A Framework for Analyzing Individual-Tree and Whole-Stand Growth by Fusing Multilevel Data: Stochastic Differential Equation and Copula Network
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Stochastic Differential Equations of Tree Size Variables
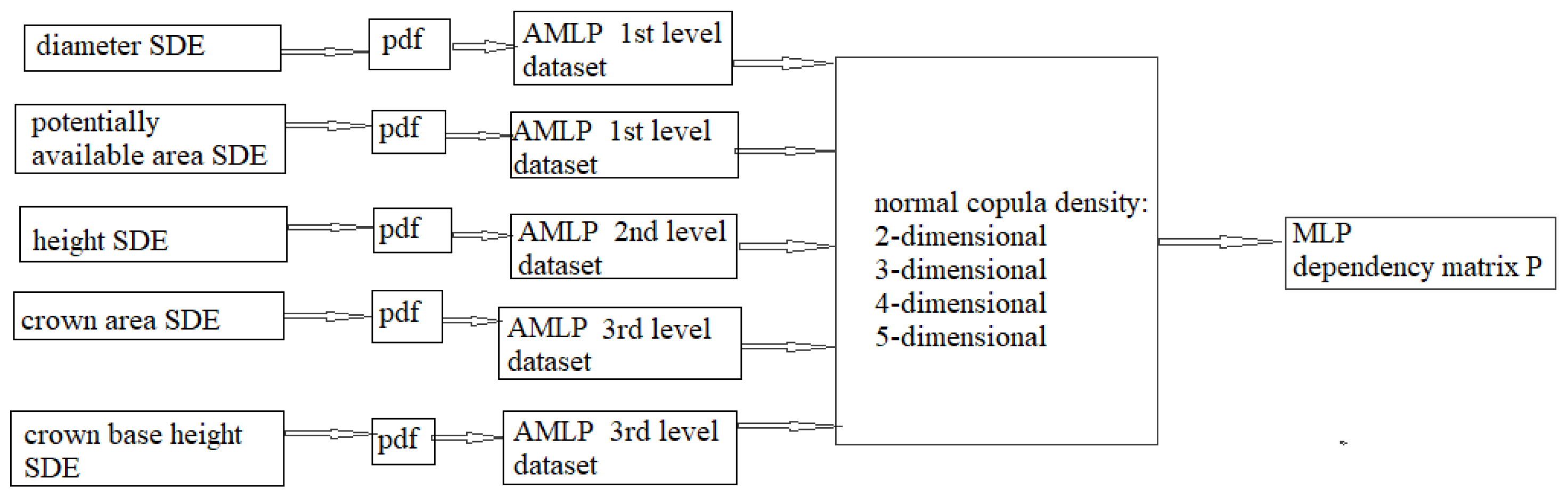
2.3. Dependence of Tree Size Variables by Copula Approach
2.4. Normalized Information Measures
2.5. Trajectories of Tree Size Variable
3. Results and Discussion
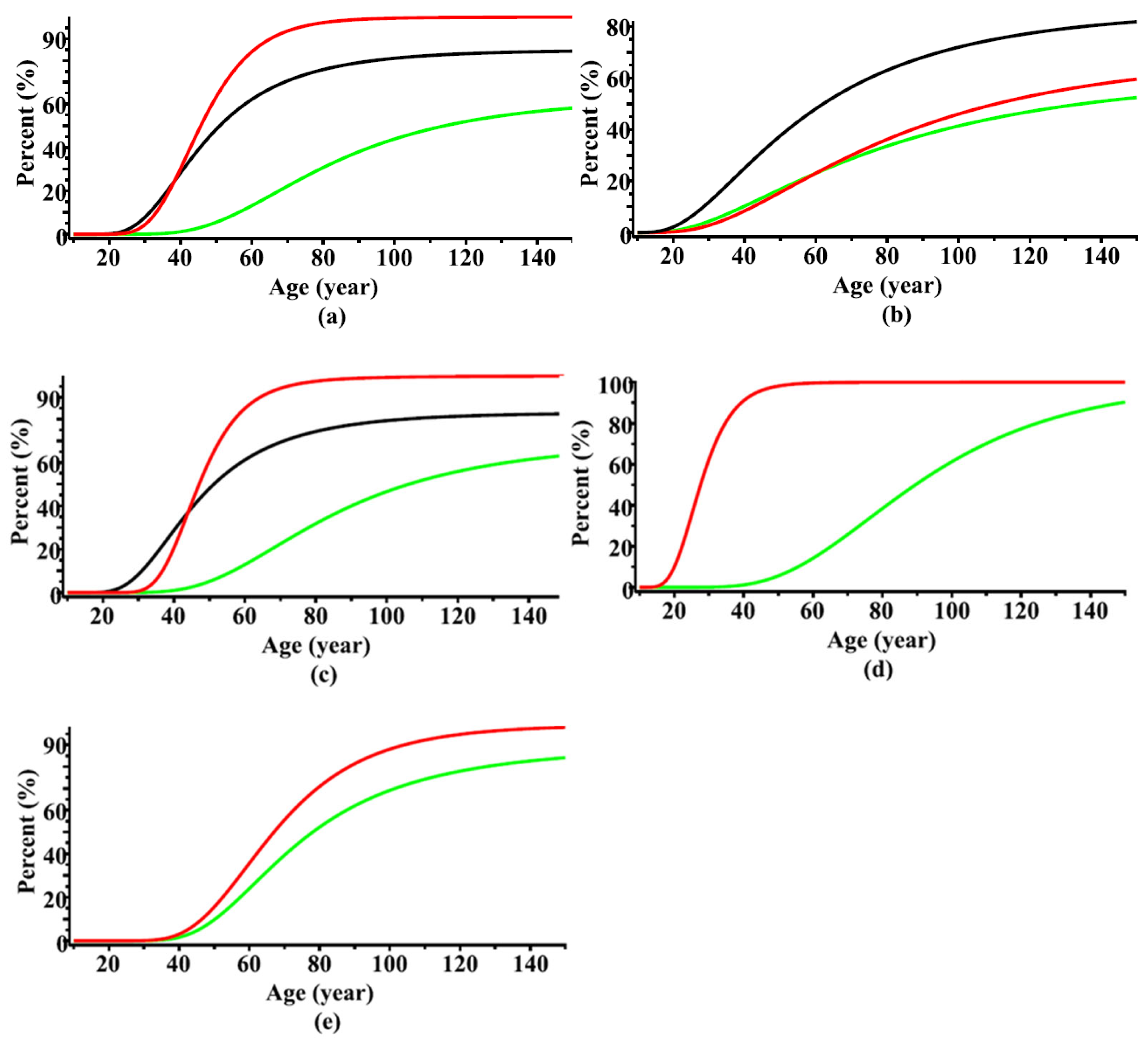
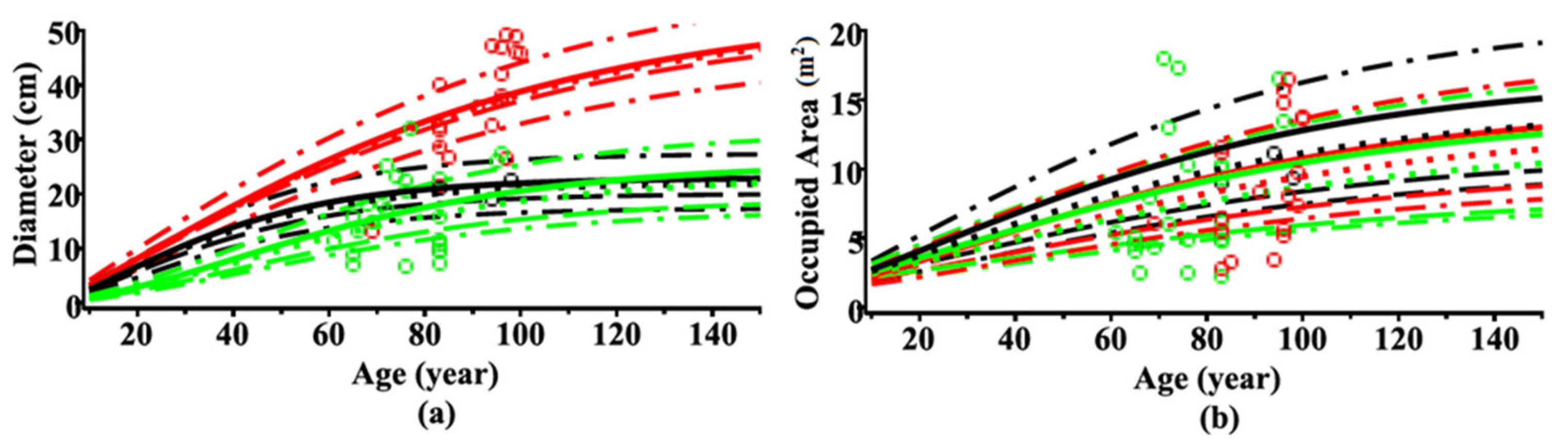
3.1. Estimating Results
3.2. Causal Effects along Different Explanatory Variables Pathways
3.3. Growth Model Pathways
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xiaoli, Z.; Lu, l.; Yanfeng, L.; Yong, W.; Jing, T.; Weiheng, X.; Leiguang, W.; Guanglong, Q. Improving the accuracy of forest aboveground biomass using Landsat 8 OLI images by quantile regression neural network for Pinus densata forests in southwestern China. Front. For. Glob. Chang. 2023, 6, 1162291. [Google Scholar] [CrossRef]
- Qiao, Y.; Zheng, G.; Du, Z.; Ma, X.; Li, J.; Moskal, L.M. Tree-Species Classification and Individual-Tree-Biomass Model Construction Based on Hyperspectral and LiDAR Data. Remote Sens. 2023, 15, 1341. [Google Scholar] [CrossRef]
- Li, Y.; Nyongesah, M.J.; Deng, L.; Haider, F.U.; Liu, S.; Mwangi, B.N.; Zhang, Q.; Chu, G.; Zhang, D.; Liu, J.; et al. Clustered tree size analysis of bio-productivity of Dinghushan National Nature Reserve in China. Front. Ecol. Evol. 2023, 11, 1118175. [Google Scholar] [CrossRef]
- Zhou, X.; Li, Z.; Liu, L.; Sharma, R.P.; Guan, F.; Fan, S. Constructing two-level nonlinear mixed-effects crown width models for Moso bamboo in China. Front. Plant Sci. 2023, 14, 1139448. [Google Scholar] [CrossRef]
- Konôpka, B.; Murgaš, V.; Pajtík, J.; Šebeň, V.; Barka, I. Tree Biomass and Leaf Area Allometric Relations for Betula pendula Roth Based on Samplings in the Western Carpathians. Plants 2023, 12, 1607. [Google Scholar] [CrossRef]
- Bui, M.H.; Phung, V.K.; Nguyen, T.B.P.; Nguyen, V.Q.; Dell, B. Allometric relationships among tree-size variables under tropical forest stages in Gia Lai, Vietnam. Ecol. Quest. 2022, 34, 1–25. [Google Scholar] [CrossRef]
- Teo, S.J.; Machado, S.A.; Filho, A.F.; Tomé, M. General height-diameter equation with biological attributes for Pinus taeda L. stands. Cerne 2017, 23, 404–411. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, H.; Zhang, X.; Lei, Y.; Huang, J.; Liu, X. An Approach to Estimate Individual Tree Ages Based on Time Series Diameter Data—A Test Case for Three Subtropical Tree Species in China. Forests 2022, 13, 614. [Google Scholar] [CrossRef]
- Fransson, P.; Brännström, Å.; Franklin, O. A tree’s quest for light-optimal height and diameter growth under a shading canopy. Tree Physiol. 2021, 41, 1–11. [Google Scholar] [CrossRef]
- Barnett, K.; Aplet, G.H.; Belote, R.T. Classifying, inventorying, and mapping mature and old-growth forests in the United States. Front. For. Glob. Change 2023, 5, 1070372. [Google Scholar] [CrossRef]
- Lu, L.; Chhin, S.; Zhang, J.; Zhang, X. Modelling tree height-diameter allometry of Chinese fir in relation to stand and climate variables through Bayesian model averaging approach. Silva Fenn. 2021, 55, 10415. [Google Scholar] [CrossRef]
- Rupšys, P.; Petrauskas, E. Development of q-exponential models for tree height, volume and stem profile. Int. J. Phys. Sci. 2010, 5, 2369–2378. [Google Scholar]
- Manso, R.; McLean, J.P.; Arcangeli, C.; Matthews, R. Dynamic top height models for several major forest tree species in Great Britain. For. Int. J. For. Res. 2021, 94, 181–192. [Google Scholar] [CrossRef]
- Arias-Rodil, M.; Barrio-Anta, M.; Diéguez-Aranda, U. Developing a dynamic growth model for Maritime pine in Asturias (NW Spain): Comparison with nearby regions. Ann. For. Sci. 2016, 73, 297–320. [Google Scholar] [CrossRef]
- Fagerberg, N.; Lohmander, P.; Eriksson, O.; Olsson, J.-O.; Poudel, B.C.; Bergh, J. Evaluation of individual-tree growth models for Picea abies based on a case study of an uneven-sized stand in southern Sweden. Scand. J. For. Res. 2022, 37, 45–58. [Google Scholar] [CrossRef]
- Souza, H.J.; Miguel, E.P.; Nascimento, R.G.M.; Cabacinha, C.D.; Rezende, A.V.; Santos, M.L. Thinning-response modifier term in growth models: An application on clonal Tectona grandis Linn F. stands at the amazonian region. For. Ecol. Manag. 2022, 511, 120109. [Google Scholar] [CrossRef]
- Caroni, C. Residuals and Influence in the Multivariate Linear Model. J. R. Stat. Soc. Ser. D Stat. 1987, 36, 365–370. [Google Scholar] [CrossRef]
- Faranak, F.; Karbalaei-Ramezanali, A.A.; Sasan, F. Application of multivariate regression on magnetic data to determine further drilling site for iron exploration. Open Geosci. 2021, 13, 138–147. [Google Scholar] [CrossRef]
- Sharma, I.; Kakchapati, S. Linear Regression Model to Identify the Factors Associated with Carbon Stock in Chure Forest of Nepal. Scientifica 2018, 2018, 1383482. [Google Scholar] [CrossRef]
- Rupšys, P. Understanding the Evolution of Tree Size Diversity within the Multivariate nonsymmetrical Diffusion Process and Information Measures. Mathematics 2019, 7, 761. [Google Scholar] [CrossRef]
- Joshua, D.; April, I.P.; Kaeli, M.; Brennan, B. Multiscale ecological niche modeling exhibits varying climate change impacts on habitat suitability of Madrean Pine-Oak trees. Front. Ecol. Evol. 2023, 11, 1086062. [Google Scholar] [CrossRef]
- Segovia, J.A.; Toaquiza, J.F.; Llanos, J.R.; Rivas, D.R. Meteorological Variables Forecasting System Using Machine Learning and Open-Source Software. Electronics 2023, 12, 1007. [Google Scholar] [CrossRef]
- Kohyama, T.S.; Potts, M.D.; Kohyama, T.I.; Kassim, A.R.; Ashton, P.S. Demographic Properties Shape Tree Size Distribution in a Malaysian Rain Forest. Am. Nat. 2015, 185, 367–379. [Google Scholar] [CrossRef] [PubMed]
- Rupšys, P.; Petrauskas, E.; Mažeika, J.A.; Deltuvas, R. The Gompertz Type Stochastic Growth Law and a Tree Diameter Distribution. Baltic For. 2007, 13, 197–206. [Google Scholar]
- Atikah, T.D.; Rahajoe, J.S.; Kohyama, T.S. Differentiation in architectural properties and functional traits of forest-floor saplings among heath, peat swamp, and mixed dipterocarp forests. Tropics 2014, 22, 157–167. [Google Scholar] [CrossRef]
- Rupšys, P.; Petrauskas, E. Quantifying Tree Diameter Distributions with One-Dimensional Diffusion Processes. J. Biol. Syst. 2010, 18, 205–221. [Google Scholar] [CrossRef]
- Bin, Y.; Ye, W.; Muller-Landau, H.C.; Wu, L.; Lian, J.; Cao, H. Unimodal tree size distributions possibly result from relatively strong conservatism in intermediate size classes. PLoS ONE 2012, 7, e52596. [Google Scholar] [CrossRef]
- Sa, Q.; Jin, X.; Pukkala, T.; Li, F. Developing Weibull-based diameter distributions for the major coniferous species in Heilongjiang Province. China J. For. Res. 2023, 34, 1803–1815. [Google Scholar] [CrossRef]
- Egonmwan, I.Y.; Ogana, F.N. Application of diameter distribution model for volume estimation in Tectona grandis L.f. stands in the Oluwa forest reserve, Nigeria. Trop. Plant Res. 2020, 7, 573–580. [Google Scholar] [CrossRef]
- Duan, A.; Zhang, J.; Zhang, X.; He, C. Stand diameter distribution modelling and prediction based on Richards function. PLoS ONE 2013, 8, e62605. [Google Scholar] [CrossRef]
- Lorimer, C.G.; Frelich, L.E. A simulation of equilibrium diameter distributions of sugar maple (Acer saccharum). Bull. Torrey Bot. Club 1984, 111, 193–199. [Google Scholar] [CrossRef]
- Kilkki, P.; Maltamo, M.; Mykkanen, R.; Paivinen, R. Use of the Weibull function in estimating the basal area dbh-distribution. Silva Fenn. 1989, 23, 311–318. [Google Scholar] [CrossRef]
- Siipilehto, J. Height distributions of Scots pine sapling stands affected by retained tree and edge stand competition. Silva Fenn. 2006, 40, 473–486. [Google Scholar] [CrossRef]
- Hafley, L.; Schreuder, H.T. Statistical distributions for fitting diameter and height data in even-aged stands. Can. J. For. Res. 1977, 7, 481–487. [Google Scholar] [CrossRef]
- Johnson, N.L. Systems of frequency curves generated by methods of translation. Biometrika 1949, 36, 149–176. [Google Scholar] [CrossRef] [PubMed]
- Mohammadalizadeh, K.H.; Namiranian, M.; Zobeiri, M.; Hourfar, A.; Marvie Mohajer, M. Modeling of frequency distribution of tree’s height in uneven-aged stands (Case study: Gorazbon district of Khyroud forest). J. For. Wood Prod. 2013, 66, 155–165. [Google Scholar]
- Mønness, E. The bivariate power-normal distribution and the bivariate Johnson system bounded distribution in forestry, including height curves. Can. J. For. Res. 2014, 45, 307–313. [Google Scholar] [CrossRef]
- Schreuder, H.T.; Hafley, W.L. A useful bivariate distribution for describing stand structure of tree heights and diameters. Biometrics 1977, 33, 471–478. [Google Scholar] [CrossRef]
- Wang, M.; Rennolls, K. Bivariate distribution modeling with tree diameter and height data. For. Sci. 2007, 53, 16–24. [Google Scholar]
- Zucchini, W.; Schmidt, M.; von Gadow, K. A model for the diameter–height distribution in an uneven-aged beech forest and a method to assess the fit of such models. Silva Fenn. 2001, 35, 169–183. [Google Scholar] [CrossRef]
- Li, F.; Zhang, L.; Davis, C.J. Modeling the joint distribution of tree diameters and heights by bivariate generalized beta distribution. For. Sci. 2002, 48, 47–58. [Google Scholar]
- Rupšys, P.; Petrauskas, E. Symmetric and Asymmetric Diffusions through Age-Varying Mixed-Species Stand Parameters. Symmetry 2021, 13, 1457. [Google Scholar] [CrossRef]
- Suzuki, T. Forest transition as a stochastic process I. J. Jpn. For. Soc. 1966, 48, 436–439. (In Japanese) [Google Scholar]
- Hara, T. A stochastic model and the moment dynamics of the growth and size distribution in plant populations. J. Theor. Biol. 1984, 109, 173–190. [Google Scholar] [CrossRef]
- Kohyama, T.; Hara, T. Frequency distribution of tree growth rate in natural forest stands. Ann. Bot. 1989, 64, 47–57. [Google Scholar] [CrossRef]
- Rupšys, P. The Use of Copulas to Practical Estimation of Multivariate Stochastic Differential Equation Mixed Effects Models. AIP Conf. Proc. 2015, 1684, 080011. [Google Scholar]
- Lin, C.R.; Buongiorno, J. Fixed versus variable-parameter matrix models of forest growth. The case of maple-birch forests. Ecol. Model. 1997, 99, 263–274. [Google Scholar] [CrossRef]
- Roitman, I.; Vanclay, J.K. Assessing size–class dynamics of a neotropical gallery forest with stationary models. Ecol. Model. 2015, 297, 118–125. [Google Scholar] [CrossRef]
- Garcia, O.A. stochastic differential equation model for the height growth of forest stands. Biometrics 1983, 39, 1059–1072. [Google Scholar] [CrossRef]
- Rennolls, K. Forest height growth modelling. For. Ecol. Manag. 1995, 71, 217–225. [Google Scholar] [CrossRef]
- Sloboda, B. Kolmogorow–Suzuki und die stochastische Differentialgleichung als Beschreibungsmittel der Bestandesevolution. Mitt. Forstl. Bundes Versuchsanst. Wien 1977, 120, 71–82. [Google Scholar]
- Rupšys, P.; Petrauskas, E. Analysis of Longitudinal Forest Data on Individual-Tree and Whole-Stand Attributes Using a Stochastic Differential Equation Model. Forests 2022, 13, 425. [Google Scholar] [CrossRef]
- Narmontas, M.; Rupšys, P.; Petrauskas, E. Models for Tree Taper Form: The Gompertz and Vasicek Diffusion Processes Framework. Symmetry 2020, 12, 80. [Google Scholar] [CrossRef]
- Rupšys, P.; Petrauskas, E. Evolution of Bivariate Tree Diameter and Height Distribution via Stand Age: Von Bertalanffy Bivariate Diffusion Process Approach. J. Forest Res. 2019, 24, 16–26. [Google Scholar] [CrossRef]
- Petrauskas, E.; Bartkevičius, E.; Rupšys, P.; Memgaudas, R. The use of stochastic differential equations to describe stem taper and volume. Baltic For. 2013, 19, 43–151. [Google Scholar]
- Rupšys, P.; Narmontas, M.; Petrauskas, E. A Multivariate Hybrid Stochastic Differential Equation Model for Whole-Stand Dynamics. Mathematics 2020, 8, 2230. [Google Scholar] [CrossRef]
- Rupšys, P. Generalized fixed-effects and mixed-effects parameters height–diameter models with diffusion processes. Int. J. Biomath. 2015, 8, 1550060. [Google Scholar] [CrossRef]
- Rupšys, P.; Petrauskas, E. A New Paradigm in Modelling the Evolution of a Stand via the Distribution of Tree Sizes. Sci. Rep. 2017, 7, 15875. [Google Scholar] [CrossRef]
- Rupšys, P.; Petrauskas, E. On the Construction of Growth Models via Symmetric Copulas and Stochastic Differential Equations. Symmetry 2022, 14, 2127. [Google Scholar] [CrossRef]
- Krikštolaitis, R.; Mozgeris, G.; Petrauskas, E.; Rupšys, P. A Statistical Dependence Framework Based on a Multivariate Normal Copula Function and Stochastic Differential EI confirmquations for Multivariate Data in Forestry. Axioms 2023, 12, 457. [Google Scholar] [CrossRef]
- Rupšys, P.; Petrauskas, E. Modeling Number of Trees per Hectare Dynamics for Uneven-Aged, Mixed-Species Stands Using the Copula Approach. Forests 2023, 14, 12. [Google Scholar] [CrossRef]
- Stigler, S.M. Who Discovered Bayes’ Theorem? Am. Stat. 1983, 37, 290–296. [Google Scholar] [CrossRef]
- Lazo, A.; Rathie, P. On the entropy of continuous probability distributions. IEEE Trans. Inf. Theory 1978, 24, 120–122. [Google Scholar] [CrossRef]
- Weiskitel, A.R.; Hann, D.W.; Kershaw, J.A., Jr.; Vanclay, J.K. Forest Growth and Yield Modeling; John Wiley & Sons: Oxford, UK, 2011; pp. 1–415. [Google Scholar]
- Sklar, A. Random variables, joint distribution functions and copulas. Kybernetika 1973, 9, 449–460. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Wiener, N. The Theory of Prediction. In Modern Mathematics for Engineers; Beckenbach, E.F., Ed.; McGraw-Hill: New York, NY, USA, 1956; pp. 165–190. [Google Scholar]
- Student. The Probable Error of a Mean. Biometrika 1908, 6, 1–25. [Google Scholar] [CrossRef]
- Stăncioiu, P.T.; Șerbescu, A.A.; Dutcă, I. Live Crown Ratio as an Indicator for Tree Vigor and Stability of Turkey Oak (Quercus cerris L.): A Case Study. Forests 2021, 12, 1763. [Google Scholar] [CrossRef]
- Põldveer, E.; Potapov, A.; Korjus, H.; Kiviste, A.; Stanturf, J.A.; Arumäe, T.; Kangur, A.; Laarmann, D. The structural complexity index SCI is useful for quantifying structural diversity of Estonian hemiboreal forests. For. Ecol. Manag. 2021, 490, 119093. [Google Scholar] [CrossRef]
- Zhou, L.; Thakur, M.P.; Jia, Z.; Hong, Y.; Yang, W.; An, S.; Zhou, X. Light effects on seedling growth in simulated forest canopy gaps vary across species from different successional stages. Front. For. Glob. Chang. 2023, 5, 1088291. [Google Scholar] [CrossRef]
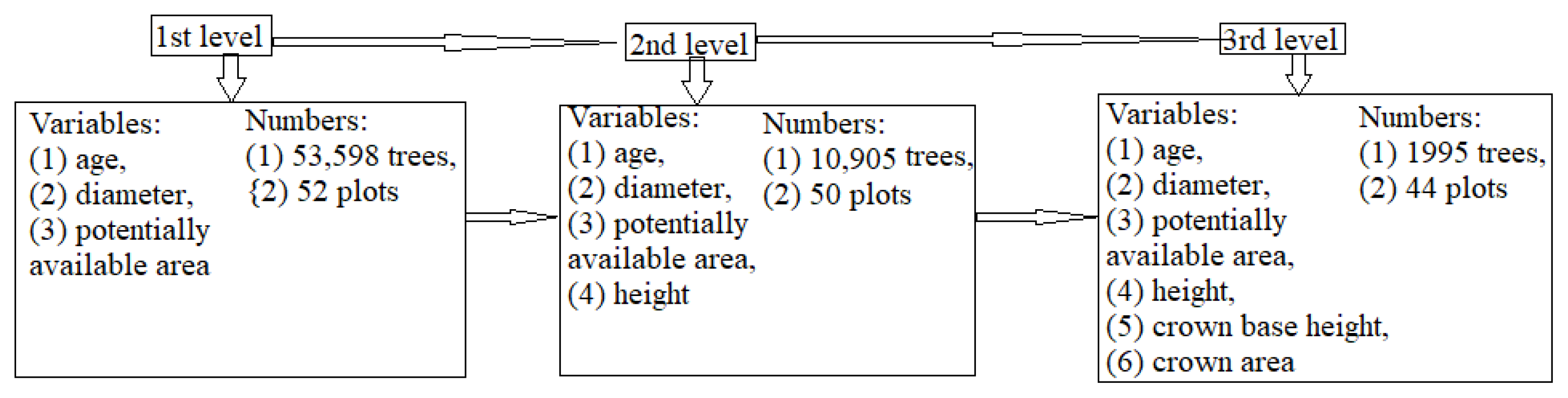

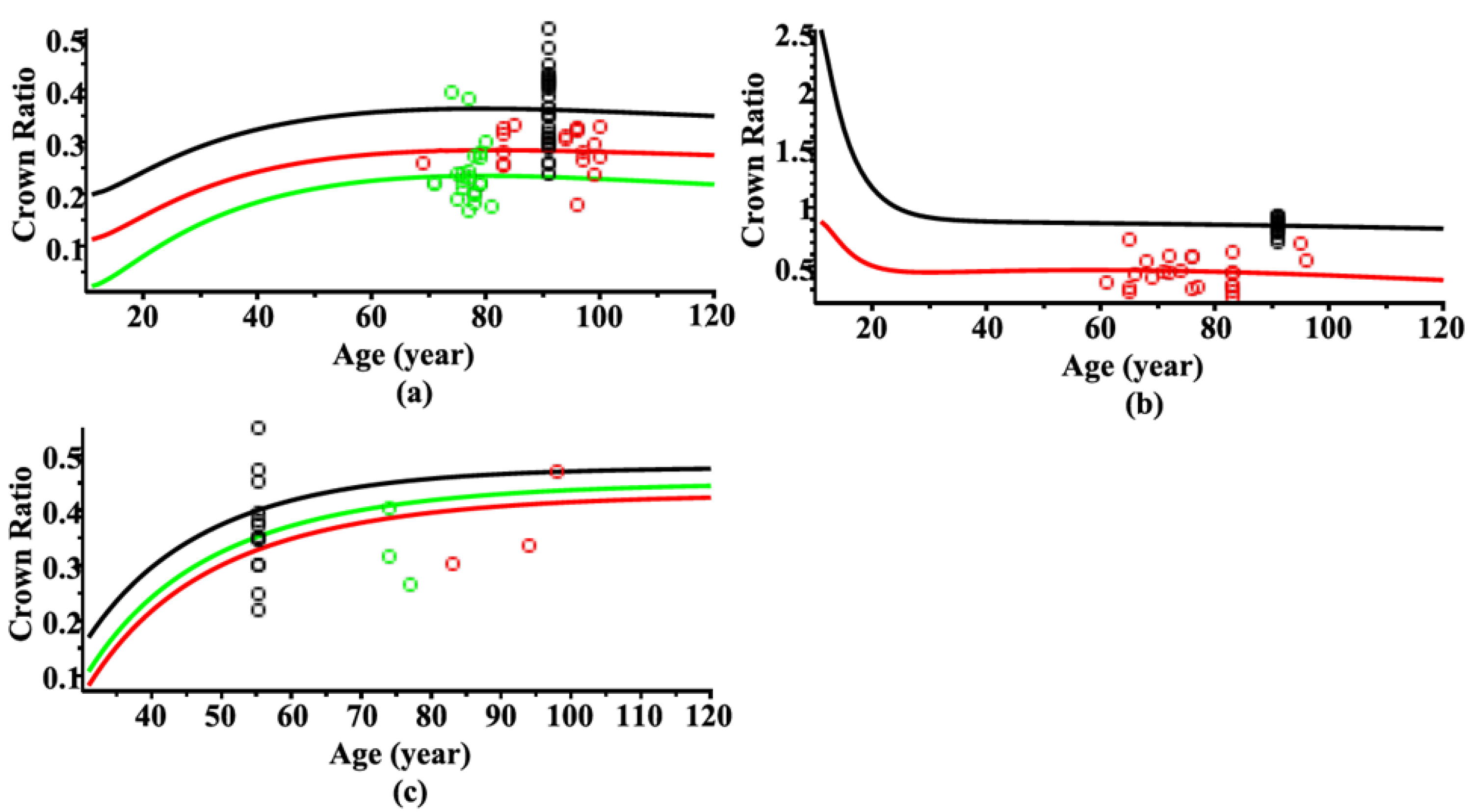
| Data Level | Tree Species | Data | Number of Trees | Min | Max | Mean | St. Dev. |
|---|---|---|---|---|---|---|---|
| First (50 plots) | Pine | t (year) | 31,173 | 7.0 | 211.0 | 59.05 | 25.69 |
| d (cm) | 31,173 | 0.20 | 61.00 | 20.44 | 10.26 | ||
| p (m2) | 31,173 | 0.09 | 124.19 | 11.07 | 8.94 | ||
| First (40 plots) | Spruce | t (year) | 20,361 | 7.0 | 207.0 | 65.63 | 23.95 |
| d (cm) | 20,361 | 0.20 | 63.80 | 13.05 | 8.65 | ||
| p (m2) | 20,361 | 0.11 | 160.24 | 9.92 | 8.52 | ||
| First (45 plots) | Birch | t (year) | 2424 | 12.0 | 129.0 | 58.26 | 21.49 |
| d (cm) | 2424 | 0.90 | 50.00 | 16.47 | 9.62 | ||
| p (m2) | 2424 | 0.33 | 173.82 | 10.24 | 8.65 | ||
| Second (45 plots) | Pine | t (year) | 6877 | 12.0 | 211.0 | 52.05 | 28.41 |
| d (cm) | 6877 | 0.20 | 59.20 | 18.61 | 10.25 | ||
| p (m2) | 6877 | 0.30 | 83.50 | 9.71 | 7.82 | ||
| h (cm) | 6877 | 1.30 | 37.90 | 17.76 | 8.48 | ||
| Second (34 plots) | Spruce | t (year) | 3507 | 7.0 | 207.0 | 53.70 | 28.09 |
| d (cm) | 3507 | 0.20 | 61.80 | 11.98 | 8.96 | ||
| p (m2) | 3507 | 0.22 | 72.72 | 8.70 | 7.49 | ||
| h (cm) | 3507 | 1.30 | 38.00 | 12.43 | 8.01 | ||
| Second (34 plots) | Birch | t (year) | 521 | 12.0 | 107.0 | 48.58 | 21.66 |
| d (cm) | 521 | 0.90 | 44.10 | 14.56 | 8.86 | ||
| p (m2) | 521 | 0.66 | 55.64 | 8.72 | 6.60 | ||
| h (cm) | 521 | 1.30 | 31.90 | 15.84 | 7.89 | ||
| Third (42 plots) | Pine | t (year) | 1340 | 46.0 | 211.0 | 83.82 | 22.67 |
| d (cm) | 1340 | 8.00 | 59.20 | 27.70 | 8.75 | ||
| p (m2) | 1340 | 1.60 | 83.49 | 15.22 | 9.38 | ||
| h (m) | 1340 | 2.30 | 37.90 | 25.76 | 4.80 | ||
| hc (m) | 1340 | 0.30 | 29.70 | 18.28 | 5.11 | ||
| wc (m) | 1340 | 0.59 | 72.10 | 12.13 | 9.41 | ||
| Third (24 plots) | Spruce | t (year) | 566 | 42.0 | 207.0 | 82.17 | 22.69 |
| d (cm) | 566 | 3.20 | 61.80 | 17.81 | 9.16 | ||
| p (m2) | 566 | 1.37 | 121.51 | 13.87 | 12.46 | ||
| h (m) | 566 | 3.80 | 36.50 | 17.80 | 6.72 | ||
| hc (m) | 566 | 0.90 | 22.80 | 7.73 | 4.03 | ||
| wc (m) | 566 | 0.07 | 55.29 | 11.69 | 8.34 | ||
| Third (22 plots) | Birch | t (year) | 89 | 55.3 | 116.0 | 78.53 | 16.71 |
| d (cm) | 89 | 5.70 | 44.10 | 20.30 | 9.25 | ||
| p (m2) | 89 | 3.29 | 36.69 | 13.25 | 6.80 | ||
| h (m) | 89 | 6.50 | 31.90 | 21.44 | 6.98 | ||
| hc (m) | 89 | 1.40 | 22.70 | 13.11 | 5.43 | ||
| wc (m) | 89 | 0.93 | 62.89 | 11.99 | 10.62 |
| Equations | α | β | ɣ | σ | δ | σϕ |
|---|---|---|---|---|---|---|
| Pine | ||||||
| Diameter | 0.0741 (0.0005) | 0.0176 (0.0001) | −22.9305 (0.2589) | 0.0007 (1.1 × 10−5) | - | 0.0027 (0.0004) |
| Potentially area | 0.0585 (0.0006) | 0.0172 (0.0002) | −1.7851 (0.0447) | 0.0078 (0.0001) | 1.6698 (0.0286) | 0.0082 (0.0012) |
| Height | 0.1243 (0.0007) | 0.0337 (0.0002) | −11.7954 (0.2856) | 0.0007 (2.1 × 10−5) | - | 0.0047 (0.0007) |
| Crown base height | 22.1587 (0.2375) | 0.0242 (0.0008) | - | 0.3654 (0.0175) | - | 4.3306 (0.4721) |
| Crown width | 0.0476 (0.0021) | 0.0124 (0.0009) | −1.5622 (0.2233) | 0.0080 (0.0007) | - | 0.0059 (0.0009) |
| Spruce | ||||||
| Diameter | 0.0893 (0.0011) | 0.0268 (0.0004) | −1.5356 (0.0566) | 0.0097 (0.0002) | - | 0.0134 (0.0022) |
| Potentially area | 0.0543 (0.0008) | 0.0171 (0.0003) | −1.0144 (0.0550) | 0.0118 (0.0003) | 2.0127 (0.0448) | 0.0107 (0.0017) |
| Height | 0.0855 (0.0003) | 0.0247 (0.0008) | −3.3666 (0.2551) | 0.0047 (0.0003) | - | 0.0071 (0.0013) |
| Crown base height | 20.3044 (1.3368) | 0.0057 (0.0004) | - | 0.1755 (0.0114) | - | 7.0771 (1.0541) |
| Crown width | 0.0685 (0.0034) | 0.0213 (0.0016) | −1.0256 (0.2429) | 0.0103 (0.0011) | - | 0.0108 (0.0024) |
| Birch | ||||||
| Diameter | 0.1316 (0.0023) | 0.0393 (0.0008) | −5.8221 (0.2373) | 0.0056 (0.0002) | - | 0.0146 (0.0022) |
| Potentially area | 0.0616 (0.0028) | 0.0189 (0.0011) | −2.0214 (0.2128) | 0.0092 (0.0006) | 1.9502 (0.1361) | 0.0101 (0.00160) |
| Height | 0.1661 (0.0099) | 0.0404 (0.0022) | −39.3068 (2.1701) | 0.0004 (3.9 × 10−5) | - | 0.0052 (0.0009) |
| Crown base height | 13.4070 (0.5751) | 0.1782 (0.0200) | - | 10.4929 (2.7817) | - | 3.0937 (0.5152) |
| Crown width | 2.6674 (0.4316) | 0.9139 (0.1543) | −0.0950 (0.0421) | 0.8690 (0.2524) | - | 0.6791 (0.1702) |
| ρi1 | ρi2 | ρi3 | ρi4 | ρi5 | |
|---|---|---|---|---|---|
| Pine | |||||
| 1 | 1 | 0.2180 (0.0053) | 0.7015 (0.0053) | 0.3507 (0.0202) | 0.7476 (0.0094) |
| 2 | 0.2180 (0.0053) | 1 | 0.0890 (0.0081) | −0.0183 (0.0236) * | 0.3232 (0.0165) |
| 3 | 0.7015 (0.0053) | 0.0890 (0.0081) | 1 | 0.6566 (0.0154) | 0.4540 (0.0165) |
| 4 | 0.3507 (0.0202) | −0.0183 (0.0236) * | 0.6566 (0.0154) | 1 | 0.1364 (0.0224) |
| 5 | 0.7476 (0.0094) | 0.3232 (0.0165) | 0.4540 (0.0165) | 0.1364 (0.0224) | 1 |
| Spruce | |||||
| 1 | 1 | 0.2374 (0.0064) | 0.8517 (0.0040) | 0.4279 (0.0157) | 0.7390 (0.0157) |
| 2 | 0.2374 (0.0040) | 1 | 0.1402 (0.0084) | −0.0479 (0.0248) * | 0.2951 (0.0248) |
| 3 | 0.8517 (0.0067) | 0.1402 (0.0084) | 1 | 0.6010 (0.0220) | 0.6071 (0.0220) |
| 4 | 0.4279 (0.0157) | −0.0316 (0.0248) * | 0.6010 (0.0220) | 1 | 0.2112 (0.0349) |
| 5 | 0.7390 (0.0157) | 0.2951 (0.0248) | 0.6071 (0.0220) | 0.2112 (0.0349) | 1 |
| Birch | |||||
| 1 | 1 | 0.1999 (0.0194) | 0.8359 (0.0102) | 0.6364 (0.0757) | 0.7478 (0.0428) |
| 2 | 0.1999 (0.0194) | 1 | 0.1395 (0.0252) | 0.1428 (0.1141) * | 0.1587 (0.1008) |
| 3 | 0.8359 (0.0102) | 0.1395 (0.0252) | 1 | 0.8190 (0.0308) | 0.6527 (0.0693) |
| 4 | 0.6364 (0.0757) | 0.1428 (0.1141) * | 0.8190 (0.0308) | 1 | 0.4274 (0.1212) |
| 5 | 0.7478 (0.0428) | 0.1587 (0.1008) | 0.6527 (0.0693) | 0.4274 (0.1212) | 1 |
| Diameter | ||||||
| k | 2 | 3 | 4 | 5 | ||
| 0.0050 | 0.1144 | 0.0148 | 0.1385 * | |||
| k, m | 2, 3 | 2, 4 | 2, 5 | 3, 4 | 3, 5 | 4, 5 |
| 0.4922 | 0.3903 | 0.5109 | 0.4941 | 0.6017 | 0.5349 | |
| k, m, n | 2, 3, 4 | 2, 3, 5 | 2, 4, 5 | 3, 4, 5 | ||
| 0.4996 | 0.6017 | 0.5350 | 0.6024 | |||
| k, m, n, s | 2, 3, 4, 5 | |||||
| 0.6024 | ||||||
| Potentially Available Area | ||||||
| k | 1 | 3 | 4 | 5 | ||
| 0.0050 | 0.0006 | 0.0002 | 0.0140 | |||
| k, m | 1, 3 | 1, 4 | 1, 5 | 3, 4 | 3, 5 | 4, 5 |
| 0.3751 | 0.3754 | 0.3834 | 0.3708 | 0.3840 | 0.3837 | |
| k, m, n | 1, 3, 4 | 1, 3, 5 | 1, 4, 5 | 3, 4, 5 | ||
| 0.3757 | 0.3840 | 0.3839 | 0.3841 | |||
| k, m, n, s | 1, 3, 4, 5 | |||||
| 0.3841 | ||||||
| Height | ||||||
| k | 1 | 2 | 4 | 5 | ||
| 0.1464 | 0.0007 | 0.0883 | 0.0490 | |||
| k, m | 1, 2 | 1, 4 | 1, 5 | 2, 4 | 2, 5 | 4, 5 |
| 0.5205 | 0.6132 | 0.5235 | 0.4615 | 0.4200 | 0.5282 | |
| k, m, n | 1, 2, 4 | 1, 2, 5 | 1, 4, 5 | 2, 4, 5 | ||
| 0.6136 | 0.5244 | 0.6135 | 0.5287 | |||
| k, m, n, s | 1, 2, 4, 5 | |||||
| 0.6134 | ||||||
| Crown Area | ||||||
| k | 1 | 2 | 3 | 5 | ||
| 0.1427 | 0.0143 | 0.0399 | 0.0013 | |||
| k, m | 1, 2 | 1, 3 | 1, 5 | 2, 3 | 2, 5 | 3, 5 |
| 0.3915 | 0.4777 | 0.3991 | 0.4688 | 0.3715 | 0.4829 | |
| k, m, n | 1, 2, 3 | 1, 2, 5 | 1, 3, 5 | 2, 3, 5 | ||
| 0.5294 | 0.5334 | 0.5235 | 0.4353 | |||
| k, m, n, s | 1, 2, 3, 5 | |||||
| 0.5335 | ||||||
| Crown Base Height | ||||||
| k | 1 | 2 | 3 | 4 | ||
| 0.0202 | 0.0003 | 0.0957 | 0.0017 | |||
| k, m | 1, 2 | 1, 3 | 1, 4 | 2, 3 | 2, 4 | 3, 4 |
| 0.5262 | 0.5188 | 0.5233 | 0.4250 | 0.3852 | 0.4210 | |
| k, m, n | 1, 2, 3 | 1, 2, 4 | 1, 3, 4 | 2, 3, 4 | ||
| 0.4786 | 0.3998 | 0.4837 | 0.4831 | |||
| k, m, n, s | 1, 2, 3, 4 | |||||
| 0.4839 | ||||||
| Diameter | ||||||
| k | 2 | 3 | 4 | 5 | ||
| 0.0119 | 0.2750 * | 0.0293 | 0.1171 | |||
| k, m | 2, 3 | 2, 4 | 2, 5 | 3, 4 | 3, 5 | 4, 5 |
| 0.6600 | 0.4146 | 0.4888 | 0.6580 | 0.7024 | 0.5244 | |
| k, m, n | 2, 3, 4 | 2, 3, 5 | 2, 4, 5 | 3, 4, 5 | ||
| 0.6646 | 0.7043 | 0.5263 | 0.7034 | |||
| k, m, n, s | 2, 3, 4, 5 | |||||
| 0.7050 | ||||||
| Potentially Available Area | ||||||
| k | 1 | 3 | 4 | 5 | ||
| 0.0117 | 0.0062 | 0.0000 | 0.0173 | |||
| k, m | 1, 3 | 1, 4 | 1, 5 | 3, 4 | 3, 5 | 4, 5 |
| 0.3810 | 0.3839 | 0.3866 | 0.3791 | 0.3855 | 0.3869 | |
| k, m, n | 1, 3, 4 | 1, 3, 5 | 1, 4, 5 | 3, 4, 5 | ||
| 0.3838 | 0.3869 | 0.3885 | 0.3873 | |||
| k, m, n, s | 1, 3, 4, 5 | |||||
| 0.3885 | ||||||
| Height | ||||||
| k | 1 | 2 | 4 | 5 | ||
| 0.2905 | 0.0067 | 0.0540 | 0.0823 | |||
| k, m | 1, 2 | 1, 4 | 1, 5 | 2, 4 | 2, 5 | 4, 5 |
| 0.6686 | 0.7069 | 0.6686 | 0.4357 | 0.4518 | 0.5195 | |
| k, m, n | 1, 2, 4 | 1, 2, 5 | 1, 4, 5 | 2, 4, 5 | ||
| 0.7068 | 0.6690 | 0.7071 | 0.5201 | |||
| k, m, n, s | 1, 2, 4, 5 | |||||
| 0.7070 | ||||||
| Crown Area | ||||||
| k | 1 | 2 | 3 | 5 | ||
| 0.1254 | 0.0188 | 0.0837 | 0.0045 | |||
| k, m | 1, 2 | 1, 3 | 1, 5 | 2, 3 | 2, 5 | 3, 5 |
| 0.5043 | 0.4974 | 0.5042 | 0.4666 | 0.3933 | 0.4653 | |
| k, m, n | 1, 2, 3 | 1, 2, 5 | 1, 3, 5 | 2, 3, 5 | ||
| 0.5046 | 0.5100 | 0.5044 | 0.4752 | |||
| k, m, n, s | 1, 2, 3, 5 | |||||
| 0.5102 | ||||||
| Crown Base Height | ||||||
| k | 1 | 2 | 3 | 4 | ||
| 0.0381 | 0.0000 | 0.0671 | 0.0055 | |||
| k, m | 1, 2 | 1, 3 | 1, 4 | 2, 3 | 2, 4 | 3, 4 |
| 0.4120 | 0.4435 | 0.4156 | 0.4429 | 0.3751 | 0.4505 | |
| k, m, n | 1, 2, 3 | 1, 2, 4 | 1, 3, 4 | 2, 3, 4 | ||
| 0.4475 | 0.4182 | 0.4515 | 0.4531 | |||
| k, m, n, s | 1, 2, 3, 4 | |||||
| 0.4838 | ||||||
| Diameter | ||||||
| k | 2 | 3 | 4 | 5 | ||
| 0.0095 | 0.2365 * | 0.0722 | 0.1126 | |||
| k, m | 2, 3 | 2, 4 | 2, 5 | 3, 4 | 3, 5 | 4, 5 |
| 0.6213 | 0.4494 | 0.4886 | 0.6126 | 0.6440 | 0.5427 | |
| k, m, n | 2, 3, 4 | 2, 3, 5 | 2, 4, 5 | 3, 4, 5 | ||
| 0.6227 | 0.6516 | 0.5469 | 0.6441 | |||
| k, m, n, s | 2, 3, 4, 5 | |||||
| 0.6518 | ||||||
| Potentially Available Area | ||||||
| k | 1 | 3 | 4 | 5 | ||
| 0.0096 | 0.0036 | 0.0027 | 0.0052 | |||
| k, m | 1, 3 | 1, 4 | 1, 5 | 3, 4 | 3, 5 | 4, 5 |
| 0.3798 | 0.3781 | 0.3783 | 0.3722 | 0.3742 | 0.3746 | |
| k, m, n | 1, 3, 4 | 1, 3, 5 | 1, 4, 5 | 3, 4, 5 | ||
| 0.3801 | 0.3799 | 0.3781 | 0.3744 | |||
| k, m, n, s | 1, 3, 4, 5 | |||||
| 0.3802 | ||||||
| Height | ||||||
| k | 1 | 2 | 4 | 5 | ||
| 0.2756 | 0.0041 | 0.1394 | 0.1008 | |||
| k, m | 1, 2 | 1, 4 | 1, 5 | 2, 4 | 2, 5 | 4, 5 |
| 0.6545 | 0.7263 | 0.6547 | 0.5124 | 0.4720 | 0.6087 | |
| k, m, n | 1, 2, 4 | 1, 2, 5 | 1, 4, 5 | 2, 4, 5 | ||
| 0.7295 | 0.6570 | 0.7349 | 0.6084 | |||
| k, m, n, s | 1, 2, 4, 5 | |||||
| 0.7384 | ||||||
| Crown Area | ||||||
| k | 1 | 2 | 3 | 5 | ||
| 0.1127 | 0.0051 | 0.0878 | 0.0216 | |||
| k, m | 1, 2 | 1, 3 | 1, 5 | 2, 3 | 2, 5 | 3, 5 |
| 0.4838 | 0.4856 | 0.4855 | 0.4603 | 0.3939 | 0.4645 | |
| k, m, n | 1, 2, 3 | 1, 2, 5 | 1, 3, 5 | 2, 3, 5 | ||
| 0.4856 | 0.4855 | 0.4913 | 0.4669 | |||
| k, m, n, s | 1, 2, 3, 5 | |||||
| 0.4914 | ||||||
| Crown Base Height | ||||||
| k | 1 | 2 | 3 | 4 | ||
| 0.0811 | 0.0030 | 0.1362 | 0.0242 | |||
| k, m | 1, 2 | 1, 3 | 1, 4 | 2, 3 | 2, 4 | 3, 4 |
| 0.4510 | 0.5090 | 0.4531 | 0.5079 | 0.3940 | 0.5155 | |
| k, m, n | 1, 2, 3 | 1, 2, 4 | 1, 3, 4 | 2, 3, 4 | ||
| 0.5093 | 0.4528 | 0.5155 | 0.5157 | |||
| k, m, n, s | 1, 2, 3, 4 | |||||
| 0.5159 | ||||||
| Diameter | ||||||
| 0.453 | ||||||
| k | 2 | 3 | 4 | 5 | ||
| 0.453 | 0.736 | 0.495 | 0.764 * | |||
| k, m | 2, 3 | 2, 4 | 2, 5 | 3, 4 | 3, 5 | 4, 5 |
| 0.744 | 0.514 | 0.764 | 0.752 | 0.860 | 0.789 | |
| k, m, n | 2, 3, 4 | 2, 3, 5 | 2, 4, 5 | 3, 4, 5 | ||
| 0.758 | 0.860 | 0.790 | 0.861 | |||
| k, m, n, s | 2, 3, 4, 5 | |||||
| 0.861 | ||||||
| Potentially Available Area | ||||||
| 0.343 | ||||||
| k | 1 | 3 | 4 | 5 | ||
| 0.367 | 0.347 | 0.345 | 0.402 | |||
| k, m | 1, 3 | 1, 4 | 1, 5 | 3, 4 | 3, 5 | 4, 5 |
| 0.373 | 0.374 | 0.404 | 0.356 | 0.405 | 0.404 | |
| k, m, n | 1, 3, 4 | 1, 3, 5 | 1, 4, 5 | 3, 4, 5 | ||
| 0.376 | 0.405 | 0.404 | 0.405 | |||
| k, m, n, s | 1, 3, 4, 5 | |||||
| 0.405 | ||||||
| Height | ||||||
| 0.617 | ||||||
| k | 1 | 2 | 4 | 5 | ||
| 0.824 | 0.618 | 0.747 | 0.704 | |||
| k, m | 1, 2 | 1, 4 | 1, 5 | 2, 4 | 2, 5 | 4, 5 |
| 0.825 | 0.873 | 0.830 | 0.751 | 0.706 | 0.808 | |
| k, m, n | 1, 2, 4 | 1, 2, 5 | 1, 4, 5 | 2, 4, 5 | ||
| 0.873 | 0.831 | 0.873 | 0.807 | |||
| k, m, n, s | 1, 2, 4, 5 | |||||
| 0.873 | ||||||
| Crown Area | ||||||
| 0.312 | ||||||
| k | 1 | 2 | 3 | 5 | ||
| 0.662 | 0.362 | 0.427 | 0.305 | |||
| k, m | 1, 2 | 1, 3 | 1, 5 | 2, 3 | 2, 5 | 3, 5 |
| 0.683 | 0.671 | 0.679 | 0.470 | 0.357 | 0.471 | |
| k, m, n | 1, 2, 3 | 1, 2, 5 | 1, 3, 5 | 2, 3, 5 | ||
| 0.690 | 0.698 | 0.680 | 0.509 | |||
| k, m, n, s | 1, 2, 3, 5 | |||||
| 0.699 | ||||||
| Crown Base Height | ||||||
| 0.727 | ||||||
| k | 1 | 2 | 3 | 4 | ||
| 0.752 | 0.727 | 0.824 | 0.729 | |||
| k, m | 1, 2 | 1, 3 | 1, 4 | 2, 3 | 2, 4 | 3, 4 |
| 0.755 | 0.833 | 0.763 | 0.826 | 0.731 | 0.835 | |
| k, m, n | 1, 2, 3 | 1, 2, 4 | 1, 3, 4 | 2, 3, 4 | ||
| 0.834 | 0.764 | 0.836 | 0.836 | |||
| k, m, n, s | 1, 2, 3, 4 | |||||
| 0.837 | ||||||
| Diameter | ||||||
| 0.455 | ||||||
| k | 2 | 3 | 4 | 5 | ||
| 0.497 | 0.891 * | 0.503 | 0.697 | |||
| k, m | 2, 3 | 2, 4 | 2, 5 | 3, 4 | 3, 5 | 4, 5 |
| 0.895 | 0.541 | 0.699 | 0.887 | 0.914 | 0.726 | |
| k, m, n | 2, 3, 4 | 2, 3, 5 | 2, 4, 5 | 3, 4, 5 | ||
| 0.891 | 0.914 | 0.726 | 0.913 | |||
| k, m, n, s | 2, 3, 4, 5 | |||||
| 0.913 | ||||||
| Potentially Available Area | ||||||
| 0.381 | ||||||
| k | 1 | 3 | 4 | 5 | ||
| 0.396 | 0.389 | 0.373 | 0.421 | |||
| k, m | 1, 3 | 1, 4 | 1, 5 | 3, 4 | 3, 5 | 4, 5 |
| 0.395 | 0.408 | 0.421 | 0.405 | 0.419 | 0.423 | |
| k, m, n | 1, 3, 4 | 1, 3, 5 | 1, 4, 5 | 3, 4, 5 | ||
| 0.406 | 0.416 | 0.424 | 0.425 | |||
| k, m, n, s | 1, 3, 4, 5 | |||||
| 0.422 | ||||||
| Height | ||||||
| 0.445 | ||||||
| k | 1 | 2 | 4 | 5 | ||
| 0.909 | 0.467 | 0.569 | 0.651 | |||
| k, m | 1, 2 | 1, 4 | 1, 5 | 2, 4 | 2, 5 | 4, 5 |
| 0.907 | 0.892 | 0.911 | 0.602 | 0.648 | 0.725 | |
| k, m, n | 1, 2, 4 | 1, 2, 5 | 1, 4, 5 | 2, 4, 5 | ||
| 0.893 | 0.908 | 0.892 | 0.727 | |||
| k, m, n, s | 1, 2, 4, 5 | |||||
| 0.892 | ||||||
| Crown Area | ||||||
| 0.396 | ||||||
| k | 1 | 2 | 3 | 5 | ||
| 0.676 | 0.458 | 0.585 | 0.403 | |||
| k, m | 1, 2 | 1, 3 | 1, 5 | 2, 3 | 2, 5 | 3, 5 |
| 0.691 | 0.679 | 0.683 | 0.616 | 0.466 | 0.596 | |
| k, m, n | 1, 2, 3 | 1, 2, 5 | 1, 3, 5 | 2, 3, 5 | ||
| 0.692 | 0.695 | 0.498 | 0.622 | |||
| k, m, n, s | 1, 2, 3, 5 | |||||
| 0.693 | ||||||
| Crown Base Height | ||||||
| k | 1 | 2 | 3 | 4 | ||
| 0.550 | 0.460 | 0.607 | 0.476 | |||
| k, m | 1, 2 | 1, 3 | 1, 4 | 2, 3 | 2, 4 | 3, 4 |
| 0.559 | 0.618 | 0.566 | 0.616 | 0.478 | 0.628 | |
| k, m, n | 1, 2, 3 | 1, 2, 4 | 1, 3, 4 | 2, 3, 4 | ||
| 0.624 | 0.571 | 0.630 | 0.632 | |||
| k, m, n, s | 1, 2, 3, 4 | |||||
| 0.633 | ||||||
| Diameter | ||||||
| 0.687 | ||||||
| k | 2 | 3 | 4 | 5 | ||
| 0.709 | 0.900 * | 0.754 | 0.835 | |||
| k, m | 2, 3 | 2, 4 | 2, 5 | 3, 4 | 3, 5 | 4, 5 |
| 0.907 | 0.768 | 0.840 | 0.900 | 0.917 | 0.861 | |
| k, m, n | 2, 3, 4 | 2, 3, 5 | 2, 4, 5 | 3, 4, 5 | ||
| 0.907 | 0.921 | 0.865 | 0.917 | |||
| k, m, n, s | 2, 3, 4, 5 | |||||
| 0.922 | ||||||
| Potentially Available Area | ||||||
| 0.345 | ||||||
| k | 1 | 3 | 4 | 5 | ||
| 0.382 | 0.361 | 0.355 | 0.358 | |||
| k, m | 1, 3 | 1, 4 | 1, 5 | 3, 4 | 3, 5 | 4, 5 |
| 0.386 | 0.381 | 0.381 | 0.360 | 0.362 | 0.362 | |
| k, m, n | 1, 3, 4 | 1, 3, 5 | 1, 4, 5 | 3, 4, 5 | ||
| 0.383 | 0.386 | 0.380 | 0.359 | |||
| k, m, n, s | 1, 3, 4, 5 | |||||
| 0.381 | ||||||
| Height | ||||||
| 0.769 | ||||||
| k | 1 | 2 | 4 | 5 | ||
| 0.938 | 0.774 | 0.867 | 0.859 | |||
| k, m | 1, 2 | 1, 4 | 1, 5 | 2, 4 | 2, 5 | 4, 5 |
| 0.939 | 0.945 | 0.938 | 0.867 | 0.859 | 0.912 | |
| k, m, n | 1, 2, 4 | 1, 2, 5 | 1, 4, 5 | 2, 4, 5 | ||
| 0.945 | 0.939 | 0.946 | 0.912 | |||
| k, m, n, s | 1, 2, 4, 5 | |||||
| 0.947 | ||||||
| Crown Area | ||||||
| 0.561 | ||||||
| k | 1 | 2 | 3 | 5 | ||
| 0.779 | 0.569 | 0.691 | 0.577 | |||
| k, m | 1, 2 | 1, 3 | 1, 5 | 2, 3 | 2, 5 | 3, 5 |
| 0.779 | 0.775 | 0.782 | 0.696 | 0.696 | 0.684 | |
| k, m, n | 1, 2, 3 | 1, 2, 5 | 1, 3, 5 | 2, 3, 5 | ||
| 0.778 | 0.787 | 0.764 | 0.688 | |||
| k, m, n, s | 1, 2, 3, 5 | |||||
| 0.763 | ||||||
| Crown Base Height | ||||||
| 0.670 | ||||||
| k | 1 | 2 | 3 | 4 | ||
| 0.752 | 0.671 | 0.759 | 0.675 | |||
| k, m | 1, 2 | 1, 3 | 1, 4 | 2, 3 | 2, 4 | 3, 4 |
| 0.751 | 0.758 | 0.754 | 0.758 | 0.674 | 0.765 | |
| k, m, n | 1, 2, 3 | 1, 2, 4 | 1, 3, 4 | 2, 3, 4 | ||
| 0.758 | 0.753 | 0.765 | 0.765 | |||
| k, m, n, s | 1, 2, 3, 4 | |||||
| 0.765 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rupšys, P.; Mozgeris, G.; Petrauskas, E.; Krikštolaitis, R. A Framework for Analyzing Individual-Tree and Whole-Stand Growth by Fusing Multilevel Data: Stochastic Differential Equation and Copula Network. Forests 2023, 14, 2037. https://doi.org/10.3390/f14102037
Rupšys P, Mozgeris G, Petrauskas E, Krikštolaitis R. A Framework for Analyzing Individual-Tree and Whole-Stand Growth by Fusing Multilevel Data: Stochastic Differential Equation and Copula Network. Forests. 2023; 14(10):2037. https://doi.org/10.3390/f14102037
Chicago/Turabian StyleRupšys, Petras, Gintautas Mozgeris, Edmundas Petrauskas, and Ričardas Krikštolaitis. 2023. "A Framework for Analyzing Individual-Tree and Whole-Stand Growth by Fusing Multilevel Data: Stochastic Differential Equation and Copula Network" Forests 14, no. 10: 2037. https://doi.org/10.3390/f14102037





