Optimizing a Regional White Spruce Tree Improvement Program: SNP Genotyping for Enhanced Breeding Values, Genetic Diversity Assessment, and Estimation of Pollen Contamination
Abstract
:1. Introduction
2. Materials and Methods
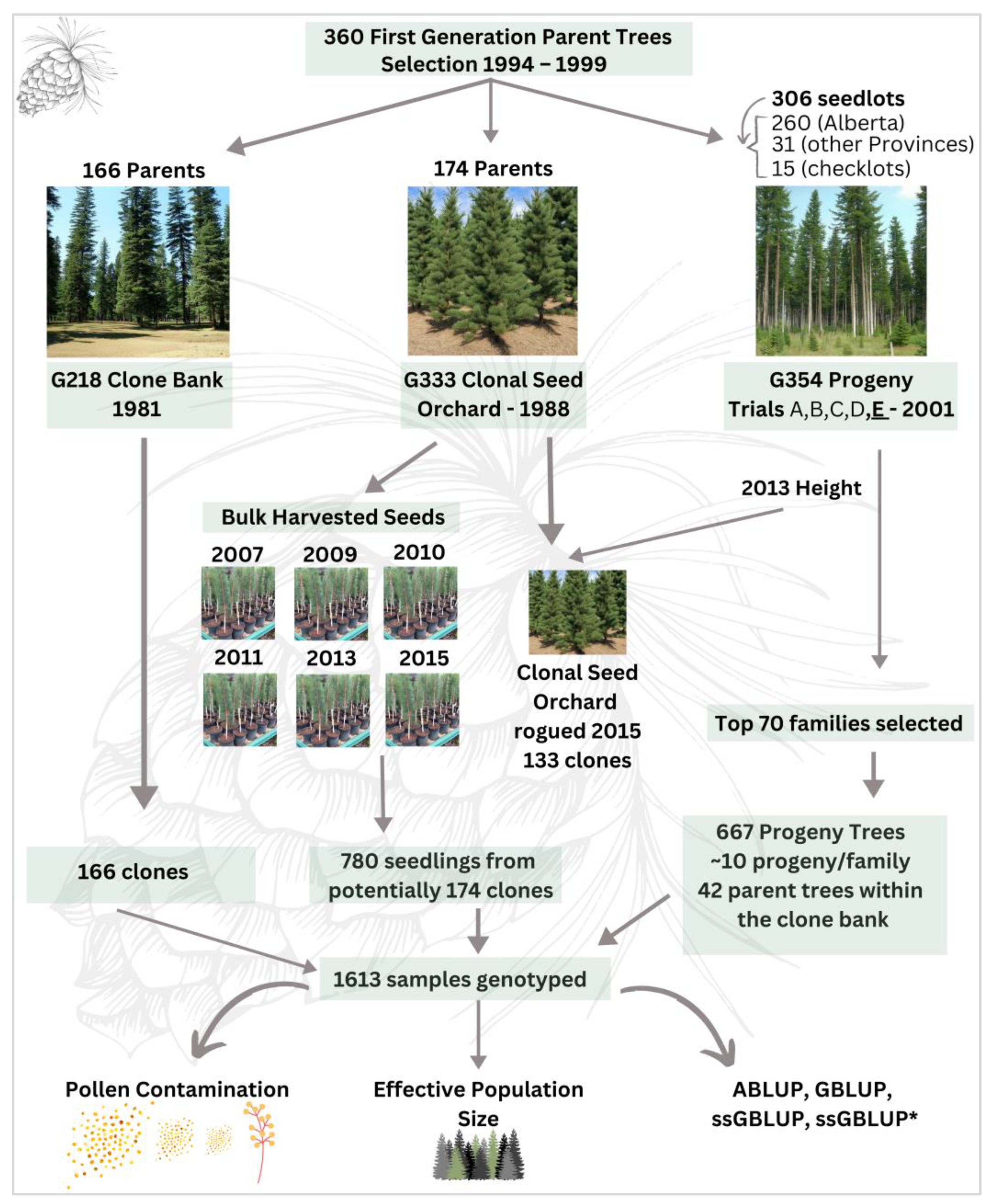
2.1. Study Area
2.2. Needle Collection and DNA Extraction
2.3. SNP Genotyping
2.4. Variance Components, Theoretical Accuracy, and Breeding Value Predictions
2.5. Genetic Diversity Analysis
2.6. Parental Assignment and Mating Dynamics
2.7. Assessment of Pollen Contamination
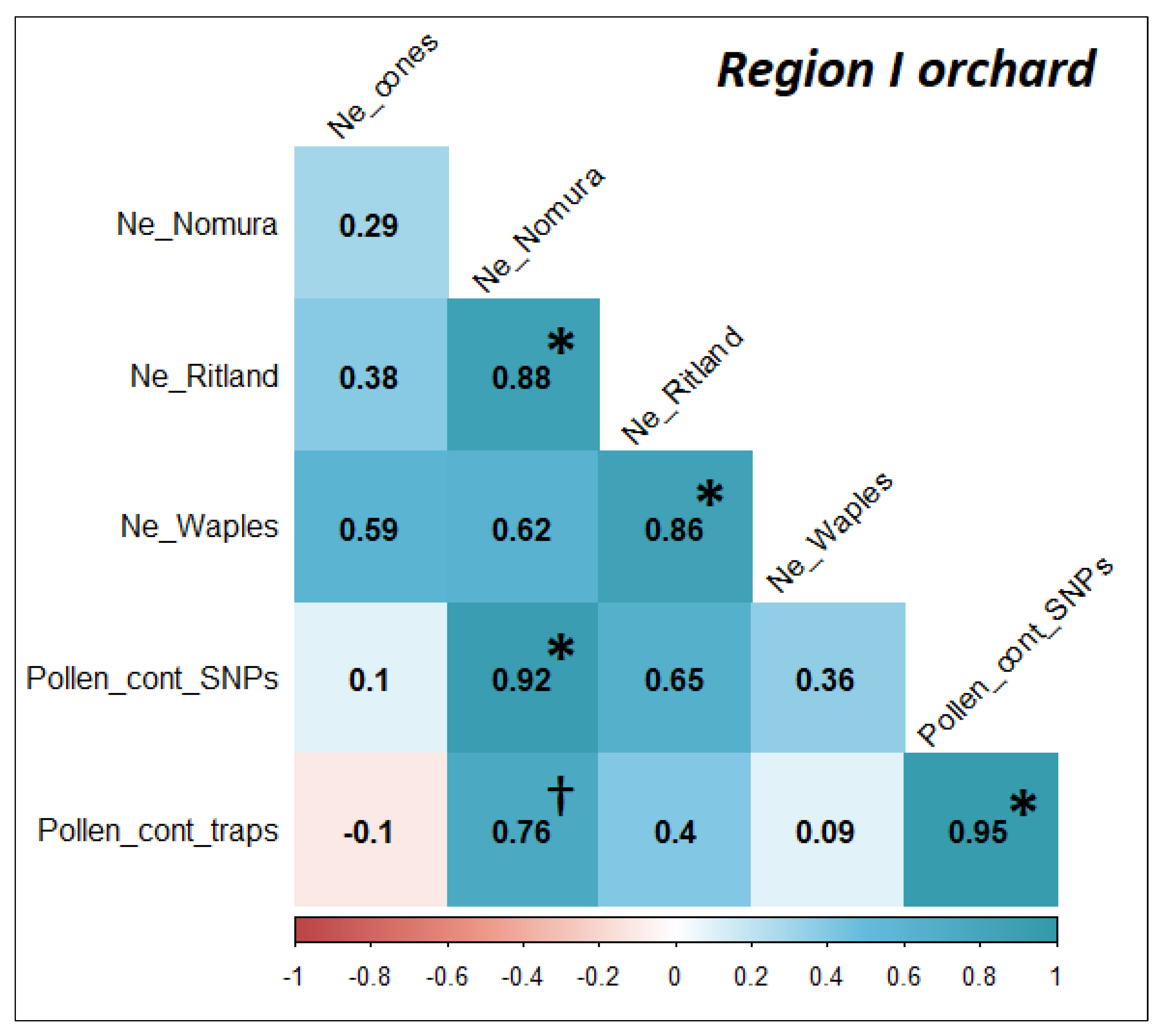
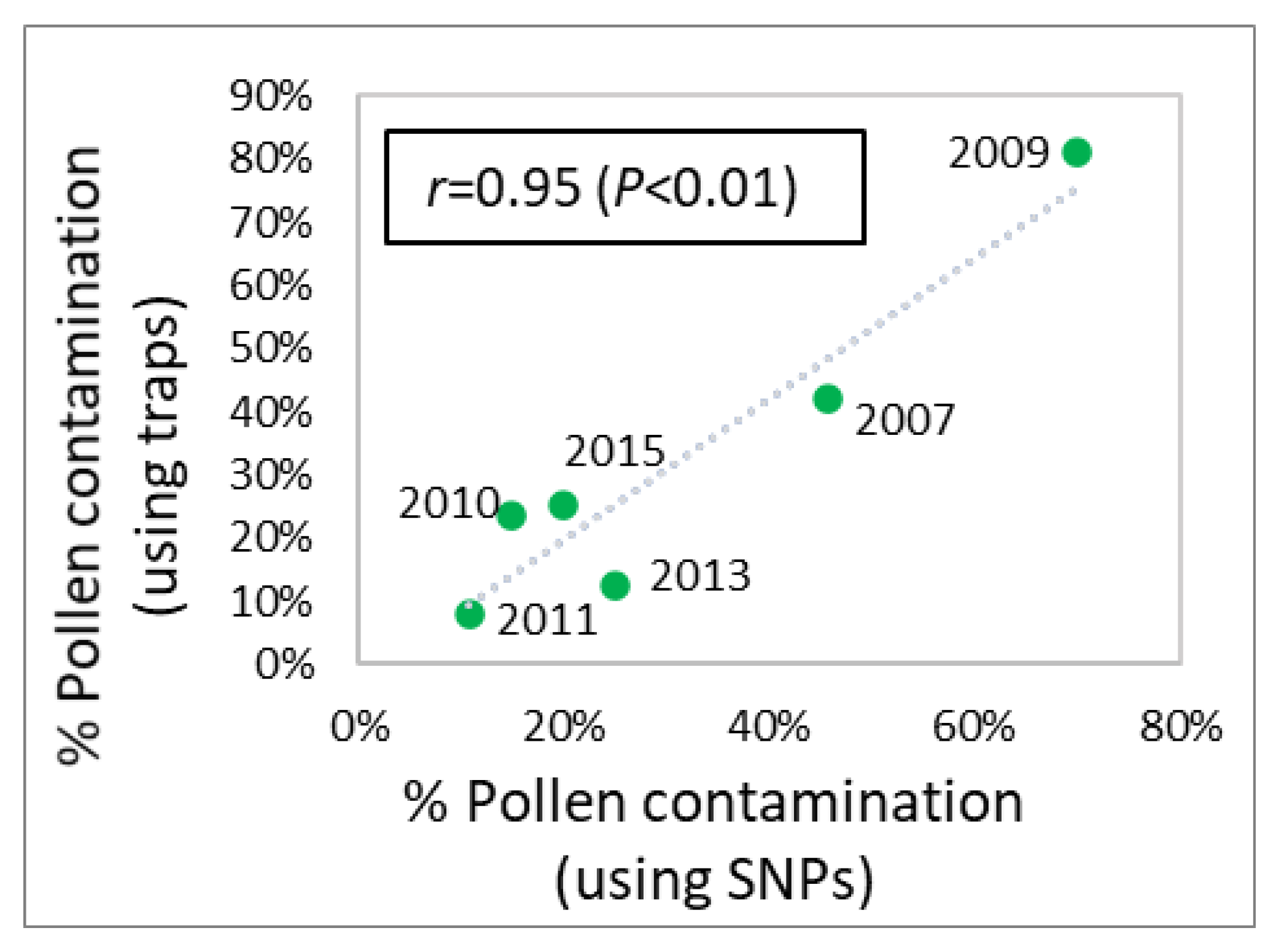
2.8. Correlations for Effective Population Size and Level of Pollen Contamination
3. Results
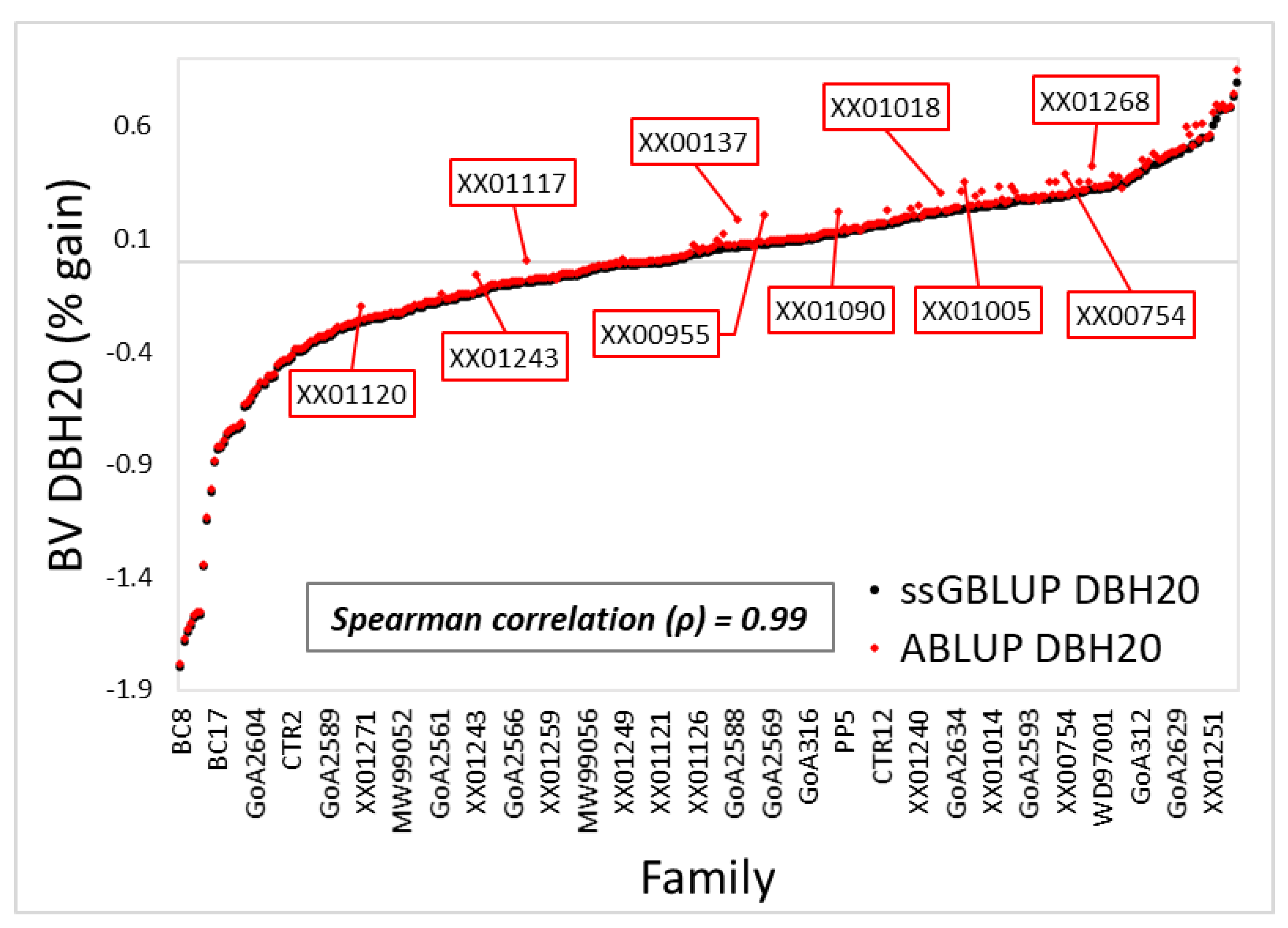
3.1. Variance Components and Predicted Breeding Values
3.2. Genetic Diversity in the White Spruce Program
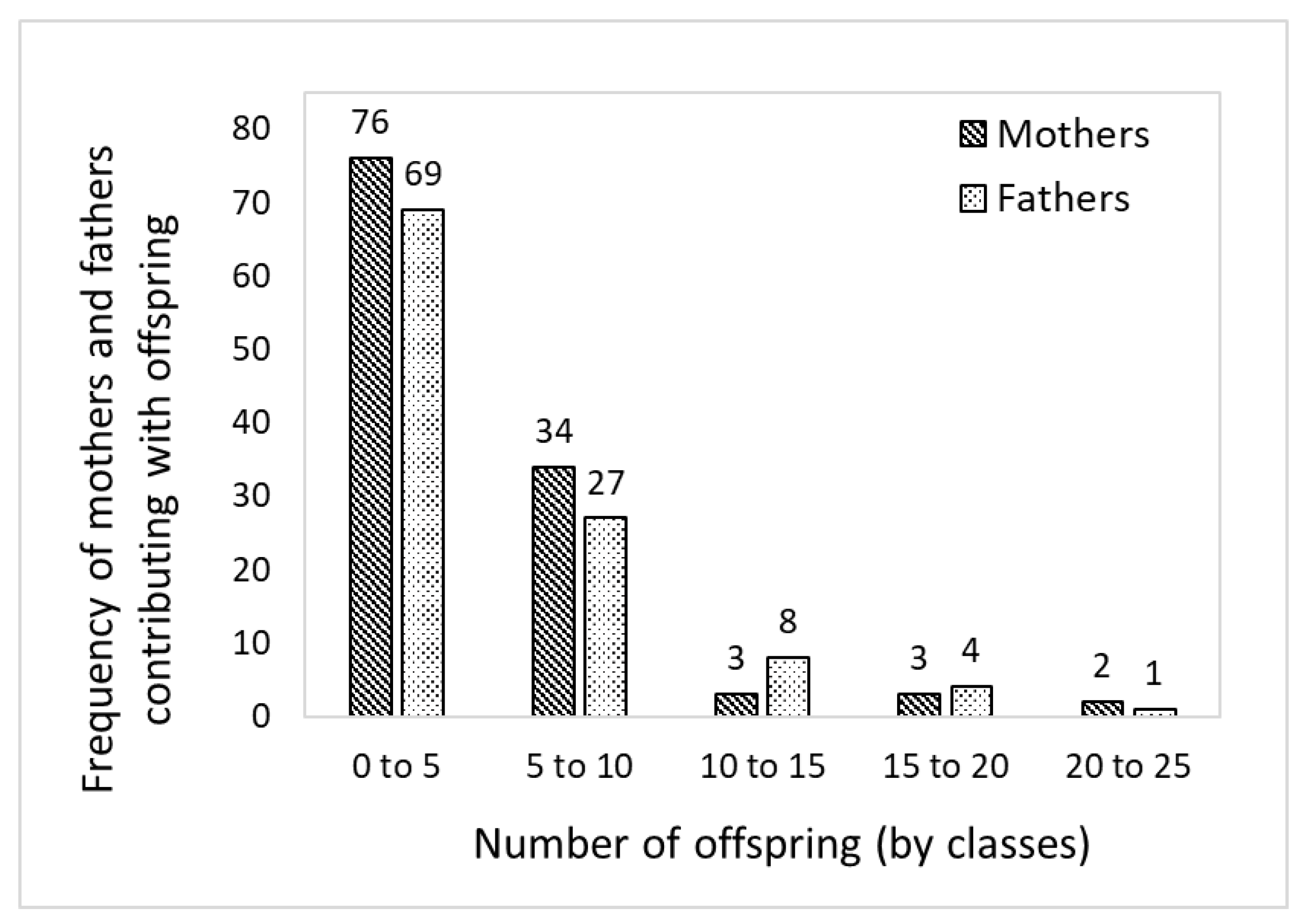
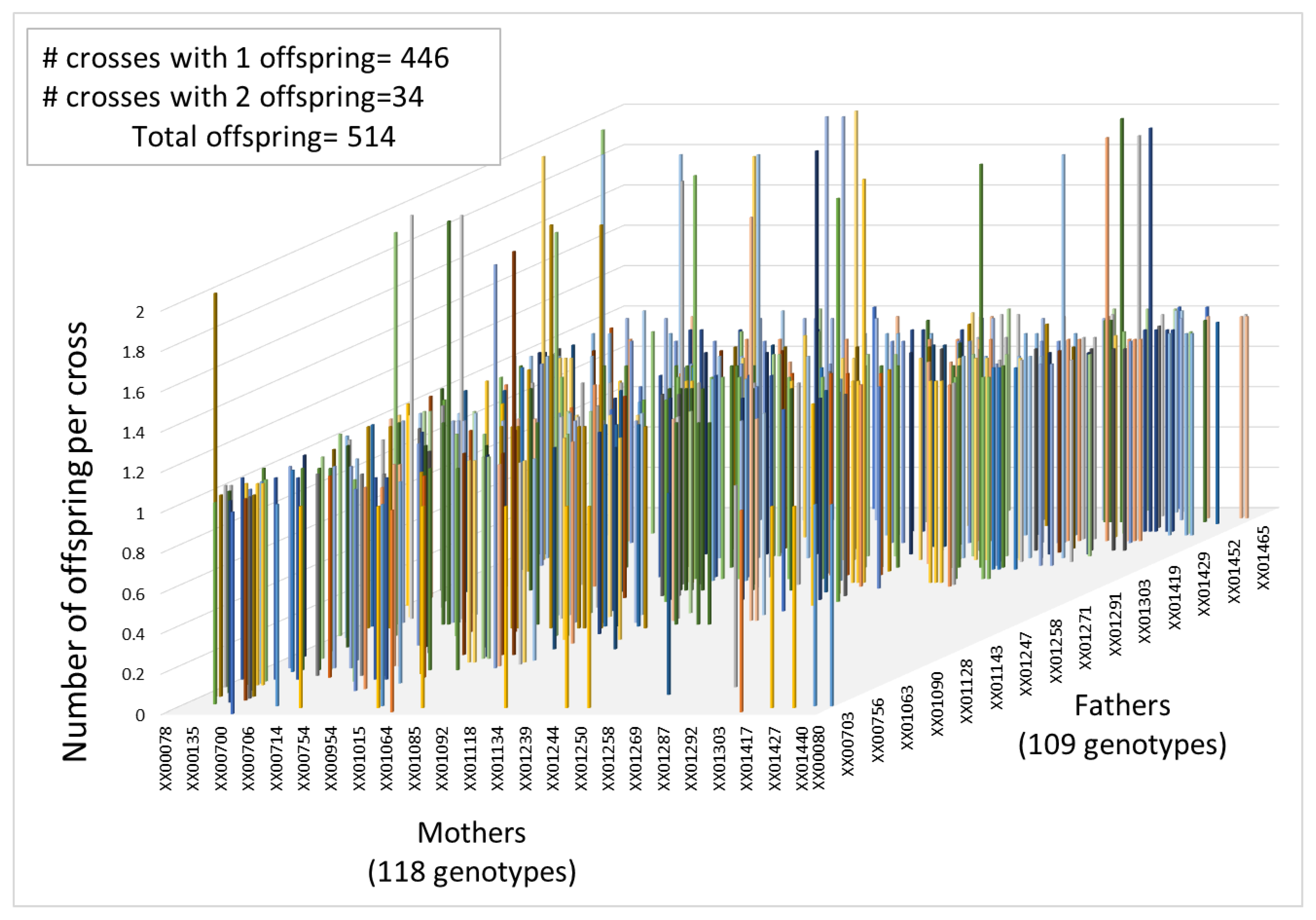
3.3. Pedigree Reconstruction
3.4. Pollen Contamination and Genetic Diversity
4. Discussion
4.1. Variance Components, Theoretical Accuracy, and Prediction of Breeding Values
4.2. Estimation of Genetic Diversity and Pollen Contamination with Appropriate Methods
4.3. Perspectives
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Uffelmann, E.; Huang, Q.Q.; Munung, N.S.; de Vries, J.; Okada, Y.; Martin, A.R.; Martin, H.C.; Lappalainen, T.; Posthuma, D. Genome-Wide Association Studies. Nat. Rev. Methods Prim. 2021, 1, 59. [Google Scholar] [CrossRef]
- Meuwissen, T.H.E.; Hayes, B.J.; Goddard, M.E. Prediction of Total Genetic Value Using Genome-Wide Dense Marker Maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [CrossRef] [PubMed]
- Borralho, N. The Impact of Individual Tree Mixed Models (BLUP) in Tree Breeding Strategies Eucalypt Plantations: Improving Fibre Yield and Quality. In Proceedings of the CRCTHF-IUFRO Conference, Hobart, Australia, 19–24 February 1995; pp. 141–145. [Google Scholar]
- Henderson, C.R. Applications of Linear Models in Animal Breeding; University of Guelph: Guelph, ON, Canada, 1984. [Google Scholar]
- Beaulieu, J.; Lenz, P.; Bousquet, J. Metadata Analysis Indicates Biased Estimation of Genetic Parameters and Gains Using Conventional Pedigree Information Instead of Genomic-Based Approaches in Tree Breeding. Sci. Rep. 2022, 12, 3933. [Google Scholar] [CrossRef] [PubMed]
- Grattapaglia, D.; Silva-Junior, O.B.; Resende, R.T.; Cappa, E.P.; Müller, B.S.F.; Tan, B.; Isik, F.; Ratcliffe, B.; El-Kassaby, Y.A. Quantitative Genetics and Genomics Converge to Accelerate Forest Tree Breeding. Front. Plant Sci. 2018, 871, 1693. [Google Scholar] [CrossRef] [PubMed]
- Beaulieu, J.; Doerksen, T.; Clément, S.; Mackay, J.; Bousquet, J. Accuracy of Genomic Selection Models in a Large Population of Open-Pollinated Families in White Spruce. Heredity 2014, 113, 343–352. [Google Scholar] [CrossRef] [PubMed]
- VanRaden, P.M. Efficient Methods to Compute Genomic Predictions. J. Dairy Sci. 2008, 91, 4414–4423. [Google Scholar] [CrossRef] [PubMed]
- Misztal, I.; Legarra, A.; Aguilar, I. Computing Procedures for Genetic Evaluation Including Phenotypic, Full Pedigree, and Genomic Information. J. Dairy Sci. 2009, 92, 4648–4655. [Google Scholar] [CrossRef]
- Christensen, O.; Lund, M. Genomic Relationship Matrix When Some Animals Are Not Genotyped. Genet. Sel. Evol. 2010, 42, 2. [Google Scholar] [CrossRef]
- Legarra, A.; Calenge, F.; Mariani, P.; Velge, P.; Beaumont, C. Use of a Reduced Set of Single Nucleotide Polymorphisms for Genetic Evaluation of Resistance to Salmonella Carrier State in Laying Hens. Poult. Sci. 2011, 90, 731–736. [Google Scholar] [CrossRef]
- Cappa, E.P.; El-Kassaby, Y.A.; Muñoz, F.; Garcia, M.N.; Villalba, P.V.; Klápště, J.; Marcucci Poltri, S.N. Improving Accuracy of Breeding Values by Incorporating Genomic Information in Spatial-Competition Mixed Models. Mol. Breed. 2017, 37, 125. [Google Scholar] [CrossRef]
- Cappa, E.P.; El-Kassaby, Y.A.; Muñoz, F.; Garcia, M.N.; Villalba, P.V.; Klápště, J.; Marcucci Poltri, S.N. Genomic-Based Multiple-Trait Evaluation in Eucalyptus Grandis Using Dominant DArT Markers. Plant Sci. 2018, 271, 27–33. [Google Scholar] [CrossRef] [PubMed]
- Ratcliffe, B.; El-Dien, O.G.; Cappa, E.P.; Porth, I.; Klápště, J.; Chen, C.; El-Kassaby, Y.A. Single-Step BLUP with Varying Genotyping Effort in Open-Pollinated Picea Glauca. G3 Genes Genomes Genet. 2017, 7, 935–942. [Google Scholar] [CrossRef] [PubMed]
- Thavamanikumar, S.; Arnold, R.J.; Luo, J.; Thumma, B.R. Genomic Studies Reveal Substantial Dominant Effects and Improved Genomic Predictions in an Open-Pollinated Breeding Population of Eucalyptus Pellita. G3 Genes Genomes Genet. 2020, 10, 3751–3763. [Google Scholar] [CrossRef] [PubMed]
- Callister, A.N.; Bradshaw, B.P.; Elms, S.; Gillies, R.A.W.; Sasse, J.M.; Brawner, J.T. Single-Step Genomic BLUP Enables Joint Analysis of Disconnected Breeding Programs: An Example with Eucalyptus Globulus Labill. G3 Genes Genomes Genet. 2021, 11, jkab253. [Google Scholar] [CrossRef] [PubMed]
- Kang, K.-S.; Bilir, N. Seed Orchards-Establishment, Management and Genetics; Kang, K.-S., Bilir, N., Eds.; The Foundation of Developing Forestry and Supporting Fire Protection Services: Altindag, Turkey, 2021; ISBN 978-975-93943-9-4. [Google Scholar]
- Galeano, E.; Bousquet, J.; Thomas, B.R. SNP-based Analysis Reveals Unexpected Features of Genetic Diversity, Parental Contributions and Pollen Contamination in a White Spruce Breeding Program. Sci. Rep. 2021, 11, 4990. [Google Scholar] [CrossRef] [PubMed]
- Wheeler, N.C.; Jech, K.S. The Use of Electrophoretic Markers in Seed Orchard Research. New For. 1992, 6, 311–328. [Google Scholar] [CrossRef]
- Sajid, M.; Ahmad, R.I.; Muhammad, A.R.; Zulfiqar, A.L.I.; Lori, H.; Tehseen, A.M. Role of SNPs in Determining QTLs for Major Traits in Cotton. J. Cott. Res. 2019, 2, 5. [Google Scholar]
- FGRMS. Alberta Forest Genetic Resource Management and Conservation Standards Volume 1: Stream 1 and Stream 2; FGRMS: Edmonton, AB, Canada, 2016; Volume 4, 165p. [Google Scholar]
- Lenz, P.R.N.; Nadeau, S.; Azaiez, A.; Gérardi, S.; Deslauriers, M.; Perron, M.; Isabel, N.; Beaulieu, J.; Bousquet, J. Genomic Prediction for Hastening and Improving Efficiency of Forward Selection in Conifer Polycross Mating Designs: An Example from White Spruce. Heredity 2020, 124, 562–578. [Google Scholar] [CrossRef]
- Isik, F.; Holland, J.; Maltecca, C. Genetic Data Analysis for Plant and Animal Breeding, 1st ed.; Isik, F., Holland, J., Maltecca, C., Eds.; Springer: Cham, Switzerland, 2017; ISBN 978-3-319-55175-3. [Google Scholar]
- Legarra, A.; Aguilar, I.; Misztal, I. A Relationship Matrix Including Full Pedigree and Genomic Information. J. Dairy Sci. 2009, 92, 4656–4663. [Google Scholar] [CrossRef]
- Aguilar, I.; Misztal, I.; Johnson, D.L.; Legarra, A.; Tsuruta, S.; Lawlor, T.J. Hot Topic: A Unified Approach to Utilize Phenotypic, Full Pedigree, and Genomic Information for Genetic Evaluation of Holstein Final Score. J. Dairy Sci. 2010, 93, 743–752. [Google Scholar] [CrossRef]
- Gezan, S.A.; de Oliveira, A.A.; Galli, G.; Murray, D. ASRgenomics: An R Package with Complementary Genomic Functions; The Comprehensive R Archive Network: Vienna, Australia, 2022. [Google Scholar]
- Butler, D.G.; Cullis, B.R.; Gilmour, A.R.; Gogel, B.J.; Thompson, R. ASReml-R Reference Manual Version 4; The Comprehensive R Archive Network: Vienna, Australia, 2017. [Google Scholar]
- Gilmour, A.R.; Thompson, R.; Cullis, B.R. Average Information REML: An Efficient Algorithm for Variance Parameter Estimation in Linear Mixed Models. Biometrics 1995, 51, 1440–1450. [Google Scholar] [CrossRef]
- Peakall, R.; Smouse, P.E. GenALEx 6.5: Genetic Analysis in Excel. Population Genetic Software for Teaching and Research—An Update. Bioinformatics 2012, 28, 2537–2539. [Google Scholar] [CrossRef] [PubMed]
- Lindgren, D.; Mullin, T.J. Relatedness and Status Number in Seed Orchard Crops. Can. J. For. Res. 1998, 28, 276–283. [Google Scholar] [CrossRef]
- Ritland, K. Estimators for Pairwise Relatedness and Individual Inbreeding Coefficients. Genet. Res. 1996, 67, 175–185. [Google Scholar] [CrossRef]
- Nomura, T. Estimation of Effective Number of Breeders from Molecular Coancestry of Single Cohort Sample. Evol. Appl. 2008, 1, 462–474. [Google Scholar] [CrossRef]
- Do, C.; Waples, R.S.; Peel, D.; Macbeth, G.M.; Tillett, B.J.; Ovenden, J.R. NeEstimator v2: Re-Implementation of Software for the Estimation of Contemporary Effective Population Size (Ne) from Genetic Data. Mol. Ecol. Resour. 2014, 14, 209–214. [Google Scholar] [CrossRef] [PubMed]
- Waples, R.S. A Bias Correction for Estimates of Effective Population Size Based on Linkage Disequilibrium at Unlinked Gene Loci. Conserv. Genet. 2006, 7, 167–184. [Google Scholar] [CrossRef]
- Kalinowski, S.T.; Taper, M.L.; Marshall, T.C. Revising How the Computer Program CERVUS Accommodates Genotyping Error Increases Success in Paternity Assignment. Mol. Ecol. 2007, 16, 1099–1106. [Google Scholar] [CrossRef]
- Thumma, B.R.; Joyce, K.R.; Jacobs, A. Genomic Studies with Preselected Markers Reveal Dominance Effects Influencing Growth Traits in Eucalyptus Nitens. G3 Genes Genomes Genet. 2022, 12, jkab363. [Google Scholar] [CrossRef]
- Ukrainetz, N.K.; Mansfield, S.D. Prediction Accuracy of Single-Step BLUP for Growth and Wood Quality Traits in the Lodgepole Pine Breeding Program in British Columbia. Tree Genet. Genomes 2020, 16, 64. [Google Scholar] [CrossRef]
- Walker, T.D.; Cumbie, W.P.; Isik, F. Single-Step Genomic Analysis Increases the Accuracy of Within-Family Selection in a Clonally Replicated Population of Pinus taeda L. For. Sci. 2022, 68, 37–52. [Google Scholar] [CrossRef]
- Gamal El-Dien, O.; Ratcliffe, B.; Klápště, J.; Chen, C.; Porth, I.; El-Kassaby, Y.A. Prediction Accuracies for Growth and Wood Attributes of Interior Spruce in Space Using Genotyping-by-Sequencing. BMC Genom. 2015, 16, 370. [Google Scholar] [CrossRef] [PubMed]
- Lenz, P.R.N.; Beaulieu, J.; Mansfield, S.D.; Clément, S.; Desponts, M.; Bousquet, J. Factors Affecting the Accuracy of Genomic Selection for Growth and Wood Quality Traits in an Advanced-Breeding Population of Black Spruce (Picea mariana). BMC Genom. 2017, 18, 335. [Google Scholar] [CrossRef] [PubMed]
- Nadeau, S.; Beaulieu, J.; Gezan, S.A.; Perron, M.; Bousquet, J.; Lenz, P.R.N. Increasing Genomic Prediction Accuracy for Unphenotyped Full- Sib Families by Modeling Additive and Dominance Effects with Large Datasets in White Spruce. Front. Plant Sci. 2023, 14, 1137834. [Google Scholar] [CrossRef] [PubMed]
- Bernardo, R. Reinventing Quantitative Genetics for Plant Breeding: Something Old, Something New, Something Borrowed, Something BLUE. Heredity 2020, 2020, 24. [Google Scholar] [CrossRef] [PubMed]
- Funda, T.; Liewlaksaneeyanawin, C.; El-Kassaby, Y.A. Determination of Paternal and Maternal Parentage in Lodgepole Pine Seed: Full versus Partial Pedigree Reconstruction. Can. J. For. Res. 2014, 44, 1122–1127. [Google Scholar] [CrossRef]
- Huang, L.S.; Song, J.; Sun, Y.Q.; Gao, Q.; Jiao, S.Q.; Zhou, S.S.; Jin, Y.; Yang, X.L.; Zhu, J.J.; Gao, F.L.; et al. Pollination Dynamics in a Platycladus Orientalis Seed Orchard as Revealed by Partial Pedigree Reconstruction. Can. J. For. Res. 2018, 48, 952–957. [Google Scholar] [CrossRef]
- Korecký, J.; El-Kassaby, Y.A. Pollination Dynamics Variation in a Douglas-Fir Seed Orchard as Revealed by Microsatellite Analysis. Silva Fenn. 2016, 50, 808. [Google Scholar] [CrossRef]
- Finžgar, B.D.; Ennos, R.; Whittet, R.; Cottrell, J. Measuring and Managing Genetic Diversity in the British Sitka Spruce Improvement Programme. Scott. For. 2023, 77, 38–44. [Google Scholar]
- El-Kassaby, Y.A.; Funda, T.; Lai, B.S.K. Female Reproductive Success Variation in a Pseudotsuga menziesii Seed Orchard as Revealed by Pedigree Reconstruction from a Bulk Seed Collection. J. Hered. 2010, 101, 164–168. [Google Scholar] [CrossRef]
- Funda, T.; Liewlaksaneeyanawin, C.; Fundova, I.; Lai, B.S.K.; Walsh, C.; van Niejenhuis, A.; Cook, C.; Graham, H.; Woods, J.; El-Kassaby, Y.A. Congruence between Parental Reproductive Investment and Success Determined by DNA-Based Pedigree Reconstruction in Conifer Seed Orchards. Can. J. For. Res. 2011, 41, 380–389. [Google Scholar] [CrossRef]
- Luikart, G.; Ryman, N.; Tallmon, D.A.; Schwartz, M.K.; Allendorf, F.W. Estimation of Census and Effective Population Sizes: The Increasing Usefulness of DNA-Based Approaches. Conserv. Genet. 2010, 11, 355–373. [Google Scholar] [CrossRef]
- Hough, J.; Williamson, R.J.; Wright, S.I. Patterns of Selection in Plant Genomes. Annu. Rev. Ecol. Evol. Syst. 2013, 44, 31–49. [Google Scholar] [CrossRef]
- Jónás, Á.; Taus, T.; Kosiol, C.; Schlötterer, C.; Futschik, A. Estimating the Effective Population Size from Temporal Allele Frequency Changes in Experimental Evolution. Genetics 2016, 204, 723–735. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Santiago, E.; Caballero, A. Prediction and Estimation of Effective Population Size. Heredity 2016, 117, 193–206. [Google Scholar] [CrossRef] [PubMed]
- Trask, A.E.; Bignal, E.M.; McCracken, D.I.; Piertney, S.B.; Reid, J.M. Estimating Demographic Contributions to Effective Population Size in an Age-Structured Wild Population Experiencing Environmental and Demographic Stochasticity. J. Anim. Ecol. 2017, 86, 1082–1093. [Google Scholar] [CrossRef]
- Bousquet, J.; Gérardi, S.; de Lafontaine, G.; Jaramillo-Correa, J.P.; Pavy, N.; Prunier, J.; Lenz, P.; Beaulieu, J. Spruce Population Genomics. In Population Genomics; Rajora, O.P., Ed.; Springer: Cham, Switzerland, 2021; pp. 1–64. [Google Scholar]


| Parameter | GBLUP | ABLUP | ssGBLUP | ssGBLUP* |
|---|---|---|---|---|
| Total No. of parents | 42 | 306 | 306 | 306 |
| No. of parents genotyped | 42 | -- | 42 | 166 |
| No. of progeny | 667 | 8658 | 8658 | 8658 |
| Total number | 709 | 8974 | 8974 | 8974 |
| HT20 | ||||
| 1517.8 (1590.4) | 6682.6 (481.7) | 7015.9 (487.3) | 6863.7 (481.5) | |
| 8077.2 (1264.3) | 6703.9 (373.2) | 6557.3 (372.2) | 6604.9 (368.4) | |
| 0.16 (0.16) | 0.49 (0.03) | 0.52 (0.03) | 0.51 (0.03) | |
| mothers | 0.43 [0.37–0.51] | 0.90 [0.90–0.90] | 0.91 [0.72–0.95] | 0.91 [0.71–0.95] |
| progeny | 0.39 [0.21–0.47] | 0.74 [0.73–0.75] | 0.76 [0.74–0.81] | 0.75 [0.74–0.80] |
| DBH20 | ||||
| 0.48 (0.3) | 2.75 (0.2) | 2.86 (0.2) | 2.78 (0.2) | |
| 3.67 (0.4) | 2.79 (0.2) | 2.77 (0.2) | 2.79 (0.2) | |
| 0.12 (0.07) | 0.49 (0.03) | 0.51 (0.03) | 0.50 (0.03) | |
| mothers | 0.55 [0.49–0.58] | 0.90 [0.90–0.90] | 0.90 [0.72–0.95] | 0.91 [0.71–0.95] |
| progeny | 0.42 [0.32–0.49] | 0.74 [0.73–0.75] | 0.76 [0.74–0.81] | 0.75 [0.74–0.80] |
| Parameter | Founders | S2007 | S2009 | S2010 | S2011 | S2013 | S2015 | Prog. Trial | |
|---|---|---|---|---|---|---|---|---|---|
| N | 166 | 120 | 180 | 120 | 120 | 120 | 120 | 667 | |
| A | Mean | 1.99 | 1.99 | 1.99 | 1.98 | 1.98 | 1.99 | 1.98 | 2 |
| (SE) | (0.001) | (0.002) | (0.001) | (0.004) | (0.003) | (0.003) | (0.004) | (0.001) | |
| I | Mean | 0.44 | 0.44 | 0.44 | 0.44 | 0.44 | 0.44 | 0.44 | 0.45 |
| (SE) | (0.006) | (0.006) | (0.006) | (0.006) | (0.006) | 0.006) | (0.006) | (0.006) | |
| He | Mean | 0.29 | 0.28 | 0.28 | 0.28 | 0.28 | 0.28 | 0.28 | 0.29 |
| (SE) | (0.004) | (0.004) | (0.004) | (0.004) | (0.004) | (0.004) | (0.004) | (0.005) | |
| Ho | Mean | 0.29 | 0.29 | 0.29 | 0.28 | 0.29 | 0.28 | 0.28 | 0.29 |
| (SE) | (0.004) | (0.003) | (0.004) | (0.005) | 0.005) | (0.005) | (0.005) | (0.005) | |
| Fi | Mean | 0.001 | 0.007 | 0.004 | −0.003 | 0.003 | 0.005 | 0.012 | −0.002 |
| (SE) | (0.002) | (0.002) | (0.002) | (0.002) | 0.002) | (0.002) | (0.002) | (0.002) | |
| Ne (Ritland) | Mean | 333.33 | 108.02 | 106.75 | 56.38 | 90.59 | 101.97 | 84.02 | 301.93 |
| Ne (Nomura) | Mean | 180.24 | 38.9 | 48.5 | 11.3 | 20.2 | 32.2 | 19.5 | 85.21 |
| (SE) | (19.36) | (5.05) | (4.03) | (2.06) | (3.57) | (3.39) | (2.93) | (10.12) | |
| Ne (Waples) | Mean | 570.82 | 209.5 | 144.4 | 81.8 | 161.6 | 160.4 | 128.9 | 358.27 |
| (SE) | (126.61) | (51.25) | (35.79) | (20.51) | 38.49) | (37.98) | (29.89) | (84.31) | |
| Ne (cones) | Mean | na | 83.9 | 59.8 | 59.9 | 79.9 | 72.3 | 28.59 | na |
| Pollen cont. (SNPs) | Mean | na | 45.8% | 70.0% | 15.0% | 10.8% | 25.0% | 20.0% | na |
| Pollen cont. (traps) | Mean | na | 42.1% | 81.0% | 23.7% | 7.8% | 12.3% | 25.2% | na |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galeano, E.; Cappa, E.P.; Bousquet, J.; Thomas, B.R. Optimizing a Regional White Spruce Tree Improvement Program: SNP Genotyping for Enhanced Breeding Values, Genetic Diversity Assessment, and Estimation of Pollen Contamination. Forests 2023, 14, 2212. https://doi.org/10.3390/f14112212
Galeano E, Cappa EP, Bousquet J, Thomas BR. Optimizing a Regional White Spruce Tree Improvement Program: SNP Genotyping for Enhanced Breeding Values, Genetic Diversity Assessment, and Estimation of Pollen Contamination. Forests. 2023; 14(11):2212. https://doi.org/10.3390/f14112212
Chicago/Turabian StyleGaleano, Esteban, Eduardo Pablo Cappa, Jean Bousquet, and Barb R. Thomas. 2023. "Optimizing a Regional White Spruce Tree Improvement Program: SNP Genotyping for Enhanced Breeding Values, Genetic Diversity Assessment, and Estimation of Pollen Contamination" Forests 14, no. 11: 2212. https://doi.org/10.3390/f14112212
APA StyleGaleano, E., Cappa, E. P., Bousquet, J., & Thomas, B. R. (2023). Optimizing a Regional White Spruce Tree Improvement Program: SNP Genotyping for Enhanced Breeding Values, Genetic Diversity Assessment, and Estimation of Pollen Contamination. Forests, 14(11), 2212. https://doi.org/10.3390/f14112212





