Number Preference as a Source of Measurement Error in the U.S. National Forest Inventory
Abstract
1. Introduction
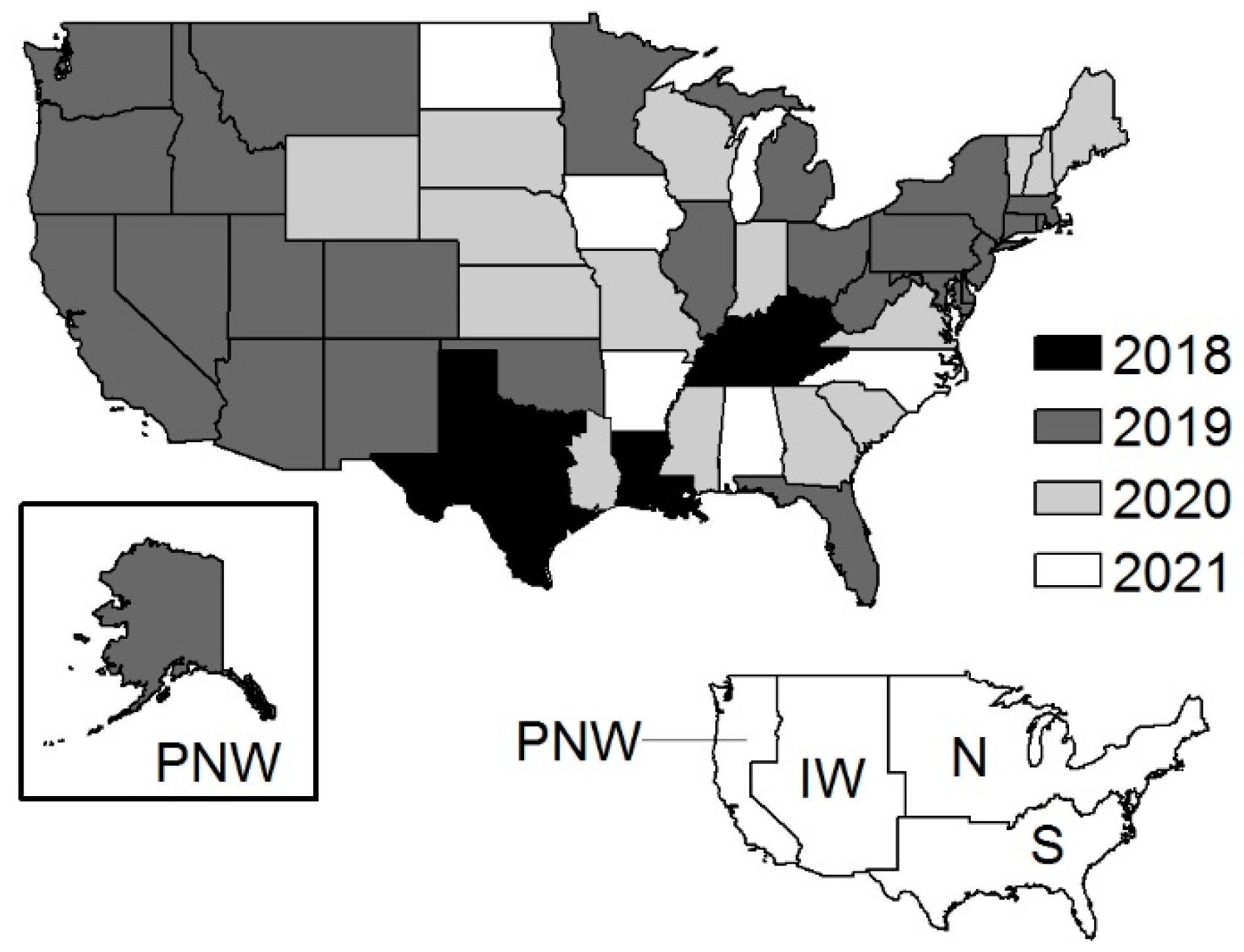
2. Materials and Methods
3. Results
3.1. Rotten/Missing Cull Volume
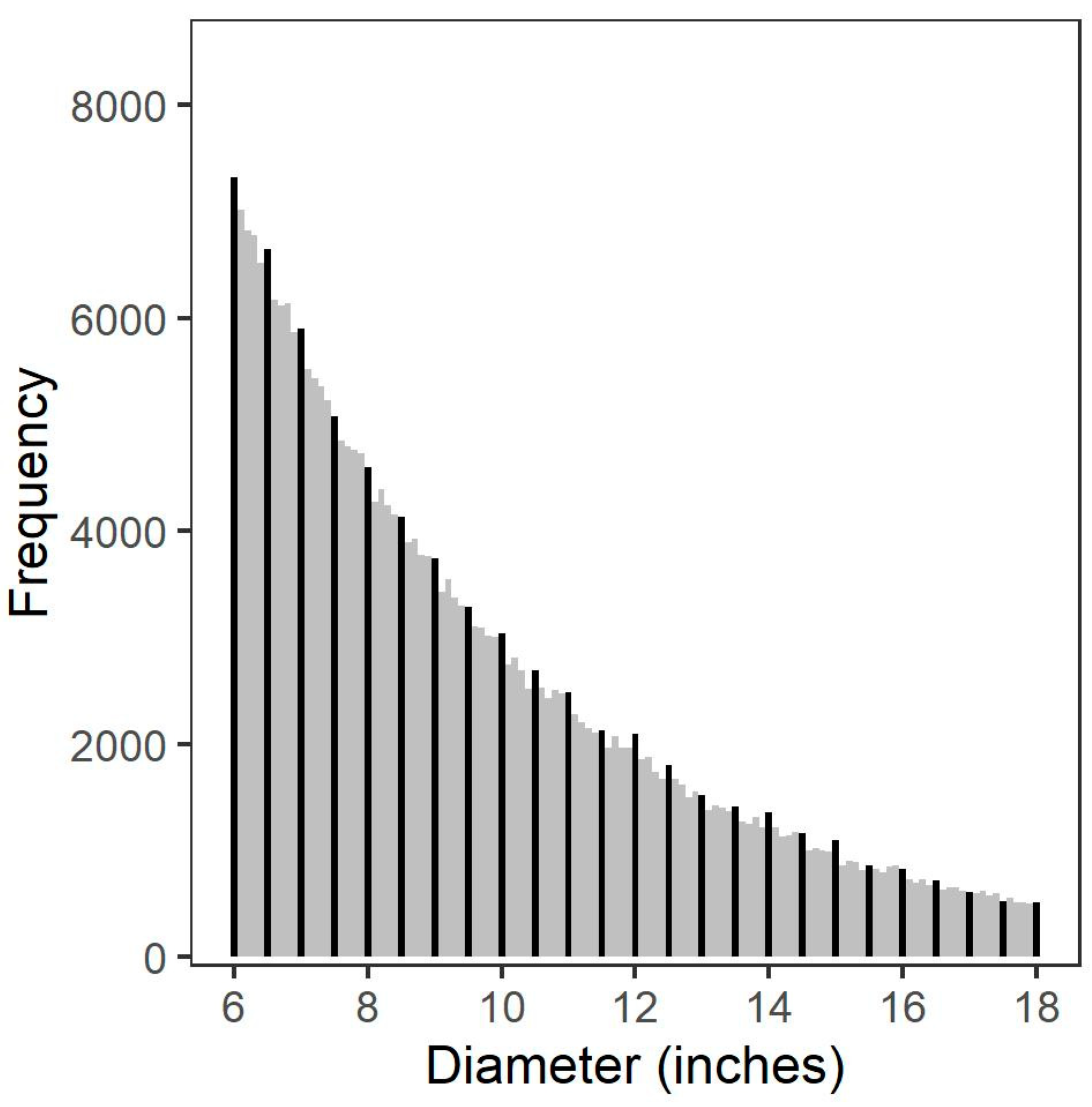
3.2. Diameter
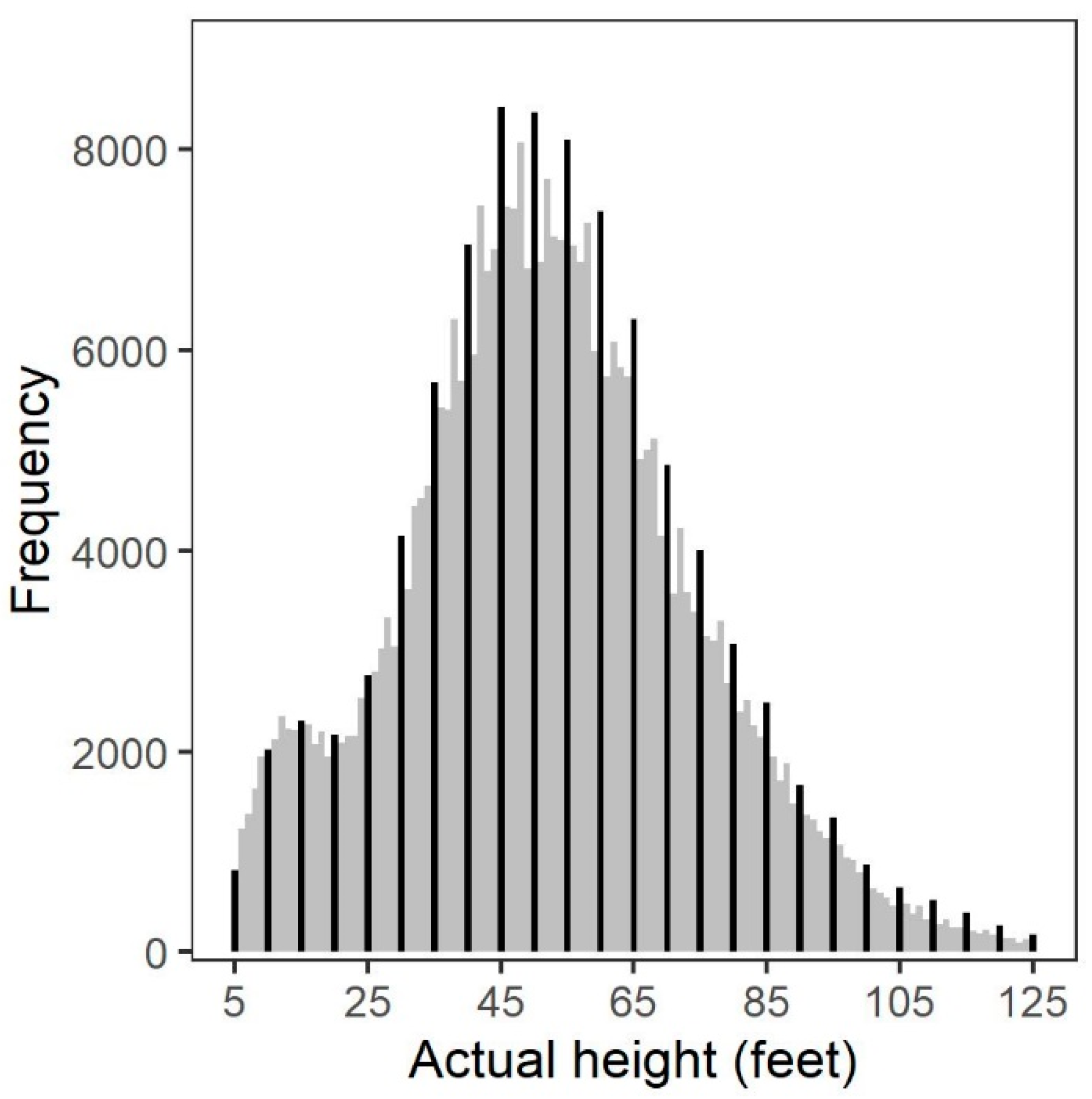
3.3. Actual Height
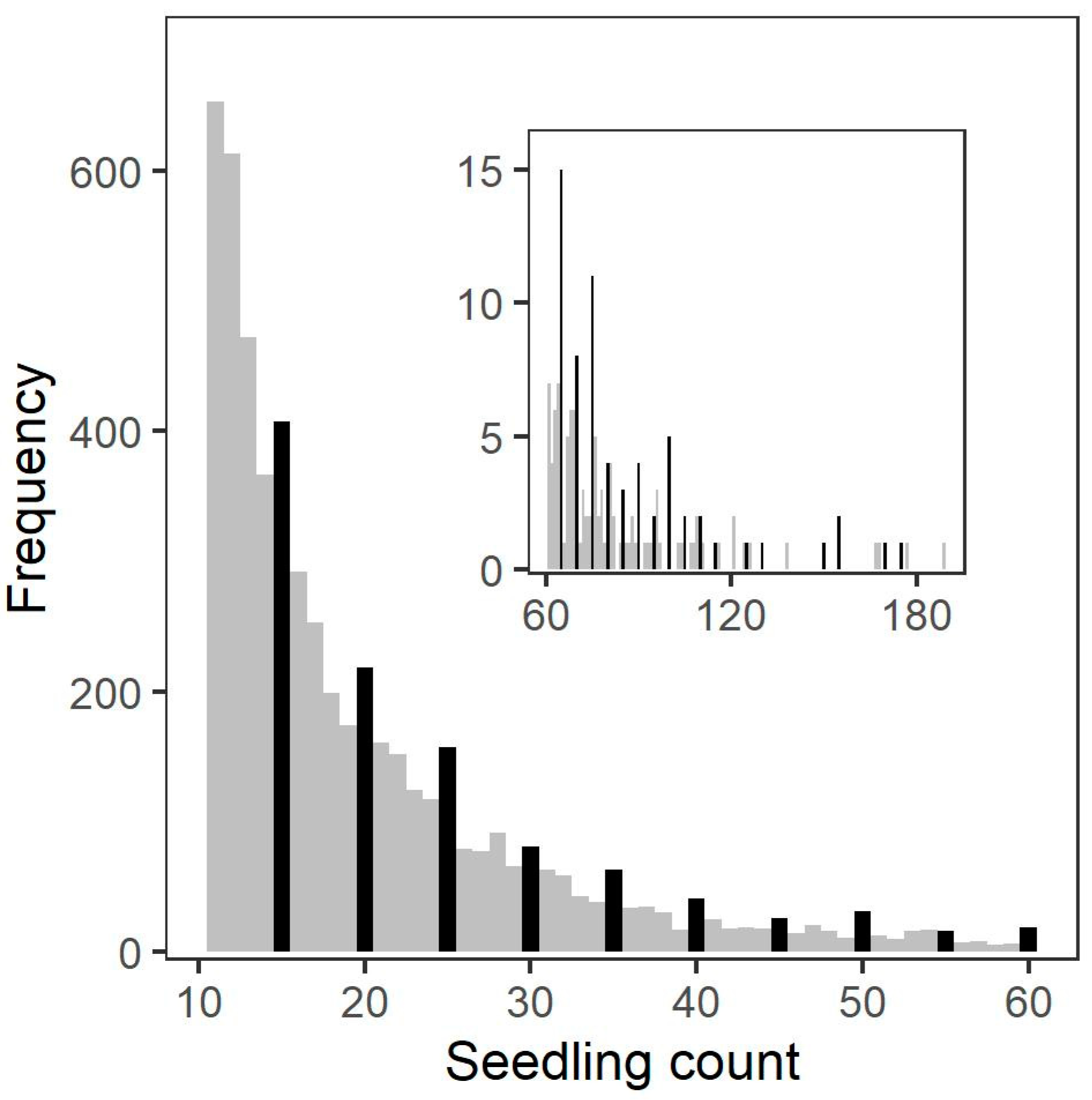
3.4. Seedling Count
4. Discussion
4.1. Considerations for Data Quality Control
4.2. Source of Number Preference
4.2.1. Task Difficulty
- Cull measurements of hardwood species due to their deliquescent crown forms [33];
- Cull measurements of trees with broken/missing tops due to their irregular crown form;
- Diameters measured above breast height or at root collar because of the awkward positioning observers must achieve in order to obtain the measurements, i.e., stretching high or crouching low;
- Heights of hardwood species due to their deliquescent crown form [33];
- Heights of trees greater than sapling size due to poorer lines of sight for the observer because the treetops are taller and farther from the observer and potentially obscured by understory vegetation;
- Seedling counts in small-sized stands and disturbed conditions due to dense understory vegetation;
- Seedling counts in conditions where the forest floor is obscured due to snow cover or water; and
- Seedling counts on steep slopes because of the precarious stance observers must maintain in order to obtain the counts.
4.2.2. Motivation and Ability
4.3. Study Limitations
5. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cunia, T. Forest inventory: On the structure of error of estimates. In State-of-the-Art Methodology of Forest Inventory: A Symposium Proceedings, Syracuse, NY, USA, 30 July–5 August 1989; PNW-GTR-263; LaBau, V.J., Cunia, T., Eds.; U.S. Department of Agriculture, Forest Service, Pacific Northwest Station: Portland, OR, USA, 1990; pp. 169–176. [Google Scholar] [CrossRef]
- Gertner, G.Z. The sensitivity of measurement error in stand volume estimation. Can. J. For. Res. 1990, 20, 800–804. [Google Scholar] [CrossRef]
- Canavan, S.J.; Hann, D.W. The two-stage method for measurement error characterization. For. Sci. 2004, 50, 743–756. [Google Scholar] [CrossRef]
- Westfall, J.A.; Patterson, P.L. Measurement variability error for estimates of volume change. Can. J. For. Res. 2007, 37, 2201–2210. [Google Scholar] [CrossRef]
- Mitchell, J. Clustering and psychological barriers: The importance of numbers. J. Futures Mark. 2001, 21, 395–428. [Google Scholar] [CrossRef]
- Pope, D.; Simonsohn, U. Round numbers as goals: Evidence from baseball, SAT Takers, and the Lab. Psychol. Sci. 2011, 22, 71–79. [Google Scholar] [CrossRef]
- Lynn, M.; Flyn, S.M.; Helion, C. Do consumers prefer round prices? Evidence from pay-what-you-want decisions and self-pumped gasoline purchases. J. Econ. Psychol. 2013, 36, 96–102. [Google Scholar] [CrossRef]
- Allen, E.J.; Dechow, P.M.; Pope, D.G.; Wu, G. Reference-dependent preferences: Evidence from marathon runners. Manag. Sci. 2017, 63, 1657–1672. [Google Scholar] [CrossRef]
- Carslaw, C.A.P.N. Anomolies in income numbers: Evidence of goal oriented behavior. Account. Rev. 1988, 63, 321–327. [Google Scholar]
- Gideon, M.; Helppie-McFall, B.; Hsu, J.W. Heaping at round numbers on financial questions: The role of satisficing. Surv. Res. Methods-Ger. 2017, 11, 189–214. [Google Scholar] [CrossRef]
- Bopp, M.; Faeh, D. End-digits preference for self-reported height depends on language. BMC Public Health 2008, 8, 342. [Google Scholar] [CrossRef]
- Crawford, F.W.; Weiss, R.E.; Suchard, M.A. Sex, lies and self-reported counts: Bayesian mixture models for heaping in longitudinal count data via birth-death process. Ann. Appl. Stat. 2015, 9, 572–596. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Shiffman, S.; Griffith, S.D.; Heitjan, D.F. Truth and memory: Linking instantaneous and retrospective self-reported cigarette consumption. Ann. Appl. Stat. 2012, 6, 1689–1706. [Google Scholar] [CrossRef]
- Schmidt, J.I.; Kellie, K.A.; Chapin, F.S., III. Detecting, estimating, and correcting for biases in harvest data. J. Wildl. Manag. 2015, 79, 1152–1162. [Google Scholar] [CrossRef]
- Zinn, S.; Würbach, A. A statistical approach to address the problem of heaping in self-reported income data. J. Appl. Stat. 2016, 43, 682–703. [Google Scholar] [CrossRef]
- Thavarajah, S.; White, W.B.; Mansoor, G.A. Terminal digit bias in a specialty hypertension faculty practice. J. Hum. Hypertens. 2003, 17, 819–822. [Google Scholar] [CrossRef]
- Hayes, S.J. Terminal digit preference occurs in pathology reporting irrespective of patient management implication. J. Clin. Pathol. 2008, 61, 1071–1072. [Google Scholar] [CrossRef]
- Bunch, A.J.; Walters, C.J.; Coggins, L.G., Jr. Measurement error in fish lengths: Evaluation and management implications. Fisheries 2013, 38, 320–326. [Google Scholar] [CrossRef]
- Beaman, J.; Vaske, J.J.; Schmidt, J.I.; Huan, T. Measuring and correcting response heaping arising from the use of prototypes. Hum. Dimens. Wildl. 2015, 20, 167–173. [Google Scholar] [CrossRef]
- Bechtold, W.A.; Patterson, P.L. (Eds.) The Enhanced Forest Inventory and Analysis Program—National Sampling Design and Estimation Procedures; Gen. Tech. Rep. SRS-80; U.S. Department of Agriculture, Forest Service, Southern Research Station: Asheville, NC, USA, 2005. [CrossRef]
- Forest Service. Forest Inventory and Analysis National Core Field Guide. Volume 1: Field Data Collection Procedures for Phase 2 Plots, Ver. 7–9. U.S. Department of Agriculture, Multiple Years. Available online: https://www.fia.fs.usda.gov/library/field-guides-methods-proc/index.php (accessed on 13 October 2019).
- Burrill, E.A.; DiTommaso, A.M.; Turner, J.A.; Pugh, S.A.; Menlove, J.; Christiansen, G.; Perry, C.J.; Conkling, B.L. The Forest Inventory and Analysis Database: Database Description and User Guide Version 9.0.1 for Phase 2. U.S. Department of Agriculture, Forest Service. 2021. Available online: https://www.fia.fs.usda.gov/library/database-documentation/current/ver90/FIADB%20User%20Guide%20P2_9-0_final.pdf (accessed on 12 August 2021).
- R Core Team. R: A Language and Environment for Statistical Computing; ver. 4.0.2 (2020-06-22): Taking Off Again; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Lumley, T. Analysis of complex survey samples. J. Stat. Softw. 2004, 9, 1–19. [Google Scholar] [CrossRef]
- Freedman Ellis, G.; Schneider, B. ‘dplyr’-Like Syntax for Summary Statistics of Survey data, ver. 1.0.0. 2020. Available online: https://CRAN.R-project.org/package=srvyr (accessed on 21 January 2021).
- Agresti, A. An Introduction to Categorical Data Analysis; John Wiley & Sons, Inc.: New York, NY, USA, 1996. [Google Scholar]
- Pollard, J.; Dunn, S. FIA Quality Assurance; U.S. Department of Agriculture, Forest Service; 2021. Available online: https://www.fia.fs.usda.gov/library/fact-sheets/data-collections/QA.pdf (accessed on 26 September 2022).
- Forest Service. Field Instructions for the Annual Inventory of Alaska; U.S. Department of Agriculture Forest Service, Pacific Northwest Research Station, Forest Inventory and Analysis Resource Monitoring and Assessment Program: Portland, OR, USA, 2019. Available online: https://www.fs.usda.gov/pnw/documents-and-media/2019-pnw-fia-alaska-field-manual (accessed on 9 August 2022).
- Forest Service. Field Instructions for the Annual Inventory of California, Oregon, and Washington; U.S. Department of Agriculture Forest Service, Pacific Northwest Research Station, Forest Inventory and Analysis Resource Monitoring and Assessment Program: Portland, OR, USA, 2019. Available online: https://www.fs.usda.gov/pnw/documents-and-media/2019-pnw-fia-ca-or-wa-field-manual (accessed on 9 August 2022).
- Camarda, C.G.; Eilers, P.H.C.; Gampa, J. Modelling trends in digit preference patterns. J. Roy. Stat. Soc. C—App. 2017, 66, 893–918. [Google Scholar] [CrossRef]
- Krosnick, J.A. Response strategies for coping with cognitive demands of attitude measures in surveys. Appl. Cogn. Psych. 1991, 5, 213–236. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Hahn, J.T.; Hefty, G.J.; Van Cleve, J.R. Variation in forest inventory field measurements. Can. J. For. Res. 1994, 24, 1766–1770. [Google Scholar] [CrossRef]
- Westfall, J.A. Differences in computed individual-tree volumes caused by differences in field measurements. North. J. Appl. For. 2008, 25, 195–201. [Google Scholar] [CrossRef]
- Nelson, M.D.; Riitters, K.H.; Coulston, J.W.; Domke, G.M.; Greenfield, E.J.; Langner, L.L.; Nowak, D.J.; O’Dea, C.B.; Oswalt, S.N.; Reeves, M.C.; et al. Defining the United States Land Base: A Technical Document Supporting the USDA Forest Service 2020 RPA Assessment; Gen. Tech. Rep. NRS-191; U.S. Department of Agriculture, Forest Service, Northern Research Station: Madison, WI, USA, 2020. [CrossRef]
- Dooley, K. Woodlands. In Forest Resources of the United States, 2017: A Technical Document Supporting the Forest Service 2020 RPA assessment; WO-GTR-97; Oswalt, S.N., Smith, W.B., Miles, P.D., Pugh, S.A., Eds.; U.S. Department of Agriculture, Forest Service, Washington Office: Washington, DC, USA, 2019; pp. 13–16. [Google Scholar] [CrossRef]
- Beaman, J.; Grenier, M. Statistical tests and measures for the presence and influence of digit preference. In Proceedings of the 1997 Northeastern Recreation Research Symposium, Bolton Landing, NY, USA, 6–9 April 1997; Vogelsong, H.G., Ed.; U.S. Department of Agriculture Forest Service, Northeastern Research Station: Radnor, PA, USA, 1998. NE-GTR-241. pp. 44–50. [Google Scholar]
- Herlambang, M.B.; Taatgen, N.A.; Cnossen, F. The role of motivation as a factor in mental fatigue. Hum. Factors 2019, 61, 1171–1185. [Google Scholar] [CrossRef] [PubMed]
- Van der Linden, D.; Frese, M.; Meijman, T.F. Mental fatigue and the control of cognitive processes: Effects on perseveration and planning. Acta Psychol. 2002, 113, 45–65. [Google Scholar] [CrossRef]
- Bowen, J.; Hinze, A.; Griffiths, C. Investigating real-time monitoring of fatigue indicators of New Zealand forestry workers. Accident Anal. Prev. 2019, 126, 122–141. [Google Scholar] [CrossRef] [PubMed]
- Pilcher, J.J.; Nadler, E.; Busch, C. Effects of hot and cold temperature exposure on performance: A meta-analytic review. Ergonomics 2002, 45, 682–698. [Google Scholar] [CrossRef]
- Beaman, J.; Vaske, J.J.; Donnelly, M.P.; Manfredo, M.J. Individual versus aggregate measures of digit preference. Hum. Dimens. Wildl. 1997, 2, 71–80. [Google Scholar] [CrossRef]

| Attribute | Region | Plots | Observations | P0,5 | LCL | UCL |
|---|---|---|---|---|---|---|
| Cull | Interior West | 1729 | 15,672 | 0.44 | 0.41 | 0.48 |
| Northern | 3878 | 17,647 | 0.30 | 0.28 | 0.31 | |
| Pacific Northwest | 1249 | 6803 | 0.59 | 0.56 | 0.62 | |
| Southern | 6245 | 42,779 | 0.55 | 0.53 | 0.56 | |
| Diameter | Interior West | 2215 | 58,445 | 0.21 | 0.21 | 0.21 |
| Northern | 4826 | 154,114 | 0.22 | 0.21 | 0.22 | |
| Pacific Northwest | 1736 | 56,689 | 0.21 | 0.21 | 0.22 | |
| Southern | 7427 | 235,078 | 0.22 | 0.21 | 0.22 | |
| Height | Interior West | 2215 | 58,445 | 0.21 | 0.20 | 0.21 |
| Northern | 4826 | 154,114 | 0.24 | 0.24 | 0.24 | |
| Pacific Northwest | 1736 | 31,818 | 0.22 | 0.22 | 0.23 | |
| Southern | 7427 | 235,074 | 0.21 | 0.21 | 0.21 | |
| Seedling count | Interior West | 398 | 662 | 0.28 | 0.23 | 0.33 |
| Northern | 1505 | 2680 | 0.19 | 0.17 | 0.21 | |
| Pacific Northwest | 388 | 708 | 0.17 | 0.14 | 0.21 | |
| Southern | 1100 | 1610 | 0.20 | 0.17 | 0.23 |
| Region | ||||||
|---|---|---|---|---|---|---|
| Parameter | Factor | xia | IW | Northern | PNW | Southern |
| α | Intercept | −0.53 *** | −0.94 *** | 1.20 *** | −0.21 *** | |
| (0.15) | (0.03) | (0.11) | (0.03) | |||
| β1 | Tree status | Standing dead | 1.27 *** | −1.42 * | −1.43 *** | 1.25 *** |
| (0.09) | (0.58) | (0.12) | (0.06) | |||
| β2 | Treetop status | Broken treetop | 0.55 *** | 0.65 *** | 0.03 | 0.64 *** |
| (0.08) | (0.06) | (0.12) | (0.05) | |||
| β3 | Species class | Softwood | −0.63 *** | 0.10 | −0.03 | −0.31 *** |
| (0.12) | (0.08) | (0.10) | (0.05) | |||
| β4 | Species type | Woodland | 0.04 | – | – | 2.00 *** |
| (0.10) | – | – | (0.15) | |||
| Region | ||||||
|---|---|---|---|---|---|---|
| Parameter | Factor | xia | IW | Northern | PNW | Southern |
| α | Intercept | −1.35 *** | −1.22 *** | −1.24 *** | −1.23 *** | |
| (0.04) | (0.01) | (0.04) | (0.01) | |||
| β1 | Method | Estimated | 0.25 * | 0.76 *** | 0.40 *** | 0.76 *** |
| (0.11) | (0.08) | (0.08) | (0.05) | |||
| β2 | Method | Different location | 0.03 | −0.15 | −0.01 | −0.04 |
| (0.04) | (0.09) | (0.05) | (0.03) | |||
| β3 | Diameter point | Above BH | 0.09 | 0.02 | 0.04 | 0.01 |
| (0.05) | (0.02) | (0.05) | (0.02) | |||
| β4 | Diameter point | Below BH | −0.02 | −0.04 | 0.05 | −0.09 |
| (0.20) | (0.03) | (0.11) | (0.07) | |||
| β5 | Diameter point | Root collar | −0.01 | −0.04 | −0.14 | 0.06 |
| (0.02) | (0.21) | (0.16) | (0.04) | |||
| β6 | Tree status | Standing dead | 0.02 | −0.01 | 0.03 | 0.05 * |
| (0.03) | (0.02) | (0.03) | (0.02) | |||
| β7 | Species class | Softwood | 0.06 | −0.01 | −0.02 | −0.02 |
| (0.03) | (0.01) | (0.03) | (0.01) | |||
| β8 | Stem size | Tree b | −0.03 | −0.09 *** | −0.09 ** | −0.09 *** |
| (0.03) | (0.02) | (0.03) | (0.01) | |||
| Region | ||||||
|---|---|---|---|---|---|---|
| Parameter | Factor | xia | IW | Northern | PNW | Southern |
| α | Intercept | −1.31 *** | −1.33 *** | −1.25 *** | −1.41 *** | |
| (0.04) | (0.06) | (0.04) | (0.01) | |||
| β1 | Method | Estimated | 0.09 | 0.15 *** | 0.10 ** | 0.08 * |
| (0.05) | (0.02) | (0.04) | (0.03) | |||
| β2 | Species type | Woodland species | −0.07 ** | −0.19 | −0.22 | −0.07 |
| (0.02) | (0.17) | (0.17) | (0.04) | |||
| β3 | Tree status | Standing dead | −0.01 | −0.13 *** | −0.03 | −0.06 |
| (0.03) | (0.02) | (0.03) | (0.03) | |||
| β4 | Species class | Softwood | 0.00 c | −0.07 *** | −0.10 ** | −0.01 |
| (0.03) | (0.02) | (0.04) | (0.01) | |||
| β5 | Stem size | Tree b | −0.01 | 0.20 *** | 0.08 * | 0.11 *** |
| (0.03) | (0.02) | (0.04) | (0.02) | |||
| Region | ||||||
|---|---|---|---|---|---|---|
| Parameter | Factor | xi a | IW | Northern | PNW | Southern |
| α | Intercept | −0.47 | −1.11 *** | −1.54 *** | −0.88 ** | |
| (0.29) | (0.22) | (0.25) | (0.32) | |||
| β1 | Stand size | Medium | −0.63 * | 0.02 | 0.17 | −0.51 |
| (0.28) | (0.15) | (0.43) | (0.27) | |||
| β2 | Stand size | Large | −0.53 * | −0.08 | −0.17 | −0.21 |
| (0.22) | (0.13) | (0.29) | (0.16) | |||
| β3 | Stand origin | Artificial | – | 0.06 | – | 0.04 |
| – | (0.25) | – | (0.20) | |||
| β4 | Disturbance | Disturbed | 0.01 | 0.06 | 0.11 | 0.41 ** |
| (0.22) | (0.12) | (0.22) | (0.16) | |||
| β5 | Treatment | Treated | – | 0.03 | 0.36 | −0.17 |
| – | (0.15) | (0.50) | (0.20) | |||
| β6 | Water depth | >3 cm | 0.33 | – | – | 0.73 ** |
| (0.43) | – | – | (0.26) | |||
| β7 | Water depth | 3–30 cm | – | 0.03 | – | – |
| – | (0.15) | – | – | |||
| β8 | Water depth | >30 cm | – | 0.27 | – | – |
| – | (0.25) | – | – | |||
| β9 | Owner group | Non-FS federal | 0.00 b | 0.08 | −0.21 | −0.51 |
| (0.33) | (0.36) | (0.35) | (0.37) | |||
| β10 | Owner group | State/local gov. | 0.29 | −0.21 | −0.13 | 0.12 |
| (0.57) | (0.21) | (0.29) | (0.34) | |||
| β11 | Owner group | Private | −0.17 | −0.42 | −0.36 | −0.47 |
| (0.26) | (0.19) | (0.33) | (0.28) | |||
| β12 | Physiography | Hydric | – | −0.12 | 0.08 | 0.64 |
| – | (0.22) | (0.30) | (0.34) | |||
| β13 | Physiography | Xeric | 0.06 | 0.01 | −0.06 | 0.23 |
| (0.23) | (0.20) | (0.41) | (0.25) | |||
| β14 | Slope | 0.00 b | −0.00 b | 0.00 b | −0.02 ** | |
| (0.00 b) | (0.00 b) | (0.01) | (0.01) | |||
| Region | ||||||
|---|---|---|---|---|---|---|
| Parameter | Factor | xi a | IW | Northern | PNW | Southern |
| α | Intercept | −0.75 ** | −1.23 *** | −0.84 *** | −0.53 * | |
| (0.26) | (0.19) | (0.25) | (0.23) | |||
| β1 | Stand size | Medium | −0.33 | 0.10 | −1.22 ** | −0.17 |
| (0.28) | (0.12) | (0.41) | (0.20) | |||
| β2 | Stand size | Large | 0.15 | 0.08 | 0.13 | −0.27 |
| (0.21) | (0.11) | (0.22) | (0.15) | |||
| β3 | Stand origin | Artificial | – | 0.24 | – | 0.14 |
| – | (0.23) | – | (0.15) | |||
| β4 | Disturbance | Disturbed | −0.12 | 0.03 | 0.22 | −0.19 |
| (0.21) | (0.10) | (0.18) | (0.13) | |||
| β5 | Treatment | Treated | – | 0.01 | −0.10 | 0.13 |
| – | (0.14) | (0.48) | (0.17) | |||
| β6 | Water depth | >3 cm | 0.25 | – | – | 0.52 * |
| (0.36) | – | – | (0.26) | |||
| β7 | Water depth | 3–30 cm | – | 0.21 | – | – |
| – | (0.13) | – | – | |||
| β8 | Water depth | >30 cm | – | 0.10 | – | – |
| – | (0.23) | – | – | |||
| β9 | Owner group | Non-FS federal | −0.26 | 0.30 | 0.12 | −0.19 |
| (0.34) | (0.35) | (0.27) | (0.30) | |||
| β10 | Owner group | State/local gov. | −0.06 | −0.07 | −0.30 | 0.08 |
| (0.40) | (0.18) | (0.24) | (0.27) | |||
| β11 | Owner group | Private | 0.00 b | 0.11 | 0.14 | −0.18 |
| (0.22) | (0.17) | (0.24) | (0.18) | |||
| β12 | Physiography | Hydric | – | 0.17 | −0.44 | −0.57 |
| – | (0.17) | (0.23) | (0.33) | |||
| β13 | Physiography | Xeric | −0.29 | 0.11 | 0.11 | 0.25 |
| (0.22) | (0.17) | (0.35) | (0.19) | |||
| β14 | Slope | −0.01 | 0.01 | 0.00 b | 0.00 b | |
| (0.00 b) | (0.00 b) | (0.00 b) | (0.00 b) | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Randolph, K.C. Number Preference as a Source of Measurement Error in the U.S. National Forest Inventory. Forests 2023, 14, 459. https://doi.org/10.3390/f14030459
Randolph KC. Number Preference as a Source of Measurement Error in the U.S. National Forest Inventory. Forests. 2023; 14(3):459. https://doi.org/10.3390/f14030459
Chicago/Turabian StyleRandolph, KaDonna C. 2023. "Number Preference as a Source of Measurement Error in the U.S. National Forest Inventory" Forests 14, no. 3: 459. https://doi.org/10.3390/f14030459
APA StyleRandolph, K. C. (2023). Number Preference as a Source of Measurement Error in the U.S. National Forest Inventory. Forests, 14(3), 459. https://doi.org/10.3390/f14030459






