Study of the Movement of Chips during Pine Wood Milling
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Theoretical Approach
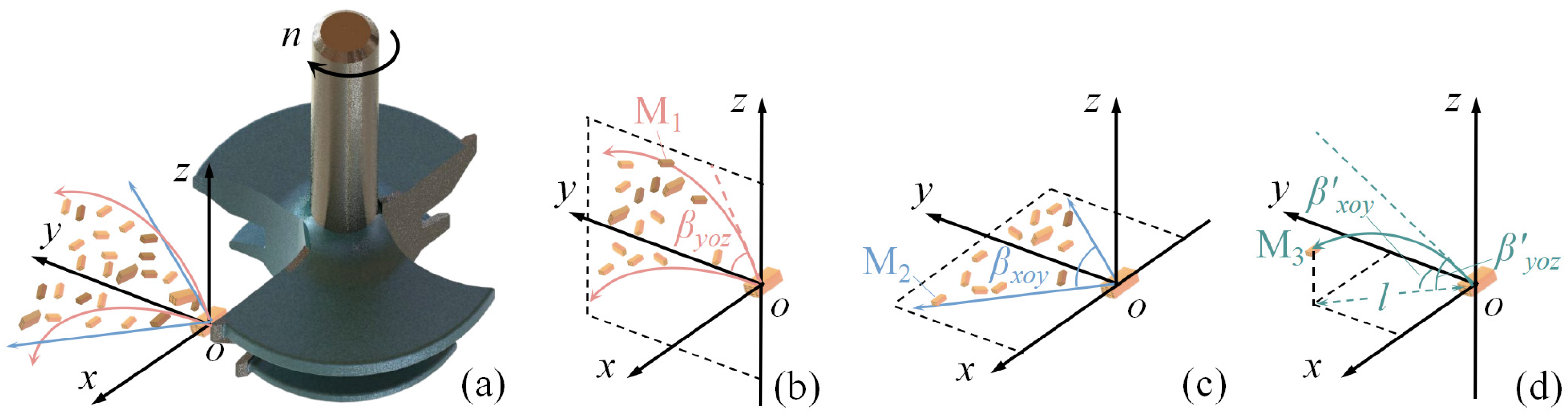
2.2.1. Analysis of Chip Morphology
2.2.2. Modeling of Chip Boundary Surface f(x,y)
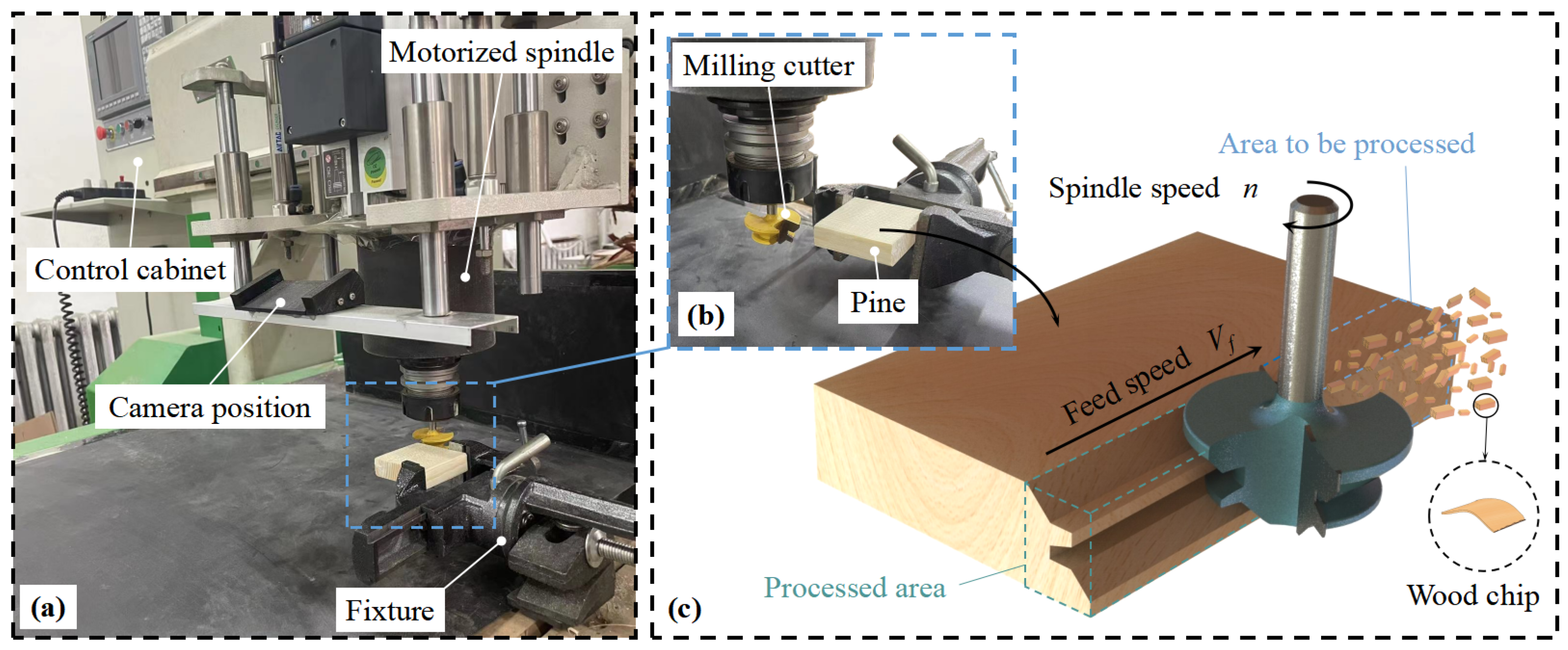
2.3. Methods
3. Results and Discussion
3.1. Effect of Milling Parameters on the Orthogonal Diffusion Angle βyoz
3.2. Effect of Milling Parameters on the Top View Diffusion Angle βxoy
3.3. Effect of Milling Parameters on the Average Chip Size La
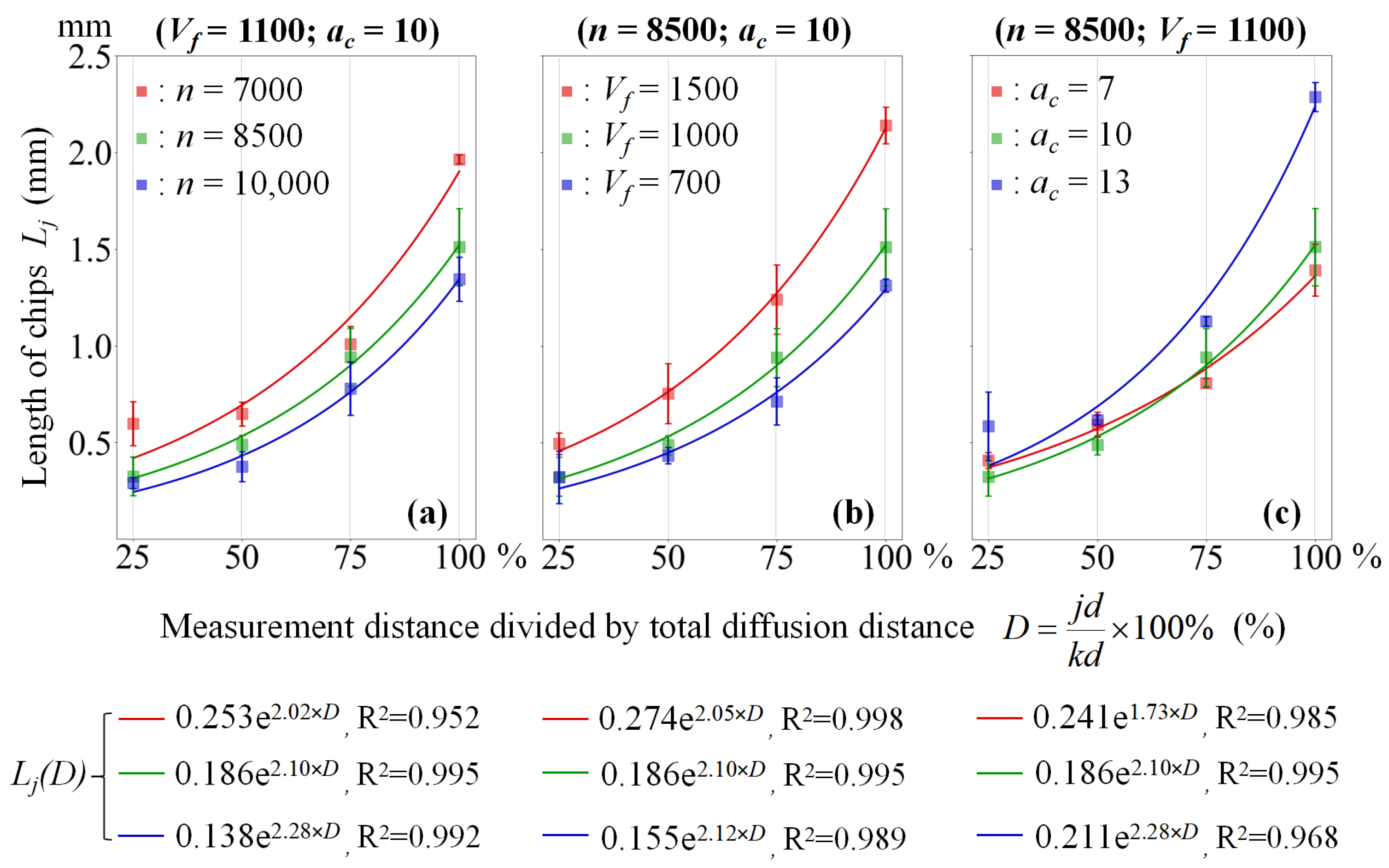
3.4. Distribution State of Chip Size
3.5. Solution of Chip Boundary Surface Model f(x,y)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Asdrubali, F.; Ferracuti, B.; Lombardi, L.; Guattari, C.; Evangelisti, L.; Grazieschi, G. A review of structural, thermo-physical, acoustical, and environmental properties of wooden materials for building applications. Build. Environ. 2017, 114, 307–332. [Google Scholar] [CrossRef]
- Magagnotti, N.; Nannicini, C.; Sciarra, G.; Spinelli, R.; Volpi, D. Determining the Exposure of Chipper Operators to Inhalable Wood Dust. Ann. Occup. Hyg. 2013, 57, 784–792. [Google Scholar]
- Shchelokov, Y.M. Upgrading designs of cyclone dust cleaner apparatuses. Russ. J. Non-Ferr. Met. 2008, 49, 478–479. [Google Scholar] [CrossRef]
- Kamata, H.; Kanauchi, T. Analysis of roughness of cutting surface with NC router (influence of grain direction in solid wood). Trans. Jpn. Soc. Mech. Eng. Ser. C. 1994, 60, 303. [Google Scholar] [CrossRef]
- Ohuchi, T.; Murase, Y. Milling of wood and wood-based materials with a computerized numerically controlled router V: Development of adaptive control grooving system corresponding to progression of tool wear. J. Wood Sci. 2006, 2, 395–398. [Google Scholar] [CrossRef]
- Budak, E.; Alintas, Y. Modeling and control of spindles radial axes for active thermal compensation. J. Manuf. Sci. Eng. 2005, 127, 77774. [Google Scholar]
- Stan, D.A.; Nezam, S.A.; Danelsson, M.; Valente, A. Chip morphology and chip formation mechanisms in orthogonal high-speed machining of Inconel 718. Procedia CIRP 2014, 16, 61–66. [Google Scholar]
- Varga, M.; Csanady, E.; Nemeth, G.; Nemeth, S. Aerodynamic assessment of the extraction attachment of cnc processing machinery. Mater. Sci. 2006, 51, 49–62. [Google Scholar]
- Barański, J.; Jewartowski, M.; Wajs, J.; Pikala, T. Experimental analysis of chip removing system in circular sawing machine. Trieskove Beztrieskove Obrabanie Dreva. 2016, 10, 25–29. [Google Scholar]
- Dong, Y.; Bouali, A.; Mechbal, N.; Bleron, L.; Raharijaona, T. Towards wood dust collection during robotic grooving. In Proceedings of the 10th International Conference on Systems and Control (ICSC), Marseille, France, 23–25 November 2022; pp. 477–481. [Google Scholar]
- Goli, G.; Fioravanti, M.; Marchal, R.; Uzielli, L. Up-milling and down-milling wood with different grain orientations theoretical background and general appearance of the chips. Eur. J. Wood Wood Prod. 2009, 67, 257–263. [Google Scholar] [CrossRef]
- Kiliç, M.; Burdurlu, E.; Aslan, S.; Altun, S.; Tümerdem, O. The effect of surface roughness on tensile strength of the medium density fiberboard (MDF) overlaid with polyvinyl chloride (PVC). Mater. Des. 2009, 30, 4580–4583. [Google Scholar] [CrossRef]
- Darmawan, W.; Azhari, M.; Rahayu, I.S.; Nandika, D.; Dumasari, L.; Malela, I.; Nishio, S. The chips generated during up-milling and down-milling of pine wood by helical router bits. J. Indian Acad. Wood Sci. 2018, 15, 9–12. [Google Scholar] [CrossRef]
- Darmawan, W.; Tanaka, C. Discrimination of coated carbide tools wear by the features extracted from parallel force and noise level. Ann. For. Sci. 2004, 61, 731–736. [Google Scholar] [CrossRef]
- Ekevad, M.; Marklund, B.; Gren, P. Wood-chip formation in circular saw blades studied by high-speed photography. Wood Mater. Sci. Eng. 2012, 7, 115–119. [Google Scholar] [CrossRef]
- Goli, G.; Fioravanti, M.; Marchal, R.; Uzielli, L.; Busoni, S. Up-milling and down-milling wood with different grain orientations—The cutting forces behaviour. Eur. J. Wood Wood Prod. 2010, 68, 385–395. [Google Scholar] [CrossRef]
- Orlowski, K.A.; Ochrymiuk, T.; Atkins, A.; Chuchala, D. Application of fracture mechanics for energetic effects predictions while wood sawing. Wood Sci. Technol. 2013, 47, 949–963. [Google Scholar] [CrossRef]
- Calzada, K.A.; Kapoor, S.G.; DeVor, R.E.; Samuel, J.; Srivastava, A.K. Modeling and interpretation of fiber orientation-based failure mechanisms in machining of carbon fiber-reinforced polymer composites. J. Manuf. Process. 2012, 14, 141–149. [Google Scholar] [CrossRef]
- Wei, W.; Cong, R.; Xue, T.; Abraham, A.D.; Yang, C. Surface Roughness and Chip Morphology of Wood Plastic Composites Manufactured via High-speed Milling. Bioresources 2021, 16, 5733–5745. [Google Scholar] [CrossRef]
- Pengcheng, D.; Bo, C.; Jinge, G.; Kun, C.; Chengfei, Z.; Yaoyu, C.; Chenyang, X.; Yongqiu, Z. 3D Radiation Temperature Measurement of Dynamic Combustion Field Based on Multi-CCD Synchronous Coupling. Infrared Laser Eng. 2022, 51, 51–60. (In Chinese) [Google Scholar]
- Wang, Z.; Wang, G.; Xu, M.; Hao, H.; Chang, Q. Preparation of dithiocarboxyl amino-methylated polyacrylamide optimized by response surface methodology. China Environ. Sci. 2017, 37, 2114–2121. (In Chinese) [Google Scholar]
- Ogun, P.S.; Jackson, M.R.; Parkin, R.M. Mechatronic approach towards surface quality improvement in rotary wood machining. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2013, 1227, 1266–1276. [Google Scholar] [CrossRef]
- Ispas, M.; Gurau, L.; Campean, M.; Hacibektasoglu, M.; Racasan, S. Milling of Heat-Treated Beech Wood (Fagus sylvatica L.) and Analysis of Surface Quality. Bioresources 2017, 11, 9095–9111. [Google Scholar] [CrossRef]
- Jones, P.D.; Fox, T.R. Wood density in Pinus taeda x Pinus rigida and response 10 years after thinning in Virginia. For. Prod. J. 2007, 57, 70–73. [Google Scholar]








| Density (kg/m3) | Compressive Strength (MPa) | Bending Strength (MPa) | Tensile Strength (MPa) | Shear Strength (MPa) | Modulus of Elasticity (MPa) | Poisson’s Ratio | Coefficient of Friction |
|---|---|---|---|---|---|---|---|
| 420 | 50 | 87 | 104 | 10 | 12,000 | 0.65 | 0.35 |
| Alpha | Spindle Speed n (r/min) | Feeding Speed Vf (mm/min) | Cutting Depth ac (mm) |
|---|---|---|---|
| +1.68 | 11,000 | 1770 | 15 |
| +1 | 10,000 | 1500 | 13 |
| 0 | 8500 | 1100 | 10 |
| −1 | 7000 | 700 | 7 |
| −1.68 | 6000 | 430 | 5 |
| No. | Factors | Indicators | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n | Vf | ac | βyoz | βxoy | La1 | La2 | La3 | La4 | La | |
| (r/min) | (mm/min) | (mm) | (°) | (°) | (mm) | (mm) | (mm) | (mm) | (mm) | |
| 1 | 7000 | 700 | 7 | 25 | 134 | 0.382 | 0.692 | 1.031 | 1.812 | 0.9792 |
| 2 | 10,000 | 700 | 13 | 31 | 107 | 0.484 | 0.541 | 0.771 | 1.396 | 0.7980 |
| 3 | 10,000 | 1500 | 13 | 73 | 135 | 0.322 | 0.559 | 1.82 | 1.9975 | 1.1746 |
| 4 * | 8500 | 1100 | 10 | 44 | 120 | 0.258 | 0.462 | 1.048 | 1.51 | 0.8195 |
| 5 | 8500 | 430 | 10 | 26 | 115 | 0.237 | 0.457 | 0.855 | 1.251 | 0.7000 |
| 6 | 11,000 | 1100 | 10 | 32 | 114 | 0.356 | 0.549 | 0.788 | 1.455 | 0.7870 |
| 7 * | 8500 | 1100 | 10 | 40 | 113 | 0.354 | 0.513 | 0.823 | 1.404 | 0.7735 |
| 8 | 7000 | 1500 | 13 | 73 | 140 | 0.514 | 1.139 | 1.793 | 2.538 | 1.4960 |
| 9 | 7000 | 700 | 13 | 28 | 114 | 0.381 | 0.563 | 1.168 | 2.47 | 1.1455 |
| 10 * | 8500 | 1100 | 10 | 43 | 115 | 0.295 | 0.488 | 0.941 | 1.455 | 0.7948 |
| 11 | 10,000 | 700 | 7 | 36 | 141 | 0.296 | 0.593 | 0.855 | 1.105 | 0.7123 |
| 12 | 8500 | 1770 | 10 | 78 | 152 | 0.542 | 0.771 | 1.357 | 2.354 | 1.2560 |
| 13 | 7000 | 1500 | 7 | 74 | 94 | 0.319 | 0.469 | 0.775 | 1.63 | 0.7983 |
| 14 | 8500 | 1100 | 15. | 45 | 137 | 0.395 | 0.668 | 0.888 | 3.11 | 1.2653 |
| 15 | 8500 | 1100 | 5 | 41 | 93 | 0.341 | 0.635 | 0.918 | 1.903 | 0.9493 |
| 16 * | 8500 | 1100 | 10 | 44 | 119 | 0.324 | 0.474 | 0.914 | 1.427 | 0.7848 |
| 17 * | 8500 | 1100 | 10 | 45 | 110 | 0.289 | 0.497 | 0.911 | 1.455 | 0.7880 |
| 18 | 10,000 | 1500 | 7 | 44 | 117 | 0.362 | 0.714 | 0.727 | 1.378 | 0.7953 |
| 19 * | 8500 | 1100 | 10 | 50 | 113 | 0.233 | 0.485 | 0.944 | 1.457 | 0.7798 |
| 20 | 6000 | 1100 | 10 | 86 | 105 | 0.291 | 0.567 | 1.4853 | 1.919 | 1.0656 |
| 21 | 10,000 | 1100 | 10 | 33 | 115 | 0.291 | 0.375 | 0.779 | 1.345 | 0.6975 |
| 22 | 7000 | 1100 | 10 | 44 | 110 | 0.597 | 0.648 | 1.008 | 1.964 | 1.0543 |
| 23 | 8500 | 1500 | 10 | 65 | 143 | 0.496 | 0.755 | 1.241 | 2.14 | 1.1580 |
| 24 | 8500 | 700 | 10 | 36 | 131 | 0.325 | 0.434 | 0.715 | 1.314 | 0.6970 |
| 25 | 8500 | 1100 | 13 | 48 | 142 | 0.585 | 0.618 | 1.127 | 2.285 | 1.1538 |
| 26 | 8500 | 1100 | 7 | 63 | 105 | 0.409 | 0.594 | 0.809 | 1.391 | 0.8008 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 5990.94 | 6 | 998.49 | 22.04 | <0.0001 |
| A–n | 1458 | 1 | 1458 | 32.19 | <0.0001 |
| B–Vf | 3922.62 | 1 | 3922.62 | 86.6 | <0.0001 |
| AB | 242 | 1 | 242 | 5.34 | 0.0378 |
| A2 | 297.09 | 1 | 297.09 | 6.56 | 0.0237 |
| B2 | 60.76 | 1 | 60.76 | 1.34 | 0.2676 |
| AB2 | 654.53 | 1 | 654.53 | 14.45 | 0.0022 |
| Residual | 588.86 | 13 | 45.3 | - | - |
| Lack of Fit | 535.53 | 8 | 66.94 | 6.28 | 0.0592 |
| Pure Error | 53.33 | 5 | 10.67 | - | - |
| Cor Total | 6579.8 | 19 | - | - | - |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 4021.77 | 8 | 502.72 | 8.19 | 0.0011 |
| A–n | 80.4 | 1 | 80.4 | 1.31 | 0.2767 |
| B–Vf | 199.72 | 1 | 199.72 | 3.25 | 0.0986 |
| C–ac | 968 | 1 | 968 | 15.77 | 0.0022 |
| AC | 220.5 | 1 | 220.5 | 3.59 | 0.0846 |
| BC | 1740.5 | 1 | 1740.5 | 28.36 | 0.0002 |
| A2 | 26.33 | 1 | 26.33 | 0.4291 | 0.5259 |
| B2 | 742.04 | 1 | 742.04 | 12.09 | 0.0052 |
| A2C | 463.85 | 1 | 463.85 | 7.56 | 0.0189 |
| Residual | 675.03 | 11 | 61.37 | - | - |
| Lack of Fit | 601.03 | 6 | 100.17 | 6.77 | 0.0566 |
| Pure Error | 74 | 5 | 14.8 | - | - |
| Cor Total | 4696.8 | 19 | - | - | - |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 0.903 | 7 | 0.129 | 19.74 | <0.0001 |
| A–n | 0.1679 | 1 | 0.1679 | 25.69 | 0.0003 |
| B–Vf | 0.1792 | 1 | 0.1792 | 27.42 | 0.0002 |
| C–ac | 0.2535 | 1 | 0.2535 | 38.79 | <0.0001 |
| AC | 0.0199 | 1 | 0.0199 | 3.04 | 0.0994 |
| BC | 0.0851 | 1 | 0.0851 | 13.02 | 0.0036 |
| B2 | 0.0514 | 1 | 0.0514 | 7.87 | 0.0159 |
| C2 | 0.1608 | 1 | 0.1608 | 24.61 | 0.0003 |
| Residual | 0.0784 | 12 | 0.0065 | - | - |
| Lack of Fit | 0.0771 | 7 | 0.011 | 42.32 | 0.06 |
| Pure Error | 0.0013 | 5 | 0.0003 | - | - |
| Cor Total | 0.9814 | 19 | - | - | - |
| No. | βyoz | βxoy | g | n | Vf | r | La | aw | dc | ρwood |
|---|---|---|---|---|---|---|---|---|---|---|
| (°) | (°) | (N/s2) | (r/min) | (mm/s) | (mm) | (mm) | (mm) | (mm) | (kg/m3) | |
| 1 | 25 | 134 | 9.8 | 7000 | 11.67 | 15 | 0.979 | 0.489 | 8.34 × 10−4 | 450 |
| 11 | 36 | 141 | 9.8 | 10,000 | 11.67 | 15 | 0.712 | 0.356 | 3.50 × 10−5 | 450 |
| 25 | 48 | 142 | 9.8 | 8500 | 18.33 | 15 | 1.154 | 2.308 | 6.47 × 10−5 | 450 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Liu, T.; Ma, Y.; Qu, W.; Ding, Y.; Zhang, T.; Song, W. Study of the Movement of Chips during Pine Wood Milling. Forests 2023, 14, 849. https://doi.org/10.3390/f14040849
Yang C, Liu T, Ma Y, Qu W, Ding Y, Zhang T, Song W. Study of the Movement of Chips during Pine Wood Milling. Forests. 2023; 14(4):849. https://doi.org/10.3390/f14040849
Chicago/Turabian StyleYang, Chunmei, Tongbin Liu, Yaqiang Ma, Wen Qu, Yucheng Ding, Tao Zhang, and Wenlong Song. 2023. "Study of the Movement of Chips during Pine Wood Milling" Forests 14, no. 4: 849. https://doi.org/10.3390/f14040849
APA StyleYang, C., Liu, T., Ma, Y., Qu, W., Ding, Y., Zhang, T., & Song, W. (2023). Study of the Movement of Chips during Pine Wood Milling. Forests, 14(4), 849. https://doi.org/10.3390/f14040849






