Estimation of Quercus Biomass in Shangri-La Based on GEDI Spaceborne Lidar Data
Abstract
:1. Introduction
2. Materials and Methods
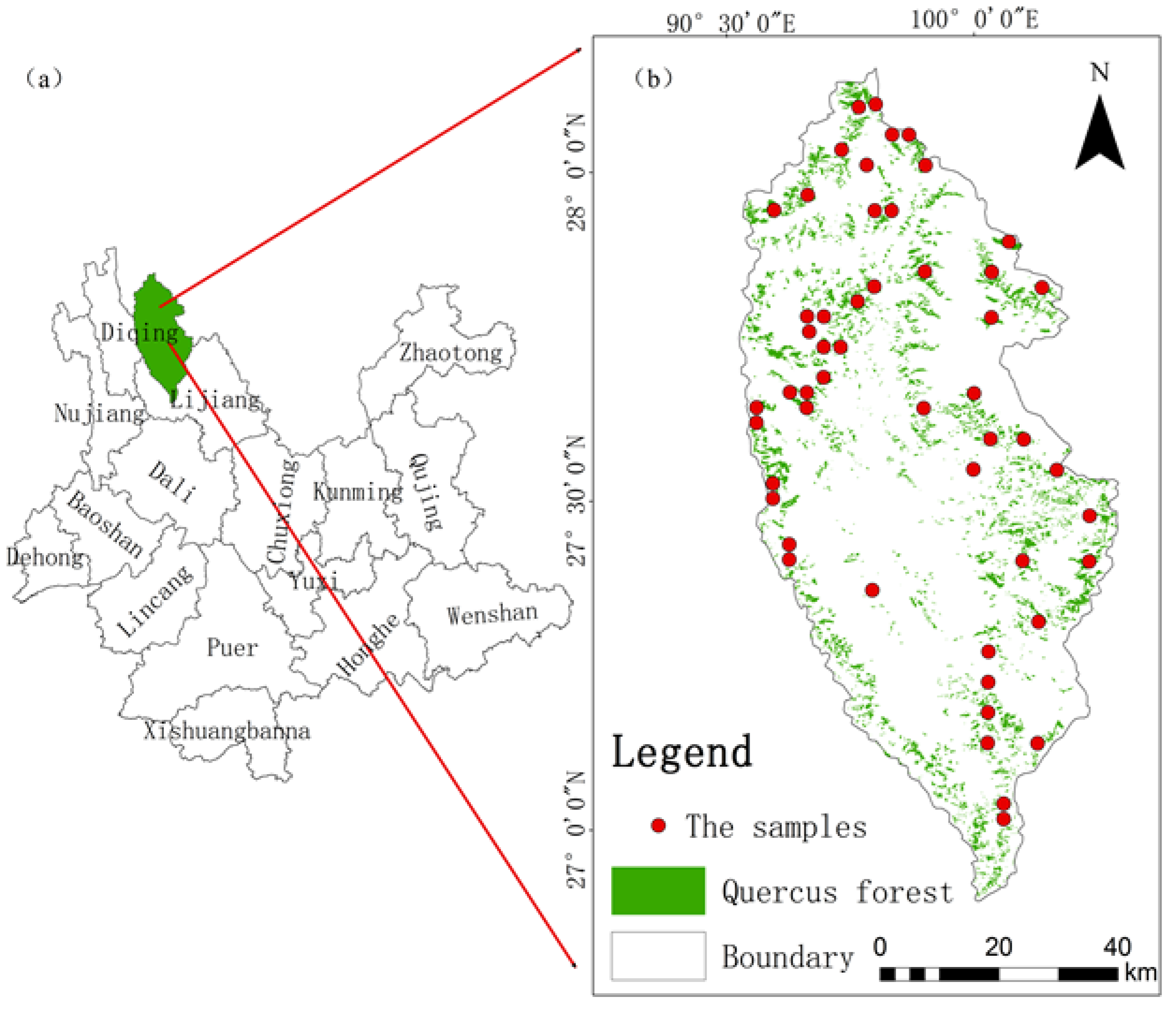
2.1. Study Area
2.2. Forest Resource Inventory Data
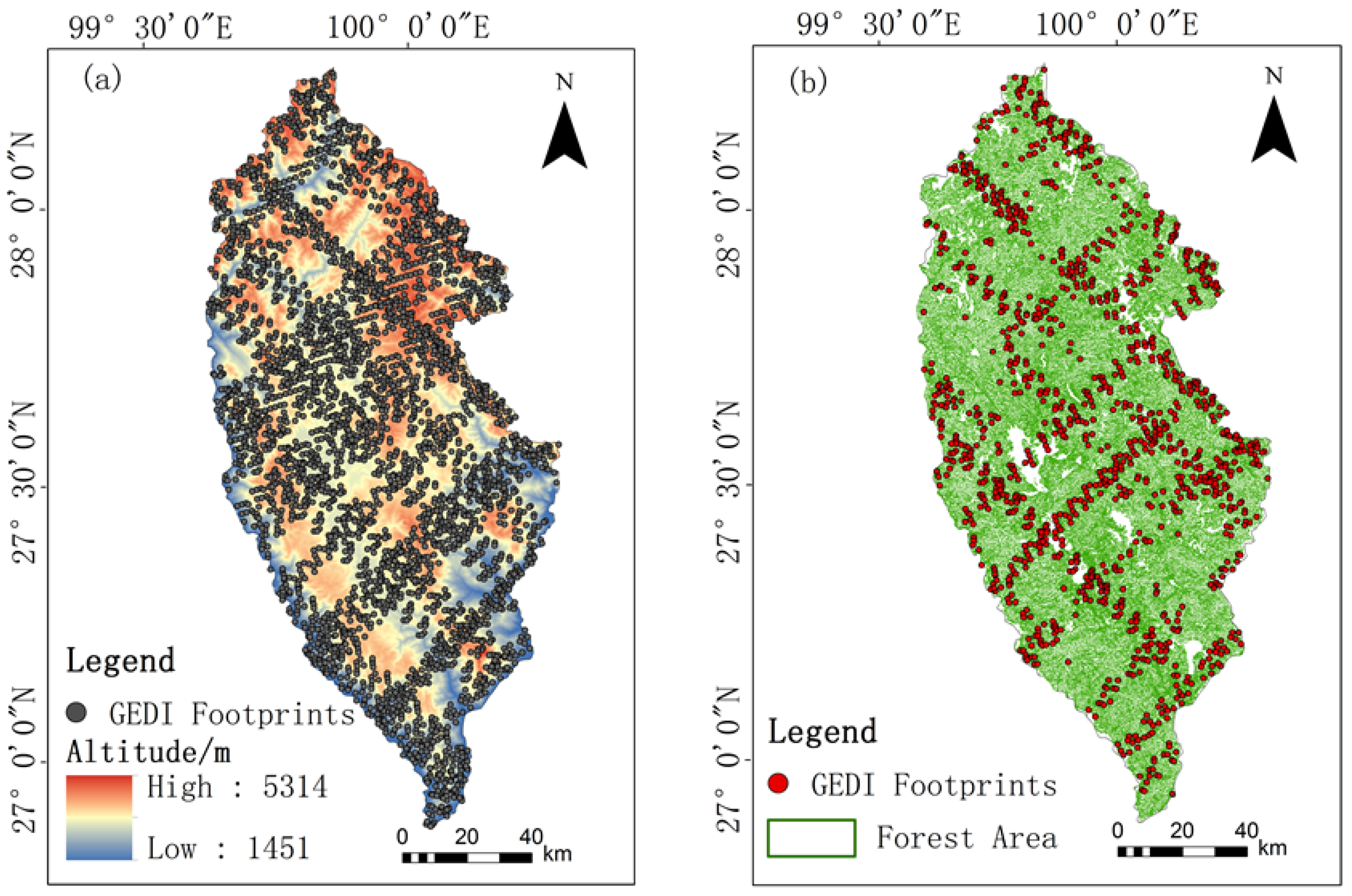
2.3. Data Acquisition and Processing of GEDI
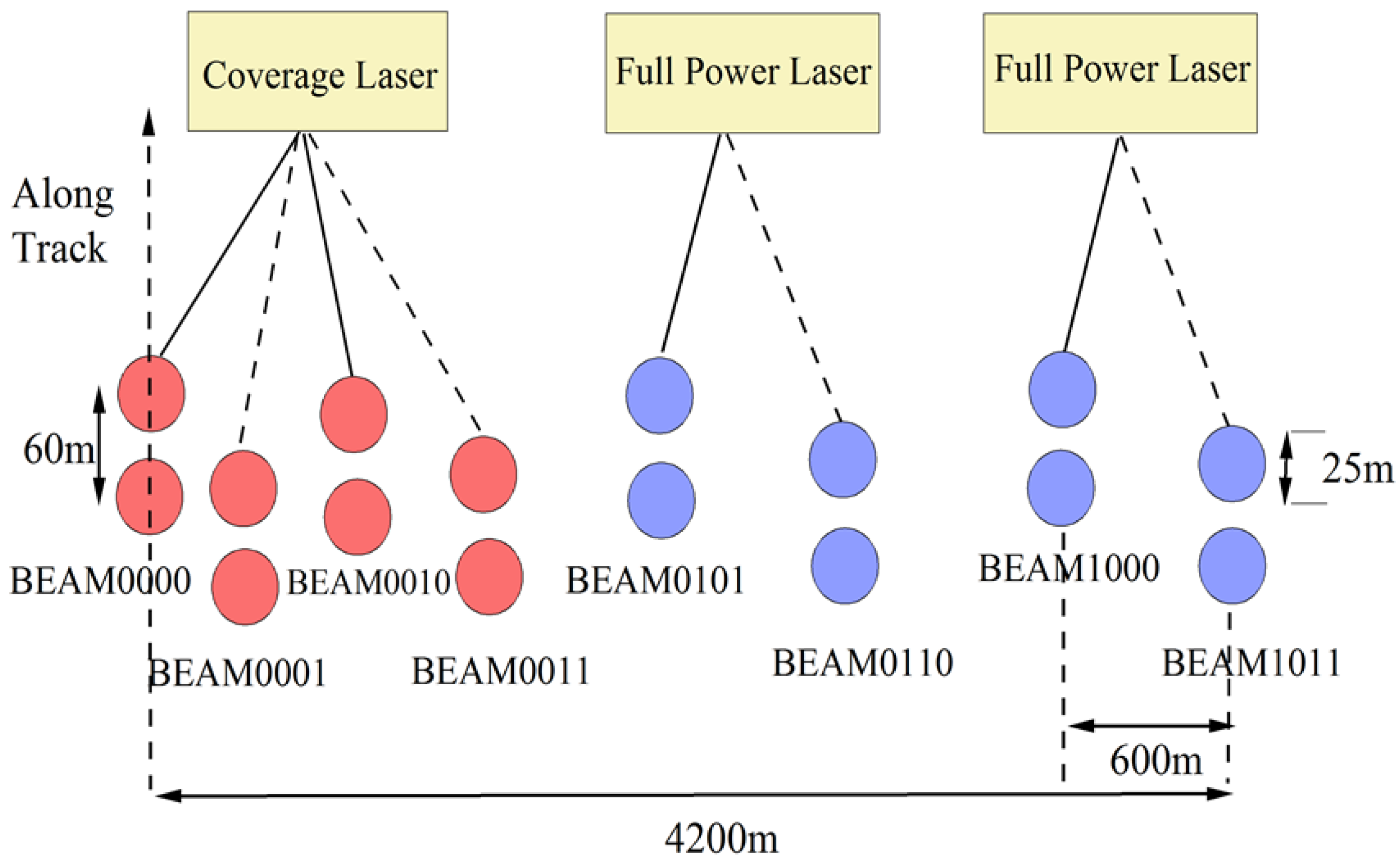
2.3.1. GEDI
2.3.2. GEDI Data Processing
- Lat_lowestmode, lon_lowestmode: Latitude and longitude can be used to find the spots’ location.
- Sensitivity: Sensitivity is greater than or equal to 0.9 indicates that the spot quality is good; thus, spots with a value less than 0.9 are deleted.
- quality_flag: A quality_flag value of 1 indicates that the laser shot meets criteria based on energy, sensitivity, amplitude, real-time surface tracking quality and difference to a DEM.
- degrade_flag: When this value is 1, it means that the state of the pointing or geolo-cated information is degraded; thus only the spots with degrade_flag = 0 is retained.
3. Methods
3.1. Geostatistical Methods
3.1.1. Variance Function
3.1.2. Kriging Interpolation
3.1.3. Evaluation of Interpolation Accuracy
3.2. Biomass Estimation Models
3.2.1. Multiple Linear Regressions
3.2.2. Support Vector Regression
3.2.3. Random Forest
3.2.4. Evaluation of Biomass Model Accuracy
4. Results
4.1. Selection of Variance Function
4.2. Validation of Interpolation Results
4.3. Variable Correlation Coefficient Matrix and Importance Analysis
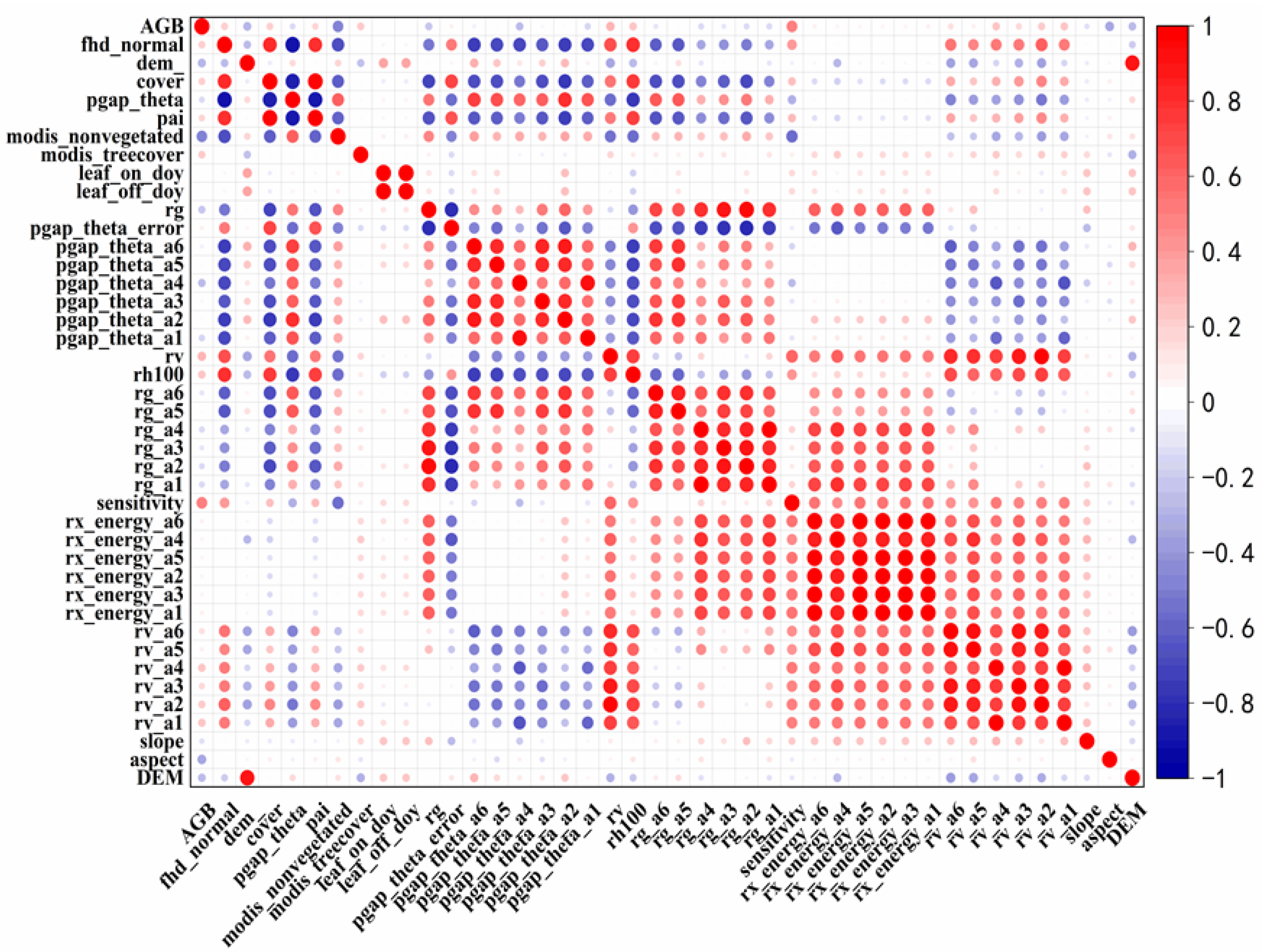
4.3.1. Correlation Analysis of Model Variables
4.3.2. Selection Results of Characteristic Variables
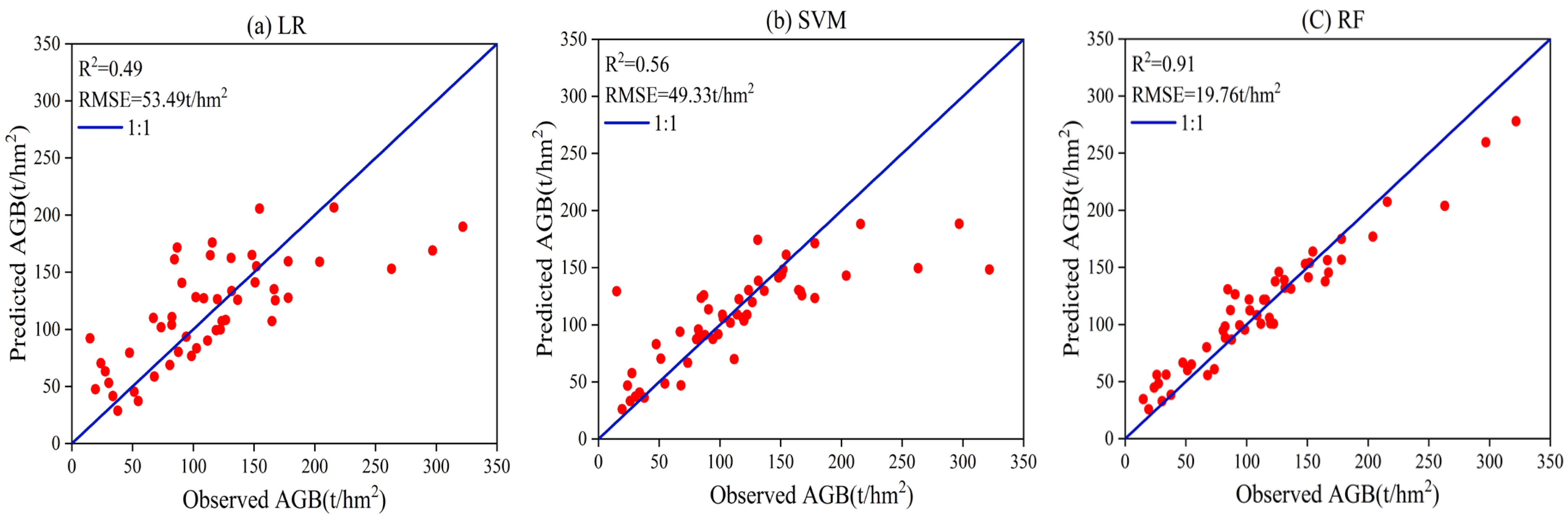
4.4. Accuracy Evaluation of Each Biomass Estimation Models
4.5. Spatial Distribution Analysis of Total Biomass
5. Discussion
5.1. Precision Analysis of Estimation Results
5.2. Analysis of the Interpolation Result
5.3. The Influence of Sample Size on Model Accuracy
5.4. Effect of Model Selection and Optimization on Estimation Accuracy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- FAO. The State of the World’s Forests 2018: Forest Pathways to Sustainable Development; United Nations: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Sandra, B. Measuring Carbon in Forests: Current Status and Future Challenges. Environ. Pollut. 2002, 116, 363–372. [Google Scholar] [CrossRef]
- Brown, S.; Gillespie, A.J.; Lugo, A.E. Biomass Estimation Methods for Tropical Forests with Applications to Forest Inventory Data. Forest Sci. 1989, 4, 881–902. [Google Scholar]
- Tuominen, S.; Eerikainen, K.; Schibalski, A.; Haakana, M.; Lehtonen, A. Mapping Biomass Variables with a Multi-Source Forest Inventory Technique. Silva Fenn. 2010, 44, 109–119. [Google Scholar] [CrossRef]
- Potapov, P.; Li, X.; Hernandez-Serna, A.; Tyukavina, A.; Hansen, M.C.; Kommareddy, A.; Pickens, A.; Turubanova, S.; Tang, H.; Silva, C.E. Mapping Global Forest Canopy Height through Integration of GEDI and Landsat Data. Remote Sens. Environ. 2021, 253, 112–165. [Google Scholar] [CrossRef]
- Liu, X.; Yang, L.; Liu, Q. Review of Forest Aboveground Biomass Inversion Methods Based on Remote Sensing Technology. Ntal. Remote Sens. Bull. 2015, 19, 62–74. (In Chinese) [Google Scholar]
- Zhao, P.; Liu, D.; Wang, G.; Wu, C.; Huang, Y.; Yu, S. Examining Spectral Reflectance Saturation in Landsat Imagery and Corresponding Solutions to Improve Forest Aboveground Biomass Estimation. Remote Sens. 2016, 8, 469. [Google Scholar] [CrossRef]
- Arévalo, P.; Baccini, A.; Woodcock, C.E.; Olofsson, P.; Walker, W.S. Continuous Mapping of Aboveground Biomass Using Landsat Time Series. Remote Sens. Environ. 2023, 288, 113–483. [Google Scholar] [CrossRef]
- Dinesh, B.I.; Frédéric, R.; Pierre, B.; Sylvie, G.; Yves, B.; David, P. Fire Disturbance Data Improves the Accuracy of Remotely Sensed Estimates of Aboveground Biomass for Boreal Forests in Eastern Canada. Remote Sens. Appl. 2017, 8, 71–82. [Google Scholar] [CrossRef]
- Zhang, J.; Rivard, B.; Sánchez-Azofeifa, A.; Castro-Esau, K. Intra-and Inter-class Spectral Variability of Tropical Tree Species at La Selva, Costa Rica: Implications for Species Identification Using HYDICE Imagery. Remote Sens. Environ. 2006, 105, 129–141. [Google Scholar] [CrossRef]
- Svein, S.; Rasmus, A.; Terje, G.; Erik, N.; Dan, J.W. Estimating Spruce and Pine Biomass with Interferometric X-band SAR. Remote Sens. Environ. 2010, 114, 2353–2360. [Google Scholar] [CrossRef]
- Atwood, D.K.; Andersen, H.-E.; Matthiss, B.; Holecz, F. Impact of Topographic Correction on Estimation of Aboveground Boreal Biomass Using Multi-temporal, L-Band Backscatter. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3262–3273. [Google Scholar] [CrossRef]
- Xi, Z.; Xu, H.; Xing, Y.; Gong, W.; Chen, G.; Yang, S. Forest Canopy Height Mapping by Synergizing ICESat-2, Sentinel-1, Sentinel-2 and Topographic Information Based on Machine Learning Methods. Remote Sens. 2022, 14, 364. [Google Scholar] [CrossRef]
- Jiang, F.; Zhao, F.; Ma, K.; Li, D.; Sun, H. Mapping the Forest Canopy Height in Northern China by Synergizing ICESat-2 with Sentinel-2 Using a Stacking Algorithm. Remote Sens. 2021, 13, 1535. [Google Scholar] [CrossRef]
- Saarela, S.; Holm, S.; Healey, S.P. Comparing Frameworks for Biomass Prediction for the Global Ecosystem Dynamics Investigation. Remote Sens. Environ. 2022, 278, 113074. [Google Scholar] [CrossRef]
- Musthafa, M.; Singh, G. Forest Above-ground Woody Biomass Estimation Using Multi-temporal Space-borne LiDAR Data in a Managed Forest at Haldwani, India. Adv. Space Res. 2022, 69, 3245–3257. [Google Scholar] [CrossRef]
- Xie, D.; Li, G.; Zhao, Y.; Yang, X.; Tang, X.; Fu, A.U.S. GEDI Space-based Laser Altimetry System and Its Applications. Space Int. 2018, 12, 39–44. (In Chinese) [Google Scholar]
- Adam, M.; Urbazaev, M.; Dubois, C.; Schmullius, C. Accuracy Assessment of GEDI Terrain Elevation and Canopy Height Estimates in European Temperate Forests: Influence of Environmental and Acquisition Parameters. Remote Sens. 2020, 12, 3948. [Google Scholar] [CrossRef]
- Hakkenberg, C.R.; Tang, H.; Burns, P.; Goetz, S.J. Canopy Structure from Space Using GEDI Lidar. Front. Ecol. Environ. 2023, 21, 55–56. [Google Scholar] [CrossRef]
- Wang, C.; Elmore, A.J.; Numata, I.; Cochrane, M.A.; Lei, S.G.; Hakkenberg, C.R.; Li, Y.; Zhao, Y.; Tian, Y. A Framework for Improving Wall-to-Wall Canopy Height Mapping by Integrating GEDI LiDAR. Remote Sens. 2022, 14, 3618. [Google Scholar] [CrossRef]
- Rishmawi, K.; Huang, C.; Zhan, X. Monitoring Key Forest Structure Attributes Across the Conterminous United States by Integrating GEDI LiDAR Measurements and VIIRS Data. Remote Sens. 2021, 13, 442. [Google Scholar] [CrossRef]
- Laura, D.; Amy, N.; Steven, H.; Nathan, T.; Temilola, F.; Marc, S.; Carlos, A.S.; John, A.; Scott, B.L.; Michelle, H.; et al. Biomass Estimation from Simulated GEDI, ICESat-2 and NISAR Across Environmental Gradients in Sonoma County, California. Remote Sens. Environ. 2020, 242, 111779. [Google Scholar] [CrossRef]
- Silva, C.A.; Duncanson, L.; Neuenschwander, A.; Thomas, N.; Hofton, M.; Fatoyinbo, L.; Simard, M.; Marshak, C. Fusing Simulated GEDI, ICESat-2 and NISAR Data for Regional Aboveground Biomass Mapping. Remote Sens. Environ. 2021, 253, 112234. [Google Scholar] [CrossRef]
- Sun, M.; Cui, L.; Park, J.; García, M.; Zhou, Y.; He, L.; Zhang, H.; Zhao, K.G. Evaluation of NASA’s GEDI Lidar Observations for Estimating Biomass in Temperate and Tropical Forests. Forests 2022, 13, 1686. [Google Scholar] [CrossRef]
- Song, F. Current Status and Characteristics of Forest Resources in Shangri-La County. J. West China For. Sci. 2008, 122, 124–128. (In Chinese) [Google Scholar]
- State Forestry Administration of China (SFAC). Tree Biomass Models and Related Parameters to Carbon Accounting for Quercus; State Forestry Administration: Beijing, China, 2016. (In Chinese)
- Chen, L.; Ren, C.; Bao, G.D.; Zhang, B.; Wang, Z.M.; Liu, M.Y.; Man, W.D.; Liu, J.F. Improved Object-Based Estimation of Forest Aboveground Biomass by Integrating LiDAR Data from GEDI and ICESat-2 with Multi-Sensor Images in a Heterogeneous Mountainous Region. Remote Sens. 2022, 14, 2743. [Google Scholar] [CrossRef]
- Han, M.; Xing, Y.; Li, G.; Huang, J.; Cai, L. Comparison of the Accuracy of the Maximum Canopy Height and Biomass Inversion of the Data of Different GEDI Algorithm. J. Cent. South Univ. For. Technol. 2022, 42, 72–82. (In Chinese) [Google Scholar]
- Liu, L.; Wang, C.; Nie, S.; Zhu, X.; Xi, X.; Wang, J. Analysis of the Influence of Different Algorithms of GEDI L2A on the Accuracy of Ground Elevation and Forest Canopy Height. J. Univ. Chin. Acad. Sci. 2022, 39, 502–511. (In Chinese) [Google Scholar]
- Cai, C.; Cao, S.; Kong, F.; Hu, L.; Liu, T.; Sun, W.; Wang, L. A Dataset of Spatial Distribution of Spruce Aboveground Biomass in Western Tianshan Mountains, Xinjiang in 2014. Chin. Sci. Data 2022, 7, 250–263. (In Chinese) [Google Scholar]
- Ying, C.L.; Ming, Y.L.; Zhen, Z.L.; Chao, L. Combining Kriging Interpolation to Improve the Accuracy of Forest Aboveground Biomass Estimation Using Remote Sensing Data. IEEE Access 2020, 8, 128124–128139. [Google Scholar] [CrossRef]
- Liao, Y.; Zhang, J.; Bao, R.; Xu, D.; Wang, S.; Han, D. Estimation of Aboveground Biomass Dynamics of Pinus densata by Introducing of Topographic Factors. Chin. J. Ecol. 2022, 1–12. (Online first Publish) (In Chinese) [Google Scholar]
- Pen, H.; Chen, G.; Chen, X.; Liu, Z.; Yao, C. Hybrid Classification of Coal and Biomass by Laser-induced Breakdown Spectroscopy Combined with K-means and SVM. Plasma Sci. Technol. 2019, 21, 64–72. [Google Scholar] [CrossRef]
- Raúl, H.; María, T.L.; Juan, D.; Darío, D.; Montealegre Antonio, L.M.; Alberto, M.; Sergio, R. Assessing GEDI-NASA System for Forest Fuels Classification Using Machine Learning Techniques. Int. J. Appl. Earth Obs. 2023, 116, 103175. [Google Scholar] [CrossRef]
- Qian, C.H.; Qiang, H.Q.; Wang, F.; Li, M.Y. Estimation of Forest Aboveground Biomass in Karst Areas Using Multi-Source Remote Sensing Data and the K-DBN Algorithm. Remote Sens. 2021, 13, 5030. [Google Scholar] [CrossRef]
- Brown, S.; Narine, L.; Gilbert, J. Using Airborne Lidar, Multispectral Imagery, and Field Inventory Data to Estimate Basal Area, Volume, and Aboveground Biomass in Heterogeneous Mixed Species Forests: A Case Study in Southern Alabama. Remote Sens. 2022, 14, 2708. [Google Scholar] [CrossRef]
- You, H. R Language Prediction in Practice; Electronic Industry Press: Beijing, China, 2016; pp. 203–204. (In Chinese) [Google Scholar]
- Liang, Z.; Li, Z.; Lai, C.; Lin, Z.; Li, T.; Zhang, J. Application of 10-fold Cross-validation in the Evaluation Generalization Ability of Prediction Models and Realization in R. Chin. J. Hosp. Stat. 2020, 27, 289–292. (In Chinese) [Google Scholar]
- Du, H.; Zhou, G.; Fan, W.; Ge, H.; Xu, X.; Shi, Y.; Fan, W. Spatial Heterogeneity and Carbon Contribution of Aboveground Biomass of Moso Bamboo by Using Geostatistical Theory. Plant Ecol. 2010, 207, 131–139. [Google Scholar] [CrossRef]
- Meng, L. Distribution of Forest Biomass for Main Forest Types in Tahe Forestry Administration of Daxinganling Based on Geostatistics; Northeast Forestry University: Harbin, China, 2017. (In Chinese) [Google Scholar]
- Ahmad, A.; Gilani, H.; Ahmad, S.R. Forest Aboveground Biomass Estimation and Mapping through High-Resolution Optical Satellite Imagery—A Literature Review. Forests 2021, 12, 914. [Google Scholar] [CrossRef]
- Wang, J.; Cheng, P.; Xu, S.; Wang, X.; Cheng, F. Forest Biomass Estimation in Shangri-La Based on Remote Sensing. J. Zhejiang AF Univ. 2013, 30, 325–329. (In Chinese) [Google Scholar]
- Xie, F. Estimation and Mapping of Forest Aboveground Biomass Based on k-NN Model and Remote Sensing; Southwest Forestry University: Kunming, China, 2019. (In Chinese) [Google Scholar]
- Guo, R.; Fu, S.; Hou, M.; Liu, J.; Miao, C.; Meng, Y.; Feng, Q.; He, J.; Qian, D.; Liang, T. Remote Sensing Retrieval of Natural Grassland Biomass in Menyuan County, Qinghai Province experimental area based on Sentinel-2 data. Acta Pratacult. Sin. 2023, 32, 15. (In Chinese) [Google Scholar]
- Liu, X.; Su, Y.; Hu, T.; Yang, Q.; Liu, B.; Deng, Y.; Tang, H.; Tang, Z.; Fang, J.; Guo, Q. Neural Network Guided Interpolation for Mapping Canopy Height of China’s Forests by Integrating GEDI and ICESat-2 Data. Remote Sens. Environ. 2022, 269, 112844. [Google Scholar] [CrossRef]
- Semko, A.; Alireza, S.; Fatemeh, S. The Soil Slope Stability in Failure with the Use of the Random Process Based on the Kriging’s Interpolation Model. J. Civ. Construct. Environ. Eng. 2022, 7, 63–72. [Google Scholar]
- Wu, C. Regional Biomass Estimation and Application Based on Remote Sensing; Zhejiang University: Hangzhou, China, 2016. (In Chinese) [Google Scholar]
- Li, H.; Mao, Z.; Shi, H.; Xiao, H. Model Uncertainty in Forest Biomass Estimation. Acta Ecol. Sin. 2017, 37, 7912–7919. [Google Scholar] [CrossRef]
- Fu, M.; Li, Z.; Qing, T. Optimizing the K-nearest Neighbors Technique for Estimating Pinus Densata Aboveground Biomass Based on Remote Sensing. J. Zhejiang A F Univ. 2019, 36, 515–523. (In Chinese) [Google Scholar]
- José, L.H.; Juan, M.D.; Kristofer, D.; Richard, B.; Fernando, T.; Alicia, P.; Juan, P.C.; Gonzalo, S.; David, L. Improving Species Diversity and Biomass Estimates of Tropical Dry Forests Using Airborne LiDAR. Remote Sens. 2014, 6, 4741–4763. [Google Scholar] [CrossRef]
- Shu, Q.; Xi, L.; Wang, K.; Xie, F.; Pang, Y.; Song, H. Optimization of Samples for Remote Sensing Estimation of Forest Aboveground Biomass at the Regional Scale. Remote Sens. 2022, 14, 4187. [Google Scholar] [CrossRef]
- Jiang, F.; Sun, H.; Li, C.; Ma, K.; Chen, S.; Long, J.; Ren, L. Retrieving the Forest Aboveground Biomass by Combined Red-edge Bands of Sentinel-2 and GF-6. Acta Ecol Sin. 2021, 41, 8222–8236. (In Chinese) [Google Scholar]
- Jiang, F.; Kutia, M.; Ma, K.; Chen, S.; Long, J.; Sun, H. Estimating the Aboveground Biomass of Coniferous Forest in Northeast China Using Spectral Variables, Land Surface Temperature and Soil Moisture. Sci. Total Environ. 2021, 785, 147335. [Google Scholar] [CrossRef]
- García-Gutiérrez, J.; Martínez-Álvarez, F.; Troncoso, A.; Riquelme, J.C. A Comparison of Machine Learning Regression Techniques for LiDAR-derived Estimation of Forest Variables. Neurocomputing 2015, 167, 24–31. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A Survey of Remote Sensing-based Aboveground Biomass Estimation Methods in Forest Ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Li, C. Evaluation of Garlic Based on Convolutional Neural Network; Shandong Agricultural University: Taian, China, 2022. (In Chinese) [Google Scholar]
- Seppanen, J.; Antropov, O.; Jagdhuber, T. Improved Characterization of Forest Transmissivity Within the L-MEB Model Using Multisensor SAR Data. IEEE Geosci. Remote Sens. 2017, 14, 1408–1412. [Google Scholar] [CrossRef]
- Song, H.; Xi, L.; Shu, Q.; Wei, Z.; Qiu, S. Estimate Forest Aboveground Biomass of Mountain by ICESat-2/ATLAS Data Interacting Cokriging. Forests 2023, 14, 13. [Google Scholar] [CrossRef]


| Forest Parameters | Value Range | Average Value | Standard Deviation |
|---|---|---|---|
| Aboveground biomass/(t/hm2) | (11.17~274.97) | 89.42 | 58.00 |
| Belowground biomass/(t/hm2) | (2.93~47.45) | 22.19 | 10.44 |
| Total biomass/(t/hm2) | (14.14~215.79) | 111.61 | 67.45 |
| Parameters | Description | Parameters | Description |
|---|---|---|---|
| cover | Total cover, defined as the percentage of the ground covered by the vertical projection of canopy material | modis_nonvegetated | Percentage non-vegetated from MODIS data |
| pgap_theta | Estimated Pgap(theta) for the selected L2A algorithm | modis_treecover | Percentage of tree cover from MODIS data |
| pai | Total Plant Area Index | dem_ | DEM from GED |
| leaf_on_doy | Leaf on day of year | leaf_off_doy | Leaf off day of year |
| pgap_theta_error | Total Pgap(theta) error | rv_aN | integral of the vegetation component in the RX waveform |
| rg_aN | Integral of the ground component in the RX waveform | sensitivity | Maximum canopy cover that can be penetrated considering the SNR of the waveform |
| rx_energy_aN | Received waveform energy between toploc and botloc with noise removed | rh100 | Height above ground of the received waveform signal start |
| fhd_normal | Foliage height diversity index calculated by vertical foliage profile normalized by total plant area index. | Lat_lowestmode Lon_lowestmode | latitude and longitude |
| quality_flag | quality flag | degrade_flag | Degrade flag |
| Parameter Name | Model | R2 | Residual SS | Nugget | Sill | Structural Ratio | Range |
|---|---|---|---|---|---|---|---|
| sensitivity | Gaussian | 0.65 | 3.14 × 10−5 | 0 | 0.05 | 0.83 | 0.05 |
| Spherical | 0.65 | 3.14 × 10−5 | 0 | 0.05 | 0.95 | 0.06 | |
| Linear | 0.13 | 7.78 × 10−5 | 0.05 | 0.06 | 0.05 | 0.93 | |
| Exponential | 0.68 | 2.90 × 10−5 | 0.01 | 0.05 | 0.89 | 0.07 | |
| rv | Gaussian | 0.52 | 5553 | 155.00 | 907.90 | 0.83 | 0.05 |
| Spherical | 0.52 | 5524 | 50.00 | 907.70 | 0.95 | 0.05 | |
| Linear | 0.04 | 11076 | 892.75 | 911.77 | 0.02 | 0.93 | |
| Exponential | 0.54 | 5364 | 103.00 | 908.10 | 0.89 | 0.05 | |
| modis_ nonvegetated | Gaussian | 0.26 | 0.26 | 0.12 | 1.28 | 0.91 | 0.06 |
| Spherical | 0.26 | 0.26 | 0 | 1.28 | 0.10 | 0.07 | |
| Linear | 0.82 | 0.06 | 1.02 | 1.48 | 0.31 | 0.93 | |
| Exponential | 0.80 | 0.07 | 1.00 | 2.04 | 0.51 | 4.91 | |
| modis_ treecover | Gaussian | 0.60 | 1.23 | 0.74 | 5.24 | 0.86 | 0.06 |
| Spherical | 0.60 | 1.23 | 0.18 | 5.24 | 0.97 | 0.07 | |
| Linear | 0.41 | 1.82 | 4.66 | 5.61 | 0.17 | 0.93 | |
| Exponential | 0.72 | 0.88 | 0.61 | 5.28 | 0.88 | 0.11 |
| Parameter Name | ME | RMSE | MSE | RMSSE | ASE | R2 | Model |
|---|---|---|---|---|---|---|---|
| sensitivity | 0.00 | 0.02 | 0.00 | 1.01 | 0.02 | 0.62 | Gaussian |
| rv | 10.18 | 3950.54 | 0.00 | 0.90 | 4378.33 | 0.71 | Spherical |
| modis_nonvegetated | 0.12 | 9.29 | 0.01 | 1.00 | 9.17 | 0.81 | Linear |
| modis_treecover | 0.00 | 0.30 | 0.00 | 0.98 | 0.31 | 0.62 | Exponential |
| Variable Filtering Method | Variable Name |
|---|---|
| Stepwise regression | Sensitivity, aspect, dem_, slope, rg_a1 |
| Random forest | Sensitivity, aspect, modis_nonvegetated, rv, modis_treecover |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Shu, Q.; Fu, H.; Zhou, W.; Luo, S.; Gao, Y.; Yu, J.; Guo, C.; Yang, Z.; Xiao, J.; et al. Estimation of Quercus Biomass in Shangri-La Based on GEDI Spaceborne Lidar Data. Forests 2023, 14, 876. https://doi.org/10.3390/f14050876
Xu L, Shu Q, Fu H, Zhou W, Luo S, Gao Y, Yu J, Guo C, Yang Z, Xiao J, et al. Estimation of Quercus Biomass in Shangri-La Based on GEDI Spaceborne Lidar Data. Forests. 2023; 14(5):876. https://doi.org/10.3390/f14050876
Chicago/Turabian StyleXu, Li, Qingtai Shu, Huyan Fu, Wenwu Zhou, Shaolong Luo, Yingqun Gao, Jinge Yu, Chaosheng Guo, Zhengdao Yang, Jinnan Xiao, and et al. 2023. "Estimation of Quercus Biomass in Shangri-La Based on GEDI Spaceborne Lidar Data" Forests 14, no. 5: 876. https://doi.org/10.3390/f14050876






