The Development of a Set of Novel Low Cost and Data Processing-Free Measuring Instruments for Tree Diameter at Breast Height and Tree Position
Abstract
:1. Introduction
1.1. Our Aims
1.2. Technical Review
2. Materials and Methods
2.1. Study Area
2.2. Methods
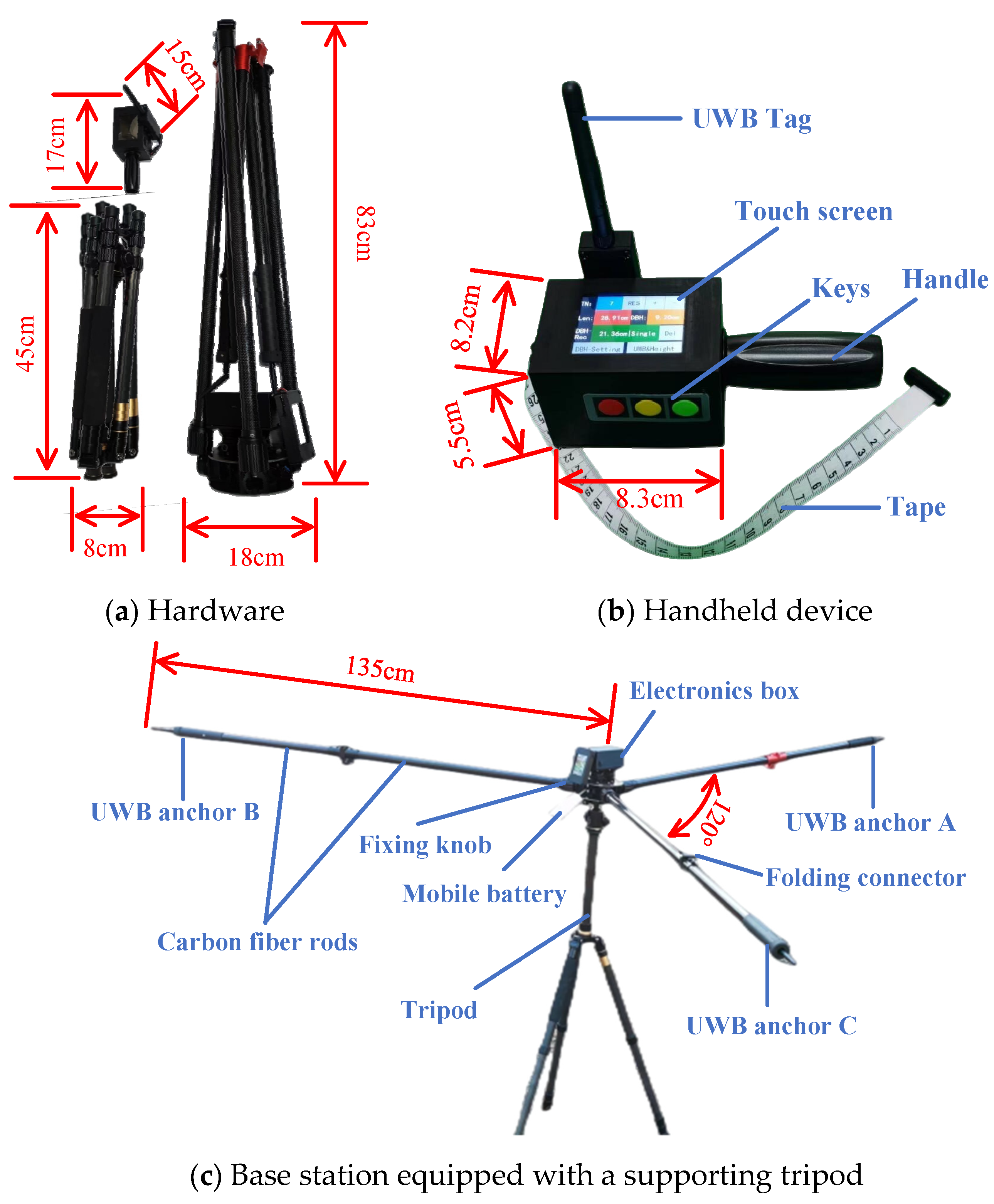
2.2.1. Hardware for Measuring Tree DBH and Tree Position
2.2.2. The Measurement Workflow
2.2.3. Measurement Algorithms for the Tree DBH Calculations
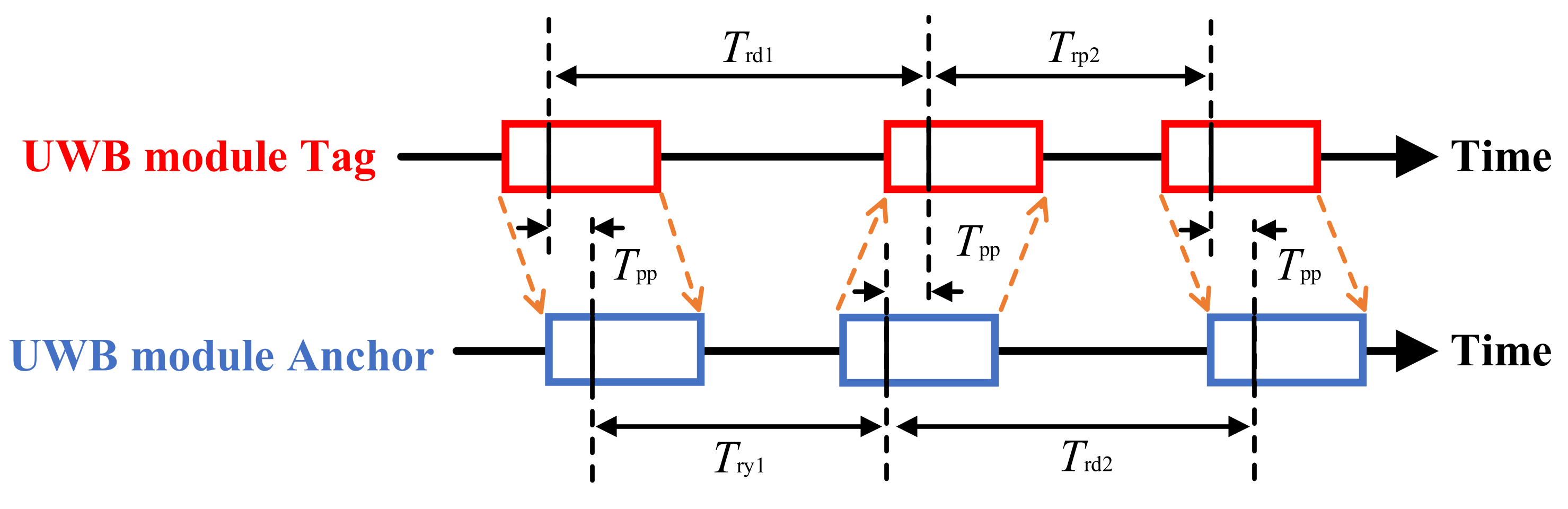
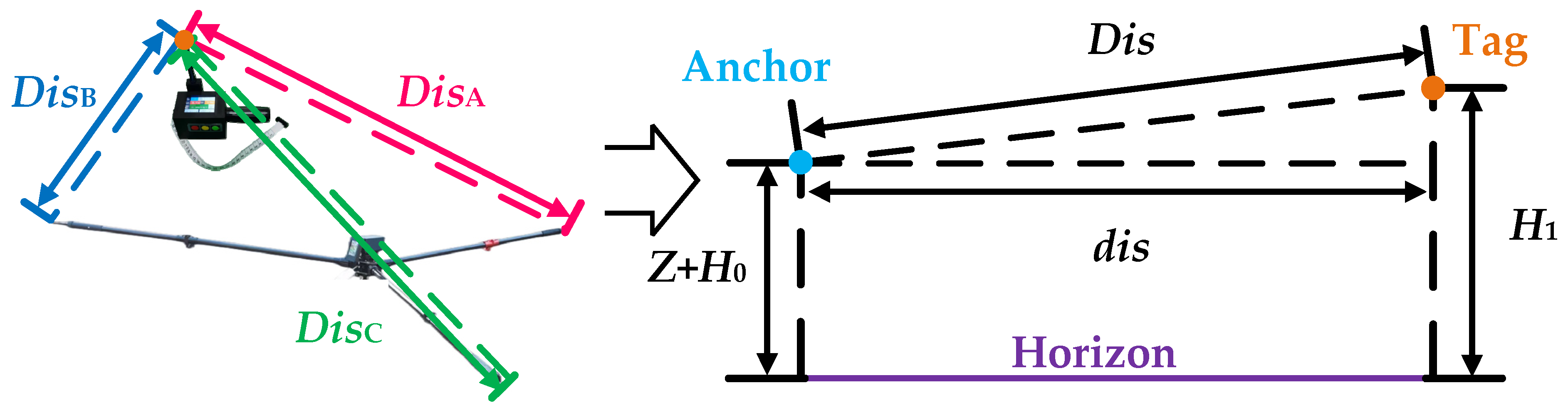
2.2.4. Measurement Algorithms for the Tree Position Estimations
2.2.5. Evaluation of the Accuracy of the Tree DBH and Tree Position
3. Results
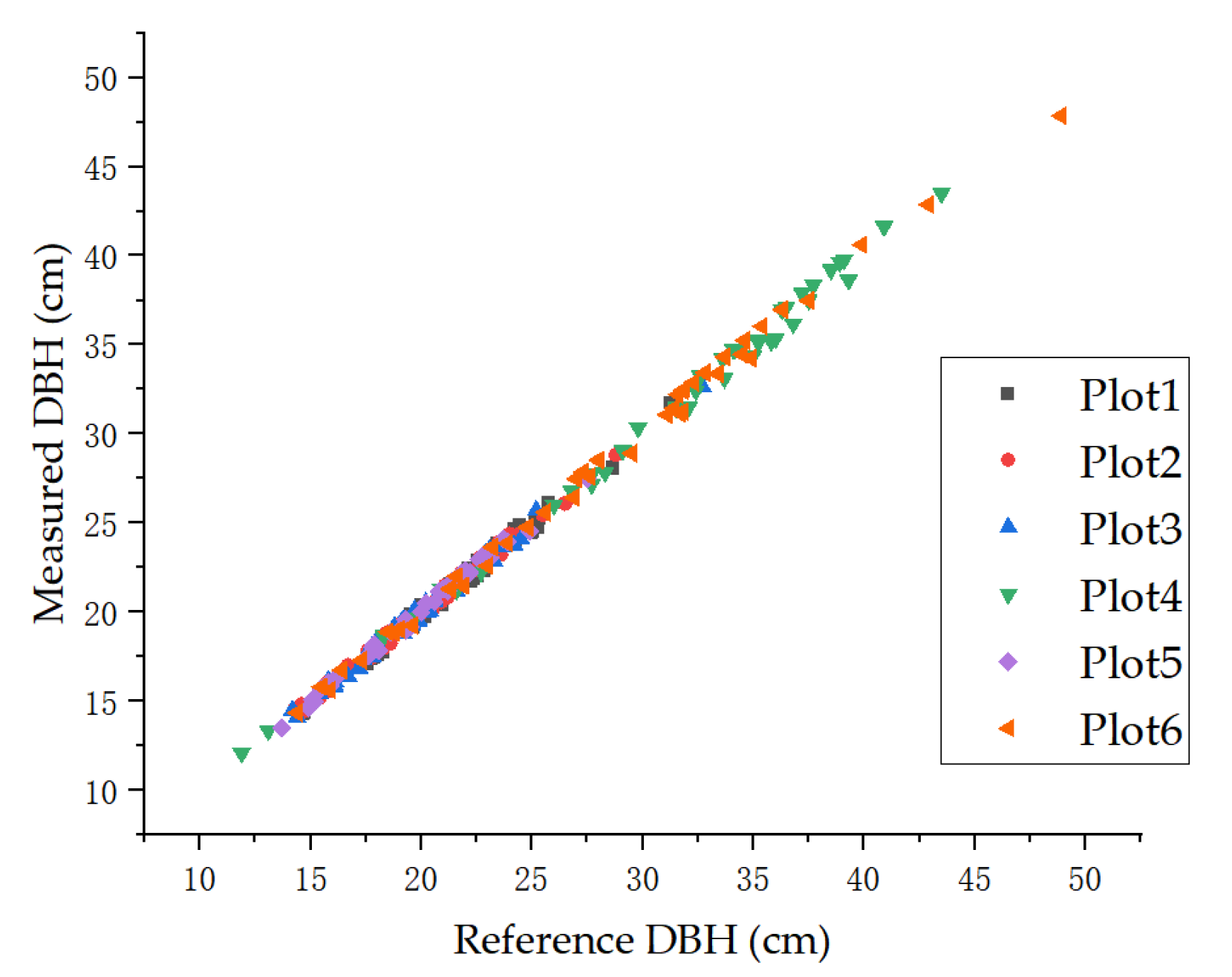
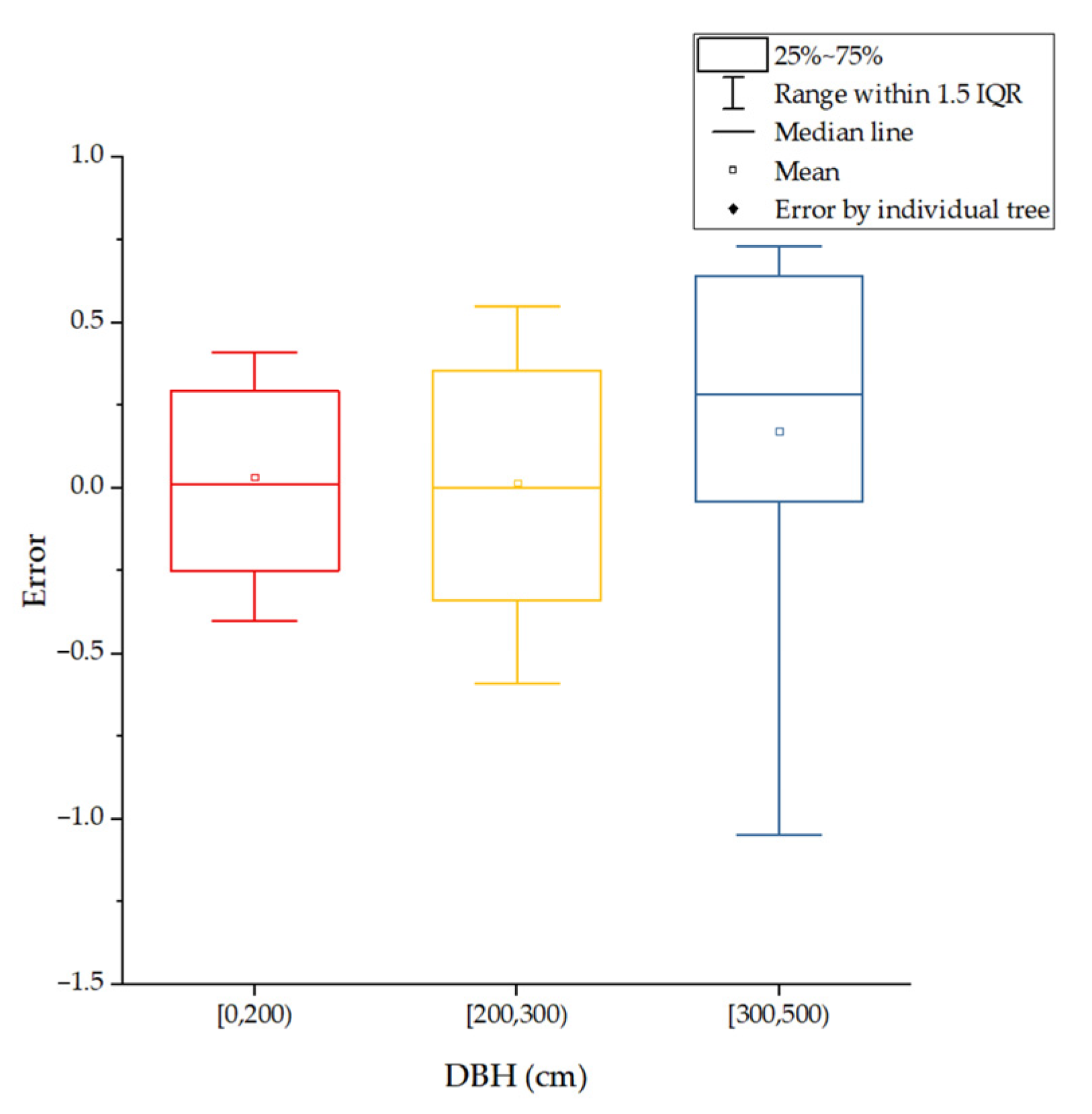
3.1. Evaluation of Tree DBH
3.2. Evaluation of Tree Position
3.3. Comparing the Efficiency of Different Methods
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Component | Type | Parameter | Function |
|---|---|---|---|
| TMR encoder | PD-1503-SDI | Bit, 12 | DBH measurement |
| MCU | STC15W4K56S4 | Flash, 56 KB | Data processing |
| UWB module | D-DWM-PG2.5 | Resolution, 1 cm and range, 130 m | Distance measurement |
| SD card | Micro SD | 2 GB | Data storage |
| Bluetooth | JDY-31 | Range, 0–15 m | Communication with smartphone |
| Display | TJC3224T124 | 320 × 240 pixels | Data display |
| Battery | ZONGCELL | 4000 mAh | Power supply |
Appendix B
| Component | Type | Parameter | Function |
|---|---|---|---|
| UWB module × 5 | D-DWM-PG2.5 | Resolution, 1 cm and range, 0–130 m | Distance measurement |
| 3D-compass | DCM250B | Resolution, 0.1° Heading range, 0~360° Heading accuracy, 0.8°, 1.5°, 2.0°, and 3.0° (inclined angle <10°, 30°, 40°, 60°) Roll and pitch range, −85°~85° Roll and pitch accuracy, 0.1°, 0.2°, and 0.3° (between ±15°, ±30°, ±60° in range) | Attitude angle measurement |
| Display | TJC3224T124 | 320 × 240 pixels | Data display |
| Mobile battery | ROMOSS | 10000 mAh | Power supply |
Appendix C

Appendix D
References
- Fan, Y.; Feng, Z.; Mannan, A.; Khan, T.U.; Shen, C.; Saeed, S. Estimating Tree Position, Diameter at Breast Height, and Tree Height in Real-Time Using a Mobile Phone with RGB-D SLAM. Remote Sens. 2018, 10, 1845. [Google Scholar] [CrossRef]
- Macdicken, K.G. Global Forest Resources Assessment 2015: What, why and how? For. Ecol. Manag. 2015, 352, 3–8. [Google Scholar] [CrossRef]
- Trumbore, S.; Brando, P.; Hartmann, H. Forest health and global change. Science 2015, 349, 814–818. [Google Scholar] [CrossRef] [PubMed]
- Tubiello, F.N.; Salvatore, M.; Ferrara, A.F.; House, J.; Federici, S.; Rossi, S.; Biancalani, R.; Condor Golec, R.D.; Jacobs, H.; Flammini, A.; et al. The contribution of agriculture, forestry and other land use activities to global warming, 1990–2012. Glob. Chang. Biol. 2015, 21, 2655–2660. [Google Scholar] [CrossRef]
- Zhang, L.; Bi, H.; Cheng, P.; Davis, C.J. Modeling spatial variation in tree diameter—Height relationships. For. Ecol. Manag. 2004, 189, 317–329. [Google Scholar] [CrossRef]
- Millar, C.I.; Stephenson, N.L. Temperate forest health in an era of emerging megadisturbance. Science 2015, 349, 823–826. [Google Scholar] [CrossRef]
- Sun, L.; Fang, L.; Weng, Y.; Zheng, S. An Integrated Method for Coding Trees, Measuring Tree Diameter, and Estimating Tree Positions. Sensors 2020, 20, 144. [Google Scholar] [CrossRef]
- Bauwens, S.; Fayolle, A.; Gourlet-Fleury, S.; Ndjele, L.M.; Mengal, C.; Lejeune, P. Terrestrial photogrammetry: A non-destructive method for modelling irregularly shaped tropical tree trunks. Methods Ecol. Evol. 2017, 8, 460–471. [Google Scholar] [CrossRef]
- Kangas, A.; Maltamo, M. Forest Inventory: Methodology and Applications; Springer Science & Business Media: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Luoma, V.; Saarinen, N.; Wulder, M.A.; White, J.C.; Vastaranta, M.; Holopainen, M.; Hyyppä, J. Assessing Precision in Conventional Field Measurements of Individual Tree Attributes. Forests 2017, 8, 38. [Google Scholar] [CrossRef]
- Binot, J.-M.; Pothier, D.; Lebel, J. Comparison of relative accuracy and time requirement between the caliper, the diameter tape and an electronic tree measuring fork. For. Chron. 1995, 71, 197–200. [Google Scholar] [CrossRef]
- Michael, K.; Steen, S.M.; Marco, M. Sampling Methods, Remote Sensing and GISMultiresourceForest Inventory; Spring-Verlag Berlin Heidelberge: Berlin, Germany, 2006. [Google Scholar]
- Wu, X.; Zhou, S.; Xu, A.; Bin, C. Passive measurement method of tree diameter at breast height using a smartphone. Comput. Electron. Agric. 2019, 163, 104875. [Google Scholar] [CrossRef]
- Tomaštík, J.; Saloň, Š.; Tunák, D.; Chudý, F.; Kardoš, M. Tango in forests—An initial experience of the use of the new Google technology in connection with forest inventory tasks. Comput. Electron. Agric. 2017, 141, 109–117. [Google Scholar] [CrossRef]
- Vastaranta, M.; Melkas, T.; Holopainen, M.; Kaartinen, H.; Hyyppae, J.; Hyyppae, H. Laser-based field measurements in tree-level forest data acquisition. Photogramm. J. Finl. 2009, 21, 51–61. [Google Scholar]
- Wang, Z.; Lu, X.; An, F.; Zhou, L.; Wang, X.; Wang, Z.; Zhang, H.; Yun, T. Integrating Real Tree Skeleton Reconstruction Based on Partial Computational Virtual Measurement (CVM) with Actual Forest Scenario Rendering: A Solid Step Forward for the Realization of the Digital Twins of Trees and Forests. Remote Sens. 2022, 14, 6041. [Google Scholar] [CrossRef]
- Zou, W.; Jing, W.; Chen, G.; Lu, Y.; Song, H. A Survey of Big Data Analytics for Smart Forestry. IEEE Access 2019, 7, 46621–46636. [Google Scholar] [CrossRef]
- Wang, Z.; Shen, Y.-J.; Zhang, X.; Zhao, Y.; Schmullius, C. Processing Point Clouds Using Simulated Physical Processes as Replacements of Conventional Mathematically Based Procedures: A Theoretical Virtual Measurement for Stem Volume. Remote Sens. 2021, 13, 4627. [Google Scholar] [CrossRef]
- Torresan, C.; Garzón, M.B.; O’Grady, M.; Robson, T.M.; Picchi, G.; Panzacchi, P.; Tomelleri, E.; Smith, M.; Marshall, J.; Wingate, L.; et al. A new generation of sensors and monitoring tools to support climate-smart forestry practices. Can. J. For. Res. 2021, 51, 1751–1765. [Google Scholar] [CrossRef]
- Barrett, F.; McRoberts, R.E.; Tomppo, E.; Cienciala, E.; Waser, L.T. A questionnaire-based review of the operational use of remotely sensed data by national forest inventories. Remote Sens. Environ. 2016, 174, 279–289. [Google Scholar] [CrossRef]
- Gougherty, A.V.; Keller, S.R.; Kruger, A.; Stylinski, C.D.; Elmore, A.J.; Fitzpatrick, M.C. Estimating tree phenology from high frequency tree movement data. Agric. For. Meteorol. 2018, 263, 217–224. [Google Scholar] [CrossRef]
- Yao, Q.; Wang, J.; Zhang, J.; Xiong, N. Error Analysis of Measuring the Diameter, Tree Height, and Volume of Standing Tree Using Electronic Theodolite. Sustainability 2022, 14, 6950. [Google Scholar] [CrossRef]
- Zhao, Z.; Feng, Z.; Liu, J.; Wang, Y. Development and Testing of a New UWB Positioning Measurement Tool to Assist in Forest Surveys. Sustainability 2022, 14, 17042. [Google Scholar] [CrossRef]
- Clark, N.; Wynne, R.; Schmoldt, D. A review of past research on dendrometers. For. Sci. 2000, 46, 570–576. [Google Scholar]
- Mokroš, M.; Výbošťok, J.; Tomaštík, J.; Grznárová, A.; Valent, P.; Slavík, M.; Merganič, J. High Precision Individual Tree Diameter and Perimeter Estimation from Close-Range Photogrammetry. Forests 2018, 9, 696. [Google Scholar] [CrossRef]
- Surový, P.; Yoshimoto, A.; Panagiotidis, D. Accuracy of reconstruction of the tree stem surface using terrestrial close-range photogrammetry. Remote Sens. 2016, 8, 123. [Google Scholar] [CrossRef]
- Jingchen, L.; Zhongke, F.; Yongxiang, F. Automatic measurement of DBH with electronic bar. Trans. Chin. Soc. Agric. Mach. 2017, 48, 1–9. [Google Scholar]
- Sun, L.; Fang, L.; Tang, L.; Liu, J. Developing portable system for measuring diameter at breast height. J. Beijing For. Univ. 2018, 40, 82–89. [Google Scholar]
- Liu, H.; Feng, Z.; Hu, N.; Liu, J.; Yu, X. Design and experiment of portable high precision equipment for tree diameter measurement. Trans. Chin. Soc. Agric. Mach. 2018, 49, 189–194. [Google Scholar]
- Sun, L.; Fang, L.; Fang, Y.; Weng, Y.; Lou, X. Development of dbh measurement device using capacitive gate sensor. Chin. J. Sens. Actuators 2019, 32, 1435–1442. [Google Scholar]
- Liang, X.; Litkey, P.; Hyyppa, J.; Kaartinen, H.; Vastaranta, M.; Holopainen, M. Automatic stem mapping using single-scan terrestrial laser scanning. IEEE Trans. Geosci. Remote Sens. 2012, 50, 661–670. [Google Scholar] [CrossRef]
- Béland, M.; Widlowski, J.-L.; Fournier, R.A.; Côté, J.-F.; Verstraete, M.M. Estimating leaf area distribution in savanna trees from terrestrial LiDAR measurements. Agric. For. Meteorol. 2011, 151, 1252–1266. [Google Scholar] [CrossRef]
- Srinivasan, S.; Popescu, S.C.; Eriksson, M.; Sheridan, R.D.; Ku, N.-W. Terrestrial laser scanning as an effective tool to retrieve tree level height, crown width, and stem diameter. Remote Sens. 2015, 7, 1877–1896. [Google Scholar] [CrossRef]
- Xie, Y.; Yang, T.; Wang, X.; Chen, X.; Pang, S.; Hu, J.; Wang, A.; Chen, L.; Shen, Z. Applying a Portable Backpack Lidar to Measure and Locate Trees in a Nature Forest Plot: Accuracy and Error Analyses. Remote Sens. 2022, 14, 1806. [Google Scholar] [CrossRef]
- Labelle, E.R.; Heppelmann, J.B.; Borchert, H. Application of Terrestrial Laser Scanner to Evaluate the Influence of Root Collar Geometry on Stump Height after Mechanized Forest Operations. Forests 2018, 9, 709. [Google Scholar] [CrossRef]
- Lian, Y.; Feng, Z.; Huai, Y.; Lu, H.; Chen, S.; Li, N. Terrestrial Videogrammetry for Deriving Key Forest Inventory Data: A Case Study in Plantation. Remote Sens. 2021, 13, 3138. [Google Scholar] [CrossRef]
- Hyyppä, J.; Virtanen, J.-P.; Jaakkola, A.; Yu, X.; Hyyppä, H.; Liang, X. Feasibility of Google Tango and Kinect for crowdsourcing forestry information. Forests 2017, 9, 6. [Google Scholar] [CrossRef]
- Prusty, S.; Sahoo, S. Detection of forest fire by using gsm & gps technology. Int. J. Intell. Comput. Appl. Sci. 2017, 5, 2322–2353. [Google Scholar]
- Keefe, F.R.; Wempe, M.A.; Becker, M.R.; Zimbelman, G.E.; Nagler, S.E.; Gilbert, L.S.; Caudill, C.C. Positioning methods and the use of location and activity data in forests. Forests 2019, 10, 458. [Google Scholar] [CrossRef]
- Pau, L.F.; Klamerus-Iwan, A.; Kormanek, M.; Goł, J.; Owsiak, K. Robotic forest harvesting process using gnss satellite positioning data: Effects of gnss inaccuracies in forest environments. In Electronic Journal of Polish Agricultural Universities; Electronic Journal of Polish Agricultural Universities: Krakow, Poland, 2016. [Google Scholar]
- Feng, T.; Chen, S.; Feng, Z.; Shen, C.; Tian, Y. Effects of Canopy and Multi-Epoch Observations on Single-Point Positioning Errors of a GNSS in Coniferous and Broadleaved Forests. Remote Sens. 2021, 13, 2325. [Google Scholar] [CrossRef]
- Agarwal, R.; Bhatti, G.; Singh, R.R.; Indragandhi, V.; Suresh, V.; Jasinska, L.; Leonowicz, Z. Intelligent Fault Detection in Hall-Effect Rotary Encoders for Industry 4.0 Applications. Electronics 2022, 11, 3633. [Google Scholar] [CrossRef]
- Meng, B.; Wang, Y.; Sun, W.; Yuan, X. A Novel Diagnosis Method for a Hall Plates-Based Rotary Encoder with a Magnetic Concentrator. Sensors 2014, 14, 13980–13998. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Wu, Z.; Peng, D.; Chen, S.; Zhang, Z.; Liu, S. Sensing Mechanism of a Rotary Magnetic Encoder Based on Time Grating. IEEE Sens. J. 2018, 18, 3677–3683. [Google Scholar] [CrossRef]
- Tomoya, N.; Hirofumi, S.; Prabhanjan, D.K.; Hitoshi, I.; Yuya, S. Tunnel magnetoresistance sensors with symmetric resistance-field response and noise properties under AC magnetic field modulation. Appl. Phys. Lett. 2022, 121, 19. [Google Scholar]
- Palacín, J.; Martínez, D. Improving the Angular Velocity Measured with a Low-Cost Magnetic Rotary Encoder Attached to a Brushed DC Motor by Compensating Magnet and Hall-Effect Sensor Misalignments. Sensors 2021, 21, 4763. [Google Scholar] [CrossRef]
- Linhao, S.; Zhongke, F.; Jueying, S.; Yakui, S.; Dangui, L.; Tiantian, M. Development and experiment of the portable high precision measurement device for tree DBH. Trans. Chin. Soc. Agric. Mach. 2022, 38, 31–41. [Google Scholar]
- Wisiak, K.; Jakić, M.; Hartlieb, P. Application of Ultra-Wide Band Sensors in Mining. Sensors 2023, 23, 300. [Google Scholar] [CrossRef] [PubMed]
- Matteo, R.; Samuel, V.D.V.; Heidi, S.; De Poorter, E. Analysis of the scalability of UWB indoor localization Solutions for High User Densities. Sensors 2018, 18, 1875. [Google Scholar]
- Xiaoping, H.; Fei, W.; Jian, Z.; Hu, Z.; Jin, J. A posture recognition method based on indoor positioning technology. Sensors 2019, 19, 1464. [Google Scholar]
- Juri, S.; Volker, S.; Norbert, S.; Arensa, M.; Hugentobler, U. Decawave UWB clock drift correction and powerself-calibration. Sensors 2019, 19, 2942. [Google Scholar]
- Gao, H.; Li, X. Tightly-Coupled Vehicle Positioning Method at Intersections Aided by UWB. Sensors 2019, 19, 2867. [Google Scholar] [CrossRef] [PubMed]
- Zabalegui, P.; De Miguel, G.; Mendizabal, J.; Adin, I. Innovation-Based Fault Detection and Exclusion Applied to Ultra-WideBand Augmented Urban GNSS Navigation. Remote Sens. 2023, 15, 99. [Google Scholar] [CrossRef]
- Yuan, F.; Chen, S.; Fang, L.; Zheng, S.; Liu, Y.; Ren, J. A Method to Locate Tree Positions Using Ultrawideband Technology. J. Sens. 2021, 2021, 5539302. [Google Scholar] [CrossRef]
- Zhu, X.; Feng, Y. RSSI-based algorithm for indoor localization. Commun. Netw. 2013, 5, 37–42. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppä, J. Automatic stem mapping by merging several terrestrial laser scans at the feature and decision levels. Sensors 2013, 13, 1614–1634. [Google Scholar] [CrossRef]
- Song, C.; Yang, B.; Zhang, L.; Wu, D. A handheld device for measuring the diameter at breast height of individual trees using laser ranging and deep-learning based image recognition. Plant Methods 2021, 17, 67. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Chen, Y.; Kukko, A.; Kaartinen, H.; Jaakkola, A.; Khoramshahi, E.; Hakala, T.; Hyyppä, J.; Holopainen, M.; Hyyppä, H. SLAM-Aided Stem Mapping for Forest Inventory with Small-Footprint Mobile LiDAR. Forests 2015, 6, 4588–4606. [Google Scholar] [CrossRef]








| Plot | Number of Trees | Dominant Species | DBH (cm) | ||
|---|---|---|---|---|---|
| Mean | Min | Max | |||
| 1 | 43 | Ginkgo biloba L. | 21.67 | 14.6 | 31.2 |
| 2 | 51 | Salix matsudana Koidz | 22.26 | 14.3 | 28.8 |
| 3 | 46 | Ginkgo biloba L. | 19.62 | 14.2 | 32.7 |
| 4 | 41 | Populus tomentosa | 30.93 | 11.9 | 43.5 |
| 5 | 40 | Salix matsudana Koidz | 19.92 | 13.7 | 27.5 |
| 6 | 43 | Populus tomentosa | 27.88 | 14.4 | 48.9 |
| Plot | BIAS (cm) | relBIAS (%) | RMSE (cm) | relRMSE (%) |
|---|---|---|---|---|
| 1 | −0.04 | −0.25 | 0.34 | 1.55 |
| 2 | 0.06 | 0.28 | 0.29 | 1.39 |
| 3 | 0.02 | 0.14 | 0.30 | 1.51 |
| 4 | 0.09 | 0.28 | 0.48 | 1.49 |
| 5 | 0.08 | 0.38 | 0.24 | 1.20 |
| 6 | 0.10 | 0.36 | 0.46 | 1.53 |
| Total | 0.05 | 0.20 | 0.36 | 1.45 |
| Plot | X (cm) | Y (cm) | ||
|---|---|---|---|---|
| BIAS | RMSE | BIAS | RMSE | |
| 1 | −6.06 | 17.81 | 10.88 | 17.51 |
| 2 | −10.30 | 18.01 | −7.34 | 18.94 |
| 3 | −7.60 | 15.27 | 3.99 | 14.49 |
| 4 | −14.42 | 29.40 | 9.12 | 27.56 |
| 5 | 9.92 | 15.63 | 3.54 | 15.48 |
| 6 | −15.92 | 28.98 | −25.90 | 34.68 |
| Total | −7.63 | 21.51 | 2.56 | 22.49 |
| Plot | Ed (cm) | |||
|---|---|---|---|---|
| Mean | Max | Min | Std 1 | |
| 1 | 22.00 | 52.32 | 3.61 | 11.83 |
| 2 | 23.73 | 45.20 | 2.02 | 10.96 |
| 3 | 19.30 | 37.83 | 4.88 | 8.36 |
| 4 | 36.89 | 77.54 | 5.85 | 16.21 |
| 5 | 19.76 | 41.12 | 6.01 | 9.66 |
| 6 | 42.06 | 71.65 | 5.46 | 16.54 |
| Total | 27.11 | 77.54 | 2.02 | 15.30 |
| Method | Number of Surveyors | Number of Trees | Filed Working Time (min) | Office Working Time (min) | Total Time (min) | Mean Time (s) |
|---|---|---|---|---|---|---|
| Traditional method | 3 | 264 | 191.08 | 21.43 | 212.51 | 48.30 |
| Presented method | 1 | 264 | 89.52 | 0 | 89.52 | 20.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Feng, Z.; Shao, Y.; Wang, L.; Su, J.; Ma, T.; Lu, D.; An, J.; Pang, Y.; Fahad, S.; et al. The Development of a Set of Novel Low Cost and Data Processing-Free Measuring Instruments for Tree Diameter at Breast Height and Tree Position. Forests 2023, 14, 891. https://doi.org/10.3390/f14050891
Sun L, Feng Z, Shao Y, Wang L, Su J, Ma T, Lu D, An J, Pang Y, Fahad S, et al. The Development of a Set of Novel Low Cost and Data Processing-Free Measuring Instruments for Tree Diameter at Breast Height and Tree Position. Forests. 2023; 14(5):891. https://doi.org/10.3390/f14050891
Chicago/Turabian StyleSun, Linhao, Zhongke Feng, Yakui Shao, Linxin Wang, Jueying Su, Tiantian Ma, Dangui Lu, Jiayi An, Yongqi Pang, Shahzad Fahad, and et al. 2023. "The Development of a Set of Novel Low Cost and Data Processing-Free Measuring Instruments for Tree Diameter at Breast Height and Tree Position" Forests 14, no. 5: 891. https://doi.org/10.3390/f14050891
APA StyleSun, L., Feng, Z., Shao, Y., Wang, L., Su, J., Ma, T., Lu, D., An, J., Pang, Y., Fahad, S., Wang, W., & Wang, Z. (2023). The Development of a Set of Novel Low Cost and Data Processing-Free Measuring Instruments for Tree Diameter at Breast Height and Tree Position. Forests, 14(5), 891. https://doi.org/10.3390/f14050891












