Estimating Forest Above-Ground Biomass in Central Amazonia Using Polarimetric Attributes of ALOS/PALSAR Images
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Acquisition of SAR and Inventory Data
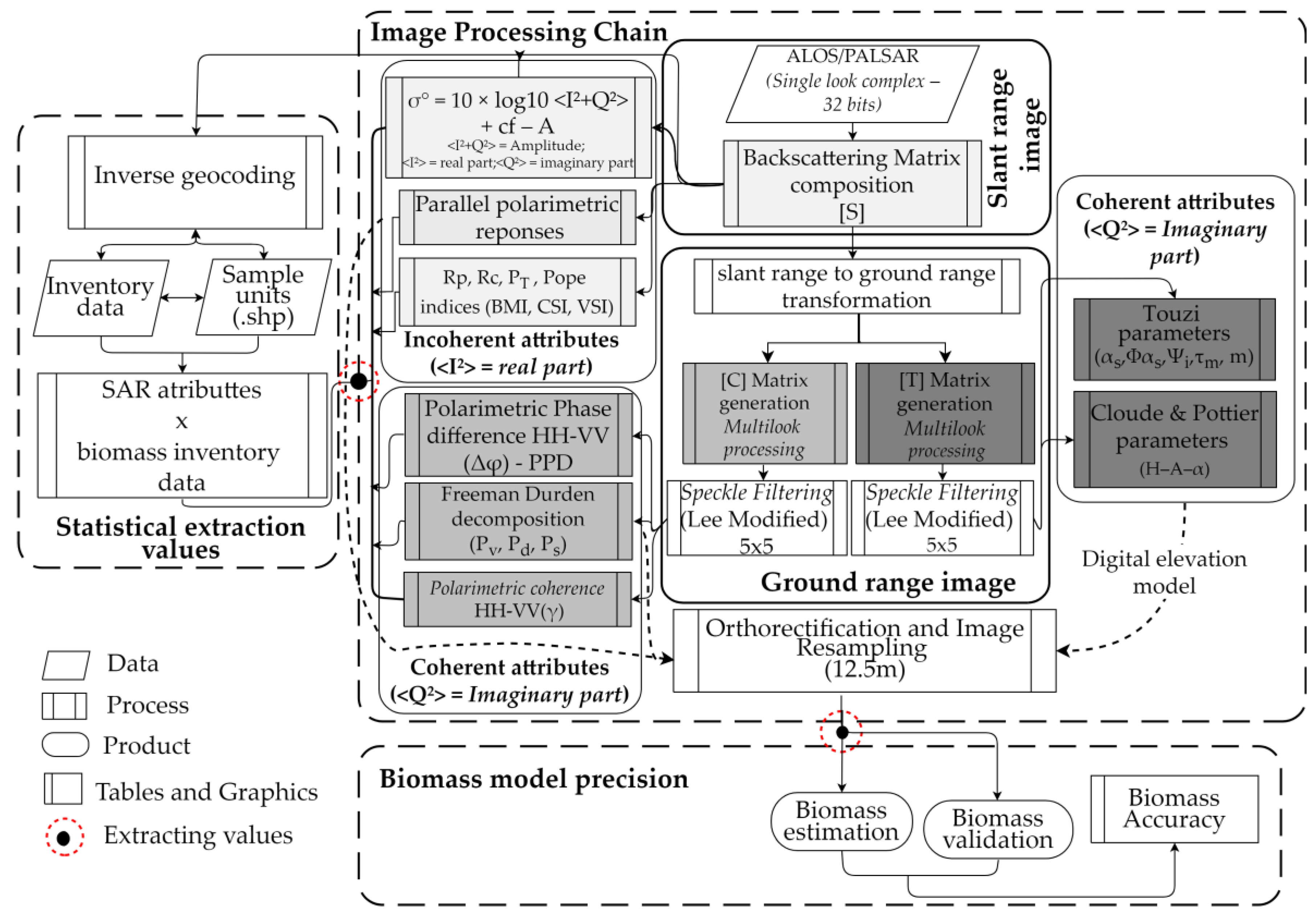
2.3. SAR Polarimetric Data Processing and Analysis
2.4. Modeling of Above-Ground Tree Biomass
3. Results
3.1. SAR, Inventory Data, and Scattering Mechanisms
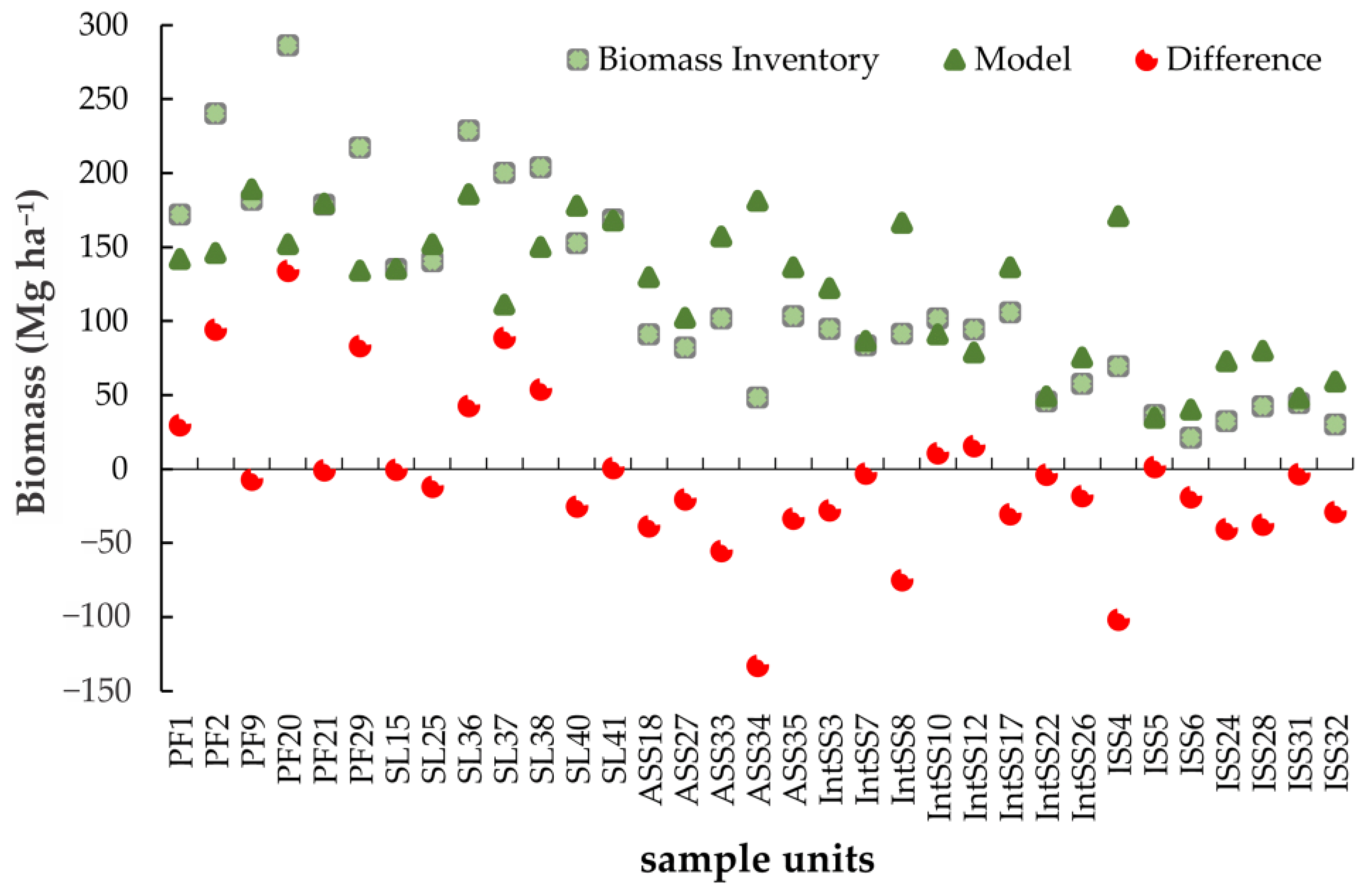
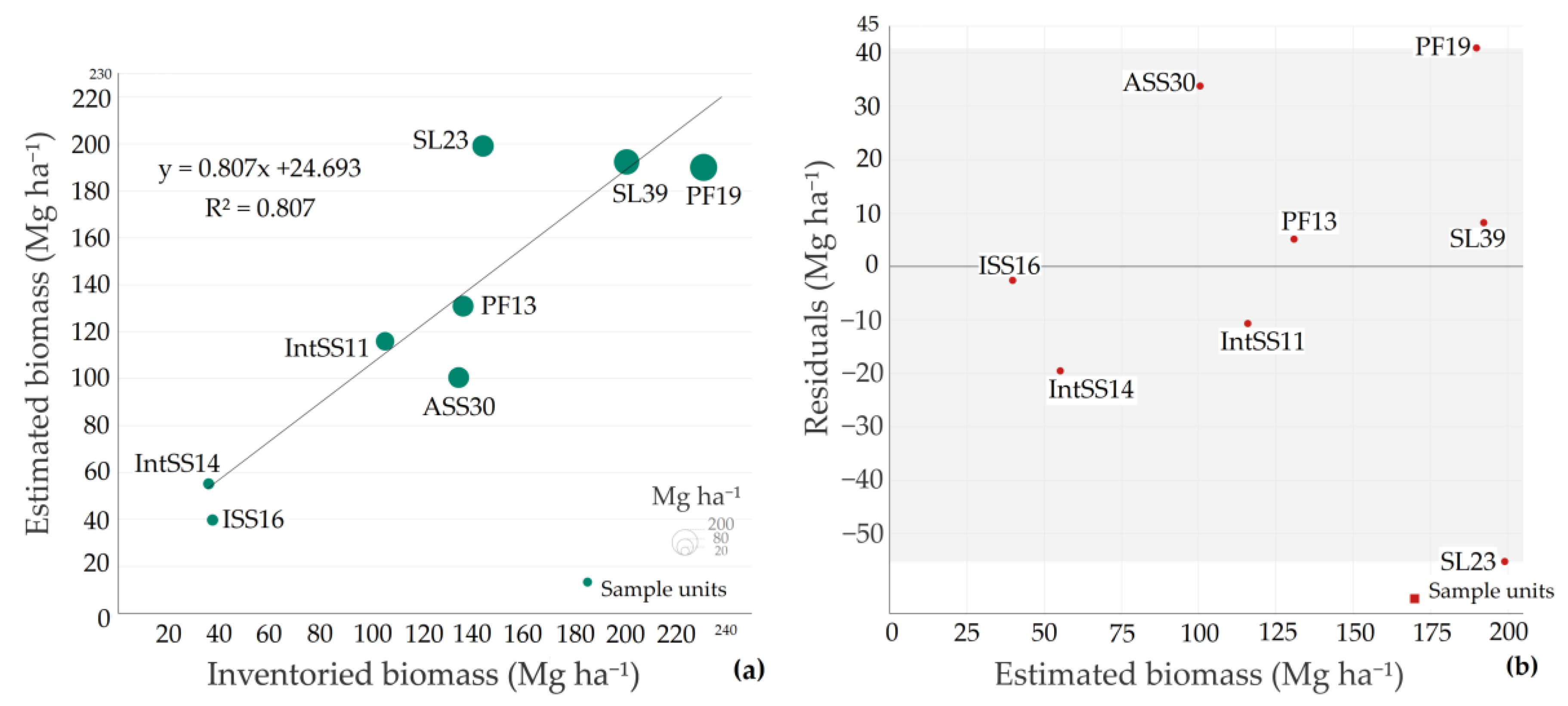
3.2. Above-Ground Tree Biomass
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Forest Inventoried Variables Used to Explain the SAR Scattering Mechanisms
| Typology | Sample Unit | Biomass (Mg ha−1) | Canopy Openness (%) * | Density (Trees ha−1) | Height (Meters) (Mean) | DBH (cm) (Mean) | G (m2 ha−1) |
|---|---|---|---|---|---|---|---|
| Primary forest (PF) | |||||||
| PF1 | 171.93 | 3.68 | 316 | 17.36 | 22.76 | 18.69 | |
| PF2 | 240.47 | 4.59 | 404 | 17.79 | 23.04 | 25.11 | |
| PF9 | 182.05 | 4.87 | 393 | 14.17 | 21.18 | 20.70 | |
| PF20 | 286.17 | 2.50 | 374 | 16.90 | 24.78 | 30.33 | |
| PF21 | 178.55 | 2.93 | 401 | 15.15 | 22.16 | 21.03 | |
| PF29 | 217.24 | 4.59 | 423 | 14.12 | 22.48 | 26.18 | |
| Total (mean) | 212.74 | 3.86 | 385 | 15.91 | 22.73 | 23.67 | |
| Selective logging (SL) | |||||||
| SL15 | 135.24 | 3.71 | 460 | 12.73 | 19.53 | 18.52 | |
| SL25 | 140.26 | 4.29 | 398 | 14.57 | 20.72 | 17.85 | |
| SL36 | 228.73 | N.D ** | 355 | 15.80 | 25.34 | 25.58 | |
| SL37 | 200.06 | N.D | 325 | 15.07 | 25.32 | 23.38 | |
| SL38 | 203.80 | N.D | 353 | 15.95 | 24.17 | 22.77 | |
| SL40 | 152.67 | N.D | 387 | 14.57 | 21.56 | 19.18 | |
| SL41 | 168.73 | N.D | 408 | 14.61 | 22.62 | 21.58 | |
| Total (mean) | 175.64 | 4.00 | 384 | 14.76 | 22.75 | 21.27 | |
| Advanced secondary succession (ASS) | |||||||
| ASS18 | 91.19 | 5.20 | 720 | 11.92 | 17.28 | 20.11 | |
| ASS27 | 82.03 | 3.17 | 680 | 12.12 | 16.83 | 17.92 | |
| ASS33 | 101.97 | 3.79 | 575 | 12.36 | 18.57 | 21.27 | |
| ASS34 | 48.43 | 5.92 | 430 | 11.98 | 16.70 | 10.68 | |
| ASS35 | 103.32 | 3.61 | 670 | 14.11 | 18.17 | 21.11 | |
| Total (mean) | 85.39 | 4.34 | 615 | 12.50 | 17.51 | 18.22 | |
| Intermediate secondary succession (IntSS) | |||||||
| IntSS3 | 94.61 | 4.77 | 780 | 12.21 | 14.43 | 18.87 | |
| IntSS7 | 83.69 | 5.29 | 1000 | 12.14 | 11.94 | 16.61 | |
| IntSS8 | 91.39 | 3.57 | 1550 | 12.82 | 10.67 | 18.60 | |
| IntSS10 | 101.77 | 7.93 | 860 | 8.99 | 11.47 | 19.58 | |
| IntSS12 | 94.48 | 3.57 | 1480 | 11.18 | 11.44 | 20.25 | |
| IntSS17 | 105.98 | 4.45 | 1070 | 10.89 | 12.87 | 21.55 | |
| IntSS22 | 45.61 | 3.62 | 1050 | 8.76 | 10.14 | 11.33 | |
| IntSS26 | 57.56 | 3.56 | 1460 | 9.21 | 10.17 | 14.15 | |
| Total (mean) | 84.39 | 4.59 | 1156 | 10.77 | 11.64 | 17.62 | |
| Initial secondary succession (ISS) | |||||||
| ISS4 | 69.42 | 6.11 | 1460 | 10.24 | 10.48 | 15.65 | |
| ISS5 | 36.37 | 7.09 | 800 | 10.00 | 9.95 | 8.51 | |
| ISS6 | 21.27 | 2.26 | 1120 | 7.60 | 7.93 | 5.94 | |
| ISS24 | 32.49 | 3.50 | 1110 | 8.81 | 9.34 | 8.46 | |
| ISS28 | 42.38 | 7.30 | 840 | 8.42 | 11.66 | 10.73 | |
| ISS31 | 44.68 | 2.67 | 1780 | 7.91 | 8.87 | 12.19 | |
| ISS32 | 30.12 | 6.49 | 1240 | 7.20 | 8.81 | 8.53 | |
| Total (mean) | 39.53 | 5.06 | 1193 | 8.60 | 9.58 | 10.00 |
References
- Food and Agriculture Organization of the United Nations (FAO). Global Forest Resources Assessment 2020—Key Findings. Available online: https://www.atibt.org/en/news/11217/fao-global-forest-resources-assessment-2020-fra-2020 (accessed on 28 April 2022).
- INPE (National Institute for Space Research). 2022. Available online: https://www.gov.br/inpe/pt-br/assuntos/ultimas-noticias/sei_01340-009084_2022_72_notatecnica_estimativa_prodes_2022_revisada_lu_lm_27_10_rev_la-002.pdf (accessed on 28 April 2022).
- Brazil. Ministério do Meio Ambiente Plano de ação para Prevenção e Controle do Desmatamento e das Queimadas no Cerrado (PCCerrado) e Plano de Ação Para Prevenção e Controle Do Desmatamento Na Amazônia Legal (PCCDAm): Fase 2016–2020; Ministério do Meio Ambiente: Brasilia, Brazil, 2018; ISBN 9788577383054. [Google Scholar]
- Frankenberg, C.; Fisher, J.B.; Worden, J.; Badgley, G.; Saatchi, S.S.; Lee, J.E.; Toon, G.C.; Butz, A.; Jung, M.; Kuze, A.; et al. New Global Observations of the Terrestrial Carbon Cycle from GOSAT: Patterns of Plant Fluorescence with Gross Primary Productivity. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Avtar, R.; Suzuki, R.; Sawada, H. Natural Forest Biomass Estimation Based on Plantation Information Using PALSAR Data. PLoS ONE 2014, 9, e86121. [Google Scholar] [CrossRef] [PubMed]
- de Sy, V.; Herold, M.; Achard, F.; Asner, G.P.; Held, A.; Kellndorfer, J.; Verbesselt, J. Synergies of Multiple Remote Sensing Data Sources for REDD+ Monitoring. Curr. Opin. Environ. Sustain. 2012, 4, 696–706. [Google Scholar] [CrossRef]
- Eckardt, R.; Berger, C.; Thiel, C.; Schmullius, C. Removal of Optically Thick Clouds from Multi-Spectral Satellite Images Using Multi-Frequency SAR Data. Remote Sens. 2013, 5, 2973. [Google Scholar] [CrossRef]
- de Jesus, J.B.; Kuplich, T.M. Applications of Sar Data to Estimate Forest Biophysical Variables in Brazil. Cerne 2020, 26, 88–97. [Google Scholar] [CrossRef]
- Wiederkehr, N.C.; Gama, F.F.; Mura, J.C.; dos Santos, J.R.; Bispo, P.C.; Sano, E.E. Analysis of the Target Decomposition Technique Attributes and Polarimetric Ratios to Discriminate Land Use and Land Cover Classes of the Tapajós Region. Boletim. Ciencias. Geodesicas. 2019, 25, e2019002. [Google Scholar] [CrossRef]
- Sinha, S.; Mohan, S.; Das, A.K.; Sharma, L.K.; Jeganathan, C.; Santra, A.; Santra Mitra, S.; Nathawat, M.S. Multi-Sensor Approach Integrating Optical and Multi-Frequency Synthetic Aperture Radar for Carbon Stock Estimation over a Tropical Deciduous Forest in India. Carbon. Manag. 2020, 11, 39–55. [Google Scholar] [CrossRef]
- Villard, L.; le Toan, T.; Tang Minh, D.H.; Mermoz, S.; Bouvet, A. Forest Biomass from Radar Remote Sensing. In Land Surface Remote Sensing in Agriculture and Forest; Baghdadi, N., Zribi, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2016; pp. 363–425. [Google Scholar] [CrossRef]
- Pichierri, M.; Hajnsek, I.; Zwieback, S.; Rabus, B. On the Potential of Polarimetric SAR Interferometry to Characterize the Biomass, Moisture and Structure of Agricultural Crops at L-, C- and X-Bands. Remote Sens. Environ 2018, 204, 596–616. [Google Scholar] [CrossRef]
- Ouchi, K. Recent Trend and Advance of Synthetic Aperture Radar with Selected Topics. Remote Sens. 2013, 5, 716–807. [Google Scholar] [CrossRef]
- Saatchi, S.; Marlier, M.; Chazdon, R.L.; Clark, D.B.; Russell, A.E. Impact of Spatial Variability of Tropical Forest Structure on Radar Estimation of Aboveground Biomass. Remote Sens. Environ. 2011, 115, 2836–2849. [Google Scholar] [CrossRef]
- Yu, Y.; Saatchi, S. Sensitivity of L-Band SAR Backscatter to Aboveground Biomass of Global Forests. Remote Sens. 2016, 8, 522. [Google Scholar] [CrossRef]
- Cassol, H.L.G.; Carreiras, J.M.d.B.; Moraes, E.C.; de Aragão, L.E.O.e.C.; Silva, C.V.d.J.; Quegan, S.; Shimabukuro, Y.E. Retrieving Secondary Forest Aboveground Biomass from Polarimetric ALOS-2 PALSAR-2 Data in the Brazilian Amazon. Remote Sens. 2019, 11, 59. [Google Scholar] [CrossRef]
- da Conceição Bispo, P.; Balzter, H.; Malhi, Y.; Slik, J.W.F.; dos Santos, J.R.; Rennó, C.D.; Espírito-Santo, F.D.; Aragão, L.E.O.C.; Ximenes, A.C.; da Conceição Bispo, P. Drivers of Metacommunity Structure Diverge for Common and Rare Amazonian Tree Species. PLoS ONE 2017, 12, e0188300. [Google Scholar] [CrossRef]
- Hojo, A.; Takagi, K.; Avtar, R.; Tadono, T.; Nakamura, F. Synthesis of L-Band Sar and Forest Heights Derived from TanDEM-X DEM and 3 Digital Terrain Models for Biomass Mapping. Remote Sens. 2020, 12, 349. [Google Scholar] [CrossRef]
- dos Santos, J.; Narvaes, I.; Graça, P.; Goncalves, F. Polarimetric Responses and Scattering Mechanisms of Tropical Forest in the Brazilian Amazon. In Advances in Geoscience and Remote Sensing; Jedlovec, G., Ed.; Intechopen: London, UK, 2009; pp. 183–206. [Google Scholar]
- dos Santos, J.R.; Gama, F.F.; da Conceição Bispo, P. Estimating Forest Biomass by Remote Sensing Radar Data in Brazil. Drewno 2014, 57, 120–132. [Google Scholar] [CrossRef]
- Neeff, T.; Vieira Dutra, L.; Roberto, J.; Santos, D.; da Costa Freitas, C.; Araujo, L.S. Tropical Forest Measurement by Interferometric Height Modeling and P-Band Radar Backscatter. For. Sci. 2005, 51, 585–594. [Google Scholar]
- Solberg, S.; Næsset, E.; Gobakken, T.; Bollandsås, O.M. Forest Biomass Change Estimated from Height Change in Interferometric SAR Height Models. Carbon Balance Manag. 2014, 9, 5. [Google Scholar] [CrossRef]
- Solberg, S.; Gizachew, B.; Næsset, E.; Gobakken, T.; Bollandsås, M.O.; Mauya, W.E.; Olsson, H.; Malimbwi, R.; Zahabu, E. Monitoring Forest Carbon in a Tanzanian Woodland Using Interferometric SAR: A Novel Methodology for REDD+. Carbon Balance Manag. 2015, 10, 14. [Google Scholar] [CrossRef]
- Gama, F.F.; dos Santos, J.R.; Mura, J.C. Continuous Monitoring of Biophysical Eucalyptus Sp. Parameters Using Interferometric Synthetic Aperture Radar Data in P and X Bands. J. Appl. Remote Sens. 2016, 10, 026002. [Google Scholar] [CrossRef]
- Kumar, S.; Khati, U.G.; Chandola, S.; Agrawal, S.; Kushwaha, S.P.S. Polarimetric SAR Interferometry Based Modeling for Tree Height and Aboveground Biomass Retrieval in a Tropical Deciduous Forest. Adv. Space Res. 2017, 60, 571–586. [Google Scholar] [CrossRef]
- Yadav, S.; Padalia, H.; Sinha, S.K.; Srinet, R.; Chauhan, P. Above-Ground Biomass Estimation of Indian Tropical Forests Using X Band Pol-InSAR and Random Forest. Remote Sens. Appl. 2021, 21, 100462. [Google Scholar] [CrossRef]
- le Toan, T.; Quegan, S.; Davidson, M.W.J.; Balzter, H.; Paillou, P.; Papathanassiou, K.; Plummer, S.; Rocca, F.; Saatchi, S.; Shugart, H.; et al. The BIOMASS Mission: Mapping Global Forest Biomass to Better Understand the Terrestrial Carbon Cycle. Remote Sens. Environ. 2011, 115, 2850–2860. [Google Scholar] [CrossRef]
- Persson, H.J.; Jonzén, J.; Nilsson, M. Combining TanDEM-X and Sentinel-2 for Large-Area Species-Wise Prediction of Forest Biomass and Volume. Int. J. Appl. Earth Obs. Geoinf. 2021, 96, 102275. [Google Scholar] [CrossRef]
- Mermoz, S.; Réjou-Méchain, M.; Villard, L.; le Toan, T.; Rossi, V.; Gourlet-Fleury, S. Decrease of L-Band SAR Backscatter with Biomass of Dense Forests. Remote Sens. Environ. 2015, 159, 307–317. [Google Scholar] [CrossRef]
- Araza, A.; de Bruin, S.; Herold, M.; Quegan, S.; Labriere, N.; Rodriguez-Veiga, P.; Avitabile, V.; Santoro, M.; Mitchard, E.T.A.; Ryan, C.M.; et al. A Comprehensive Framework for Assessing the Accuracy and Uncertainty of Global Above-Ground Biomass Maps. Remote Sens. Environ. 2022, 272, 112917. [Google Scholar] [CrossRef]
- Santoro, M.; Cartus, O.; Carvalhais, N.; Rozendaal, D.M.A.; Avitabile, V.; Araza, A.; de Bruin, S.; Herold, M.; Quegan, S.; Rodríguez-Veiga, P.; et al. The Global Forest Above-Ground Biomass Pool for 2010 Estimated from High-Resolution Satellite Observations. Earth. Syst. Sci. Data 2021, 13, 3927–3950. [Google Scholar] [CrossRef]
- Santoro, M.; Cartus, O.; Wegmüller, U.; Besnard, S.; Carvalhais, N.; Araza, A.; Herold, M.; Liang, J.; Cavlovic, J.; Engdahl, M.E. Global Estimation of Above-Ground Biomass from Spaceborne C-Band Scatterometer Observations Aided by LiDAR Metrics of Vegetation Structure. Remote Sens. Environ. 2022, 279, 113114. [Google Scholar] [CrossRef]
- Muhammad Waqar, M.; Sukmawati, R.; Ji, Y.; Tetuko, J.; Sumantyo, S.; Segah, H.; Prasetyo, L.B. Retrieval of Tropical Peatland Forest Biomass from Polarimetric Features in Central Kalimantan, Indonesia. Prog. Electromagn. Res. C 2020, 98, 109–125. [Google Scholar] [CrossRef]
- Ji, Y.; Xu, K.; Zeng, P.; Zhang, W. GA-SVR Algorithm for Improving Forest above Ground Biomass Estimation Using SAR Data. IEEE J. Sel. Top. Appl. Earth. Obs. Remote Sens 2021, 14, 6585–6595. [Google Scholar] [CrossRef]
- Zeng, P.; Zhang, W.; Li, Y.; Shi, J.; Wang, Z. Forest Total and Component Above-Ground Biomass (AGB) Estimation through C-and L-Band Polarimetric SAR Data. Forests 2022, 13, 442. [Google Scholar] [CrossRef]
- Huang, W.; Sun, G.; Ni, W.; Zhang, Z.; Dubayah, R. Sensitivity of Multi-Source SAR Backscatter to Changes in Forest Aboveground Biomass. Remote Sens. 2015, 7, 9587–9609. [Google Scholar] [CrossRef]
- Sun, G.; Ranson, K.J.; Kharuk, V.I. Radiometric Slope Correction for Forest Biomass Estimation from SAR Data in the Western Sayani Mountains, Siberia. Remote Sens. Environ. 2002, 79, 279–287. [Google Scholar] [CrossRef]
- Bar-On, Y.M.; Phillips, R.; Milo, R. The Biomass Distribution on Earth. Proc. Natl. Acad. Sci. USA 2018, 115, 6506–6511. [Google Scholar] [CrossRef] [PubMed]
- Erb, K.H.; Kastner, T.; Plutzar, C.; Bais, A.L.S.; Carvalhais, N.; Fetzel, T.; Gingrich, S.; Haberl, H.; Lauk, C.; Niedertscheider, M.; et al. Unexpectedly Large Impact of Forest Management and Grazing on Global Vegetation Biomass. Nature 2018, 553, 73–76. [Google Scholar] [CrossRef] [PubMed]
- Pereira, L.O.; Furtado, L.F.A.; Novo, E.M.L.M.; Sant’Anna, S.J.S.; Liesenberg, V.; Silva, T.S.F. Multifrequency and Full-Polarimetric SAR Assessment for Estimating above Ground Biomass and Leaf Area Index in the Amazon Várzea Wetlands. Remote Sens. 2018, 10, 1355. [Google Scholar] [CrossRef]
- Touzi, R. Target Scattering Decomposition in Terms of Roll-Invariant Target Parameters. IEEE Trans. Geosci. Remote Sens. 2007, 45, 73–84. [Google Scholar] [CrossRef]
- Touzi, R.; Deschamps, A.; Rother, G. Phase of Target Scattering for Wetland Characterization Using Polarimetric C-Band SAR. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3241–3261. [Google Scholar] [CrossRef]
- Bispo, P.C.; Santos, J.R.; Valeriano, M.M.; Touzi, R.; Seifert, F.M. Integration of Polarimetric PALSAR Attributes and Local Geomorphometric Variables Derived from SRTM for Forest Biomass Modeling in Central Amazonia. Can. J. Remote Sens. 2014, 40, 26–42. [Google Scholar] [CrossRef]
- van der Sanden, J. Radar Remote Sensing to Support Tropical Forest Management. Doctoral Thesis, Wageningen Agricultural University, Wageningen, The Netherlands, 1997. [Google Scholar]
- EMBRAPA—CPATU Pesquisas Sobre Utilização e Conservação Do Solo Na Amazônia Oriental—Relatório Final Do Convênio EMBRAPA-CPATU-GTZ; Belém-PA, Brazil: 1986. Available online: https://www.embrapa.br/en/busca-de-publicacoes/-/publicacao/403080/pesquisas-sobre-utilizacao-e-conservacao-do-solo-na-amazonia-oriental-relatorio-final-do-convenio-embrapa-cpatu-gtz (accessed on 28 April 2022).
- Paula da Cruz Gato, A.; Guerreiro Martorano, L.; Makelle de Oliveira Lopes, M.; Conceição da Silva, W. Regime térmico-hídrico climatológico comparado aos valores registrados em 2017 na estação meteorológica de Belterra, Pará. In Proceedings of the Seminário de Iniciação Científica da Embrapa Amazônia Oriental, 22, 2018, Belém, PA, Brazil, 26–27 November 2018; Embrapa Amazônia Oriental: Belém, PA, Brazil, 2018; pp. 134–138. [Google Scholar]
- Brazil. RADAMBRASIL. Departamento Nacional de Produção Mineral. Folha AS.21-Santarém: Geologia, Geomorfologia, Pedologia, Vegetação e Uso Potencial da Terra. Rio de Janeiro: DNPM, 1976. 510p. (Levantamento Dos Recursos Naturais, 10); Ministério das Minas e Energia: Rio de Janeiro, Brazil, 1976; p. 510. [Google Scholar]
- de Almeida, C.A.; Coutinho, A.C.; Esquerdo, J.C. dalla M.; Adami, M.; Venturieri, A.; Diniz, C.G.; Dessay, N.; Durieux, L.; Gomes, A.R. High Spatial Resolution Land Use and Land Cover Mapping of the Brazilian Legal Amazon in 2008 using Landsat-5/TM and MODIS Data. Acta Amaz. 2016, 46, 291–302. [Google Scholar] [CrossRef]
- Jennings, S.B.; Brown, N.D.; Sheil, A.D. Introduction Assessing Forest Canopies and Understorey Illumination: Canopy Closure, Canopy Cover and Other Measures. Forestry 1999, 72, 59–73. [Google Scholar] [CrossRef]
- Neter, J.; Kutner, M.H.; Nachtsheim, C.J.; Wasserman, W. Applied Linear Statistical Models; Irwin: Chicago, IL, USA, 1983; Volume 1, ISBN 0-256-02547-9. [Google Scholar]
- Augustynczik, A.L.D.; Machado, S.D.A.; Figueiredo Filho, A.; Netto, S.P. Avaliação Do Tamanho de Parcelas e de Intensidade de Amostragem Em Inventários Florestais Evaluation of a Plot Sizes and Sampling Intensities in Forest Inventories. Sci. For. 2016, 41, 291–302. [Google Scholar]
- Narvaes, I.D.S. Avaliação de Dados SAR Polarimétricos para Estimativa de Biomassa em Diferentes Fitofisionomias de Florestas Tropicais. Doctoral Thesis, National Institute for Space Research (INPE), São José dos Campos, Brazil, 2010. Available online: http://mtc-m16d.sid.inpe.br/col/sid.inpe.br/mtc-m19@80/2010/08.09.22.43/doc/publicacao.pdf (accessed on 13 July 2022).
- Brown, S.; Gillespie, A.J.R.; Lugo, A.E. Biomass estimation methods for tropical forests with applications to forest inventory data. For. Sci. 1989, 35, 881–902. [Google Scholar] [CrossRef]
- Uhl, C.; Buschbacher, R.; Serrao, E.A.S. Abandoned Pastures in Eastern Amazonia. I. Patterns of Plant Succession. J. Ecol. 1988, 76, 663–681. [Google Scholar] [CrossRef]
- Lee, J.-S.; Grunes, M.R.; Grandi, G. de Polarimetric SAR Speckle Filtering and Its Implication for Classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2363–2373. [Google Scholar] [CrossRef]
- L3HARRIS FAST.FORWARD. ENVI® SARscape® Products. ENVI’s SAR Module. Available online: https://www.l3harrisgeospatial.com/portals/0/pdfs/NV5_SARscape_Analytics_WEB.pdf (accessed on 27 August 2022).
- Woodhouse, I.H. Introduction to Microwave Remote Sensing; Taylor and Francis Group: Boca Raton, FL, USA, 2006. [Google Scholar]
- Cloude, R.; Pottier, E. A Review of Target Decomposition Theorems in Radar Polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S.L. A Three-Component Scattering Model for Polarimetric SAR Data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- Pope, K.O.; Rey-Benayas, J.M.; Paris, J.F. Radar Remote Sensing of Forest and Wetland Ecosystems in the Central American Tropics. Remote Sens. Environ. 1994, 48, 205–219. [Google Scholar] [CrossRef]
- Shimada, M.; Isoguchi, O.; Tadono, T.; Isono, K. PALSAR Radiometric and Geometric Calibration. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3915–3932. [Google Scholar] [CrossRef]
- Mather, P.M.; Koch, M. Computer Processing of Remotely-Sensed Images: An Introduction, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011; ISBN 1119956404. [Google Scholar]
- Tuong, T.T.C.; Tani, H.; Wang, X.; Thang, N.Q.; Bui, H.M. Combination of SAR Polarimetric Parameters for Estimating Tropical Forest Aboveground Biomass. Pol. J. Environ. Stud. 2020, 29, 3353–3365. [Google Scholar] [CrossRef]
- Da Silva Narvaes, I.; Dos Santos, J.R.; De Queiroz Da Silva, A. Analysis of structural parameters of forest typologies using l-band SAR data. Bull. Geod. Sci. 2010, 16, 475–489. [Google Scholar]
- Zebker, H.A.; Norikane, L. Radar Polarimeter Measures Orientation of Calibration Corner Reflectors. Proc. IEEE 1987, 75, 1686–1688. [Google Scholar] [CrossRef]
- Gonçalves, F.G.; Santos, J.R.; Treuhaft, R.N. Stem Volume of Tropical Forests from Polarimetric Radar. Int. J. Remote Sens. 2011, 32, 503–522. [Google Scholar] [CrossRef]
- Jafari, M.; Maghsoudi, Y.; Valadan Zoej, M.J. A New Method for Land Cover Characterization and Classification of Polarimetric SAR Data Using Polarimetric Signatures. IEEE J. Sel. Top. Appl. Earth. Obs. Remote. Sens 2015, 8, 3595–3607. [Google Scholar] [CrossRef]
- Mcnairn, H.; Duguay, C.; Brisco, B.; Pultz, T.J. The Effect of Soil and Crop Residue Characteristics on Polarimetric Radar Response. Remote Sens. Environ. 2002, 80, 308–320. [Google Scholar] [CrossRef]
- Martins, F.; dos Santos, J.R.; Galvão, L.S.; Xaud, H.A.M. Sensitivity of ALOS/PALSAR Imagery to Forest Degradation by Fire in Northern Amazon. Int. J. Appl. Earth Obs. Geoinf. 2016, 49, 163–174. [Google Scholar] [CrossRef]
- Evans, D.L.; Farr, T.G.; van Zyl, J.J.; Zebker, H.A. Radar Polarimetry: Analysis Tools and Applications. IEEE Trans. Geosci. Remote Sens. 1988, 26, 774–789. [Google Scholar] [CrossRef]
- Jafari, M.; Maghsoudi, Y.; Zoej, M.J.V. A New Component Scattering Model Using Polarimetric Signatures Based Pattern Recognition on Polarimetric SAR Data. J. Indian Soc. Remote Sens. 2016, 44, 297–306. [Google Scholar] [CrossRef]
- Bispo, P.D.C.; dos Santos, J.R.; Valeriano, M.d.M.; Graça, P.M.L.d.A. Efeito da topografia da resposta polarimétrica de floresta tropical em imagens PALSAR/ALOS/Effect of topography on the polarimetric response of tropical forest in PALSAR/ALOS. Revista Ambiência 2012, 8, 501–510. [Google Scholar] [CrossRef]
- Baker, P.J.; Wilson, J.S. A Quantitative Technique for the Identification of Canopy Stratification in Tropical and Temperate Forests. For. Ecol. Manag. 2000, 127, 77–86. [Google Scholar] [CrossRef]
- Cao, L.; Coops, N.C.; Innes, J.; Dai, J.; She, G. Mapping above- and below-ground biomass components in subtropical forests using small-footprint LiDAR. Forests 2014, 5, 1356–1373. [Google Scholar] [CrossRef]
- Astiani, D.; Mujiman; Rafiastanto, A. Forest Type Diversity on Carbon Stocks: Cases of Recent Land Cover Conditions of Tropical Lowland, Swamp, and Peatland Forests in West Kalimantan, Indonesia. Biodiversitas 2017, 18, 137–144. [Google Scholar] [CrossRef]
- Touzi, R.; Boerner, W.M.; Lee, J.S.; Lueneburg, E. A Review of Polarimetry in the Context of Synthetic Aperture Radar: Concepts and Information Extraction. Can. J. Remote Sens. 2004, 30, 380–407. [Google Scholar] [CrossRef]
- Ningthoujam, R.K.; Joshi, P.K.; Roy, P.S. Retrieval of Forest Biomass for Tropical Deciduous Mixed Forest Using ALOS PALSAR Mosaic Imagery and Field Plot Data. Int. J. Appl. Earth Obs. Geoinf. 2018, 69, 206–216. [Google Scholar] [CrossRef]
- Liu, Z.; Michel, O.O.; Wu, G.; Mao, Y.; Hu, Y.; Fan, W. The Potential of Fully Polarized ALOS-2 Data for Estimating Forest Above-Ground Biomass. Remote Sens. 2022, 14, 669. [Google Scholar] [CrossRef]
- Carstairs, H.; Mitchard, E.T.A.; McNicol, I.; Aquino, C.; Burt, A.; Ebanega, M.O.; Dikongo, A.M.; Bueso-Bello, J.L.; Disney, M. An Effective Method for InSAR Mapping of Tropical Forest Degradation in Hilly Areas. Remote Sens. 2022, 14, 452. [Google Scholar] [CrossRef]
- Homeier, J.; Breckle, S.W.; Günter, S.; Rollenbeck, R.T.; Leuschner, C. Tree Diversity, Forest Structure and Productivity along Altitudinal and Topographical Gradients in a Species-Rich Ecuadorian Montane Rain Forest. Biotropica 2010, 42, 140–148. [Google Scholar] [CrossRef]
- Sinha, S.; Jeganathan, C.; Sharma, L.K.; Nathawat, M.S. A Review of Radar Remote Sensing for Biomass Estimation. Int. J. Environ. Sci. Technol. 2015, 12, 1779–1792. [Google Scholar] [CrossRef]
- Köhl, M.; Neupane, P.R.; Mundhenk, P. REDD+ Measurement, Reporting and Verification—A Cost Trap? Implications for Financing REDD+MRV Costs by Result-Based Payments. Ecol. Econ. 2020, 168, 106513. [Google Scholar] [CrossRef]

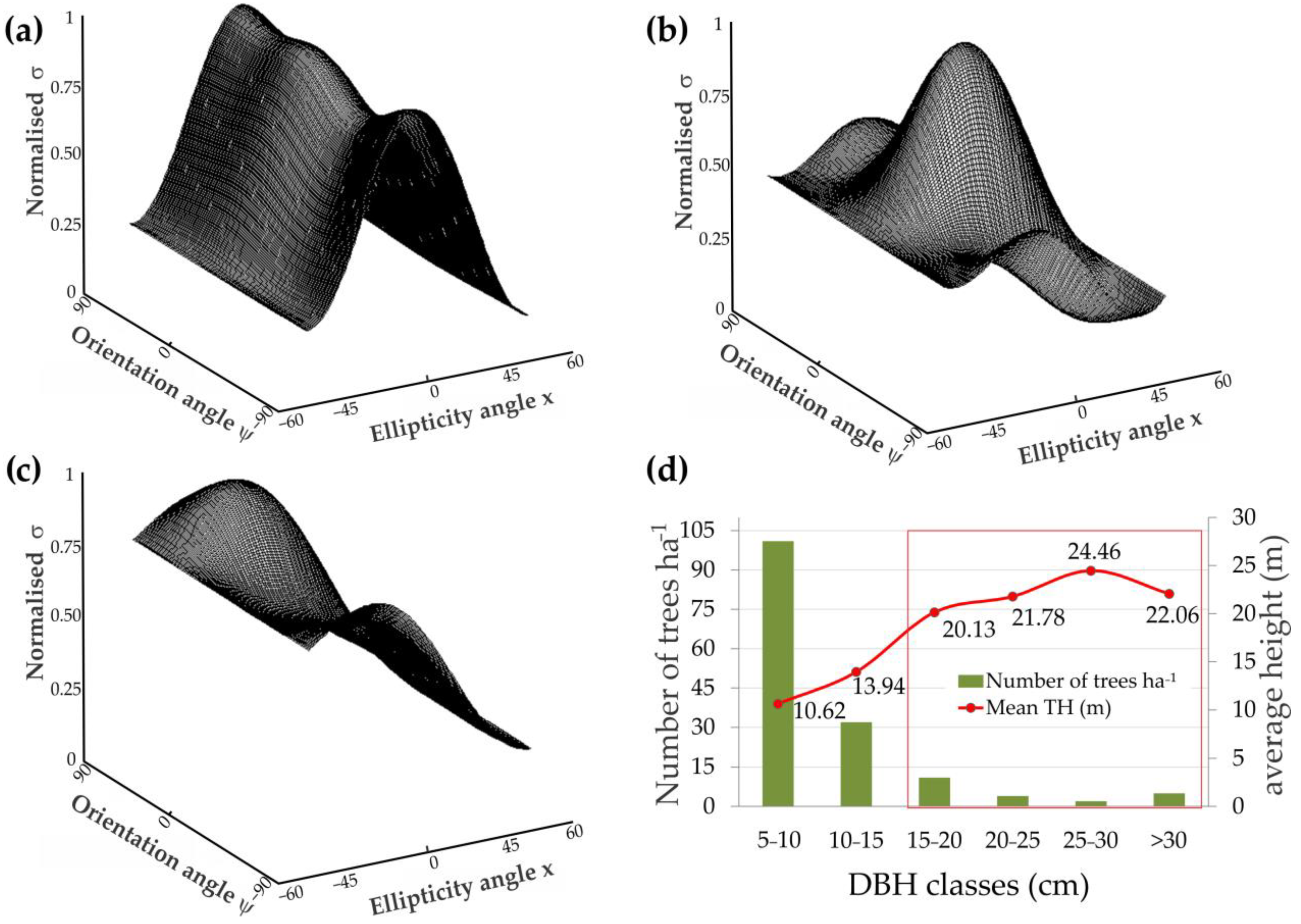

| Typology | Scattering Mechanism | HH Response to VV | Average Pedestal Height (σ) |
|---|---|---|---|
| Primary forest (PF) | |||
| PF1, PF20, PF21, PF29 | multiple and volumetric scattering | HH > VV | 0.142; 0.121; 0.137 and 0.125 |
| PF2, PF9 | multiple scattering | HH < VV or HH ≈ VV | 0.251; 0.151 |
| Mean | 0.155 | ||
| Selective logging (SL) | |||
| SL25 | multiple scattering | HH < VV or HH ≈ VV | 0.16 |
| SL15, SL36, SL37 | multiple and volumetric scattering | HH > VV | 0.199; 0.155; 0.122, |
| SL38, SL40, SL41 | 0.147; 0.141; 0.148 | ||
| Mean | 0.153 | ||
| Advanced secondary succession (ASS) | |||
| ASS18, ASS27 | multiple and volumetric scattering | HH > VV | 0.142; 0.097 |
| ASS33, ASS34, ASS35 | multiple scattering | HH < VV or HH ≈ VV | 0.116; 0.147; 0.144 |
| Mean | 0.129 | ||
| Intermediate secondary succession (IntSS) | |||
| IntSS3, IntSS8, | multiple scattering | HH < VV or HH ≈ VV | 0.141; 0.157; |
| IntSS10, IntSS17 | 0.126; 0.088 | ||
| IntSS7, IntSS12, | multiple and volumetric scattering | HH > VV | 0.107; 0.094, |
| IntSS22, IntSS26 | 0.141; 0.099 | ||
| Mean | 0.119 | ||
| Initial secondary succession (ISS) | |||
| ISS4, ISS5, ISS6 | multiple scattering | HH < VV or HH ≈ VV | 0.161; 0.089; 0.109 |
| ISS28 | 0.133 | ||
| ISS24, ISS31, ISS32 | multiple and volumetric scattering | HH > VV | 0.112; 0.121; 0.117 |
| Mean | 0.127 |
| Variable | βk | Sk | t * | p * | VIF |
|---|---|---|---|---|---|
| Constant | −1221.37 | 442.3 | −2.76 | 0.010 | |
| σ°HH | −70.31 | 26.818 | −2.62 | 0.014 | 4.43 |
| Pv | 1064.65 | 327.2 | 3.25 | 0.003 | 4.91 |
| αS2 | 6.28 | 2.916 | 2.15 | 0.041 | 2.07 |
| ΦS2 | −2.42 | 1.264 | −1.91 | 0.067 | 1.16 |
| ΦS3 | 3.44 | 1.294 | 2.66 | 0.013 | 1.57 |
| τm | 6.05 | 3.474 | 1.74 | 0.094 | 1.29 |
| SAR Sensor | Biomass Saturation (Mg ha−1) | Precision (R2) | RMSE (Mg ha−1) | Technique | Forest Type | Author (s) |
|---|---|---|---|---|---|---|
| ALOS-1/ PALSAR-1 | ~210 | 0.67 | 56.9 | Full polarimetric (coherent and incoherent attributes) | Tropical forest in different successional stages | This study |
| ALOS-1/ PALSAR-1 | 300 | 0.53–0.55 | 92–94 | Michigan Microwave Canopy Scattering model (MIMICS-I) | Deciduous mixed forest | [77] |
| ALOS-1/ PALSAR-1 | ≥100 | not provided | 20 | Polarised data (HV polarization) | Eleven forest types | [15] |
| ~80 | not provided | 20 | Fresh water swamp forests | |||
| ~250 | not provided | 20 | Needleleaf forests | |||
| AIRSAR (L band) | ≤150 | 0.42–0.91 | 23.8 | Full polarimetric | Tropical wet forest | [14] |
| (P-band) | ˂300 | 0.68–0.91 | 22.6 | Full polarimetric | ||
| (C-band) | ≤150 + 40% | 0.79 | 29 | PolinSAR (L + InSAR height index) | ||
| ˂300 + 20% | 0.93 | 15.1 | PolinSAR (P + InSAR height index) | |||
| TerraSAR-X | ~280 | 0.73 | 58 | Radargrammetric height | Spruce forest | [23] |
| Tandem-X | ~300 | 0.66 | 65 | Interferometric height | Spruce forest | [22] |
| ALOS-2/PALSAR-2 and RADARSAT-2 | >120 | 0.562 (site I) 0.461 (site II) | 16.02 (site I) 28.46 (site II) | Polarimetric attributes | China’s temperate forest areas | [35] |
| ALOS-1/ PALSAR-1 | ~210 | 44.70% | 54.3 | Full polarimetric (coherent attributes) | Dense and open ombrophilous forest | [43] |
| ~210 | 44.90% | 50.6 | Full polarimetric (coherent attributes + cosine factor (terrain) | |||
| ~210 | 79.40% | 33.2 | Full polarimetric (coherent attributes + elevation + slope) | |||
| ALOS-2/ PALSAR-2 | 150 | 0.90 | 14.24 | Full polarimetric (coherent and incoherent attributes) + terrain factors + RF + PCA + ridge regression (to solve the problem of collinearity) | Mixed forest of coniferous and broad-leaved trees | [78] |
| ALOS-1/PALSAR -1; Envisar ASAR; GLAS | 147 | 57.1% | 10.6 | WDBEF (Wood Density Biomass Expansion Factor) + sigma nought ground + sigma nought vegetation layers = GSV (growing stock volume (m3 ha−1) | Global estimation | [31] |
| GlobBiomass 2010; CCI Biomass 2017 v.1 (SAR backscattered intensity images); Baccini 2000 (LiDAR footprints + Landsat Reflectance); GEOCARBON 2007–2010 map (combining a refined pantropical map and radar backscatter intensity) | 200–250 | not provided | 76.75 (in average) | Global biomass maps and NFIs | Global estimation | [30] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Narvaes, I.d.S.; Santos, J.R.d.; Bispo, P.d.C.; Graça, P.M.d.A.; Guimarães, U.S.; Gama, F.F. Estimating Forest Above-Ground Biomass in Central Amazonia Using Polarimetric Attributes of ALOS/PALSAR Images. Forests 2023, 14, 941. https://doi.org/10.3390/f14050941
Narvaes IdS, Santos JRd, Bispo PdC, Graça PMdA, Guimarães US, Gama FF. Estimating Forest Above-Ground Biomass in Central Amazonia Using Polarimetric Attributes of ALOS/PALSAR Images. Forests. 2023; 14(5):941. https://doi.org/10.3390/f14050941
Chicago/Turabian StyleNarvaes, Igor da Silva, João Roberto dos Santos, Polyanna da Conceição Bispo, Paulo Maurício de Alencastro Graça, Ulisses Silva Guimarães, and Fábio Furlan Gama. 2023. "Estimating Forest Above-Ground Biomass in Central Amazonia Using Polarimetric Attributes of ALOS/PALSAR Images" Forests 14, no. 5: 941. https://doi.org/10.3390/f14050941
APA StyleNarvaes, I. d. S., Santos, J. R. d., Bispo, P. d. C., Graça, P. M. d. A., Guimarães, U. S., & Gama, F. F. (2023). Estimating Forest Above-Ground Biomass in Central Amazonia Using Polarimetric Attributes of ALOS/PALSAR Images. Forests, 14(5), 941. https://doi.org/10.3390/f14050941








