Laurel Regeneration Management by Smallholders to Generate Agroforestry Systems in the Ecuadorian Amazon Upper Basin: Growth and Yield Models
Abstract
:1. Introduction
2. Materials and Methods
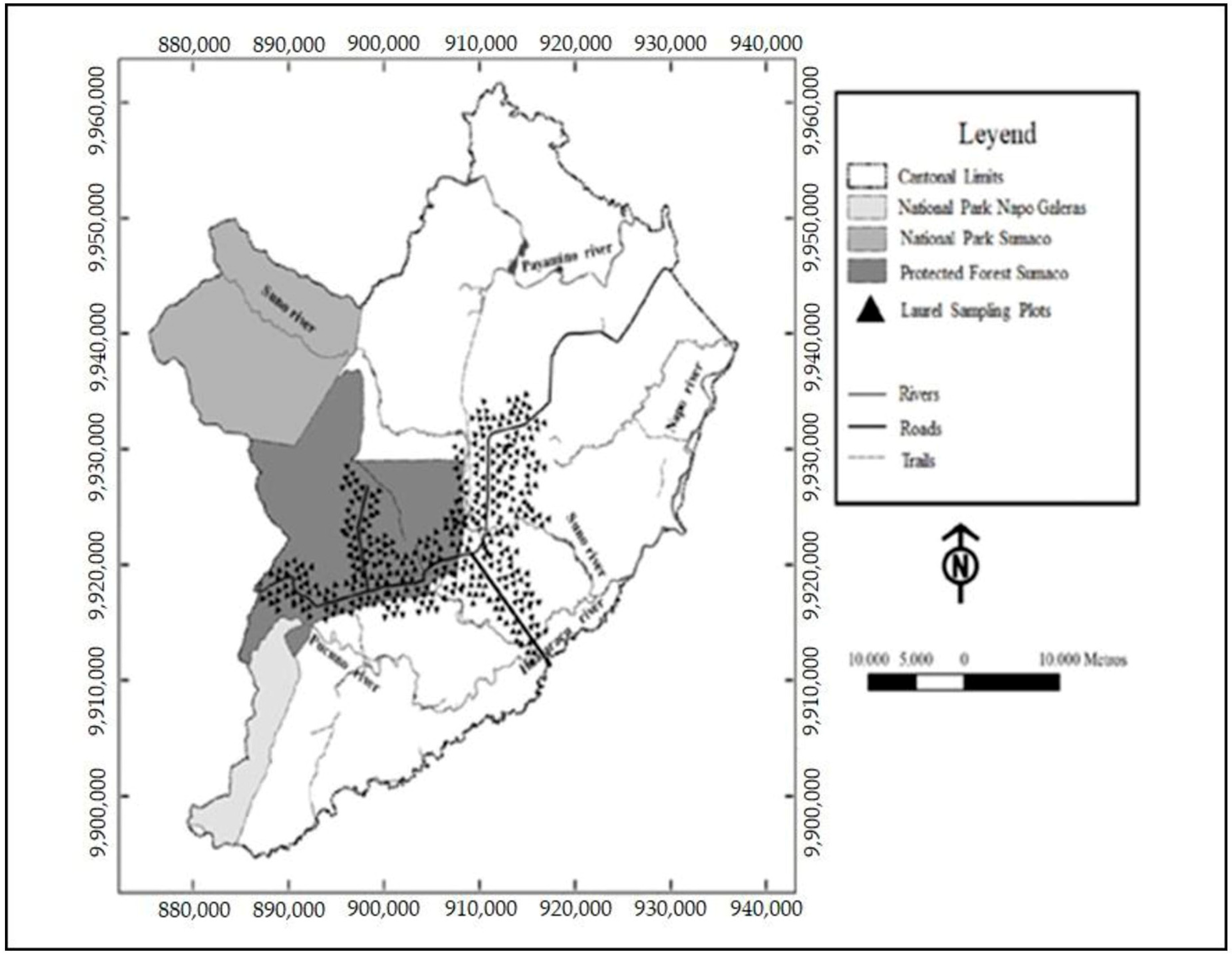
2.1. Study Area
2.2. Tree Competition Index for DBH Analysis in Agroforestry Systems Amazon Upper Basin
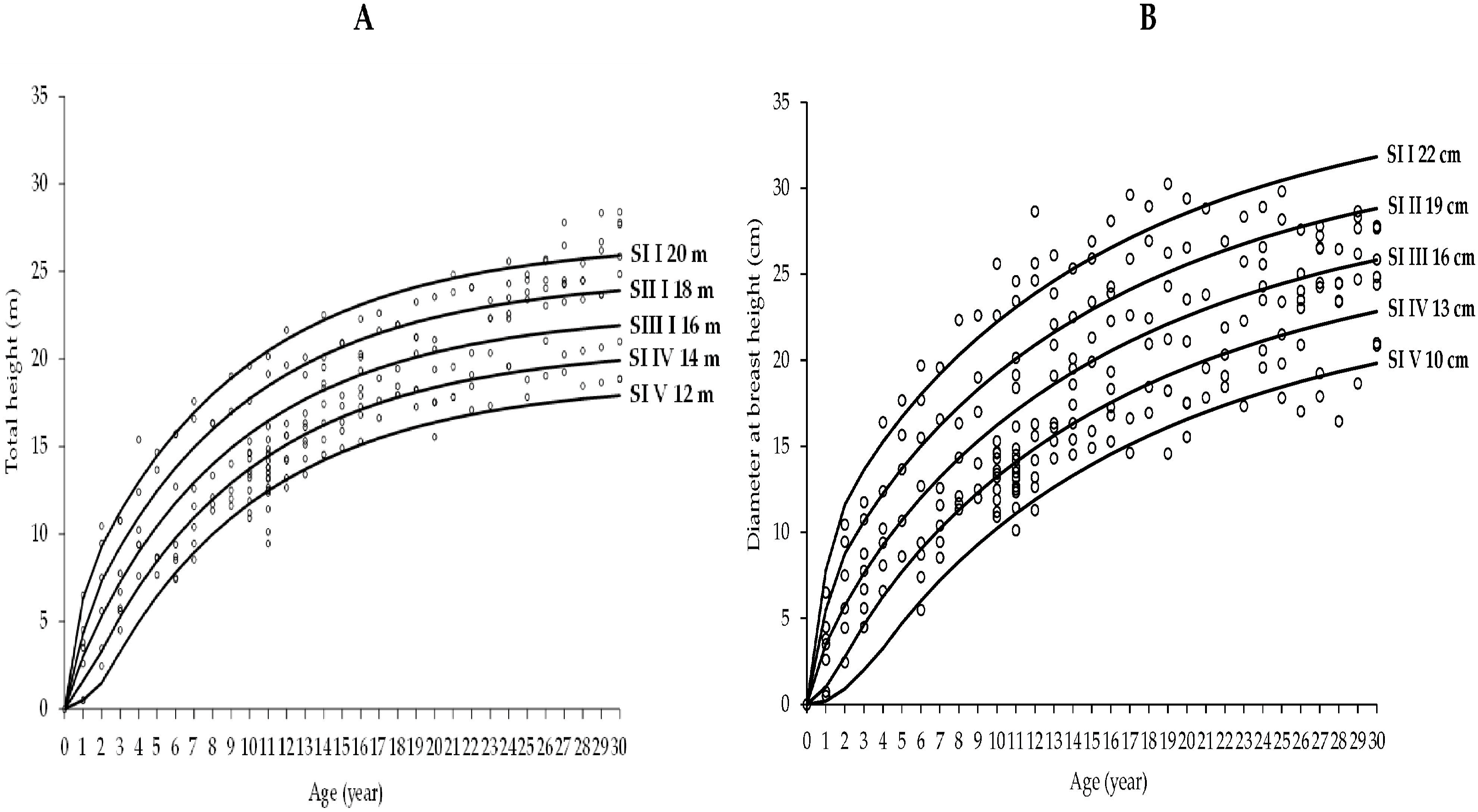
2.3. Site Index
2.4. Volume Estimation
3. Results
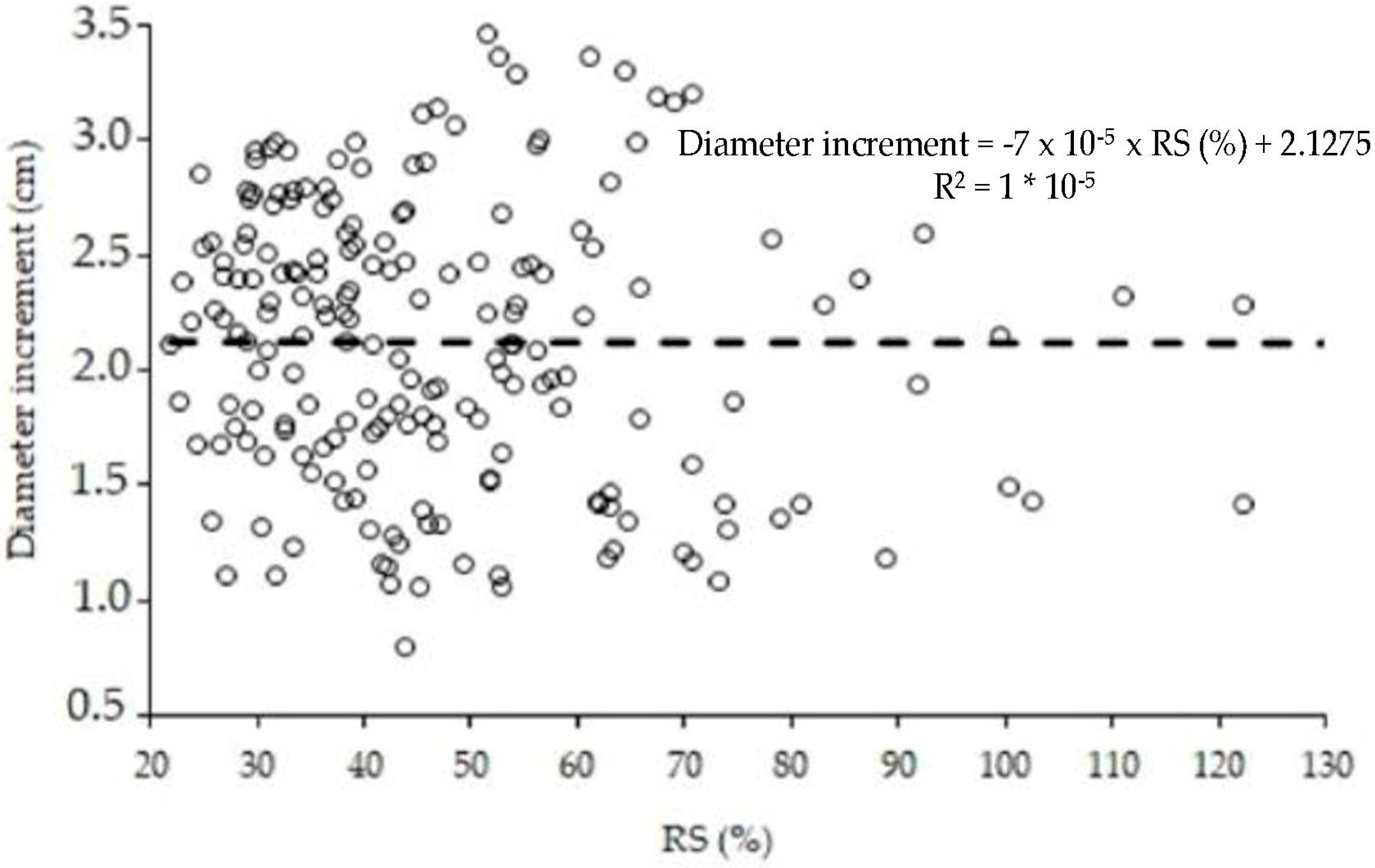
3.1. Tree Competiton Factor in Agroforestry Systems
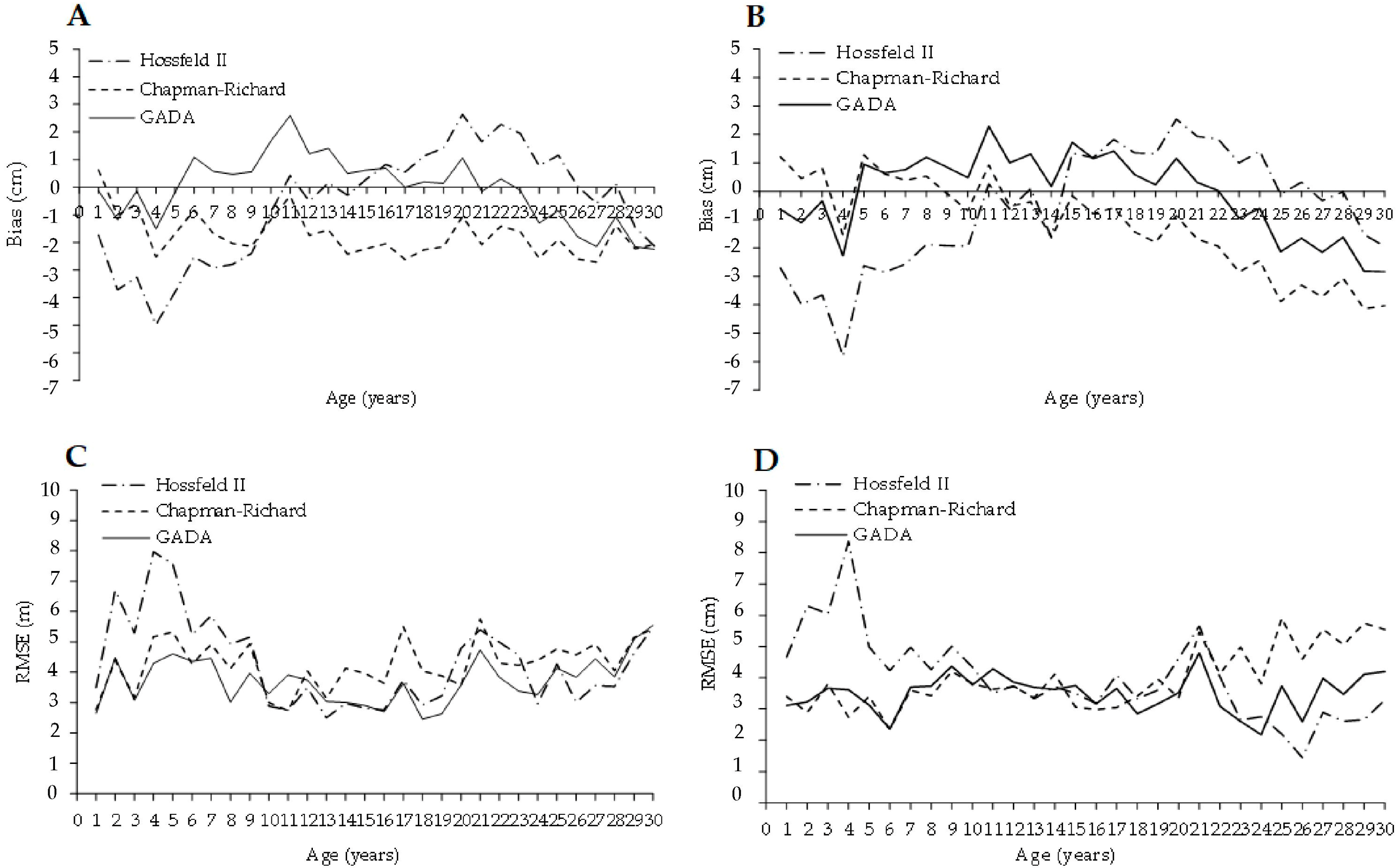
3.2. Growth Models for Laurel Height and Diameter-Age Growth
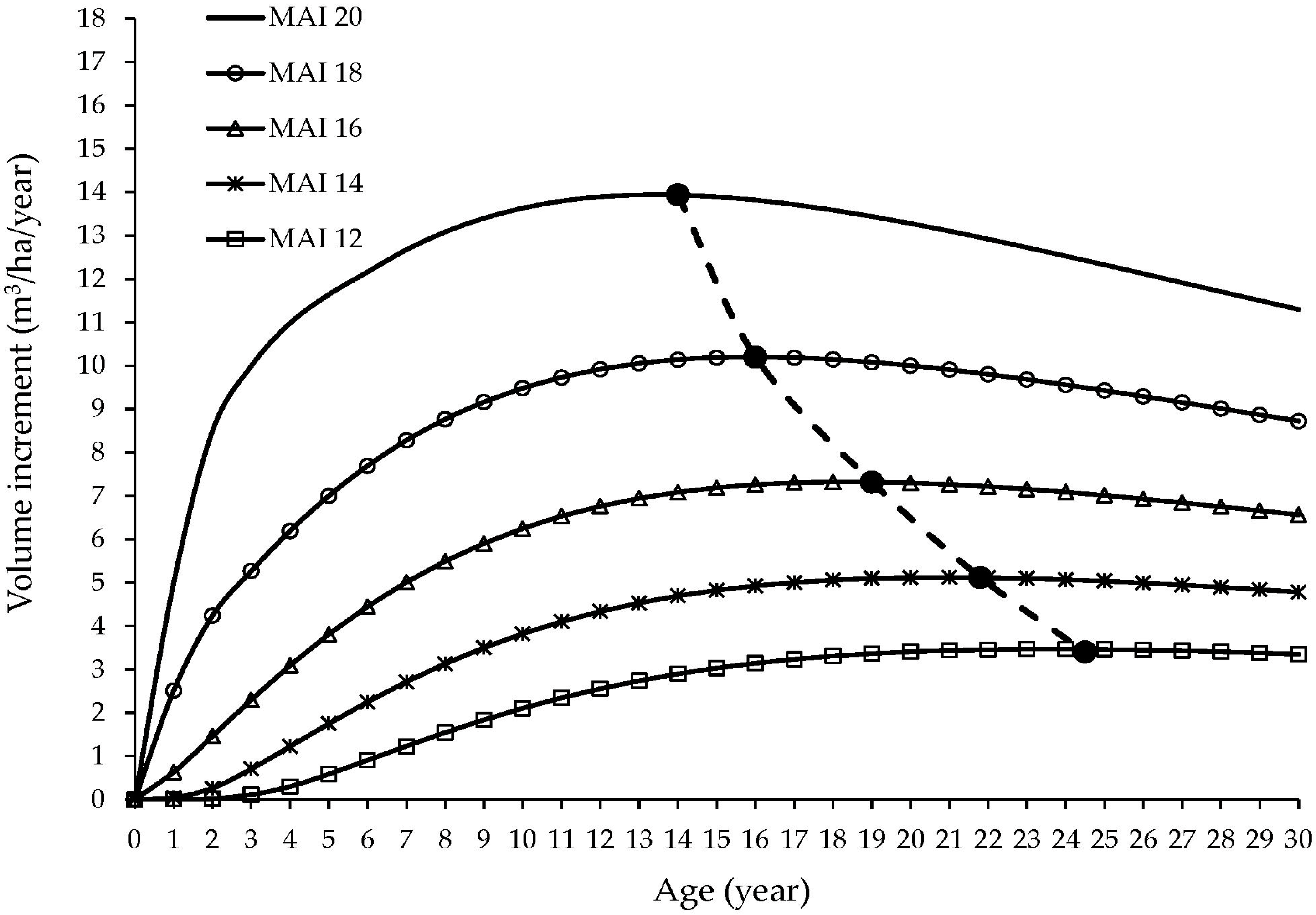
3.3. Estimation of Laurel Total Volume and Yield
4. Discussion
4.1. Competition Index in Laurel Agroforestry System
4.2. Height and Diameter Laurel Growth
4.3. Laurel Total Volume
4.4. Laurel Yield in Agroforestry System
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Soler, R.; Peri, P.L.; Bahamonde, H.; Gargaglione, V.; Ormaechea, S.; Herrera, A.H.; Jardón, L.S.; Lorenzo, C.; Pastur, G.M. Assessing knowledge production for agrosilvopastoral systems in South America. Rangel. Ecol. Manag. 2018, 71, 637–645. [Google Scholar] [CrossRef]
- Jarrett, C.; Cummins, I.; Logan-Hines, E. Adapting indigenous agroforestry systems for integrative landscape management and sustainable supply chain development in Napo, Ecuador. In Integrating Landscapes: Agroforestry for Biodiversity Conservation and Food Sovereignty; Montagnini, F., Ed.; Springer: Cham, Switzerland, 2017; Volume 12, pp. 283–309. [Google Scholar]
- Cañadas, L. El Mapa Ecológico y Bioclimático del Ecuador; Editores Asociados Cia: Quito, Ecuador, 1983; pp. 90–98. [Google Scholar]
- Cañadas-López, A.; Rade Loor, D.; Andrade Candell, J.; Hernández-Díaz, J.C.; Molina Hidrovo, C.; Zambrano Zambrano, M.; Wehenkel, C.H. Gap edge attributes in Neotropical rain forest, Ecuador. Rev. De Biol. Trop. 2018, 66, 149–163. [Google Scholar] [CrossRef] [Green Version]
- Velázquez, M. Identificación, Fenología, Usos y Clasificación de Los Árboles y Arbustos del Bosque Seco de Guápalas. Ph.D. Thesis, Universidad Nacional de Loja, Loja, Ecuador, 1998. [Google Scholar]
- BCE (Banco Central del Ecuador). Información Estadística Mensual. 2020. Available online: https://contenido.bce.fin.ec/home1/estadisticas/cntrimestral/CNTrimestral.html (accessed on 5 December 2022).
- Miller, R.P.; Nair, P.R. Indigenous agroforestry systems in Amazonia: From prehistory to today. Agrofor. Syst. 2006, 66, 151–164. [Google Scholar] [CrossRef]
- De Almeida-Souza, M.; Hernández-Velazco, M.R.; Brazão-Protázio, J.M.; Escobar-Flores, J.G.; López-Sánchez, C.A.; Hernández-Díaz, J.C.; Wehenkel, C.H. A Proposal for a Hybrid Model Based on the Weibull Growth Equation in the Adjustment of Growth Curves applied to Pine Forest Species in Northern Mexico. Environ. Sci. Proc. 2021, 4, 107. [Google Scholar] [CrossRef]
- Porro, R.; Miller, R.P.; Tito, M.R.; Donovan, J.A.; Vivan, J.L.; Trancoso, R.; Van Kanten, R.F.; Grijalva, J.E.; Ramirez, B.L.; Gonçalves, A.L. Agroforestry in the Amazon region: A pathway for balancing conservation and development. In Agroforestry-The Future of Global Land Use; Nair, P., Garrity, D., Eds.; Springer: Dordrecht, The Netherland, 2012; Volume 9, pp. 391–428. [Google Scholar]
- Da Silva, C.B.R.; dos Santos Junior, J.A.; Araújo, A.J.C.; Sales, A.; Siviero, M.A.; Andrade, F.W.; Castro, J.P.; de Figueiredo Latorraca, J.V.; de Lima Melo, L.E. Properties of juvenile wood of Schizolobium parahyba var. amazonicum (paricá) under different cropping systems. Agrofor. Syst. 2020, 94, 583–595. [Google Scholar] [CrossRef]
- Clutter, J.L.; Fortson, J.C.; Pienaar, L.V.; Brister, G.H.; Bailey, R.L. Timber Management: A Quantitative Approach; John Wiley & Sons, Inc.: New York, NY, USA, 1983; pp. 45–130. [Google Scholar]
- Pretzsch, H. Forest Dynamics, Growth, and Yield; Springer: Berlin/Heidelberg, Germany, 2009; Volume 684. [Google Scholar]
- Montoro-Girona, M.; Morin, H.; Lussier, J.M.; Walsh, D. Radial growth response of black spruce stands ten years after experimental shelterwoods and seed-tree cuttings in boreal forest. Forests 2016, 7, 240. [Google Scholar] [CrossRef] [Green Version]
- Alder, D.; Montenegro, F.A. A yield model for Cordia alliodora plantation in Ecuador. Int. For. Rev. 1999, 1, 242–250. [Google Scholar]
- Ricker, M.; Río, R.D. Projecting diameter growth in tropical trees: A new modelling approach. For. Sci. 2004, 50, 213–224. [Google Scholar] [CrossRef]
- Olschewski, R.; Benítez, P.C. Secondary forests as temporary carbon sink? The economic impact of accounting methods on reforestation projects in the tropics. Ecol. Econ. 2005, 55, 380–394. [Google Scholar] [CrossRef]
- Olschewski, R.; Benítez, P.C. Economic trade-offs between carbon sequestration, timber production, and crop pollination in tropical forested landscapes. Ecol. Complex. 2010, 7, 314–319. [Google Scholar] [CrossRef]
- Olschewski, R.; Benítez, P.C. Optimizing joint production of timber and carbon 466 sequestration of afforestation projects. J. For. Econ. 2010, 16, 1–10. [Google Scholar] [CrossRef]
- De Koning, F.; Olschewski, R.; Veldkamp, E.; Benítez-Ponce, P.C.; Laclau, P.; López, M.; Urquiza, M.; Schlichter, T. Evaluation of the CO2 Sequestration Potential of Afforestation Projects and Secondary Forests in Two Different Climate Zones of South America; Deutsche, Gesellschaft für Technische Zusammenarbeit: Eschborn, Germany, 2002; pp. 25–100. [Google Scholar]
- De Koning, F.; Olschewski, R.; Veldkamp, E.; López-Ulloa, P.; Schlichter, T.; Urquiza, M. The ecological and economic potential of carbon sequestration in forests: Examples from South America. Ambio 2005, 34, 224–230. [Google Scholar] [CrossRef] [PubMed]
- Parresol, B.R.; Devall, M.S. Patterns of diametric growth in stem-analyzed laurel trees (Cordia alliadora) in a Panamanian forest. Southwest Nat. 2013, 55, 170–178. [Google Scholar] [CrossRef]
- Somarriba, E.; Suárez-Islas, A.; Calero-Borge, W.; Villota, A.; Castillo, C.; Vílchez, S.; Deheuvels, O.; Cerda, R. Cocoa–timber agroforestry systems: Theobroma cacao—Cordia alliodora in Central America. Agrofor. Syst. 2014, 88, 1001–1019. [Google Scholar] [CrossRef] [Green Version]
- Cieszewski, C.J.; Bailey, R.L. Generalized algebraic difference approach: Theory-based derivation of dynamic site equations with polymorphism and variable asymptotes. For. Sci. 2000, 46, 116–126. [Google Scholar] [CrossRef]
- Cieszewski, C.J. Three methods of deriving advanced Dynamic site equations demonstrated on inland Douglas-fir site curves. Can. J. For. Res. 2001, 31, 165–173. [Google Scholar] [CrossRef]
- Cieszewski, C.J. Comparing fixed- and variable-base-age site equations having single versus multiple asymptotes. For. Sci. 2002, 48, 7–23. [Google Scholar] [CrossRef]
- Cieszewski, C.J. Developing a well-behaved dynamic sit equation using a modified Hossfeld IV function 3 m m1 Y=(ax)/(c=x), a simplified mixed-model and scant subalpine fir dat. For. Sci. 2003, 49, 539–554. [Google Scholar] [CrossRef]
- Wehenkel, C.H.; Cruz-Cobos, F.; Carrillo, A.; Lujan-Soto, J.E. Estimating bark volumes for 16 native tree species on the Sierra Madre Occidental, Mexico. Scand. J. For. Res. 2012, 27, 578–585. [Google Scholar] [CrossRef]
- Simental-Cano, B.; López-Sánchez, C.A.; Wehenkel, C.H.; Vargas-Larreta, B.; Álvarez González, J.G.; Corral-Rivas, J.J. Species-specific and regional volume models for 12 forest species in Durango, Mexico. Rev. Chapingo Ser. Cienc. For. Ambiente 2017, 23, 155–171. [Google Scholar] [CrossRef]
- Tewari, V.P.; Sukumar, R.; Kumar, R.; Gadow, K. Forest observational studies in India: Past developments and considerations for the future. For. Ecol. Manag. 2014, 316, 32–46. [Google Scholar] [CrossRef]
- Cañadas-López, A. Providing Information about Natural Resources as a Base to Support the Decentralization of the Forest Sector in Canton Loreto; Research Centre of Forest Ecology: Göttingen, Germany, 2005; pp. 20–150. [Google Scholar]
- Cañadas-López, A.; Camargo, J.C.; Reyes, X. Community classification as a base for the understanding of dynamics of the land use in Protected Forest Sumaco. In International Research on Food Security, Natural Resource Management and Rural Development, Rural Proverty Reduction through Research for Development and Transformation, 1st ed.; Peters, K., Kirschke, D., Bürkert, A., Schultze-Kraft, R., Bharati, L., Bonte-Friedheim, C., Deininger, A., Bhandari, N., Weitkamp, H., Eds.; Druckhaus Köthen GmbH: Berlin, Germany, 2004; p. 160. [Google Scholar]
- Cañadas-López, A.; Rivadeneira, T.; Andrade, J.; Aguirre, P. Las áreas protegidas como una contribución al desarrollo sustentable: Caso del bosque protector Sumaco, Ecuador. Sustentabilidades 2013, 8, 1–14. [Google Scholar]
- Cañadas-López, A.; Nenadić, O.; Bolte, A. Effects of different land use intensities on the succession of secondary forests in the protected forest Sumaco, Ecuador. In International Research on Food Security, Natural Resource Management and Rural Development, Rural Proverty Reduction through Research for Development and Transformation, 1st ed.; Peters, K., Kirschke, D., Bürkert, A., Schultze-Kraft, R., Bharati, L., Bonte-Friedheim, C., Deininger, A., Bhandari, N., Weitkamp, H., Eds.; Druckhaus Köthen GmbH: Berlin, Germany, 2004; p. 298. [Google Scholar]
- Arroyo-Rodríguez, V.; Melo, F.P.L.; Martínez-Ramos, M.; Bongers, F.; Chazdon, R.L.; Meave, J.A.; Norden, N.; Santos, B.A.; Leal, I.R.; Tabarelli, M. Multiple successional pathways in human-modified tropical landscapes: New insights from forest succession, forest fragmentation and landscape ecology research. Biol. Rev. 2017, 92, 326–340. [Google Scholar] [CrossRef] [PubMed]
- Wilson, F.G. Numerical expression of stocking in terms of height. J. For. 1946, 44, 758–761. [Google Scholar] [CrossRef]
- Long, J.N. A practical approach to density management. For. Chron. 1985, 61, 23–27. [Google Scholar] [CrossRef] [Green Version]
- Cañadas-López, A.; Rade, D.; Siegmund-Schultze, M.; Moreira, C.G.; Vargas-Hernández, J.; Wehenkel, C.H. Growth and yield models for Balsa wood plantations in the coastal lowlands Ecuador. Forests 2019, 10, 733. [Google Scholar] [CrossRef] [Green Version]
- Cañadas-López, A.; Andrade-Candell, J.; Domínguez-Andrade, J.M.; Molina-Hidrovo, C.; Schnabel-Delgado, O.; Vargas-Hernández, J.J.; Wehenkel, C. Growth and yield models for teak planted as living fences in coastal Ecuador. Forests 2018, 9, 55. [Google Scholar] [CrossRef] [Green Version]
- Richards, F.J. A flexible growth function for empirical use. J. Exp. Bot. 1959, 10, 290–300. [Google Scholar] [CrossRef]
- Peschel, W. Mathematical methods for growth studies of trees and forest stands and the results of their application. Tharandter Forstl. Jahrburch 1938, 89, 169–247. [Google Scholar]
- Curtis, R.O. A stem-analysis approach to site-index curves. For. Sci. 1964, 10, 241–256. [Google Scholar] [CrossRef]
- Bailey, R.L.; Clutter, J.L. Base-age invariant polymorphic site curves. For. Sci. 1974, 20, 155–159. [Google Scholar] [CrossRef]
- Burkhart, H.E.; Tomé, M. Modeling Forest Trees and Stands; Springer: Dorcrecht, The Nederlands, 2012; pp. 10–120. [Google Scholar]
- R Foundation for Statistical Computing. Available online: http://www.R-project.org/ (accessed on 22 October 2022).
- STATISTICA 10.0 TIBCO Statistica® Data Scientist. 2023. Available online: https://statistica.software.informer.com/10.0/ (accessed on 20 October 2022).
- Schumacher, F.X.; Hall, F.S. Logarithmic expression of timber-tree volume. J. Agric. Res. 1933, 47, 719–734. [Google Scholar]
- Spurr, S.H. Forest Inventory; Ronald Press Co.: New York, NY, USA, 1952; p. 476. [Google Scholar]
- Avery, T.E.; Burkhart, H.E. Forest Measurements, 5th ed.; McGraw-Hill: New York, NY, USA, 2002; p. 456. [Google Scholar]
- Ruiz, R.M.; Martínez, G.E.R.; Mata, J.J. Análisis del crecimiento y producción de látex en plantaciones forestales comerciales de hule (Hevea brasiliensis Muell Arg.) en el estado de Oaxaca, México. Ra Ximhai 2007, 3, 565–578. [Google Scholar] [CrossRef]
- Honer, T.G. A new total cubic foot volume function. For. Chron. 1965, 41, 476–493. [Google Scholar] [CrossRef]
- Newnham, R.M. Variable-form taper functions for four Alberta tree species. Can. J. For. Res. 1992, 22, 210–223. [Google Scholar] [CrossRef]
- Snipes, M.; Taylor, D.C. Model selection and Akaike Information Criteria: An example from wine ratings and prices. Wine Econ. Policy 2014, 3, 3–9. [Google Scholar] [CrossRef] [Green Version]
- Pretzsch, H. Facilitation and competition reduction in tree species mixtures in Central Europe: Consequences for growth modeling and forest management. Ecol. Model. 2022, 464, 109812. [Google Scholar] [CrossRef]
- Gonzalez de Andres, E.; Camarero, J.J.; Blanco, J.A.; Imbert, J.B.; Lo, Y.H.; Sangüesa-Barreda, G.; Castillo, F.J. Tree-to-tree competition in mixed European beech–Scots pine forests has different impacts on growth and water-use efficiency depending on site conditions. J. Ecol. 2018, 106, 59–75. [Google Scholar] [CrossRef] [Green Version]
- Gea-Izquierdo, G.; Cañellas, I.; Montero, G. Site index in agroforestry systems: Age-dependent and age-independent dynamic growth models for Quercus ilex in Iberian open oak woodlands. Can. J. For. Res. 2008, 38, 101–113. [Google Scholar] [CrossRef] [Green Version]
- Grau, O.; Peñuelas, J.; Ferry, B.; Freycon, V.; Blanc, L.; Desprez, M.; Baraloto, C.; Chave, J.; Descroix, L.; Dourdain, A.; et al. Nutrient-cycling mechanisms other than the direct absorption from soil may control forest structure and dynamics in poor Amazonian soils. Sci. Rep. 2017, 7, 45017. [Google Scholar] [CrossRef] [Green Version]
- Cañadas-López, A.; Gamboa-Trujillo, P.; Buitrón-Garrido, S.; Medina-Torres, B.; Vargas-Hernández, J.J.; Wehenkel, C.H. Thinning Levels of Laurel natural regeneration to establish Traditional Agroforestry Systems, Ecuadorian Amazon Upper Basin. Forests 2023, 14, 667. [Google Scholar] [CrossRef]
- Toraño Caicoya, A.; Pretzsch, H. Stand density biases the estimation of the site index especially on dry sites. Can. J. For. Res. 2021, 51, 1050–1064. [Google Scholar] [CrossRef]
- Ding, Y.; Zang, R.; Huang, J.; Xu, Y.; Lu, X.; Guo, Z.; Ren, W. Intraspecific trait variation and neighborhood competition drive community dynamics in an old-growth spruce forest in northwest China. Sci. Total Environ. 2019, 678, 525–532. [Google Scholar] [CrossRef]
- Guamán, L.A. Turno Biológico de Corta para Cordia alliodora (Ruiz y Pav.) Oken A Través de Métodos Dendrocronológicos en la Quinta Experimental “El Padmi”, Zamora Chinchipe. Bachelor’s Thesis, Universidad Nacional de Loja, Loja, Ecuador, 2019. [Google Scholar]
- Bílek, L.; Böhm, M.; Veloz, L.; Montenegro, F. Production improvement of Cordia alliodora (Ruiz & Pavon) Oken plantations in lowland tropics of Ecuador. Agric. Trop. Et Subtrop. 2011, 44, 77–82. [Google Scholar]
- Mora, B. Índices de Crecimiento del Laurel (Cordia Alliodora) en la Zona de Santo Domingo de Los Colorados. Bachelor’s Thesis, Universidad Central del Ecuador, Quito, Ecuador, 1972. [Google Scholar]
- Briceño-J, A.M.; Rangel-Ch, J.O.; Bogino, S.M. Tree ring study of Cordia alliodora (Ruiz & Pav.) in Colombia. Colomb. For. 2016, 19, 219–232. [Google Scholar] [CrossRef] [Green Version]
- Martínez, H.; Vargas, R.; Leguízamo-Barbosa, A.; Vega-González, L.E.; Neyra-Román, M.G.; Silva, L.J.; Jairo, L.F. Resultados del Comportamiento de Especies Forestales Plantadas en Líneas de Enriquecimiento en Bajo Calima, San José del Guaviare y Tumaco, Colombia, Serie Técnica No 19; ICA/CONIF/FAO: Bogotá, Colombia, 1986; pp. 25–60. [Google Scholar]
- Giraldo, L.G.; Del Valle, J.I.; Escobar, M. El Crecimiento del Nogal (Cordia alliodora) Ruiz & Pavon Oken en Relación con Algunos Factores Climáticos, Edáficos y Fisiográficos en el Suroeste de Antioquia (Colombia). Rev. Fac. Nac. Agron. Medellín 1980, 33, 21–32. [Google Scholar]
- Sebbenn, A.M.; Boshier, D.H.; Freitas, M.L.; Zanatto, A.C.S.; Sato, A.S.; Ettori, L.C.; Moraes, E. Results of an International Provenance Trial of Cordia alliodora in Sao Paulo, Brazil at Five and 23 Years of Age. Silvae Genet. 2007, 56, 110–116. [Google Scholar] [CrossRef] [Green Version]
- Greaves, A.; McCarter, P.S. Cordia Alliodora: A Promising Tree for Tropical Agroforestry; Oxford Forestry Institute, University of Oxford: Oxford, UK, 1990; pp. 15–49. [Google Scholar]
- Somarriba, E.; Valdivieso, R.; Vásquez, W.; Galloway, G. Survival, growth, timber productivity and site index of Cordia alliadora in forestry and agroforestry. Agrofor. Syst. 2001, 51, 111–118. [Google Scholar] [CrossRef]
- Somarriba, E.; Beer, J.W. Dimensions, volumes and growth of Cordia alliodora in agroforestry systems. For. Ecol. Manag. 1987, 18, 113–126. [Google Scholar] [CrossRef]
- Lamprecht, H. Silviculture in the Tropics: Tropical Forest Ecosystems and Their Tree Species: Possibilities and Methods for Their Long-term Utilization; Deutsche Gesellschaft für Technische Zusammenarbeit: Eschborn, Germany, 1989; pp. 130–190. [Google Scholar]
- Heuveldop, J.; Fassbemder, H.W.; Alpizar, L.; Enriquez, G.; Fölster, H. Modelling agroforestry systems of cocoa (Theobroma cacao) in Costa Rica. II. Cacao and wood production, litter production and decomposition. Agrofor. Syst. 1988, 6, 37–48. [Google Scholar] [CrossRef]
- Johnson, P.; Morales, R. A Review of Cordia alliodora (Ruiz & Pav.) Oken. Turrialba 1972, 22, 210–220. [Google Scholar]
- Hummel, S. Height, diameter and crown dimensions of Cordia alliodora associated with tree density. For. Ecol. Manag. 2000, 127, 31–40. [Google Scholar] [CrossRef]
- Beer, J.; Bonnemann, A.; Chávez, W.; Fassbender, H.W.; Imbach, A.C.; Martel, I. Modelling agroforestry systems of cacao (Theobroma cacao) with laurel (Cordia alliodora) or poro (Erythrina poeppigiana) in Costa Rica. Agrofor. Syst. 1990, 12, 229–249. [Google Scholar] [CrossRef]
- Hallé, F.; Oldeman, R.A.; Tomlinson, P.B. Tropical Trees and Forests: An Architectural Analysis; Springer Science & Business Media: Berlin, Heidelberg, NY, USA, 2012; pp. 10–120. [Google Scholar]
- Bergmann, C.; Stuhrmann, M.; Zech, W. Site factors, foliar nutrient levels and growth of Cordia alliodora plantations in the humid lowlands of Northern Costa Rica. Plant Soil 1994, 166, 193–202. [Google Scholar] [CrossRef]
- Kleinn, C. Lecture Notes for the Teaching Module Forest Inventory and Remote Sensing. In Ed Faculty of Forest Science and Forest Ecology; Georg-August Universität Göttingen: Göttingen, Germany, 2007; pp. 10–70. [Google Scholar]
- Cañadas-López, A. Volumen y perfil de fuste para Cordia alliodora en sistemas agroforestales, Bosque Protector Sumaco. Bosques Latid. Cero 2007, 3, 15–20. [Google Scholar]
- Cañadas-López, A.; Vilčko, F.; Rade, D.; Zambrano, C.; Molina, C. Hacia una descripción de fuste para Laurel (Cordia alliodora) en sistemas agroforestales, Bosque Protector Sumaco. ACI Av. Cienc. Ing. 2014, 6, 24–31. [Google Scholar] [CrossRef]
- Chazdon, R.L.; Broadbent, E.N.; Rozendaal, D.M.; Bongers, F.; Zambrano, A.M.A.; Aide, T.M.; Balvanera, P.; Becknell, J.M.; Boukili, V.; Brancalion, P.H.; et al. Carbon sequestration potential of second-growth forest regeneration in the Latin American tropics. Sci. Adv. 2016, 2, e1501639. [Google Scholar] [CrossRef] [Green Version]
- Piotto, D.; Montagnini, F.; Ugalde, L.; Kanninen, M. Performance of forest plantations in small and medium-sized farms in the Atlantic lowlands of Costa Rica. For. Ecol. Manag. 2003, 175, 195–204. [Google Scholar] [CrossRef]
- Alves, D.; Viera, S.; Scaranello, M.; Camargo, P.B.; Santos, F.A.M.; Joly, C.A.; Martinelli, L.A. Forest structure and live aboveground biomass variation along an elevational gradient of tropical Atlantic moist forest (Brazil). For. Ecol. Manag. 2010, 260, 679–691. [Google Scholar] [CrossRef]
- Antúnez, P.; Wehenkel, C.H.; Kukunda, C.B.; Hernández-Díaz, J.C. Climatic Variables Differentially Influence Neotropical Plant Species of Conservation Concern. J. Sustain. For. 2021, 12, 43–58. [Google Scholar] [CrossRef]
- Salas, G.; Valencia, J.E. Notas Sobre la Reforestación con Cordia Alliodora (Ruiz & Pav.) Oken en dos Zonas Tropicales de Cajura: Tumaco y Carare-Opón Colombia. Serie Técnica No 10; CONIF: Medellín, Colombia, 1979; pp. 20–50. [Google Scholar]
- Hudson, J.M. A note on Cordia alliodora in Vanuatu. Commonw. For. Rev. 1984, 63, 181–183. [Google Scholar]
- Vega, L. Plantaciones de Cordia Alliodora en Combinación con Cultivos Agrícolas, una Alternativa de Manejo en Surinam; Instituto Forestal Latino Americano de Investigación y Capacitación: Mérida, Venezuela, 1978; pp. 21–38. [Google Scholar]
- Beer, J. Dimensiones, Volúmenes y Crecimiento de Cordia Alliodora en Sistemas Agroforestales; CATIE: Turrialba, Costa Rica, 1986; pp. 12–80. [Google Scholar]
- Beer, J. Experiences with Coffee-Shade Trees in Costa Rica. Advances in Agroforestry Research; CATIE: Turrialba, Costa Rica, 1987; pp. 40–80. [Google Scholar]
- EME (Ministerio del Ambiente de la Republica del Ecuador). Texto Unificado de la Legislación Ambiental Secundaria (Tulas); MAE: Quito, Ecuador, 2003; Available online: https://www.ambiente.gob.ec (accessed on 5 December 2022).
- Cañadas, A.; Rade, D.; Domínguez, J.M.; Murillo, I.; Molina, C. Modelación Forestal Como Innovación Tecnológica Para el Manejo Silvicultural y Aprovechamiento Económico de la Balsa, Región Costa-Ecuador; Yala, A., Ed.; INIAP, Estación Experimental Portoviejo: Quito, Ecuador, 2016; pp. 20–40. ISBN 978-9942-09360-8. [Google Scholar]
| Characterization of the Data Used in the Fitting Process | Variable | Average | Maximum | Minimum | Standard Error (±) |
|---|---|---|---|---|---|
| Stand information of 226 plots | Age in years | 15.10 | 30.00 | 1.00 | 0.55 |
| Diameter at breast height (cm) | 18.30 | 31.45 | 0.98 | 0.46 | |
| Total height (m) | 16.68 | 28.41 | 0.50 | 0.39 | |
| Laurel sample tree for volume fitted (195 trees) | Diameter at Breast height (cm) | 16.97 | 30.24 | 4.30 | 2.91 |
| Height (m) | 14.03 | 30.23 | 5.00 | 1.87 | |
| Volume (m3) | 0.25 | 0.99 | 0.02 | 0.01 |
| Model | Expression | Equation |
|---|---|---|
| Schumacher–Hall (allometric) [46] | (10) | |
| Spurr [47] | (11) | |
| Spurr potential [47] | (12) | |
| Spurr with an independent term [47] | (13) | |
| Incomplete generalized combined variable [48] | (14) | |
| Australian formula [49] | (15) | |
| Honer [50] | (16) | |
| Newnham [51] | (17) |
| Parameter | Model | Parameter | Estimated Value | Standard Error | p-Value | RMSE |
|---|---|---|---|---|---|---|
| Height-age | Equation (1) | a1 a2 a3 | 41.748 0.015 0.550 | 16.86 0.02 0.07 | <0.001 <0.001 <0.001 | 3.17 |
| Equation (2) | a1 a2 a3 | 0.181 −0.133 0.130 | 0.24 0.08 0.12 | <0.001 <0.001 <0.001 | 3.22 | |
| Equation (8) | b1 b2 b3 | 0.109 −12.593 42.093 | 0.03 3.50 11.81 | <0.001 <0.001 <0.001 | 2.92 | |
| Diameter-age | Equation (1) | a1 a2 a3 | 154.363 0.0005 0.449 | 2513.90 0.02 0.07 | <0.001 <0.001 <0.001 | 3.11 |
| Equation (2) | a1 a2 a3 | 1.508 −1.046 1.045 | 0.34 0.01 9.34 | <0.001 <0.001 <0.001 | 3.15 | |
| Equation (8) | b1 b2 b3 | 0.059 −5.094 19.809 | 0.002 0.48 0.32 | <0.001 <0.001 <0.001 | 2.83 |
| Model | MSE | R2Adj | Parameter | Estimator | SE | AIC |
|---|---|---|---|---|---|---|
| Spurr potential | 0.12 | 0.96 | a | 0.00007 | <0.00 | −11.66 |
| b | 1.44231 | 0.05 | ||||
| Schumacher-Hall (allometric) | 0.05 | 0.94 | a | 0.00036 | <0.00 | −7.28 |
| b | −0.08518 | 0.09 | ||||
| c | 2.48693 | 0.08 | ||||
| Australian formula | 0.05 | 0.94 | a | −0.17367 | 0.02 | −7.21 |
| b | −0.00068 | <0.00 | ||||
| c | 0.02476 | <0.00 | ||||
| d | 0.00004 | <0.00 | ||||
| Incomplete generalized combined variable | 0.09 | 0.88 | a | −0.30835 | 0.02 | −6.60 |
| b | 0.03523 | <0.00 | ||||
| c | 0.00001 | <0.00 | ||||
| Honer | 0.17 | 0.87 | a | −343.79 | <0.00 | −6.02 |
| b | 29876.01 | 0.03 | ||||
| Spurr with an independent term | 0.19 | 0.87 | a | 0.00795 | 0.01 | −5.9 |
| b | 0.00004 | <0.00 | ||||
| Newnham | 0.78 | 0.49 | a | 0.24198 | 0.02 | −4.48 |
| b | 0.000001 | <0.00 | ||||
| c | −0.01904 | 1.23 | ||||
| d | −1995.99 | 822.10 | ||||
| Spurr | 0.19 | 0.43 | a | 0.00045 | <0.00 | −0.67 |
| Author | Country | Age (Years) | Best Site | Worst Site | Best Site | Worst Site | ||
|---|---|---|---|---|---|---|---|---|
| Height (m) | DBH (cm) | Height (m) | DBH (cm) | Volume (m3 ha−1) | Volume (m3 ha−1) | |||
| Current study | Ecuador Amazon Region | 10 | 19.7 | 22.2 | 11.7 | 10.2 | 136 (300 trees ha−1) | 21 (300 trees ha−1) |
| 14 | 22.2 | 25.3 | 14.2 | 13.3 | 195 (300 trees ha−1) | 41 (300 trees ha−1) | ||
| 24 | 25.2 | 30.1 | 17.2 | 18.1 | 300 (300 trees ha−1) | 83 (300 trees ha−1) | ||
| Cañadas-López [30] | Ecuador Amazon region | 10 | 14.6 | |||||
| Alder and Montenegro [14] | Ecuador coast lowland region | 10 | 28.0 | 18.2 | ||||
| 14 | 296 (300 trees ha−1) | 83 (300 trees ha−1) | ||||||
| Guamán [60] | Ecuador Amazon region Zamora Chinchipe | 31 | 32.3 | |||||
| Bílek et al. [61] | Ecuador Río Pitzara coast lowland region | 1.2 | 5.4 | |||||
| Mora [62] | Ecuador Sto. Domingo Coast lowland region | 6 | 70 (708 trees ha−1) | |||||
| Briceño et al. [63] | Tropical Dry Forest, Tolima Colombia | 64 | 205.5 | |||||
| Martínez et al. [64] | Colombia La Espirrilla | 7 | 40 (357 trees ha−1) | |||||
| Giraldo et al. [65] | Colombia in higher altitudes | 50 | 30 | 16 | ||||
| Sebbenn et al. [66] | Brazil São Paulo | 23 | 8.8 | 11.7 | 14.1 | |||
| Greaves and McCarter [67] | Central and South America | 20–30 | 35 | 55 | 30 | 40 | ||
| Somarriba et al. [22] | Central America | 9 | 48 (204 trees ha−1) | |||||
| Parresol and Devall [21] | Panamá | 14 | 15.7 | |||||
| Somarriba et al. [68] | Costa Rica TalamancaPanamá Changuinola | 5 | 21 | 28.5 | 15 | 15.6 | ||
| 5 | 114 (300 trees ha−1) | 74 (300 trees ha−1) | ||||||
| Somarriba and Beer [69] | Costa Rica Province Limón | 34 | 690 (68–290 trees ha−1) | 298 (68–290 trees ha−1) | ||||
| Lamprecht [70] | Costa Rica Turrialba | 10 | 12.5 | 16 | ||||
| Heuveldop et al. [71] | Costa Rica Turrialba | 8 | 14.0 | 26.7 | 14.6 | |||
| Johnson and Morales [72] | Costa Rica Turrialba | 13 | 19.6 | 22.2 | ||||
| Costa Rica Turrialba | 3 | 5.2 | 8.9 | |||||
| Hummel [73] | Costa Rica low elevation Atlantic coast | 10 | 17.1 | 21.3 | ||||
| Beer et al. [74] | Costa Rica Atlantic coast | 10.5 | 15 | 24 | 77.6 (278 trees ha−1) | |||
| Johnson and Morales [72] | Costa Rica Atlantic coast | 24 | 29.3 | 37.8 | ||||
| Hallé, et al. [75] | Tropical rain forest | 5 | 12 | 10.5 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cañadas-López, Á.; Gamboa-Trujillo, P.; Buitrón-Garrido, S.; Medina-Torres, B.; Velasco, C.; Vargas-Hernández, J.d.J.; Wehenkel, C. Laurel Regeneration Management by Smallholders to Generate Agroforestry Systems in the Ecuadorian Amazon Upper Basin: Growth and Yield Models. Forests 2023, 14, 1174. https://doi.org/10.3390/f14061174
Cañadas-López Á, Gamboa-Trujillo P, Buitrón-Garrido S, Medina-Torres B, Velasco C, Vargas-Hernández JdJ, Wehenkel C. Laurel Regeneration Management by Smallholders to Generate Agroforestry Systems in the Ecuadorian Amazon Upper Basin: Growth and Yield Models. Forests. 2023; 14(6):1174. https://doi.org/10.3390/f14061174
Chicago/Turabian StyleCañadas-López, Álvaro, Paul Gamboa-Trujillo, Santiago Buitrón-Garrido, Byron Medina-Torres, Christian Velasco, José de Jesús Vargas-Hernández, and Christian Wehenkel. 2023. "Laurel Regeneration Management by Smallholders to Generate Agroforestry Systems in the Ecuadorian Amazon Upper Basin: Growth and Yield Models" Forests 14, no. 6: 1174. https://doi.org/10.3390/f14061174
APA StyleCañadas-López, Á., Gamboa-Trujillo, P., Buitrón-Garrido, S., Medina-Torres, B., Velasco, C., Vargas-Hernández, J. d. J., & Wehenkel, C. (2023). Laurel Regeneration Management by Smallholders to Generate Agroforestry Systems in the Ecuadorian Amazon Upper Basin: Growth and Yield Models. Forests, 14(6), 1174. https://doi.org/10.3390/f14061174






