Tree Skeletonization with DBSCAN Clustering Using Terrestrial Laser Scanning Data
Abstract
:1. Introduction
1.1. Background
1.2. Related Work
2. Materials and Methods
2.1. Field Data Collection and Processing
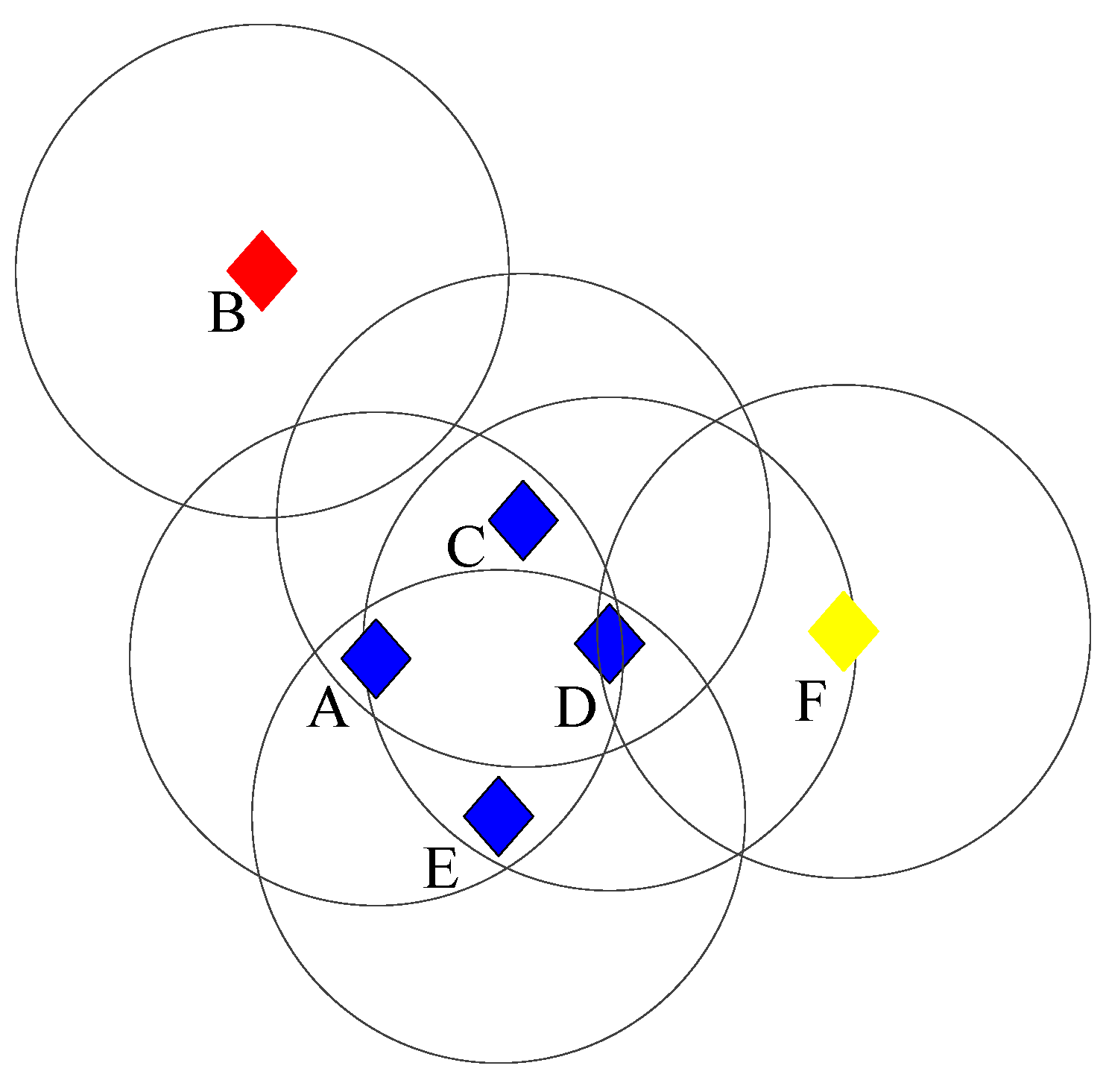
2.2. DBSCAN
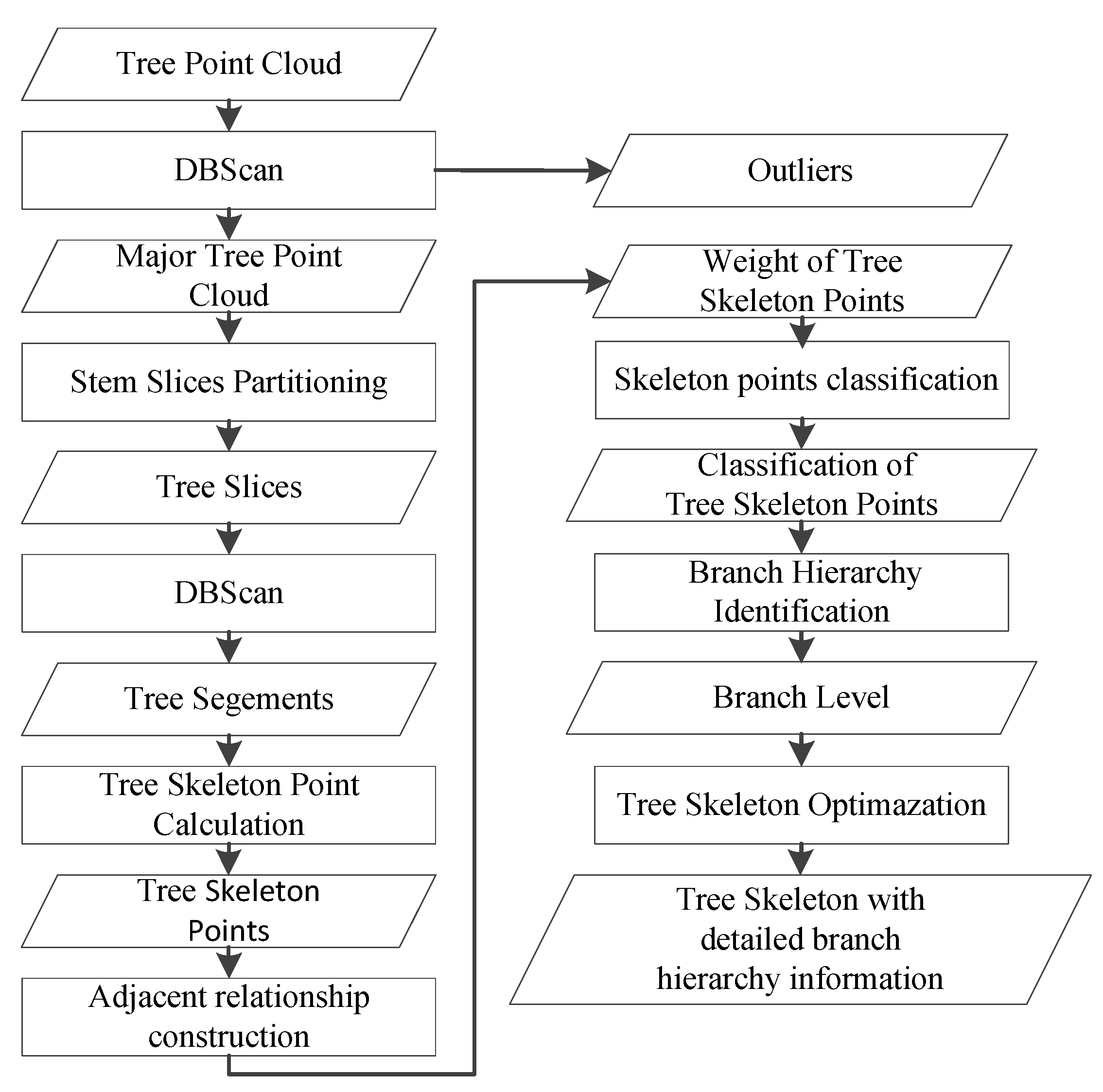
2.3. Tree-Skeletonization Method
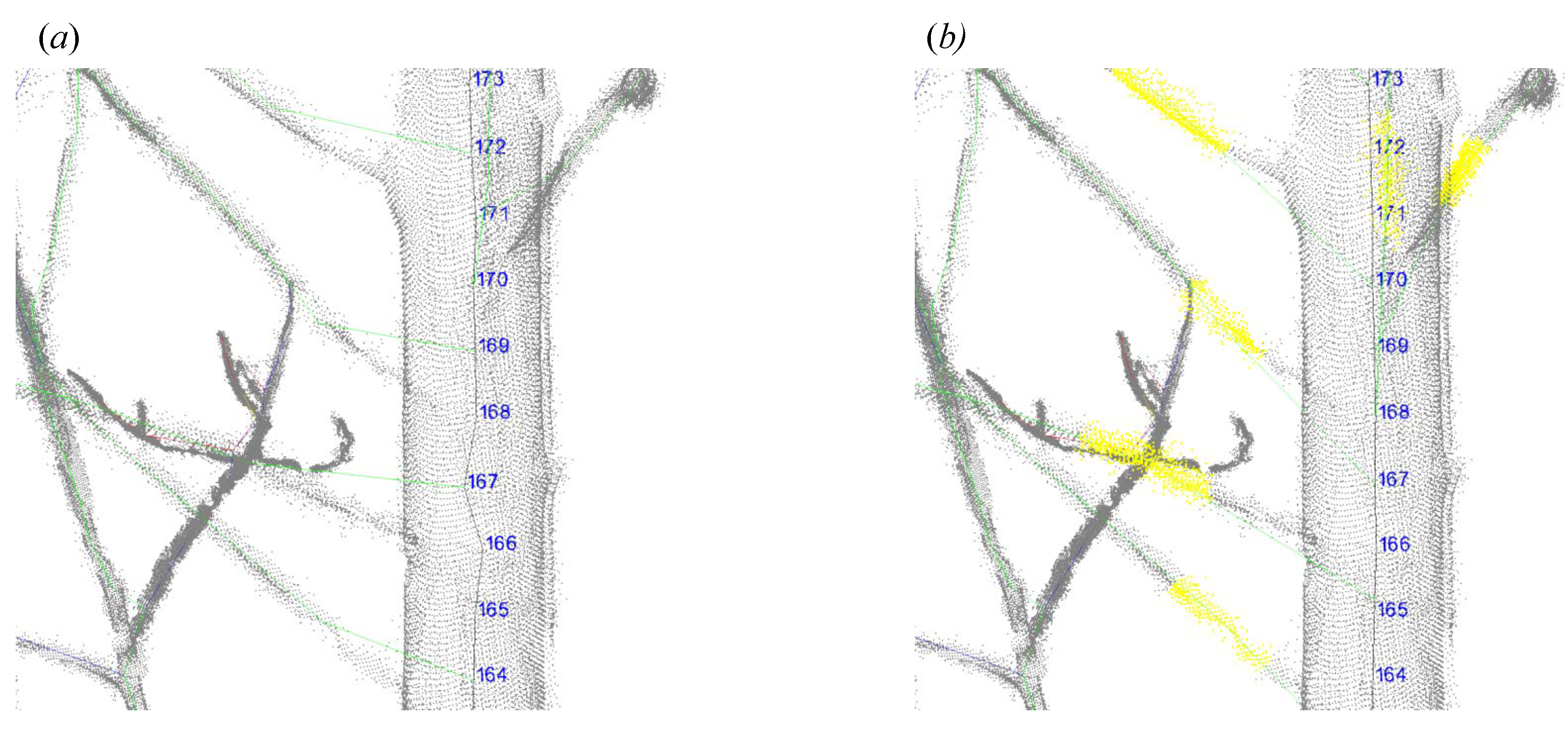
2.3.1. Outlier Removal and Recorded Traversal Order
2.3.2. Tree Slice and Segment Generation
2.3.3. Tree Skeleton Point Calculation with Point-Inversion Transformations
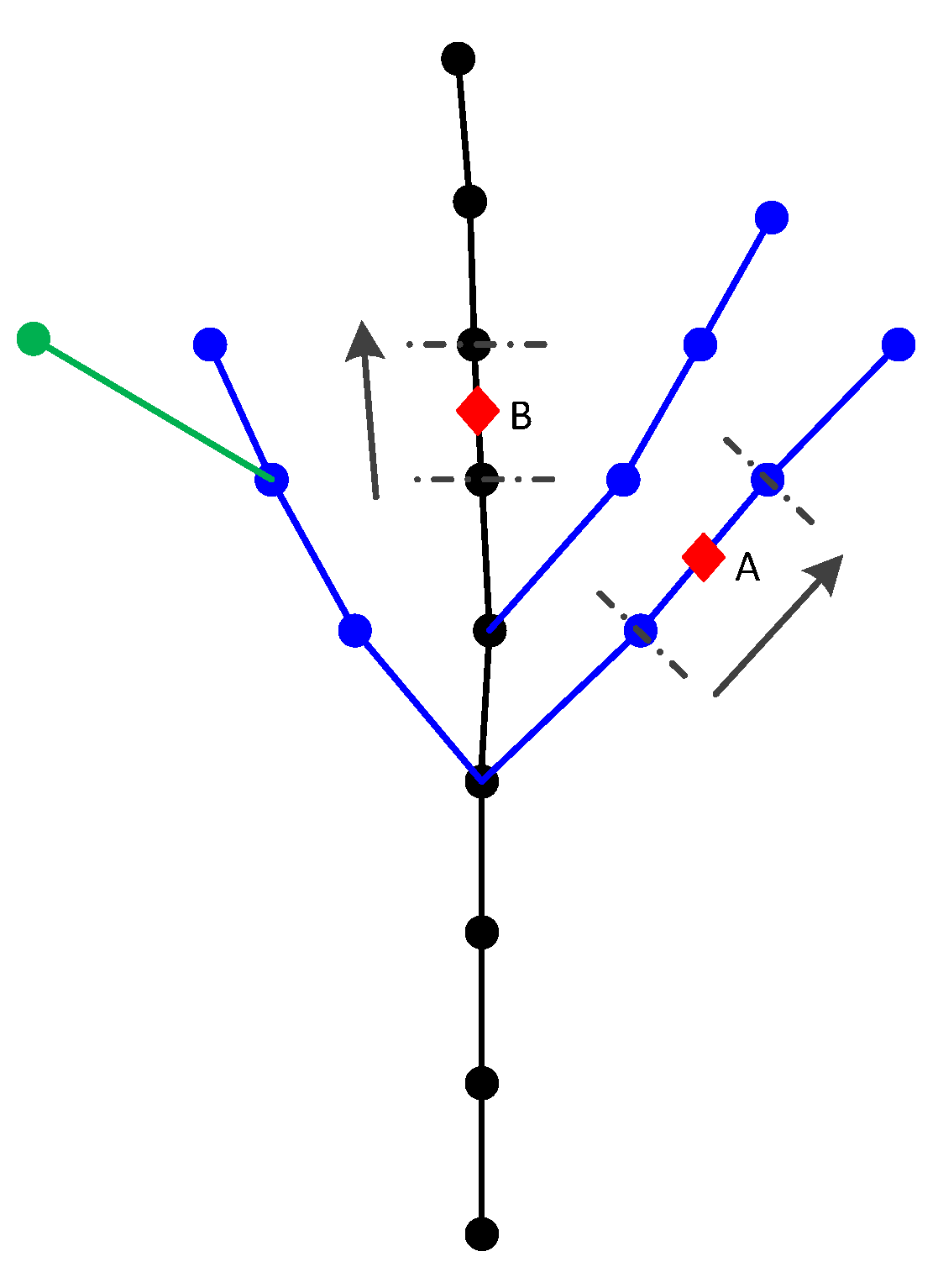
2.3.4. Adjacent Relationship Construction
2.3.5. Skeleton Point Classification and Branch Hierarchy Identification
2.3.6. Tree Skeleton Optimization
2.4. Assessment Indices
3. Results
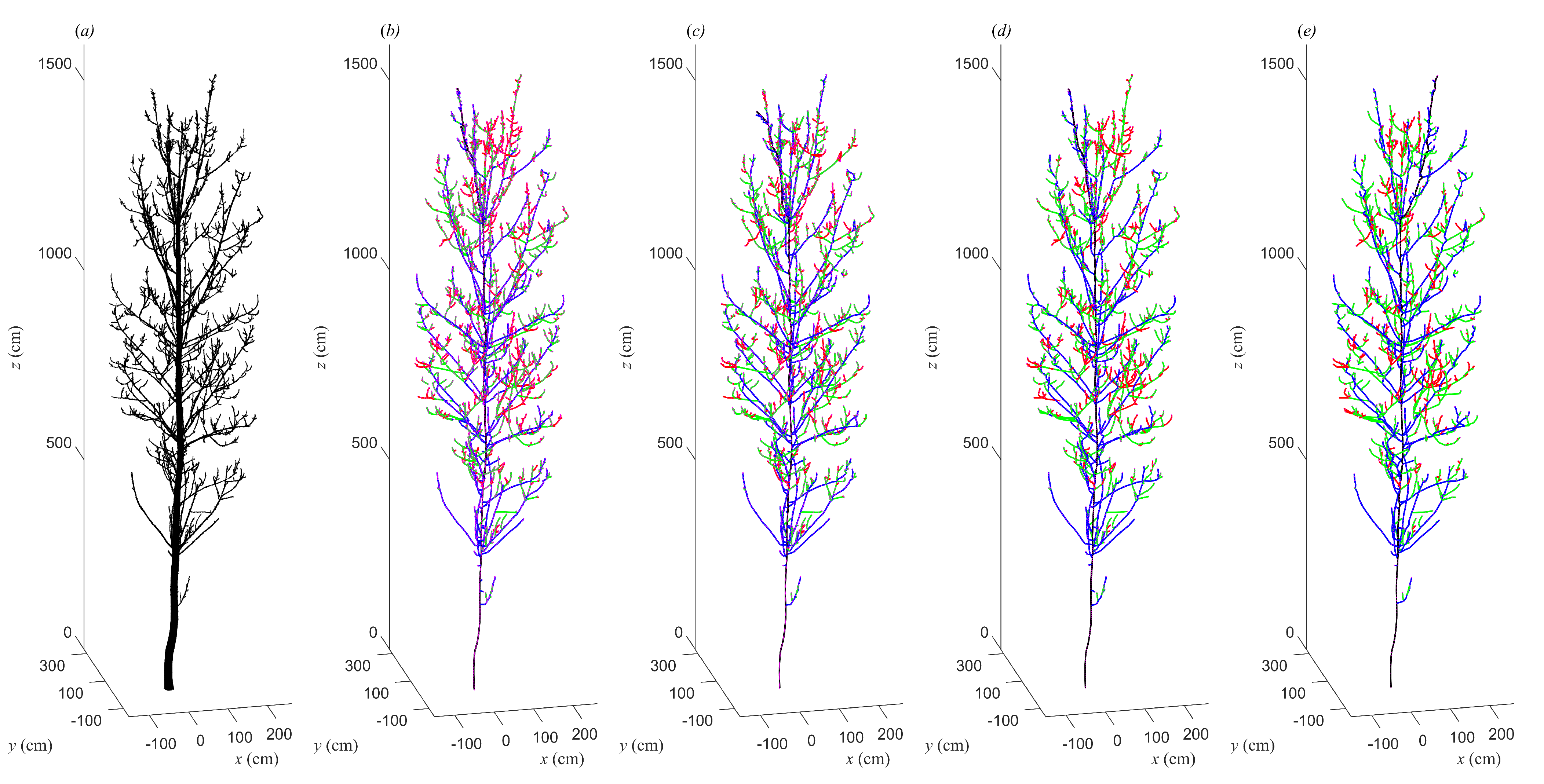
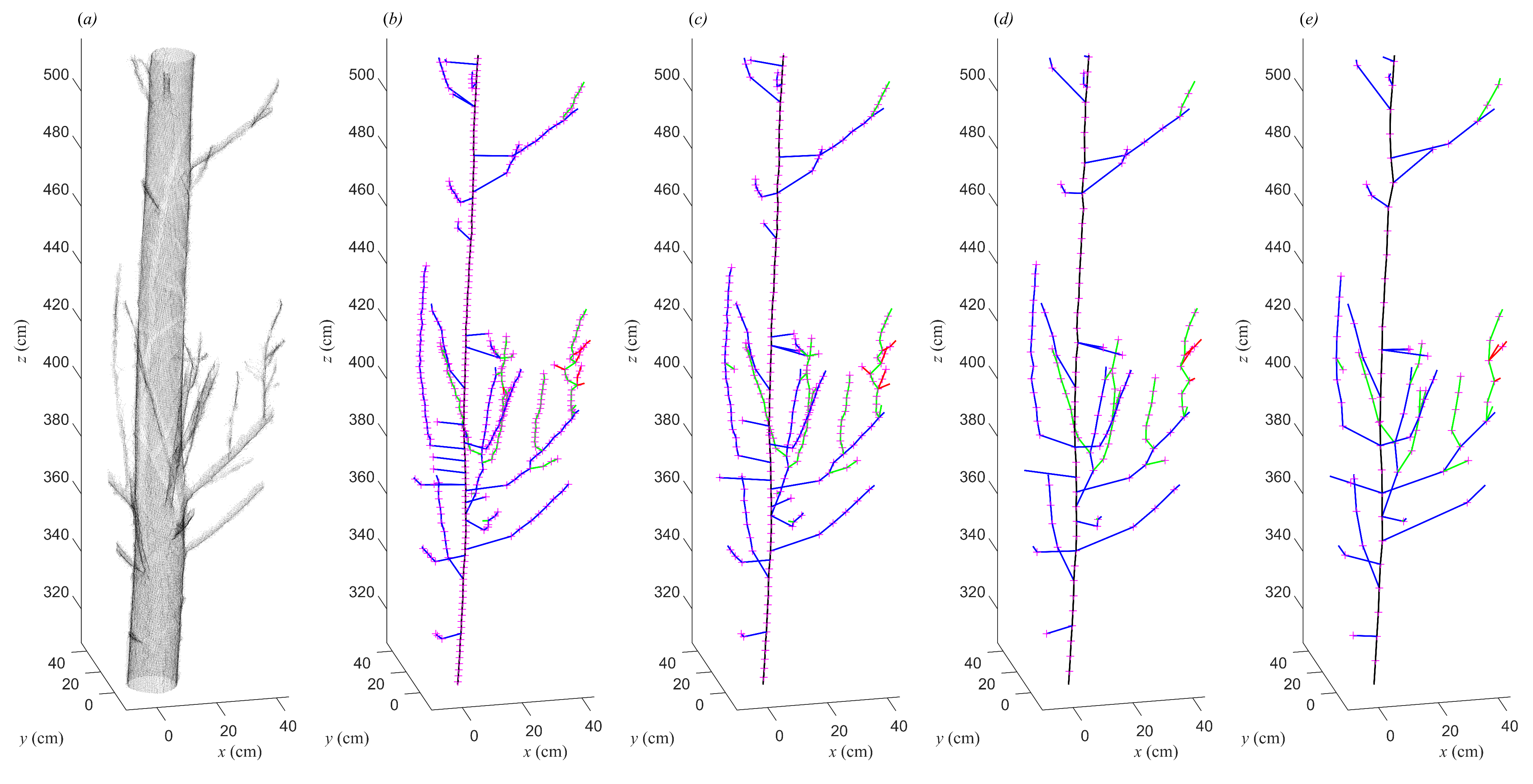
3.1. Results of the Constructed Tree Skeleton with Four Groups of Parameter Values
3.2. Visualizations of Four Constructed Tree Skeletons with a Group of Parameter Values
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Raumonen, P.; Kaasalainen, M.; Åkerblom, M.; Kaasalainen, S.; Kaartinen, H.; Vastaranta, M.; Holopainen, M.; Disney, M.; Lewis, P. Fast Automatic Precision Tree Models from Terrestrial Laser Scanner Data. Remote Sens. 2013, 5, 491. [Google Scholar] [CrossRef] [Green Version]
- Abegg, M.; Bösch, R.; Kükenbrink, D.; Morsdorf, F. Tree volume estimation with terrestrial laser scanning-Testing for bias in a 3D virtual environment. Agric. For. Meteorol. 2023, 331, 109348. [Google Scholar] [CrossRef]
- Huang, H.; Wu, S.; Cohen-Or, D.; Gong, M.; Zhang, H.; Li, G.; Chen, B. L1-Medial Skeleton of Point Cloud. ACM Trans. Graph. 2013, 32, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Jiang, A.; Liu, J.; Zhou, J.; Zhang, M. Skeleton Extraction from Point Clouds of Trees with Complex Branches via Graph Contraction. Vis. Comput. 2021, 27, 2235–2251. [Google Scholar]
- Xu, Y.; Hu, C.; Xie, Y. An improved space colonization algorithm with DBSCAN clustering for a single tree skeleton extraction. Int. J. Remote Sens. 2022, 43, 3692–3713. [Google Scholar] [CrossRef]
- Li, J.; Wu, H.; Xiao, Z.; Lu, H. 3D modeling of laser-scanned trees based on skeleton refined extraction. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102943. [Google Scholar] [CrossRef]
- Su, Z.; Zhao, Y.; Zhao, C.; Guo, X.; Li, Z. Skeleton extraction for tree models. Math. Comput. Model. 2011, 54, 1115–1120. [Google Scholar] [CrossRef]
- Pueschel, P. The influence of scanner parameters on the extraction of tree metrics from FARO Photon 120 terrestrial laser scans. ISPRS J. Photogramm. Remote Sens. 2013, 78, 58–68. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppä, J.; Kaartinen, H.; Lehtomäki, M.; Pyörälä, J.; Pfeifer, N.; Holopainen, M.; Brolly, G.; Francesco, P.; Hackenberg, J.; et al. International benchmarking of terrestrial laser scanning approaches for forest inventories. ISPRS J. Photogramm. Remote Sens. 2018, 144, 137–179. [Google Scholar] [CrossRef]
- Livny, Y.; Yan, F.; Olson, M.; Chen, B.; Zhang, H.; El-Sana, J. Automatic reconstruction of tree skeletal structures from point clouds. ACM Trans. Graph. (TOG) 2010, 29, 151. [Google Scholar] [CrossRef] [Green Version]
- Yan, D.M.; Wintz, J.; Mourrain, B.; Wang, W.; Boudon, F.; Godin, C. Efficient and robust reconstruction of botanical branching structure from laser scanned points. In Proceedings of the 2009 11th IEEE International Conference on Computer-Aided Design and Computer Graphics, Huangshan, China, 19–21 August 2009; pp. 572–575. [Google Scholar] [CrossRef] [Green Version]
- Bucksch, A.; Lindenbergh, R.; Menenti, M. SkelTre - Robust skeleton extraction from imperfect point clouds. Vis. Comput. 2010, 26, 1283–1300. [Google Scholar] [CrossRef] [Green Version]
- He, G.; Yang, J.; Behnke, S. Research on geometric features and point cloud properties for tree skeleton extraction. Pers. Ubiquitous Comput. 2018, 22, 903–910. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, J.; Benes, B.; Deussen, O.; Zhang, X.; Huang, H. TreePartNet Neural Decomposition of Point Clouds for 3D Tree Reconstruction. ACM Trans. Graph. 2021, 40, 232:1–232:16. [Google Scholar] [CrossRef]
- Sun, J.; Wang, P.; Li, R.; Zhou, M.; Wu, Y. Fast Tree Skeleton Extraction Using Voxel Thinning Based on Tree Point Cloud. Remote Sens. 2022, 14, 2558. [Google Scholar] [CrossRef]
- Liu, L.; Pan, g.Y.; Li, Z. Individual Tree DBH and Height Estimation Using Terrestrial Laser Scanning (TLS) in A Subtropical Forest. Sci. Silvae Sin. 2016, 52, 26–37. [Google Scholar] [CrossRef]
- Rusu, R.B.; Cousins, S. 3d is here: Point cloud library (pcl). In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1–4. [Google Scholar]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xiaowei, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise; AAAI Press: Washington, DC, USA, 1996; pp. 226–231. [Google Scholar]
- You, L.; Guo, J.; Pang, Y.; Tang, S.; Song, X.; Zhang, X. 3D stem model construction with geometry consistency using terrestrial laser scanning data. Int. J. Remote Sens. 2021, 42, 714–737. [Google Scholar] [CrossRef]
- You, L.; Tang, S.; Song, X.; Lei, Y.; Zang, H.; Lou, M.; Zhuang, C. Precise Measurement of Stem Diameter by Simulating the Path of Diameter Tape from Terrestrial Laser Scanning Data. Remote Sens. 2016, 8, 717. [Google Scholar] [CrossRef] [Green Version]
- You, L.; Wei, J.; Liang, X.; Lou, M.; Pang, Y.; Song, X. Comparison of Numerical Calculation Methods for Stem Diameter Retrieval Using Terrestrial Laser Data. Remote Sens. 2021, 13, 1780. [Google Scholar] [CrossRef]
- Qin, H.; Han, J.; Li, N.; Huang, H.; Chen, B. Mass-Driven Topology-Aware Curve Skeleton Extraction from Incomplete Point Clouds. IEEE Trans. Vis. Comput. Graph. 2020, 26, 2805–2817. [Google Scholar] [CrossRef] [PubMed]
- Yifan, W.; Wu, S.; Huang, H.; Cohen-Or, D.; Sorkine-Hornung, O. Patch-based progressive 3d point set upsampling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5958–5967. [Google Scholar]





| Tree ID | Tree Height (m) | Point Number | (cm) | h (cm) | k | Skeleton Height (m) | Skeleton Point Number | Height Error (m) | (cm) | (cm) | (cm) | (○) | (○) | (○) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0213 | 15.927 | 2,289,875 | 1.0 | 6 | 8 | 3 | 15.829 | 3473 | 0.099 | 4.211 | 0.017 | 0.429 | 50.346 | 0.121 | 4.548 |
| 5 | 5 | 15.880 | 5574 | 0.048 | 7.766 | 0.006 | 0.320 | 50.089 | 0.055 | 6.130 | |||||
| 3 | 8 | 15.891 | 9467 | 0.037 | 9.983 | 0.005 | 0.310 | 50.206 | 0.012 | 7.831 | |||||
| 2 | 10 | 15.896 | 14445 | 0.031 | 6.431 | 0.008 | 0.288 | 54.609 | 0.015 | 11.169 | |||||
| 0111 | 15.922 | 1,349,179 | 1.0 | 6 | 8 | 3 | 15.840 | 1983 | 0.083 | 8.177 | 0.009 | 0.423 | 47.506 | 0.090 | 4.025 |
| 5 | 5 | 15.884 | 3183 | 0.038 | 8.177 | 0.009 | 0.365 | 48.969 | 0.068 | 5.479 | |||||
| 3 | 8 | 15.894 | 5434 | 0.028 | 8.177 | 0.007 | 0.339 | 48.969 | 0.063 | 6.802 | |||||
| 2 | 10 | 15.898 | 8290 | 0.024 | 8.538 | 0.005 | 0.354 | 54.232 | 0.045 | 8.860 | |||||
| 0510 | 10.108 | 833,913 | 1.0 | 6 | 8 | 3 | 10.049 | 992 | 0.058 | 7.226 | 0.016 | 0.424 | 49.142 | 0.041 | 6.817 |
| 5 | 5 | 10.050 | 1613 | 0.058 | 7.226 | 0.016 | 0.409 | 45.146 | 0.041 | 7.149 | |||||
| 3 | 8 | 10.075 | 2838 | 0.033 | 11.367 | 0.013 | 0.525 | 50.526 | 0.022 | 8.763 | |||||
| 2 | 10 | 10.079 | 4444 | 0.029 | 6.711 | 0.008 | 0.430 | 54.415 | 0.018 | 13.802 | |||||
| 0406 | 17.827 | 3,027,495 | 1.5 | 6 | 8 | 3 | 17.746 | 3910 | 0.081 | 15.290 | 0.009 | 0.543 | 51.734 | 0.028 | 7.239 |
| 5 | 5 | 17.751 | 6186 | 0.077 | 15.290 | 0.009 | 0.512 | 51.734 | 0.033 | 7.551 | |||||
| 3 | 8 | 17.759 | 10543 | 0.081 | 15.290 | 0.008 | 0.476 | 53.679 | 0.016 | 9.380 | |||||
| 2 | 10 | 17.778 | 16035 | 0.049 | 15.290 | 0.008 | 0.444 | 53.679 | 0.007 | 12.311 | |||||
| 0305 | 17.128 | 3,378,374 | 1.5 | 6 | 8 | 3 | 17.038 | 5107 | 0.090 | 12.168 | 0.010 | 0.464 | 51.928 | 0.033 | 6.954 |
| 5 | 5 | 17.085 | 8285 | 0.043 | 12.168 | 0.010 | 0.444 | 48.858 | 0.046 | 7.443 | |||||
| 3 | 8 | 17.095 | 14107 | 0.033 | 12.168 | 0.008 | 0.415 | 52.264 | 0.022 | 9.324 | |||||
| 2 | 10 | 17.097 | 21521 | 0.030 | 17.298 | 0.006 | 0.400 | 53.596 | 0.011 | 14.309 | |||||
| 0407 | 14.350 | 2,192,439 | 1.5 | 6 | 8 | 3 | 14.231 | 2989 | 0.119 | 13.366 | 0.006 | 0.426 | 53.806 | 0.019 | 11.750 |
| 5 | 5 | 14.301 | 4830 | 0.049 | 7.672 | 0.010 | 0.469 | 51.360 | 0.131 | 7.564 | |||||
| 3 | 8 | 14.310 | 8197 | 0.040 | 9.514 | 0.006 | 0.417 | 53.806 | 0.019 | 12.114 | |||||
| 2 | 10 | 14.320 | 12446 | 0.030 | 7.672 | 0.006 | 0.398 | 53.806 | 0.019 | 13.061 | |||||
| 0511 | 15.674 | 1,218,069 | 1.0 | 6 | 8 | 3 | 15.596 | 1929 | 0.078 | 8.605 | 0.015 | 0.512 | 53.294 | 0.081 | 6.632 |
| 5 | 5 | 15.633 | 3175 | 0.041 | 8.605 | 0.015 | 0.512 | 53.294 | 0.150 | 7.692 | |||||
| 3 | 8 | 15.891 | 5406 | 0.037 | 9.983 | 0.005 | 0.310 | 50.206 | 0.012 | 7.831 | |||||
| 2 | 10 | 15.896 | 8456 | 0.031 | 9.983 | 0.005 | 0.296 | 54.609 | 0.012 | 9.959 | |||||
| 0617 | 15.551 | 2,825,789 | 1.0 | 6 | 8 | 3 | 15.437 | 4252 | 0.114 | 8.709 | 0.007 | 0.409 | 53.984 | 0.046 | 6.253 |
| 5 | 5 | 15.495 | 6859 | 0.056 | 4.990 | 0.007 | 0.383 | 52.103 | 0.046 | 6.549 | |||||
| 3 | 8 | 15.530 | 11826 | 0.021 | 13.255 | 0.005 | 0.363 | 53.984 | 0.025 | 0.025 | |||||
| 2 | 10 | 15.535 | 18109 | 0.016 | 13.255 | 0.004 | 0.343 | 54.107 | 0.009 | 9.957 | |||||
| 0514 | 13.193 | 1,203,242 | 1.0 | 6 | 8 | 3 | 13.107 | 1913 | 0.087 | 17.298 | 0.008 | 0.417 | 50.521 | 0.040 | 6.876 |
| 5 | 5 | 13.098 | 3191 | 0.095 | 17.298 | 0.008 | 0.401 | 50.521 | 0.040 | 6.979 | |||||
| 3 | 8 | 13.137 | 5591 | 0.057 | 17.298 | 0.008 | 0.465 | 54.493 | 0.026 | 9.050 | |||||
| 2 | 10 | 13.160 | 8610 | 0.033 | 17.298 | 0.008 | 0.468 | 53.514 | 0.011 | 13.004 | |||||
| 0519 | 14.171 | 1,246,086 | 1.0 | 6 | 8 | 3 | 14.074 | 1436 | 0.096 | 9.448 | 0.006 | 0.444 | 48.738 | 0.097 | 7.199 |
| 5 | 5 | 14.1354 | 2394 | 0.035 | 9.448 | 0.010 | 0.451 | 48.738 | 0.097 | 7.947 | |||||
| 3 | 8 | 14.149 | 4108 | 0.021 | 12.644 | 0.005 | 0.507 | 49.850 | 0.027 | 9.817 | |||||
| 2 | 10 | 14.154 | 6375 | 0.016 | 7.860 | 0.008 | 0.397 | 52.283 | 0.031 | 12.820 |
| h (cm) | k | Average of Height Error (m) | Average of (cm) | Average of (cm) | Average of (cm) | Average of (○) | Average of (○) | Average of (○) |
|---|---|---|---|---|---|---|---|---|
| 2 | 10 | 0.029 | 11.034 | 0.007 | 0.382 | 53.885 | 0.018 | 11.925 |
| 3 | 8 | 0.039 | 11.968 | 0.007 | 0.413 | 51.798 | 0.024 | 8.094 |
| 5 | 5 | 0.054 | 9.864 | 0.010 | 0.427 | 50.081 | 0.071 | 7.048 |
| 8 | 3 | 0.090 | 10.450 | 0.010 | 0.449 | 51.100 | 0.060 | 6.829 |
| - | - | 0.053 | 10.829 | 0.008 | 0.418 | 51.716 | 0.043 | 8.474 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, L.; Sun, Y.; Liu, Y.; Chang, X.; Jiang, J.; Feng, Y.; Song, X. Tree Skeletonization with DBSCAN Clustering Using Terrestrial Laser Scanning Data. Forests 2023, 14, 1525. https://doi.org/10.3390/f14081525
You L, Sun Y, Liu Y, Chang X, Jiang J, Feng Y, Song X. Tree Skeletonization with DBSCAN Clustering Using Terrestrial Laser Scanning Data. Forests. 2023; 14(8):1525. https://doi.org/10.3390/f14081525
Chicago/Turabian StyleYou, Lei, Yian Sun, Yong Liu, Xiaosa Chang, Jun Jiang, Yan Feng, and Xinyu Song. 2023. "Tree Skeletonization with DBSCAN Clustering Using Terrestrial Laser Scanning Data" Forests 14, no. 8: 1525. https://doi.org/10.3390/f14081525
APA StyleYou, L., Sun, Y., Liu, Y., Chang, X., Jiang, J., Feng, Y., & Song, X. (2023). Tree Skeletonization with DBSCAN Clustering Using Terrestrial Laser Scanning Data. Forests, 14(8), 1525. https://doi.org/10.3390/f14081525






