A Review on Acoustics of Wood as a Tool for Quality Assessment
Abstract
:1. Introduction
2. Theoretical Aspects Related to the Acoustical Characterization of Wood
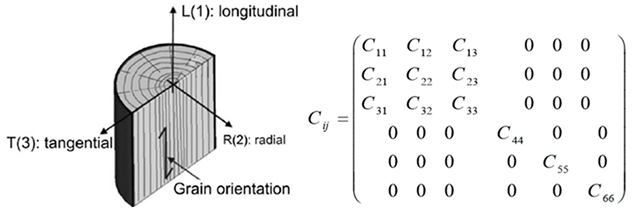
2.1. Elastic Symmetry of Propagation Media
2.1.1. Isotropic Solid
2.1.2. Anisotropic Solids
- -
- S11, S22, S33 relate an extensional stress to an extensional strain, both in the same direction. For the particular symmetry of solid wood this relation gives the Young’s moduli EL, ER, and ET.
- -
- S12, S13, S23 relate an extensional strain to a perpendicular extensional stress. In this way the six Poisson’s ratios can be calculated.
- -
- S44, S55, S66 relate a shear strain to a shear stress in the same plane, and are the inverse of the terms C44, C55, C66, corresponding to planes 23, 13, 12.
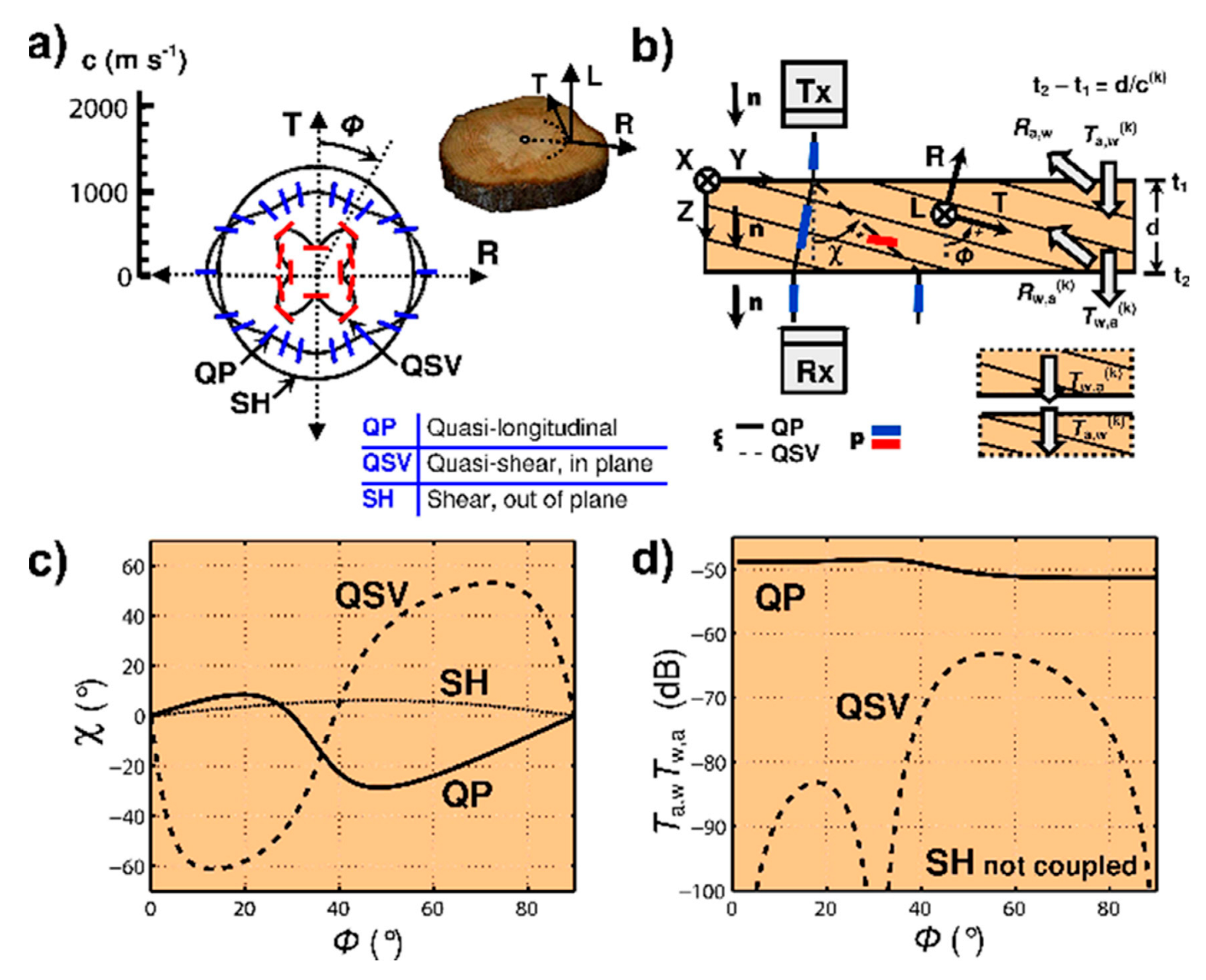
2.2. Wave Propagation in Anisotropic Media
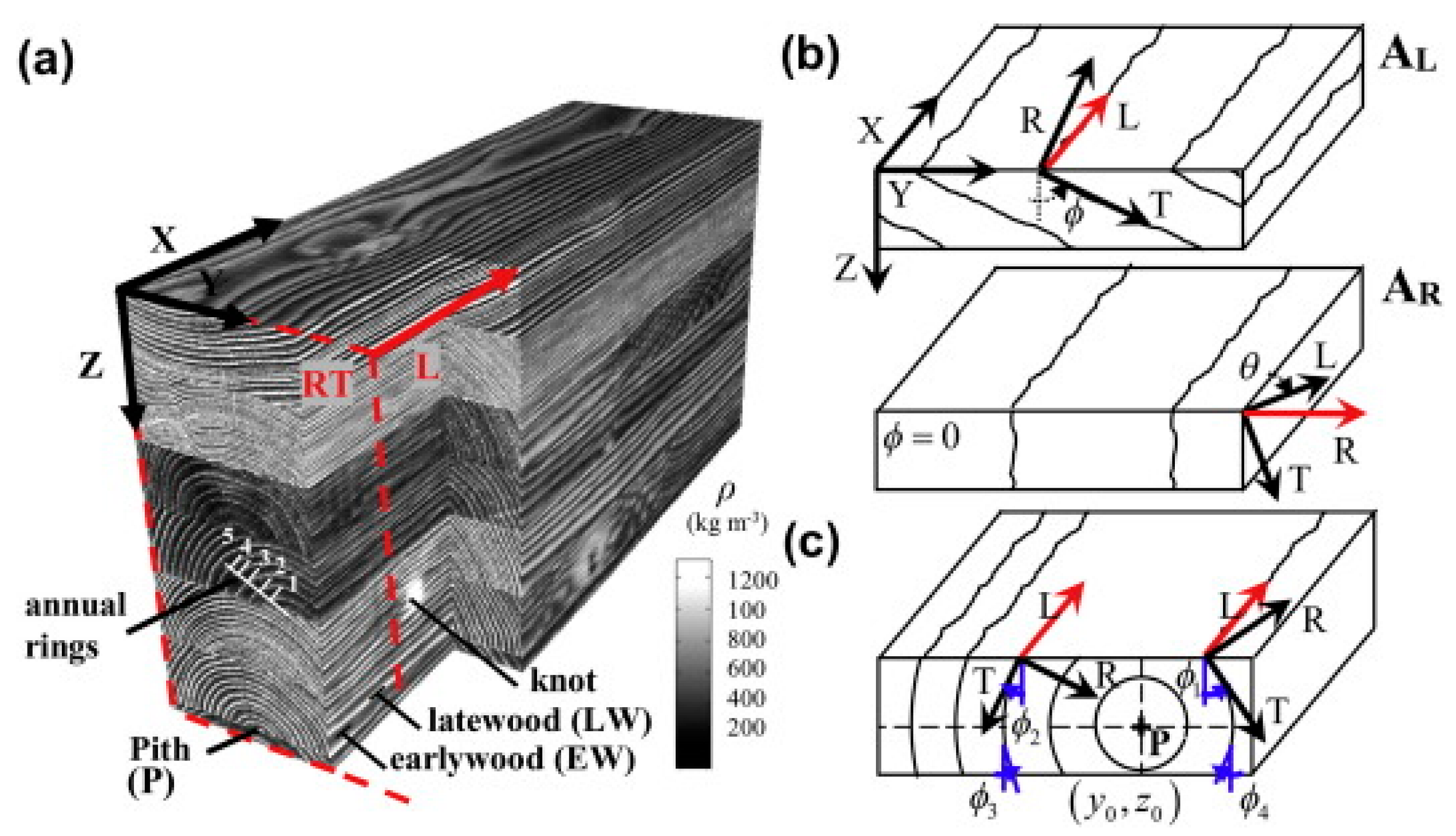
2.2.1. Wood Structure and Propagation Phenomena
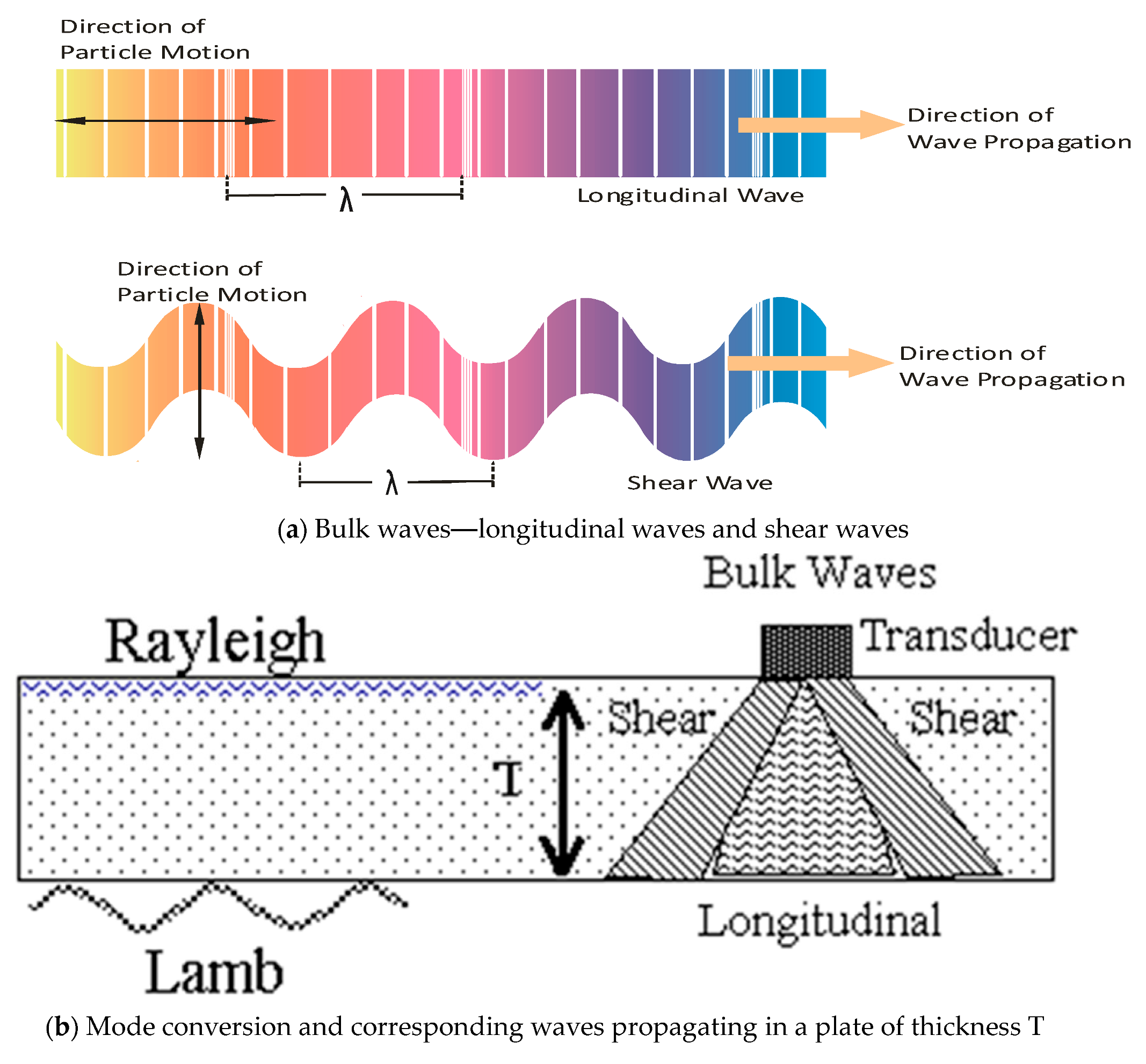
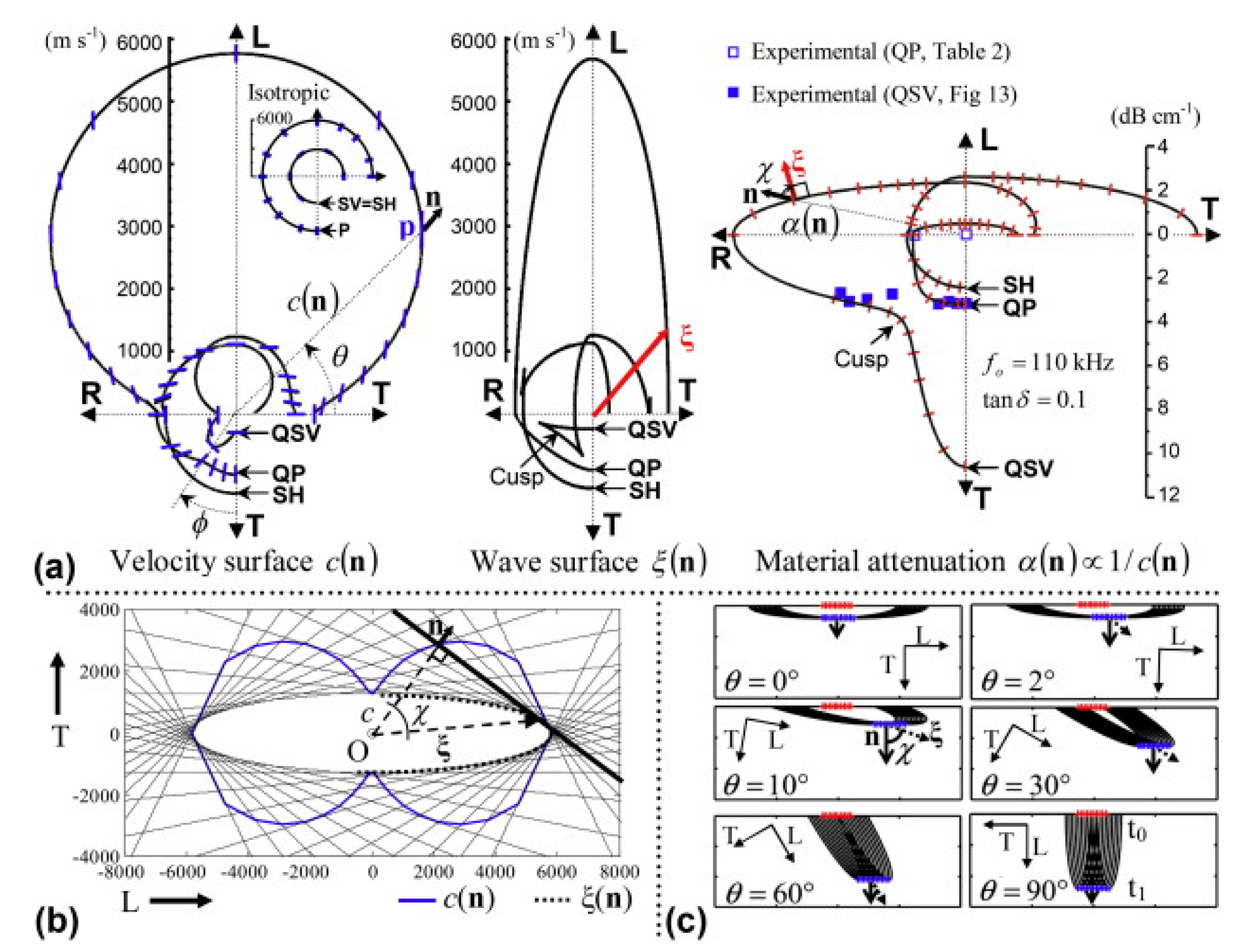
2.2.2. Type of Waves Propagation in an Anisotropic Solid
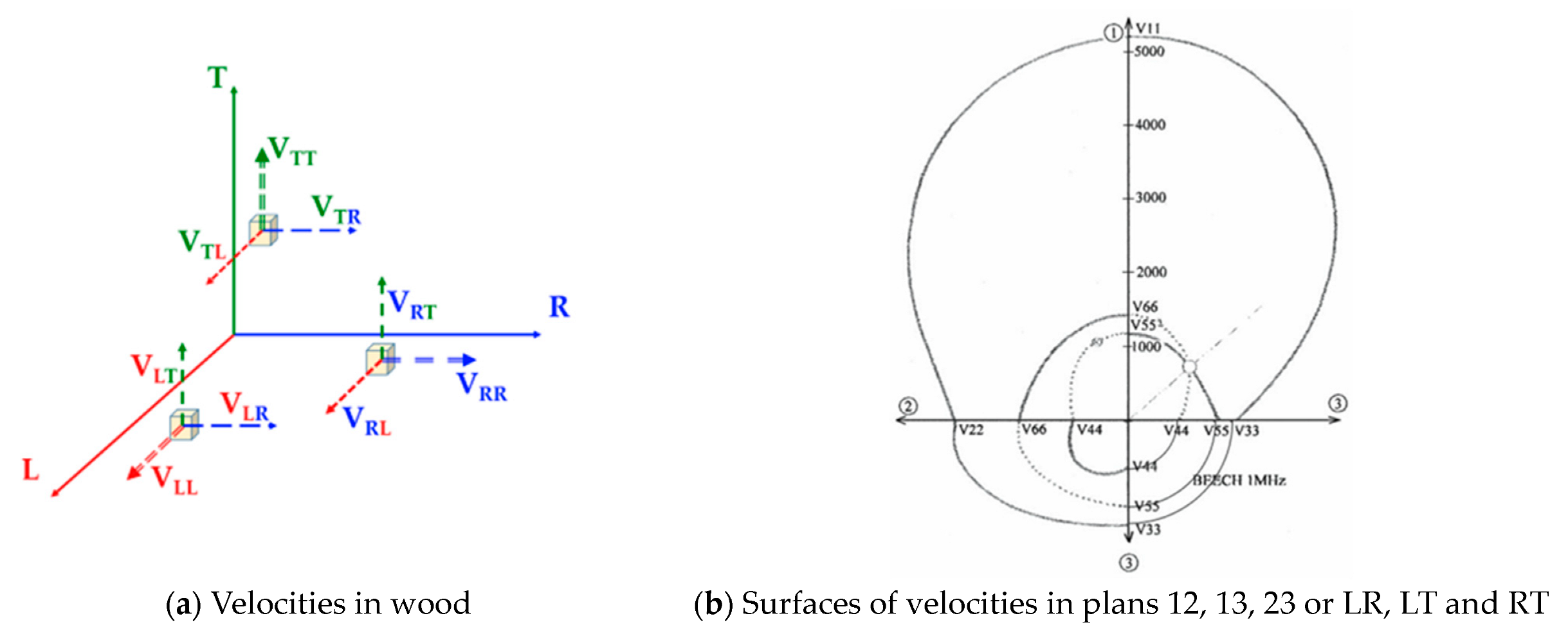
2.2.3. Velocity of Waves and the Elastic Constants
- (a)
- The Eigenvalues of Christoffel’s Equations
- -
- In symmetry plane 12: n1 = cos α; n2 = sin α; n3 = 0 and the stiffnesses C11; C22; C66; and Γ11 = C11n12 + C66n22; Γ22 = C22n22 + C66n12; Γ12 = (C12 + C66)n1n2;
- -
- In symmetry plane 13: n1 = cos α; n3 = sin α; n2 = 0 and the stiffnesses C11; C33; C55; and Γ11 = C11n12 + C55n32; Γ33 = C33n3 2 + C55n12; Γ23 = (C13 + C55)n1n3;
- -
- In symmetry plane 23: n2 = cos α; n3 = sin α; n1 = 0 and the stiffnesses C22; C33; C44; and Γ22 = C22n22 + C44n32; Γ33 = C33n32 + C44n22; Γ23 = (C23 + C44)n2n3;
- (b)
- The Eigenvectors of Christoffel’s Equations
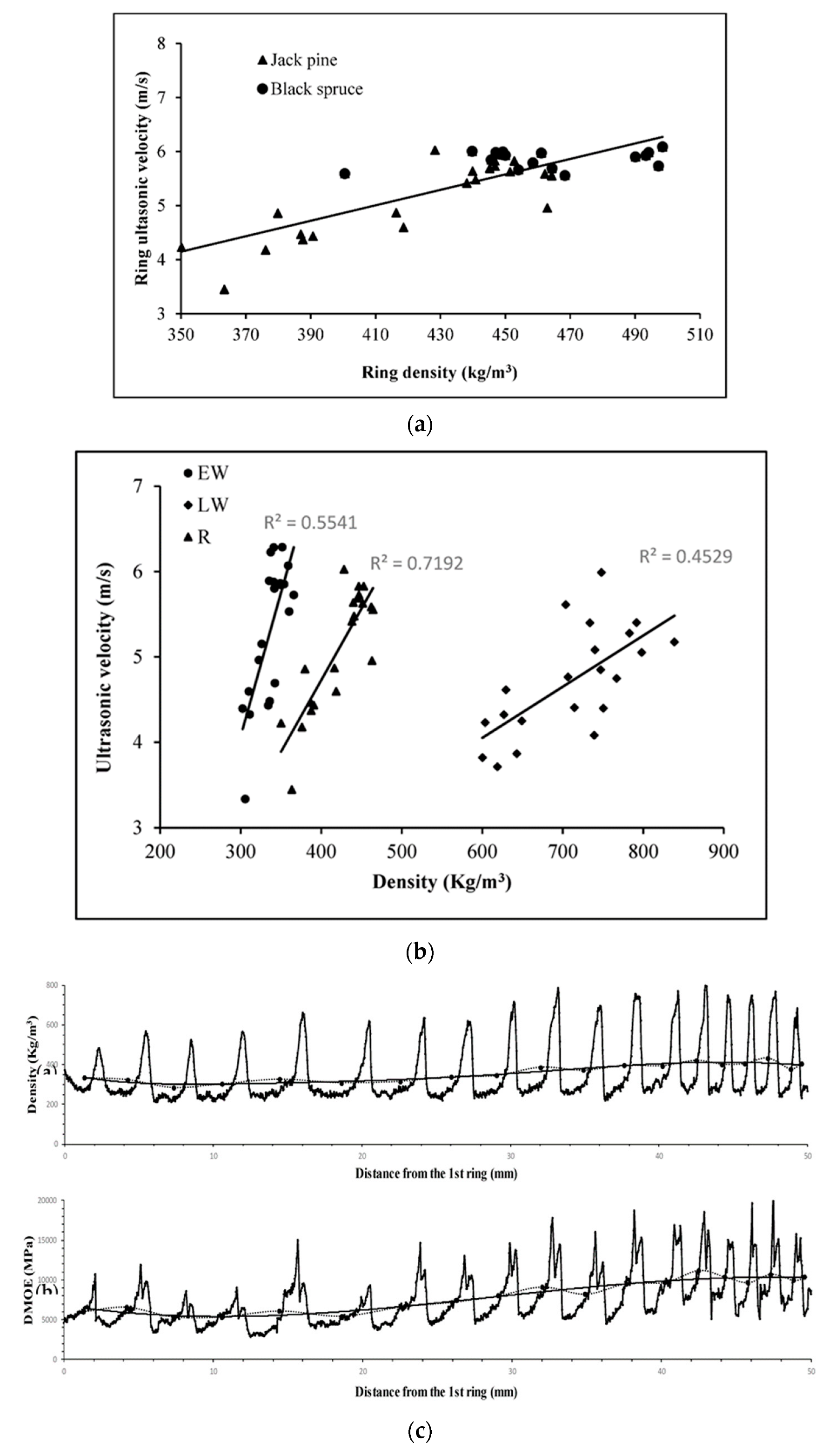
2.3. Effect of Density on Ultrasonic Velocity
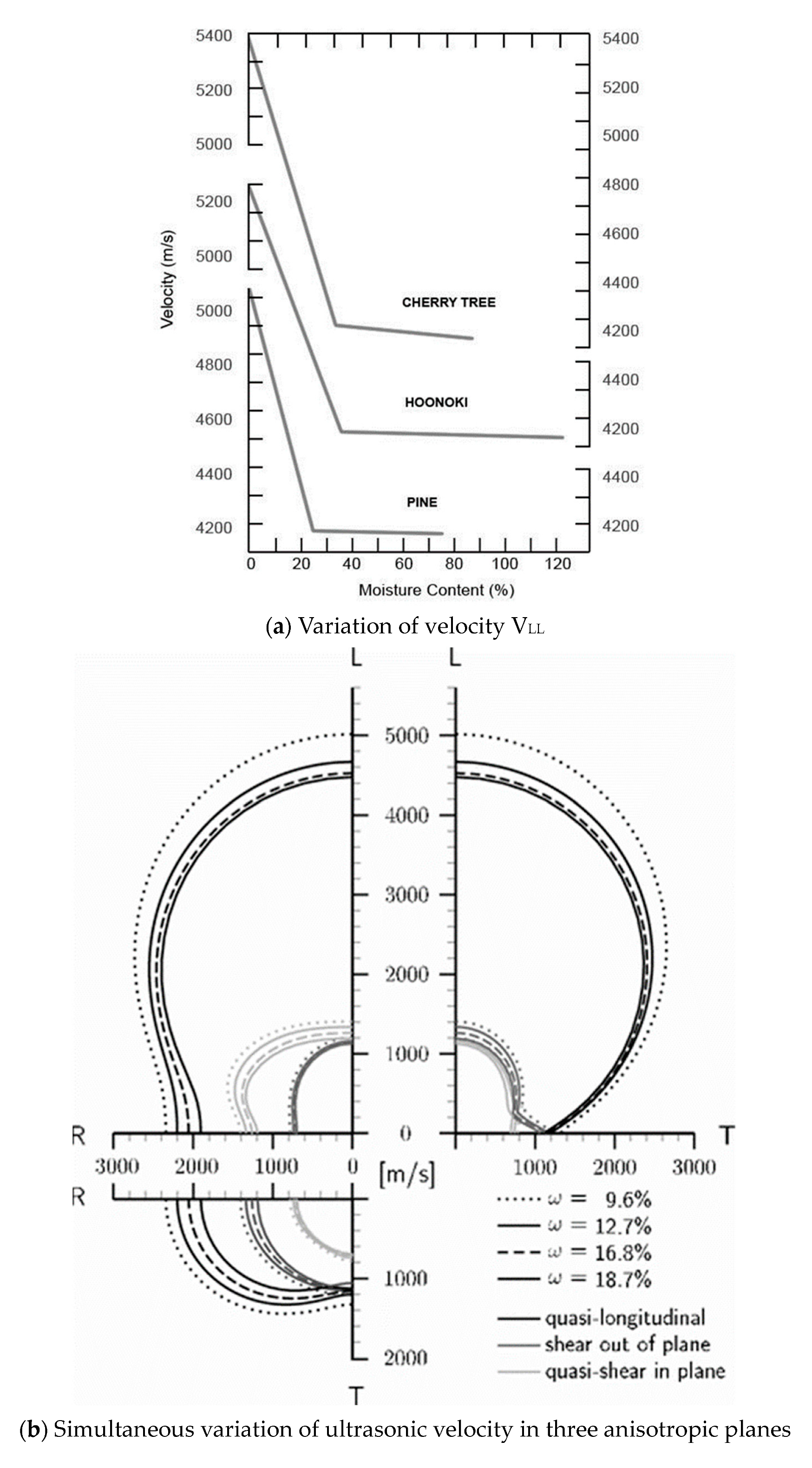
2.4. Effect of Moisture Content on Ultrasonic Velocity
2.4.1. Ultrasonic Method Effect
- -
- The Poisson ratios increase with decreasing moisture content.
- -
- The planes LT and LR are mostly affected (ν ij increased with about 40%) by moisture content increasing from 9.6% to 18.7%. Water migration is firstly along the L axis and secondly along axis R.
- -
- The RT plane is affected by about 25% (the ν RT ij increased by about 22% and ν TR 30%) by moisture content increasing from 9.6% to 18.7%. Axis T is more resistant to deformation than axis R. Migration of water is along the R axis.
2.4.2. Static Compression Effect
- -
- The Poisson ratios decrease with moisture content.
- -
- The LT and LR planes are mostly affected (the ν ij decreased with about 40%) by moisture content increasing from 9.6% to 18.7%. Water migration occurs firstly along the L axis and secondly along the R axis.
- -
- the RT plane is less affected (3%) by moisture content increasing from 9.6% to 18.7%. There is no difference between the R axis and the T axis.
2.5. Ultrasonic Resonance Spectroscopy
2.6. Methods in the Low-Frequency Domain for Elastic Constant Determination
- -
- Bar length in L, transverse section RT, moduli EL, GLR, G LT, and ν LR and ν LT
- -
- Bar length in R, transverse section LT, moduli ER, GRL, G RT, and ν RL and ν RT
- -
- Bar length in T, transverse section RL, moduli ET, GTL, G TR, and ν TL and ν TR
3. Acoustic Methods for Quality Assessment of Trees, Logs and Lumber
3.1. The Background
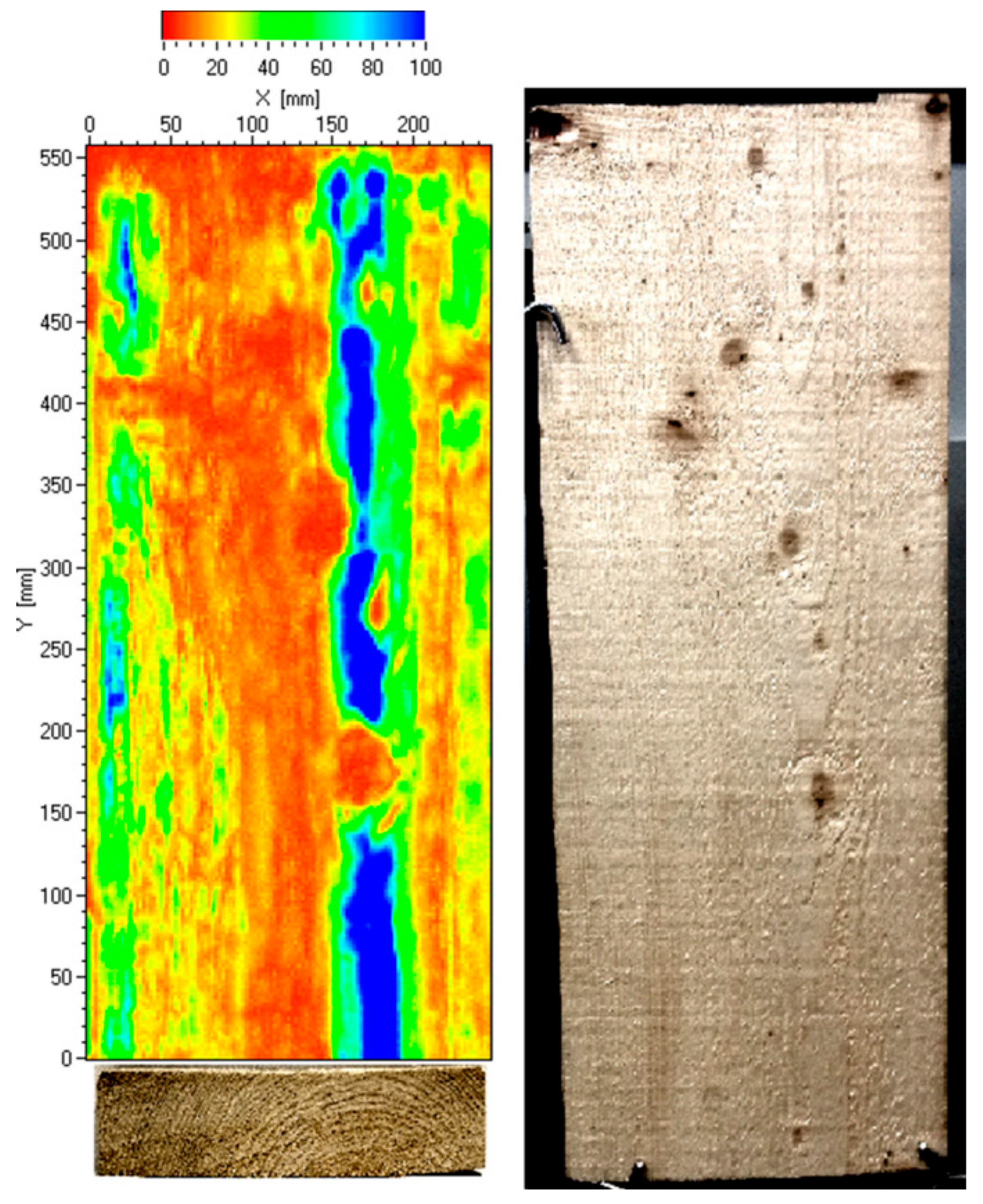
3.2. Quality Assessment of Standing Trees and Green Logs
3.2.1. Scattering Based Techniques
3.2.2. Ultrasonic Tomography
- -
- Techniques based on the projection-slice theorem (filtered back-projection and direct Fourier transform), which are fast but restricted to projection data that are sets of straight rays.
- -
- Techniques based on iteration procedures (algebraic reconstruction techniques and simultaneous iterative reconstruction techniques), which are relatively slow but may be used with complex sampling geometries and a bending ray path.
- -
- ART—algebraic reconstruction technique—in which each equation corresponds to a ray projection. The computed ray sums are a poor approximation to the measured ones and the image suffers from significant noise.
- -
- SIRT—simultaneous iterative reconstructive technique—reduces the noise of ART by relaxation and produces better images than ART. The relaxation parameter becomes progressively smaller with an increasing number of iterations.
3.3. Quality Assessment of Standing Trees
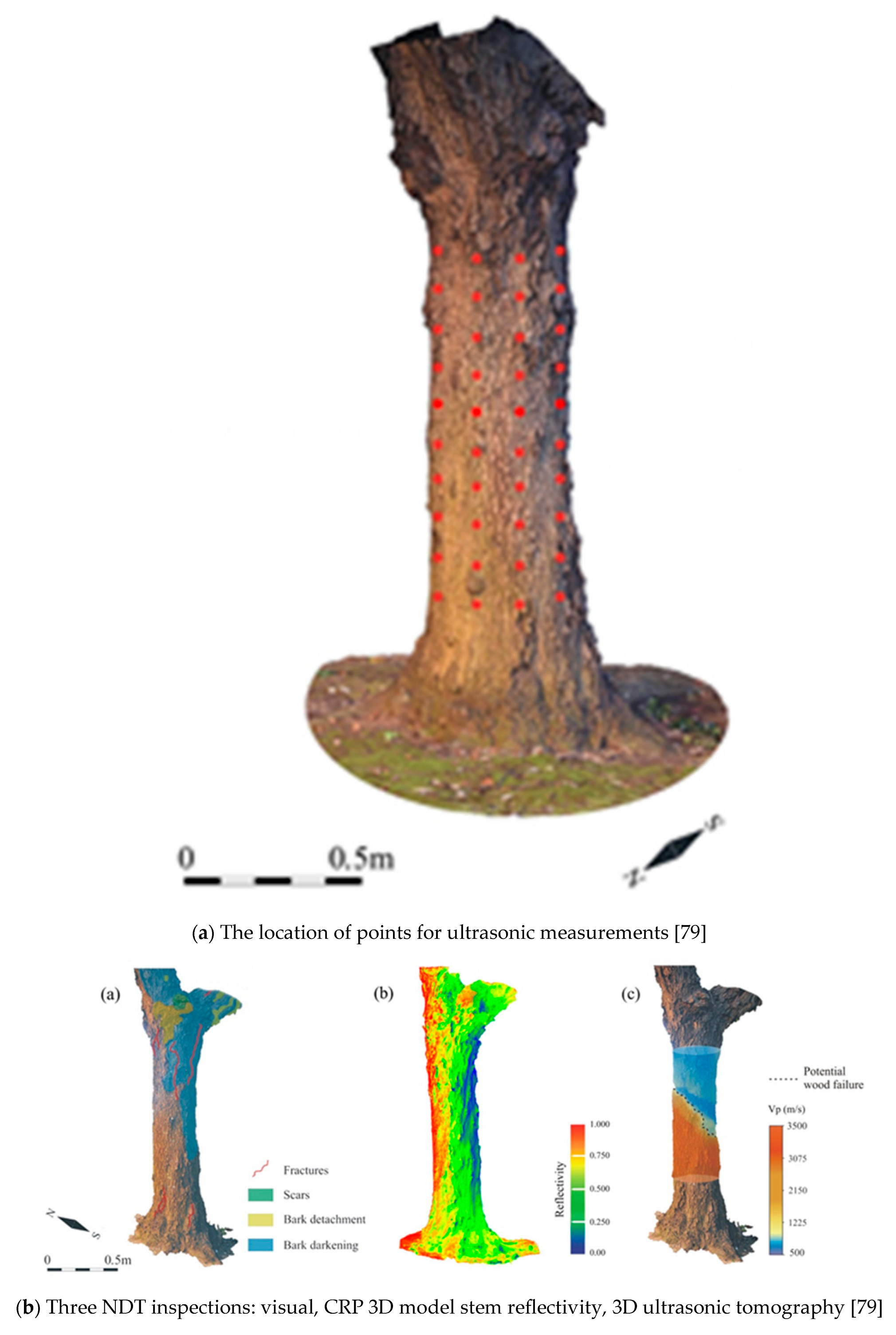
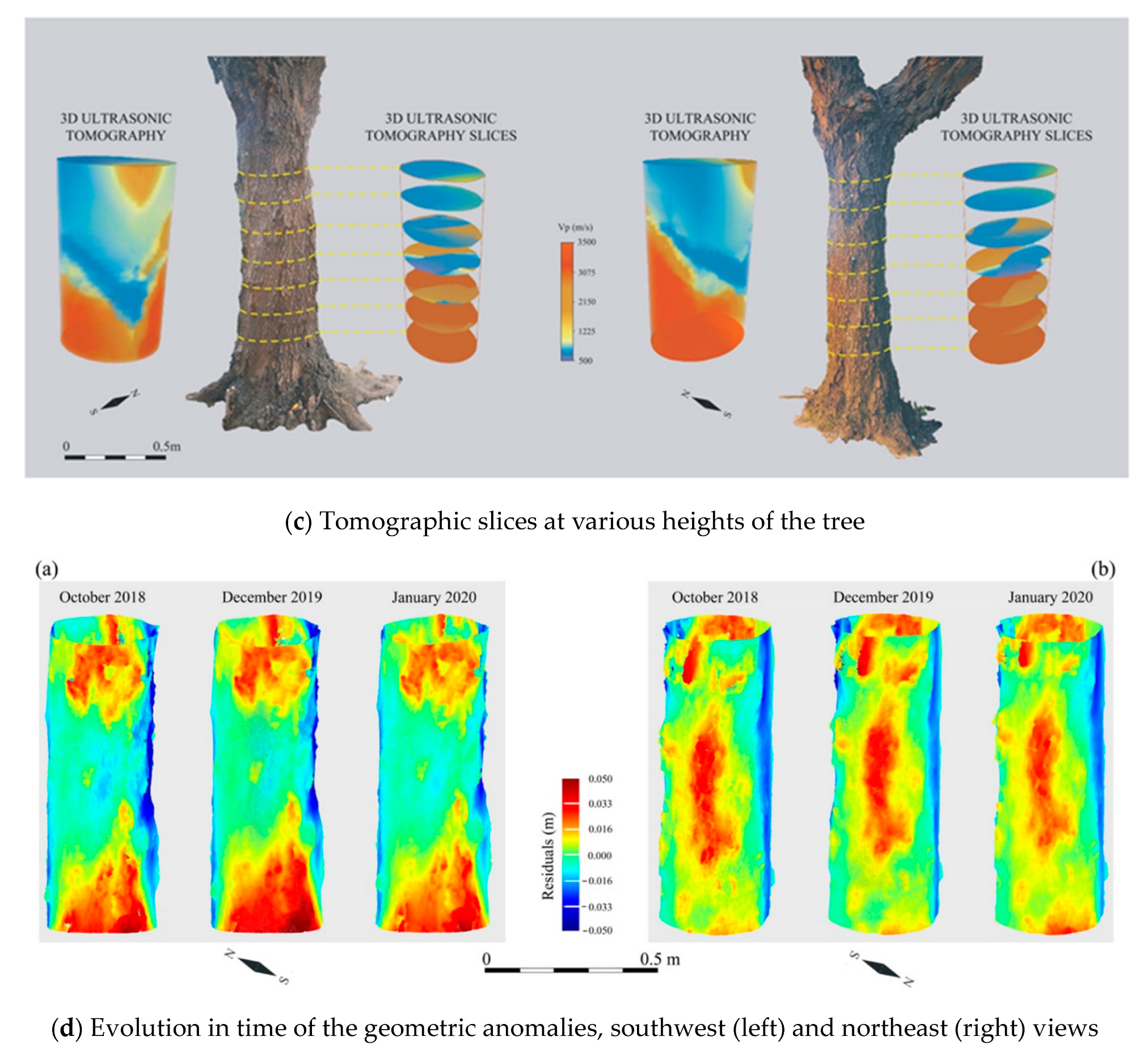
3.3.1. Urban Trees
3.3.2. Forest Trees
- (a)
- Detection of rot in old standing trees
- (b)
- Effect of thinning
- -
- An increase with age of the diameter of the tree at breast height (DBH) and of the height of the tree;
- -
- Increasing velocity after the second thinning in standing trees and in logs;
- -
- The velocity, VL, measured on standing trees with a greater VL measured on green logs by about 20%. This can be explained by the fact that the velocity on trees is measured under the stress created by the mass of the crown, the branches, the leaves.
3.3.3. Trees from Plantations
- (a)
- Plantation of Pinus radiata
- (b)
- Plantation of Sitka spruce
- (c)
- Eucalyptus species
- -
- Modulus of rupture in static cantilever test and the velocities—mean and minimum
- -
- Velocities (m/s) and diameter (m) of the tree
- -
- Multiple regression modulus of rupture, the velocities and the diameter
3.4. The Quality of Logs and Lumber for Structural Purpose
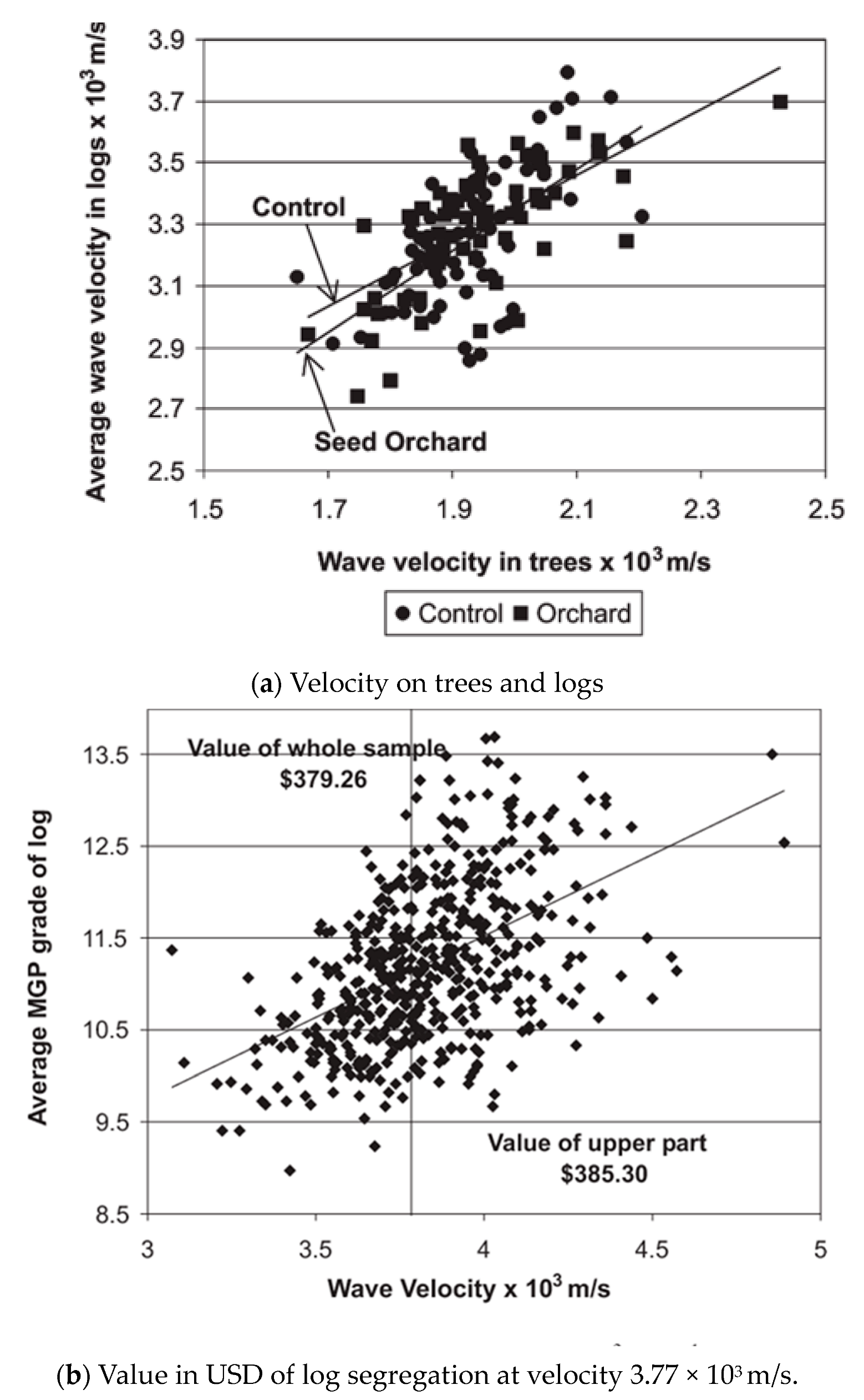
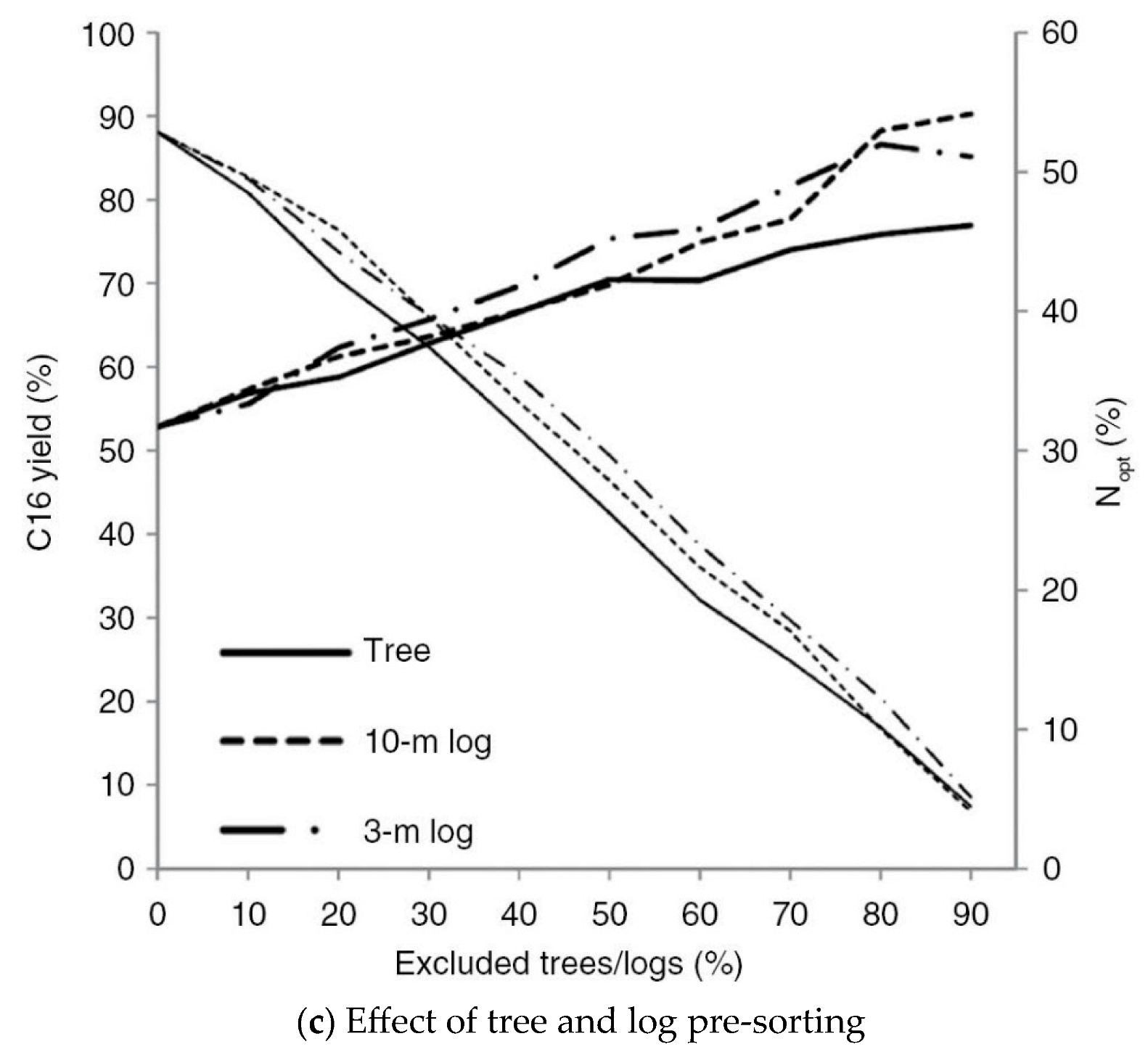
3.4.1. Stress Wave Method on Logs and Lumber
- -
- For log grade F1, the value in USD is 178 for logs, 243 for dimension lumber and 329 for factory lumber.
- -
- For log grade F2, the value in USD is 99 for logs, 236 for dimension lumber and 272 for factory lumber.
- -
- For log grade F3, the value in USD is 81 for logs, 211 for dimension lumber and 227 for factory lumber.
- -
- The first class has the highest velocity of the stress waves (3676 m/s) and the highest MOE (13.51 GPa). For lumber, the MOE is in the same range (13.79 GPa)
- -
- The last class has the lowest velocity (3048 m/s), the lowest MOE (9.29 GPa). For lumber, the MOE is 8.27 GPa.
- -
- Comparing the class G1 to G4, note the decrease in velocity of 17% for logs and of
- -
- 30% in the MOE for logs and 40% for lumber.
- -
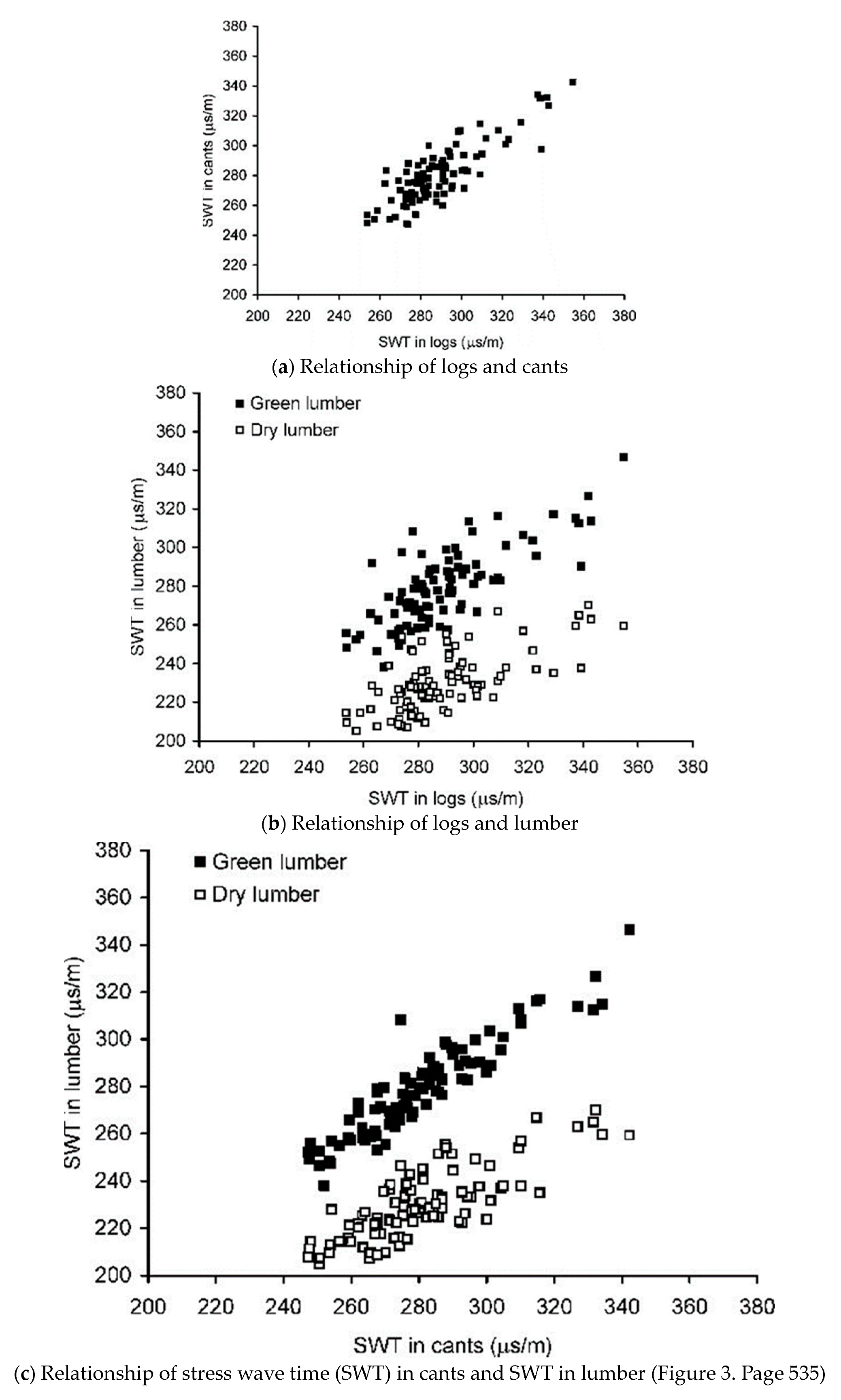
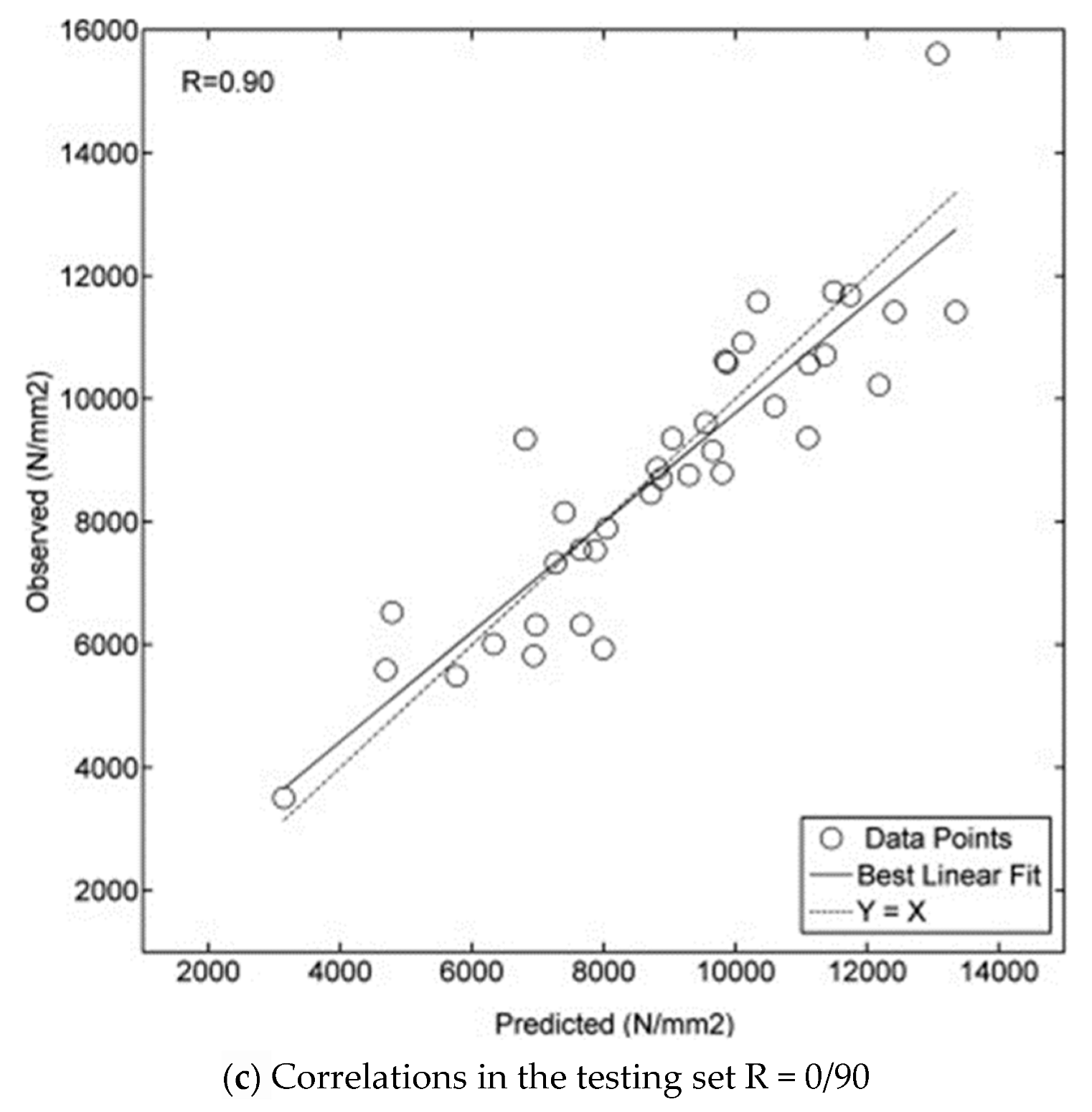
- Correlation coefficients between the stress wave propagation time in logs and cants or lumber are highly significant, between 0.72 and 0.95 (Figure 18).
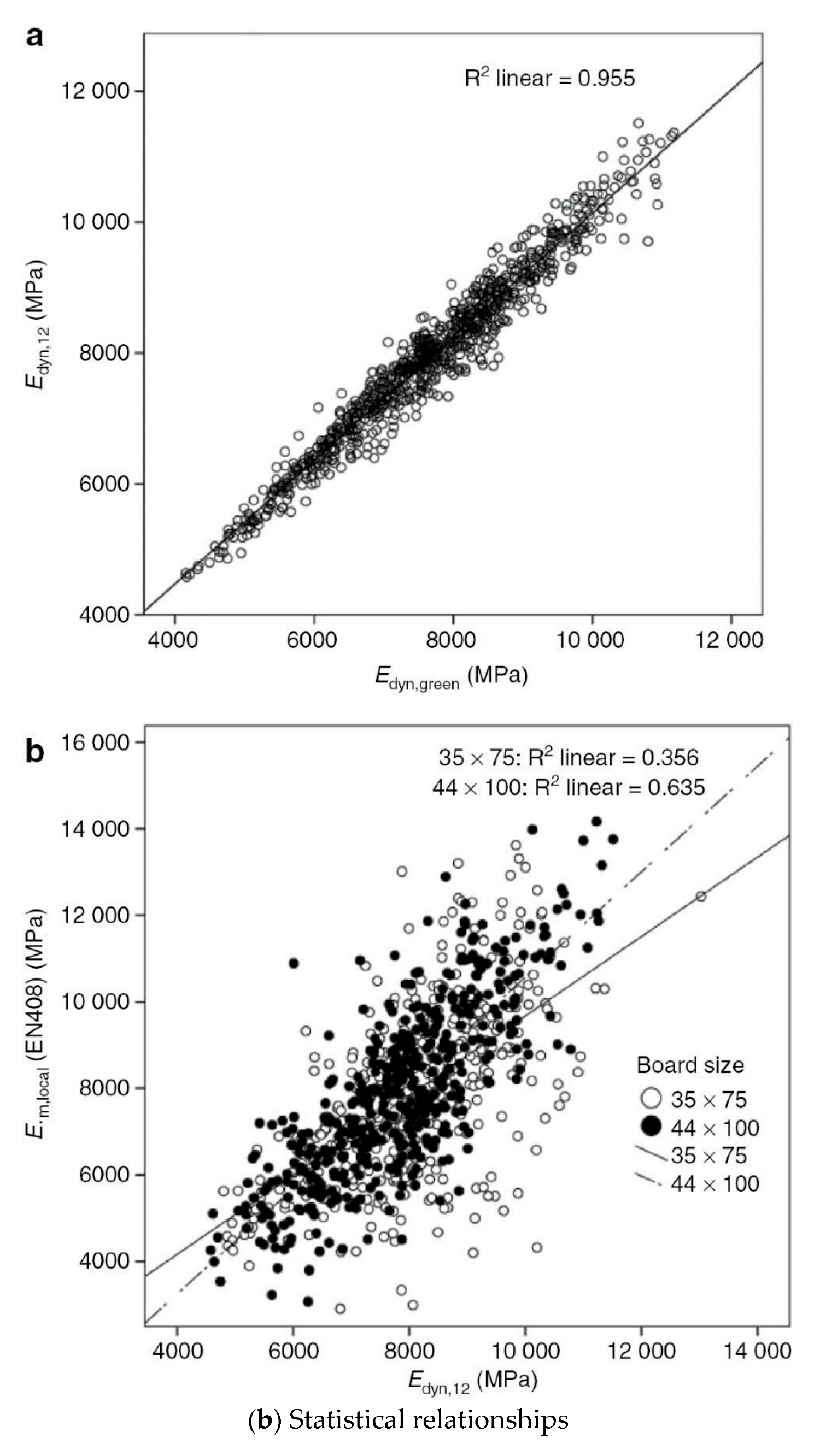
3.4.2. Frequency Resonance Method on Lumber
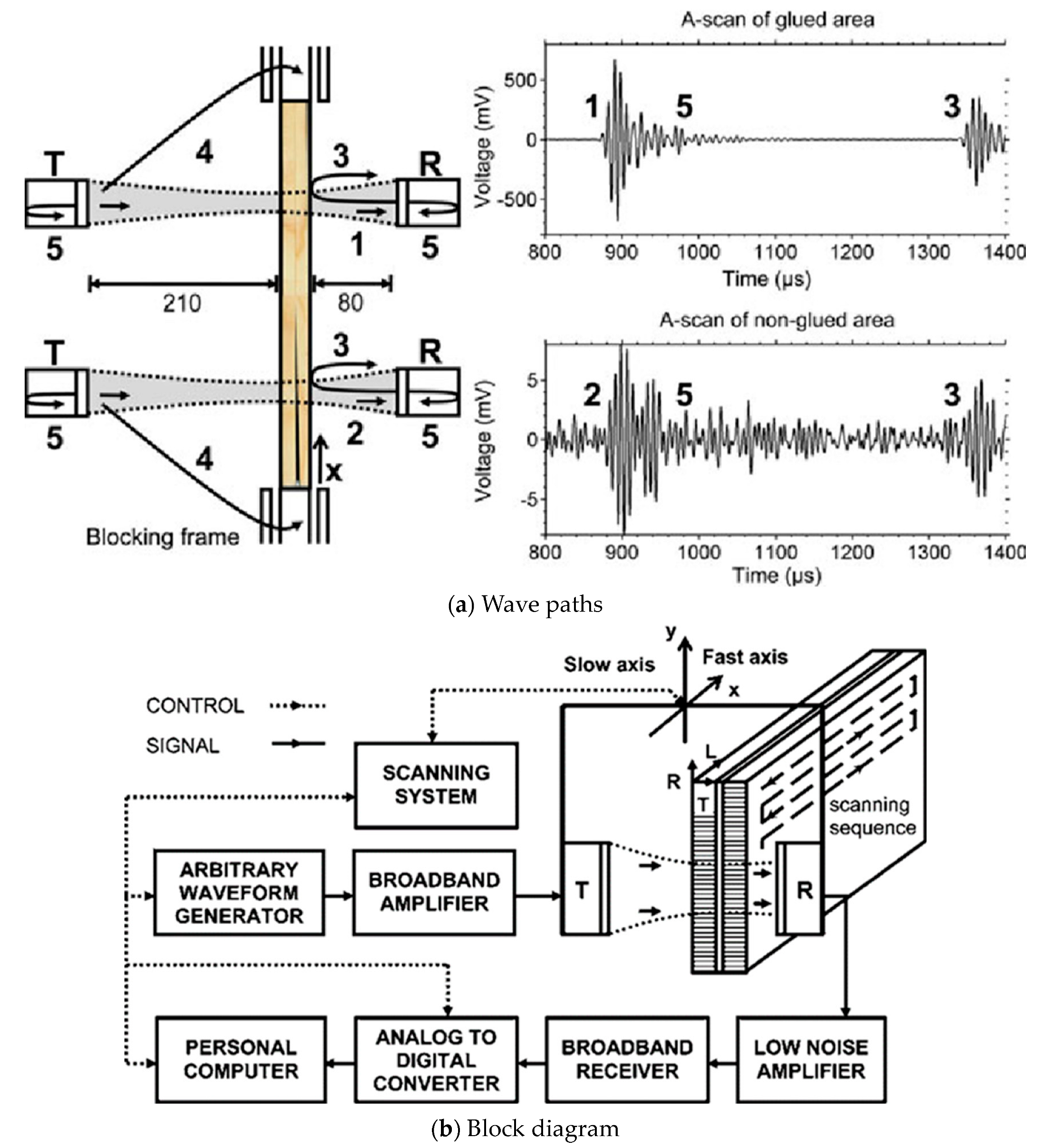
3.4.3. Ultrasonic Method by Direct Contact
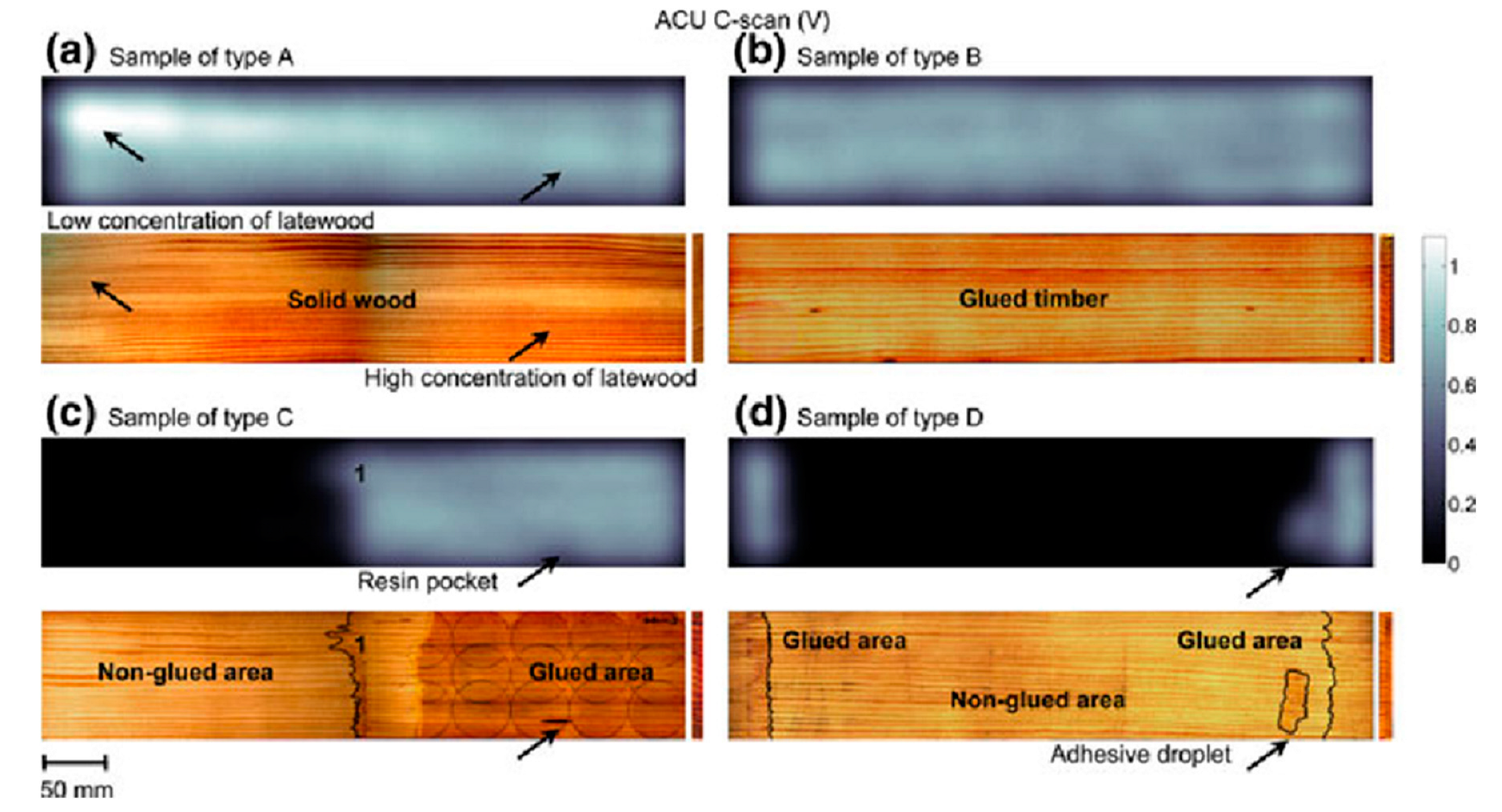
3.4.4. Air-Coupled Ultrasound on Lumber
3.4.5. Acoustic Technology and Machine Grading
| Acoustic Method | Parameters Measured | Maximum Feed Speed | Company |
|---|---|---|---|
| Pieces/Min | |||
| longitudinal resonance | dynamic stiffness, without density | 100–240 | Dynalyse AB, Sweden |
| longitudinal resonance | dynamic stiffness, without density | 180 | Viscan (ViSCAN) Italy |
| longitudinal resonance combined X-ray | dynamic stiffness X-ray density, knots size and position | 150 –acoustic 80–300 X-ray | EuroGrecomat-706, Italy |
| longitudinal resonance | dynamic stiffness with density | manual operation | MTG 960., The Netherlands |
| longitudinal resonance | dynamic stiffness with density | 180 | Precigrader Dynalyse AB, Sweden |
| longitudinal resonance, combined optical scanner for knots | dynamic stiffness with density | 25 and 180 | Grademaster Illertissen, Germany |
| flexural resonance | dynamic stiffness with density | 20 | Xyloclass, France |
| edgewise flexural resonance | dynamic stiffness with density | 4 | SARL Esteves, France |
| ultrasonic time of flight, and pin indentation density | dynamic stiffness with density | 30–40 | Triomatic, France |

4. Acoustic Methods for Quality Assessment of Structural Composite Timber Products and of Wood-Based Composite Boards
4.1. The Background, LVL and Glulam
4.2. Stress Wave Timing Inspection of Glulam Beams
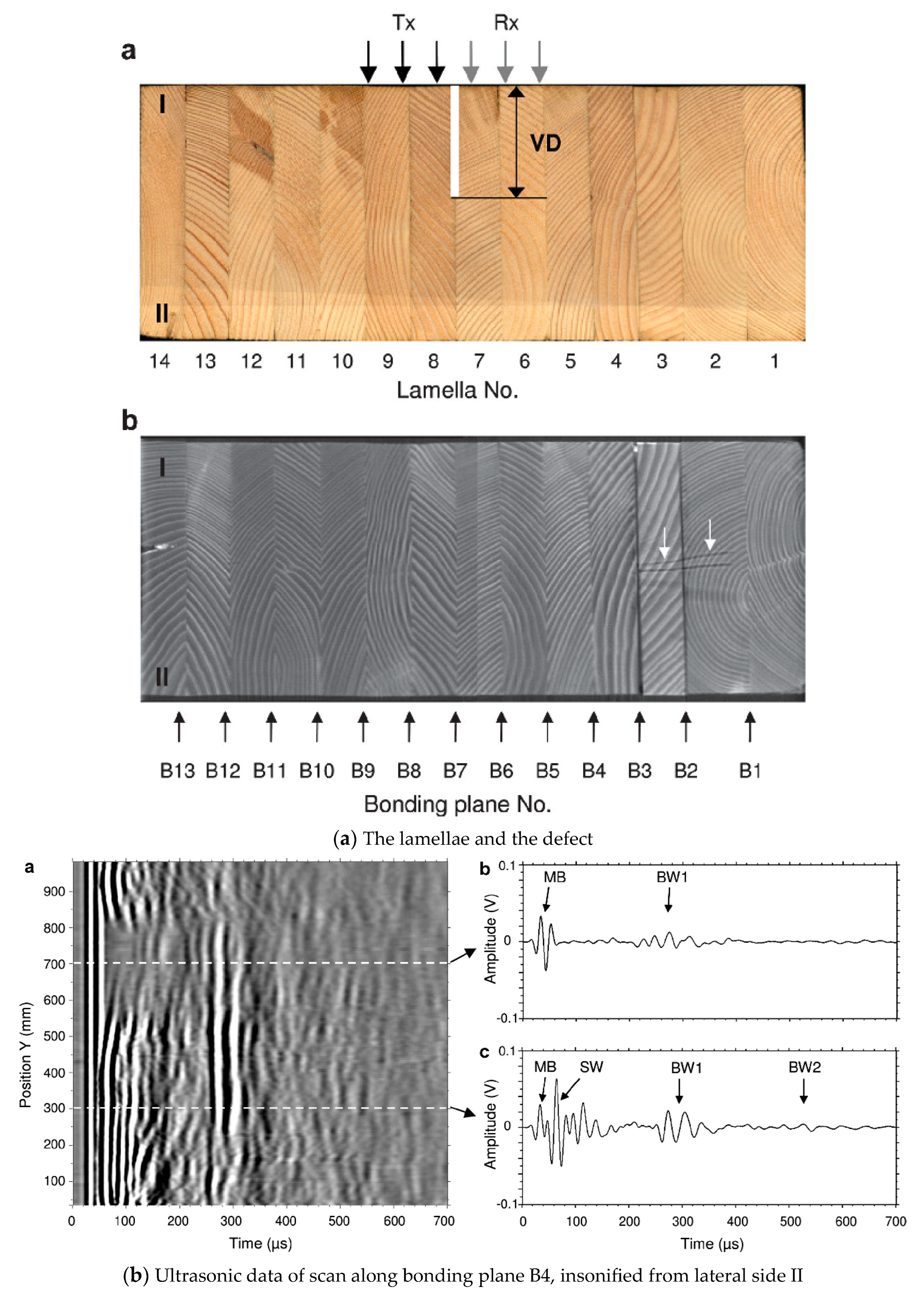
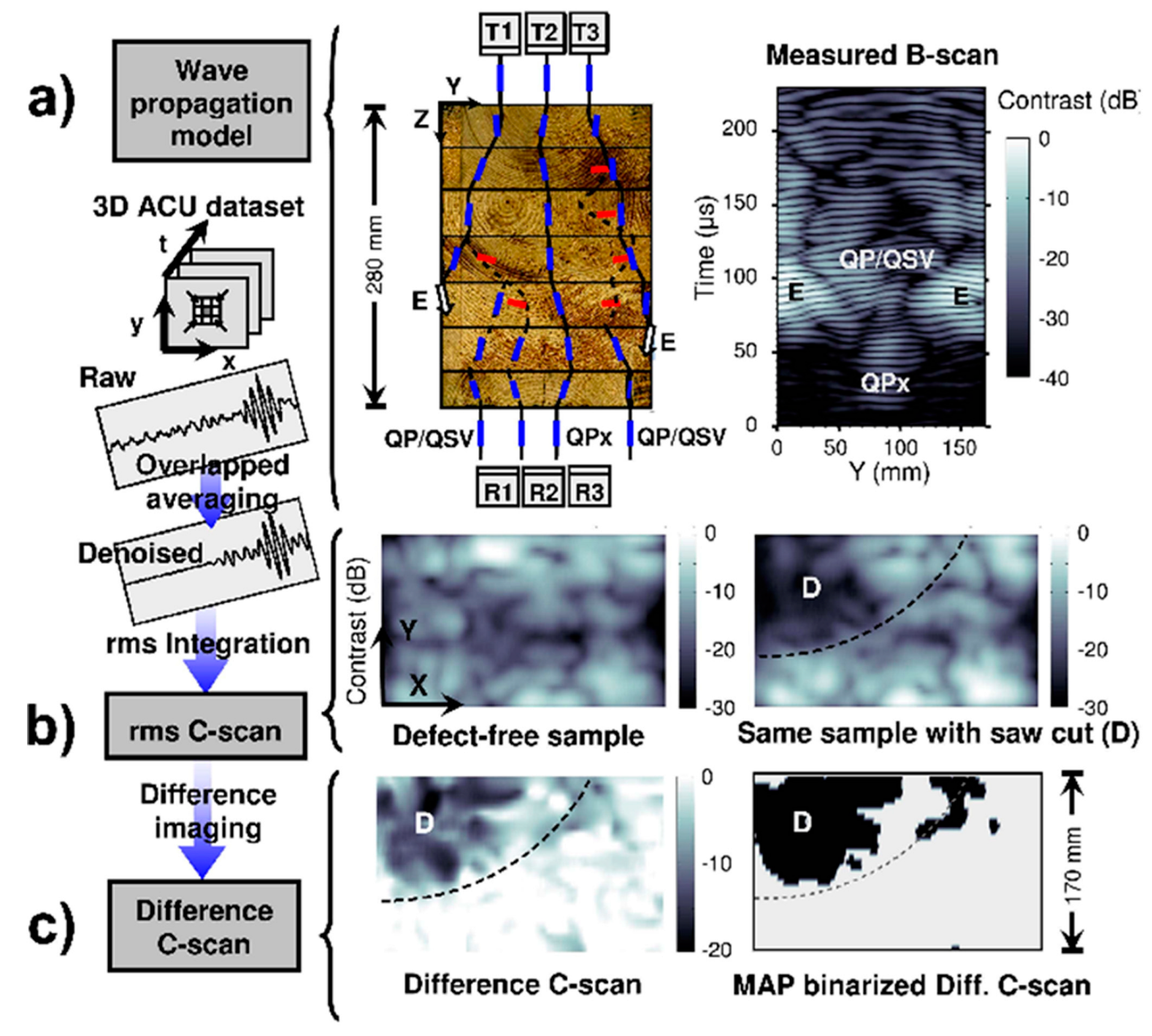
4.3. Glued Laminated Timber Scanning by Dry-Point-Contact Ultrasound
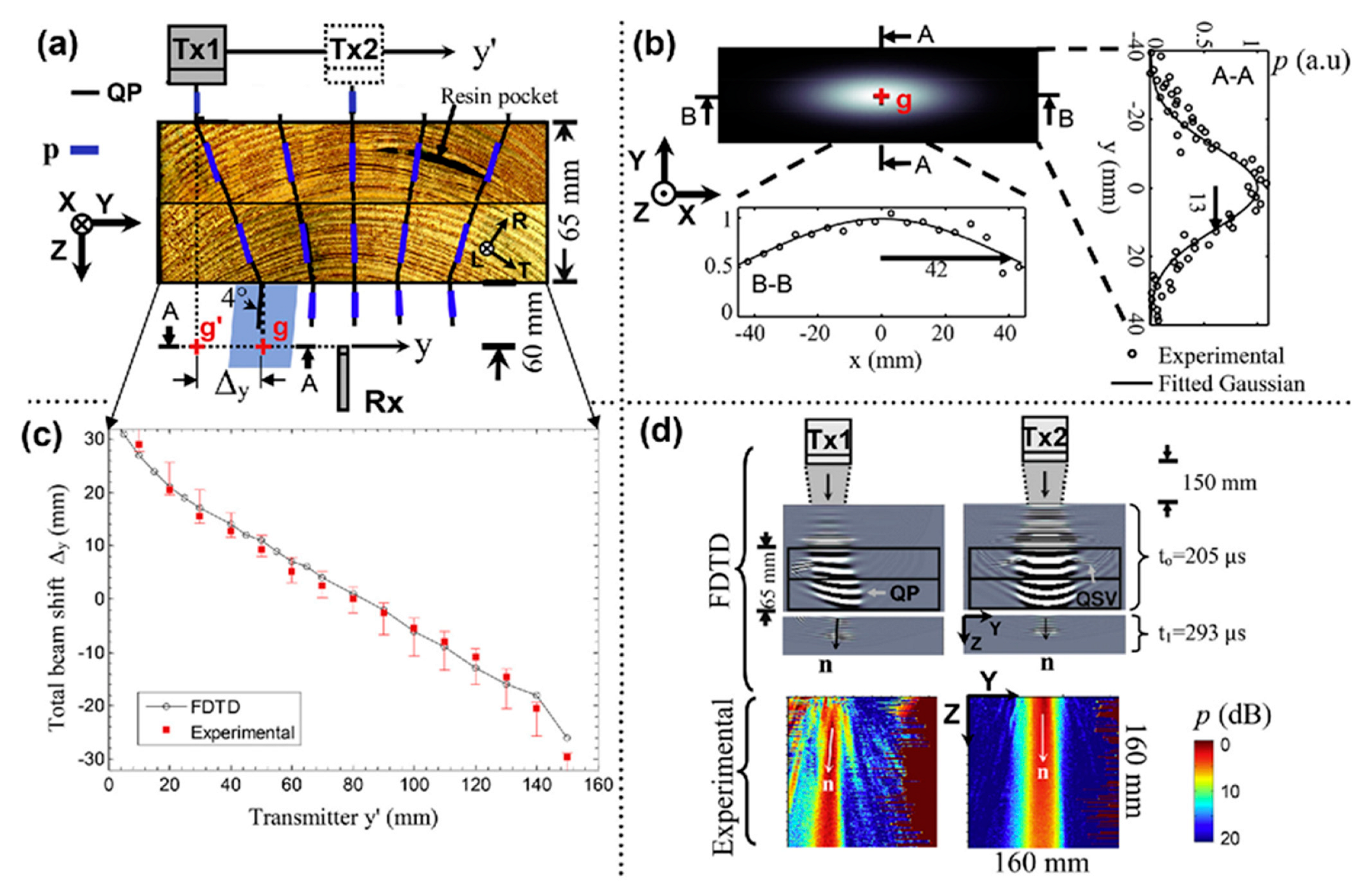
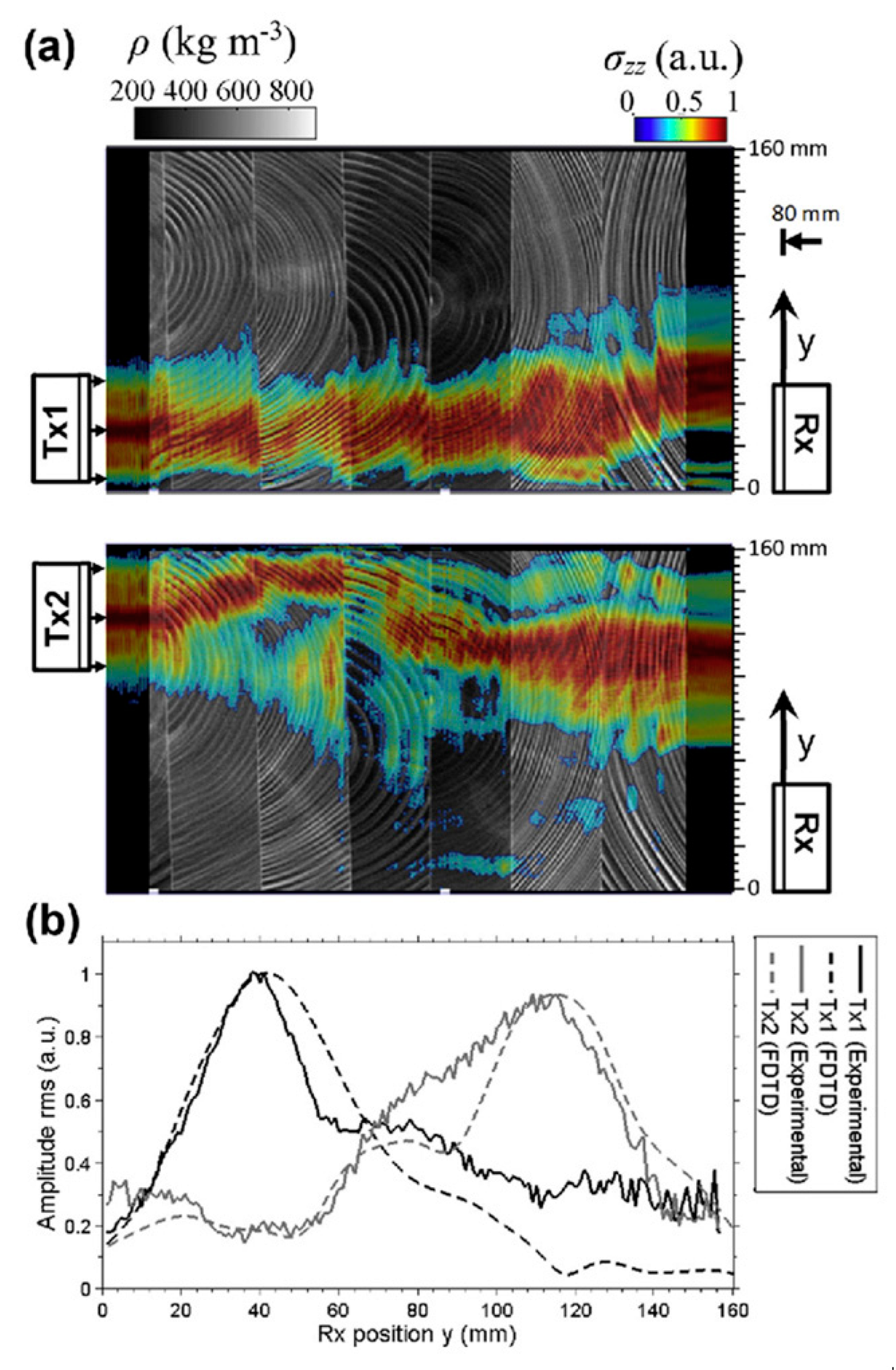
4.4. Air-Coupled Ultrasound Inspection of Glued Laminated Timber
- (a)
- A single, unbonded timber lamella with curved growth rings in RT plane
- -
- The velocity surface, the wave surface and the attenuation in three anisotropic planes of solid wood;
- -
- The effect of the annual ring in a multilayer glulam;
- -
- Air-coupled ultrasonic wave propagation in a glulam structure composed of several lamellae.
- (b)
- Velocity surface, wave surface and attenuation in three anisotropic planes of solid wood.
- (c)
- the wave path in a structure made of two lamellae
- (d)
- The wave path in a structure made of seven lamellae
- -
- The coordinate transformation with respect to the pith of the tree, for a cylindrical stem model, for the analysis of vibration modes in a defect clear specimen.
- -
- The calculation of the elastic properties of the glulam
- -
- The first path having the QPx mode at the center of the beam.
- -
- The secondary paths having interference of the QP/QSV modes with small total shifts and edge reflection, E coupled at all sample width positions in the B-scan
- -
- in the RT plane and beam skewing leads to position dependent wave paths.
- -
- C-scan image of the structure without defect.
- -
- C-scan image with the delamination of a saw cut defect. Defects larger than 100 mm × 100 mm can be imaged. The maximum height of the glulam was 280 mm. Accurate segmentation of the geometry of the defect was obtained with a MAP binarization procedure described by [139].
- -
- For the 7-lamella system, a very complex QP/QSV interference pattern and edge reflections were identified and were imaged with the C-scan mode.
5. High-Power Ultrasound
5.1. Introduction
5.2. Wood Drying
- (a)
- High-power ultrasound and infrared radiation
- (b)
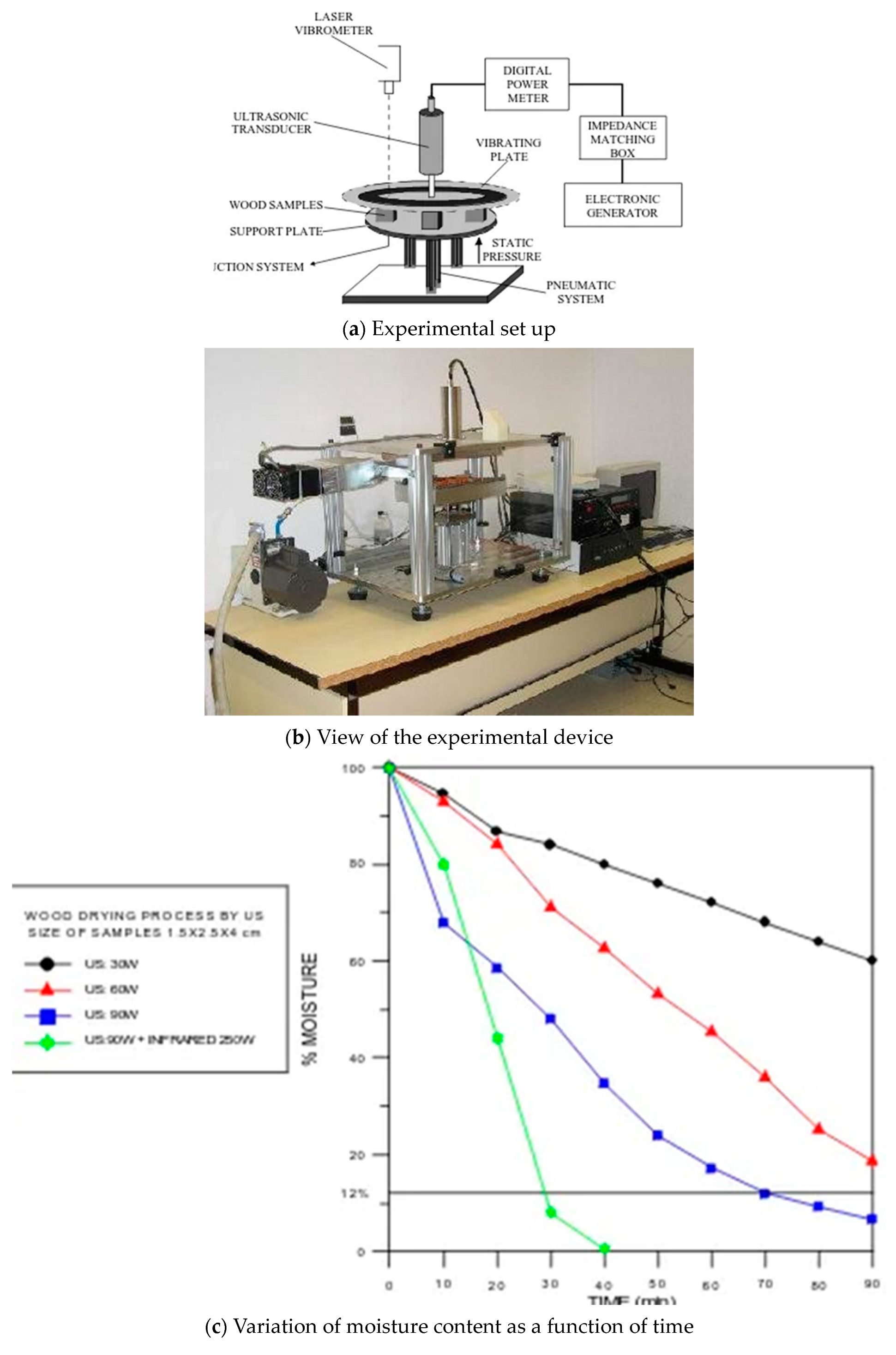
- High-power ultrasound and vacuum
- -
- The ultrasonic sub ensemble is composed of a generator and of an ultrasonic transducer 66 mm in diameter, weighing 0.9 kg with a frequency 20 kHz and power of 100 W. The samples are in direct contact with the transducer.
- -
- The vacuum sub ensemble, where the air velocity is controlled by pulse modulation. Air velocity was set at 2 m/s.
- -
- The heating sub ensemble (the nature of the heating source is not specified). The temperature monitor and the heat generator were designed for a maximum achievable temperature of 200 °C. Wood drying temperature was set at 60 °C and the absolute pressure was set at 0.02 MPa.
- -
- The specimens’ initial moisture content 130%. The final moisture content of the specimens was 10%. Water evaporation is only from the surface of the specimen (450 mm × 100 mm). During ultrasonic treatment water migration is only along the thickness of the specimen, from the central zone to the surface.
- -
- The drying process was followed through the calculation of the water diffusion coefficient and by observing its variation during the drying time.
5.3. Wood Preservation and Sterilization with High-Power Ultrasound
6. Acoustical Properties of Wood Species for Musical Instruments
6.1. Wood Species
6.2. Specimens
6.3. Methods
6.4. Acoustical and Mechanical Properties
| Velocities (m/s) | Elastic Moduli (108 N/m2) | |||||||
|---|---|---|---|---|---|---|---|---|
| Longitudinal Velocities | Shear Velocities | Young’s Moduli | Shear Moduli | |||||
| Density | VLL | VRR | VLT | VRT | EL | ER | GLT | GRT |
| Spruce | ||||||||
| 480 | 5600 | 1299 | 1307 | 359 | 150 | 7.4 | 8.2 | 0.62 |
| 440 | 6000 | 1100 | 1215 | 316 | 160 | 5.0 | 6.5 | 0.44 |
| Maple | ||||||||
| 750 | 3800 | 1700 | 110 | 20 | 17 | 0.89 | ||
| 760 | 3800 | 1900 | 110 | 26 | 13 | 0.49 | ||
| Wood Species | Density | Velocities (m/s) | |||||
|---|---|---|---|---|---|---|---|
| kg/m3 | VLL | VRR | VTT | VRT | VLT | VLR | |
| Picea | |||||||
| P. abies | 400 | 5050 | 2000 | 1425 | 300 | 1310 | 1340 |
| P rubens | 485 | 6000 | 2150 | 1600 | 330 | 1240 | 1320 |
| P. sitchensis | 370 | 5600 | 2150 | 1450 | 300 | 1340 | 1400 |
| Acer spp | |||||||
| A pseudoplatanus | 670 | 4600 | 2500 | 1870 | 925 | 1529 | 1835 |
| A platanoides | 740 | 4940 | 2491 | 1942 | 937 | 1350 | 1698 |
| A. macrophylum | 600 | 4500 | 2340 | 1550 | 900 | 1340 | 1720 |
| Wood Species | Density | Young’s Moduli | Shear Moduli | ||||
|---|---|---|---|---|---|---|---|
| kg/m3 | EL | ER | ET | GRT | GLT | GLR | |
| Picea | |||||||
| P. abies | 400 | 82.79 | 1.56 | 1.03 | 0.36 | 8.12 | 7.56 |
| P rubens | 485 | 150.89 | 3.13 | 1.75 | 0.53 | 7.45 | 8.46 |
| P. sitchensis | 370 | 99.95 | 9.49 | 4.30 | 0.33 | 6.64 | 7.25 |
| Acer spp | |||||||
| A pseudoplatanus | 670 | 98.59 | 26.25 | 12.93 | 5.73 | 15.68 | 22.56 |
| A platanoides | 740 | 89.53 | 29.08 | 16.99 | 7.20 | 13.68 | 21.34 |
| A. macrophylum | 600 | 11.20 | 27.66 | 11.71 | 4.86 | 10.77 | 17.75 |
6.5. Factors Affecting Acoustical Properties of Wood for Musical Instruments
6.5.1. Wood Anisotropy
- -
- Wood anisotropy has no effect on the vibrations patterns for modes 1 to 6. In this table, only mode 6 is illustrated. For mode 6 and the isotropic, transverse isotropic and orthotropic cases, the frequencies are respectively 202.42 Hz, 205.95 Hz and 219.55 Hz. The vibrating surface of high amplitude (yellow and red) is very small. Mode 7, f = 247.59 Hz, shows identical patterns for isotropic and transverse isotropy and is different from orthotropic symmetry for which the upper bout (in blue) is not vibrating. Mode 8—the patterns are different for the three cases. The orthotropic plate vibrates (red and yellow) mostly on the wider lower bout, at f = 248.18 Hz. Mode 9—the patterns are different for the three elastic symmetries, but have some similarities—mainly the central part of the lower bout vibrates. Mode 10, f = 285.9 Hz, the center bout vibrates identically for the plates in the three cases of anisotropy. At superior modes, above 588 Hz, the patterns are different for each case of anisotropy. However, in the case of the orthotropic plate, Mode 49, at f = 595.16 Hz the upper bout does not vibrate. At frequencies higher than 1500 Hz, the vibrating surfaces of small amplitude are distributed equally on the plate surface. No large amplitudes (red color) were observed.
- -
- Wood anisotropy has no effect on the vibration patterns for modes 1 to 4. Only mode 4 is illustrated in this Table 3. For mode 4 and the isotropic, transverse isotropic and orthotropic cases, the frequencies are respectively 135.66 Hz, 138.35 Hz and 173.38 Hz. The vibrating surface (+, yellow and red) is in the lower bout. Mode 6 shows identical patterns for the isotropic and transverse isotropic cases and is different from orthotropic symmetry for which the central bout vibrates mostly. Mode 7—the patterns are very similar for isotropic and transverse isotropic cases and different for the orthotropic case. The orthotropic plate vibrates (+ red and yellow) mostly on the wider lower bout, at f = 217.44 Hz. Mode 9—the patterns are similar for the isotropic and transverse isotropic cases, and it is the central part of the lower bout which vibrates mostly. In the orthotropic case, the vibration pattern is more complex with a vibrating zone on the central and lower bouts. Mode 10, the center bout vibrates identically for the isotropic and transverse isotropic plates. The orthotropic plate vibrates mostly on the lower bout at f = 257.72 Hz. Mode 11, the vibration patterns of the isotropic and transverse isotropic cases are similar, and all bouts vibrate. The orthotropic plate pattern, f = 274.93 Hz, is very different, and the upper and central bouts vibrate more than the lower bout. At superior modes, over 438 Hz, the patterns are different for each case of anisotropy. However, in case of the orthotropic plate, mode 58, f = 593.89 Hz, the central bout does not vibrate. At frequencies higher than 1000 Hz, the small amplitude vibrating surfaces are distributed equally on the plate surface. Only very small zones of large amplitude (red color) were observed on the orthotropic plate on the lower bout.
- -
- The vibration of flat isotropic plates involves firstly flexural bending wave displacements, perpendicular to the surface. The modal frequency depends on the Young’s modulus E, density ρ, plate thickness t, and k = 2π/λ, where λ is the spatially averaged characteristic wave length of two-dimensional standing waves. The frequency is given by the expression f modal = [E/ρ] ½ (t k2) = V t 4π2/λ2, where V is the standing wave velocity.
- -
- The vibration of flat orthotropic plates involves flexural plate modes which are two dimensional, and the frequency depends on several elastic parameters of the anisotropic media. Moreover, there is the necessity of fitting an integral number of half wave length standing waves within the upper and lower bout area of the plate.
6.5.2. Factors Related to the Environmental Conditions
- (a)
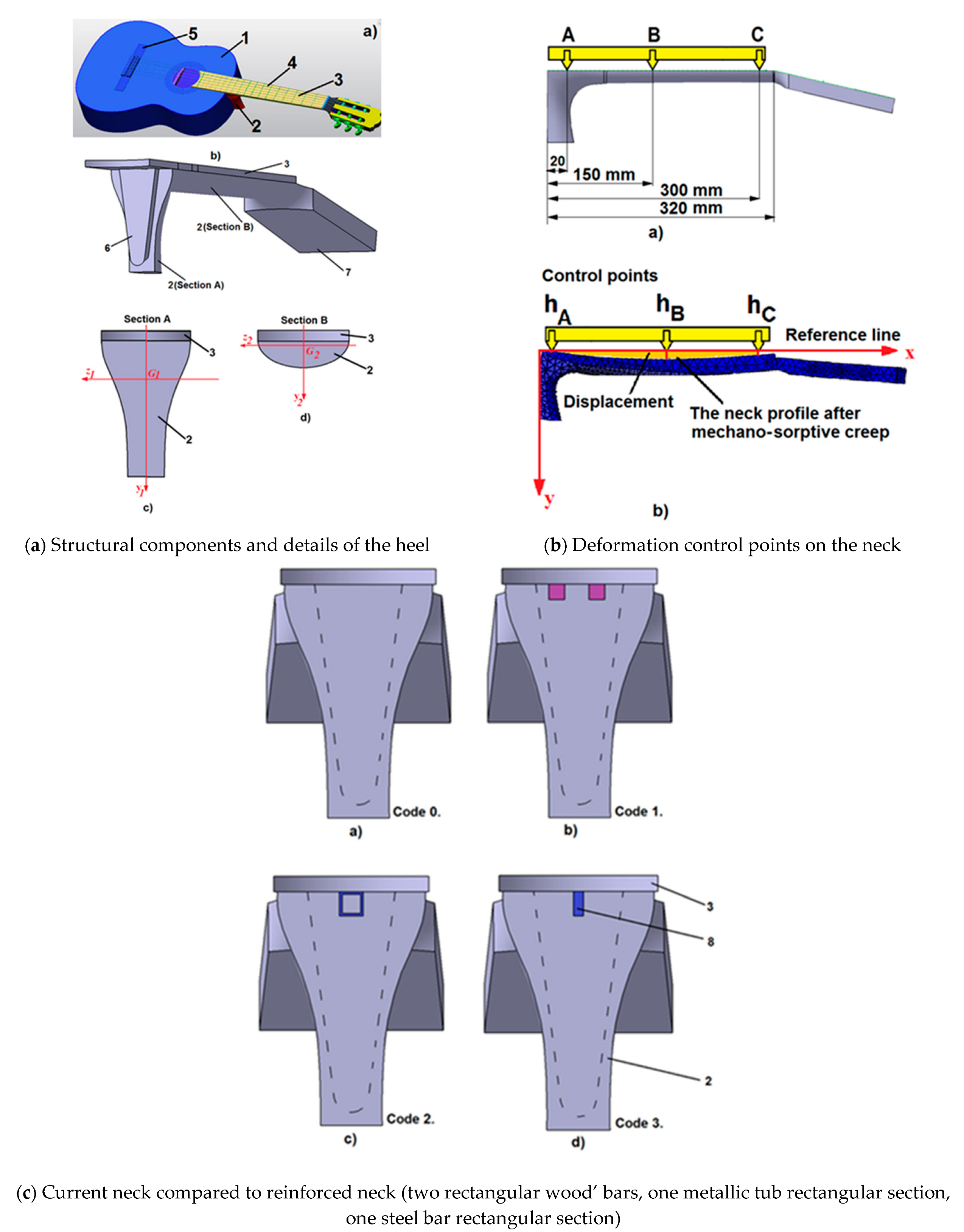
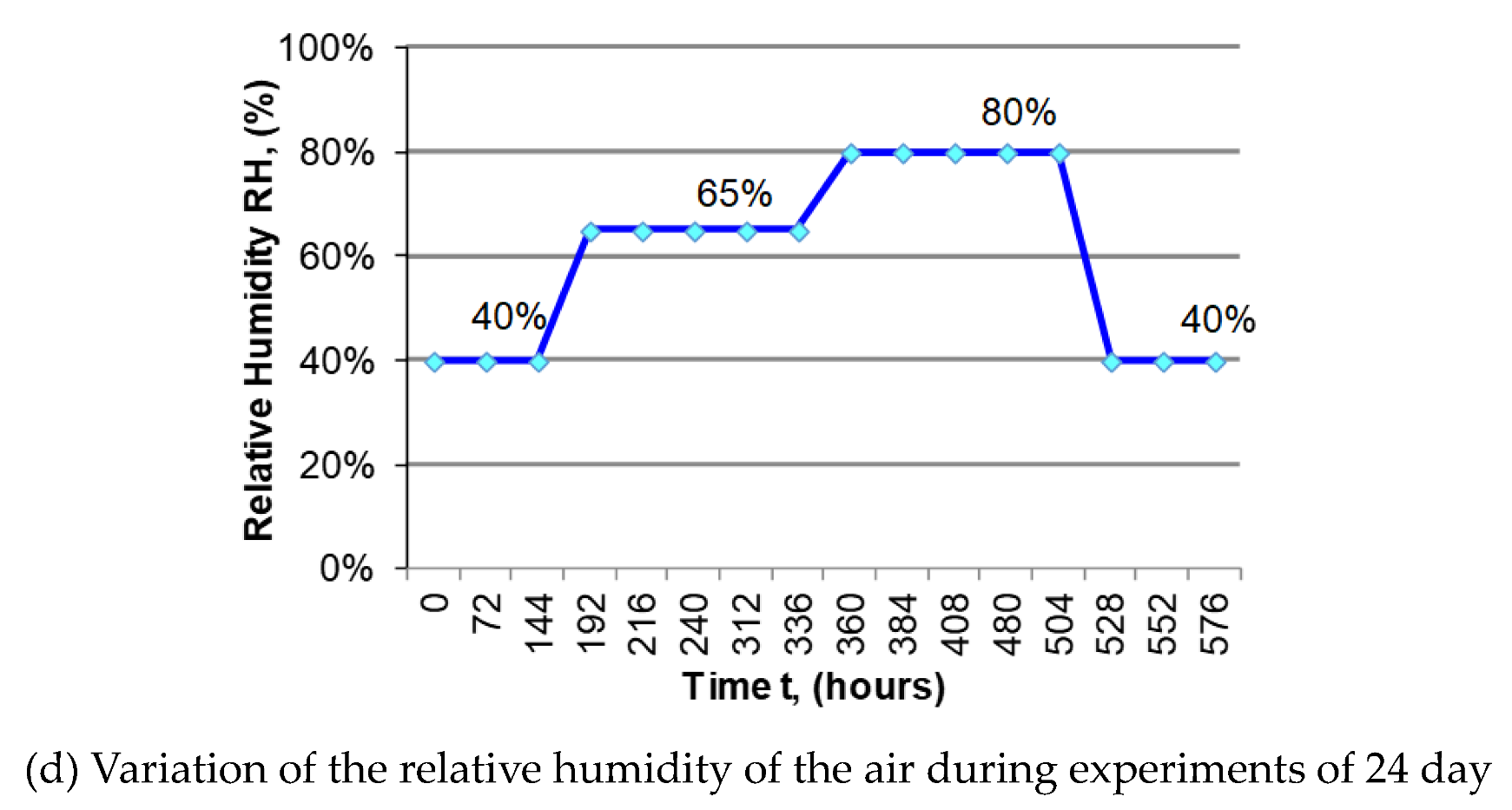
- Effect of moisture content variation on elastic properties of a blank of a guitar
- (b)
- Wood moisture variation and the induced deformation in the neck of a guitar
6.5.3. Factors Related to the Natural Aging of Wood
- -
- Lignin slightly decreases with aging because of its oxidizability. This effect is evident in the color and the perfumed odors of old wood. The density of old wood is in general lower than that of the new wood because of lignin oxidizability.
- -
- Hemicelluloses are the most unstable components, easily hydrolyzable in oligosaccharides.
- -
- Cellulose is the most stable chemical component of wood and is quantitatively unchangeable with age. However, the index of crystallinity of cellulosic crystal varies with age. Ref. [180] stated that the index of crystallinity in Japanese cypress has a maximum at 350 years and decreases gradually with age until 1400 years.
- -
- The effects of aging are usually attributed to irreversible chemical changes in wood polymers, such as the recrystallization of cellulose and depolymerization of hemicelluloses [181].
- -
- Long-term loading of wood can have an effect on the piezoelectric properties of wood [182].
6.5.4. Factors Related to the Long-Term Loading of Wood in Static or Dynamic Regimes
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
List of Notations and Abbreviations
| Coordinate systems | |
| L, R, T | Natural axes of wood |
| L | Longitudinal growth direction of tree, fiber main orientation direction |
| R | Radial direction with respect to annual growth ring |
| T | Tangential direction with respect to annual growth ring. The corresponding planes are LR, LT, RT. |
| 1,2,3 | Anisotropic axes of a solid in general |
| X Y Z | Laminate axes—length, width, depth/height |
| A | Transformation matrix LRT to XYZ |
| t | Time |
| Mechanic and acoustic parameter | |
| σijkl or σij | Stress tensor (N/m2) |
| [εkl] | Strain tensor |
| n | Wave normal vector |
| p | Polarization vector |
| u | Particle displacement field (m) |
| ξ | Ray velocity/energy flux vector (m/s) |
| α | Attenuation coefficient is expressed in dB/m or in Np/m |
| V | Wave velocity (m/s) |
| f | Frequency (Hz) |
| ω | Angular frequency = 2 π f(s-1) |
| λ | Wavelength (m) |
| χ | Beam shift/skew angle |
| Z | Acoustic impedance (kg m−2 s−1) |
| Cijkl | Stiffness tensor (N/m2) or Cij or [C] |
| Sijkl | Compliance tensor or Sij or [S]; [C]−1 = [S] |
| ρ | Density (kg/m3) |
| tan δ | Loss tangent |
| Θ | Grain angle |
| Φ | Ring angle |
| Technical constants | |
| E is Young’s modulus (which is the ratio of longitudinal stress to longitudinal strain in the same direction of a rod, and in static test); G is the shear modulus (which is the ratio of the deviatoric stress to the deviatoric strain); ν is the Poisson’s ratio (the ratio of the transverse contraction of a sample to its longitudinal extension, under tensile stress). | |
| Abbreviations for wave types | |
| P, SV SH | Longitudinal or compressional, shear in plane, shear out of plane |
| QP QSV | Quasi P, quasi SV |
| ACU | Air-coupled ultrasound |
| FDTD | Finite difference time domain |
| Tx, Rx | Transmitter, receiver transducers |
References
- Beall, F.C. Overview of the use of ultrasonic technologies in research on wood properties. Wood Sci. Technol. 2002, 36, 197–212. [Google Scholar] [CrossRef]
- Bucur, V. Acoustics of Wood, 2nd ed.; First edition was published in 1995 by CRC Boca Raton; Springer: New York, NY, USA, 2006. [Google Scholar]
- Ross, R.J. Nondestructive Evaluation of Wood, 2nd ed.; General Technical Report FPL-GTR-238; Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2015.
- Hearmon, R.F.S. An Introduction to Applied Anisotropic Elasticity; Oxford University Press: Oxford, UK, 1961. [Google Scholar]
- Hearmon, R.F.S. The Elasticity of Wood and Plywood; Forest Products Research Special Report No. 7; HMSO: London, UK, 1948. [Google Scholar]
- Musgrave, M.J.P. Crystal Acoustics; Oxford University Press: Oxford, UK, 1970. [Google Scholar]
- Green, R.E., Jr. Ultrasonic Investigation of Mechanical Properties; Academic Press: New York, NY, USA, 1973; Volume 3. [Google Scholar]
- Chevalier, Y.; Vinh, J.T. Chapter 10 Characterization of isotropic and anisotropic materials by progressive ultrasonic waves. In Mechanics of Viscoelastic Materials and Wave Dispersion; Wiley: London, UK, 2010; pp. 513–554. [Google Scholar]
- Jones, R.M. Mechanics of Composite Materials; Mc Graw Hill: Washington, DC, USA, 1975. [Google Scholar]
- Lipsett, A.W.; Beltzer, A.I. Re-examination of dynamic problem of elasticity for negative poisson ratios. J. Acoust. Soc. Am. 1988, 86, 2179–2186. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure & Properties; Pergamon Press: Oxford, UK, 1988. [Google Scholar]
- Bucur, V.; Archer, R.R. Elastic constants for wood by an ultrasonic method. Wood Sci. Technol. 1984, 18, 255–265. [Google Scholar] [CrossRef]
- McIntyre, M.E.; Woodhouse, J. On measuring wood properties, Part 3. J. Catgut Acoust. Soc. 1986, 45, 14–23. [Google Scholar]
- Trinca, A.J. Methodology for Determination of Elastic Constants of Wood with Ultrasound. Ph.D. Thesis, Unicamp Campinas, Campinas, Brazil, 2011. (In Portuguese). [Google Scholar]
- Gonçalves, R.; Garcia, G.H.L.; Brazolin, S.; Bertoldo, C.; Ruy, M. Methodology for the characterization of elastic constants of wood from tree branches. BioResources 2019, 14, 8439–8454. [Google Scholar] [CrossRef]
- Watanabe, U.; Norimoto, M. Three dimensional analysis of elastic constants of the wood cell wall. Wood Res. Bull. Wood Res. Inst. Kyoto Univ. 2000, 87, 1–7. [Google Scholar]
- Bucur, V.; Kazemi-Najafi, S.K. Negative Poisson ratios in wood and Particleboard with Ultrasonic Technique. In Nondestructive Characterization of Materials XI, Proceedings of the 11th International Symposium Berlin, Germany, 24–28 June 2002; Springer Nature: Berlin/Heidelberg, Germany, 2002; Volume 6, p. 47. [Google Scholar]
- Bodig, J.; Goodmann, J.R. Prediction of elastic parameter of wood. Wood Sci. 1973, 5, 249–264. [Google Scholar]
- Bodig, J.; Jayne, B.A. Mechanics of Wood and Wood Composites; van Nostrand Reinhold: New York, NY, USA, 1982. [Google Scholar]
- Guitard, D. Mécanique du Matériau Bois et Composites; Cépaduès: Paris, France, 1987. [Google Scholar]
- Sotomayor Castellanos, J.R. Dynamic characteristics of 22 woods determined by the transverse vibration method. Rev. Mex. De Cienc. For. 2018, 9, 181–202. [Google Scholar]
- Dinulică, F.; Bucur, V.; Albu, C.T.; Vasilescu, M.M.; Curtu, A.L.; Nicolescu, N.V. Relevant phenotypic descriptors of the resonance Norway spruce standing trees for the acoustical quality of wood for musical instruments. Eur. J. For. Res. 2021, 140, 105–125. [Google Scholar] [CrossRef]
- Dinulica, F.; Stanciu, M.D.; Savin, A. Correlation between anatomical grading and acoustic–elastic properties of resonant spruce wood used for musical instruments. Forests 2021, 12, 1122. [Google Scholar] [CrossRef]
- Rocaboy, F.; Bucur, V. About the physical properties of wood of twentieth century violins. Catgut Acoust. Soc. J. Ser. II 1990, 1, 21–28. Available online: https://stacks.stanford.edu/file/druid:gh900xs0490/CAS_gh900xs0490.pdf#page=23 (accessed on 4 July 2022).
- Mason, E.G.; Hayes, M.; Pink, N. Validation of ultrasonic velocity estimates of wood properties in discs of radiata pine. N.Z. J. For. Sci. 2017, 47, 16. [Google Scholar] [CrossRef]
- Rose, J.L. Ultrasonic Waves in Solid Media; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Achenbach, J. Wave Propagation in Elastic Solids; Elsevier: New York, NY, USA, 2012. [Google Scholar]
- Berndt, H.; Johnson, G.C. Examination of Wave Propagation in Wood from a microstructural Perspective. In Review of Progress in Quantitative Nondestructive Evaluation; Springer: Boston, MA, USA, 1995; pp. 1661–1668. [Google Scholar]
- Berndt, H.; Schniewind, A.P.; Johnson, G.C. High resolution ultrasonic imaging of wood. Wood Sci. Technol. 1999, 33, 185–198. [Google Scholar] [CrossRef]
- Berndt, H.; Schniewind, A.P.; Johnson, G.C. Ultrasonic energy propagation through wood: Where, when, how much. In Proceedings of the 12th International Symposium on Nondestructive Testing of Wood University of Western Hungary, Sopron, Hungary, 13–15 September 2000; pp. 57–65. [Google Scholar]
- Bucur, V.; Berndt, H. Ultrasonic energy flux and off diagonal elastic constants of wood. In Proceedings of the IEEE Ultrasonics Symposium joint World Congress Ultrasonics, Atlanta, GA, USA, 7–10 October 2001; Volume 1, pp. 697–700. [Google Scholar]
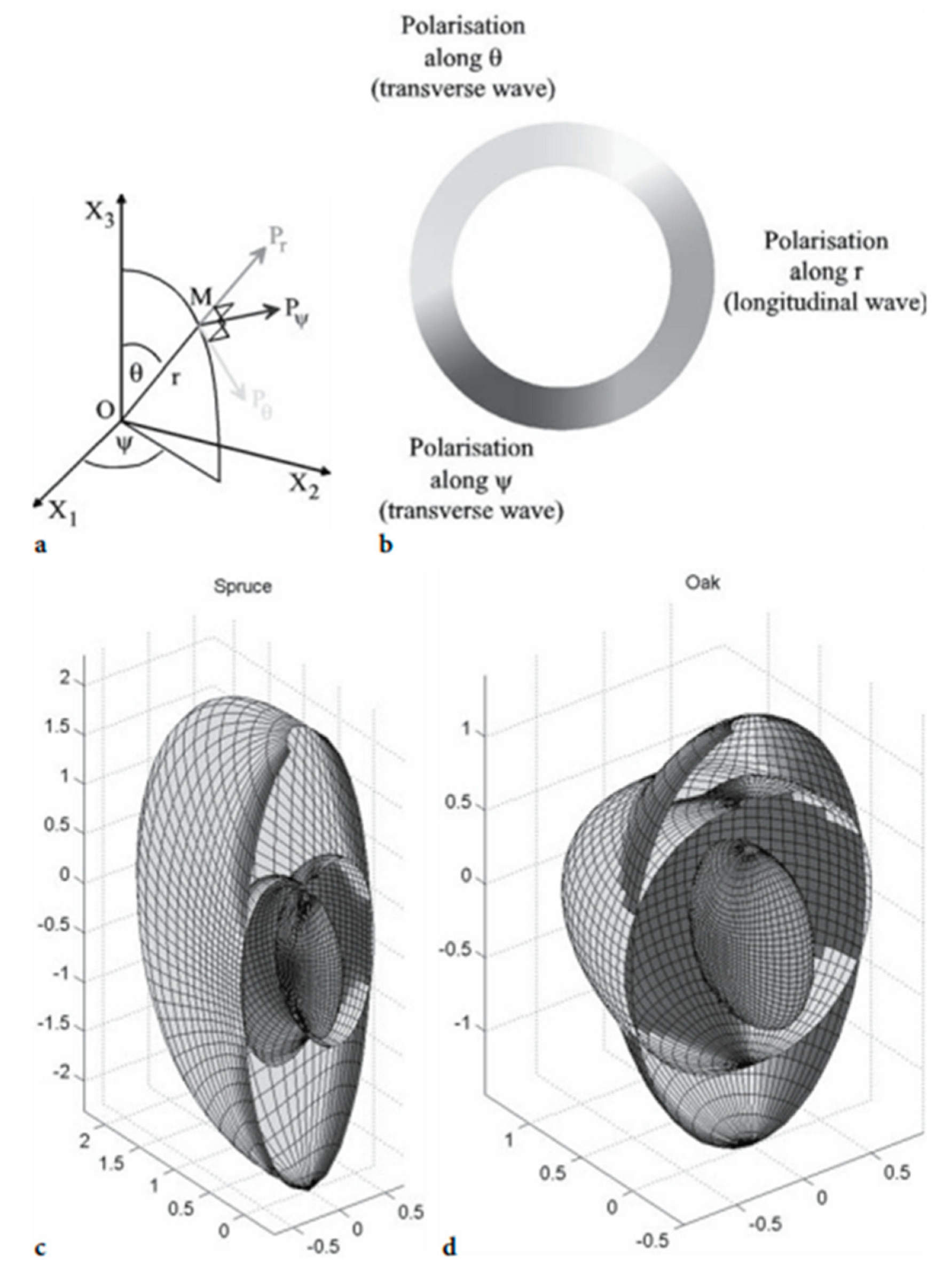
- Lanceleur, P.; de Belleval, J.P.; Mercier, N. Synthetic tridimensional representation of slowness surfaces of anisotropic materials. Acta Acust. United Acust. 1998, 84, 1047–1054. [Google Scholar]
- Bucur, V.; Lanceleur, P.; Roge, B. Acoustic properties of wood in tridimensional representation of slowness surfaces. Ultrasonics 2002, 40, 537–541. [Google Scholar] [CrossRef]
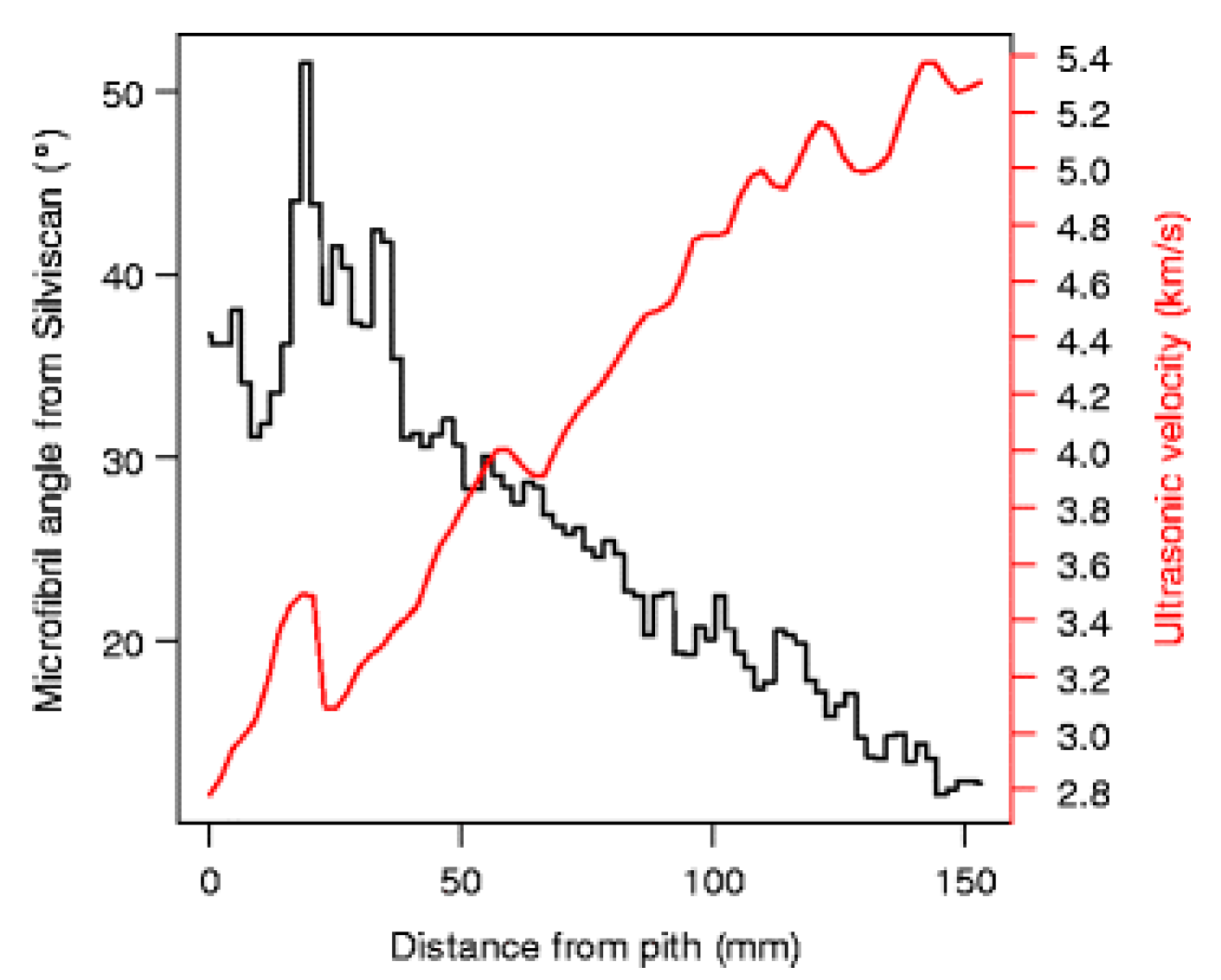
- Kharrat, W.; Koubaa, A.; Khlif, M.; Bradai, C. Intra-ring wood density and dynamic modulus of elasticity profiles for black spruce and jack pine from x-ray densitometry and ultrasonic wave velocity measurement. Forests 2019, 10, 569. [Google Scholar] [CrossRef]
- Moliński, W.; Fabisiak, E.; Roszyk, E. The propagation velocity of ultrasound waves along the grain in juvenile, mature, normal and reaction wood of pine (Pinus sylvestris L.). Ann. Wars. Univ. Life Sci. SGGW For. Wood Technol. 2007, 62, 200–206. [Google Scholar]
- Sandoz, J.L. Moisture content and temperature effect on ultrasound timber grading. Wood Sci. Technol. 1993, 27, 373–380. [Google Scholar] [CrossRef]
- Sakai, H.; Minamisawa, A.; Takagi, K. Effect of moisture content on ultrasonic velocity and attenuation in woods. Ultrasonics 1990, 28, 382–385. [Google Scholar] [CrossRef]
- Ozyhar, T.; Hering, S.; Sanabria, S.J.; Niemz, P. Determining moisture-dependent elastic characteristics of beech wood by means of ultrasonic waves. Wood Sci. Technol. 2013, 47, 329–341. [Google Scholar] [CrossRef]
- Hering, S.; Keunecke, D.; Niemz, P. Moisture-dependent orthotropic elasticity of beech wood. Wood Sci Technol. 2012, 46, 927–938. [Google Scholar] [CrossRef]
- Crespo, J.; Aira, J.R.; Vázquez, C.; Guaita, M. Comparative analysis of the elastic constants measured via conventional, ultrasound, and 3-D digital image correlation methods in Eucalyptus globulus. BioResources 2017, 12, 3728–3743. [Google Scholar] [CrossRef]
- Bucur, V. Les termes non diagonaux de la matrice des rigidités du bois. Holzforschung 1986, 40, 315–324. [Google Scholar] [CrossRef]
- Schubert, S. Acousto-Ultrasound Assessment of Inner Wood Decay in Standing Trees: Possibilities and Limitations. Doctoral Dissertation, ETH Zurich, Zurich, Switzerland, 2007. [Google Scholar]
- Schubert, S.; Gsell, D.; Dual, J.; Motavalli, M.; Niemz, P. Rolling shear modulus and damping factor of spruce and decayed spruce estimated by modal analysis. Holzforschung 2006, 60, 78–84. [Google Scholar] [CrossRef]
- Longo, R.; Delaunay, T.; Laux, D.; El Mouridi, M.; Arnould, O.; Le Clezio, E. Wood elastic characterization from a single sample by resonant ultrasound spectroscopy. Ultrasonics 2012, 52, 971–974. [Google Scholar] [CrossRef]
- Pellerin, R.F.; Ross, R.J. Nondestructive Evaluation of Wood; Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2002.
- Schimleck, L.; Dahlen, J.; Apiolaza, L.A.; Downes, G.; Emms, G.; Evans, R.; Moore, J.; Pâques, L.; Van den Bulcke, J.; Wang, X. Non-destructive evaluation techniques and what they tell us about wood property variation. Forests 2019, 10, 728. [Google Scholar] [CrossRef]
- Legg, M.; Bradley, S. Measurement of stiffness of standing trees and felled logs using acoustics: A review. J. Acoust. Soc. Am. 2016, 138, 588–604. [Google Scholar]
- Rudnicki, M.; Wang, X.; Ross, R.J.; Allison, B.A.; Perzynski, K. Measuring Wood Quality in Standing Trees—A Review; General Technical Reports FPL-GTR-248; Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2017; p. 248.
- McDonald, K.A.; Cox, R.G.; Bulgrin, E.H. Locating Lumber Defects by Ultrasonics; Research Paper Forests Products Lab: Madison, WI, USA, 1969.
- Waubke, N.V. Fundamental Investigations on the Suitability of Ultrasound Pulse Duration Measurements as Simplified and Accurate Method for Sorting Timber; Institute for Materials Science and Physics of the University of the Bundeswehr: Munich, Germany, 1981. [Google Scholar]
- Waubke, N.V. Use of flight time measurement for sorting timber. Holzbauforschung 1988, 40, 152–154. [Google Scholar]
- Bucur, V. Delamination in Wood, Wood Products and Wood-Based Composites; Springer Dordrecht: Berlin, Germany, 2011. [Google Scholar]
- Ross, R.J.; McDonald, K.A.; Green, D.W.; Schad, K.C. Relationship between log and lumber modulus of elasticity. For. Prod. J. 1997, 47, 89–92. [Google Scholar]
- Ross, R.J.; Brashaw, B.K.; Pellerin, R.F. Nondestructive evaluation of wood. For. Prod J. 1998, 48, 15–19. [Google Scholar]
- Green, D.W.; Ross, R.J. Linking log quality with product performance. In Proceedings of the IUFRO all division 5 International Conference, Pullman, WA, USA, 7–12 July 1997; International Union of Forestry Research Organizations: Rome, Italy, 1997. [Google Scholar]
- Sandoz, J.L. Mechanical assessment of conical roundwood for Swiss spruce. In De la Forêt Cultivée a l’industrie de Demain’, Proceedings of the Actes du 3eme Colloque Sciences et Industries du Bois, Bordeaux, France, 14–15 May 1990; Association pour la Recherche sur la Production Forestière et le Bois en Région Aquitaine (ARBORA): Bordeaux, France, 1990; Volume 1, pp. 145–157. [Google Scholar]
- Bartholomeu, A. Ultrasonic Grading of Wooden Beams. Ph.D. Dissertation, University of Campinas, Campinas, Brazil, 2001. (In Portuguese). [Google Scholar]
- Dickson, R.L.; Raymond, C.A.; Joe, W.; Wilkinson, C.A. Segregation of Eucalyptus dunnii logs using acoustics. For. Ecol. Manag. 2003, 179, 243–251. [Google Scholar] [CrossRef]
- Wang, X.; Ross, R.J.; Green, D.W.; Brashaw, B.; Englund, K.; Wolcott, M. Stress wave sorting of red maple logs for structural quality. Wood Sci. Technol. 2004, 37, 531–537. [Google Scholar] [CrossRef]
- Arriaga, F.; Íñiguez-Gonzalez, G.; Esteban, M.; Divos, F. Vibration method for grading of large cross—Section coniferous timber species. Holzforschung 2012, 66, 381–387. [Google Scholar] [CrossRef]
- Bertoldo, C.; Gonҫalves, R. Influence of measurement position, tree diameter, and bulk wood density on models 38 trees that predict wave propagation velocity in logs according to the velocity in trees. For. Prod. J. 2015, 65, 166–172. [Google Scholar] [CrossRef]
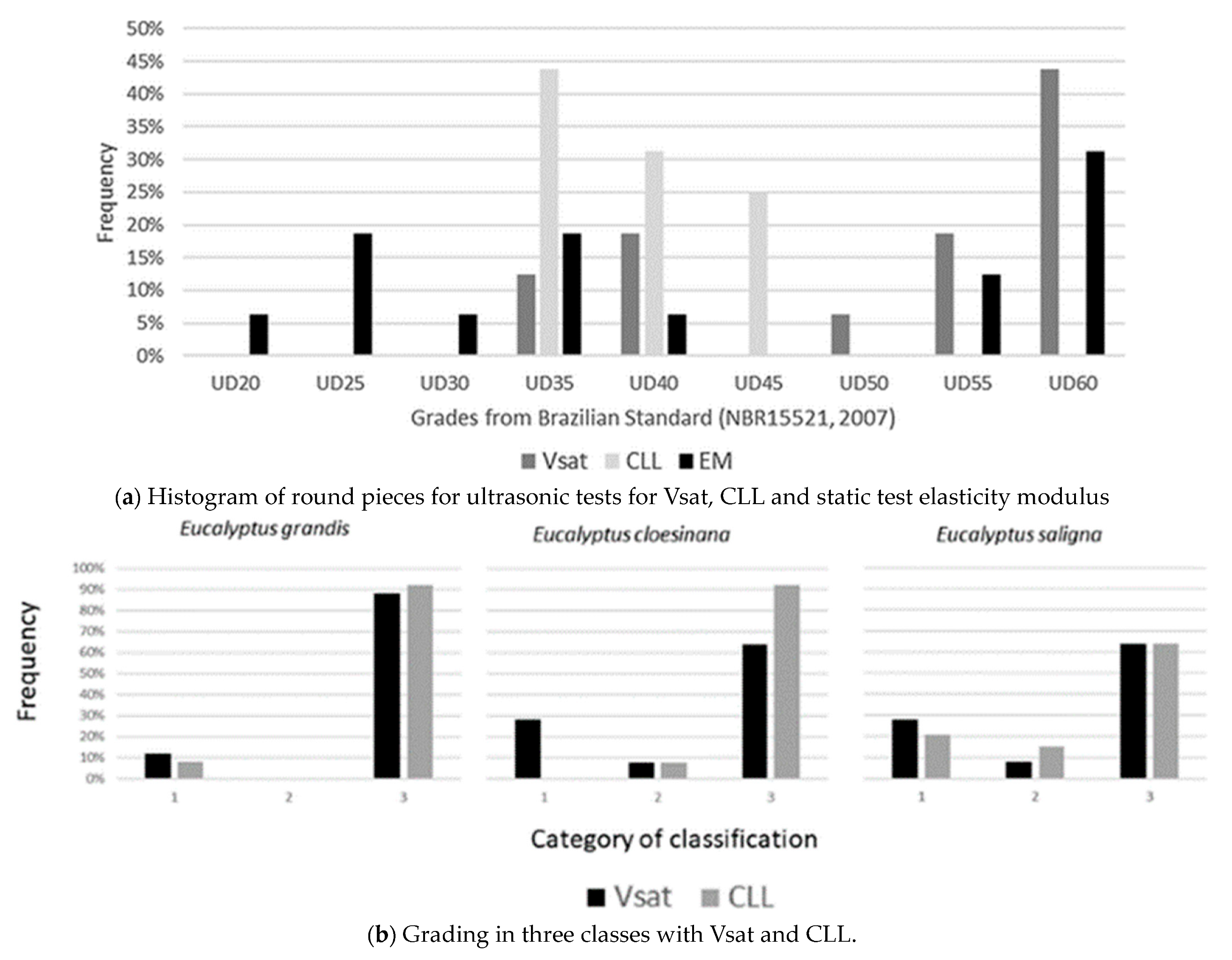
- Ruy, M.; Gonçalves, R.; Pereira, D.M.; Lorensani, R.G.M.; Bertoldo, C. Ultrasound grading of round Eucalyptus timber using the Brazilian standard. Eur. J. Wood Wood Prod. 2018, 76, 889–898. [Google Scholar] [CrossRef]
- Kovryga, A.; Sarnaghi, A.K.; van de Kuilen, J.W.G. Strength grading of hardwoods using transversal ultrasound. Eur. J. Wood Wood Prod. 2020, 78, 951–960. [Google Scholar] [CrossRef]
- Bucur, V. Ultrasonic techniques for nondestructive testing of standing trees. Ultrasonics 2005, 43, 237–239. [Google Scholar] [CrossRef]
- Bucur, V. Chapter 5 Ultrasonic imaging In Nondestructive Characterization and Imaging of Wood; Springer: Berlin/Heidelberg, Germany, 2003; pp. 181–213. [Google Scholar]
- Bucur, V. Urban Forest Acoustics; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Sandoz, J.L. Standing tree quality assessments using ultrasound. Int. Symp. Urban Tree Health 1997, 496, 269–278. [Google Scholar] [CrossRef]
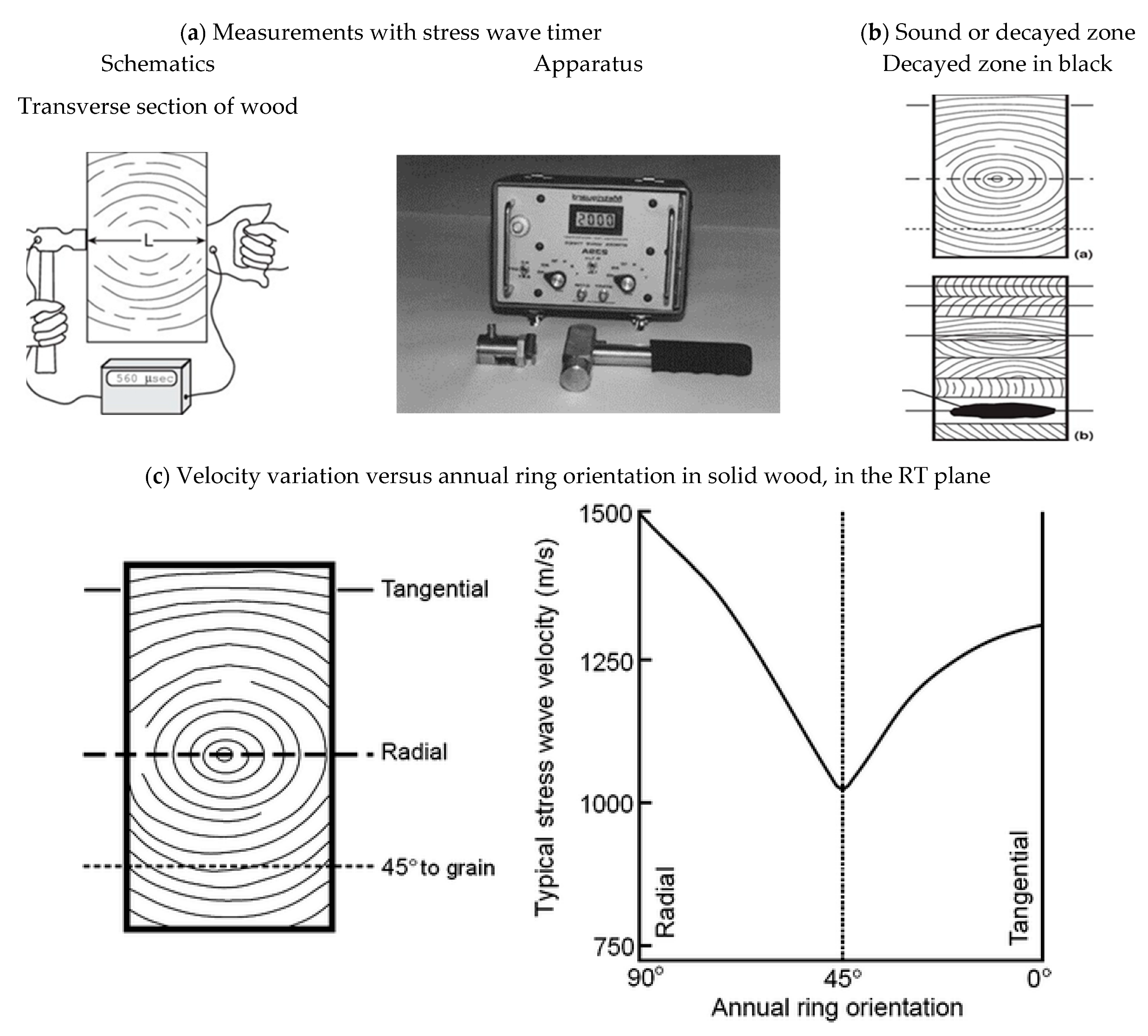
- Ouis, D. Detection of rot in standing trees by means of an acoustic technique. Arboric. J. 2001, 25, 117–152. [Google Scholar] [CrossRef]
- McDonald, K.A. Lumber Defect Detection by Ultrasonics; Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 1978; Volume 311.
- Chazelas, J.L.; Vergne, A.; Bucur, V. Analyse de la variation des propriétés physiques et mécaniques locales du bois autour des nœuds. In Actes du Colloque Comportement Mécanique du Bois; G.S. Rhéologie du Bois: Bordeaux, France, 1988; pp. 376–386. [Google Scholar]
- Martinis, R. Nondestructive Techniques for Decay Diagnosis on Standing Trees. Ph.D. Thesis, University of Florence Dipartimento di Biotecnologie, Agrarie, Italy, 2002. (In Italian). [Google Scholar]
- Martinis, R.; Socco, V.; Sambuelli, L.; Schmitt, O.; Bucur, V. Tomographie ultrasonore pour les arbres sur pied. Ann. For. Sci. 2004, 61, 157–162. [Google Scholar] [CrossRef]
- Nicolotti, G.; Socco, L.V.; Martinis, R.; Godio, A.; Sambuelli, L. Application and comparison of three tomographic techniques for detection of decay in trees. J. Arboric. 2003, 29, 66–78. [Google Scholar]
- Arciniegas, A.; Prieto, F.; Brancheriau, L.; Lasaygues, P. Literature review of acoustic and ultrasonic tomography in standing trees. Trees 2014, 28, 1559–1567. [Google Scholar] [CrossRef]
- Espinosa, L.; Brancheriau, L.; Cortes, Y.; Prieto, F.; Lasaygues, P. Ultrasound computed tomography on standing trees: Accounting for wood anisotropy permits a more accurate detection of defects. Ann. For. Sci. 2020, 77, 68. [Google Scholar]
- Wang, X.; Carter, P. Acoustic assessment of wood quality in trees and logs. In Nondestructive Evaluation of Wood, 2nd ed.; Ross, R.J., Ed.; General Technical Report FPL-GTR-238; Forest Product Laboratory: Madison, WI, USA, 2015; pp. 87–102. [Google Scholar]
- Mattheck, C.G.; Bethge, K.A. Detection of decay in trees with Metriguard stress wave timer. J. Arboric. 1993, 19, 374. [Google Scholar] [CrossRef]
- Allison, R.B.; Wang, X.; Senalik, C.A. Methods for nondestructive testing of urban trees. Forests 2020, 11, 1341. [Google Scholar] [CrossRef]
- Puxeddu, M.; Cuccuru, F.; Fais, S.; Casula, G.; Bianchi, M.G. 3D Imaging of CRP- (close range photometry) and Ultrasonic Tomography to Detect Decay in a Living Adult Holm Oak (Quercus ilex L.) in Sardinia (Italy). Appl. Sci. 2021, 11, 1199. [Google Scholar] [CrossRef]
- Bucur, V. Wood structural anisotropy estimated by invariants. Bull. Int. Assoc. Wood Anat. 1988, 9, 67–74. [Google Scholar] [CrossRef]
- Bucur, V. An ultrasonic method for measuring the elastic, constants of wood increment cores bored from living trees. Ultrasonics 1983, 21, 116–126. [Google Scholar] [CrossRef]
- Bucur, V.; Perrin, A. Détermination du module d’Young du bois par une méthode dynamique sur carottes de sondage. Ann. Des Sci. For. 1981, 38, 283–298. [Google Scholar] [CrossRef]
- Wessels, C.B.; Malan, F.S.; Rypstra, T. A review of measurement methods used on standing trees for the prediction 549 of some mechanical properties of timber. Eur. J. For. Res. 2011, 130, 881–893. [Google Scholar] [CrossRef]
- Bauer, C.; Kilbertus, G.; Bucur, V. Technique ultrasonore de caractérisation du degré d’altération des bois de hêtre et de pin soumis a l’attaque de différents champignons. Holzforschung 1991, 45, 41–46. [Google Scholar] [CrossRef]
- Bucur, V.; Navarrete, A.; De Troya, M.T.; Sanchez, E.; Garros, S.; Diez, R. Fungi decay in wood by combined nondestructive techniques. In Proceedings of the Ultrasonics International 93 Conference, Vienna, Austria, 6–8 July 1993; Technical University of Vienna: Vienna, Austria, 1993; pp. 287–290. [Google Scholar]
- Kazemi-Najafi, S.; Shalbafan, A.; Ebrahimi, G. Internal decay assessment in standing beech trees using ultrasonic velocity measurement. Eur. J. For. Res. 2009, 128, 345–350. [Google Scholar] [CrossRef]
- Krajnc, L.; Kadunc, A.; Straže, A. The use of ultrasound velocity and damping for the detection of internal structural defects in standing trees of European beech and Norway spruce. Holzforschung 2019, 73, 807–816. [Google Scholar] [CrossRef]
- Bucur, V.; Feeney, F. Attenuation of ultrasound in solid wood. Ultrasonics 1992, 30, 76–81. [Google Scholar] [CrossRef]
- Llana, D.F.; Short, I.; Harte, A.M. Use of non-destructive test methods on Irish hardwood standing trees and small-diameter round timber for prediction of mechanical properties. Ann. For. Sci. 2020, 77, 62. [Google Scholar]
- Dickson, R.L.; Matheson, A.C.; Joe, B.; Ilic, J.; Owen, J.V. Acoustic segregation of Pinus radiata logs for sawmilling. N. Z. J. Forest. Sci. 2004, 34, 175–189. [Google Scholar]
- Matheson, A.C.; Dickson, R.L.; Spencer, D.J.; Joe, B.; Ilic, J. Acoustic segregation of Pinus radiata logs according to stiffness. Ann. For. Sci. 2002, 59, 471–477. [Google Scholar] [CrossRef]
- Simic, K.; Gendvilas, V.; O’Reilly, C.; Harte, A.M. Predicting structural timber grade-determining properties using acoustic and density measurements on young Sitka spruce trees and logs. Holzforschung 2019, 73, 139–149. [Google Scholar] [CrossRef]
- European Standard. EN 14081-2; Timber Structures—Strength Graded Structural Timber with Rectangular Cross Section—Part 2: Machine Grading, Additional Requirements for Type Testing. European Committee of Standardization (CEN): Brussels, Belgium, 2009. [Google Scholar]
- European Standard. EN 408; Timber Structures: Structural Timber and Glued Laminated Timber—Determination of Some Physical and Mechanical Properties. European Committee of Standardization (CEN): Brussels, Belgium, 2010. [Google Scholar]
- Gonçalves, R.; Batista, F.A.F.; Lorensani, R.G.M. Selecting Eucalyptus clones using ultrasound test on standing trees. For. Prod. J. 2013, 63, 112–118. [Google Scholar]
- NBR 15521; Nondestructive Testing, Ultrasonic Testing, Mechanical Classification of Dicotyledonous Sawn Wood. National Board of Revenue: Dhaka, Bangladesh, 2007.
- McDonald, K.A.; Green, D.W.; Dwyer, J.; Whipple, J.W. Red maple stressgraded 2 by 4 dimension lumber from factory-grade logs. For. Prod. J. 1993, 43, 13–18. [Google Scholar]
- Green, D.W.; McDonald, K.A. Mechanical properties of red maple structural lumber. Wood Fiber Sci. 1993, 25, 365–374. [Google Scholar]
- Sinalik, C.A.; Green, D.W. Chapter 4 Grading and properties of hardwood structural lumber. In Under Evaluated Hardwoods for Engineering Materials and Components, 2nd ed.; Ross, R.J., Erikson, J.R., Eds.; Edition General Technical Report FPL-GTR-275; U.S. Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2020; pp. 27–38. [Google Scholar]
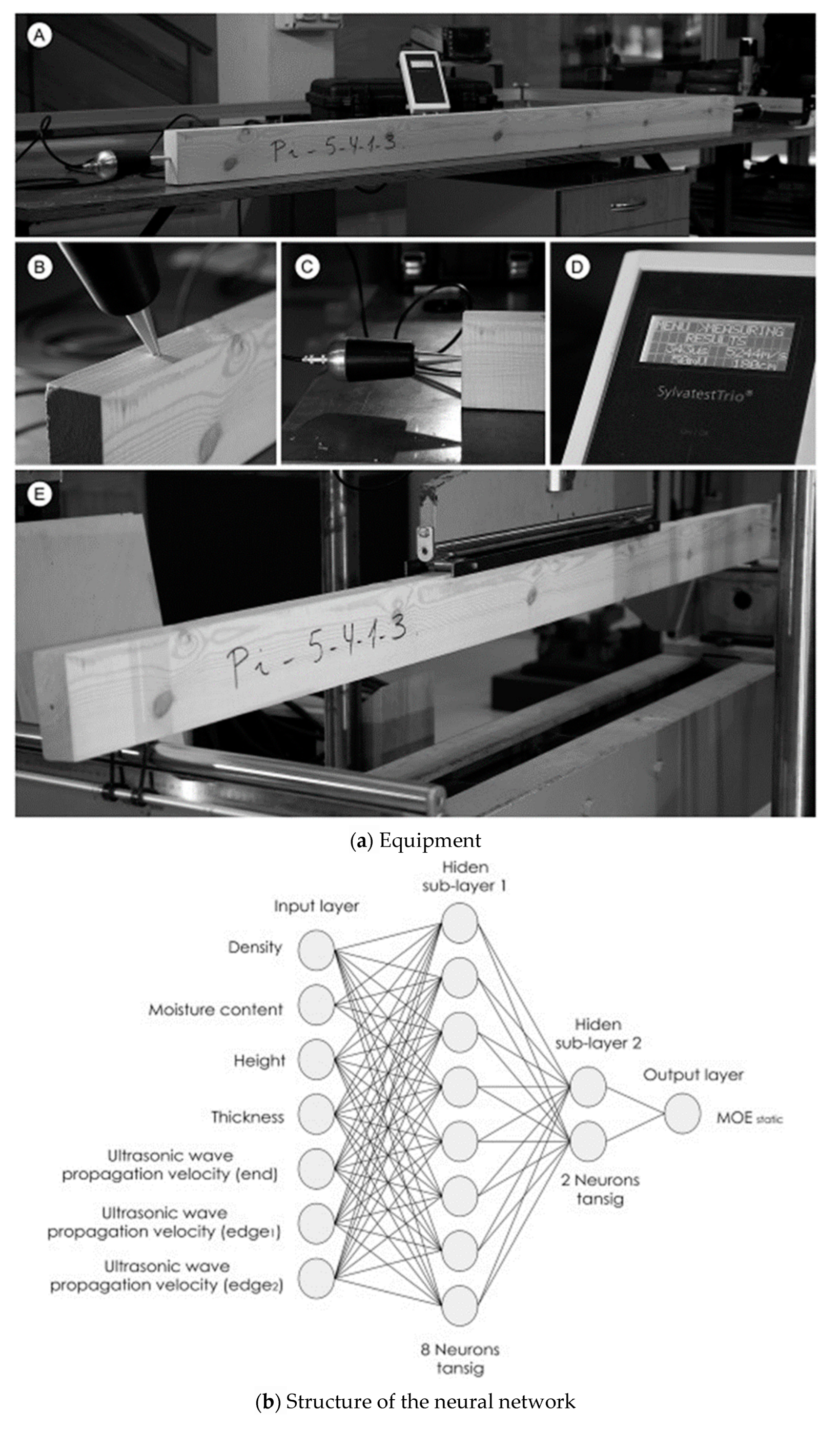
- García-Iruela, A.; Fernández, F.G.; Esteban, L.G.; De Palacios, P.; Simón, C.; Arriaga, F. Comparison of modelling using regression techniques and an artificial neural network for obtaining the static modulus of elasticity of Pinus radiata D. Don. timber by ultrasound. Compos. Part B-Eng. 2016, 96, 112–118. [Google Scholar]
- Arriaga, F.; Monton, J.; Segues, E.; Íñiguez-Gonzalez, G. Determination of the mechanical properties of radiata pine timber by means of longitudinal and transverse vibration methods. Holzforschung 2014, 68, 299–305. [Google Scholar] [CrossRef]
- Feeney, F.E.; Chivers, R.C.; Evertsen, J.A.; Keating, J. The influence of the inhomogeneity on the propagation of ultrasound in wood. Ultrasonics 1996, 36, 449–453. [Google Scholar] [CrossRef]
- Schafer, M.E. Ultrasound for defect detection and grading in wood and lumber. In Proceedings of the 2000 IEEE Ultrasonics Symposium. Proceedings. An International Symposium (Cat. No. 00CH37121), San Juan, PR, USA, 22–25 October 2000; Volume 1, pp. 771–778. [Google Scholar]
- Yaitskova, N.; Nadkernychnyy, Y.; Franjga, R.; Monroy Gonzalez Plata, R. TUS: A Breadboard for Development of New Wood Grading Algorithms Using Ultrasound. 2015. Available online: https://www.researchgate.net/profile/Natalia-Yaitskova/publication/272664728_TUS_a_breadboard_for_development_of_new_wood_grading_algorithms_using_ultrasound/links/54eaf77a0cf27a6de11559f8/TUS-a-breadboard-for-development-of-new-wood-grading-algorithms-using-ultrasound.pdf (accessed on 26 January 2022).
- Bhardwaj, M.C. High efficiency non-contact transducers and a very high coupling piezoelectric composite. In Proceedings of the 16th World Conference on Nondestructive Testing, Montreal, QC, Canada, 30 August–3 September 2004. [Google Scholar]
- Gan, T.H.; Hutchins, D.A.; Green, R.J.; Andrews, M.K.; Harris, P.D. Noncontact, high-resolution ultrasonic imaging of wood samples using coded chirp waveforms. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 280–288. [Google Scholar] [CrossRef]
- Marchetti, B.; Munaretto, R.; Revel, G.; Tomasini, E.P.; Bianche, V.B. Non-contact ultrasonic sensor for density measurement and defect detection on wood. In Proceedings of the 16th World Conference on Nondestructive Testing, Montreal, QC, Canada, 30 August–3 September 2004. [Google Scholar]
- Machado, J.; Sardinha, R.; Cruz, H. Feasibility of automatic detection of knots in maritime pine timber by acousto-ultrasonic scanning. Wood Sci. Technol. 2004, 38, 277–284. [Google Scholar] [CrossRef]
- Vun, R.Y.; Hoover, K.; Janowiak, J.; Bhardwaj, M.C. Calibration of non-contact ultrasound as an online sensor for wood characterization: Efects of temperature, moisture, and scanning direction. Appl. Phys. A 2008, 90, 191–196. [Google Scholar]
- Solodov, I.; Pfleiderer, K.; Busse, G. Nondestructive characterization of wood by monitoring of local elastic anisotropy and dynamic nonlinearity. Holzforschung 2004, 58, 504–510. [Google Scholar] [CrossRef]
- Tiitta, M.; Tiitta, V.; Gaal, M.; Heikkinen, J.; Lappalainen, R.; Tomppo, L. Air-coupled ultrasound detection of natural defects in wood using ferroelectret and piezoelectric sensors. Wood Sci. Technol. 2020, 54, 1051–1064. [Google Scholar] [CrossRef]
- Galligan, W.L.; Courteau, R.W. Measurement of elasticity of timber with longitudinal stress waves and the piezoelectric effect in wood. In Proceedings of the 2nd Nondestructive Testing of Wood Symposium, Pullman, WA, USA, April 1965; pp. 223–244. [Google Scholar]
- Galligan, W.; Kerns, J.; Brashaw, B.K. Chapter 11. Machine grading of lumber. In Nondestructive Evaluation of Wood, 2nd ed.; FPL GTR 238; Ross, R.J., Ed.; Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2015; pp. 115–139. [Google Scholar]
- Entsminger, E.D.; Brashaw, B.K.; Seale, R.D.; Ross, R.J. Machine Grading of Lumber—Practical Concerns for Lumber Producers; General Technical Report FPL-GTR-279; Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2020.
- Edinburgh Napier University, UK. Available online: https://blogs.napier.ac.uk/cwst/grading-machines-speeds/ (accessed on 21 October 2021).
- Available online: https://blogs.napier.ac.uk/cwst/wp-content/uploads/sites/23/2016/12/DSC04840-e1480930831237.jpg (accessed on 21 October 2021).
- Available online: https://sahateollisuuskirja.fi/wp-content/uploads/precigrader_3_13_3_2_square-compressor-330x331.jpg (accessed on 21 October 2021).
- Available online: https://sahateollisuuskirja.fi/wp-content/uploads/resonanssivarahtelyn_mittaus_3_13_3_3-compressor-330x330.jpg (accessed on 26 January 2022).
- Nocetti, M.; Brunetti, M.; Bacher, M. Efficiency of the machine grading of chestnut structural timber: Prediction of strength classes by dry and wet measurements. Mater Struct. 2016, 49, 4439–4450. [Google Scholar]
- European Standard. EN 338; Structural Timber—Strength Classes. European Committee of Standardization (CEN): Brussels, Belgium, 2009. [Google Scholar]
- Dietsch, P.; Tannert, T. Assessing the integrity of glued-laminated timber elements. Constr. Build. Mater. 2015, 101, 1259–1270. [Google Scholar] [CrossRef]
- Huang, C.L. Chapter 11: Industry prospective of delamination in wood and wood products. In Delamination in Wood and Wood Products and Wood-Based Composites; Bucur, V., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 215–236. [Google Scholar]
- Aicher, S.; Stapf, G. Block glued glulam—Bridges, beams and arches. In Proceedings of the World Conference on Timber Engineering (WCTE 2014), Quebec City, QC, Canada, 10–14 August 2014. Session 4.8 Timber Bridges paper 714. [Google Scholar]
- Pieters, A.R. Ultrasonic energy: A new method for veneer grading. In Proceedings of the ASCE Convention, Boston, MA, USA, 2–6 April 1979; Preprint #3534; American Society of Civil Engineer: Reston, VA, USA, 1979. [Google Scholar]
- Brashaw, B.K. Chapter 10 Ultrasonic veneer grading. In Nondestructive Evaluation of Wood; FPL GTR 238; Ross, R.J., Ed.; USDA: Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2015; pp. 109–113. [Google Scholar]
- Breyer, D.E.; Fridley, K.J.; Cobeen, K.E.; Pollock, D.G. Design of Wood Structures, 8th ed.; ASD/LRFD; McGraw Hill Education: New York, NY, USA, 2019. [Google Scholar]
- Sanabria, S.J.; Furrer, R.; Neuenschwander, J.; Niemz, P.; Sennhauser, U. Air-coupled ultrasound wave propagation in glued laminated timber structures applied to bonding quality assessment. In Proceedings of the 2010 IEEE International Ultrasonics Symposium, San Diego, CA, USA, 11–14 October 2010. [Google Scholar]
- Dimanche, M.; Capretti, S.; Del Senno, M.; Facaoaru, I. Validation of theoretical approach for the detection of delamination in glued laminated beams. In Proceedings of the First European Symposium on Nondestructive Evaluation of Wood, Sopron, Hungary, 21–23 September 1994; pp. 250–260. [Google Scholar]
- Sanabria, S.J.; Furrer, R.; Neuenschwander, J.; Niemz, P.; Sennhauser, U. Air-coupled ultrasound inspection of glued laminated timber. Holzforschung 2011, 65, 377–387. [Google Scholar] [CrossRef]
- Sanabria, S.J.; Mueller, C.; Neuenschwander, J.; Niemz, P.; Sennhauser, U. Air-coupled ultrasound as an accurate and reproducible method for bonding assessment of glued timber. Wood Sci. Technol. 2011, 45, 645–659. [Google Scholar] [CrossRef]
- Sanabria, S.; Furrer, R.; Neuenschwander, J.; Niemz, P.; Schütz, P. Analytical modelling, finite-difference simulation and experimental validation of air-coupled ultrasound beam refraction and damping through timber laminates, with application to non-destructive testing. Ultrasonics 2015, 63, 65–85. [Google Scholar] [CrossRef]
- Bucur, V.; Böhnke, I. Factors affecting ultrasonic measurements in solid wood. Ultrasonics 1994, 32, 385–390. [Google Scholar] [CrossRef]
- Feeney, F. Ultrasonic Characterisation of the Structure and Properties of Wood. Doctor Dissertation, Department of Physics University of Surrey Guildford, University of Surrey, Surrey, UK, 1999. [Google Scholar]
- Feeney, B.; Chivers, R. Macroscopic considerations of Ultrasonic Propagation in Wood-Attenuation. Mol. Quantum Acoust. 2001, 22, 45–56. [Google Scholar]
- Hoyle, R.J.; Pellerin, R.F. Stress wave inspection of a wood structure. In Proceedings of the Fourth Symposium on Nondestructive Testing of Wood, Vancouver, BC, Canada, 28–30 August 1978; 1978; pp. 33–45. [Google Scholar]
- Ross, R.J.; Pellerin, R.F. Chapter 12: Inspection of timber structures using stress wave timing nondestructive evaluation tools. In Nondesrtructive Evaluation of Wood, 2nd ed.; Ross, E., Ed.; General Technical Report 238; Forest Products Laboratory: Madison WI, USA, 2015; pp. 141–148. [Google Scholar]
- Neuenschwander, J.; Sanabria, S.J.; Schuetz, P.; Widmann, R.; Vogel, M. Delamination detection in a 90-year-old glulam block with scanning dry point-contact ultrasound. Holzforschung 2013, 67, 949–957. [Google Scholar] [CrossRef]
- Kunkle, J.; Vun, R.; Eischeild, T.; Langron, M. Phenomenal advancements in transducers and piezoelectric composites for non-contact ultrasound and other applications. In Ultrasonics. In Proceedings of the 9th European Conference for Non-Destructive Testing; Berlin, Germany, 25–29 September 2006.
- Sanabria, S.J.; Wyss, P.; Neuenschwander, J.; Niem, P.; Sennhauser, U. Assessment of glued timber integrity by limited-angle microfocus X-ray computed tomography. Eur. J. Wood Wood Prod. 2011, 69, 605–617. [Google Scholar] [CrossRef]
- Gallego Juárez, J.A. Macrosonics: Phenomena, transducers and applications. In Proceedings of the Forum Acusticum Sevilla 2002, Keynote Lecture; Sociedad Española de Acústica: 2002. Available online: http://hdl.handle.net/10261/7977 (accessed on 4 July 2022).
- Gallego-Juarez, J.A.; Rodriguez-Corral, G.; Gálvez Moraleda, J.C.; Yang, T.S. A new high-intensity ultrasonic technology for food dehydration. Drying Tech. 1999, 17, 597–608. [Google Scholar] [CrossRef]
- Gallego-Juárez, J.A.; Graff, K.F. (Eds.) Power Ultrasonics: Applications of High-Intensity Ultrasound; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Legay, M.; Gondrexon, N.; Le Person, S.; Boldo, P.; Bontemps, A. Power ultrasonics: Applications of high-intensity ultrasound. Int. J. Chem. Eng. 2011, 2011, 670108. [Google Scholar]
- Khmelev, V.N.; Khmelev, S.S.; Tsyganok, S.N.; Titov, G.A. Ultrasonic drying of birch veneer. In Proceedings of the 2011 International Conference and Seminar on Micro/Nanotechnologies and Electron Devices Proceedings, Erlagol, Russia, 30 June 2011–4 July 2011; pp. 295–299. [Google Scholar]
- Mazela, B.; Perdoch, W.; Peplińska, B.; Zieliński, M. Influence of chemical pre-treatments and ultrasonication on the dimensions and appearance of cellulose fibers. Materials 2020, 13, 5274. [Google Scholar] [CrossRef]
- Sinn, G.; Zettl, B.; Mayer, H.; Stanzl-Tschegg, S. Ultrasonic-assisted cutting of wood. J. Mater. Process. Technol. 2005, 170, 42–49. [Google Scholar] [CrossRef]
- Postnikov, V.V.; Kamalova, N.S.; Kalchenko, S.V. Ultrasonic plasticization of lignin in modified wood. Bull. Russ. Acad. Sci. Phys. 2010, 74, 1319–1320. [Google Scholar] [CrossRef]
- Proszyk, S.; Pradzyński, W. On the possibilities of the use of ultrasound for regeneration of aged glue urea-formaldehyde resins. Holzforshung 1990, 44, 173–176. [Google Scholar] [CrossRef]
- Gfeller, B.; Zanetti, M.; Properzi, M.; Pizzi, A.; Pichelin, F.; Lehmann, M.; Delmotte, L. Wood bonding by vibrational welding. J. Adhes. Sci. Technol. 2003, 17, 1573–1589. [Google Scholar] [CrossRef]
- Lam, J.F.; Avramidis, S.; Lee, G. Effect of ultrasonic vibration on convective heat transfer between water and wood cylinders. Wood Fiber Sci. 1992, 24, 154–160. [Google Scholar]
- Kauman, W. Cell collapse in wood. Holz als Roh und Werk Part 1–22. 1964, 5, 185–196, Part 2–22, 1964, 12, 465–472. [Google Scholar]
- Neylon, M. Ultrasonic drying of eucalyptus. a preliminary study. Aust. For. Ind. J. 1978, 44, 16–18. [Google Scholar]
- Valentino, G.A.; Leija, L.; Riera, E.; Rodriguez, G.; Gallego-Juárez, J.A. Wood drzying by Using High Power Ultrasound and Infrared Radiation. 2002. Available online: https://digital.csic.es/bitstream/10261/7976/1/ult02005.pdf (accessed on 21 December 2022).
- Tanaka, T.; Avramidis, S.; Shida, S. A preliminary study on ultrasonic treatment effect on transverse wood permeability. Maderas-Cienc. Tecnol. 2010, 12, 3–9. [Google Scholar] [CrossRef]
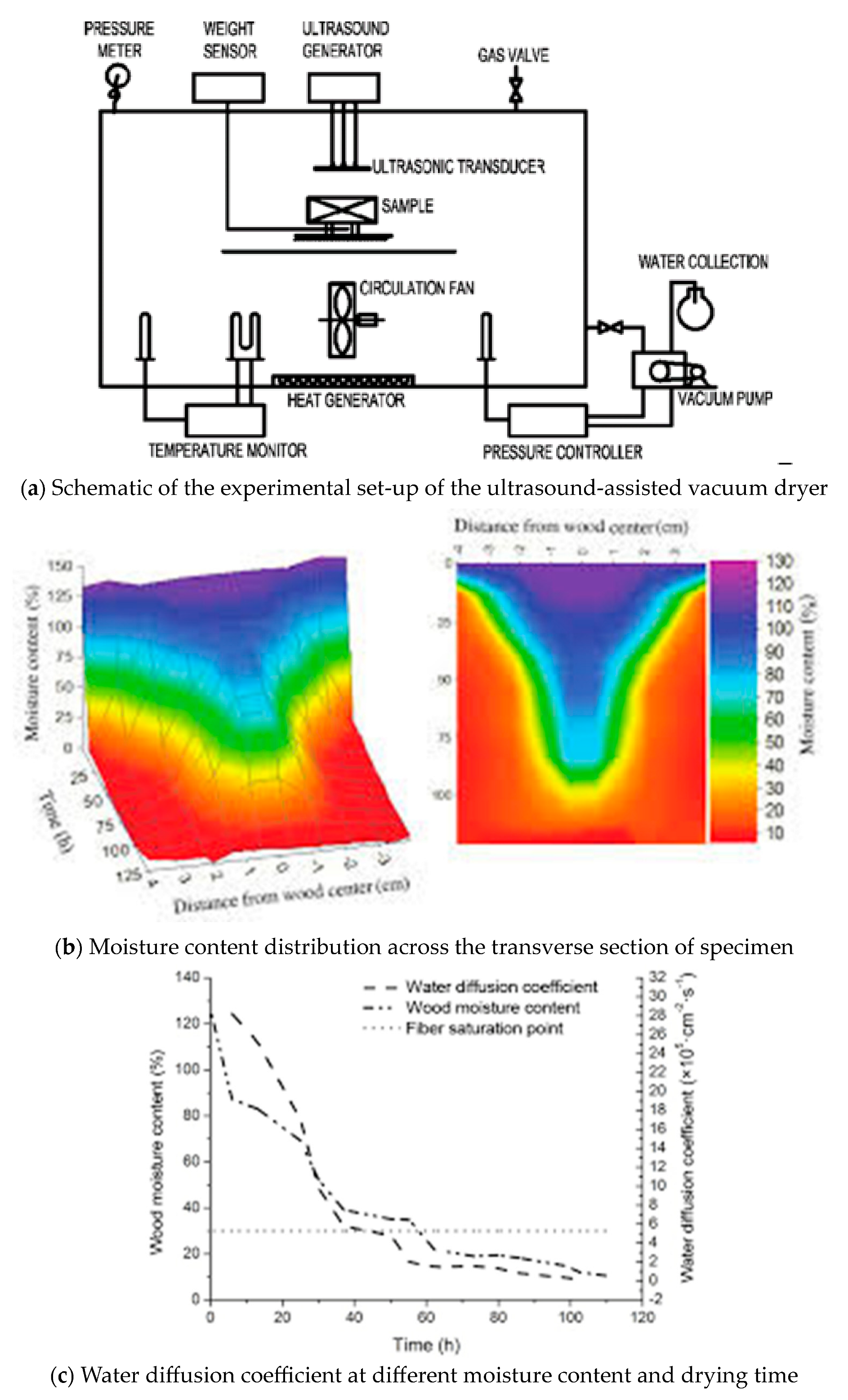
- He, Z.; Wang, Z.; Lv, H.; Zhang, Z.; Yi, S. Effects of ultrasound on mass transfer within the boundary layer during wood vacuum drying. BioResources 2015, 10, 5267–5277. [Google Scholar] [CrossRef]
- He, Z.; Zhang, Y.; Qiu, S.; Zhao, Z.; Yi, S. Water distribution during ultrasound-assisted vacuum drying of wood. Wood Res. 2016, 61, 341–350. [Google Scholar]
- Gallego-Juárez, J.A.; Riera, E.; De la Fuente Blanco, S.; Rodríguez-Corral, G.; Acosta-Aparicio, V.M.; Blanco, A. Application of high-power ultrasound for dehydration of vegetables: Processes and devices. Dry. Technol. 2007, 25, 1893–1901. [Google Scholar] [CrossRef]
- Breniaux, M.; Renault, P.; Ghidossi, R. Impact of high-power ultrasound for barrel regeneration on the extraction of wood volatile and non-volatile compounds. Processes 2021, 9, 959. [Google Scholar] [CrossRef]
- Breniaux, M.; Renault, P.; Meunier, F.; Ghidossi, R. Study of high-power ultrasound for oak wood barrel regeneration: Impact on wood properties and sanitation effect. Beverages 2019, 5, 10. [Google Scholar]
- Albu, C.T.; Dinulica, F.; Bartha, S.; Vasilescu, M.M.; Tereșneu, C.C.; Vlad, I.A. Musical instrument lumber recovery from Romanian resonance spruces. BioResources 2020, 15, 967–986. [Google Scholar] [CrossRef]
- Carlier, C.; Brémaud, I.; Gril, J. Characteristics of “resonance wood” as viewed by violin makers or by wood scientists: Part 1–a survey on the relation between luthiers and their raw material». In Proceedings of the International symposium WoodSciCraft 2014 «Wood Science and Craftsmanship: Cross perspective between Europe and Japan», Montpellier, France, 8–12 September 2014. [Google Scholar]
- Bremaud, I. What do we know on “resonance wood” properties? Selective review and ongoing research. In Proceedings of the Meetings on Acoustics 2012, Nantes, France, 23–27 April 2012. [Google Scholar]
- Bucur, V. Handbook of Materials for String Musical Instruments; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Bucur, V. Handbook of Materials for Wind Musical Instruments; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Perez Martínez, M.A.; Poletti, P.; Gil Espert, L. Vibration testing for the evaluation of the effects of moisture content on the in-plane elastic constants of wood used in musical instruments. In Vibration and Structural Acoustics Analysis: Current Research and Related Technologies; Vasques, C.M.A., Rodrigues, J.D., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 21–57. [Google Scholar]
- François, M. Vers une mesure non destructive de la qualité des bois de lutherie. Revue des Composites et des Materiaux Avances. arXiv 2000, arXiv:0911.4641. [Google Scholar]
- Longo, R.; Laux, D.; Pagano, S.; Delaunay, T.; Le Clézio, E.; Arnould, O. Elastic characterization of wood by Resonant Ultrasound Spectroscopy (RUS): A comprehensive study. Wood Sci. Technol. 2018, 52, 383–402. [Google Scholar] [CrossRef]
- Bucur, V.; Rasolofosaon, P.N. Dynamic elastic anisotropy and nonlinearity in wood and rock. Ultrasonics 1998, 36, 813–824. [Google Scholar] [CrossRef]
- Gonçalves, R.; Trinca, A.J.; Pellis, B.P. Elastic constants of wood determined by ultrasound using three geometries of specimens. Wood Sci. Technol. 2014, 48, 269–287. [Google Scholar] [CrossRef]
- Haines, D.W. On musical instrument wood. Catgut Acoust. Soc. Newsl. 1979, 31, 23–32. [Google Scholar]
- Stanciu, M.D.; Coşereanu, C.; Dinulică, F.; Bucur, V. Effect of wood species on vibration modes of violins plates. Eur. J. Wood Wood Prod. 2020, 78, 785–799. [Google Scholar] [CrossRef]
- Rodgers, O.E. Initial result on finite elements analysis of violin backs. J. Catgut Acoust. Soc. Ser. I 1986, 46, 18–23. [Google Scholar]
- Szalai, J. Anisotropic Strength and Elasticity of Wood and Wood-Based Composites, Private ed; University of West Hungary: Sopron, Hungary,, 1994. [Google Scholar]
- Gough, C. The violin: Chladni patterns, plates, shells and sounds. The Eur. Phys. J.-Spec. Top. 2007, 145, 77–101. [Google Scholar]
- Woodhouse, J. The acoustics of the violin: A review. Rep. Prog. Phys. 2014, 77, 115901. [Google Scholar] [CrossRef] [PubMed]
- Stanciu, M.D.; Bucur, V.; Munteanu, V.M.; Georgescu, S.V.; Năstac, S.M. Moisture-induced deformation in the neck of a classical guitar. Holzforschung 2019, 73, 371–379. [Google Scholar] [CrossRef]
- Barducci, I.; Pasqualini, G. Misura dell’attrito interno e delle costanti elastiche del legno. Il Nuovo C. 1948, 5, 416–446. [Google Scholar] [CrossRef]
- Zimmermann, M.H. Letter to C M Hutchins concerning wood seasoning. Catgut Acoust. Soc Newsl. 1978, 30, 7. [Google Scholar]
- Fengel, D.; Wegene, G. Wood: Chemistry, Ultrastructure, Reactions; Walter de Gruyter: Berlin, Germany, 1989. [Google Scholar]
- Fukada, E. Piezoelectricity as a fundamental property of wood. Wood Sci. Techn. 1965, 2, 299–307. [Google Scholar] [CrossRef]
- Obataya, E. Effects of natural and artificial ageing on the physical and acoustic properties of wood in musical instruments. J. Cult. Herit. 2017, 27, S63–S69. [Google Scholar] [CrossRef]
- Nakai, T.; Yamamoto, H.; Hamatake, M.; Nakao, T. Initial shapes of stress-strain curve of wood specimen subjected to repeated combined compression and vibration stresses and the piezoelectric behaviour. J. Wood Sci. 2006, 52, 539–543. [Google Scholar] [CrossRef]
- Sobue, N.; Okayasu, S. Effects of continuous vibration on dynamic visco-eslaticity of wood. Zair.—Jap. J. Soc. Mat. Scie. 1992, 41, 164–169. [Google Scholar] [CrossRef]
- Sobue, N. Effect of continuous vibration on dynamic viscoelasticity of wood. In Proceedings of the International Symposium ISMA 1995 Durdin, Cannes, France, 13–15 September 1995. [Google Scholar]
- Le Conte, S.; Vaiedelich, S.; François, M. A wood viscoelasticity measurement technique and applications to musical instruments: First results. J. Violin Soc. Am. VSA Papers 2007, 21, 1–7. [Google Scholar]
- Hutchins, C.M.; Rogers, O.E. Methods of changing the frequency spacing between the A1 and B1 modes of violins. Catgut Acoust. Soc. J. Ser. II 1992, 2, 13–19. [Google Scholar]





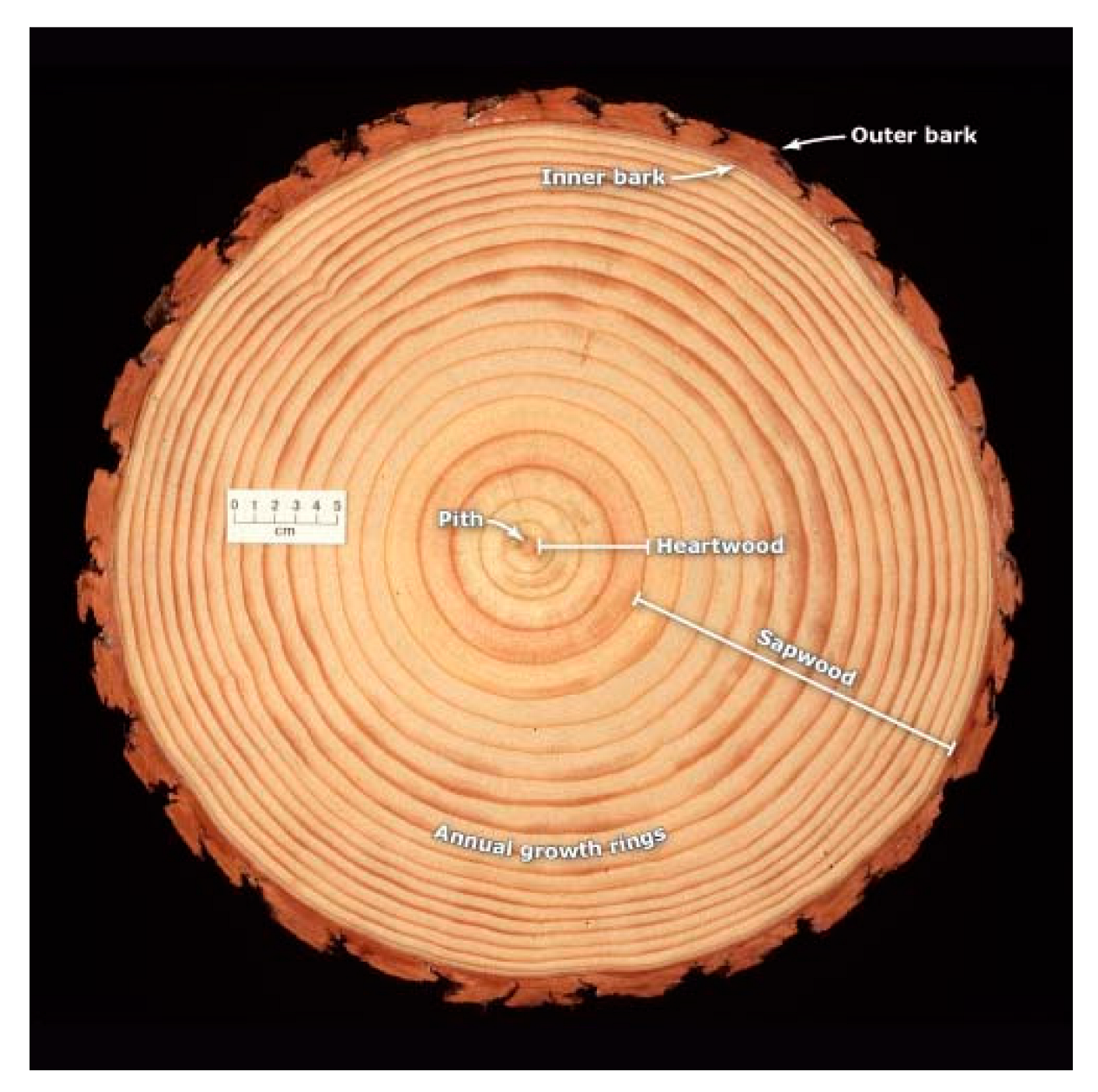
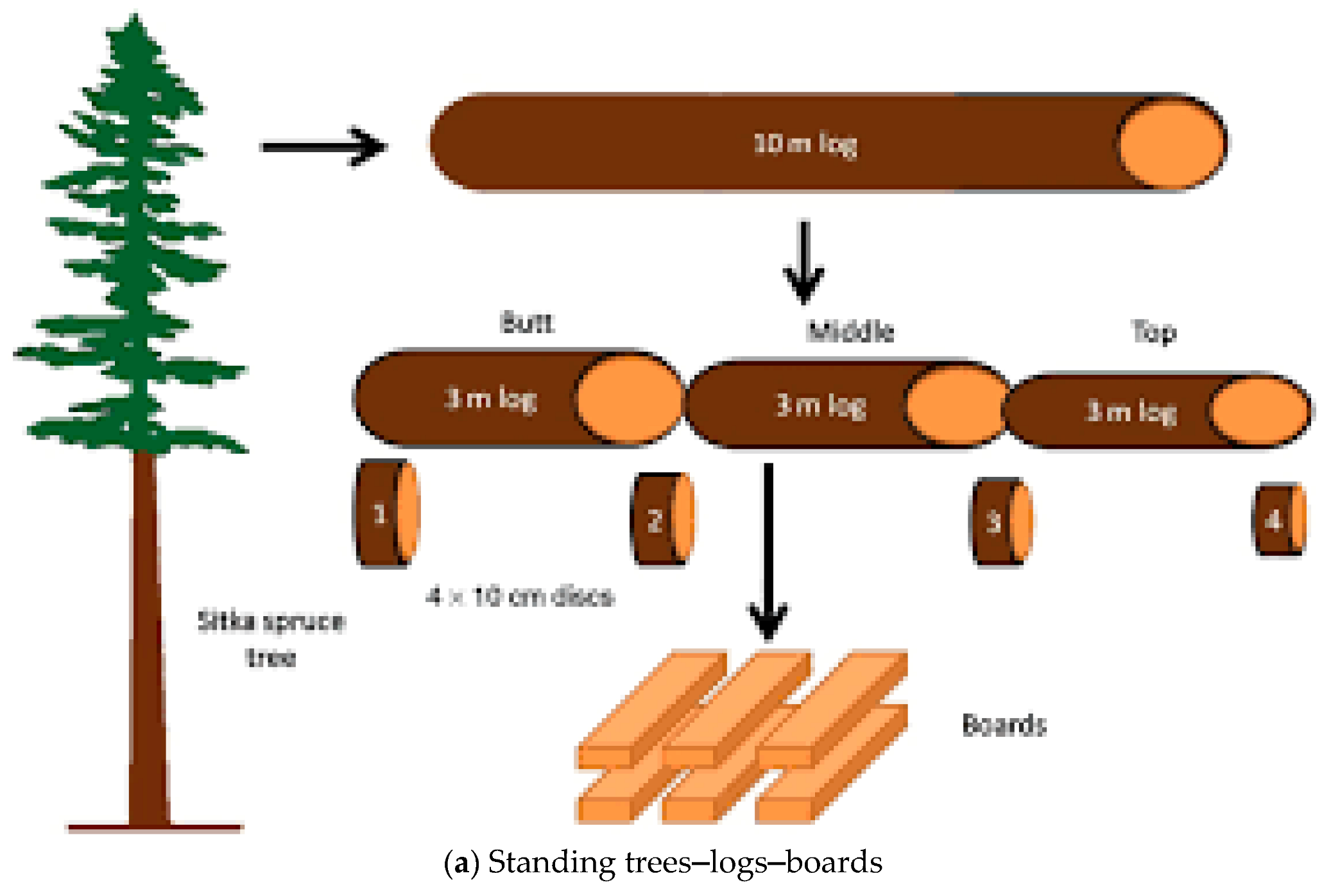













| (a). Axes of Symmetry of Wood and the Terms of the Stiffness Matrix |
|---|
| In general for wood: C11 > C22 > C33 > C66 > C55 > C44; and C1 2> C13 > C23; Poisson ratios 1 – νij. νji > 0 |
 |
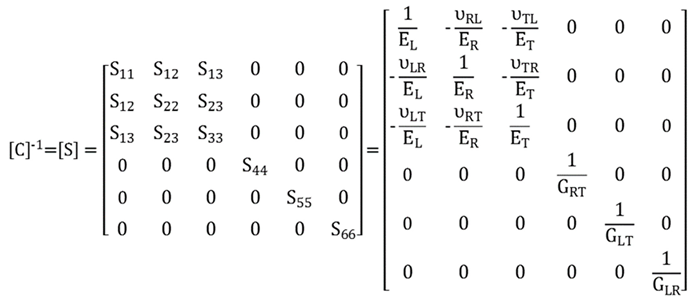
| (b). Compliance matrix, the corresponding engineering constants E, G and Poisson ratio ν |
 |
| Species | Density | Engineering Constants of Wood 108 N/m2 | |||||
|---|---|---|---|---|---|---|---|
| Young’s Moduli | Shear Moduli | ||||||
| kg/m3 | EL | ER | ET | GRT | GLT | GLR | |
| Balsa | 200 | 6.3 | 3.0 | 1.0 | 0.30 | 2.0 | 3.1 |
| Spruce | 440 | 159 | 6.9 | 3.9 | 0.36 | 7.7 | 7.5 |
| Oak | 660 | 158 | 15.1 | 8.0 | 2.70 | 8.9 | 13.4 |
| Species | Density | Poisson Ratios ν ij | |||||
|---|---|---|---|---|---|---|---|
| kg/m3 | ν12 = ν LR | ν21 = ν RL | ν13 = ν LT | ν31 = ν TL | ν23 = ν RT | ν32 = ν TR | |
| Balsa | 200 | 0.23 | 0.018 | 0.49 | 0.009 | 0.66 | 0.24 |
| Spruce | 440 | 0.44 | 0.028 | 0.38 | 0.013 | 0.47 | 0.25 |
| Oak | 660 | 0.33 | 0.130 | 0.50 | 0.086 | 0.64 | 0.30 |
| Variables | Units | Range | Ring Width | Ring Regularity | Latewood Width | Latewood Proportion | |
| mm | % | mm | % | ||||
| Average | |||||||
| 1.27 | 0.29 | 23 | |||||
| 0.71–2.38 | 0.18–0.54 | 25.03–23.64 | |||||
| Correlation coefficients | |||||||
| 1 | Density | kg/m3 | 381–446 | 0.395 | 0.396 | 0.402 | −293 |
| 2 | Velocity VLL | m/s | 4283–5006 | −0.708 | −0.639 | −0.708 | 0.229 |
| 3 | Velocity VRR | m/s | 1594–1703 | 0.057 | −0.012 | 0.075 | 0.253 |
| 4 | Velocity VTT | m/s | 1227–1409 | 0.289 | 0.217 | 0.258 | 0.214 |
| Young’s moduli | |||||||
| 5 | EL | MPa | 7011–10,250 | −0.287 | −0.273 | −0.339 | 0.125 |
| 6 | ER | MPa | 993–1221 | −0.184 | −0.239 | −0.166 | 0.123 |
| 7 | ET | MPa | 564–839 | −0.065 | −0.147 | −0.088 | 0.162 |
| Shear moduli | |||||||
| 8 | GRT | MPa | 599–781 | −0.117 | −0.127 | −0.062 | 0.210 |
| 9 | GLT | MPa | 738–937 | −0.239 | −0.259 | −0.186 | 0.247 |
| 10 | GLR | MPa | 759–1030 | 0.244 | 0.171 | 0.248 | 0.292 |
| Propagation Direction of Waves along Axis | Wave Normal | Polarization Vector along Axis | Wave Type | Velocities and Stiffnesses |
|---|---|---|---|---|
| Axis X1 | n1 = 1 | X1 | L—longitudinal wave | V112 × ρ = C11 |
| n2 = 0 | X2 | T—shear wave | V662 × ρ = C66 | |
| n3 = 0 | X3 | T—shear wave | V552 × ρ = C55 | |
| Axis X2 | n1 = 0 | X1 | T—shear wave | V662 × ρ = C66 |
| n2 = 1 | X2 | L—longitudinal wave | V222 × ρ = C22 | |
| n3 = 0 | X3 | T—shear wave | V442 × ρ = C44 | |
| Axis X3 | n1 = 0 | X1 | T—shear | V552 × ρ = C55 |
| n2 = 0 | X2 | T—shear | V442 × ρ = C44 | |
| n3 = 1 | X3 | L—longitudinal | V332 × ρ = C33 |
| Wave Normal | Polarization Vector | Wave Type |
|---|---|---|
| Plane X1 X2 | ||
| n1, n2 n3 = 0 | p1/p2 = Γ12/(ρV2 − Γ11) = (ρV2 − Γ22)/Γ12 along axis X3 | QL and QT 2ρV2 QL, QT = (Γ11 + Γ22) ± [(Γ11 − Γ22)2 + 4Γ122] ½ T ρVT 2 = C55 n1 2 + C44 n2 2 |
| Plane X1 X3 | ||
| n1, n3 n2 = 0 | p1/p3 = Γ13/(ρV2 − Γ11) = (ρV2 − Γ33)/Γ13 along axis X2 | QL and QT 2ρV2 QL, QT = (Γ11 + Γ33) ± [(Γ11 − Γ33)2 + 4Γ132] ½ T ρVT 2 = C66 n1 2 + C44 n2 2 |
| Plane X1 X3 | ||
| n2, n3 n1 = 0 | p2/p3 = Γ23/(ρV2 − Γ22) = (ρV2 − Γ33)/Γ13 along axis X2 | QL and QT 2ρV2 QL, QT = (Γ22 + Γ33) ± [(Γ22 − Γ33)2 +4Γ232] ½ T ρVT 2 = C55 n1 2 + C66 n2 2 |
| Moisture Content | Ultrasonic Velocities (m/s) | |||||
|---|---|---|---|---|---|---|
| % | VLL | VRR | VTT | VLR | VLT | VRT |
| 9.6 | 5029 | 2350 | 1331 | 1485 | 1333 | 786 |
| 12.7 | 4681 | 2207 | 1204 | 1413 | 1413 | 754 |
| 16.8 | 4524 | 2057 | 1199 | 1395 | 1395 | 727 |
| 18.7 | 4480 | 1960 | 1090 | 1166 | 1166 | 659 |
| Moisture Content | Young’s Moduli 103 MPa | Poisson Ratios Calculated from Ultrasonic Constants [C] and [S] = [C] −1 with an Optimization Procedure | |||||||
|---|---|---|---|---|---|---|---|---|---|
| % | EL | ER | ET | ν LR | ν RL | ν LT | ν TL | ν RT | ν TR |
| 9.6 | 11.18 | 2.31 | 0.56 | 0.01 | 0.04 | 0.11 | 2.21 | 0.26 | 1.09 |
| 12.7 | 9.56 | 2.79 | 0.49 | 0.02 | 0.08 | 0.11 | 2.26 | 0.23 | 1.02 |
| 16.8 | 8.20 | 2.04 | 0.44 | 0.03 | 0.11 | 0.13 | 2.43 | 0.20 | 0.90 |
| 18.7 | 8.80 | 1.89 | 0.42 | 0.04 | 0.20 | 0.12 | 2.37 | 0.70 | 0.77 |
| Moisture Content | Variation of Velocities % | Variation of Young’s Moduli % | |||||||
|---|---|---|---|---|---|---|---|---|---|
| % | V LR | V RL | V LT | V TL | V RT | V TR | EL | ER | ET |
| Increasing | Decreasing | Decreasing | |||||||
| 9.6 to18.7 | −10.9 | −16.5 | −17.4 | −21.5 | −21.8 | −16.2 | −21.3 | −22.2 | −25.0 |
| Moisture Content | Variation of Poisson Ratios % | |||||
|---|---|---|---|---|---|---|
| % | ν LR | ν RL | ν LT | ν TL | ν RT | ν TR |
| Increasing | Increasing | |||||
| 9.6 to 18.7 | +300 | +400 | +9.6 | +7.2 | +160 | +29.7 |
| Order 9.6 | 2 | 1 | 5 | 6 | 3 | 4 |
| Moisture Content | Poisson Ratios | |||||
|---|---|---|---|---|---|---|
| % | Ultrasonic method | |||||
| ν LR | ν RL | ν LT | ν TL | ν RT | ν TR | |
| 9.6 | 0.01 | 0.04 | 0.11 | 2.21 | 0.26 | 1.09 |
| 12.7 | 0.02 | 0.08 | 0.11 | 2.26 | 0.23 | 1.02 |
| 16.8 | 0.03 | 0.11 | 0.13 | 2.43 | 0.20 | 0.90 |
| 18.7 | 0.04 | 0.20 | 0.12 | 2.37 | 0.70 | 0.77 |
| Static test [39] | ||||||
| 9.6 | 0.09 | 0.31 | 0.10 | 0.26 | 0.29 | 0.65 |
| 12.7 | 0.07 | 0.27 | 0.09 | 0.28 | 0.27 | 0.64 |
| 16.8 | 0.06 | 0.24 | 0.06 | 0.18 | 0.27 | 0.64 |
| 18.7 | 0.05 | 0.24 | 0.06 | 0.18 | 0.28 | 0.63 |
| Moisture Content | Variation of Poisson Ratios Static Measurements % | |||||
|---|---|---|---|---|---|---|
| % | ν LR | ν RL | ν:LT | ν TL | ν RT | ν TR |
| Increasing | Ultrasound—ν ij increasing | |||||
| 9.6 to 18.7 | 40 | 2.4 | 44 | 3.1 | 22.5 | 30.7 |
| Static—ν ij decreasing | ||||||
| Increasing | ||||||
| 9.6 to 18.7 | −44 | −23 | −40 | −31 | −3 | −3 |
| Static Method | Ultrasound | ||
|---|---|---|---|
| Relationship | Main Effect | Relationships | Main Effect |
| ν LR ≈ ν LT | Effect axis L | ν LT ≈ 10 ν LR | Effect axis L (x10) |
| ν TR ≈ 2 ν RT | Effect plan RT, axis R x2 | ν TR > 3 ν RT | Effect plan RT axis R x3 |
| ν TL ≈ ν RL | Secondar effect axis L | ν TL ≈ 3 ν RL | Secondar effect axis L |
| General relationship ν TR > ν RL > ν RT > ν TL > ν LT > ν LR | General relationship ν TL > ν TR > ν RT > ν LT > ν RL > ν LR | ||
| High contribution of axis T Low Contribution of planes LT and LR Symmetry TL and LT | High Contribution of axis T Low Contribution of axis L Symmetry RL and LR | ||
| Conclusion Axis T is the stiff axis | Conclusion Express better the migration of moisture content | ||
| Engineering Constants | Methods | ||
|---|---|---|---|
| Ultrasonic Method /Optimization for Cij Sample at 45° | Static Test Compression Test (Strain Gauges) | Optical Method 3D Image Correlation Method | |
| Young’s moduli (MPa) | |||
| EL | 21,939 | 18,055 | 25,659 |
| ER | 2420 | 1775 | 1820 |
| ET | 1165 | 686 | 821 |
| Shear moduli (MPa) | |||
| GLR | 1756 | 1690 | 1926 |
| GLT | 969 | - | - |
| GRT | 533 | - | - |
| Poisson ratio | |||
| ν RT | 0.696 | 0.688 | 0.635 |
| ν LT | 0.588 | 0.599 | 0.606 |
| ν LR | 0.452 | 0.424 | 0.448 |
| ν TR | 0.325 | - | - |
| ν RL | 0.052 | 0.036 | 0.032 |
| ν TL | 0.032 | - | - |
| Species | Diameter at Breast Height | Velocity at Stump Level (m/s) | Anisotropy | |
|---|---|---|---|---|
| Radial Direction | Tangential Direction | VR/VT | ||
| Spruce | <25 cm | 1340 | 1130 | 1.185 |
| >25 cm | 1330 | 1180 | 1.127 | |
| Differences % | 0.7 | −4.4 | 4.8 | |
| Measurement Radial Direction R— for Four Cases Named | Tree | Velocity-Radial Direction m/s | Damping in Radial Direction ×10−3 | ||
|---|---|---|---|---|---|
| At Stump Level | Above Stump Level | At Stump Level | Above Stump Level | ||
| Parallel | Sound | 1450 | 1390 | 17 | 20 |
| With rot | 1170 | 1150 | 18 | 17 | |
| Difference % | −19.3 | −17.2 | +5.5 | −15.0 | |
| Perpendicular | Sound | 1320 | 1290 | 13 | 19 |
| With rot | 1140 | 1230 | 15 | 19 | |
| Difference % | −13.6 | −4.6 | +15.3 | 0.0 | |
| At—45° | Sound | 1230 | - | - | - |
| With rot | 1040 | - | - | - | |
| Difference % | −15.4 | ||||
| At—+45° | Sound | 1120 | - | - | - |
| With rot | 1040 | - | -- | - | |
| Difference % | −7.14 | - | - | - | |
| (a). Measurements at stump level with reference with 4 points (Figure 1, page 808) | |||||
 | |||||
| (b). Damping of the ultrasonic signal in time domain (Figure 3, page 809) | |||||
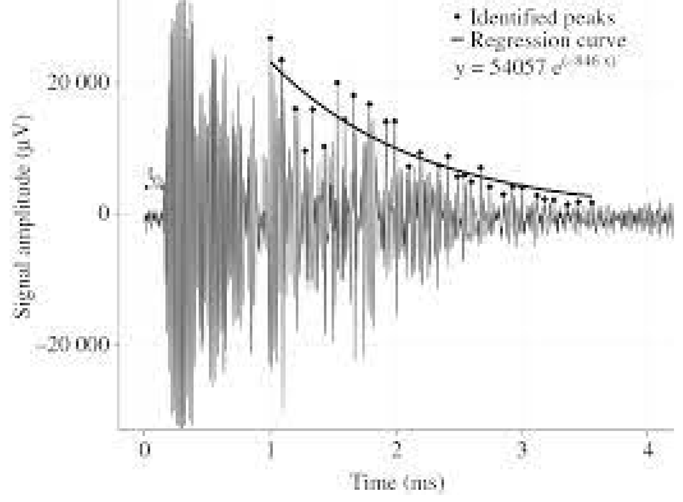 | |||||
| Species | Model | Overall Prediction Accuracy | Sensitivity | Specificity |
|---|---|---|---|---|
| Spruce | With radial velocity | 0.83 | 0.83 | 0.70 |
| With radial damping | 0.82 | 0.82 | 1.00 |
| Species | Treatment | Tree Characteristics | Stress Wave Velocity Along Axis L | ||||
|---|---|---|---|---|---|---|---|
| Thinning | Tree Age Years | DBH mm | Height .m | Standing Tree m/s | Green log m/s | Differences % | |
| Alder | 1st | 15 | 127 | 13.6 | 3609 | 3053 | 18.2 |
| 2nd | 21 | 132 | 12.6 | 4254 | 3419 | 24.4 | |
| Ash | 1st | 15 | 127 | 13.6 | 4738 | 4088 | 15.9 |
| 2nd | 21 | 133 | 13.8 | 4928 | 4185 | 17.8 | |
| Sycamore | 1st | 15 | 118 | 9.0 | 3537 | 3138 | 12.7 |
| 2nd | 23 | 151 | 18.6 | 4661 | 4037 | 15.5 | |
| Values | Φ mm | Density kg/m3 | Ultrasonic Test | Static Test | Ratio CLL/EL | ||
|---|---|---|---|---|---|---|---|
| Velocity | Stiffness | Modulus | |||||
| VL Saturated .m/s | CLL MPa | EL MPa | |||||
| E. grandis | Average | 207 | 751 | 4560 | 18.452 | 15.844 | 1.16 |
| Coeff. Var. % | 24.6 | 7.0 | 6.7 | 9.1 | 38.3 | - | |
| E. cloeziana | Average | 151 | 820 | 4517 | 23.451 | 20.091 | 1.16 |
| Coeff. Var. % | 58 | 7.0 | 8.7 | 17 | 55 | - | |
| E. saligna | Average | 182 | 740 | 4148 | 17.470 | 13.003 | 1.34 |
| Coeff. Var. % | 32 | 14 | 10.9 | 12 | 20 | - | |
| Materials | Specific Time Reading (μ/m) | Velocity-Calculated (m/s) | |||||
|---|---|---|---|---|---|---|---|
| Mean | Standard Dev. | Min | Max | Mean | Min | Max | |
| Log | 289 | 20.1 | 257 | 355 | 3469 | 2816 | 3891 |
| Cants | 281 | 19.8 | 247 | 342 | 3558 | 2923 | 4048 |
| Green lumber | 270 | 17.8 | 238 | 347 | 3703 | 2880 | 4201 |
| Dry lumber | 230 | 15.1 | 199 | 270 | 4347 | 3704 | 5025 |
| Log Classes | Log Number | Logs Characteristics | Lumber | ||
|---|---|---|---|---|---|
| Stress Wave Testing on Logs | MOE | ||||
| Timer Measured | Velocity Longitudinal Waves-Calculated * | MOE Calculated | Stress Waves Measured | ||
| μs/m | m/s | GPa | GPa | ||
| G 1 | 17 | <272 | >3676 | >13.51 | >13.79 |
| G 2 | 56 | 272–298 | 3676–3355 | 11.25–13.51 | 11.10–13.49 |
| G 3 | 15 | 298–328 | 3355–3048 | 9.29–11.25 | 8.27–11.02 |
| G 4 | 7 | >328 | <3048 | <9.29 | <8.27 |
| Variables Stress Wave Time on Logs, Cants, Lumber | Linear Regression Model | Correlation Coefficient | Standard Error Estimate | |
|---|---|---|---|---|
| Y | X | y = a + b x | .r | % |
| SWT of cant | SWT of log | y = 40.4 + 0.8316x | 0.82 | 10.93 |
| SWT of green lumber | SWT of log | y = 60.5 + 0.7560x | 0.75 | 12.81 |
| SWT of green lumber | SWT of cant | y = 21.1 + 0.9187x | 0.92 | 7.63 |
| SWT of dry lumber | SWT of log | y = 82.3 + 0.5107x | 0.68 | 11.17 |
| SWT of dry lumber | SWT of cant | y = 58.7 + 0.6096x | 0.80 | 9.06 |
| Variables | Units | Mean | Standard Deviation | Coefficient of Variation | Minimum | Maximum |
|---|---|---|---|---|---|---|
| Width | mm | 39.3 | 1.7 | 4.4 | 31.9 | 43.7 |
| Height | mm | 99.8 | 0.6 | 0.6 | 95.8 | 100.8382 |
| Velocity ends | m/s | 5368 | 382 | 7.3 | 3997 | 6045 |
| Velocity edge 1 | m/s | 5151 | 611 | 12.0 | 1071 | 6117 |
| Velocity edge 2 | m/s | 5150 | 552 | 11.0 | 1634 | 6104 |
| Moisture content | % | 10.5 | 0.6 | 6.1 | 9.1 | 12.1 |
| Density | kg/m3 | 489 | 62.7 | 12.8 | 353 | 808 |
| MOE static | N/mm2 | 9011 | 2209 | 25.2 | 2293 | 13,912 |
| Variables | Eigen Values | Percentage of Variance | Accumulated Percentage |
|---|---|---|---|
| Width | 2.47 | 35.5 | 35.35 |
| Height | 1.24 | 17.71 | 53.06 |
| Velocity -ends | 1.20 | 17.02 | 70.15 |
| Velocity edge 1 | 0.74 | 10.59 | 80.74 |
| Velocity edge 2 | 0.64 | 9.21 | 89.94 |
| Moisture content | 0.48 | 6.81 | 96.76 |
| Density | 0.23 | 3.24 | 100.00 |
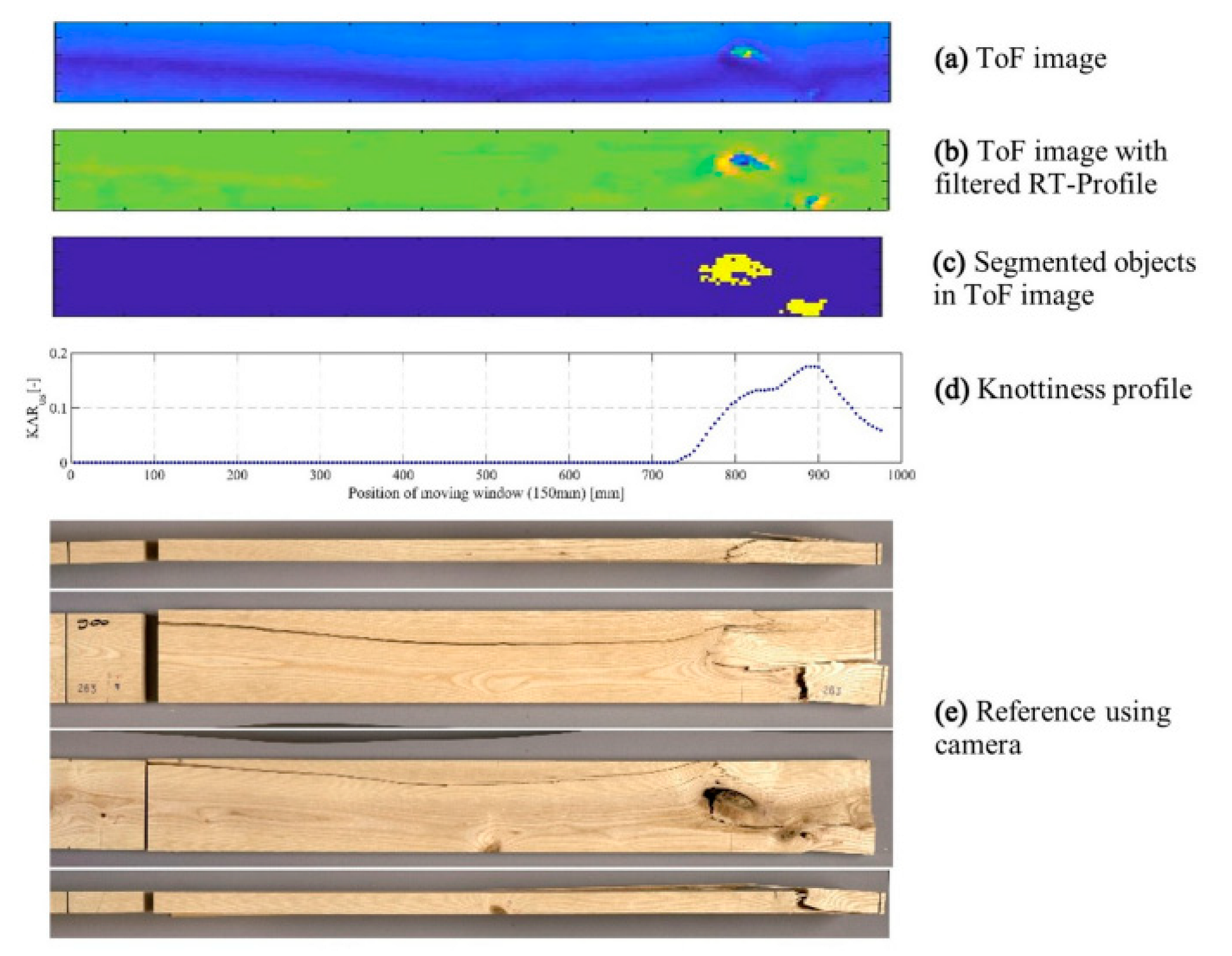
| Variables’ Relationships | Linear Regression Equation | Coefficient R2 |
|---|---|---|
| Knottiness in general and CKDR | ||
| Elastic moduli | MOE static = 1229 + 0.7566 MOE dyn, end frequency | 0.87 |
| MOE static = 823 + 0.8112 MOE dyn, edge. frequency | 0.86 | |
| Rupture modulus | MOR = 7.26 + 0.00349 MOE dyn. end. frequency | 0.46 |
| MOR = 3.25 + 0.00346 MOE dyn. edge. frequency | 0.50 | |
| Knottiness in the central position of the beam and CKDRcentral | ||
| Elastic moduli | MOE static = 695 + 0.7779 MOE dyn, end. frequency + 988 CKDRcentral | 0.87 |
| MOE static = 78.30 + 0843 MOE dyn, edge. frequency + 1324 CKDRc | 0.86 | |
| Rupture modulus | MOR = 22.09 + 0.00289 MOE dyn, end. frequency − 27.228 CKDRc | 0.50 |
| MOR = 16.63 + 0.00338 MOE dyn, edge. frequency − 23.571 CKDRc | 0.54 | |
| Path Length | Direction of Stress Wave Measurements versus Wood Anisotropy | |||||
|---|---|---|---|---|---|---|
| Radial | Tangential | 45° to Grain | ||||
| Time | Velocity | Time | Velocity | Time | Velocity | |
| mm | μs | m/s | μs | m/s | μs | m/s |
| 64 | 43 | 1488 | 51 | 1254 | 64 | 1000 |
| 89 | 60 | 1483 | 71 | 1253 | 88 | 1011 |
| 140 | 94 | 1489 | 112 | 1250 | 139 | 1007 |
| 292 | 195 | 1497 | 234 | 1248 | 290 | 1007 |
| 394 | 264 | 1492 | 315 | 1250 | 392 | 1005 |
| 444 | 297 | 1494 | 355 | 1250 | 442 | 1004 |
| 495 | 331 | 1495 | 396 | 1250 | 492 | 1006 |
| Terms with | Terms of the Stiffness Matrix GPa | ||
|---|---|---|---|
| Diagonal-P wave | CLL = C11 = 16.60 | CRR = C22 = 0.79 | CTT = C33 = 0.45 |
| Diagonal-S wave | GRT = C 44 = 0.04 | GLT = C55 = 0.78 | GLR = C 66 = 0.63 |
| Off diagonal | CLR = C12 = 0.44 | CLT -= C 13 = 0.32 | CRT = C23 = 0.20 |
| Treatment | Effective Water Diffusivity × 10−11 m2 s−1 | Time Reduction (%) | ||||
|---|---|---|---|---|---|---|
| Frequency | With 28 kHz | When Compare Frequencies | ||||
| 28 kHz | 40 kHz | Δ% | Versus Control | 28 kHz versus 40 kHz | ||
| 1 | Duration 30 min | 1.22 | 1.26 | 3.2 | 17 | 4.7 |
| 2 | Duration 60 min | 1.30 | 1.34 | 4.6 | 21 | 3.3 |
| 3 | Duration 90 min | 1.38 | 1.50 | 8.6 | 26 | 9.2 |
| 4 | Effect of drying time (Figure 4, page 5270 [157]) | |||||
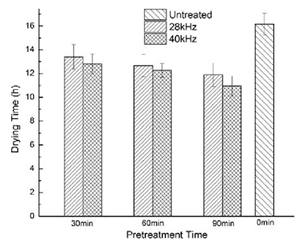 | ||||||
| Elastic Parameters | Units | First Hypothesis Isotropic Solid | Second Hypothesis * Transverse Isotropic * | Third Hypothesis Orthotropic | |||
|---|---|---|---|---|---|---|---|
| Spruce | Maple | Spruce | Maple | Spruce | Maple | ||
| Density | kg/m3 | 400 | 600 | 400 | 700 | 430 | 590 |
| Young’s moduli | MPa | 15,000 | 10,000 | ||||
| EL | MPa | 13,000 | 10,000 | 13,500 | 10,000 | ||
| ER | MPa | 700 | 2000 | 890 | 1570 | ||
| ET | MPa | 700 * | 2000 * | 480 | 870 | ||
| Shear moduli | 840 | 700 | |||||
| G RT | MPa | 60 | 720 | 32 | 290 | ||
| G LT | MPa | 900 | 1600 | 500 | 1100 | ||
| G LR | MPa | 900 * | 1600 * | 720 | 1222 | ||
| Poisson ratios | 0.37 | 0.37 | |||||
| ν LR | 0.37 | 0.47 | 0.45 | 0.46 | |||
| ν RL | 0.03 | 0.093 | |||||
| ν LT | 0.42 | 0.50 | 0.54 | 0.50 | |||
| ν TL | 0.019 | 0.038 | |||||
| ν RT | 0.47 | 0.50 | 0.56 | 0.82 | |||
| ν TR | 0.30 | 0.40 | |||||
| Mode | Isotropic Symmetry | Transverse Isotropic | Orthotropic Symmetry |
|---|---|---|---|
| Lower Modes | |||
| 6 | Mode 6, f = 202.42 Hz | Mode 6, f = 205.95 Hz | Mode 6, f = 219.55 Hz |
| Mode: Identical Frequency: very near | 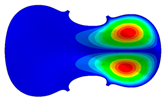 | 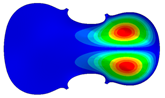 | 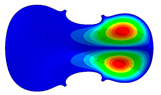 |
| 7 | Mode 7, f = 219.56 Hz | Mode 7, f = 229.82 Hz | Mode 7, f = 247.59 Hz |
| Mode: identical Frequency: very near |  | 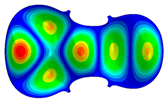 | 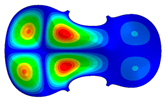 |
| 8 | Mode 8, f = 224.71 Hz | Mode 8, f = 230.65 Hz | Mode 8, f = 248.18 Hz |
| Mode: identical Frequency: very near | 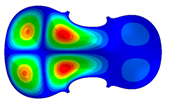 | 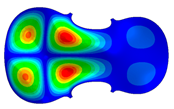 | 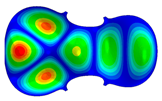 |
| 9 | Mode 9, f = 232.74 Hz | Mode 9, f = 239.71 Hz | Mode 9, f = 257.02 Hz |
| Mode: Identical Frequency: very near | 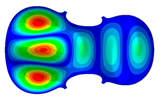 | 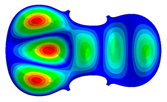 | 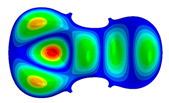 |
| 10 | Mode 10, f = 256.79 Hz | Mode 10, f = 267.25 Hz | Mode 10, f = 285.93 Hz |
| Mode: Identical Frequency: very near | 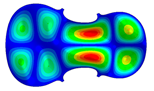 | 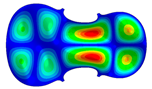 | 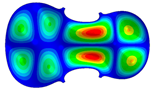 |
| 12 | Mode 12, f = 276.84 Hz | Mode 12, f = 288.70 Hz | Mode 12, f = 310.52 Hz |
| Mode: Identical Frequency: Different | 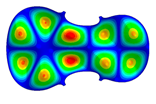 | 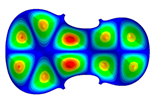 | 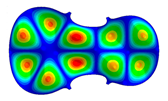 |
| Superior modes | |||
| 49–66 | Mode 66, f = 588.15 Hz | Mode 56, f = 591.70 Hz | Mode 49, f = 595.16 Hz |
| Mode: different Frequency: very near | 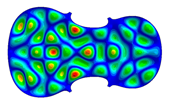 | 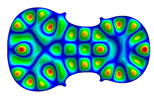 | 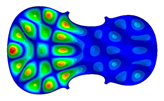 |
| 358–508 | Mode 508, f = 1568.4 | Mode 423, f = 1568,2 Hz | Mode 358, f = 1568.3 Hz |
| Mode: different Frequency: Identical |  | 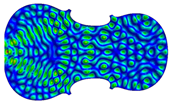 |  |
| Mode | Isotropic Symmetry | Transverse Isotropic | Orthotropic Symmetry |
|---|---|---|---|
| Lower Modes | |||
| 4 | Mode 4, f = 135.66 Hz | Mode 4, f = 138.35 Hz | Mode 4, f = 173.38 Hz |
| Mode identical Frequency Near | 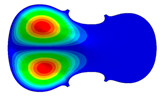 | 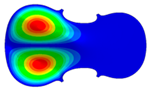 | 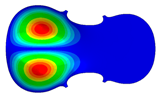 |
| 6 | Mode 6, f = 164.63 Hz | Mode 6, f = 169.86 Hz | Mode 6, f = 216.50 Hz |
| Mode identical Frequency Different | 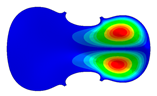 | 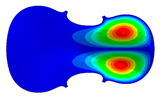 | 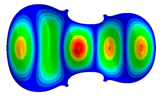 |
| 7 | Mode 7; f = 178.74 Hz | Mode 7; f = 189.26 Hz | Mode 7; f = 217.44 Hz |
| Mode identical Frequency Different | 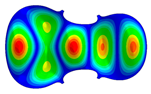 |  | 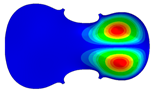 |
| 9 | Mode 9; f = 189.49 Hz | Mode 9; f = 197.58 Hz | Mode 9; f = 248.31 Hz |
| Mode identical Frequency Different |  | 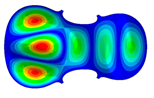 | 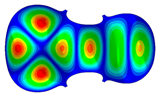 |
| 10 | Mode 10; f = 208.99 Hz | Mode 10; f = 218.92 Hz | Mode 10; f = 257.72 Hz |
| Mode identical Frequency Different | 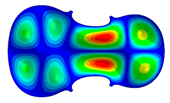 | 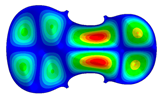 | 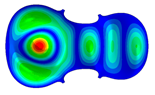 |
| 11 | Mode 11, f = 210.48 Hz | Mode 11, f = 224.05 Hz | Mode 11, f = 274.93 Hz |
| Mode identical Frequency Different | 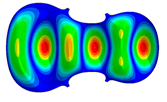 | 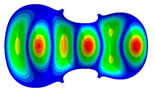 | 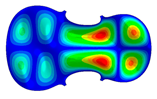 |
| 12 | Mode 12, f = 225.42 Hz | Mode 12, f = 237.20 Hz | Mode 12, f = 286.02 Hz |
| Mode identical Frequency Different | 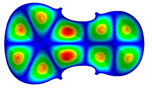 | 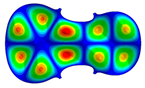 | 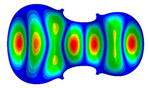 |
| Superior modes | |||
| 48–58 | Mode 55, f = 438.65 Hz | Mode 48, f = 441.69 Hz | Mode 58, f = 593.89 Hz |
| Mode different Frequency Different | 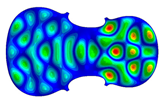 | 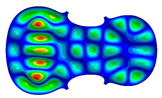 | 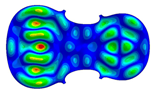 |
| 188–335 | Mode 335, f = 1046.9 Hz | Mode 288, f = 1046.2 Hz | Mode 188, f = 1047.2 Hz |
| Mode different Frequency Identical | 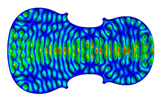 |  | 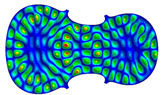 |
| Modes | Species | Modal Frequency (Hz) | ||
|---|---|---|---|---|
| Isotropic | Transverse Isotropic | Orthotropic | ||
| Mode 6 | Spruce | 203.42 | 205.95 | 219.55 |
| Maple | 164.5 | 169.85 | 216.50 | |
| Difference % | 18.92 | 17.52 | 1.38 | |
| Mode 9 | Spruce | 232.74 | 239.71 | 257.06 |
| Maple | 201.99 | 218.92 | 257.92 | |
| Difference % | 13.21 | 8.67 | 0.00 | |
| Mode 10 | Spruce | 256.79 | 267.25 | 265.93 |
| Maple | 208.98 | 218.92 | 257.72 | |
| Difference % | 18.60 | 18.08 | 3.08 | |
| Mode 12 | Spruce | 276.84 | 288.70 | 310.52 |
| Maple | 225.42 | 237.20 | 286.02 | |
| Difference % | 18.57 | 17.83 | 7.88 | |
| Modes | Species | Effect of Elastic Hypothesis on Modal Frequency (%) | ||
|---|---|---|---|---|
| Orthotropic/ Over Transverse Isotropic | Transverse Isotropic Over Isotropic | Orthotropic Over Isotropic | ||
| Mode 6 | Spruce | 6.8 | 1 | 7.8 |
| Maple | 27.8 | 2.9 | 31.7 | |
| Mode 9 | Spruce | 7.5 | 3.0 | 10.7 |
| Maple | 17.8 | 8.4 | 27.8 | |
| Mode 10 | Spruce | −0.7 | 4.2 | 3.5 |
| Maple | 17.8 | 4.8 | 23.5 | |
| Mode 12 | Spruce | 7.6 | 4.3 | 12.3 |
| Maple | 20.6 | 5.3 | 27.1 | |
| Elastic Moduli | Units | Moisture Content (%) | |||||
|---|---|---|---|---|---|---|---|
| 1.43 | 6.01 | 9.38 | 15.73 | 24.71 | |||
| Water Content and Wood Structure | |||||||
| Near Owen Dry | One Molecular Water Layer | Indoor Moisture Content | Air Dried | Near Fiber Saturation Point | |||
| 1 | EL | MPa | 13,871 | 13,080 | 12,439 | 12,065 | 9491 |
| 2 | ER | MPa | 923 | 938 | 890 | 725 | 497 |
| 3 | GLR | MPa | 914 | 1004 | 947 | 942 | 668 |
| Anisotropy ratio | |||||||
| 4 | EL/ER | - | 15.1 | 13.8 | 13.8 | 15.6 | 19.23 |
| 5 | EL/G LR | - | 15.1 | 12.9 | 12.8 | 12.8 | 14.3 |
| 6 | ER/G LR | - | 1.01 | 0.93 | 0.91 | 0.76 | 0.74 |
| Age | Density | Velocity (m/s) | Quality Factor | Origin Country | ||
|---|---|---|---|---|---|---|
| kg/m3 | VLL | VRR | Ratio | Q L | ||
| Spruce | ||||||
| 1 year | 460 | 5350 | 1400 | 125 | Italy | |
| 10 years | 410 | 5700 | 1150 | 4.95 | 125 | Italy |
| 52 years | 440 | 5400 | 1500 | 4.70 | 130 | Tyrol |
| 390 years | 450 | 4200 | 950 | 4.40 | 95 | Italy |
| Maple | ||||||
| 1 year | 720 | 3050 | 80 | Italy | ||
| 13 years | 665 | 4300 | 105 | Italy | ||
| 17 years | 785 | 4150 | 80 | France | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bucur, V. A Review on Acoustics of Wood as a Tool for Quality Assessment. Forests 2023, 14, 1545. https://doi.org/10.3390/f14081545
Bucur V. A Review on Acoustics of Wood as a Tool for Quality Assessment. Forests. 2023; 14(8):1545. https://doi.org/10.3390/f14081545
Chicago/Turabian StyleBucur, Voichita. 2023. "A Review on Acoustics of Wood as a Tool for Quality Assessment" Forests 14, no. 8: 1545. https://doi.org/10.3390/f14081545
APA StyleBucur, V. (2023). A Review on Acoustics of Wood as a Tool for Quality Assessment. Forests, 14(8), 1545. https://doi.org/10.3390/f14081545






