Research on the Performance and Control Strategy of Electro-Hydraulic Servo System for Selective Hole Digging Tree Planter
Abstract
1. Introduction
2. Materials and Methods
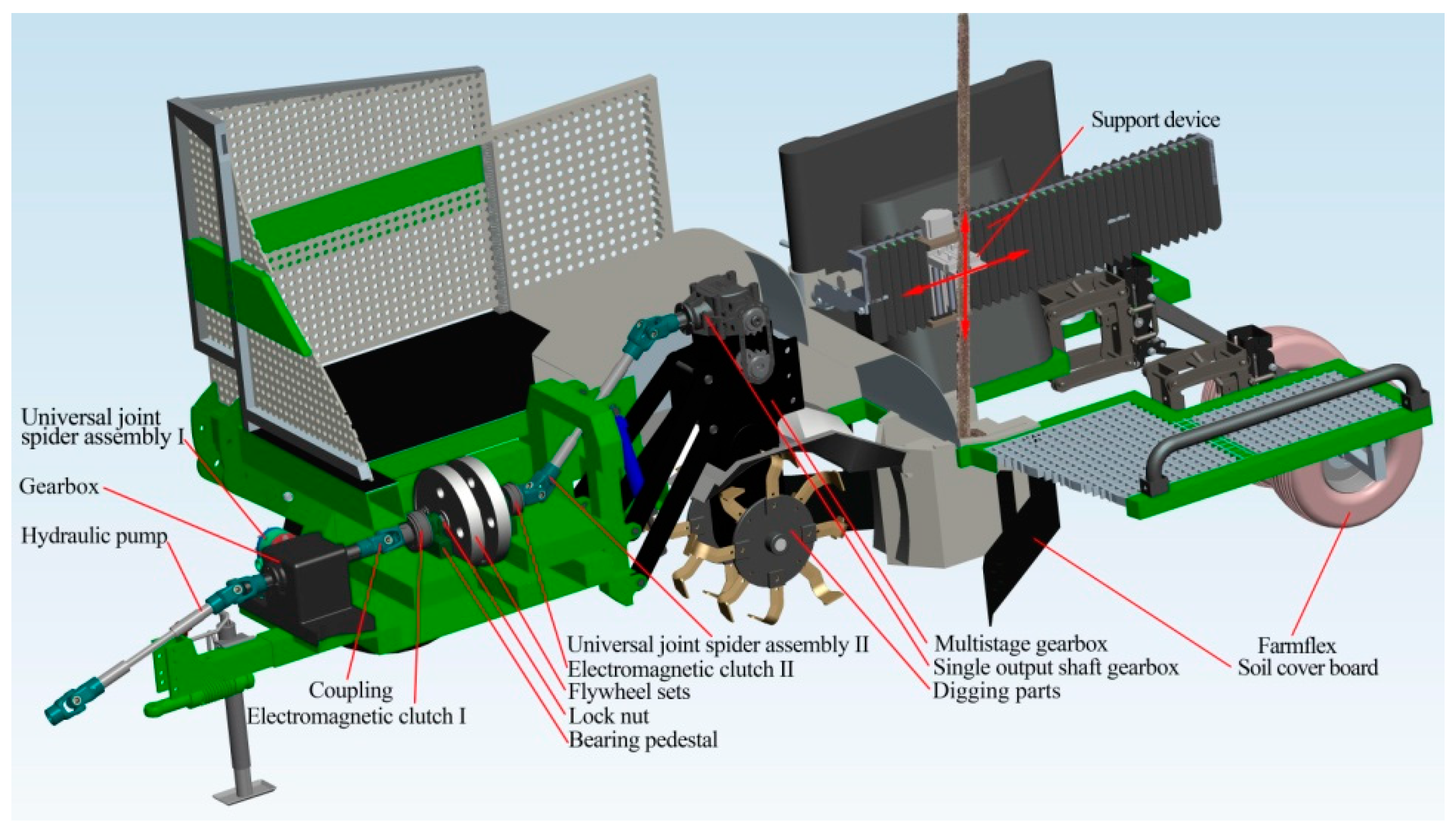
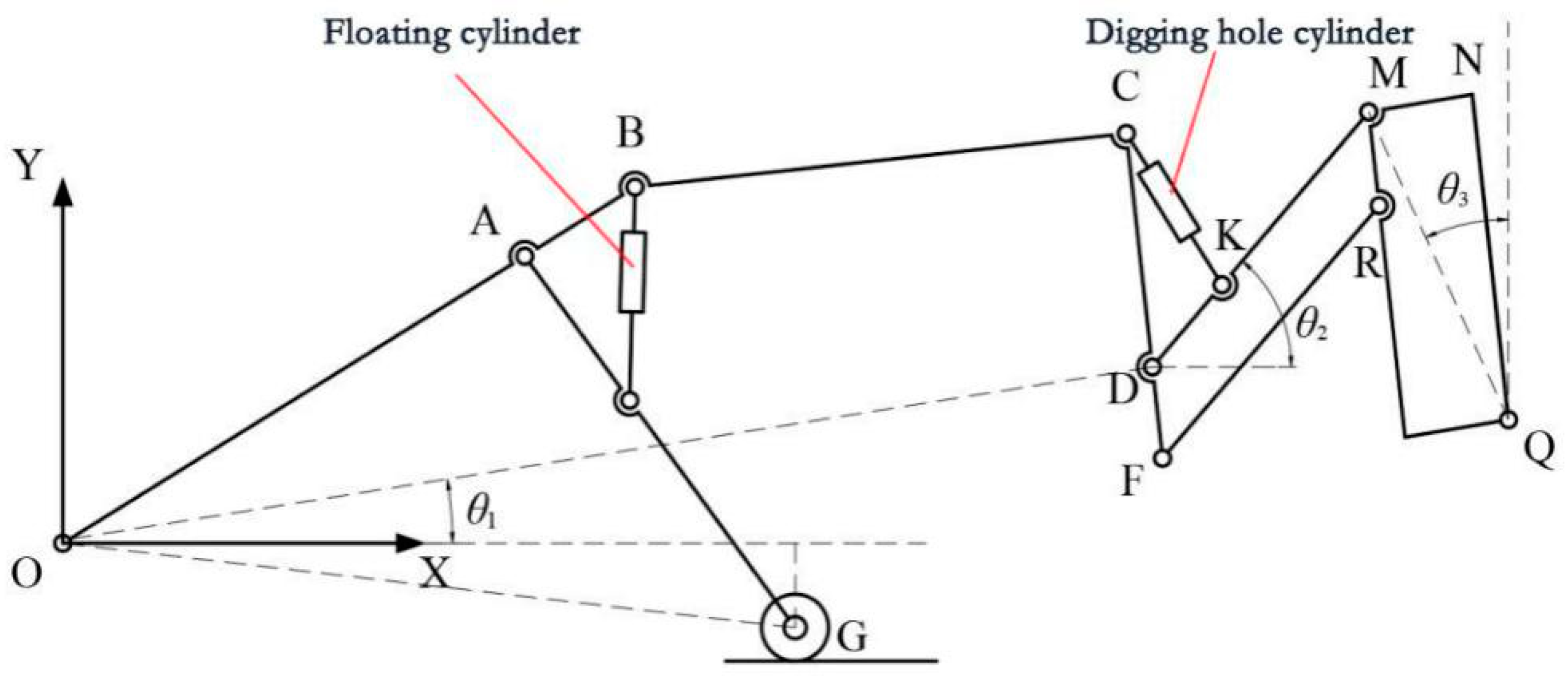
2.1. Modeling of Trajectory of Intermittent Digging Mechanism
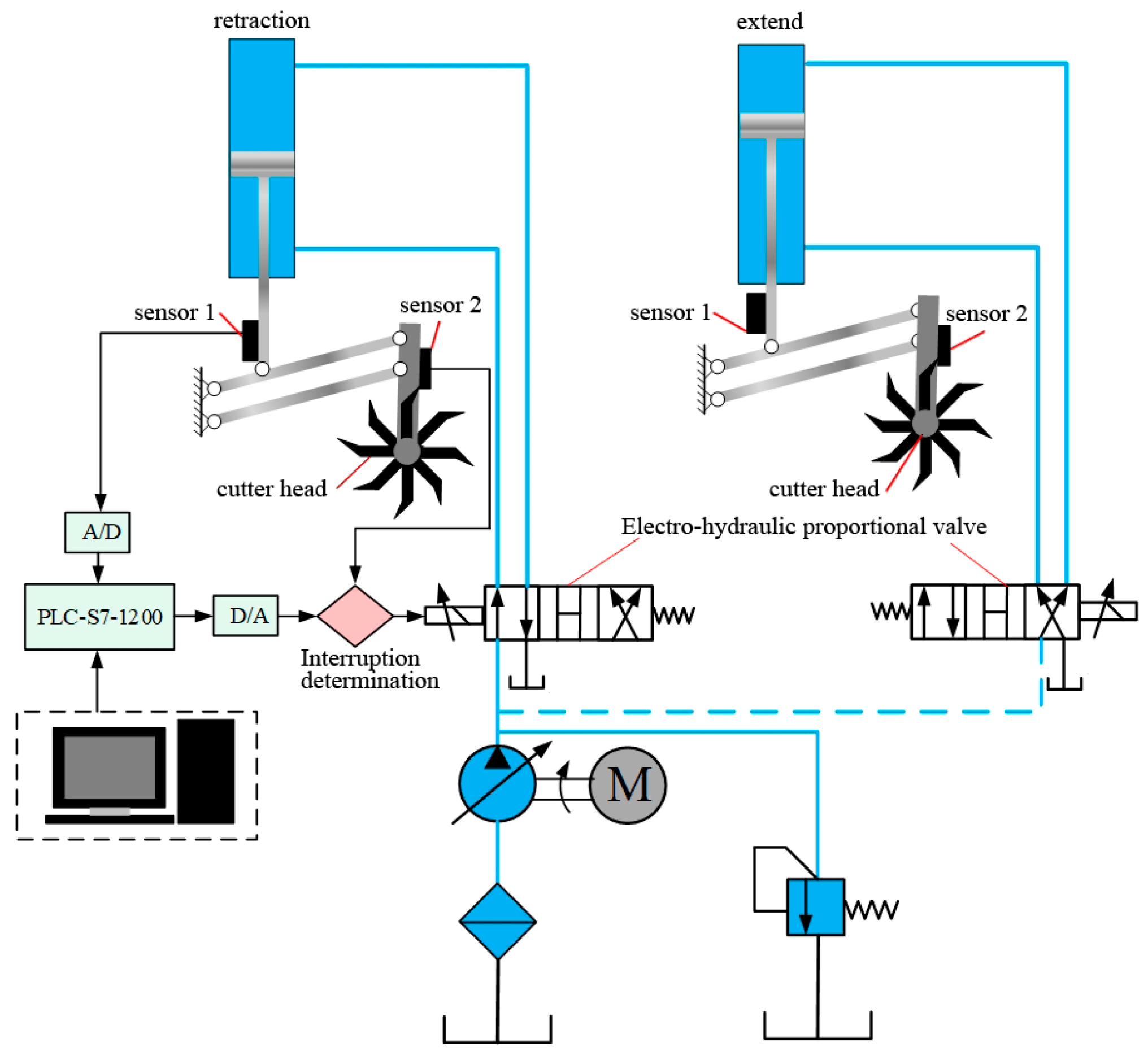
2.2. Mathematical Modeling of Electrohydraulic Servo Systems
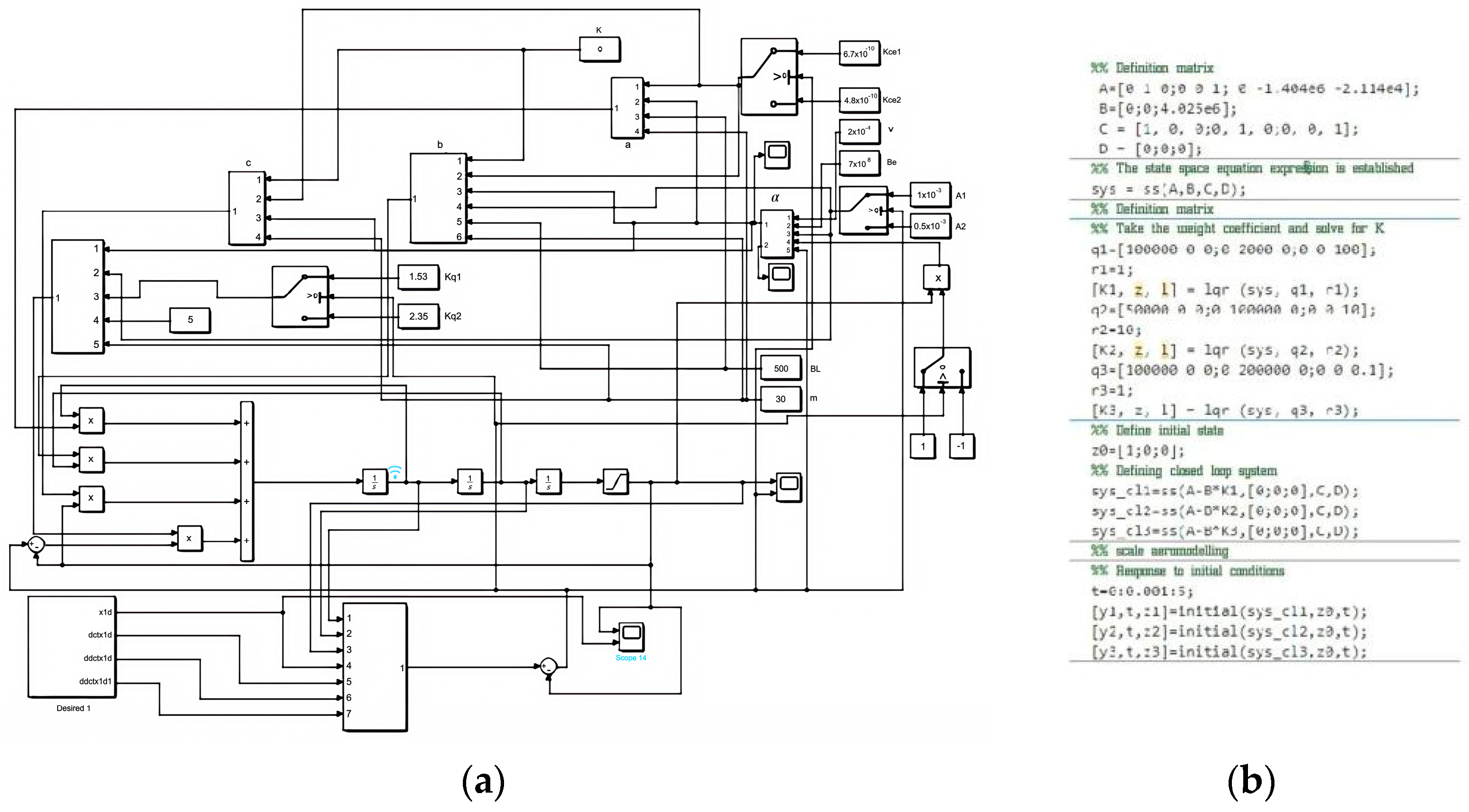
2.3. Design of Linear State Feedback Controller with Feedforward Based on a Linear Quadratic Regulator
3. Results and Discussion
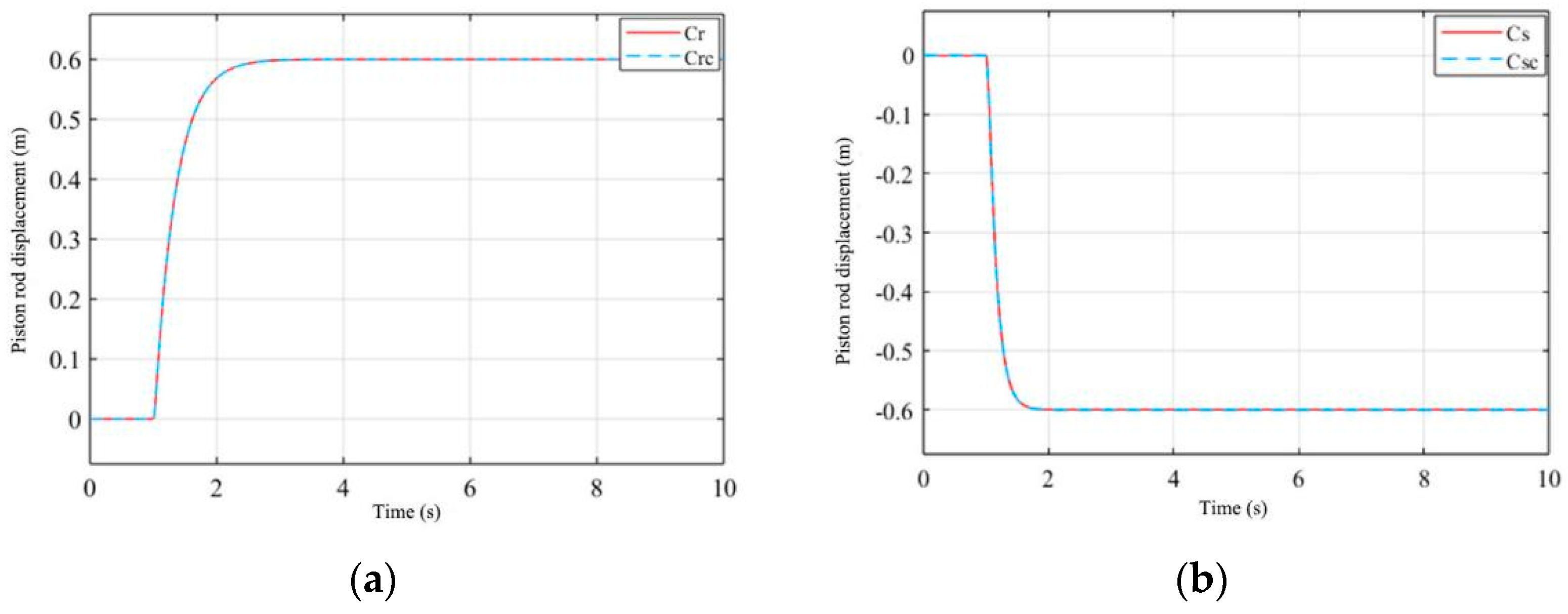
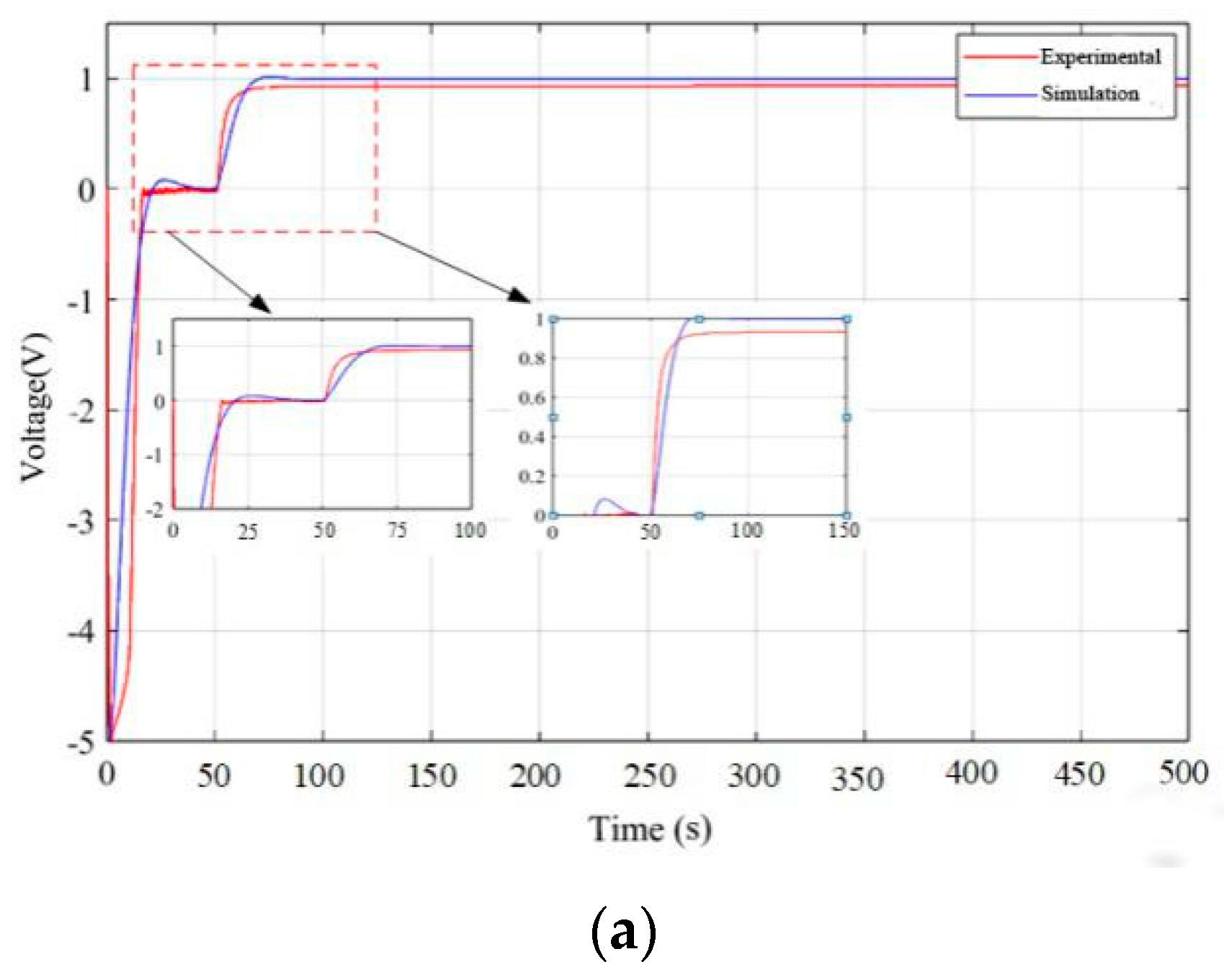
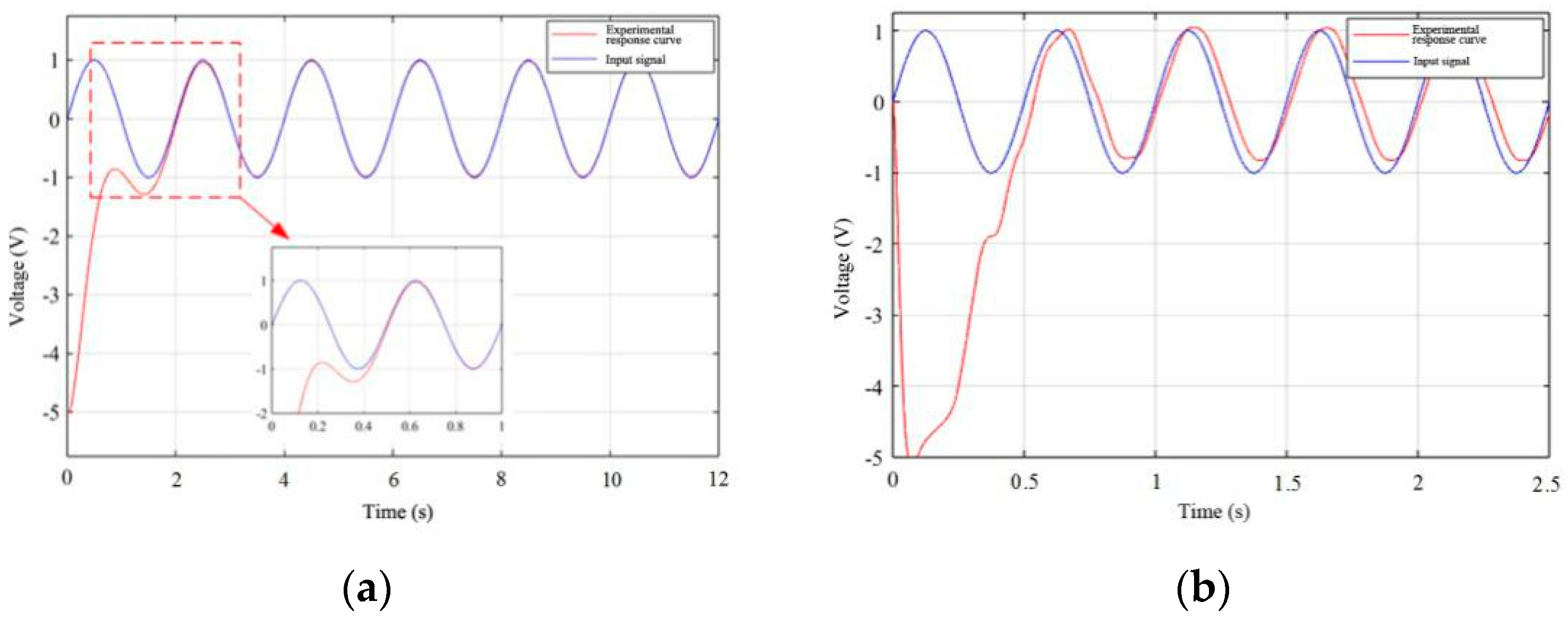
3.1. Electro-Hydraulic Servo System Performance Analysis
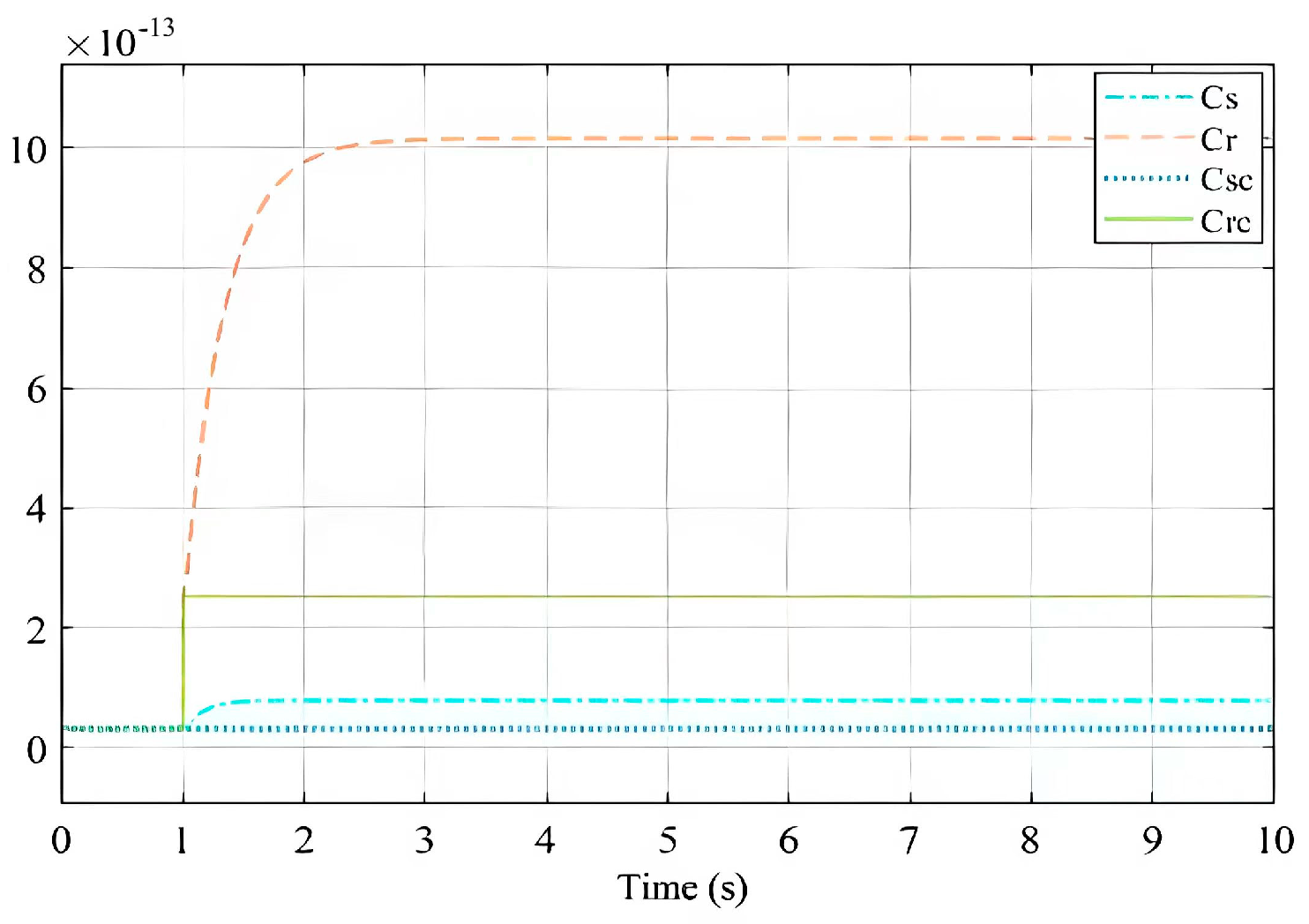
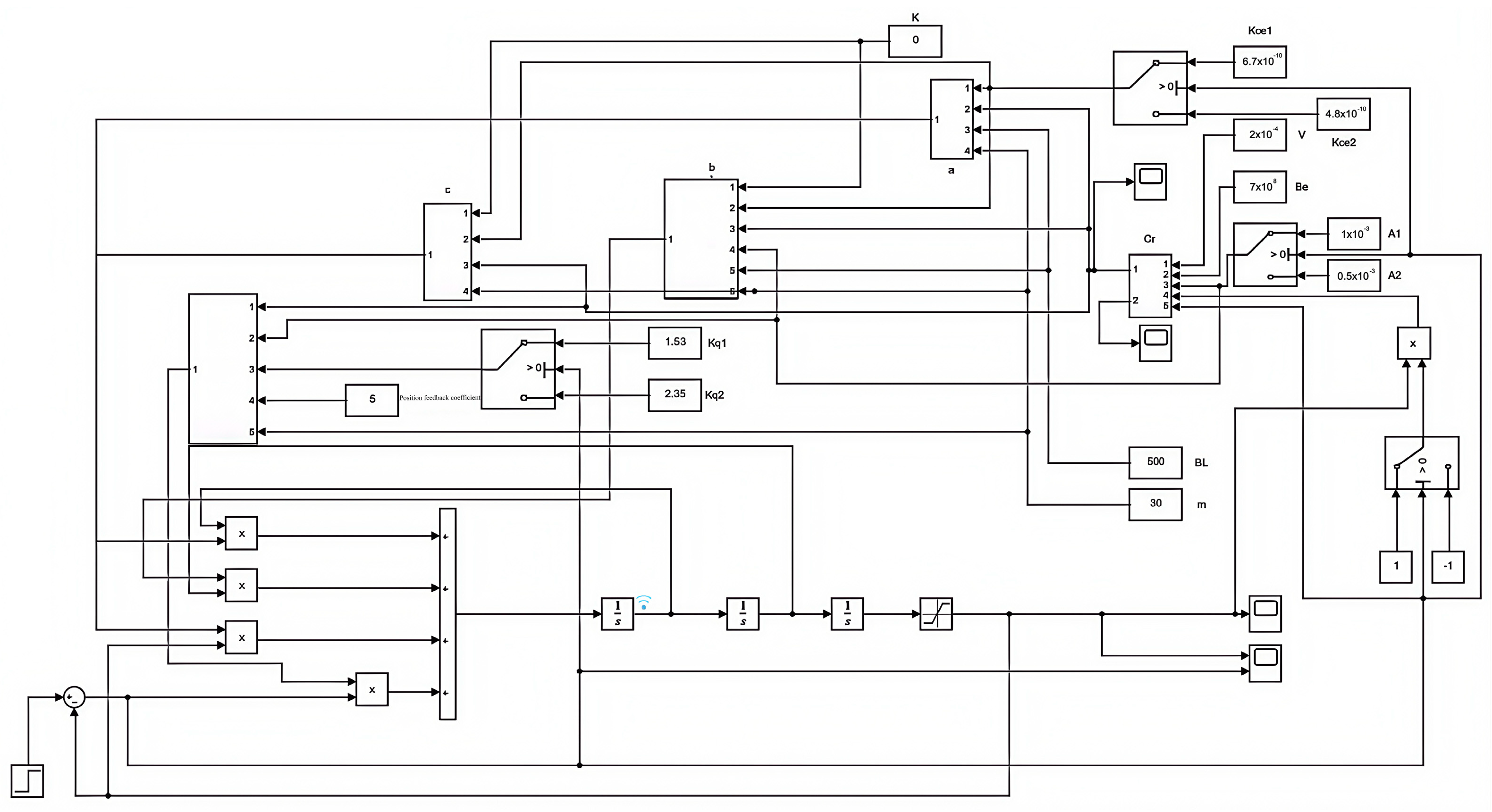
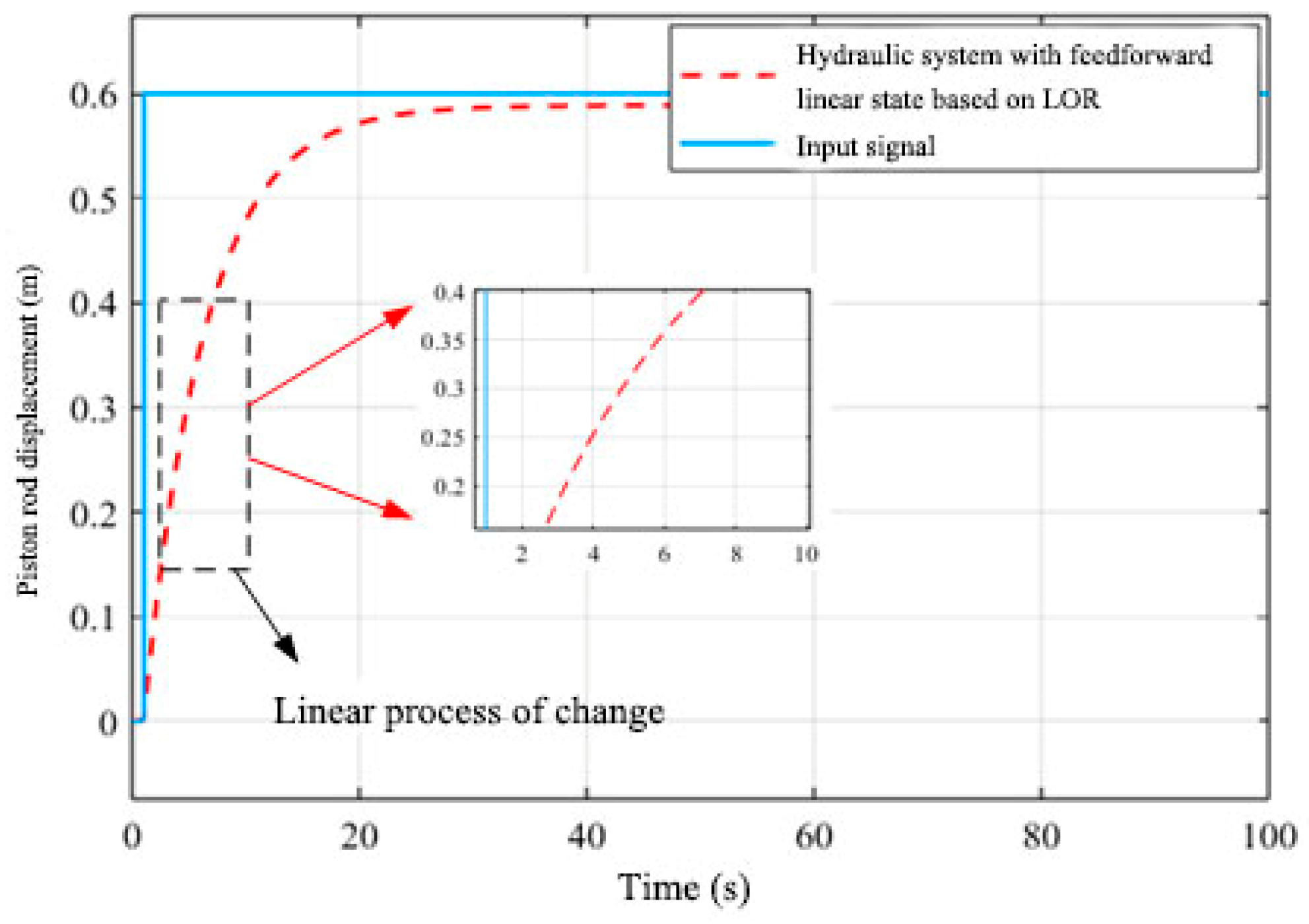
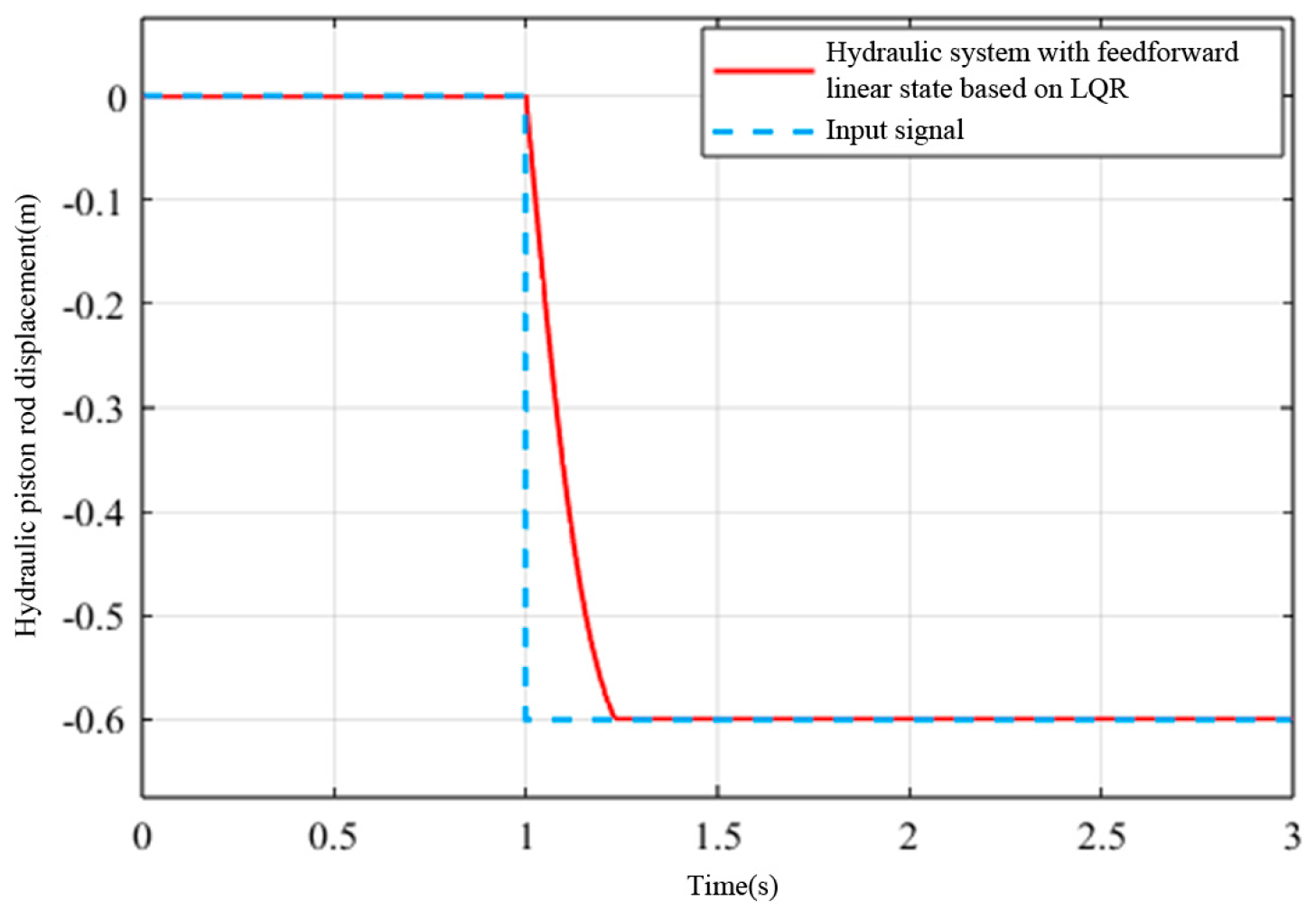
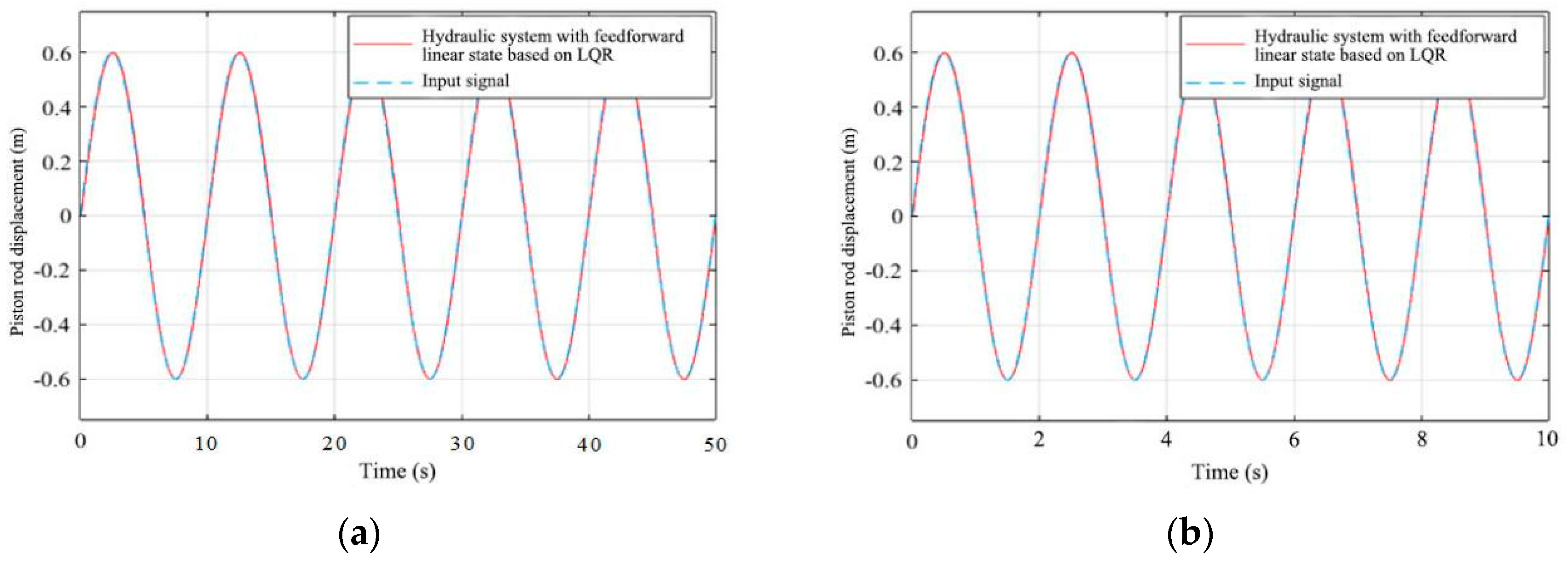
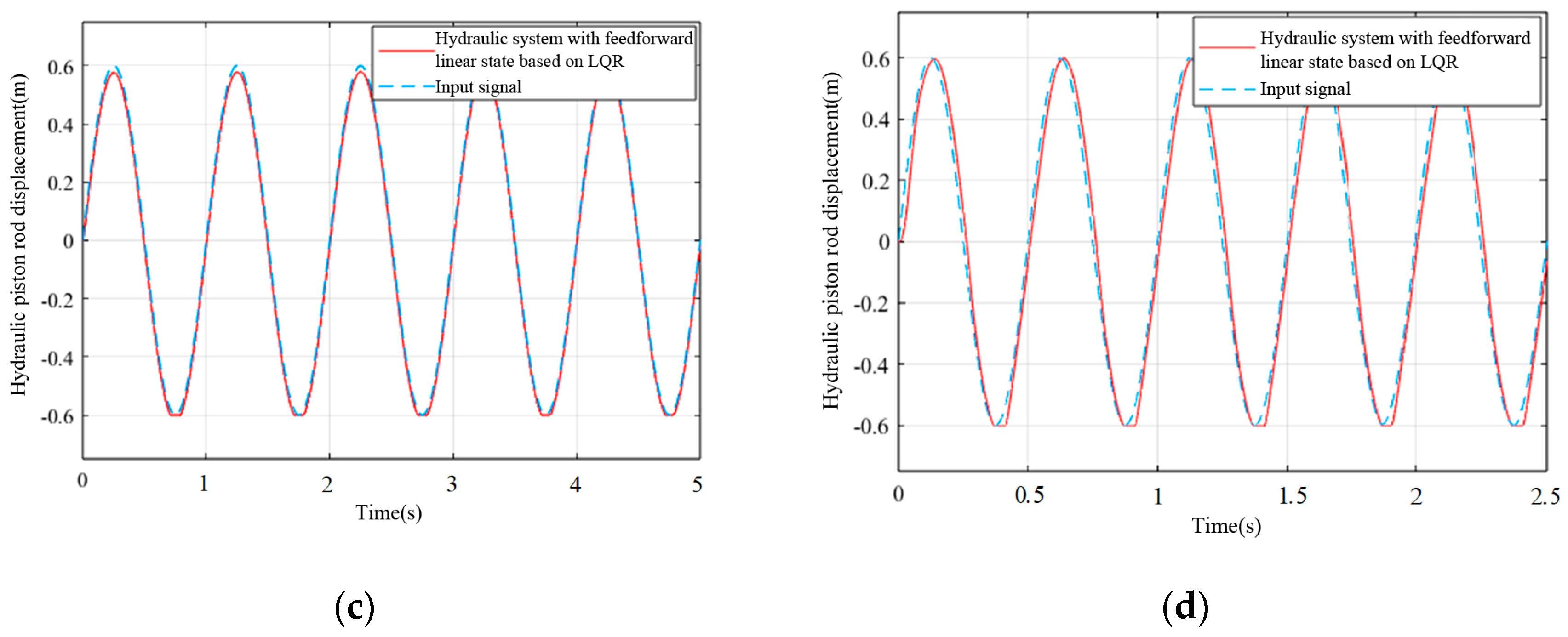
3.2. Simulation and Analysis of a Hydraulic System Based on LQR Linear State Feedback Control with Feedforward
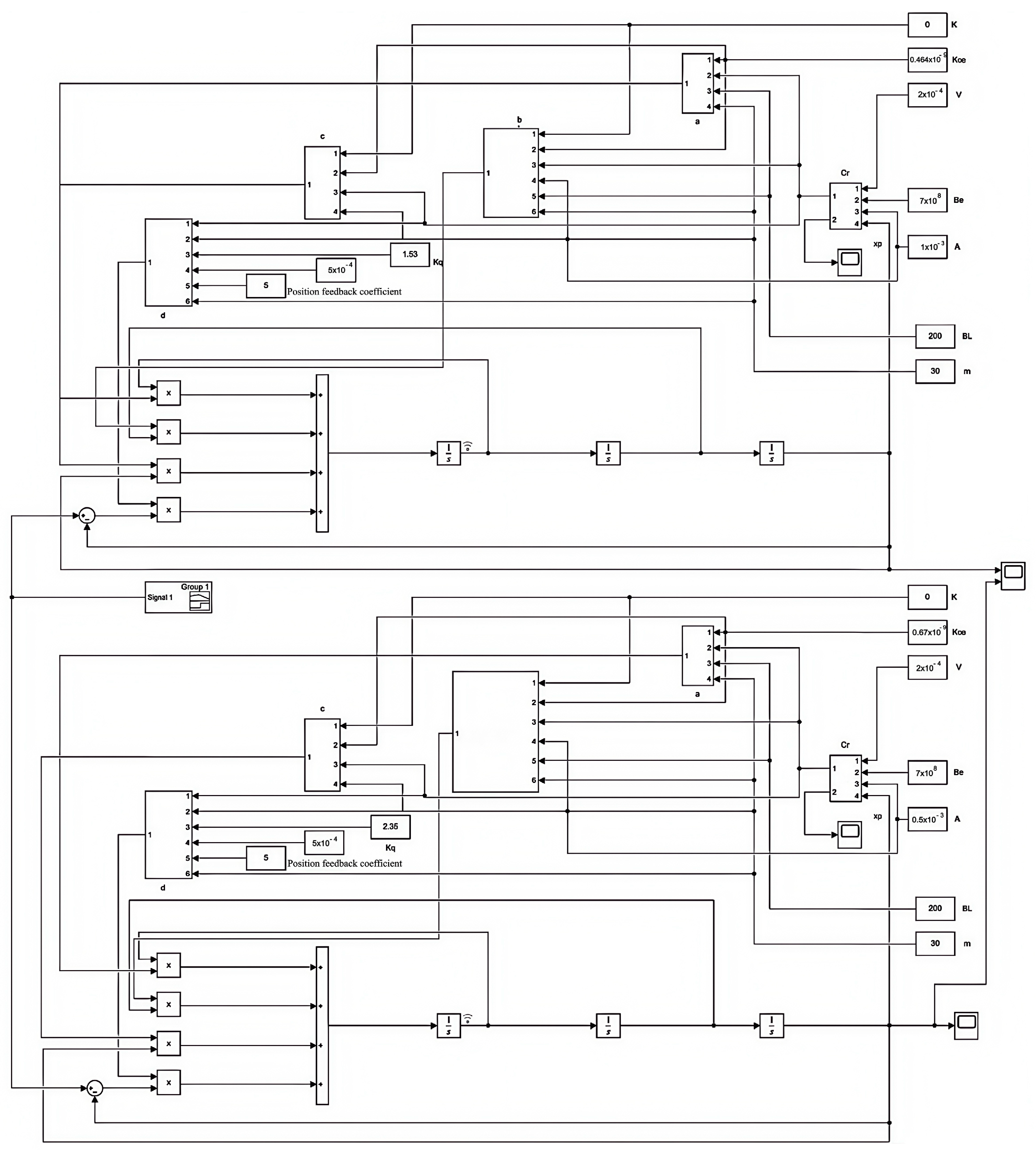
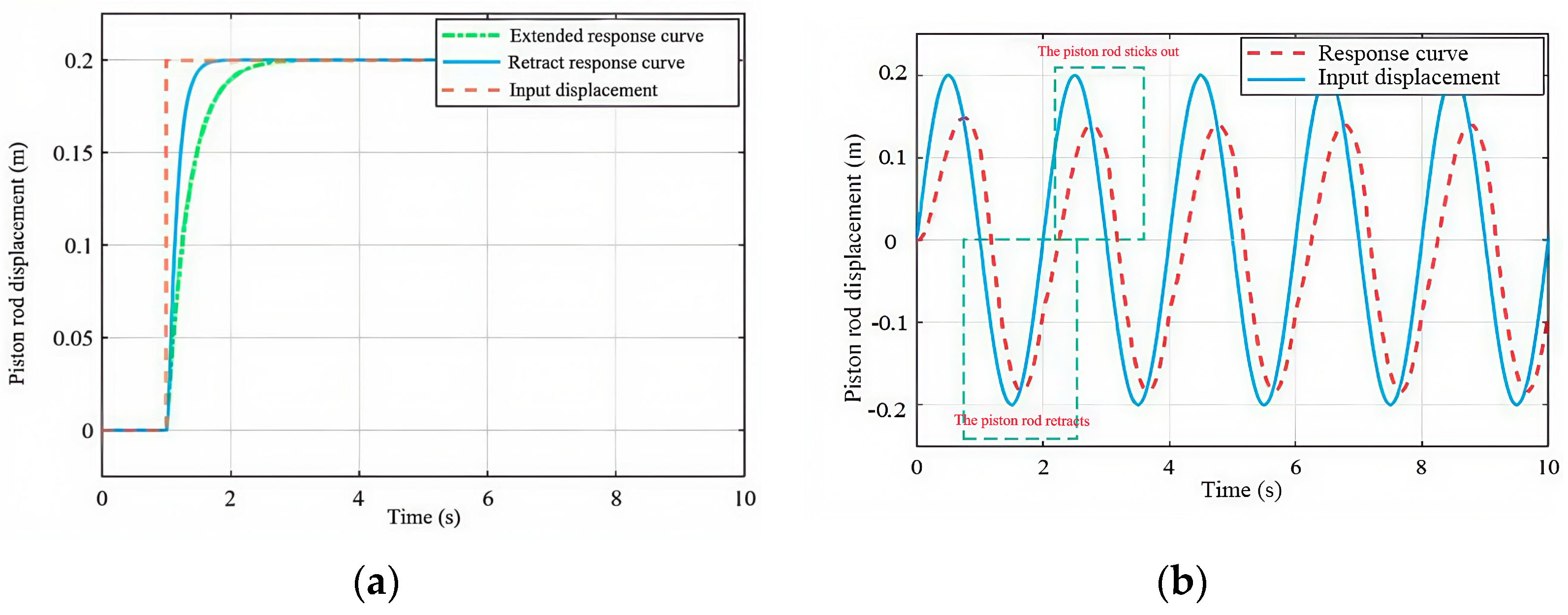
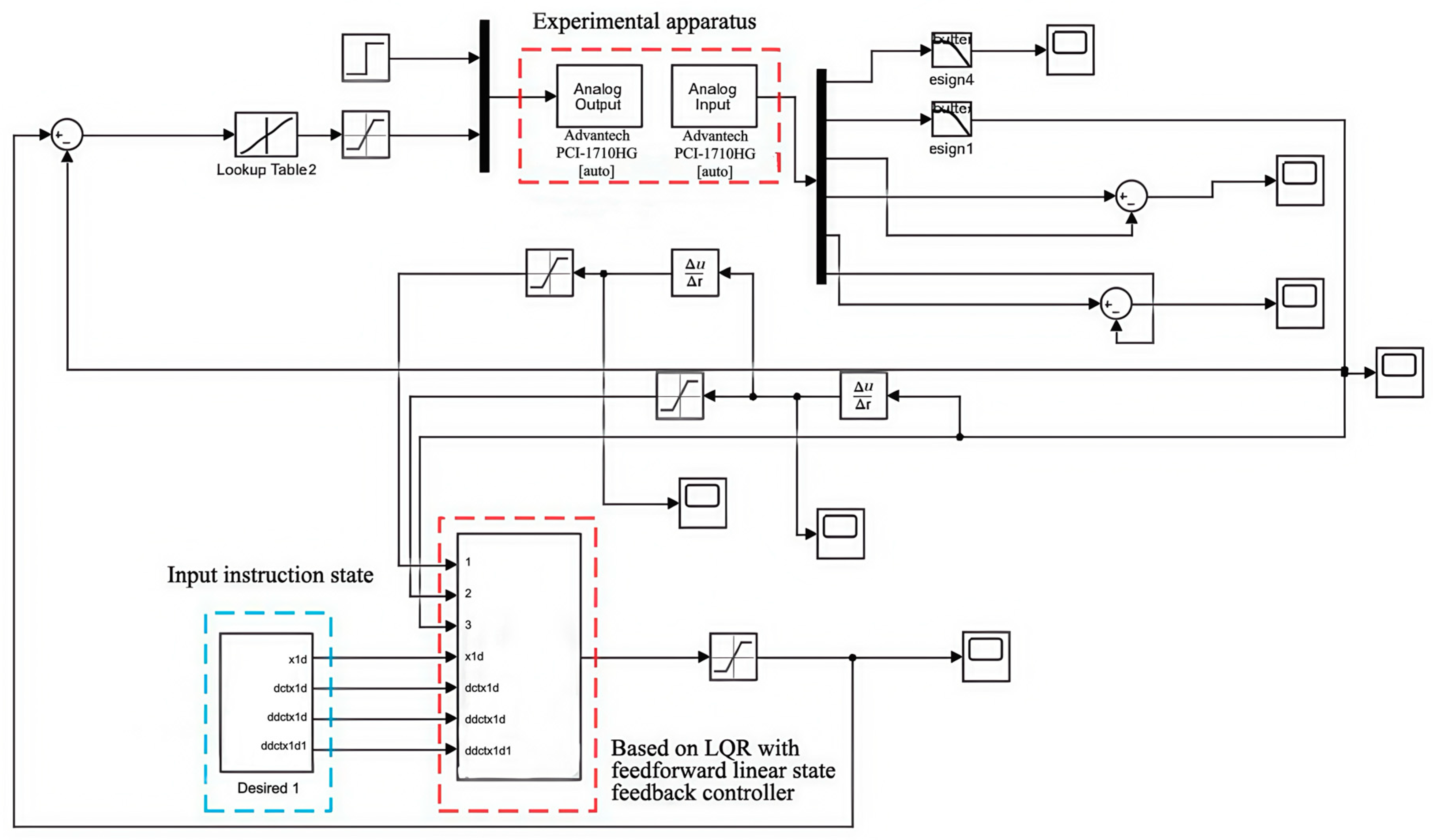
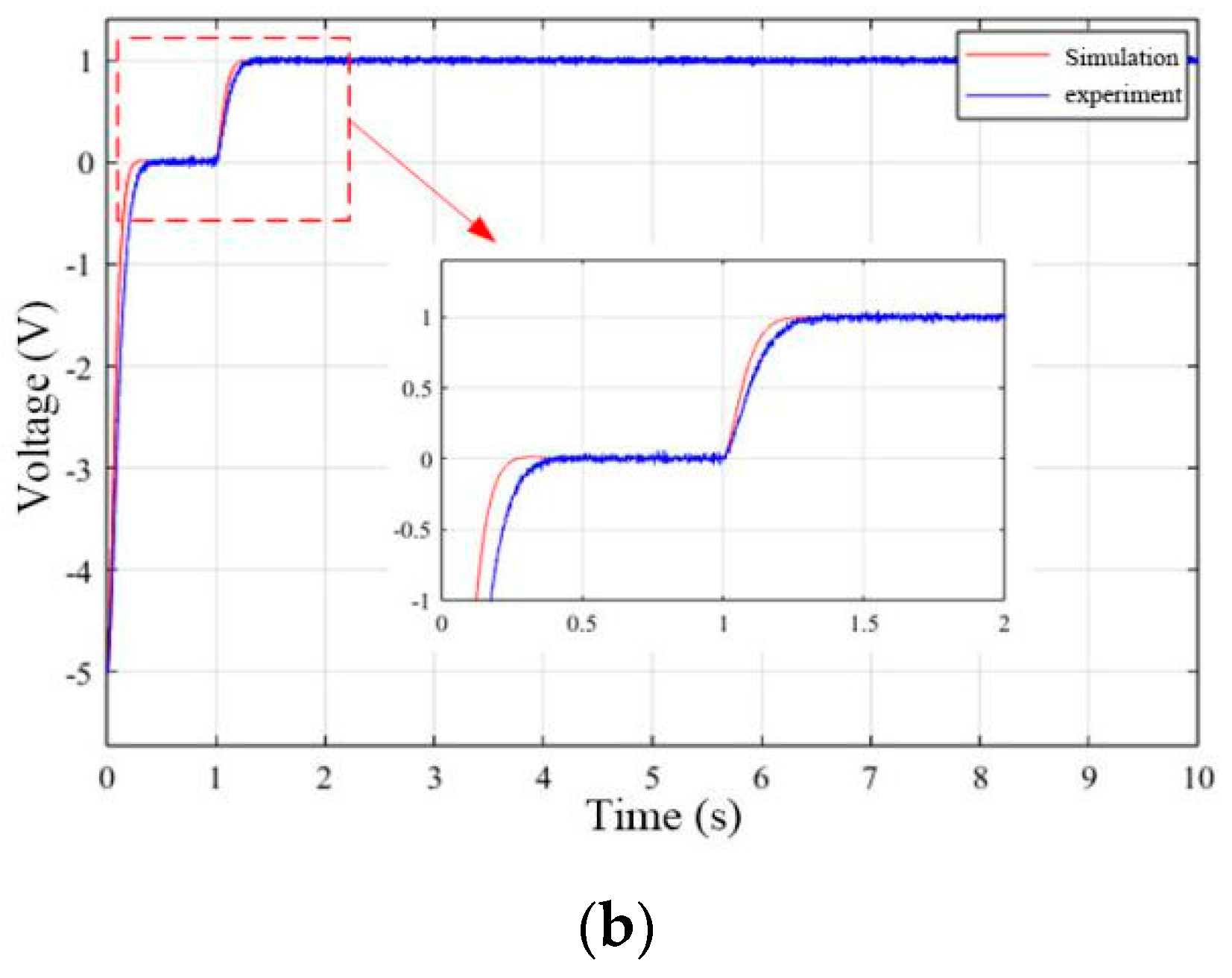
3.3. Experiments on a Hydraulic System Based on LQR Linear State Feedback Control with Feedforward
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ersson, B.T.; Laine, T.; Saksa, T. Mechanized tree planting in Sweden and Finland: Current state and key factors for future growth. Forests 2018, 9, 370. [Google Scholar] [CrossRef]
- Freedman, B.; Keith, T. Planting trees for carbon credits: A discussion of context, issues, feasibility, and environmental benefits. Environ. Rev. 2011, 4, 100–111. [Google Scholar] [CrossRef]
- Živković, M.; Urošević, M.; Komnenić, V. Technological and technical aspects of mechanized fruit tree planting. Poljopr. Teh. 2008, 33, 33–39. [Google Scholar]
- Zhu, B.; Yu, H.; Li, C. Design and Analysis of Intermittent Hole Digging Transplanter. For. Eng. 2020, 36, 39–44. [Google Scholar]
- Rantala, J.; Harstela, P.; Saarinen, V.-M.; Tervo, L. A Techno-Economic Evaluation of Bracker and M-Planter Tree Planting Device. Silva Fenn. 2009, 43, 659–667. [Google Scholar] [CrossRef]
- Zhang, P.; Wu, Z.; Yin, L. Research on Tree Planting Robots Based on Intelligent Control. Sci. Technol. Commun. 2017, 9, 42–43. [Google Scholar]
- Xu, C.; Lv, Z.; Xin, L.; Zhao, Y. Optimization Design and Experiment of Fully Automatic Strawberry Bowl Seedling Transplanting Mechanism. J. Agric. Mach. 2019, 50, 97–106. [Google Scholar]
- Liepins, K.; Lazdina, D.; Lazdins, A. Productivity and Cost-effectiveness of the M-Planter Tree Planting Machine in Latvian Conditions. Balt. For. 2011, 17, 308–311. [Google Scholar]
- Ma, L.; Wang, J.; Zong, W.; Huang, X.; Feng, J. Design and experiment of automatic feed mechanism with half nuts structure of portable digging machine. Trans. Chin. Soc. Agric. Eng. 2017, 33, 25–31. [Google Scholar]
- Jiang, C.; Yu, G. Development and experiment of efficient deep planting earth auger. Trans. Chin. Soc. Agric. Eng. 2013, 29, 75–83. [Google Scholar]
- Tang, Q.; Wu, J.; Jiang, L.; Wu, C.; Xiao, T.; Jiang, T. Design and experiment of hydraulic profiling system for rapeseed tillage and transplanting joint operation machine. J. Agric. Mach. 2021, 52, 95–102. [Google Scholar]
- Tang, Q.; Wu, C.; Wu, J.; Qin, C.; Jiang, L.; Wang, G. Research on the Electro hydraulic Proportional Control System for the Hole Distance of Rapeseed Rotary Tillage and Transplanting Joint Operation Machine. J. Agric. Mach. 2020, 51, 228–235. [Google Scholar]
- Fu, W.; Luo, X.; Zeng, S.; Wang, Z.; Wang, C.; Yuan, Q. Design and experiment of electro-hydraulic proportional control system for precise dry hole sowing machine for rice. J. Agric. Eng. 2015, 31, 25–31. [Google Scholar]
- Burce, M.E.; Kataoka, T.; Okamoto, H. Development of Seeding Depth Control System for Conservation Tillage Cultivation. J. Soc. Agric. Food Work. 2014, 76, 62–69. [Google Scholar]
- Yin, R.; Yuan, J.; Liu, X. Design and Test of Electro-Hydraulic Control System for Intelligent Fruit Tree Planter. In Advanced Manufacturing and Automation IX 9th; Springer: Singapore, 2020. [Google Scholar]
- Jin, K.; Song, J.; Li, Y.; Zhang, Z.; Zhou, H.; Chang, X. Linear active disturbance rejection control for the electro-hydraulic position servo system. Sci. Prog. 2021, 104, 15–23. [Google Scholar] [CrossRef]
- Li, J.; Li, W.; Du, X. Research on the characteristics of electro-hydraulic position servo system of RBF neural network under fuzzy rules. Sci. Rep. 2024, 14, 15332. [Google Scholar] [CrossRef]
- Sa, Y.; Zhu, Z.; Tang, Y.; Li, X.; Shen, G. Adaptive dynamic surface control using nonlinear disturbance observers for position tracking of electro-hydraulic servo systems. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2022, 236, 634–653. [Google Scholar] [CrossRef]
- Nguyen, M.; Dao, H.; Ahn, K. Active disturbance rejection control for position tracking of electro-hydraulic servo systems under modeling uncertainty and external load. Actuators 2021, 10, 20. [Google Scholar] [CrossRef]
- Nguyen, M.; Dao, H.; Ahn, K. Adaptive robust position control of electro-hydraulic servo systems with large uncertainties and disturbances. Appl. Sci. 2022, 12, 794. [Google Scholar] [CrossRef]
- Naveen, C.; Meenakshipriya, B.; Tony, T.A.; Sathiyavathi, S.; Sathishbabu, S. Real-time implementation of iterative learning control for an electro-hydraulic servo system. IETE J. Res. 2023, 69, 649–664. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, S.; Chen, Y.; Gu, C.C. Neural direct adaptive active disturbance rejection controller for electro-hydraulic servo system. Int. J. Control Autom. Syst. 2022, 20, 2402–2412. [Google Scholar] [CrossRef]
- Sun, C.; Dong, X.; Wang, M.; Li, J. Sliding mode control of electro-hydraulic position servo system based on adaptive reaching law. Appl. Sci. 2022, 12, 6897. [Google Scholar] [CrossRef]
- He, J.; Su, S.; Wang, H.; Chen, F.; Yin, B. Online PID Tuning Strategy for Hydraulic Servo Control Systems via SAC-Based Deep Reinforcement Learning. Machines 2023, 11, 593. [Google Scholar] [CrossRef]
- Wu, Z. Hydraulic Control System; Higher Education Press: Beijing, China, 2008; pp. 106–201. [Google Scholar]

| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Piston rodless chamber area A1 (m2) | 1 × 10−3 | Piston rodless cavity area A2 (m2) | 0.5 × 10−3 |
| Initial volume of hydraulic cylinder Vt (m3) | 2 × 10−4 | Viscous friction of hydraulic system Bp (N/(m/s)) | 500 |
| Effective volume modulus of elasticity of hydraulic fluid βe (Pa) | 7 × 108 | Electro-hydraulic proportional valve flow gain Kqr | 1.53 |
| Electro-hydraulic proportional valve flow gain Kqs | 2.35 | Rated supply pressure Ps (MPa) | 21 |
| Load mass m (kg) | 30 | Hydraulic oil density ρ (kg/m3) | 850 |
| Total hydraulic cylinder flow-pressure coefficient Kcs (m3/s·Pa) | 4.6 × 10−9 | Total hydraulic cylinder flow-pressure coefficient Kcr (m3/s·Pa) | 6.7 × 10−9 |
| Electro-hydraulic proportional valve gain Kv (mm/V) | 5 × 10−4 | Displacement sensor feedback gain Kx (V/m) | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, B.; Liu, J.; Yu, H.; Yu, L.; Wang, Z.; Zhou, H.; Yang, C. Research on the Performance and Control Strategy of Electro-Hydraulic Servo System for Selective Hole Digging Tree Planter. Forests 2024, 15, 1744. https://doi.org/10.3390/f15101744
Zhu B, Liu J, Yu H, Yu L, Wang Z, Zhou H, Yang C. Research on the Performance and Control Strategy of Electro-Hydraulic Servo System for Selective Hole Digging Tree Planter. Forests. 2024; 15(10):1744. https://doi.org/10.3390/f15101744
Chicago/Turabian StyleZhu, Binhai, Jiuqing Liu, Hang Yu, Li Yu, Zhenli Wang, Huan Zhou, and Chunmei Yang. 2024. "Research on the Performance and Control Strategy of Electro-Hydraulic Servo System for Selective Hole Digging Tree Planter" Forests 15, no. 10: 1744. https://doi.org/10.3390/f15101744
APA StyleZhu, B., Liu, J., Yu, H., Yu, L., Wang, Z., Zhou, H., & Yang, C. (2024). Research on the Performance and Control Strategy of Electro-Hydraulic Servo System for Selective Hole Digging Tree Planter. Forests, 15(10), 1744. https://doi.org/10.3390/f15101744





