Numerical Simulation and Bayesian Optimization CatBoost Prediction Method for Characteristic Parameters of Veneer Roller Pressing and Defibering
Abstract
:1. Introduction
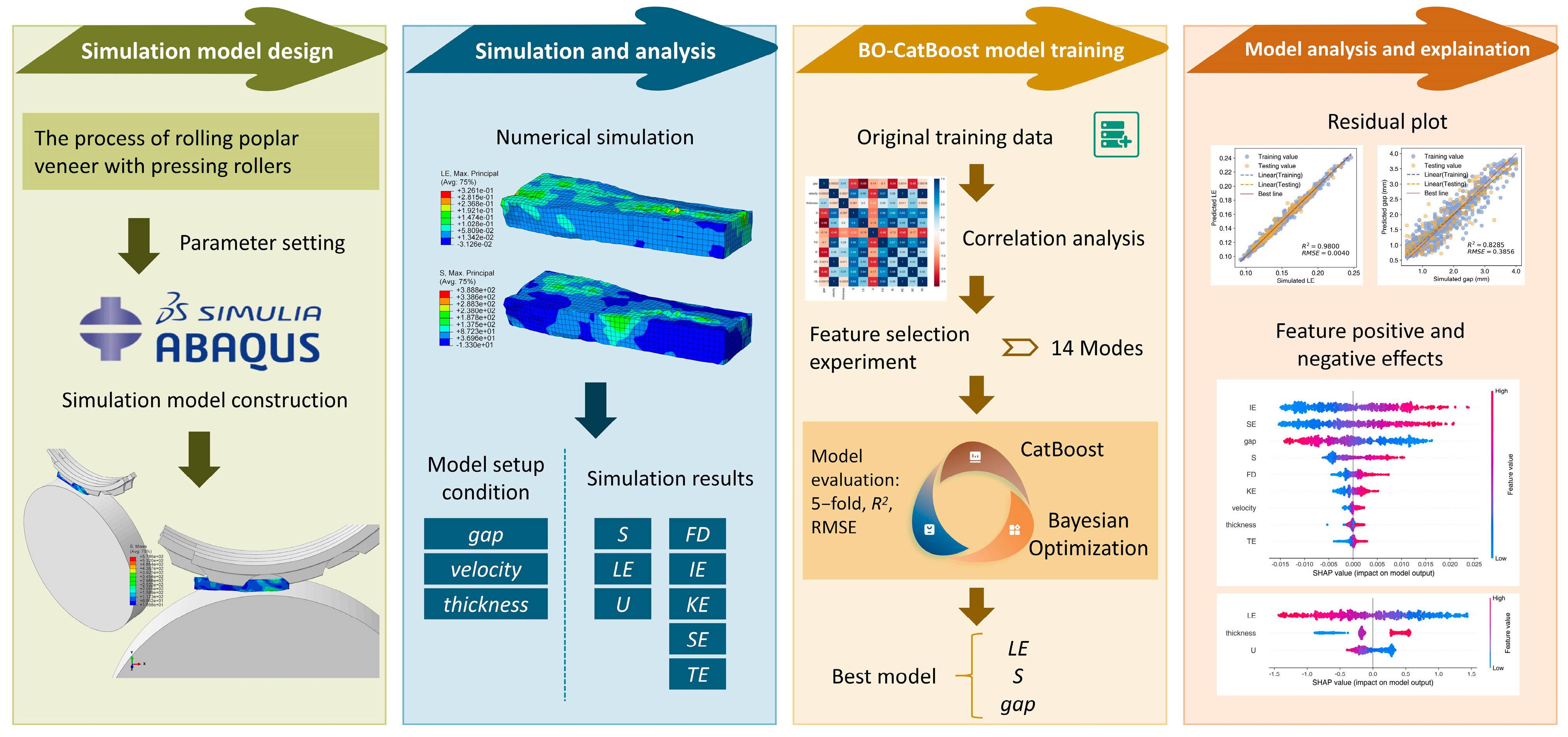
- (1)
- Establishing an FEM model of veneer rolled by the unit of the pressing roller.
- (2)
- Analyzing the effects of key characteristic parameters on the stress, strain, and energy fields of the veneer to determine the characteristic parameters of veneer roller pressing and defibering that will ultimately be involved in the prediction task, based on the FEM model created in task (1).
- (3)
- Using the numerical simulation results as the main research data, the CatBoost model is improved by using the BO algorithm, and constructs the BO-CatBoost prediction model for the characteristic parameters of veneer roller pressing and defibering.
- (4)
- The features that significantly affect the prediction results are analyzed using the Shapley Additive Explanation (SHAP) method, thus providing a more profound understanding of the decision-making process.
2. Research Methodology
2.1. Force Analysis and Simulation of Rolling Process
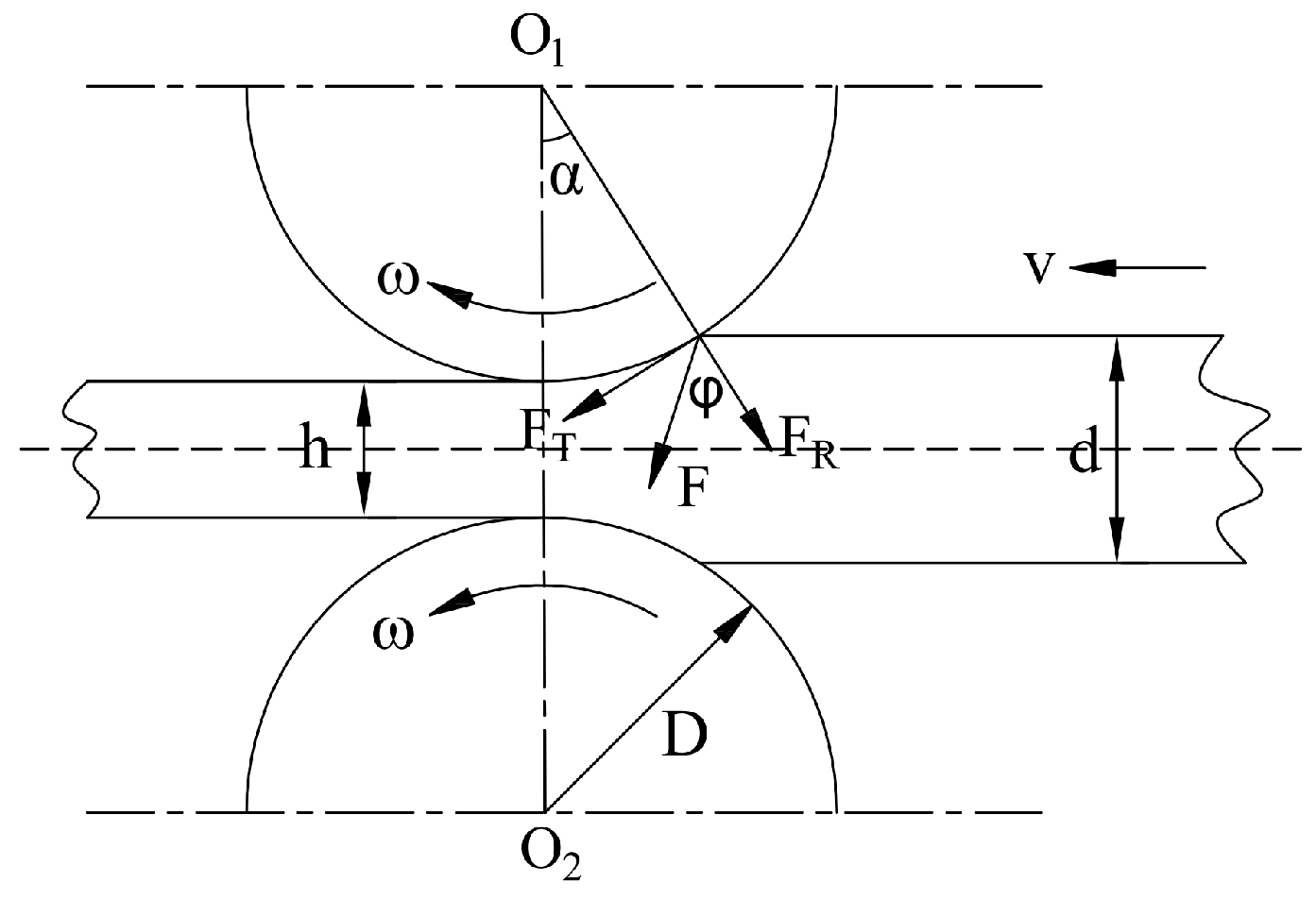
2.1.1. Force Analysis
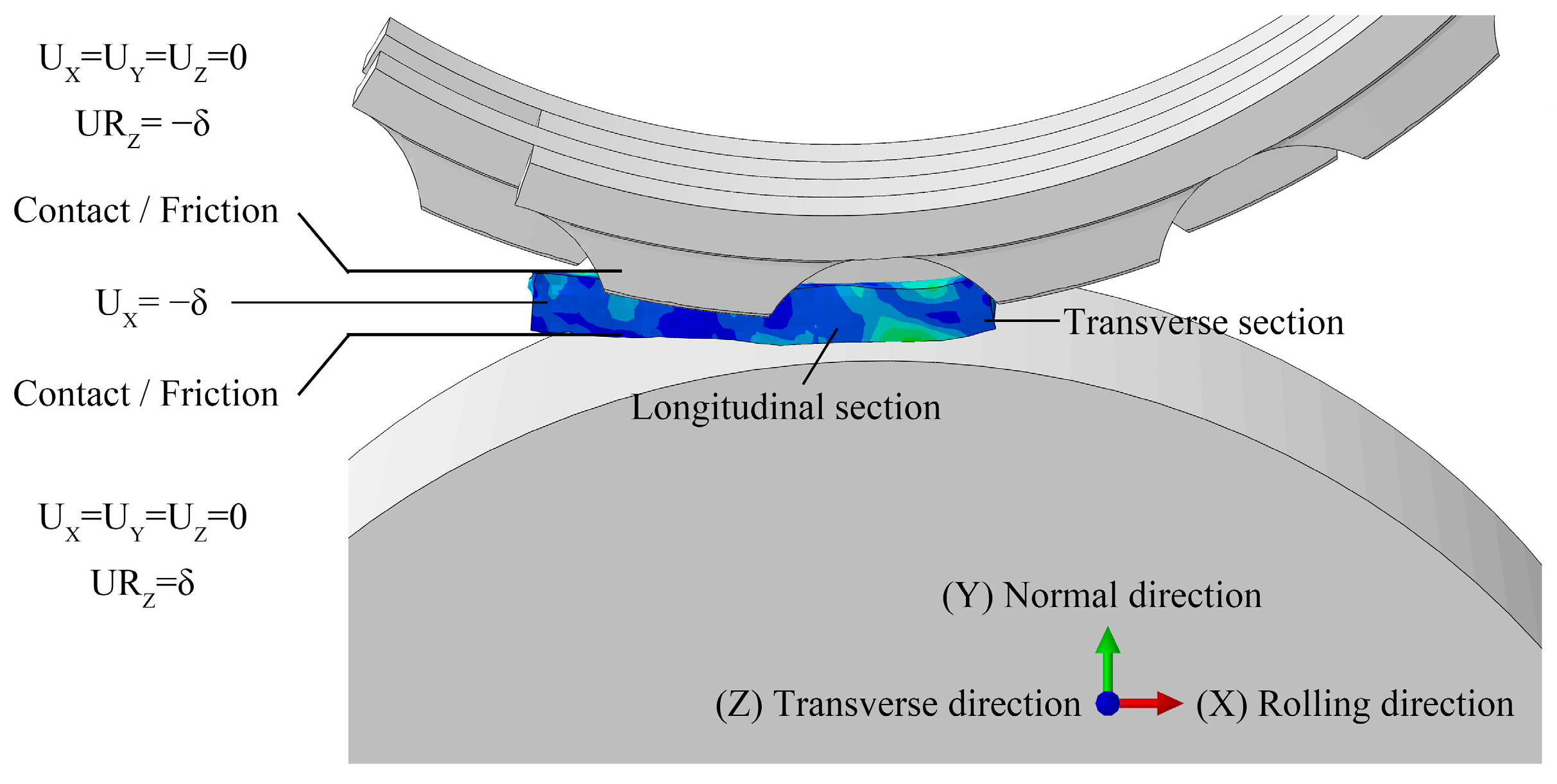
2.1.2. FEM Model Establishment
2.2. BO-CatBoost
2.3. Cross-Validation and Evaluation Criteria
3. Experimental Setup and Result Analysis
3.1. Simulated Analysis of Veneer Roller Pressing and Defibering
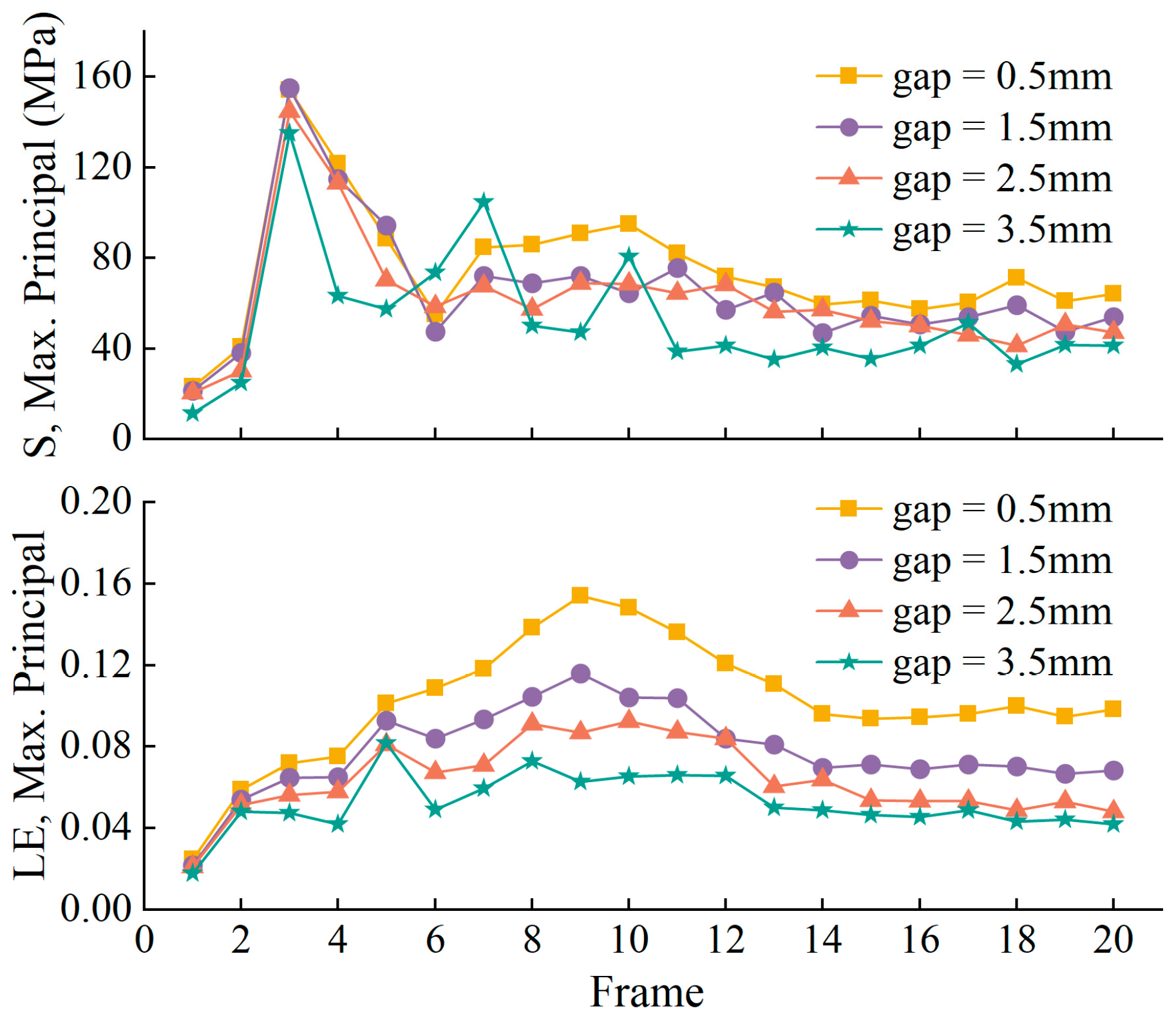
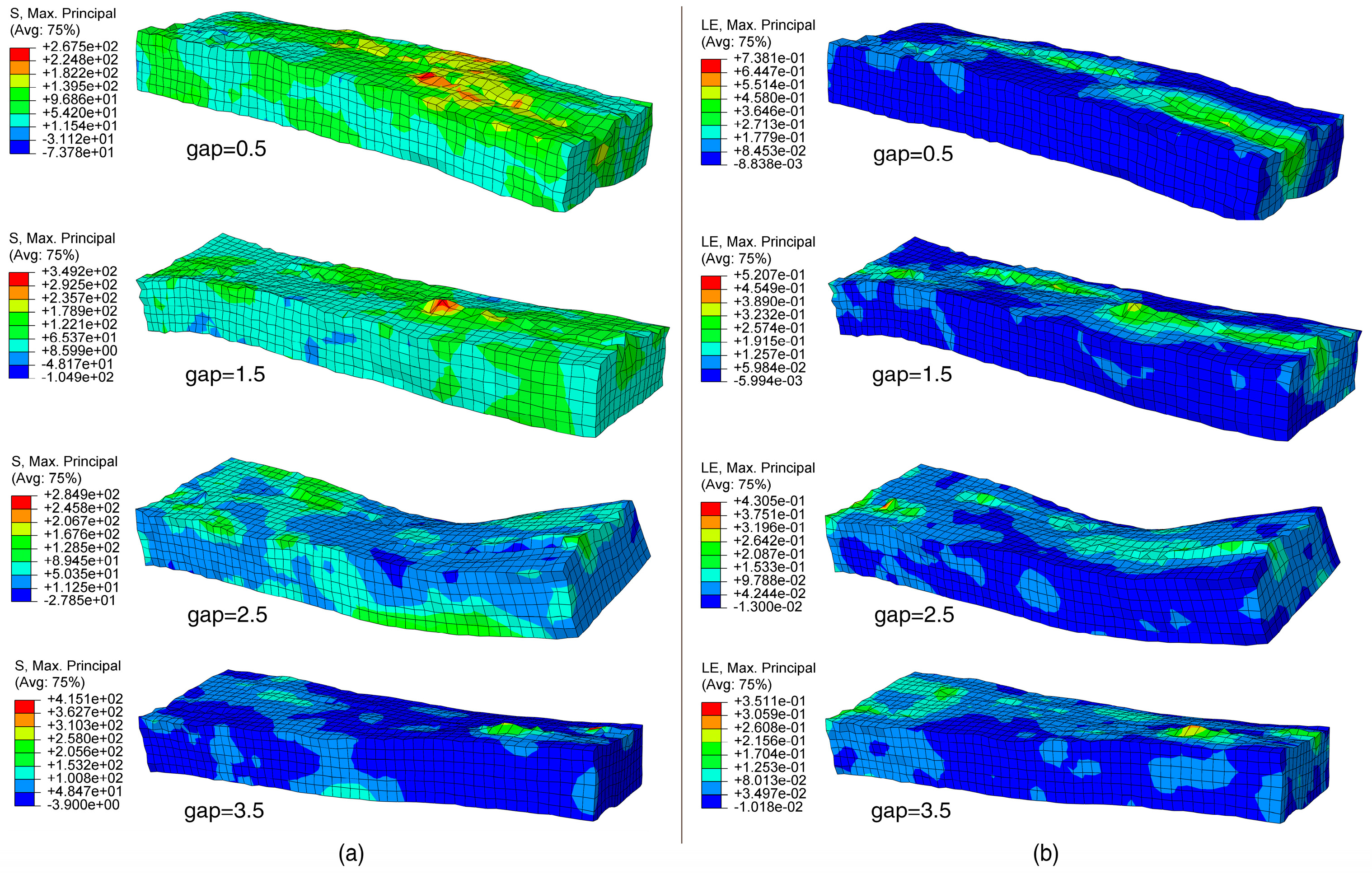
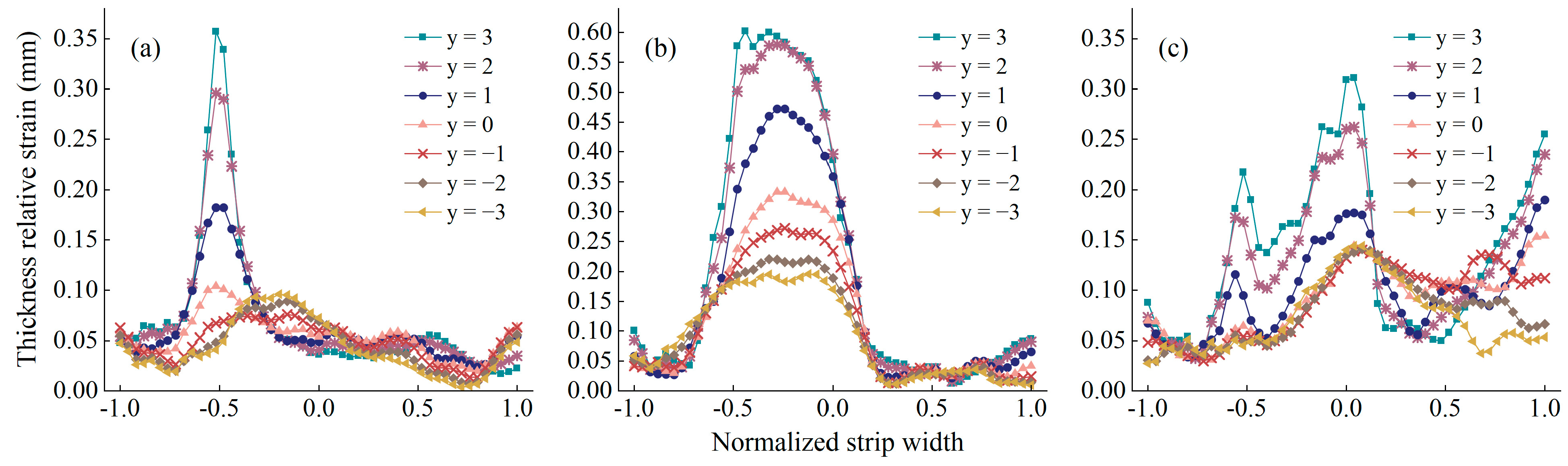
3.1.1. The Effect of Roller Gap in Defibering
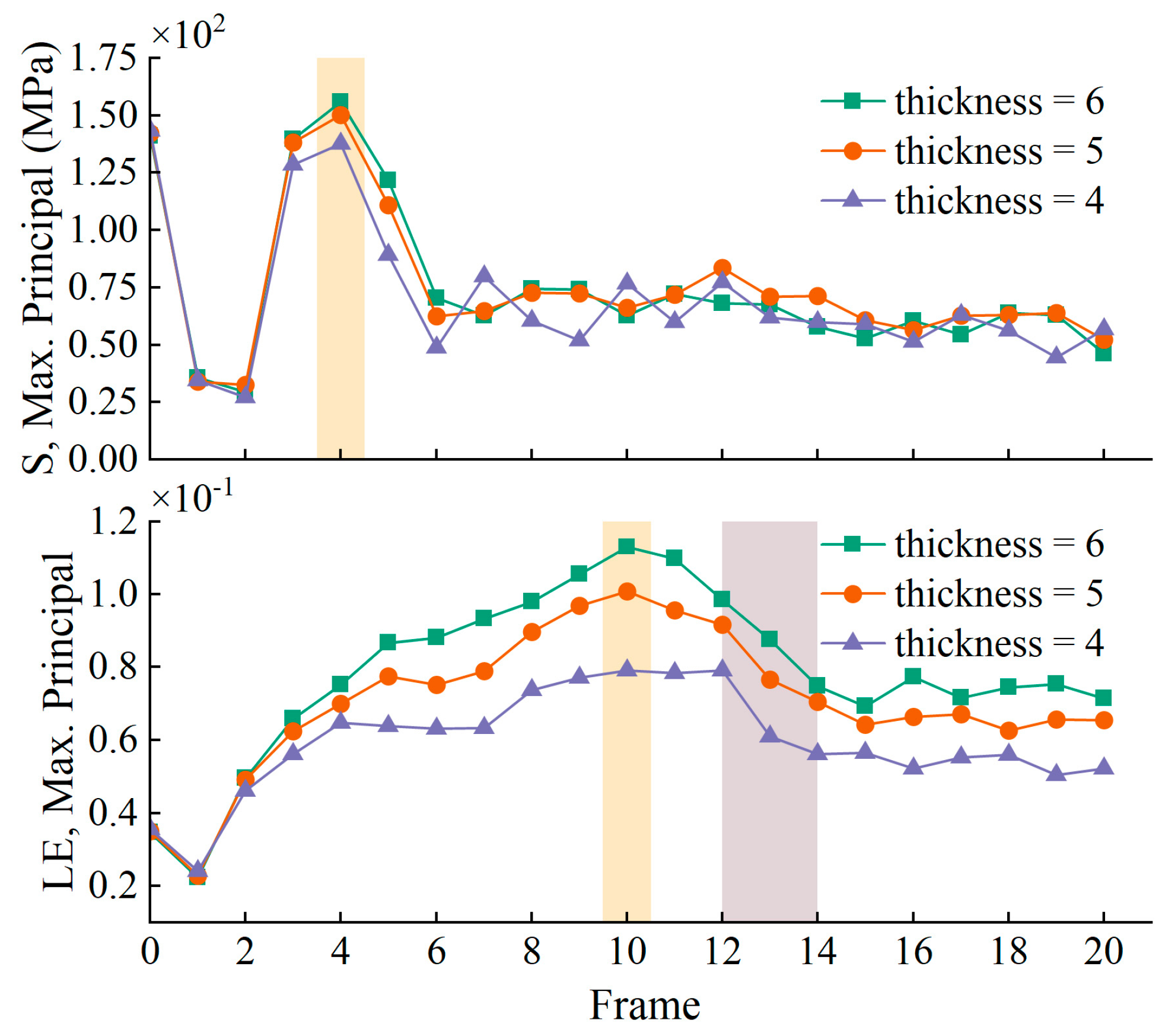
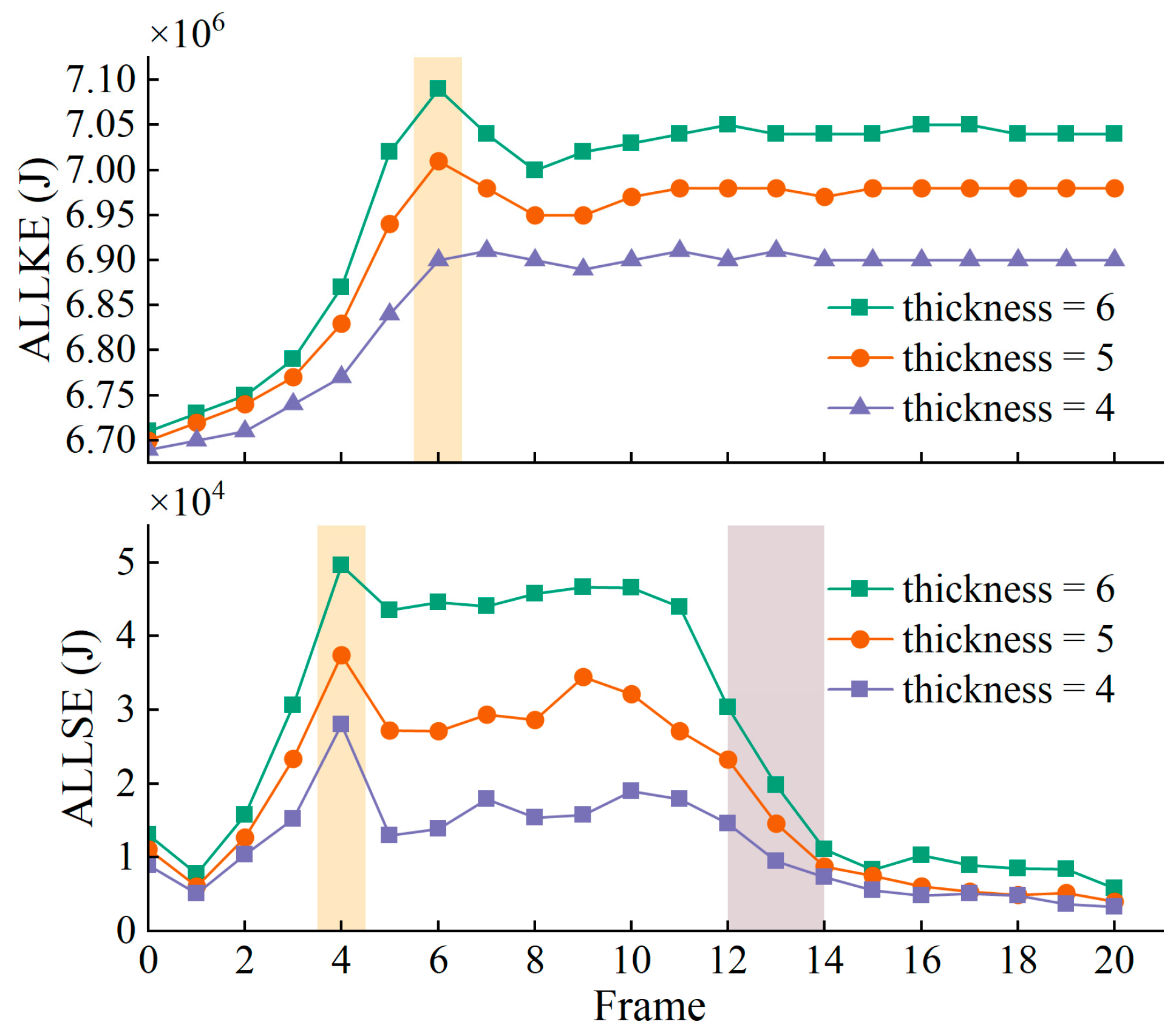
3.1.2. The Effect of Veneer Thickness in Defibering
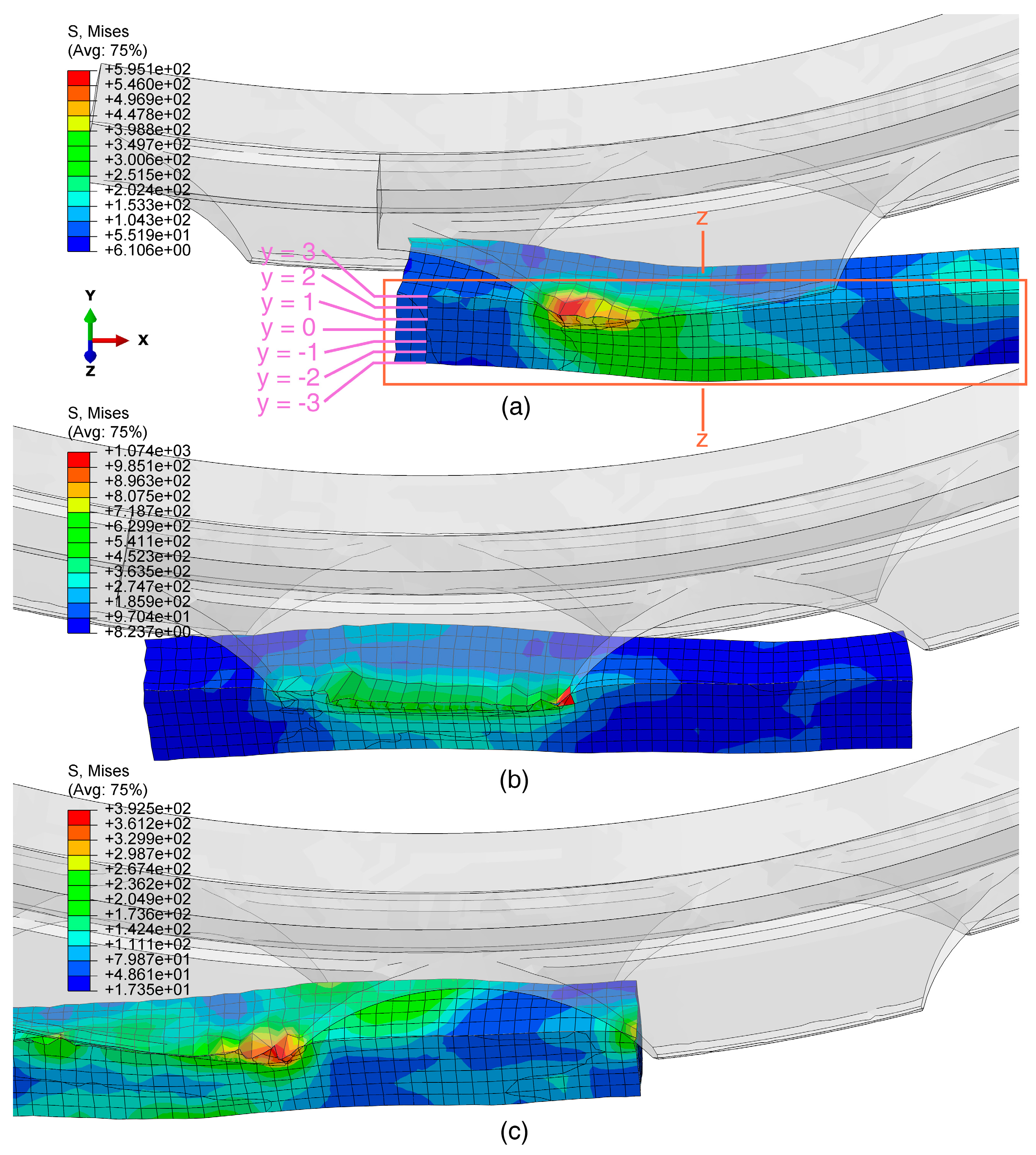
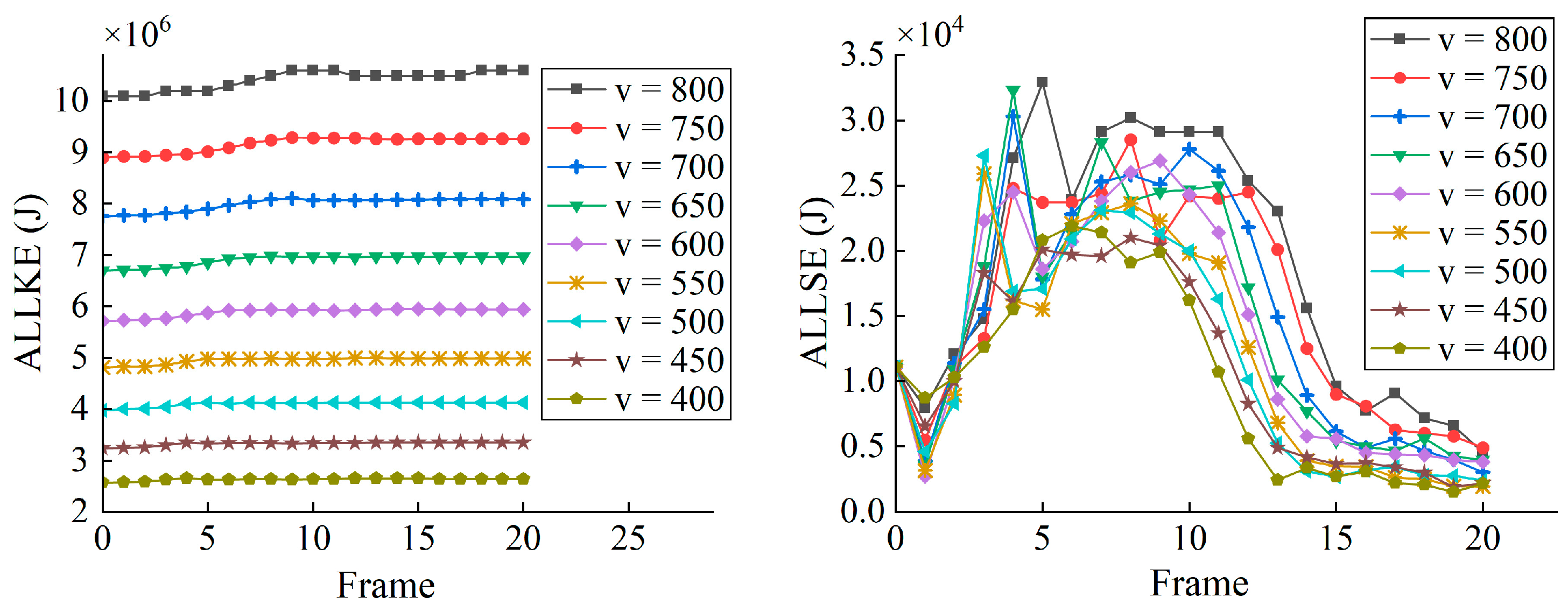
3.1.3. The Effect of Roller Velocity in Defibering
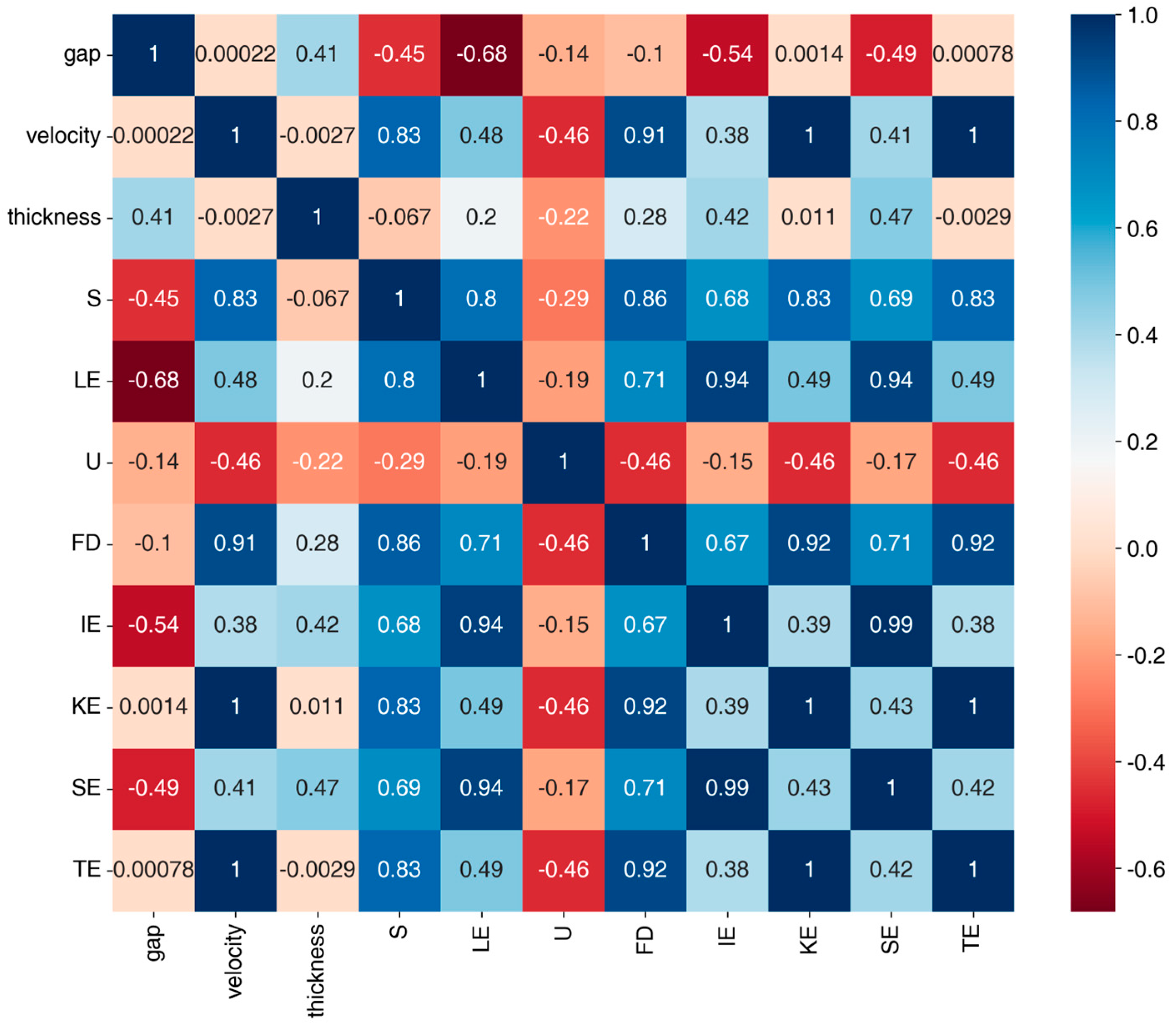
3.2. Feature Selection and Prediction Results Analysis
3.2.1. Dataset Generation and Modes Creation
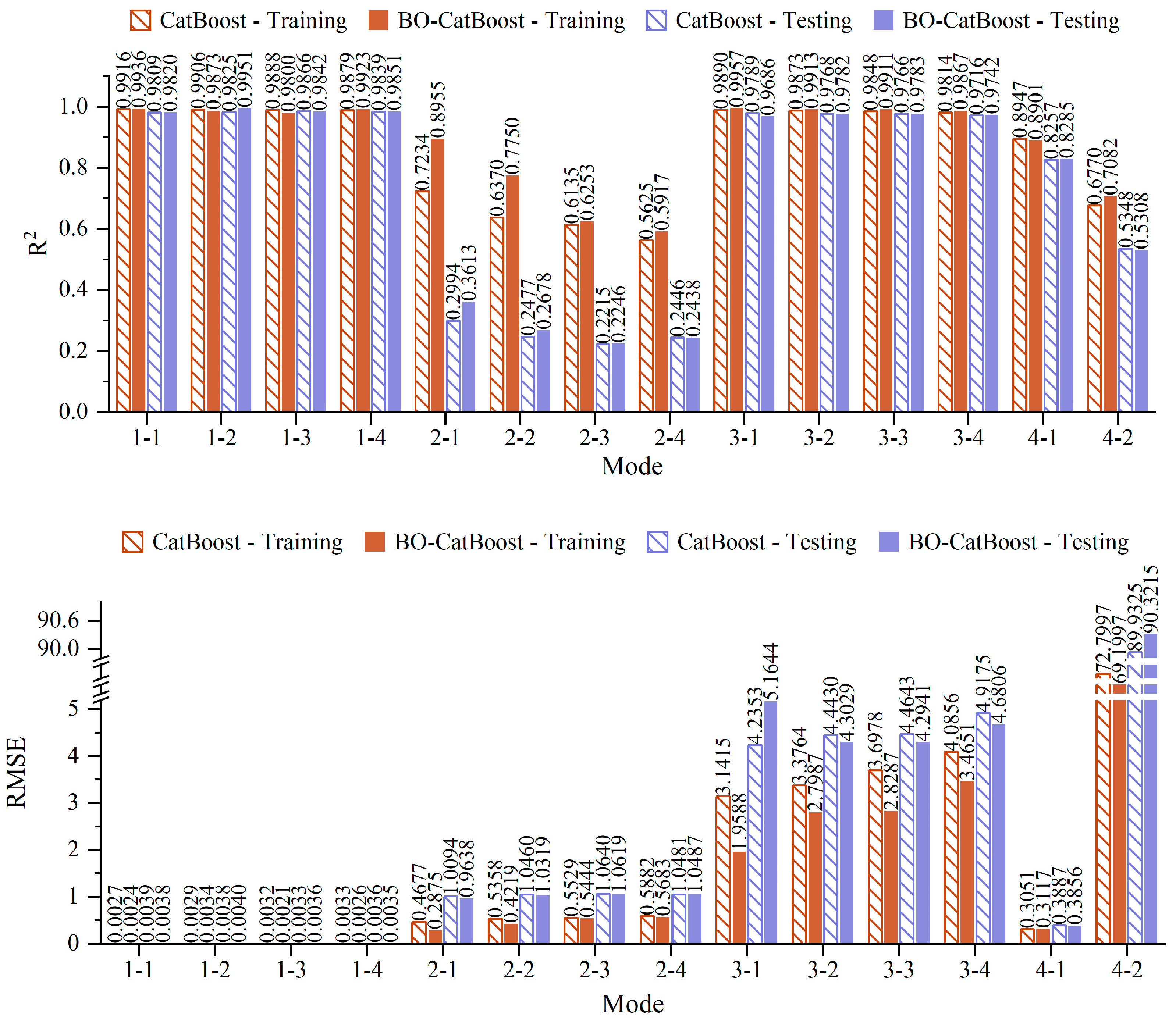
3.2.2. Performance Analysis Before and After Hyperparameter Optimization
3.2.3. Interpretability Analysis Using SHAP Values
4. Conclusions and Prospects
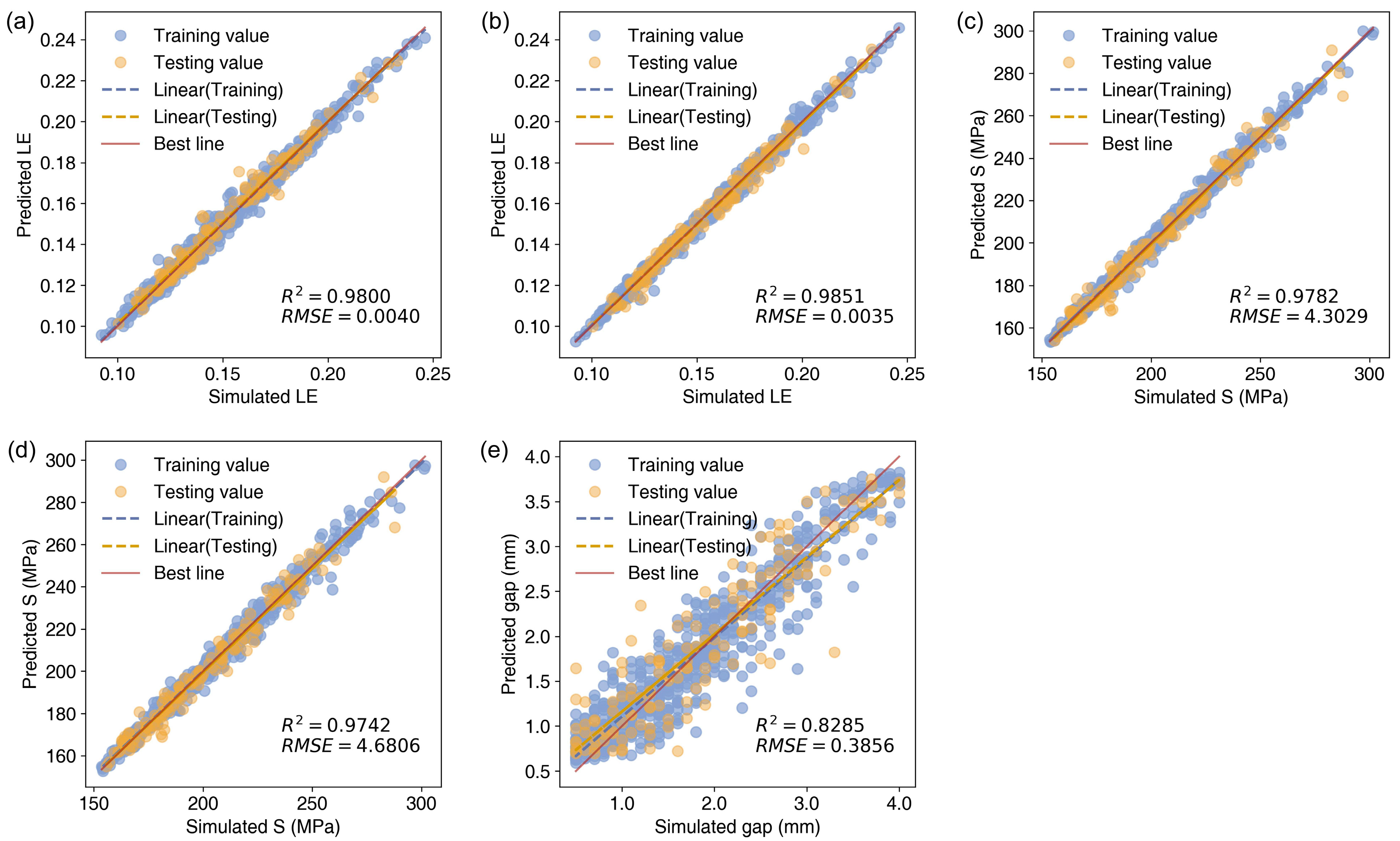
- BO-CatBoost improved the model performance to varying degrees, significantly improving the and generalization of the model and reducing the prediction error.
- The model demonstrated notable efficacy in strain prediction, attaining an of 0.98 for both the training and test sets, with a mean value of 0.9 or greater for the 5-fold cross-validation results. The for stress prediction also reached 0.97. However, the 5-fold cross-validation results indicated that the model’s generalization ability required improvement.
- In practical applications, the roller gap prediction may also take into account factors such as the tree species, the moisture content of the veneer, and changes in width and thickness before and after defibering. Despite there being few features related to roller gap prediction in the current simulation, the method demonstrated excellent prediction performance, thereby underscoring its potential for application in intelligent decision-making systems.
- By reducing the number of input features when predicting the same goal, it was possible to analyze the correlation between features. The model was also observed to exhibit reduced complexity and enhanced execution efficiency while maintaining the fundamental performance characteristics. The optimal input feature combinations were Mode 1-4 and Mode 3-4.
- The analysis of the input characteristics of the prediction model based on the SHAP algorithm revealed that the influence of different variables varies across different models. To illustrate, roller gap exerted a considerable influence on strain, whereas roller velocity exerted a more pronounced effect on stress, and veneer thickness exerted a comparatively lesser effect on stress.
- The prediction model of veneer defibering key parameters, established by applying the BO-CatBoost algorithm, could accurately evaluate the key variables, thereby providing crucial data reference and theoretical support for the realization of online regulation of the roller defibering process.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, Y.; Ji, Y.; Yu, W. Development of Bamboo Scrimber: A Literature Review. J. Wood Sci. 2019, 65, 25. [Google Scholar] [CrossRef]
- Sun, X.; He, M.; Liang, F.; Li, Z.; Wu, L.; Sun, Y. Experimental Investigation into the Mechanical Properties of Scrimber Composite for Structural Applications. Constr. Build. Mater. 2021, 276, 122234. [Google Scholar] [CrossRef]
- Li, X.; Rao, F.; Li, N.; Lei, W.; Bao, M.; Bao, Y.; Li, L.; Duan, Z.; Zu, Q.; Zhang, Y.; et al. High-Performance Bamboo Scrimber Composite Prepared from Heat-Treated Bambusa Chungii Units with Different Resin Contents for Outdoor Use. Ind. Crops Prod. 2023, 205, 117503. [Google Scholar] [CrossRef]
- Li, X.; Li, L.; Li, N.; Bao, M.; Bao, Y.; Wu, Z.; Wang, J.; Rao, F.; Chen, Y. Sustainable Production of Engineered Bamboo Scrimber Composites for Construction and Flooring Applications. Constr. Build. Mater. 2022, 347, 128615. [Google Scholar] [CrossRef]
- Coleman, J.; Hills, S. Reconsolidated Wood Product. US Patent 4232067, 4 November 1980. [Google Scholar]
- Yu, W. Current Status and Future Trend of Science and Technology for Reconstituted Materials in China. Chin. J. Wood Sci. and Technol. 2023, 37, 1–7. [Google Scholar] [CrossRef]
- Nugroho, N.; Ando, N. Development of Structural Composite Products Made from Bamboo I: Fundamental Properties of Bamboo Zephyr Board. J. Wood Sci. 2000, 46, 68–74. [Google Scholar] [CrossRef]
- Nugroho, N.; Ando, N. Development of Structural Composite Products Made from Bamboo II: Fundamental Properties of Laminated Bamboo Lumber. J. Wood Sci. 2001, 47, 237–242. [Google Scholar] [CrossRef]
- Zhu, A.; Hong, Y.; Zhang, X.; Yu, H.; Wang, H.; Wang, Y.; Yu, W. Research Progress on Carbon Footprint of Wood/Bamboo Products Based on the Life Cycle. China For. Prod. Ind. 2023, 60, 83–87. [Google Scholar] [CrossRef]
- Gao, Q.; Lin, Q.; Huang, Y.; Hu, J.; Yu, W. High-Performance Wood Scrimber Prepared by a Roller-Pressing Impregnation Method. Constr. Build. Mater. 2023, 368, 130404. [Google Scholar] [CrossRef]
- Yang, N.; Zhang, Y. Technological Innovation for Bamboo Scrimber and Its Key Technical Problems Faced. World Bamboo Rattan 2021, 19, 64–68. [Google Scholar]
- Wang, Q.; Zhang, Y.; Yan, C.; Liu, Z.; Wang, X. Research Status of the Scrimber Roller Press Equipment and System Intelligent Development Trend. World For. Res. 2024, 37, 74–79. [Google Scholar] [CrossRef]
- Adachi, K.; Inoue, M.; Kawai, S. Deformation Behavior of Wood by Roller Pressing. Mokuzai Gakkaishi 2005, 51, 234–242. [Google Scholar] [CrossRef]
- Kocovic, V.; Dzunic, D.; Kostic, S.; Brzakovic, L.; Tadic, B.; Prica, M.; Vukelic, D. Investigation into the Effects of Roller Pressing on Hardness, Roughness and Elastic Modulus of Wooden Workpieces. Appl. Sci. 2022, 12, 5575. [Google Scholar] [CrossRef]
- Zhou, S.-R.; Shi, L.-L.; Xiong, G.; Kang, S.-B.; Qin, Y.-L.; Yan, H.-Q. Global Buckling Behaviour of Bamboo Scrimber Box Columns under Axial Compression: Experimental Tests and Numerical Modelling. J. Build. Eng. 2023, 63, 105435. [Google Scholar] [CrossRef]
- Wei, Y.; Tang, S.; Ji, X.; Zhao, K.; Li, G. Stress-Strain Behavior and Model of Bamboo Scrimber under Cyclic Axial Compression. Eng. Struct. 2020, 209, 110279. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, L.; Qu, P.; Li, S.; Jiang, Z.; Li, W. Surface Texture Transfer in Skin-Pass Rolling with the Effect of Roll Surface Wear. Wear 2021, 476, 203764. [Google Scholar] [CrossRef]
- Yang, Z.; Deng, X.; Li, Z. Numerical Modeling of Dynamic Frictional Rolling Contact with an Explicit Finite Element Method. Tribol. Int. 2019, 129, 214–231. [Google Scholar] [CrossRef]
- Song, J.; Lan, J.; Zhu, L.; Jiang, Z.; Zhang, Z.; Han, J.; Ma, C. Finite Element Simulation and Microstructural Analysis of Roll Forming for DP590 High-Strength Dual-Phase Steel Wheel Rims. Materials 2024, 17, 3795. [Google Scholar] [CrossRef]
- Yu, J.; Zhangzhong, L.; Lan, R.; Zhang, X.; Xu, L.; Li, J. Ensemble Learning Simulation Method for Hydraulic Characteristic Parameters of Emitters Driven by Limited Data. Agronomy 2023, 13, 986. [Google Scholar] [CrossRef]
- Cherif, E.K.; Lucas, R.; Ait Tchakoucht, T.; Gama, I.; Ribeiro, I.; Domingos, T.; Proença, V. Predicting Fractional Shrub Cover in Heterogeneous Mediterranean Landscapes Using Machine Learning and Sentinel-2 Imagery. Forests 2024, 15, 1739. [Google Scholar] [CrossRef]
- Mienye, I.D.; Sun, Y.; Wang, Z. Prediction Performance of Improved Decision Tree-Based Algorithms: A Review. Procedia Manuf. 2019, 35, 698–703. [Google Scholar] [CrossRef]
- Nguyen, N.-H.; Tong, K.T.; Lee, S.; Karamanli, A.; Vo, T.P. Prediction Compressive Strength of Cement-Based Mortar Containing Metakaolin Using Explainable Categorical Gradient Boosting Model. Eng. Struct. 2022, 269, 114768. [Google Scholar] [CrossRef]
- Hancock, J.; Khoshgoftaar, T.M. CatBoost for Big Data: An Interdisciplinary Review. J. Big Data 2020, 7, 94. [Google Scholar] [CrossRef]
- Islam, A.M.; Masud, F.B.; Ahmed, M.R.; Jafar, A.I.; Ullah, J.R.; Islam, S.; Shatabda, S.; Islam, A.K.M.M. An Attention-Guided Deep-Learning-Based Network with Bayesian Optimization for Forest Fire Classification and Localization. Forests 2023, 14, 2080. [Google Scholar] [CrossRef]
- Ma, Y.; Xu, Q.; Yang, C. Cutting principle and mechanical analysis of scrimber rolling fluffer. Wood Process. Mach. 2016, 27, 698. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased Boosting with Categorical Features. arXiv 2019, arXiv:1706.09516. [Google Scholar]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A Comparative Analysis of Gradient Boosting Algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Hassanali, M.; Soltanaghaei, M.; Javdani Gandomani, T.; Zamani Boroujeni, F. Software Development Effort Estimation Using Boosting Algorithms and Automatic Tuning of Hyperparameters with Optuna. J. Softw. Evol. Process 2024, 36, e2665. [Google Scholar] [CrossRef]
- Kong, Q.; He, C.; Liao, L.; Xu, J.; Yuan, C. Hyperparameter Optimization for Interfacial Bond Strength Prediction between Fiber-Reinforced Polymer and Concrete. Structures 2023, 51, 573–601. [Google Scholar] [CrossRef]
- Levesque, J.-C.; Durand, A.; Gagne, C.; Sabourin, R. Bayesian Optimization for Conditional Hyperparameter Spaces. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 286–293. [Google Scholar] [CrossRef]
- Sjöberg, A.; Önnheim, M.; Gustavsson, E.; Jirstrand, M. Architecture-Aware Bayesian Optimization for Neural Network Tuning. In Artificial Neural Networks and Machine Learning—ICANN 2019: Deep Learning; Tetko, I.V., Kůrková, V., Karpov, P., Theis, F., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2019; Volume 11728, pp. 220–231. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Gupta, S.; Rana, S.; Venkatesh, S. Stable Bayesian Optimization. In Advances in Knowledge Discovery and Data Mining; Kim, J., Shim, K., Cao, L., Lee, J.-G., Lin, X., Moon, Y.-S., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2017; Volume 10235, pp. 578–591. [Google Scholar] [CrossRef]
- Hebbal, A.; Balesdent, M.; Brevault, L.; Melab, N.; Talbi, E.-G. Deep Gaussian Process for Multi-Objective Bayesian Optimization. Optim. Eng. 2023, 24, 1809–1848. [Google Scholar] [CrossRef]
- He, B.; Zhang, S.; Yang, F.; Yan, C.; Zhou, D.; Zeng, X. An Efficient Bayesian Optimization Approach for Analog Circuit Synthesis via Sparse Gaussian Process Modeling. In Proceedings of the 2020 Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 9–13 March 2020; pp. 67–72. [Google Scholar] [CrossRef]
- Vasinek, M.; Plato, J.; Snasel, V. Limitations on Low Variance K-Fold Cross Validation in Learning Set of Rules Inducers. In Proceedings of the 2016 International Conference on Intelligent Networking and Collaborative Systems (INCoS), Ostrava, Czech Republic, 7–9 September 2016; pp. 207–214. [Google Scholar] [CrossRef]
- Yu, S.; Gu, C.; Liu, W.; O’Neill, M. Deep Learning-Based Hardware Trojan Detection with Block-Based Netlist Information Extraction. IEEE Trans. Emerg. Top. Comput. 2022, 10, 1837–1853. [Google Scholar] [CrossRef]
- Lundberg, S.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. arXiv 2017, arXiv:1705.07874. [Google Scholar]
- Liu, F.; Wang, X.; Li, T.; Huang, M.; Hu, T.; Wen, Y.; Su, Y. An Automated and Interpretable Machine Learning Scheme for Power System Transient Stability Assessment. Energies 2023, 16, 1956. [Google Scholar] [CrossRef]
- Rastgoo, A.; Khajavi, H. A Novel Study on Forecasting the Airfoil Self-Noise, Using a Hybrid Model Based on the Combination of CatBoost and Arithmetic Optimization Algorithm. Expert Syst. Appl. 2023, 229, 120576. [Google Scholar] [CrossRef]
- Huang, R.; Ni, J.; Qiao, P.; Wang, Q.; Shi, X.; Yin, Q. An Explainable Prediction Model for Aerodynamic Noise of an Engine Turbocharger Compressor Using an Ensemble Learning and Shapley Additive Explanations Approach. Sustainability 2023, 15, 13405. [Google Scholar] [CrossRef]
- Feng, Z.; Champliaud, H. Analyses of Profile Radial-Axial Ring Rolling Process Based on Explicit Finite Element Method. In Volume 2: Computer Technology and Bolted Joints; American Society of Mechanical Engineers: Anaheim, CA, USA, 2014; p. V002T02A013. [Google Scholar] [CrossRef]




| (MPa) | (MPa) | (MPa) | (MPa) | (MPa) | (MPa) | |||
|---|---|---|---|---|---|---|---|---|
| 4170 | 900 | 480 | 700 | 620 | 170 | 0.13 | 0.7 | 0.75 |
| Properties | Parts | Types | Value |
|---|---|---|---|
| Geometrical features | Veneer | Length | 50 mm |
| Thickness | 4–6 mm | ||
| Width | 15 mm | ||
| Rollers | Radius | 95 mm | |
| Depth | 30 mm | ||
| Materials | Veneer | - | Table 1 shows |
| Defibering roller | - | Q345 | |
| Friction roller | - | 45# steel | |
| Mesh | Veneer | - | Tetrahedral mesh |
| Defibering roller | - | Tetrahedral mesh (medial axis algorithm) | |
| Friction roller | - | Hexahedral unit | |
| Maxps Damage | Veneer | Max Principal Stress | 100 Mpa |
| Damage Stabilization Cohesive | 1 × 10−5 | ||
| Tangential Behavior | Veneer and Rollers | Friction Coeff | 0.5 |
| Analysis step | - | - | Dynamic, Explicit |
| Load | Veneer (transverse section direction) | pressure | 100 Mpa |
| Defibering roller | Z-axis rotation | −400–−800 mm/s | |
| Friction roller | Z-axis rotation | 400–800 mm/s |
| Parameters | Type | Range Value | Explanations |
|---|---|---|---|
| iterations | int | [500, 1500] | Determines the number of gradient lifting of the algorithm. |
| learning_rate | float | [0.02, 0.5] | Helps the algorithm to better control the contribution of weak learners in each iteration, improving the accuracy of the overall model. |
| depth | int | [4, 10] | Controls the depth of the tree to be used. |
| l2_leaf_reg | float | [1, 10] | Controls the degree of regularization of the model to avoid overfitting. |
| rsm | float | [0.6, 1.0] | Able to add diversity to the model training process to improve the accuracy of the model. |
| random_seed | int | [100, 500] | Can control the initialization state of the stochastic process used to ensure the reproducibility of the experiment. |
| subsample | float | [0.6, 1.0] | Used primarily for data sampling to reduce the risk of model overfitting and improve model generalization. |
| Veneer Thickness (mm) | Roller Velocity (mm/s) | ROLLER Gap (mm) | Simulation Result Array |
|---|---|---|---|
| 4 | [400, 800, 50] | [0.5, 2, 0.1] | 9 × 16 = 144 |
| 5 | [400, 800, 50] | [0.5, 3, 0.1] | 9 × 26 = 234 |
| 6 | [400, 800, 50] | [0.5, 4, 0.1] | 9 × 36 = 324 |
| Variables | Symbol | Unit | Minimum | Maximum | Mean | Standard Deviation |
|---|---|---|---|---|---|---|
| Roller gap | gap | mm | 0.50 | 4.00 | 1.88 | 0.94 |
| Roller velocity | velocity | mm/s | 400.00 | 800.00 | 600.21 | 129.16 |
| Veneer thickness | thickness | mm | 4.00 | 6.00 | 5.26 | 0.77 |
| Maximum principal stress | S | Mpa | 153.59 | 301.60 | 205.18 | 29.88 |
| Maximum principal strain | LE | - | 0.09 | 0.25 | 0.15 | 0.03 |
| Spatial displacement | U | mm | 0.18 | 5.66 | 1.41 | 0.97 |
| Frictional dissipation | FD | J | 20,340.77 | 186,125.41 | 83,960.99 | 39,101.63 |
| Internal energy | IE | J | 7787.11 | 79,670.33 | 27,514.78 | 13,554.63 |
| Kinetic energy | KE | J | 2,607,400.00 | 10,547,661.90 | 6,175,309.59 | 2,532,188.00 |
| Strain energy | SE | J | 5555.07 | 42,857.25 | 17,223.59 | 7163.84 |
| Total energy | TE | J | 2,508,794.00 | 10,073,704.76 | 5,930,829.35 | 2,450,048.91 |
| Mode Labels | Gap | Velocity | Thickness | S | LE | U | FD | IE | KE | SE | TE |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mode 1-1 | √ | √ | √ | √ | ★ | √ | √ | √ | √ | √ | |
| Mode 1-2 | √ | √ | √ | √ | ★ | √ | |||||
| Mode 1-3 | √ | √ | √ | √ | ★ | ||||||
| Mode 1-4 | √ | √ | √ | ★ | |||||||
| Mode 2-1 | √ | √ | √ | √ | ★ | √ | √ | √ | √ | √ | |
| Mode 2-2 | √ | √ | √ | √ | ★ | √ | |||||
| Mode 2-3 | √ | √ | √ | √ | ★ | ||||||
| Mode 2-4 | √ | √ | √ | ★ | |||||||
| Mode 3-1 | √ | √ | √ | ★ | √ | √ | √ | √ | √ | √ | |
| Mode 3-2 | √ | √ | √ | ★ | √ | √ | √ | ||||
| Mode 3-3 | √ | √ | √ | ★ | √ | ||||||
| Mode 3-4 | √ | √ | √ | ★ | |||||||
| Mode 4-1 | ★ | √ | √ | √ | |||||||
| Mode 4-2 | ★ | √ | √ | √ |
| Mode Labels | CatBoost | BO-CatBoost | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAE | MSE | RMSE | 5-Fold | MAE | MSE | RMSE | 5-Fold | |||
| Mode 1-1 | 0.9809 | 0.0027 | 0 | 0.0039 | 0.9378 | 0.9820 | 0.0027 | 0 | 0.0038 | 0.9672 |
| Mode 1-2 | 0.9825 | 0.0026 | 0 | 0.0038 | 0.9302 | 0.9800 | 0.0028 | 0 | 0.0040 | 0.9664 |
| Mode 1-3 | 0.9866 | 0.0024 | 0 | 0.0033 | 0.9021 | 0.9842 | 0.0027 | 0 | 0.0036 | 0.9228 |
| Mode 1-4 | 0.9839 | 0.0027 | 0 | 0.0036 | 0.8679 | 0.9851 | 0.0027 | 0 | 0.0035 | 0.9089 |
| Mode 2-1 | 0.2994 | 0.6569 | 1.0188 | 1.0094 | 0.1601 | 0.3613 | 0.6298 | 0.9289 | 0.9638 | 0.1705 |
| Mode 2-2 | 0.2477 | 0.6636 | 1.0940 | 1.0460 | 0.1334 | 0.2678 | 0.6552 | 1.0648 | 1.0319 | 0.0834 |
| Mode 2-3 | 0.2215 | 0.6758 | 1.1321 | 1.0640 | 0.0436 | 0.2246 | 0.6717 | 1.1276 | 1.0619 | 0.0701 |
| Mode 2-4 | 0.2446 | 0.6699 | 1.0985 | 1.0481 | 0.1500 | 0.2438 | 0.6683 | 1.0997 | 1.0487 | 0.1528 |
| Mode 3-1 | 0.9789 | 3.1608 | 17.9375 | 4.2353 | −0.0904 | 0.9686 | 3.8480 | 26.6710 | 5.1644 | 0.4175 |
| Mode 3-2 | 0.9768 | 3.2730 | 19.7403 | 4.4430 | −0.2302 | 0.9782 | 3.1775 | 18.5146 | 4.3029 | 0.3210 |
| Mode 3-3 | 0.9766 | 3.3956 | 19.9298 | 4.4643 | −0.1626 | 0.9783 | 3.2740 | 18.4391 | 4.2941 | 0.3768 |
| Mode 3-4 | 0.9716 | 3.7366 | 24.1821 | 4.9175 | −0.2905 | 0.9742 | 3.4929 | 21.9081 | 4.6806 | 0.2747 |
| Mode 4-1 | 0.8257 | 0.2950 | 0.1511 | 0.3887 | 0.7794 | 0.8285 | 0.2898 | 0.1487 | 0.3856 | 0.7825 |
| Mode 4-2 | 0.5348 | 71.0299 | 8087.8579 | 89.9325 | −17.2478 | 0.5308 | 69.1023 | 8157.977 | 90.3215 | −17.3382 |
| Mode Labels | Optimal Parameters | Default Parameters | ||||||
|---|---|---|---|---|---|---|---|---|
| Iterations | Learning_Rate | Depth | l2_leaf_reg | rsm | Random_Seed | Subsample | ||
| Mode 1-1 | 677 | 0.132 | 3 | 5.954 | 0.816 | 154 | 0.804 | ‘loss_function’: ‘RMSE’, ‘iterations’: 500, ‘learning_rate’: 0.03, ‘random_seed’: 500, ‘l2_leaf_reg’: 3, ‘subsample’: 0.6, ‘best_model_min_trees’: 50, ‘depth’: 6, ‘min_data_in_leaf’: 300, ‘one_hot_max_size’: 4, ‘rsm’: 0.6, |
| Mode 1-2 | 595 | 0.02 | 3 | 1 | 1 | 428 | 0.6 | |
| Mode 1-3 | 826 | 0.223 | 5 | 5.429 | 0.749 | 295 | 0.769 | |
| Mode 1-4 | 525 | 0.5 | 3 | 1.245 | 0.624 | 361 | 0.613 | |
| Mode 2-1 | 916 | 0.106 | 6 | 8.945 | 0.772 | 391 | 0.6 | |
| Mode 2-2 | 778 | 0.044 | 5 | 5.672 | 0.673 | 299 | 0.773 | |
| Mode 2-3 | 890 | 0.02 | 5 | 8.494 | 0.789 | 348 | 0.6 | |
| Mode 2-4 | 776 | 0.02 | 8 | 1 | 0.6 | 385 | 0.6 | |
| Mode 3-1 | 838 | 0.411 | 4 | 6.841 | 0.623 | 380 | 0.889 | |
| Mode 3-2 | 635 | 0.291 | 3 | 1.42 | 0.91 | 250 | 0.733 | |
| Mode 3-3 | 521 | 0.5 | 3 | 10 | 1 | 215 | 0.6 | |
| Mode 3-4 | 606 | 0.146 | 4 | 4.722 | 0.921 | 461 | 0.716 | |
| Mode 4-1 | 558 | 0.02 | 4 | 1.226 | 0.6 | 493 | 0.6 | |
| Mode 4-2 | 801 | 0.053 | 5 | 4.367 | 0.818 | 209 | 0.985 | |
| Prediction Modes | 1-1 | 1-2 | 1-3 | 1-4 | 3-1 | 3-2 | 3-3 | 3-4 | 4-1 |
|---|---|---|---|---|---|---|---|---|---|
| Execution Time (ms) | 979 | 639 | 1280 | 390 | 2760 | 827 | 565 | 528 | 1030 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Yan, C.; Zhang, Y.; Xu, Y.; Wang, X.; Cui, P. Numerical Simulation and Bayesian Optimization CatBoost Prediction Method for Characteristic Parameters of Veneer Roller Pressing and Defibering. Forests 2024, 15, 2173. https://doi.org/10.3390/f15122173
Wang Q, Yan C, Zhang Y, Xu Y, Wang X, Cui P. Numerical Simulation and Bayesian Optimization CatBoost Prediction Method for Characteristic Parameters of Veneer Roller Pressing and Defibering. Forests. 2024; 15(12):2173. https://doi.org/10.3390/f15122173
Chicago/Turabian StyleWang, Qi, Chenglin Yan, Yahui Zhang, Yang Xu, Xinxu Wang, and Pu Cui. 2024. "Numerical Simulation and Bayesian Optimization CatBoost Prediction Method for Characteristic Parameters of Veneer Roller Pressing and Defibering" Forests 15, no. 12: 2173. https://doi.org/10.3390/f15122173
APA StyleWang, Q., Yan, C., Zhang, Y., Xu, Y., Wang, X., & Cui, P. (2024). Numerical Simulation and Bayesian Optimization CatBoost Prediction Method for Characteristic Parameters of Veneer Roller Pressing and Defibering. Forests, 15(12), 2173. https://doi.org/10.3390/f15122173






