Simulation of Radial Growth of Mongolian Pine (Pinus sylvestris var. mongolica) and Dahurian Larch (Larix gmelinii) Using the Vaganov–Shashkin Model in the Greater Khingan Range, Northeast China
Abstract
:1. Introduction
2. Materials and Methods
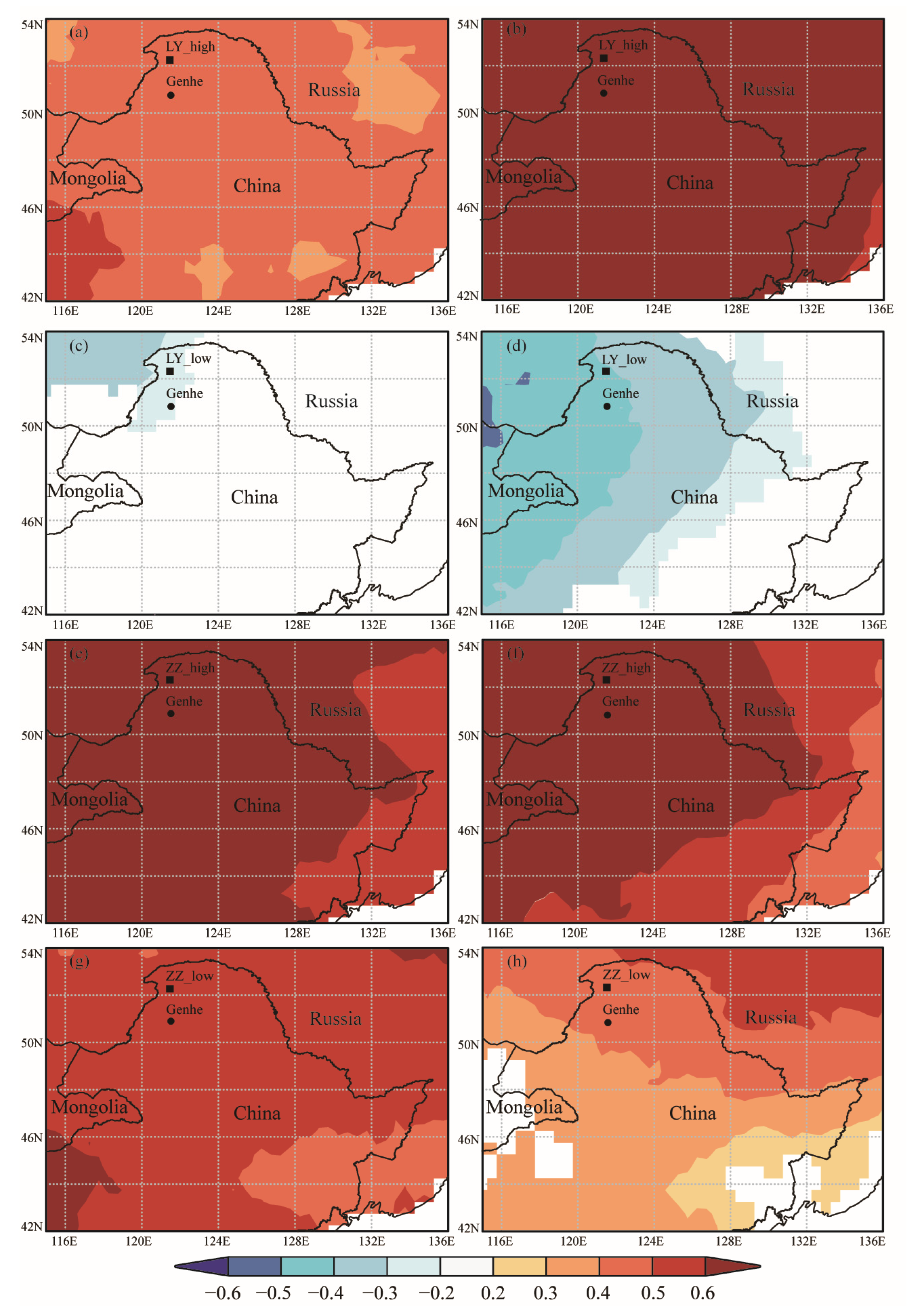
2.1. Study Area and Climate
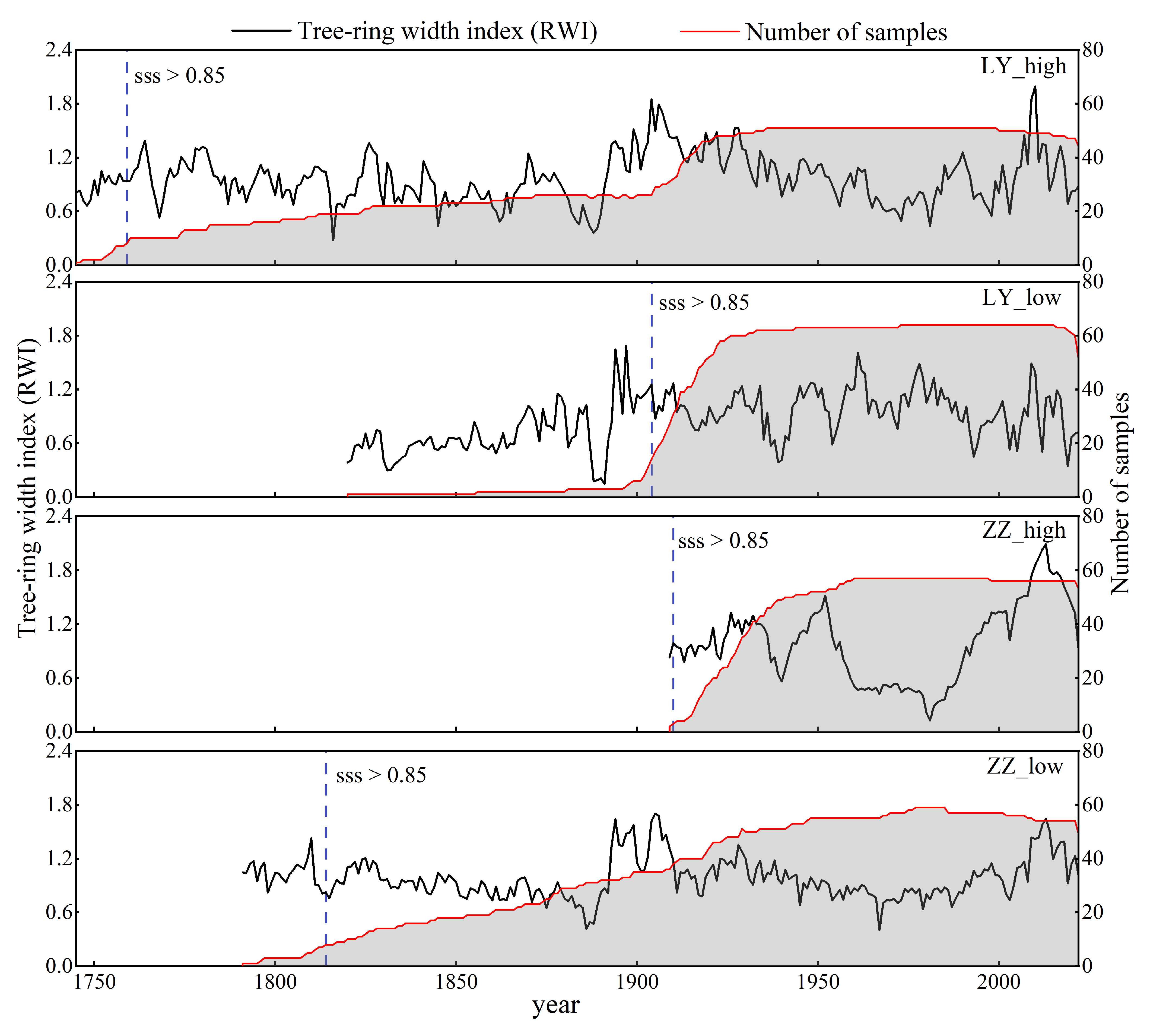
2.2. Tree-Ring Data
2.3. Vaganov–Shashkin Process-Based Model
- (a)
- Tree growth response to temperature. Tree growth begins when a suitable cumulative temperature (Tbeg) has been reached. Trees do not grow when the temperature is below the minimum growth temperature (Tmin1), and tree growth increases linearly with increasing temperatures when the temperature exceeds Tmin1 but is below the lower limit of the optimum growth temperature (Topt1). Maximum tree growth occurs when the temperature is between Topt1 and the upper limit of the Topt2. When the temperature exceeds Topt2 but is less than the maximum growth temperature (Tmax), the tree growth decreases linearly with an increase in temperature.
- (b)
- Tree growth response to soil moisture. The response of tree growth to soil moisture is similar to that of temperature. Four parameters are used (Wmin1, Wopt1, Wopt2, and Wmax) with a complicated calculation process. The daily change in the soil water content dW is expressed by the soil dynamic equilibrium equation:
- (c)
- Tree growth response to sunlight. The sunlight-influenced tree growth rate, (ignoring the Earth’s eccentricity as it orbits the sun and atmospheric transmittance), is expressed in terms of the latitude (φ), angle of incidence of the sun (θ), and day length (Φ) as follows:
2.4. Simulation Process and Parameter Selection
3. Results
3.1. Process Model Results
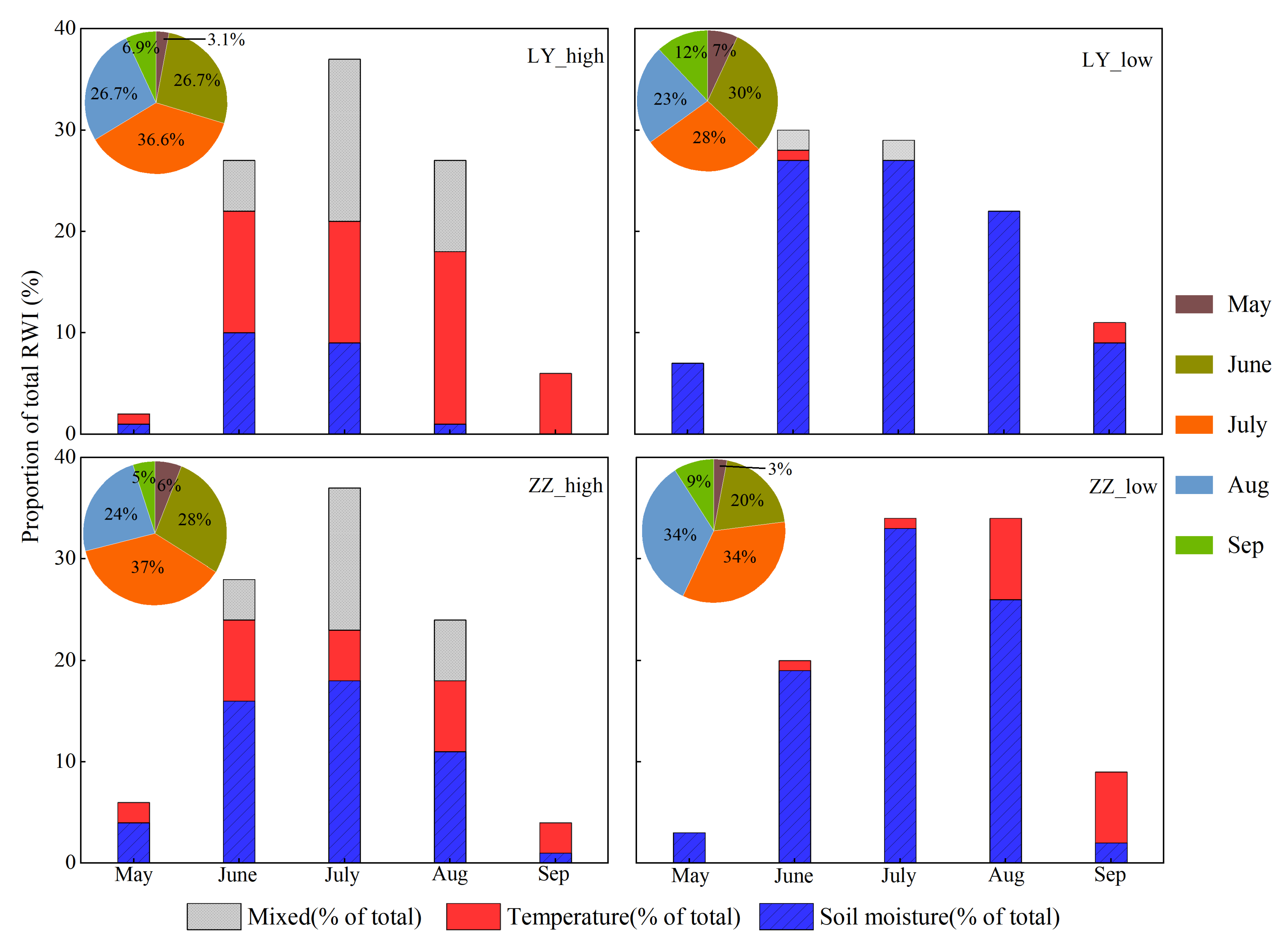
3.2. Standardized Chronology and Tree Response to Climatic Factors Analysis
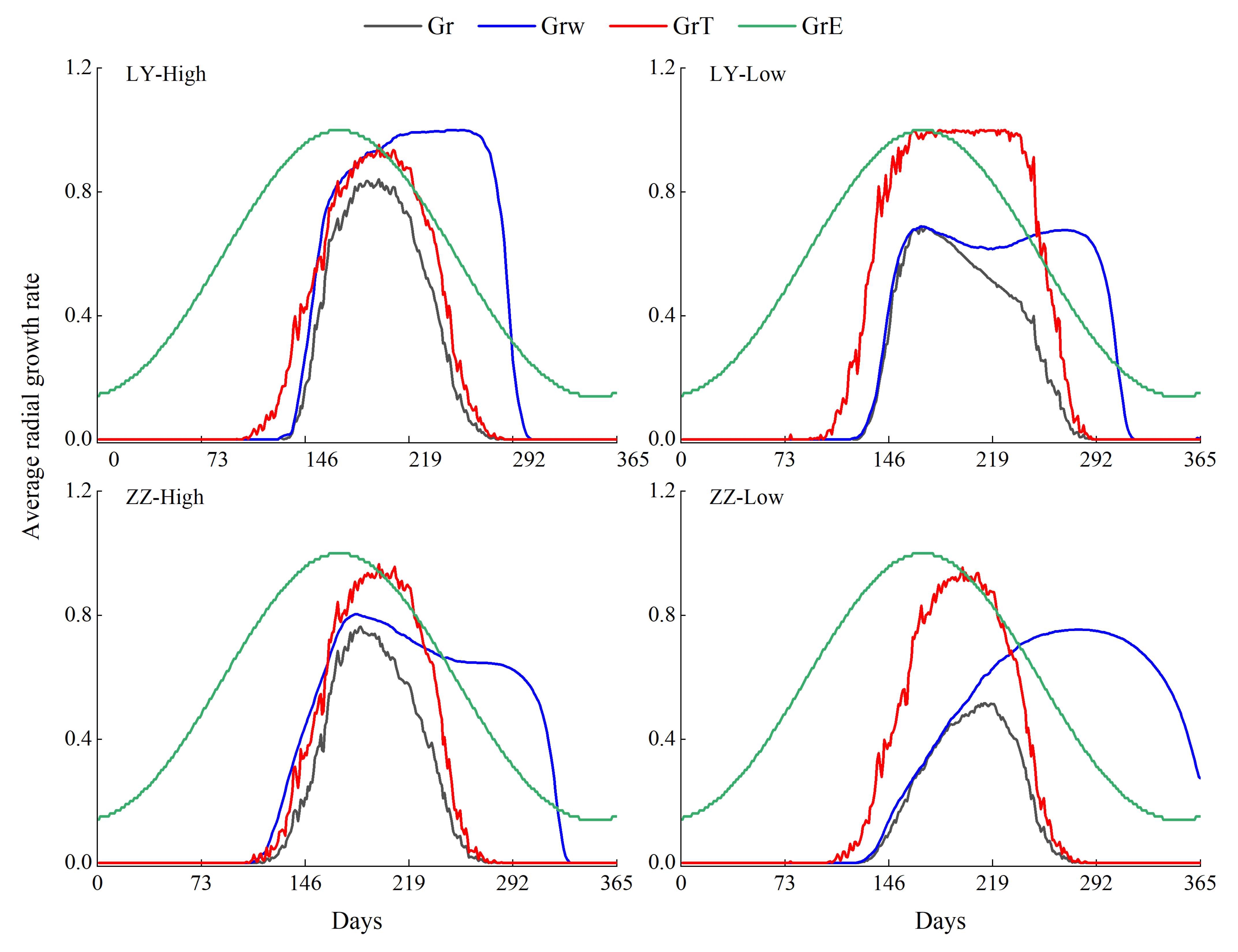
3.3. Radial Growth Rate and Growth Start and Cessation Dates
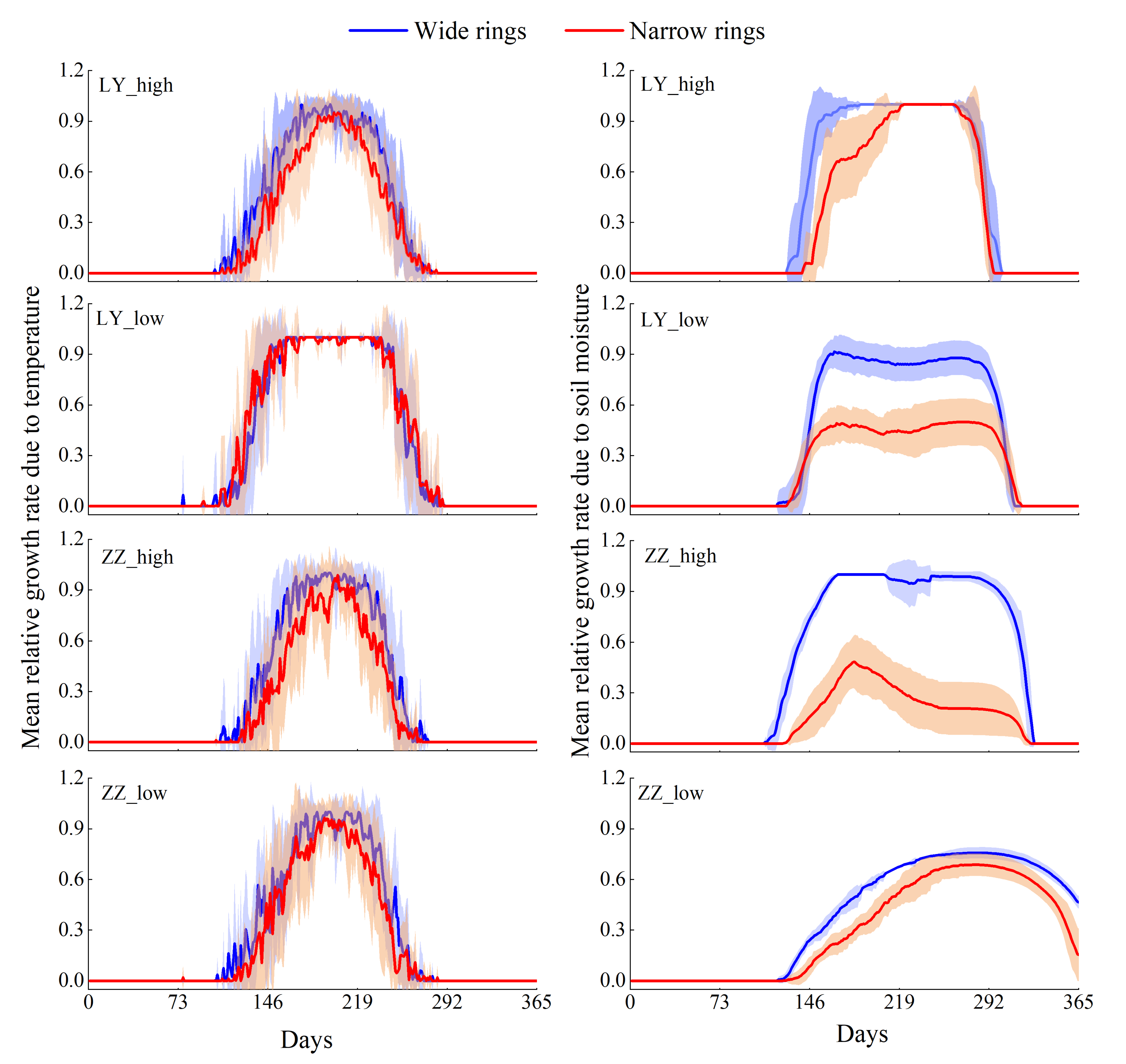
3.4. Intra-Annual Comparison of Wide and Narrow Rings
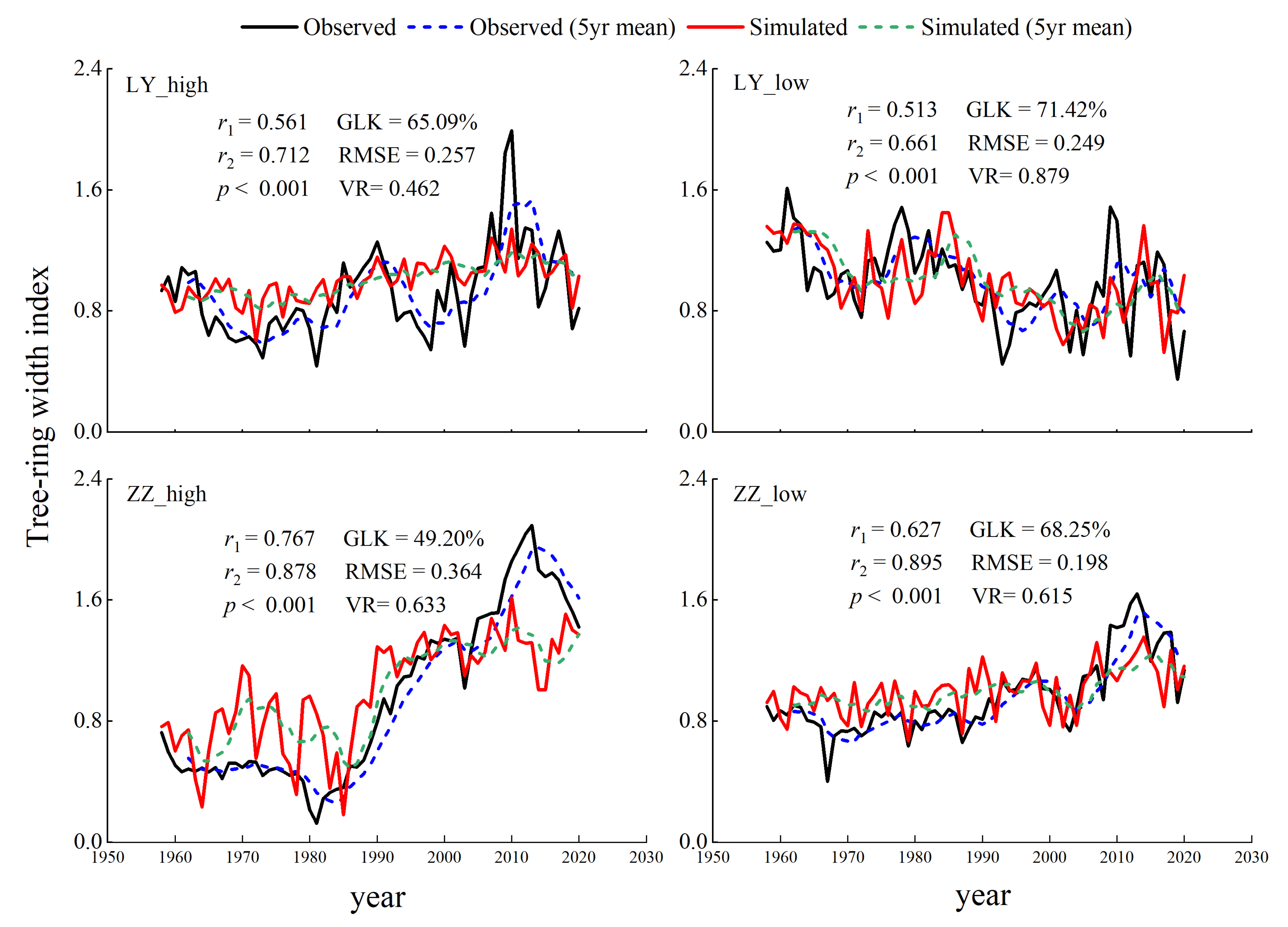
3.5. Validation of the RWI
4. Discussion
4.1. Tree Physiological Parameters
4.2. Growth Rate and Phenological Period
4.3. Limiting Climatic Factors
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiao, L.; Wang, D. Climate change, the evaporation paradox, and their effects on streamflow in Lijiang watershed. Pol. J. Environ. Stud. 2018, 27, 2585–2591. [Google Scholar] [CrossRef]
- Alkama, R.; Cescatti, A. Biophysical climate impacts of recent changes in global forest cover. Science 2016, 351, 600–604. [Google Scholar] [CrossRef]
- Zhao, K.; Jackson, R.B. Biophysical forcings of land-use changes from potential forestry activities in North America. Ecol. Monogr. 2014, 84, 329–353. [Google Scholar] [CrossRef]
- Engelbrecht, B.M. Forests on the brink. Nature 2012, 491, 675–676. [Google Scholar] [CrossRef]
- Allen, C.D.; Macalady, A.K.; Chenchouni, H.; Bachelet, D.; McDowell, N.; Vennetier, M.; Kitzberger, T.; Rigling, A.; Breshears, D.D.; Hogg, E.T. A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manag. 2010, 259, 660–684. [Google Scholar] [CrossRef]
- Meng, Y.; Liu, X.; Ding, C.; Xu, B.; Zhu, L. Analysis of ecological resilience to evaluate the inherent maintenance capacity of a forest ecosystem using a dense Landsat time series. Ecol. Inform. 2020, 57, 101064. [Google Scholar] [CrossRef]
- Sánchez-Salguero, R.; Camarero, J.J.; Gutiérrez, E.; Gonzalez Rouco, F.; Gazol, A.; Sangüesa-Barreda, G.; Andreu-Hayles, L.; Linares, J.C.; Seftigen, K. Assessing forest vulnerability to climate warming using a process-based model of tree growth: Bad prospects for rear-edges. Glob. Chang. Biol. 2017, 23, 2705–2719. [Google Scholar] [CrossRef] [PubMed]
- Qi, Z.; Liu, H.; Wu, X.; Hao, Q. Climate-driven speedup of alpine treeline forest growth in the Tianshan Mountains, Northwestern China. Glob. Chang. Biol. 2015, 21, 816–826. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Yin, Y.; Hao, Q.; Liu, G. Sensitivity of temperate vegetation to Holocene development of East Asian monsoon. Quat. Sci. Rev. 2014, 98, 126–134. [Google Scholar] [CrossRef]
- Drobyshev, I.; Gewehr, S.; Berninger, F.; Bergeron, Y. Species specific growth responses of black spruce and trembling aspen may enhance resilience of boreal forest to climate change. J. Ecol. 2013, 101, 231–242. [Google Scholar] [CrossRef]
- Soh, W.K.; Yiotis, C.; Murray, M.; Parnell, A.; Wright, I.J.; Spicer, R.A.; Lawson, T.; Caballero, R.; McElwain, J.C. Rising CO2 drives divergence in water use efficiency of evergreen and deciduous plants. Sci. Adv. 2019, 5, eaax7906. [Google Scholar] [CrossRef]
- Fritts, H. Tree Rings and Climate; Academic Press Inc.: London, UK, 1976; Volume 562. [Google Scholar]
- Mann, M.E.; Jones, P.D. Global surface temperatures over the past two millennia. Geophys. Res. Lett. 2003, 30, 1–4. [Google Scholar] [CrossRef]
- Zhang, Z. Tree-rings, a key ecological indicator of environment and climate change. Ecol. Indic. 2015, 51, 107–116. [Google Scholar] [CrossRef]
- Hughes, M.K. Dendrochronology in climatology–the state of the art. Dendrochronologia 2002, 20, 95–116. [Google Scholar] [CrossRef]
- Zhang, R.; Yuan, Y.; Wei, W.; He, Q.; Shang, H.; Zhang, T.; Zhao, Y. Changes of wet and dry in the past hundred years in eastern Kyrgyzstan by tree-ring. Arid Land Geogr. 2013, 36, 691–699. [Google Scholar] [CrossRef]
- Saladyga, T.; Maxwell, R.S. Temporal variability in climate response of eastern hemlock in the Central Appalachian Region. Southeast. Geogr. 2015, 55, 143–163. [Google Scholar] [CrossRef]
- D’Arrigo, R.; Wilson, R.; Liepert, B.; Cherubini, P. On the ‘divergence problem’in northern forests: A review of the tree-ring evidence and possible causes. Glob. Planet. Chang. 2008, 60, 289–305. [Google Scholar] [CrossRef]
- Wilmking, M.; Juday, G.P.; Barber, V.A.; Zald, H.S. Recent climate warming forces contrasting growth responses of white spruce at treeline in Alaska through temperature thresholds. Glob. Chang. Biol. 2004, 10, 1724–1736. [Google Scholar] [CrossRef]
- Wu, G.; Xu, G.; Chen, T.; Liu, X.; Zhang, Y.; An, W.; Wang, W.; Fang, Z.-a.; Yu, S. Age-dependent tree-ring growth responses of Schrenk spruce (Picea schrenkiana) to climate—A case study in the Tianshan Mountain, China. Dendrochronologia 2013, 31, 318–326. [Google Scholar] [CrossRef]
- Schwab, N.; Kaczka, R.J.; Janecka, K.; Böhner, J.; Chaudhary, R.P.; Scholten, T.; Schickhoff, U. Climate change-induced shift of tree growth sensitivity at a central Himalayan treeline ecotone. Forests 2018, 9, 267. [Google Scholar] [CrossRef]
- Cook, E.R.; Kairiukstis, L.A. Methods of Dendrochronology: Applications in the Environmental Sciences; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Wu, Y.; Gan, M.; Yu, R.; Yang, M.; Guo, Y.; Zhao, P. Process-based modeling radial growth of Picea schrenkiana in the eastern Tianshan Mountains. Arid Land Geogr. 2020, 43, 64–71. [Google Scholar] [CrossRef]
- Zhang, Y.; Shao, X.; Xu, Y.; Wilmking, M. Process-based modeling analyses of Sabina przewalskii growth response to climate factors around the northeastern Qaidam Basin. Chin. Sci. Bull. 2011, 56, 1518–1525. [Google Scholar] [CrossRef]
- Anchukaitis, K.; Evans, M.; Kaplan, A.; Vaganov, E.; Hughes, M.; Grissino-Mayer, H.; Cane, M. Forward modeling of regional scale tree-ring patterns in the southeastern United States and the recent influence of summer drought. Geophys. Res. Lett. 2006, 33, 347–360. [Google Scholar] [CrossRef]
- Touchan, R.; Shishov, V.; Meko, D.; Nouiri, I.; Grachev, A. Process based model sheds light on climate sensitivity of Mediterranean tree-ring width. Biogeosciences 2012, 9, 965–972. [Google Scholar] [CrossRef]
- Shishov, V.V.; Tychkov, I.I.; Popkova, M.I.; Ilyin, V.A.; Bryukhanova, M.V.; Kirdyanov, A.V. VS-oscilloscope: A new tool to parameterize tree radial growth based on climate conditions. Dendrochronologia 2016, 39, 42–50. [Google Scholar] [CrossRef]
- Fritts, H.; Shashkin, A.; Downes, G. A simulation model of conifer ring growth and cell structure. In Tree-Ring Analysis: Biological, Methodological and Environmental Aspects; CABI Publishing: Wallingford, UK, 1999; pp. 3–32. [Google Scholar]
- Vaganov, E. Analysis of a seasonal growth patterns of trees and modelling in dendrochronology. Tree-Rings Clim. Humanit. Radiocarb. 1996, 1996, 73–87. [Google Scholar]
- Zhang, Y.; Shao, X.; Xu, Y.; WILMKING, M. Response processes of Qilian cypress to climatic factors at the northeastern edge of Qaidam simulated by physiological modeling. Chin. Sci. Bull. 2011, 56, 975–982. [Google Scholar]
- Chen, L.; Huang, J.-G.; Stadt, K.J.; Comeau, P.G.; Zhai, L.; Dawson, A.; Alam, S.A. Drought explains variation in the radial growth of white spruce in western Canada. Agric. For. Meteorol. 2017, 233, 133–142. [Google Scholar] [CrossRef]
- Sánchez-Salguero, R.; Camarero, J.J.; Rozas, V.; Génova, M.; Olano, J.M.; Arzac, A.; Gazol, A.; Caminero, L.; Tejedor, E.; de Luis, M. Resist, recover or both? Growth plasticity in response to drought is geographically structured and linked to intraspecific variability in Pinus pinaster. J. Biogeogr. 2018, 45, 1126–1139. [Google Scholar] [CrossRef]
- Tumajer, J.; Altman, J.; Štěpánek, P.; Treml, V.; Doležal, J.; Cienciala, E. Increasing moisture limitation of Norway spruce in Central Europe revealed by forward modelling of tree growth in tree-ring network. Agric. For. Meteorol. 2017, 247, 56–64. [Google Scholar] [CrossRef]
- Shi, J.; Liu, Y.; Vaganov, E.A.; Li, J.; Cai, Q. Statistical and process-based modeling analyses of tree growth response to climate in semi-arid area of north central China: A case study of Pinus tabulaeformis. J. Geophys. Res. Biogeosci 2008, 113, 1–10. [Google Scholar] [CrossRef]
- Zhang, J.; Gou, X.; Zhang, Y.; Lu, M.; Xu, X.; Zhang, F.; Liu, W.; Gao, L. Forward modeling analyses of Qilian Juniper (Sabina przewalskii) growth in response to climate factors in different regions of the Qilian Mountains, northwestern China. Trees 2016, 30, 175–188. [Google Scholar] [CrossRef]
- Xiao-Ying, W.; Chun-Yu, Z.; Qing-Yu, J. Impacts of climate change on forest ecosystems in Northeast China. Adv. Clim. Chang. Res. 2013, 4, 230–241. [Google Scholar] [CrossRef]
- Luo, X.; Liang, Y.; He, H.; Hang, C.; Zhang, Q. Long-term effects of climate change and different silvicultural strategies on stand information and aboveground biomass of forest major species in the Great Xing’an Mountains. Acta Ecol. Sin. 2019, 39, 7656–7669. [Google Scholar] [CrossRef]
- Xie, A.; Suan, Y.; Bai, R. Arid Climate Trend over Northeastern China and Its Response to Global Warming. Acta Geogr. Sin. 2003, 58, 75–82. [Google Scholar] [CrossRef]
- Guo, X.; Wang, Z.; Zhang, N.; Zhang, D. Responses of radial growth of Pinus sylvestris var.mongolica and Larix gmelinii to climate change. Chin. J. Appl. Ecol. 2021, 32, 3405–3414. [Google Scholar] [CrossRef]
- Sun, Z.; Zhao, H.; Zhu, L.; Li, Z.; Zhang, Y.; Wang, X. Differences in response of Larix gmelinii growth to rising temperature under different precipitation gradients in northern Daxing’an Mountains of northeastern China. J. Beijing For. Univ. 2019, 41, 1–14. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, F.; Tie, N. Relationship between Radial Growth of Larix gmelinii Forest and Climatic Factors. For. Inventory Plan. 2021, 46, 106–113. [Google Scholar] [CrossRef]
- Bao, G.; Liu, Z.; Liu, N.; Wu, M. Simulation analysis of the radial growth characteristics of Pinus sylvestris var.mongolica in Hulunbuir Sandy Land by Vaganov-Shashkin Model. Chin. J. Appl. Ecol. 2021, 32, 3448–3458. [Google Scholar] [CrossRef]
- Weng, D.; Suan, Z.-a. A preliminary study of the lapse rate of surface air temperature over mountainous regions of China. Geogr. Res. 1984, 3, 24–34. Available online: https://www.dlyj.ac.cn/CN/10.11821/yj1984020003 (accessed on 20 May 2023).
- Holmes, R.L. Computer-assisted quality control in tree-ring dating and measurement. Tree-Ring Bull. 1983, 43, 69–78. [Google Scholar] [CrossRef]
- Cook, E.R. A Time Series Approach to Tree-Ring Standardization. Ph.D. Thesis, University of Arizona, Tucson, AZ, USA, 1985. [Google Scholar]
- Chen, K.; Jiao, L.; Liu, X.; Qi, C.; Xue, R. Evaluation of the response stability of two dominant conifer species to climate change in the southern margin of the Tengger Desert. Glob. Ecol. Conserv. 2021, 25, e01439. [Google Scholar] [CrossRef]
- Arzac, A.; Garcia-Cervigon, A.I.; Vicente-Serrano, S.M.; Loidi, J.; Olano, J.M. Phenological shifts in climatic response of secondary growth allow Juniperus sabina L. to cope with altitudinal and temporal climate variability. Agric. For. Meteorol. 2016, 217, 35–45. [Google Scholar] [CrossRef]
- Evans, M.; Reichert, B.; Kaplan, A.; Anchukaitis, K.; Vaganov, E.; Hughes, M.; Cane, M. A forward modeling approach to paleoclimatic interpretation of tree-ring data. J. Geophys. Res. Biogeosci. 2006, 111, 1–13. [Google Scholar] [CrossRef]
- Shi, J.; Liu, Y.; Cai, Q.; Yi, L. A case study of physiological characteristics of statistical correlation between Pinus tabulaeformis tree-ring widths and climatic factors. Acta Ecol. Sin. 2006, 26, 697–705. [Google Scholar]
- Vaganov, E.A.; Anchukaitis, K.J.; Evans, M.N. How well understood are the processes that create dendroclimatic records? A mechanistic model of the climatic control on conifer tree-ring growth dynamics. In Dendroclimatology: Progress and Prospects; Spring: Berlin/Heidelberg, Germany, 2011; pp. 37–75. [Google Scholar] [CrossRef]
- Tychkov, I.I.; Sviderskaya, I.V.; Babushkina, E.A.; Popkova, M.I.; Vaganov, E.A.; Shishov, V.V. How can the parameterization of a process-based model help us understand real tree-ring growth? Trees 2019, 33, 345–357. [Google Scholar] [CrossRef]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 2020, 7, 109. [Google Scholar] [CrossRef] [PubMed]
- Vaganov, E.A.; Hughes, M.K.; Shashkin, A.V. Growth Dynamics of Conifer Tree Rings: Images of Past and Future Environments; Springer Science & Business Media: Berlin, Germany, 2006; Volume 183. [Google Scholar]
- Wang, Y.F.; Zhang, Y.X.; Gou, X.H.; Gao, L.L.; Wang, F. Climate response mechanism of radial growth of Picea crassifolia in low altitude area of middle Qili. Acta Ecol. Sin. 2020, 40, 161–169. [Google Scholar] [CrossRef]
- Jevšenak, J.; Tychkov, I.; Gričar, J.; Levanič, T.; Tumajer, J.; Prislan, P.; Arnič, D.; Popkova, M.; Shishov, V.V. Growth-limiting factors and climate response variability in Norway spruce (Picea abies L.) along an elevation and precipitation gradients in Slovenia. Int. J. Biometeorol. 2021, 65, 311–324. [Google Scholar] [CrossRef]
- Chen, L.; Li, S.; Hou, L.; Shi, A.; Bai, H. Response of Larix chinensis radial growth to climatic factors based on the Vaganov-Shashkin model. Chin. J. Appl. Ecol. 2017, 28, 2470–2480. [Google Scholar] [CrossRef]
- Zhu, J.; Kang, H.; Li, Z.; Wang, G.; Zhang, R. Impact of water stress on survival and photosynthesis of Mongolian pine seedlings on sandy land. Acta Ecol. Sin. 2005, 25, 2527–2533. [Google Scholar] [CrossRef]
- Kang, H.; Zhu, J.; Li, Z.; Xu, M. Natural distribution of Pinus sylvestris var. mongolica on sandy land and its cultivation as an exotic species. Chin. J. Ecol. 2004, 23, 134–139. Available online: https://www.cje.net.cn/CN/Y2004/V/I5/134 (accessed on 13 October 2023).
- Jiang, Y.; Zhang, Y.; Guo, Y.; Kang, M.; Wang, M.; Wang, B. Intra-annual xylem growth of Larix principis-rupprechtii at its upper and lower distribution limits on the Luyashan mountain in North-Central China. Forests 2015, 6, 3809–3827. [Google Scholar] [CrossRef]
- Wu, Y.; Gan, M.; Yu, R. Effect of climate on the radial growth of Larix sibirica and its phenological features in the eastern Tianshan Mountains. Chin. J. Appl. Environ. Biol. 2019, 25, 1301–1311. [Google Scholar] [CrossRef]
- Zhang, Y.; Wilmking, M.; Gou, X. Changing relationships between tree growth and climate in Northwest China. In Forest Ecology: Recent Advances in Plant Ecology; Spring: Berlin/Heidelberg, Germany, 2009; pp. 39–50. [Google Scholar] [CrossRef]
- Zhang, T.; Yuan, Y.; Wei, W.; Shang, H.-m.; Yu, S.; Zhang, R.; Chen, F.; Fan, Z.; Qin, L. Developments and Analysis of Multi-Tree-Ring Width Chronologies of Meyer Spruce in the Ortindag Sand Land. Desert Oasis Meteorol. 2016, 10, 47–53. [Google Scholar] [CrossRef]
- Yu, D.; Wang, G.G.; Dai, L.; Wang, Q. Dendroclimatic analysis of Betula ermanii forests at their upper limit of distribution in Changbai Mountain, Northeast China. For. Ecol. Manag. 2007, 240, 105–113. [Google Scholar] [CrossRef]
- Gao, L.; Gou, X.; Deng, Y.; Yang, M.; Zhang, F. Assessing the influences of tree species, elevation and climate on tree-ring growth in the Qilian Mountains of northwest China. Trees 2017, 31, 393–404. [Google Scholar] [CrossRef]
- Zhou, P.; Huang, J.-G.; Liang, H.; Rossi, S.; Bergeron, Y.; Shishov, V.V.; Jiang, S.; Kang, J.; Zhu, H.; Dong, Z. Radial growth of Larix sibirica was more sensitive to climate at low than high altitudes in the Altai Mountains, China. Agric. For. Meteorol. 2021, 304, 108392. [Google Scholar] [CrossRef]
- Bai, X.; Zhang, X.; Li, J.; Duan, X.; Jin, Y.; Chen, Z. Altitudinal disparity in growth of Dahurian larch (Larix gmelinii Rupr.) in response to recent climate change in northeast China. Sci. Total Environ. 2019, 670, 466–477. [Google Scholar] [CrossRef]
- Li, W.; Jiang, Y.; Dong, M.; Du, E.; Wu, F.; Zhao, S.; Xu, H. Species-specific growth-climate responses of Dahurian larch (Larix gmelinii) and Mongolian pine (Pinus sylvestris var. mongolica) in the Greater Khingan Range, northeast China. Dendrochronologia 2021, 65, 125803. [Google Scholar] [CrossRef]
- Zeng, X.; Wei, C.; Liu, X.; Zhang, L. Qinghai spruce (Picea crassifolia) and Chinese pine (Pinus tabuliformis) show high vulnerability and similar resilience to early-growing-season drought in the Helan Mountains, China. Ecol. Indic. 2020, 110, 105871. [Google Scholar] [CrossRef]
- Qin, L.; Yuan, Y.; Zhang, R.; Wei, W.; Yu, S.; Fan, Z.; Chen, F.; Zhang, T.; Shang, H. Tree-ring response to snow cover and reconstruction of century annual maximum snow depth for northern Tianshan Mountains, China. Geochronometria 2016, 43, 9–17. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, X.; Zhang, Q.; Zeng, X.; Xu, G.; Wu, G.; Wang, W. Species-specific tree growth and intrinsic water-use efficiency of Dahurian larch (Larix gmelinii) and Mongolian pine (Pinus sylvestris var. mongolica) growing in a boreal permafrost region of the Greater Hinggan Mountains, Northeastern China. Agric. For. Meteorol. 2018, 248, 145–155. [Google Scholar] [CrossRef]
- Dinis, L.; Savard, M.M.; Gammon, P.; Bégin, C.; Vaive, J. Influence of climatic conditions and industrial emissions on spruce tree-ring Pb isotopes analyzed at ppb concentrations in the Athabasca oil sands region. Dendrochronologia 2016, 37, 96–106. [Google Scholar] [CrossRef]
- Yu, D.; Wang, Q.; Wang, G.G.; Dai, L. Dendroclimatic response of Picea jezoensis along an altitudinal gradient in Changbai Mountains. Sci. China Ser. E Technol. Sci. 2006, 49, 150–159. [Google Scholar] [CrossRef]
- Baltzer, J.L.; Veness, T.; Chasmer, L.E.; Sniderhan, A.E.; Quinton, W.L. Forests on thawing permafrost: Fragmentation, edge effects, and net forest loss. Glob. Chang. Biol. 2014, 20, 824–834. [Google Scholar] [CrossRef]
- Feng, X.; Zhang, Y.; Chang, X. Analysis of heat and water transferring characteristics in the active layer of permafrost in the wetland of the Greater Khingan Mountains. J. Glaciol. Geocryol. 2021, 43, 1468–1479. [Google Scholar] [CrossRef]
- Guo, Y.; Song, C.; Wan, Z.; Lu, Y.; Qiao, T.; Tan, W.; Wang, L. Dynamics of dissolved organic carbon release from a permafrost wetland catchment in northeast China. J. Hydrol. 2015, 531, 919–928. [Google Scholar] [CrossRef]
- Reyes, F.R.; Lougheed, V.L. Rapid nutrient release from permafrost thaw in arctic aquatic ecosystems. Arct. Antarct. Alp. Res. 2015, 47, 35–48. [Google Scholar] [CrossRef]



| Species | Sampling Sites | Latitude (E) | Longitude (N) | Elevation (m) | Slope Direction | Slope Degree (°) | Canopy Density | Number of Samples/Number of Trees |
|---|---|---|---|---|---|---|---|---|
| Dahurian larch | LY_high | 121.47° | 52.18° | 1100–1200 | N | 5 | 0.8 | 51/24 |
| LY_low | 121.5° | 52.16° | 800–900 | SW | 5 | 0.9 | 64/22 | |
| Mongolian pine | ZZ_high | 121.47° | 52.19° | 1100–1200 | EN | 5 | 0.8 | 57/21 |
| ZZ_low | 121.53° | 52.13° | 800–900 | SE | 30 | 0.8 | 59/22 |
| Statistical Parameter | LY_High | LY_Low | ZZ_High | ZZ_Low | ||||
|---|---|---|---|---|---|---|---|---|
| STD | RES | STD | RES | STD | RES | STD | RES | |
| Expressing population signal (EPS) | 0.964 | 0.965 | 0.958 | 0.964 | 0.990 | 0.944 | 0.962 | 0.955 |
| Mean sensitivity (MS) | 0.155 | 0.174 | 0.191 | 0.190 | 0.115 | 0.116 | 0.110 | 0.142 |
| Standard deviation (SD) | 0.194 | 0.162 | 0.211 | 0.130 | 0.214 | 0.128 | 0.279 | 0.125 |
| The first-order auto correlation coefficient (AC1) | 0.770 | 0.001 | 0.733 | −0.004 | 0.957 | 0.166 | 0.802 | 0.054 |
| Correlation coefficient (R) | 0.379 | 0.385 | 0.280 | 0.315 | 0.680 | 0.261 | 0.360 | 0.320 |
| Signal-to-noise ratio (SNR) | 26.87 | 27.53 | 22.95 | 27.16 | 101.91 | 16.95 | 25.35 | 21.17 |
| Parameter | Description | Value | |||
|---|---|---|---|---|---|
| LY_High | LY_Low | ZZ_High | ZZ_Low | ||
| Tmin | Minimum temperature for tree growth (°C) | 4 | 4 | 6.5 | 7.5 |
| Topt1 | Lower value of the optimal temperature range (°C) | 14.5 | 8 | 13.5 | 15 |
| Topt2 | Upper value of the optimal temperature range (°C) | 22 | 21 | 25 | 24 |
| Tmax | Maximum temperature for tree growth (°C) | 29 | 29 | 29 | 30 |
| Wmin | Minimum soil moisture for tree growth (V/V) | 0.01 | 0.005 | 0.01 | 0.005 |
| Wopt1 | Lower value of the optimal soil moisture range (V/V) | 0.2 | 0.5 | 0.125 | 0.275 |
| Wopt2 | Upper value of the optimal soil moisture range (V/V) | 0.6 | 0.6 | 0.475 | 0.6 |
| Wmax | Maximum soil moisture for tree growth (V/V) | 0.9 | 0.9 | 0.9 | 0.9 |
| Tbeg | Cumulative temperature at the start of tree growth (°C) | 99 | 98 | 98 | 101 |
| Droot | Depth of root system (mm) | 450 | 450 | 450 | 450 |
| Pmax | Maximum daily precipitation for saturated soil (mm) | 20 | 20 | 22 | 23 |
| K1 | Fraction of precipitation penetrating soil (dimensionless) | 0.53 | 0.29 | 0.48 | 0.51 |
| K2 | First coefficient for calculating transpiration (mm/day) | 0.07 | 0.075 | 0.105 | 0.05 |
| K3 | Second coefficient for calculating transpiration (1/°) | 0.17 | 0.21 | 0.175 | 0.165 |
| Kr | Coefficient for soil water infiltration (dimensionless) | 0.001 | 0.000 | 0.000 | 0.005 |
| Λ | Cambial model time step (days) | 0.2 | 0.2 | 0.2 | 0.2 |
| Vcr | Minimum cambial cell growth rate (μm/days) | 0.11 | 0.09 | 0.06 | 0.08 |
| D0 | Initial cambial cell size (μm) | 4 | 4 | 4 | 4 |
| Dcr | Cell size at which mitotic cycle begins (μm) | 8 | 8 | 8 | 8 |
| Vm | Growth rate during mitotic cycle (μm/days) | 1 | 1 | 1 | 1 |
| Dm | Cambial cell size at which mitosis occurs (μm) | 10 | 10 | 10 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, S.; Wang, Z.; Zhang, D.; Luo, T.; Wang, X.; Mi, T. Simulation of Radial Growth of Mongolian Pine (Pinus sylvestris var. mongolica) and Dahurian Larch (Larix gmelinii) Using the Vaganov–Shashkin Model in the Greater Khingan Range, Northeast China. Forests 2024, 15, 243. https://doi.org/10.3390/f15020243
Zhong S, Wang Z, Zhang D, Luo T, Wang X, Mi T. Simulation of Radial Growth of Mongolian Pine (Pinus sylvestris var. mongolica) and Dahurian Larch (Larix gmelinii) Using the Vaganov–Shashkin Model in the Greater Khingan Range, Northeast China. Forests. 2024; 15(2):243. https://doi.org/10.3390/f15020243
Chicago/Turabian StyleZhong, Shubing, Zhaopeng Wang, Dongyou Zhang, Taoran Luo, Xinrui Wang, and Tingxuan Mi. 2024. "Simulation of Radial Growth of Mongolian Pine (Pinus sylvestris var. mongolica) and Dahurian Larch (Larix gmelinii) Using the Vaganov–Shashkin Model in the Greater Khingan Range, Northeast China" Forests 15, no. 2: 243. https://doi.org/10.3390/f15020243
APA StyleZhong, S., Wang, Z., Zhang, D., Luo, T., Wang, X., & Mi, T. (2024). Simulation of Radial Growth of Mongolian Pine (Pinus sylvestris var. mongolica) and Dahurian Larch (Larix gmelinii) Using the Vaganov–Shashkin Model in the Greater Khingan Range, Northeast China. Forests, 15(2), 243. https://doi.org/10.3390/f15020243





