Optimizing Stand Spatial Structure at Different Development Stages in Mixed Hard Broadleaf Forests
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Classifying Development Stages of Mixed Hard Broadleaf Forests
2.3. Stand Spatial Structure Optimization
2.3.1. SS Parameters Selection
2.3.2. SpS Optimization Model
2.3.3. Optimization Simulation
3. Results
3.1. Classifying Development Stages of Mixed Hard Broadleaf Forests
3.1.1. Twinspan Classification Results
3.1.2. Stand Growth Analysis for TWINSPAN Classification
3.2. Stand Spatial Structure Optimization
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Král, K.; McMahon, S.M.; Janík, D.; Adam, D.; Vrška, T. Patch mosaic of developmental stages in central European natural forests along vegetation gradient. For. Ecol. Manag. 2014, 330, 17–28. [Google Scholar] [CrossRef]
- Gong, Z.; Kang, X.; Gu, L. Quantitative division of succession and spatial patterns among different stand developmental stages in Changbai Mountains. J. Mt. Sci. 2019, 16, 2063–2078. [Google Scholar] [CrossRef]
- Dai, L.; Qi, L.; Wang, Q. Changes in forest structure and composition on Changbai Mountain in Northeast China. Ann. For. Sci. 2011, 68, 889–897. [Google Scholar] [CrossRef]
- Collins, R.J.; Carson, W.P. The effects of environment and life stage on Quercus abundance in the eastern deciduous forest, USA: Are sapling densities most responsive to environmental gradients? For. Ecol. Manag. 2004, 201, 241–258. [Google Scholar] [CrossRef]
- Hao, Z.; Zhang, J.; Song, B.; Ye, J.; Li, B. Vertical structure and spatial associations of dominant tree species in an old-growth temperate forest. For. Ecol. Manag. 2007, 252, 1–11. [Google Scholar] [CrossRef]
- Král, K.; Vrška, T.; Hort, L.; Adam, D.; Šamonil, P. Developmental phases in a temperate natural spruce-fir-beech forest: Determination by a supervised classification method. Eur. J. For. Res. 2009, 129, 339–351. [Google Scholar] [CrossRef]
- Glatthorn, J.; Feldmann, E.; Tabaku, V.; Leuschner, C.; Meyer, P. Classifying development stages of primeval European beech forests: Is clustering a useful tool? BMC Ecol. 2018, 18, 47. [Google Scholar] [CrossRef]
- Huber, M.O. Statistical models to identify stand development stages by means of stand characteristics. Can. J. For. Res. 2011, 41, 111–123. [Google Scholar] [CrossRef]
- Uhl, C.; Buschbacher, R.; Serrao, E.A.S. Abandoned Pastures in Eastern Amazonia. I. Patterns of Plant Succession. J. Ecol. 1988, 76, 663. [Google Scholar] [CrossRef]
- Leibundgut, H. Uber Zweck und Methodik der Strukturund Zuwachsanalyse von Urw€aldern. Schweiz. Z. Forstwes. 1959, 110, 111–124. [Google Scholar]
- Leibundgut, H. Uber die Dynamik europaischer Urwalder. Allg. Forst Z. 1978, 33, 686–690. [Google Scholar]
- Goodell, L.; Faber-Langendoen, D. Development of stand structural stage indices to characterize forest condition in Upstate New York. For. Ecol. Manag. 2007, 249, 158–170. [Google Scholar] [CrossRef]
- Podlaski, R. Suitability of the selected statistical distributions for fitting diameter data in distinguished development stages and phases of near-natural mixed forests in the Świętokrzyski National Park (Poland). For. Ecol. Manag. 2006, 236, 393–402. [Google Scholar] [CrossRef]
- Zenner, E.K.; Peck, J.E.; Hobi, M.L.; Commarmot, B. Validation of a classification protocol: Meeting the prospect requirement and ensuring distinctiveness when assigning forest development phases. Appl. Veg. Sci. 2016, 19, 541–552. [Google Scholar] [CrossRef]
- Feldmann, E.; Glatthorn, J.; Hauck, M.; Leuschner, C. A novel empirical approach for determining the extension of forest development stages in temperate old-growth forests. Eur. J. For. Res. 2018, 137, 321–335. [Google Scholar] [CrossRef]
- Gao, T.; Hedblom, M.; Emilsson, T.; Nielsen, A.B. The role of forest stand structure as biodiversity indicator. For. Ecol. Manag. 2014, 330, 82–93. [Google Scholar] [CrossRef]
- Ali, A. Forest stand structure and functioning: Current knowledge and future challenges. Ecol. Indic. 2019, 98, 665–677. [Google Scholar] [CrossRef]
- Baran, J.; Pielech, R.; Kauzal, P.; Kukla, W.; Bodziarczyk, J. Influence of forest management on stand structure in ravine forests. For. Ecol. Manag. 2020, 463, 118018. [Google Scholar] [CrossRef]
- Hui, G.; Zhang, G.; Zhao, Z.; Yang, A. Methods of Forest Structure Research: A Review. Curr. For. Rep. 2019, 5, 142–154. [Google Scholar] [CrossRef]
- Aguirre, O.; Hui, G.; von Gadow, K.; Jiménez, J. An analysis of spatial forest structure using neighbourhood-based variables. For. Ecol. Manag. 2003, 183, 137–145. [Google Scholar] [CrossRef]
- Gadow, K.V.; Zhang, C.Y.; Wehenkel, C.; Pommerening, A.; Corral-Rivas, J.; Korol, M.; Myklush, S.; Hui, G.Y.; Kiviste, A.; Zhao, X.H. Forest Structure and Diversity. In Continuous Cover Forestry; Springer: Dordrecht, The Netherlands, 2011; pp. 29–83. [Google Scholar] [CrossRef]
- Pastorella, F.; Paletto, A. Stand structure indices as tools to support forest management: An application in Trentino forests (Italy). J. For. Sci. 2013, 59, 159–168. [Google Scholar] [CrossRef]
- Ye, S.; Zheng, Z.; Diao, Z.; Ding, G.; Bao, Y.; Liu, Y.; Gao, G. Effects of Thinning on the Spatial Structure of Larix principis-rupprechtii Plantation. Sustainability 2018, 10, 1250. [Google Scholar] [CrossRef]
- Lopes, J.F.B.; Lopes, F.B.; Araújo, I.C.D.S.; Pereira, E.C.B.; Brandão, M.L.S.M.; Feitosa, E.D.O.; Luna, N.R.D.S.; Sousa, G.G.D.; Amorim, A.V.; Iwata, B.D.F.; et al. How Forest Management with Clear-Cutting Affects the Regeneration, Diversity and Structure of a Seasonally Dry Tropical Forest in Brazil. Forests 2023, 14, 1870. [Google Scholar] [CrossRef]
- Dittrich, S.; Hauck, M.; Jacob, M.; Rommerskirchen, A.; Leuschner, C. Response of ground vegetation and epiphyte diversity to natural age dynamics in a Central European Mountain spruce forest. J. Veg. Sci. 2012, 24, 675–687. [Google Scholar] [CrossRef]
- Hill, M.O. TWINSPAN: A fortran program of arranging multivariate data in an ordered two way table by classification of individual and attributes. In Section of Ecology and Systematics; Cornell University: Ithaca, NY, USA, 1979. [Google Scholar]
- Roleček, J.; Tichý, L.; Zelený, D.; Chytrý, M. Modified TWINSPAN classification in which the hierarchy respects cluster heterogeneity. J. Veg. Sci. 2009, 20, 596–602. [Google Scholar] [CrossRef]
- Hu, Y.; Bo, H.Y.; Bo, X.H. Structured Forest Management; China Forestry Publishing: Beijing, China, 2007; pp. 56–60. ISBN 9787503847639. [Google Scholar]
- Li, Y.; Hui, G.; Zhao, Z.; Hu, Y. The bivariate distribution characteristics of spatial structure in natural Korean pine broad-leaved forest. J. Veg. Sci. 2012, 23, 1180–1190. [Google Scholar] [CrossRef]
- Hui, G.Y.; Von Gadow, K.; Hu, Y.B.; Chen, B.W. Characterizing Forest spatial distribution pattern with the mean value of uniform angle index. Acta Ecol. Sin. 2004, 24, 1225–1229. (In Chinese) [Google Scholar]
- Pukkala, T.; Ketonen, T.; Pykäläinen, J. Predicting timber harvests from private forests—A utility maximisation approach. For. Policy Econ. 2003, 5, 285–296. [Google Scholar] [CrossRef]
- Schwartz, J.W.; Nagel, L.M.; Webster, C.R. Effects of uneven-aged management on diameter distribution and species composition of northern hardwoods in Upper Michigan. For. Ecol. Manag. 2005, 211, 356–370. [Google Scholar] [CrossRef]
- Gadow, K.V.; Hui, G. Modelling Forest Development; Forestry Sciences Series; Springer: Dordrecht, The Netherlands, 1999. [Google Scholar] [CrossRef]
- Hui, G.Y.; Hu, Y.B.; Liu, R.H. Methods of Analyzing Stand Spatial Dominance in Forest Observational Studies. Res. Inst. For. 2019, 2, 12. (In Chinese) [Google Scholar]
- Neto, T.; Constantino, M.; Martins, I.; Pedroso, J.P. A multi-objective Monte Carlo tree search for forest harvest scheduling. Eur. J. Oper. Res. 2020, 282, 1115–1126. [Google Scholar] [CrossRef]
- Gu, L.; O’Hara, K.L.; Li, W.; Gong, Z. Spatial patterns and interspecific associations among trees at different stand development stages in the natural secondary forests on the Loess Plateau, China. Ecol. Evol. 2019, 9, 6410–6421. [Google Scholar] [CrossRef] [PubMed]
- Gokturk, A.; Tiras, H. Stand structure and spatial distribution of trees at different developmental stages and stand layers in mixed stands in Artvin region, Turkey. Appl. Ecol. Environ. Res. 2020, 18, 6163–6179. [Google Scholar] [CrossRef]
- Zhang, M.; Kang, X.; Meng, J.; Zhang, L. Distribution patterns and associations of dominant tree species in a mixed coniferous-broadleaf forest in the Changbai Mountains. J. Mt. Sci. 2015, 12, 659–670. [Google Scholar] [CrossRef]
- Petritan, I.C.; Marzano, R.; Petritan, A.M.; Lingua, E. Overstory succession in a mixed Quercus petraea—Fagus sylvatica old growth forest revealed through the spatial pattern of competition and mortality. For. Ecol. Manag. 2014, 326, 9–17. [Google Scholar] [CrossRef]
- Christensen, N.L.; Peet, R.K. Convergence During Secondary Forest Succession. J. Ecol. 1984, 72, 25. [Google Scholar] [CrossRef]
- Zhou, C.F.; Zhang, H.R.; Lu, J.; Zhang, X.H. Disturbances and Succession Laws of Main Natural Secondary Forests in Northeast China. For. Res. 2021, 34, 175–183. [Google Scholar] [CrossRef]
- Zhou, Y.L.; Zhao, G.Y. Types, distribution and succession patterns of natural secondary forests Lesser Khingan Mountains—Changbai Mountain forest area. J. Northeast. For. Univ. 1964, 33–45. (In Chinese) [Google Scholar]
- Lu, L.L. Study on Community Structure Characteristics of Different Succession Stages of Broad-leaved Korean Pine Forest in Changbai Mountain. Ph.D. Thesis, BeiHua University, Changchun, China, 2019. [Google Scholar]
- Drössler, L.; Feldmann, E.; Glatthorn, J.; Annighöfer, P.; Kucbel, S.; Tabaku, V. What Happens after the Gap?—Size Distributions of Patches with Homogeneously Sized Trees in Natural and Managed Beech Forests in Europe. Open J. For. 2016, 6, 177–190. [Google Scholar] [CrossRef]
- McElhinny, C.; Gibbons, P.; Brack, C.; Bauhus, J. Forest and woodland stand structural complexity: Its definition and measurement. For. Ecol. Manag. 2005, 218, 1–24. [Google Scholar] [CrossRef]
- Wang, H.X.; Huang, S.X.; Zhang, S.S.; Peng, H.; Cao, K.F. Localized neighborhood species mingling is correlated with individual tree size inequality in natural forests in South China. Ann. For. Sci. 2021, 78, 102. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Cao, X.; Liu, Z.; Lv, Y. The Multivariate Distribution of Stand Spatial Structure and Tree Size Indices Using Neighborhood-Based Variables in Coniferous and Broad Mixed Forest. Forests 2023, 14, 2228. [Google Scholar] [CrossRef]
- Li, Y.; Hui, G.; Wang, H.; Zhang, G.; Ye, S. Selection priority for harvested trees according to stand structural indices. iFor.-Biogeosci. For. 2017, 10, 561–566. [Google Scholar] [CrossRef]
- Li, Y.; Ye, S.; Hui, G.; Hu, Y.; Zhao, Z. Spatial structure of timber harvested according to structure-based forest management. For. Ecol. Manag. 2014, 322, 106–116. [Google Scholar] [CrossRef]
- State Forestry Bureau. Regulations for Forest Tending; China Standards Press: Beijing, China, 2015. (In Chinese) [Google Scholar]
- Dong, L.; Wei, H.; Liu, Z. Optimizing Forest Spatial Structure with Neighborhood-Based Indices: Four Case Studies from Northeast China. Forests 2020, 11, 413. [Google Scholar] [CrossRef]
- Qiu, H.; Zhang, H.; Lei, K.; Hu, X.; Yang, T.; Jiang, X. A New Tree-Level Multi-Objective Forest Harvest Model (MO-PSO): Integrating Neighborhood Indices and PSO Algorithm to Improve the Optimization Effect of Spatial Structure. Forests 2023, 14, 441. [Google Scholar] [CrossRef]
- Dong, L.; Bettinger, P.; Liu, Z. Optimizing neighborhood-based stand spatial structure: Four cases of boreal forests. For. Ecol. Manag. 2022, 506, 119965. [Google Scholar] [CrossRef]
- Liu, H.; Dong, X.; Meng, Y.; Gao, T.; Mao, L.; Gao, R. A novel model to evaluate spatial structure in thinned conifer-broadleaved mixed natural forests. J. For. Res. 2023, 34, 1881–1898. [Google Scholar] [CrossRef]
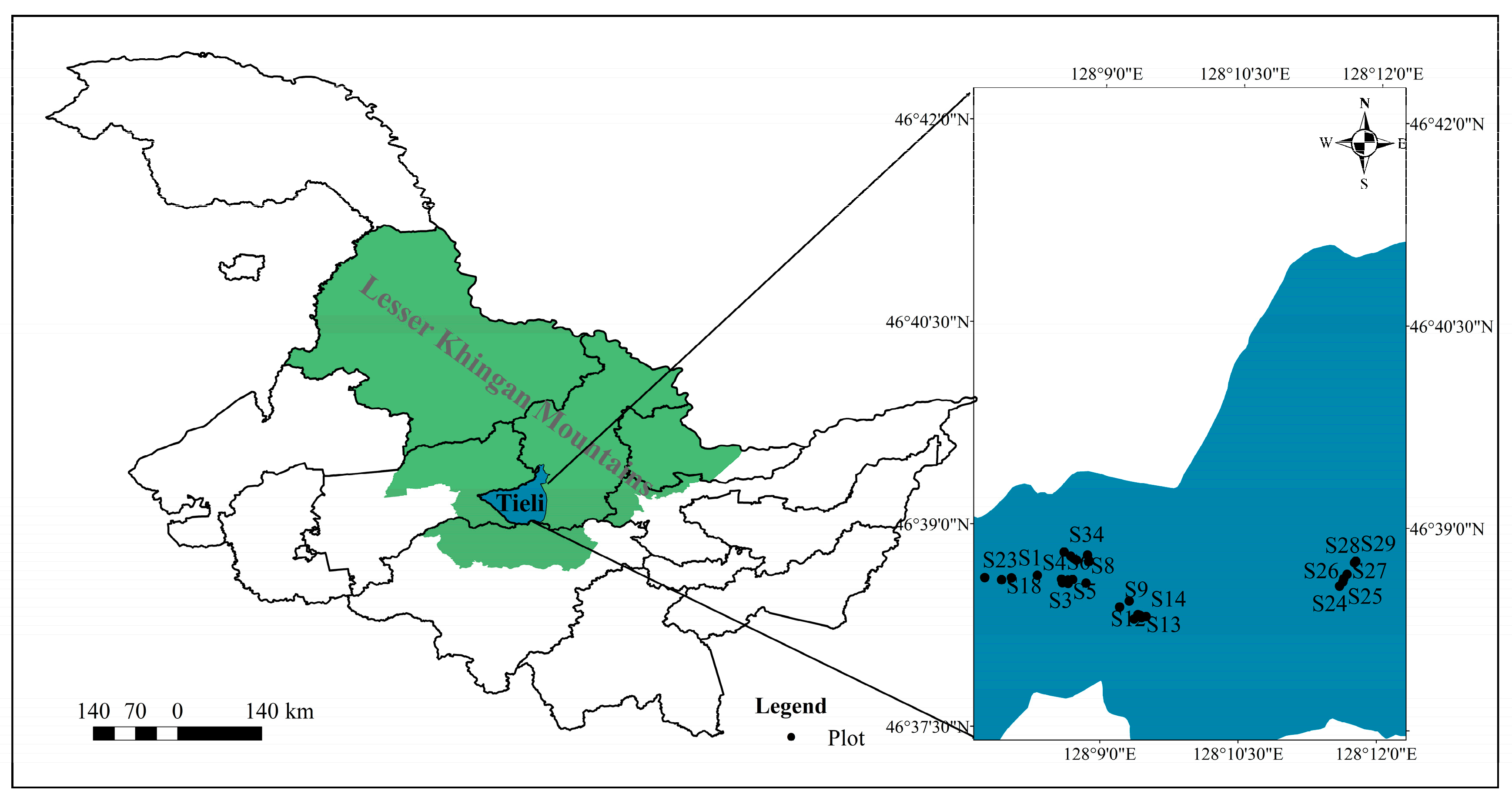
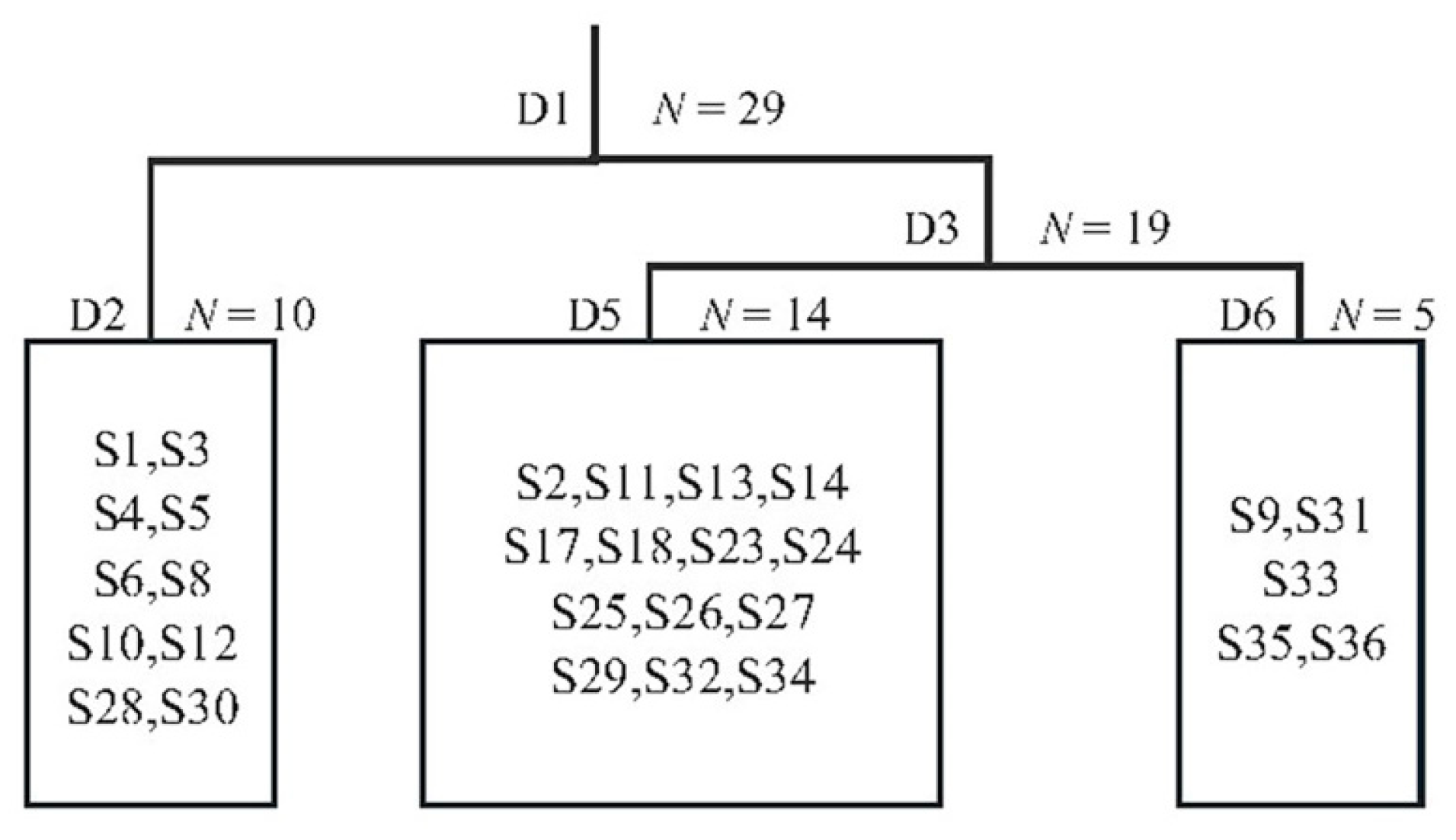
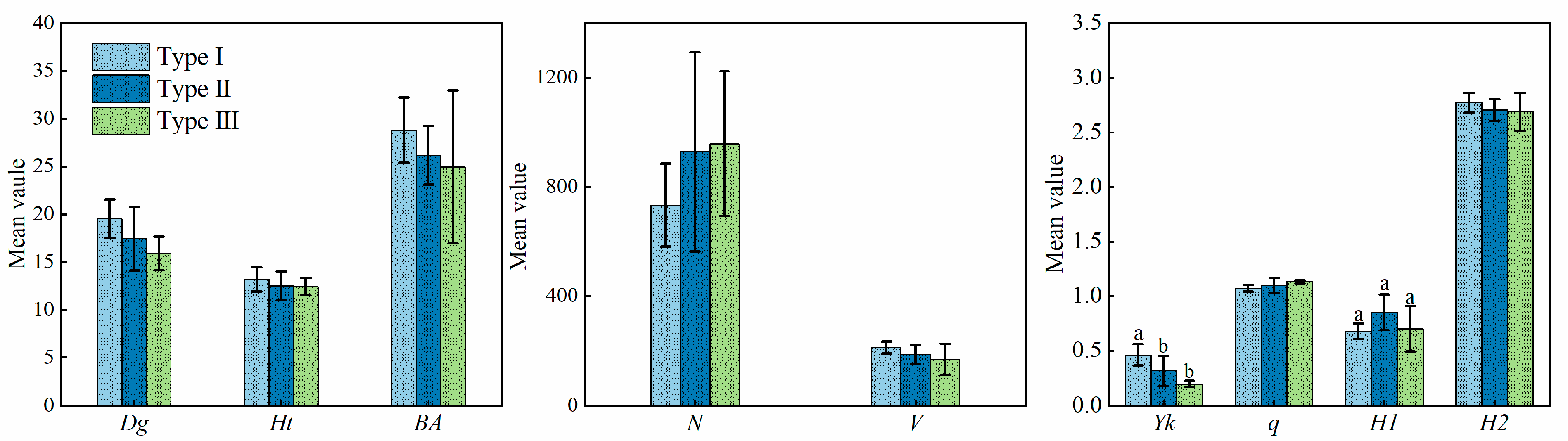
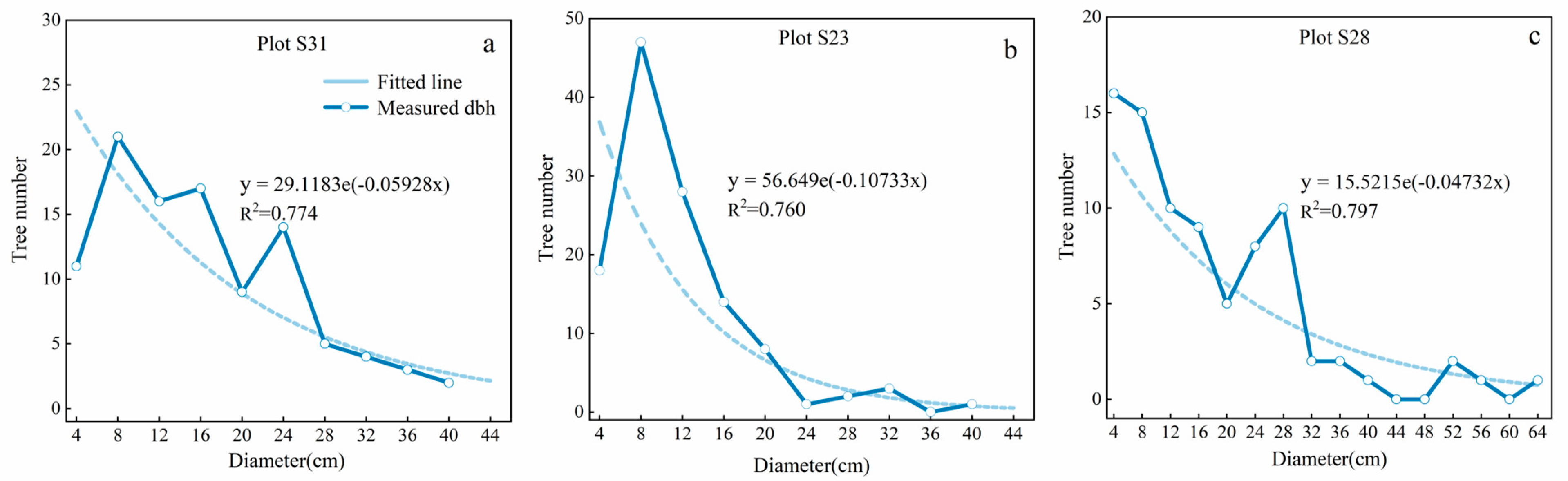

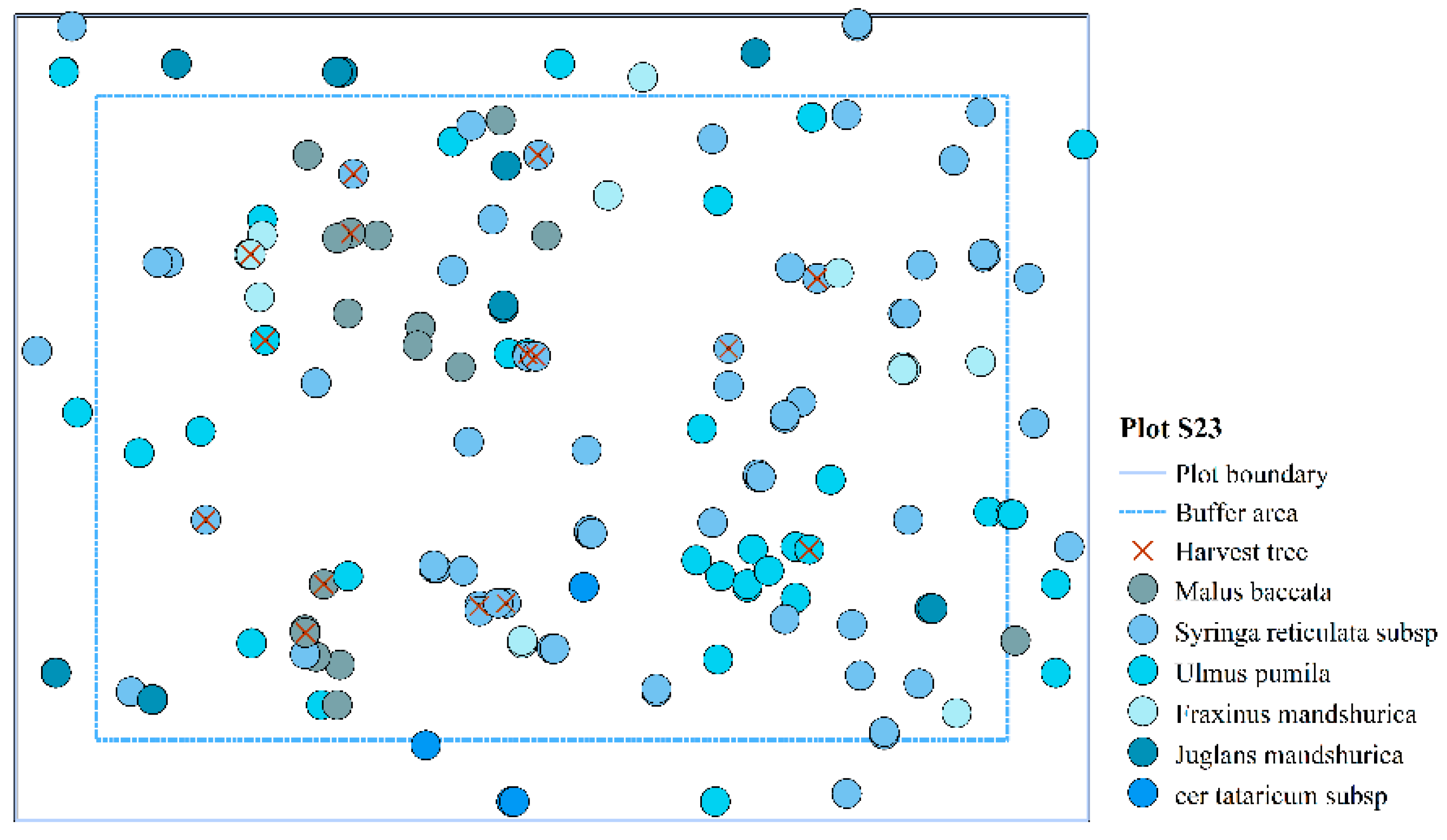
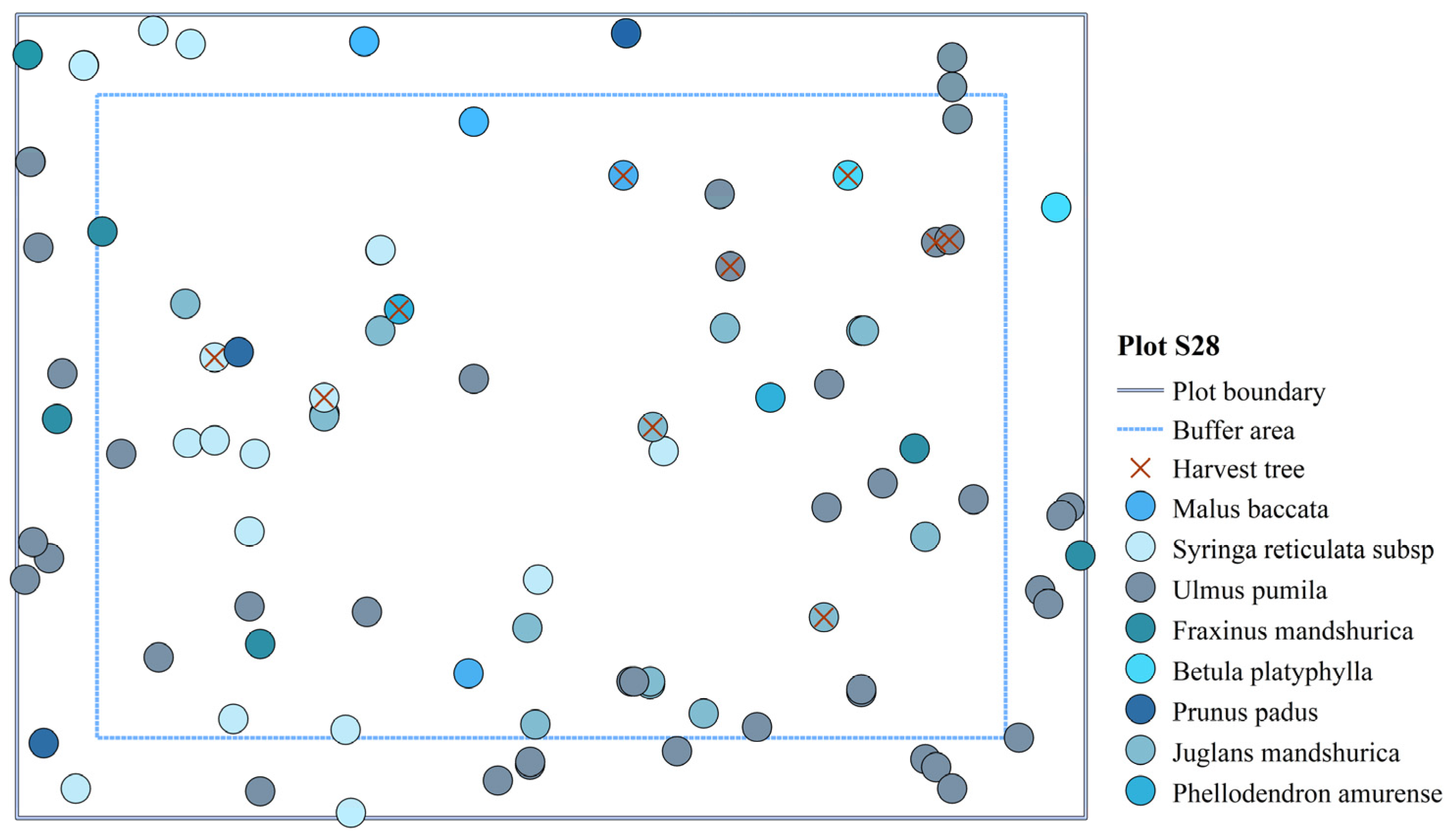
| Plot | Mean Elevation (m) | Slope (°) | Mean DBH (cm) | Density (Tree/ha) | Number of Species |
|---|---|---|---|---|---|
| S1 | 321 | <5 | 20.31 | 725 | 6 |
| S2 | 341 | <5 | 17.51 | 700 | 9 |
| S3 | 338 | <5 | 21.85 | 533 | 5 |
| S4 | 451 | <5 | 17.45 | 733 | 8 |
| S5 | 339 | <5 | 24.08 | 541 | 6 |
| S6 | 378 | <5 | 21.12 | 542 | 6 |
| S8 | 296 | <5 | 21.01 | 600 | 11 |
| S9 | 343 | <5 | 17.64 | 825 | 8 |
| S10 | 329 | <5 | 22.83 | 450 | 8 |
| S11 | 331 | <5 | 18.38 | 758 | 7 |
| S12 | 271 | <5 | 18.72 | 625 | 6 |
| S13 | 252 | <5 | 20.18 | 741 | 10 |
| S14 | 337 | <5 | 12.39 | 1266 | 10 |
| S17 | 305 | <5 | 20.57 | 625 | 6 |
| S18 | 296 | 5~15 | 22.92 | 508 | 6 |
| S23 | 323 | <5 | 11.89 | 1383 | 6 |
| S24 | 325 | <5 | 18.26 | 641 | 10 |
| S25 | 345 | <5 | 21.47 | 500 | 10 |
| S26 | 352 | <5 | 19.94 | 616 | 9 |
| S27 | 346 | <5 | 22.62 | 566 | 9 |
| S28 | 356 | <5 | 17.26 | 775 | 8 |
| S29 | 357 | 15~20 | 15.34 | 741 | 14 |
| S30 | 376 | 5~15 | 18.08 | 958 | 10 |
| S31 | 370 | 15~25 | 16.78 | 1050 | 10 |
| S32 | 352 | <5 | 17.68 | 775 | 11 |
| S33 | 360 | <5 | 17.44 | 991 | 11 |
| S34 | 367 | <5 | 16.65 | 750 | 10 |
| S35 | 354 | <5 | 14.99 | 1050 | 7 |
| S36 | 354 | <5 | 17.8 | 708 | 9 |
| Index | Formula | Definition |
|---|---|---|
| Complete mingling index (Mc) | Where is the number of different tree species in paired neighbours; is the degree of isolation of the nearest neighbour to the reference tree; is the number of nearest neighboring trees; is the Simpson index of the SpS unit i, is the tree species of the SpS unit I; is the proportion of trees of the jth species; is a simple mingling index, , where , if reference tree i and its neighbor tree j are the same white tree species, otherwise, | |
| Uniform angle index (W) | Where ; and α is the angle between two adjacent trees | |
| Dominance index (U) | where zij takes the value 1 if the jth neighbor (dj) is smaller than the reference tree i(di), and the value 0, otherwise, | |
| Stand layer index (S) | where Sij = 0, indicating that the neighbour tree and the reference tree are not in the same vertical layer; otherwise, Sij = 1 | |
| Hegyi competition index (CI) | where di is the diameter of the reference tree, dj is the diameter of the neighbouring trees, and Lij is the Euclidean distance between them | |
| Open degree (K) | where Hj is the height of the neighboring tree j, and Dij is the distance between them |
| Plot | Intensity | Number (Tree) | Mc | S | CI | W | U | q | Q(x) | RIP |
|---|---|---|---|---|---|---|---|---|---|---|
| S31 | 0% | 126 | 0.601 | 0.573 | 2.610 | 0.526 | 0.497 | 1.267 | 178.425 | |
| 10% | 12 | 0.661 | 0.603 | 2.220 | 0.516 | 0.500 | 1.260 | 607.397 | 124.04 | |
| 20% | 24 | 0.685 | 0.631 | 2.124 | 0.497 | 0.500 | 1.208 | 677.869 | 11.60 | |
| 30% | 36 | 0.667 | 0.618 | 1.946 | 0.503 | 0.506 | 1.339 | 733.350 | 8.18 | |
| S23 | 0% | 166 | 0.400 | 0.386 | 3.043 | 0.523 | 0.486 | 1.536 | 57.312 | |
| 10% | 16 | 0.439 | 0.556 | 2.275 | 0.500 | 0.479 | 1.500 | 248.586 | 333.74 | |
| 20% | 32 | 0.455 | 0.530 | 2.042 | 0.510 | 0.474 | 1.507 | 395.122 | 58.94 | |
| 30% | 48 | 0.503 | 0.540 | 1.823 | 0.491 | 0.479 | 1.449 | 530.569 | 34.27 | |
| S28 | 0% | 92 | 0.455 | 0.486 | 2.372 | 0.533 | 0.515 | 1.227 | 172.444 | |
| 10% | 10 | 0.469 | 0.593 | 2.096 | 0.513 | 0.513 | 1.212 | 373.914 | 116.83 | |
| 20% | 20 | 0.465 | 0.598 | 1.969 | 0.511 | 0.511 | 1.228 | 407.176 | 8.89 | |
| 30% | 30 | 0.470 | 0.560 | 1.972 | 0.5000 | 0.495 | 1.200 | 309.324 | −24.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheng, Q.; Dong, L.; Liu, Z. Optimizing Stand Spatial Structure at Different Development Stages in Mixed Hard Broadleaf Forests. Forests 2024, 15, 1653. https://doi.org/10.3390/f15091653
Sheng Q, Dong L, Liu Z. Optimizing Stand Spatial Structure at Different Development Stages in Mixed Hard Broadleaf Forests. Forests. 2024; 15(9):1653. https://doi.org/10.3390/f15091653
Chicago/Turabian StyleSheng, Qi, Lingbo Dong, and Zhaogang Liu. 2024. "Optimizing Stand Spatial Structure at Different Development Stages in Mixed Hard Broadleaf Forests" Forests 15, no. 9: 1653. https://doi.org/10.3390/f15091653
APA StyleSheng, Q., Dong, L., & Liu, Z. (2024). Optimizing Stand Spatial Structure at Different Development Stages in Mixed Hard Broadleaf Forests. Forests, 15(9), 1653. https://doi.org/10.3390/f15091653






