Multi-Level Matching Optimization Design of Thin-Walled Beam Cross-Section for Tri-Axle Unmanned Forestry Vehicle Frame
Abstract
1. Introduction
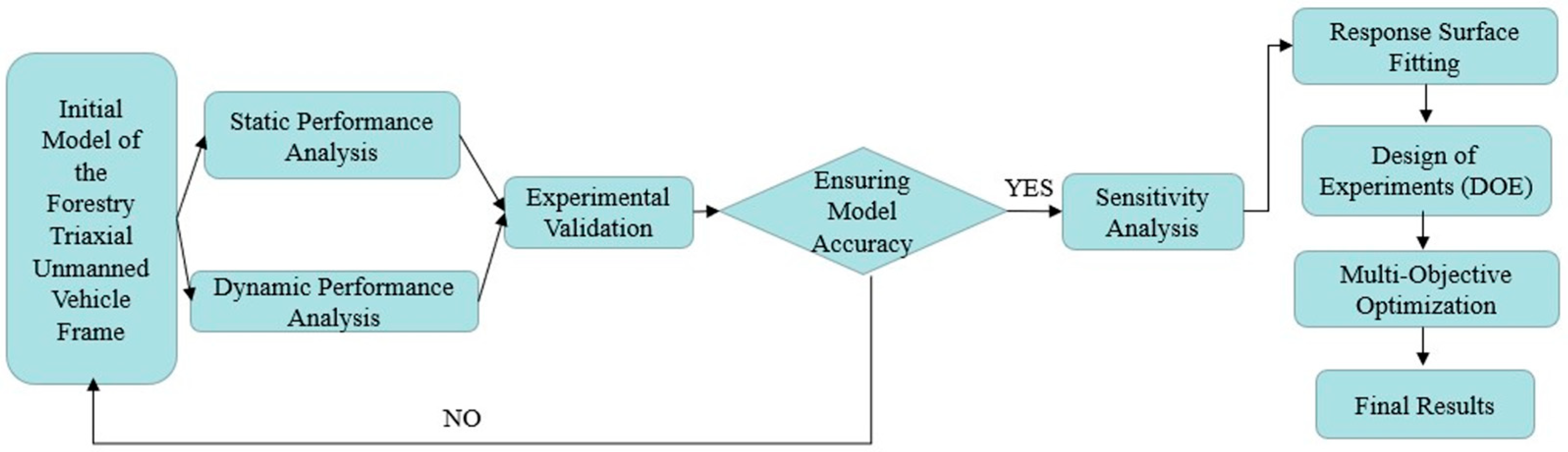
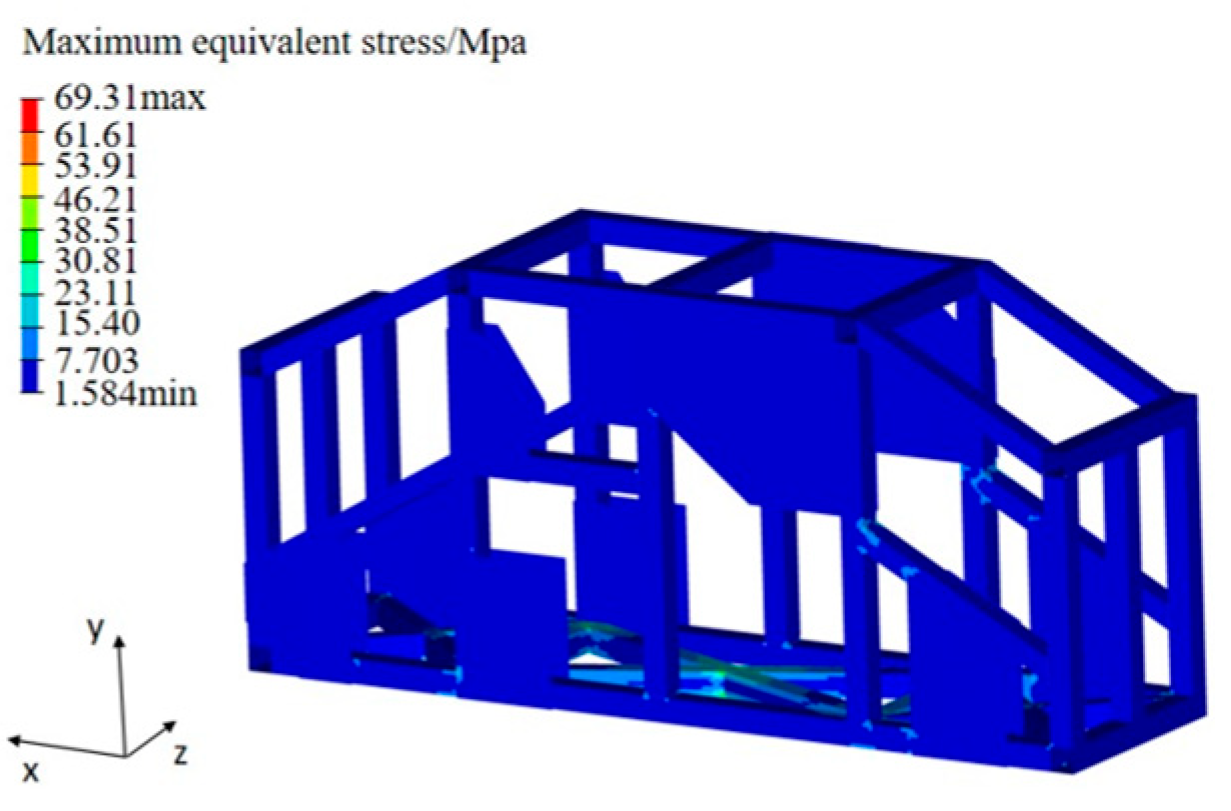
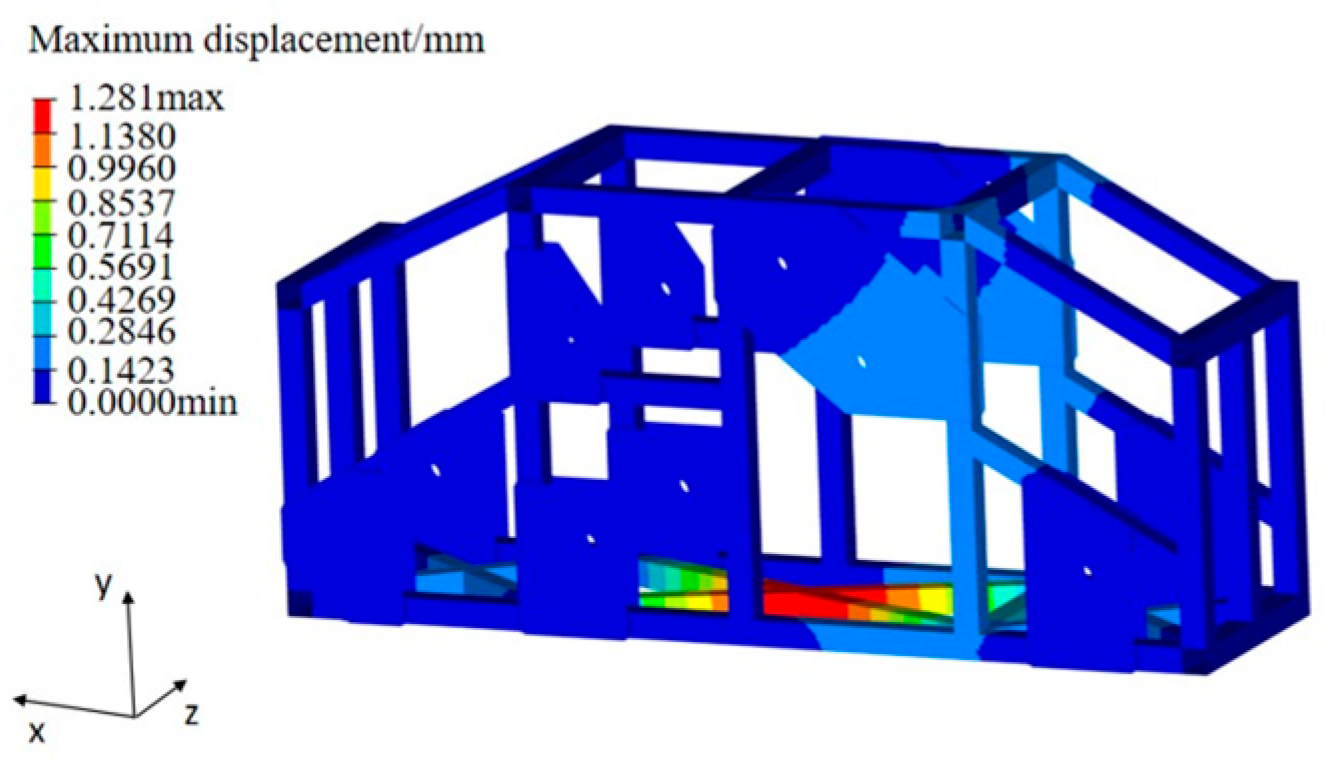
2. Performance Analysis of the Three-Axle Unmanned Vehicle Frame
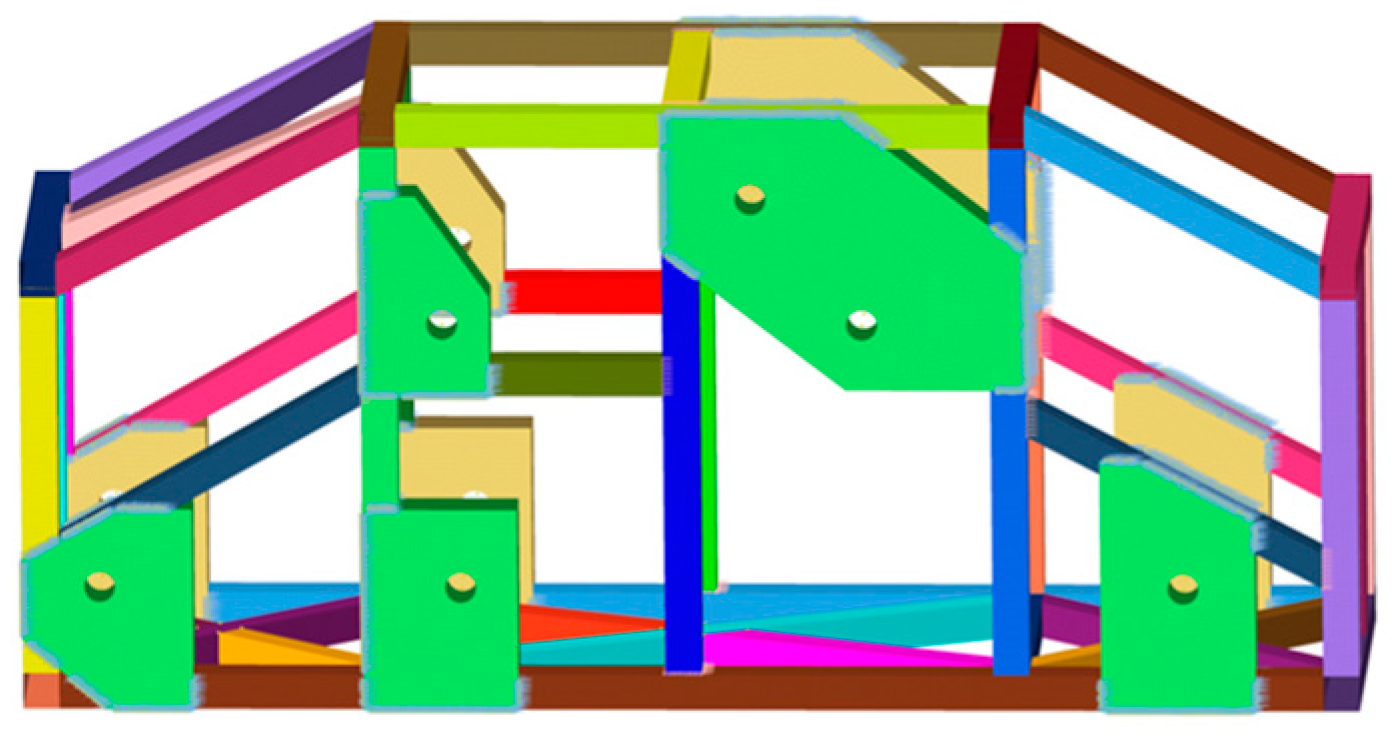
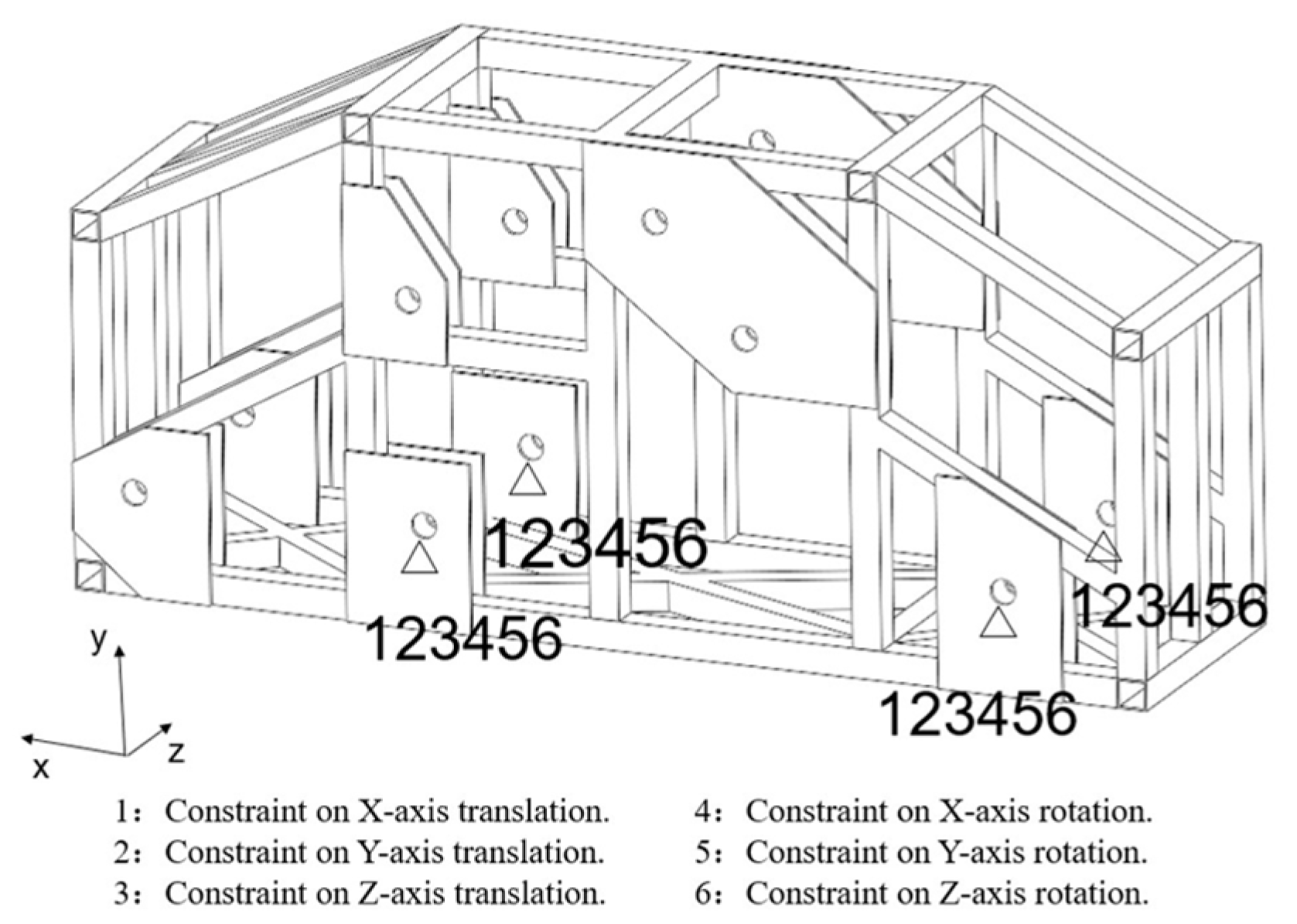
2.1. Establishment of the Vehicle Frame Structural Model
2.2. Frame Structure Model Establishment
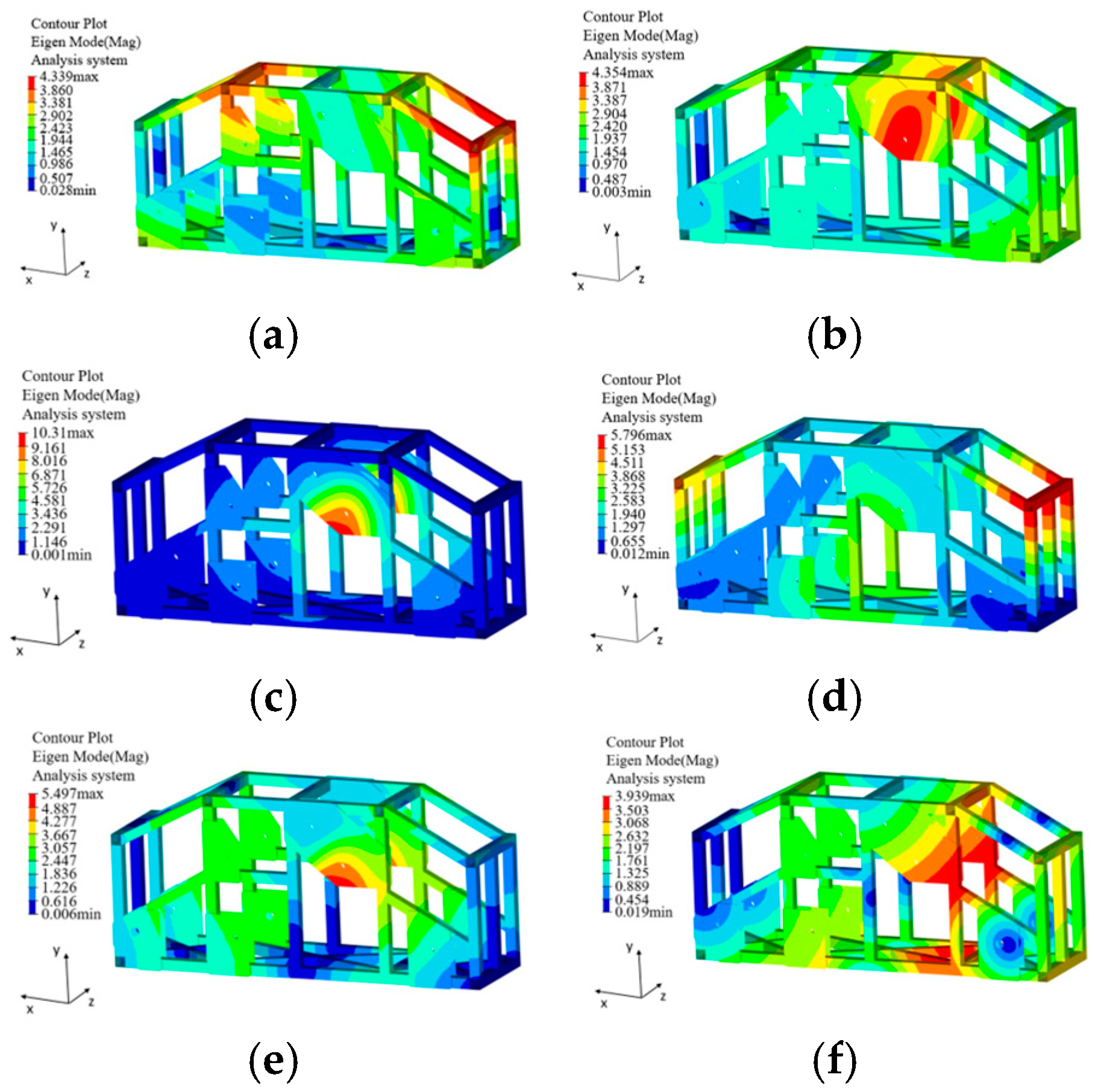
2.3. Modal Analysis
3. Experimental Validation of the Tri-Axle Unmanned Vehicle Frame
3.1. Experimental Validation Method
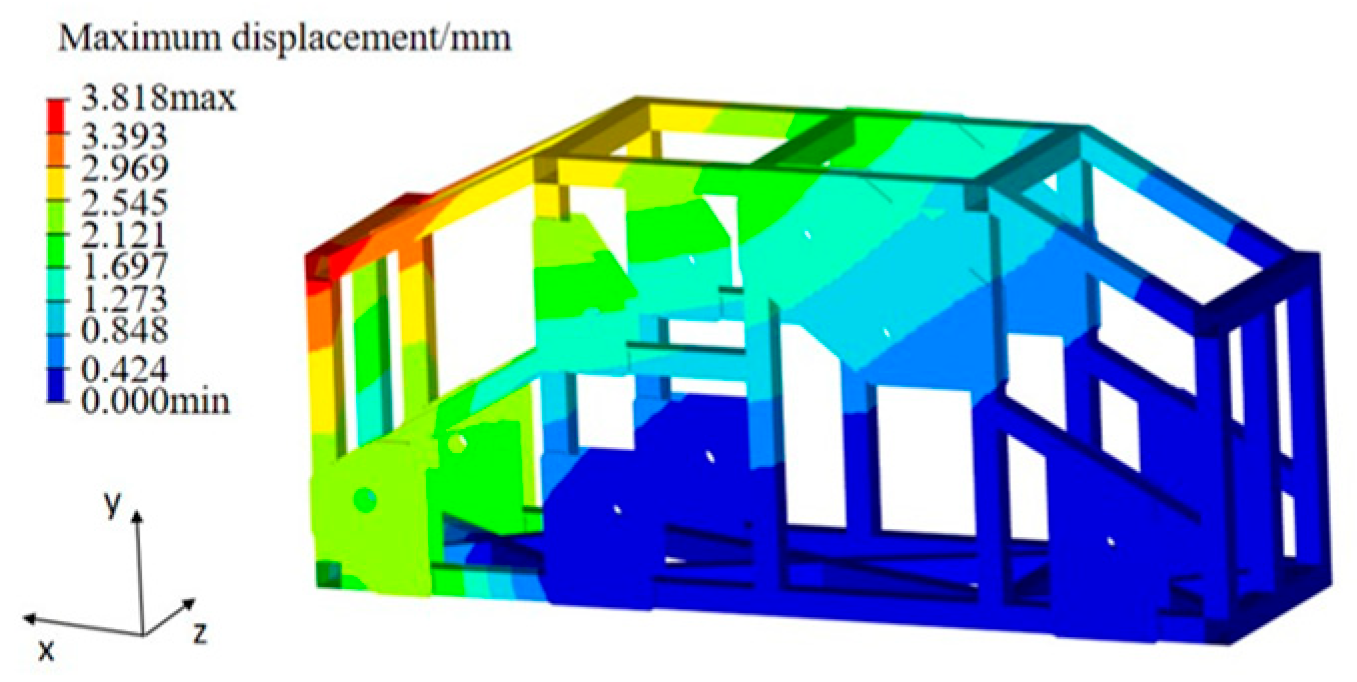
3.2. Bending and Torsion Tests of the Tri-Axle Unmanned Vehicle Frame
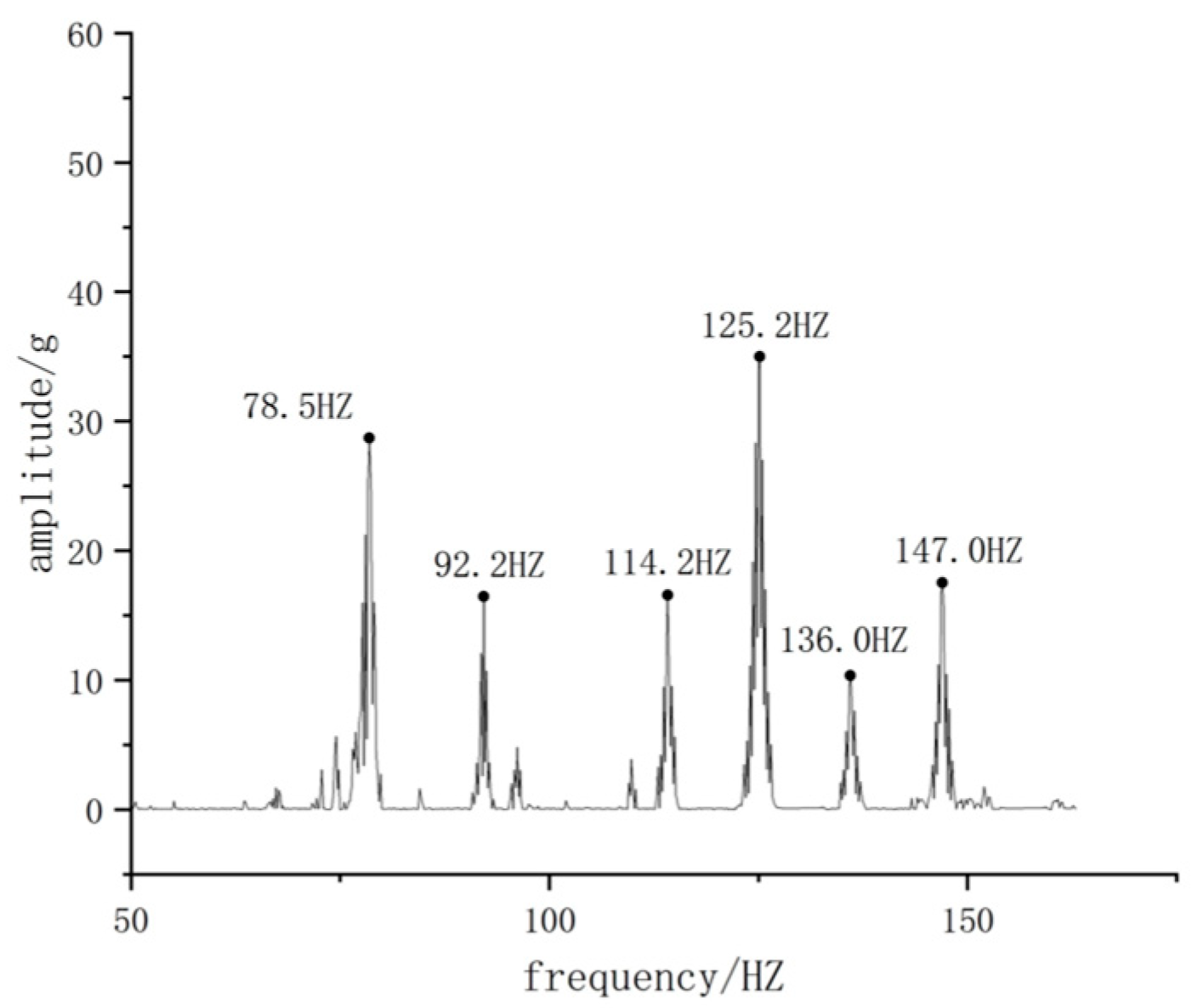
3.3. Modal Test of the Tri-Axle Unmanned Vehicle Frame
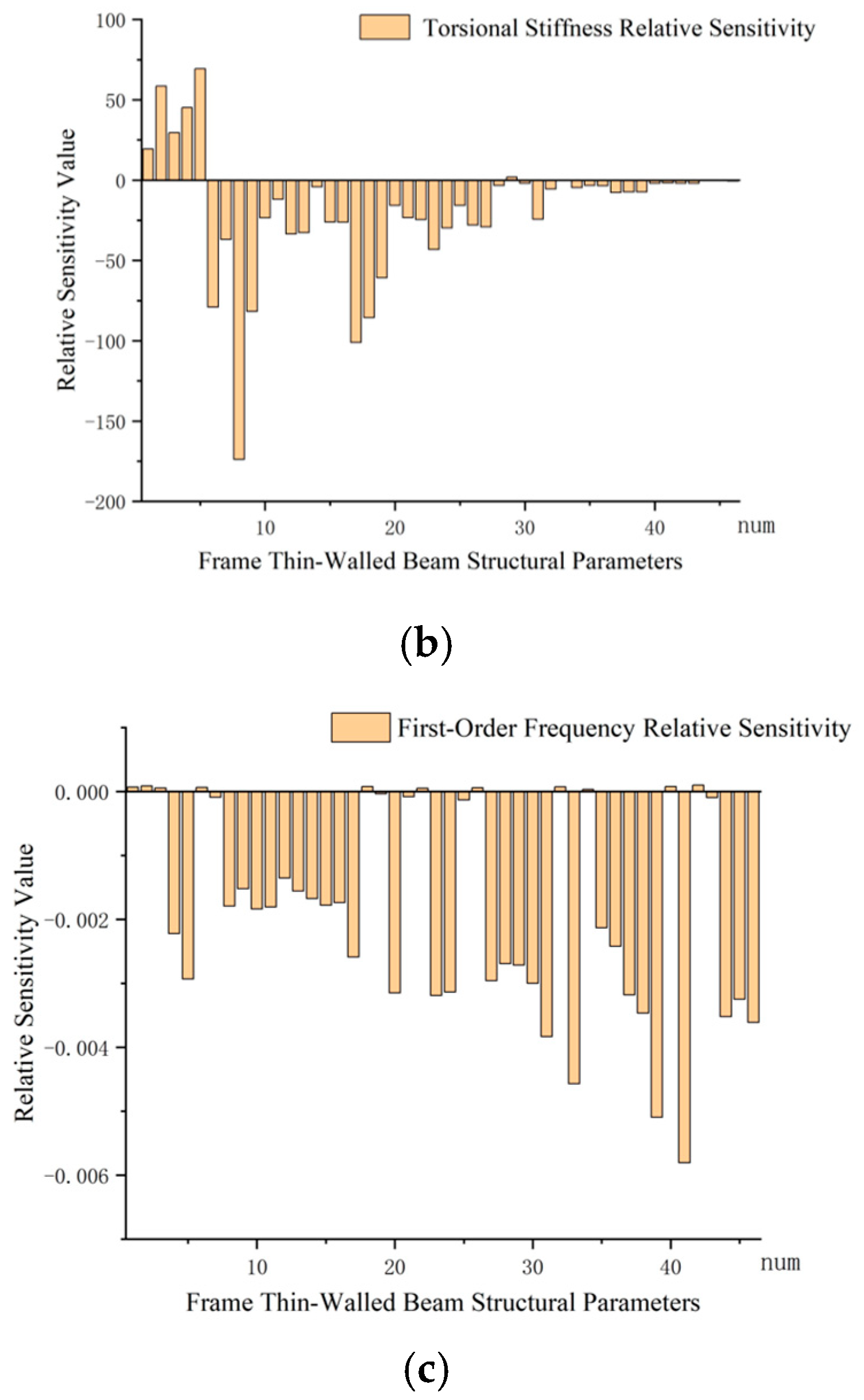
4. Sensitivity Analysis of Thin-Walled Beam Cross-Sections in the Frame
4.1. Sensitivity Analysis
4.2. Sensitivity Analysis Results
4.3. Selection of Design Variables
5. Multi-Objective Optimization Design of the Frame
5.1. DOE (Design of Experiment)
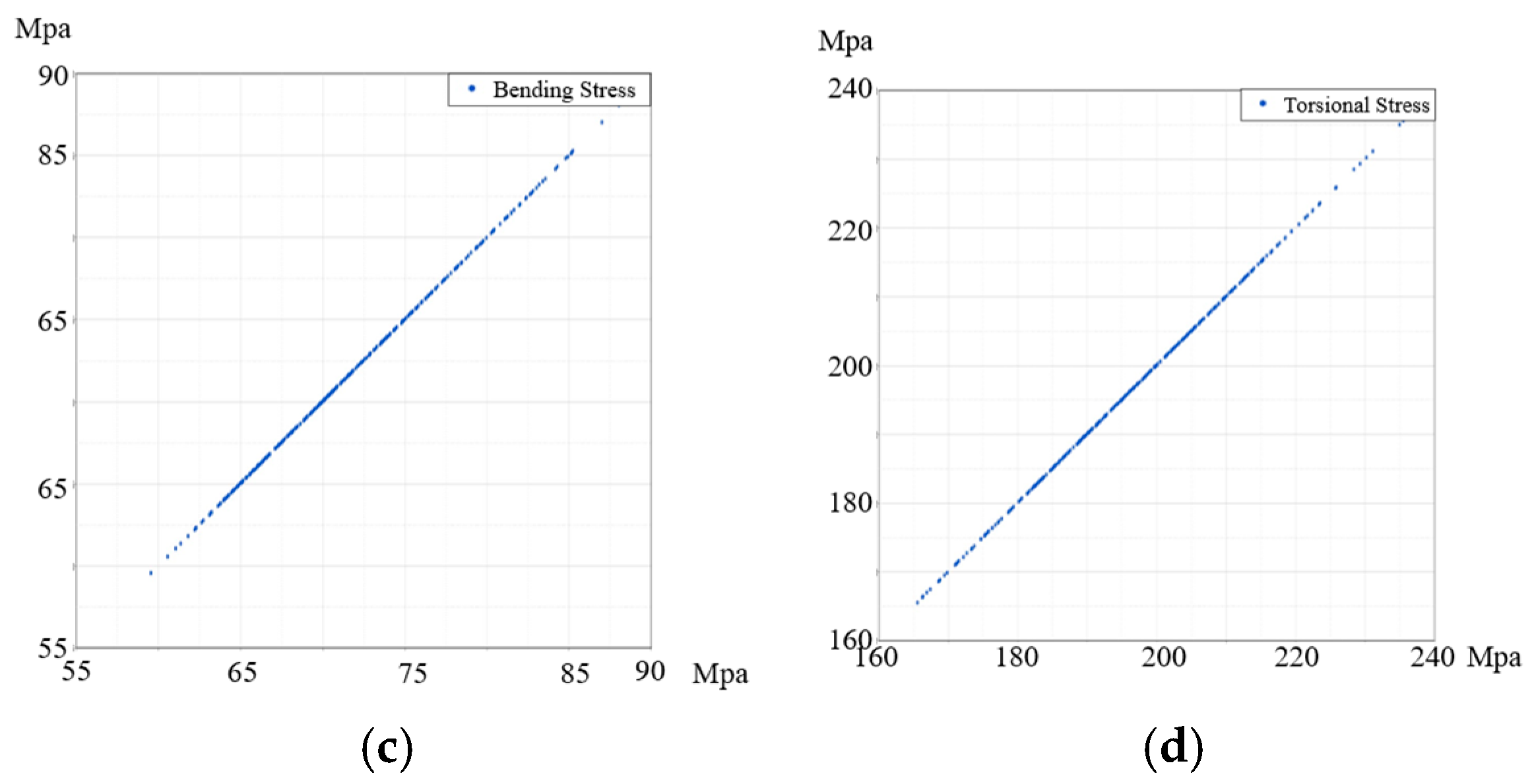
5.2. Response Surface Fitting
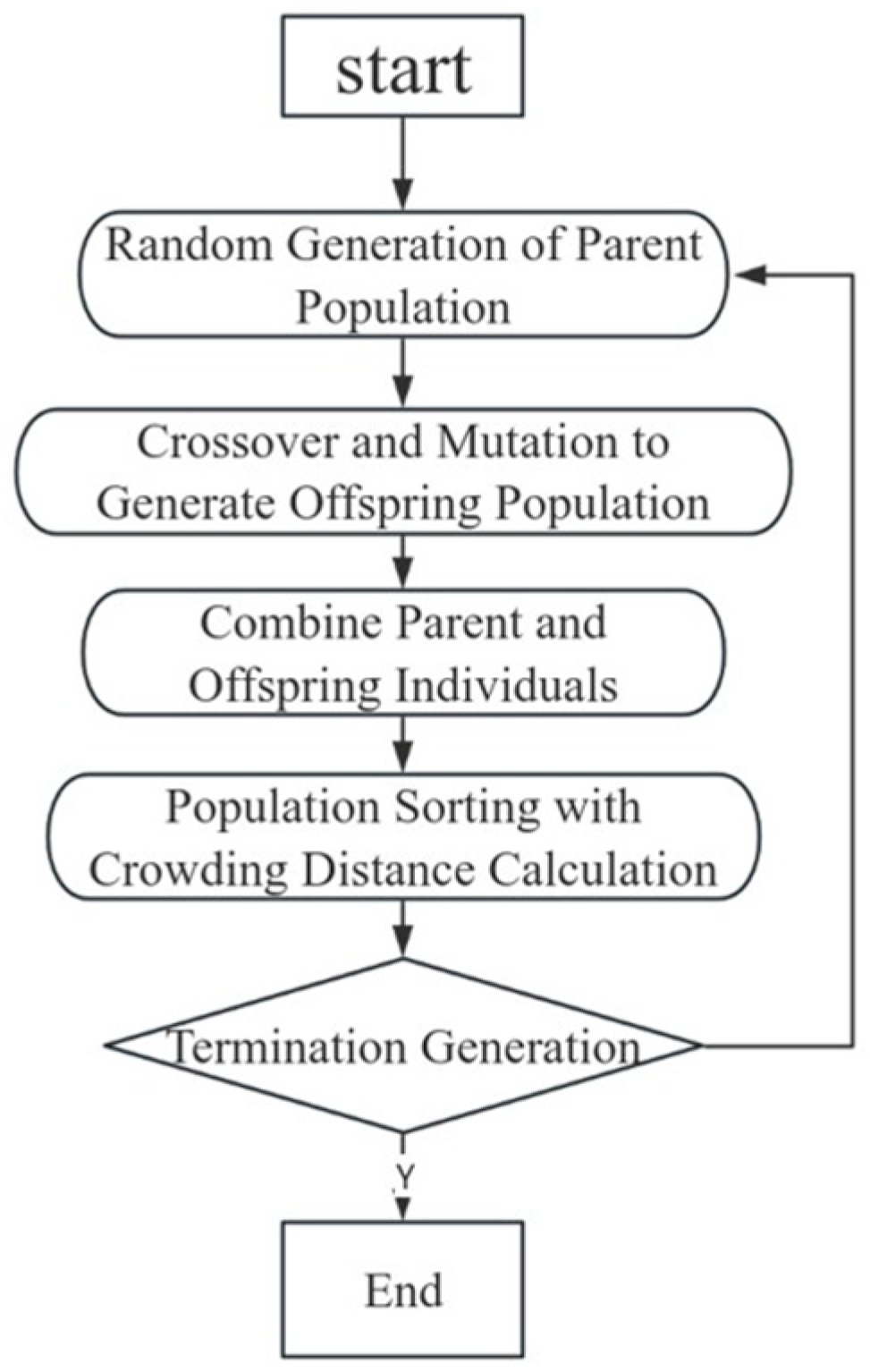
5.3. Optimization Design of the Frame Based on the MOGA Multi-Objective Genetic Algorithm
5.4. Comparison of Optimization Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kalyashov, V.; Mikheev, A.; Kunickaya, O.; Grigorev, I.; Tikhonov, E.; Grigorev, G.; Storodubtseva, T.; Lavrov, M. Design and analysis of electric power-assisted steering in vehicles for mountain forests. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023, 237, 3494–3504. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, D.; Li, Z.; Shi, Y.; Wang, N. Optimum design and trafficability analysis for an articulated wheel-legged forestry chassis. J. Mech. Des. 2022, 144, 013301. [Google Scholar] [CrossRef]
- Rybansky, M. Determination the ability of military vehicles to override vegetation. J. Terramechanics 2020, 91, 129–138. [Google Scholar] [CrossRef]
- Anandan, N.; Arronde Pérez, D.; Mitterer, T.; Zangl, H. Design and evaluation of capacitive smart transducer for a forestry crane gripper. Sensors 2023, 23, 2747. [Google Scholar] [CrossRef] [PubMed]
- Scolaro, E.; Beligoj, M.; Estevez, M.P.; Alberti, L.; Renzi, M.; Mattetti, M. Electrification of agricultural machinery: A review. IEEE Access 2021, 9, 164520–164541. [Google Scholar] [CrossRef]
- Zhang, J.; Deng, Y.; Zheng, B.; Qi, X. Lightweight design of low-load electric vehicle frame. J. Comput. Methods Sci. Eng. 2021, 21, 423–433. [Google Scholar] [CrossRef]
- Ju, Y.J.; Jeon, E.S. Topology optimization of seat cushion frame with dissimilar materials for lightweight strength optimization. Int. J. Manuf. Mater. Mech. Eng. (IJMMME) 2019, 9, 1–12. [Google Scholar] [CrossRef]
- Wang, D.; Xie, C.; Liu, Y.; Xu, W.; Chen, Q. Multi-objective collaborative optimization for the lightweight design of an electric bus body frame. Automot. Innov. 2020, 3, 250–259. [Google Scholar] [CrossRef]
- Liu, J.; Dai, R.; Wu, T.; Zhou, P.; Yang, X. Reliability optimisation of an electric bus frame orienting side impact safety and lightweight. Int. J. Veh. Perform. 2023, 9, 225–249. [Google Scholar] [CrossRef]
- Zheng, B. Analysis of Static and Dynamic Characteristics and Lightweight Design of Titanium Alloy Frame. Manuf. Technol. 2024, 24, 507–519. [Google Scholar] [CrossRef]
- Longye, P.; Zhu, X.; Yang, L.; Guan, T. Lightweight Design of an Electric Tricycle Frame Considering Dynamic Stress in Driving Conditions. Int. J. Automot. Technol. 2021, 22, 1075–1085. [Google Scholar]
- Cheng, L.; Lin, H.B.; Zhang, Y.L. Optimization design and analysis of mobile pump truck frame using response surface methodology. PLoS ONE 2023, 18, e0290348. [Google Scholar] [CrossRef]
- Shangguan, Y.; Wang, W.; He, A.; Ma, W.; Tian, H. Lightweight design for the aluminum alloy-carbon fiber hybrid structure of the EMU car body. J. Mech. Sci. Technol. 2023, 37, 6441–6452. [Google Scholar] [CrossRef]
- Wang, F.C.; Gao, H.L.; Song, X.G.; Lei, Y.X. Designand Manufacture of an All-Terrain Six Wheel Mobile Robot. Mach. Des. Manuf. 2020, 253–256. [Google Scholar]
- Spinelli, R.; Magagnotti, N.; Pari, L.; De Francesco, F. A comparison of tractor-trailer units and high-speed forwarders used in Alpine forestry. Scand. J. For. Res. 2015, 30, 470–477. [Google Scholar] [CrossRef]
- Sun, S.; Wu, J.; Ren, C.; Tang, H.; Chen, J.; Ma, W.; Chu, J. Chassis trafficability simulation and experiment of a LY1352JP forest tracked vehicle. J. For. Res. 2021, 32, 1315–1325. [Google Scholar] [CrossRef]
- Fang, Z.L.; Song, Y.L.; Kang, J.; Zhang, X.H.; Zhang, D. Lightweight Design and Optimization of Integrated Die Casting Aluminum Alloy Front Cabin. Automot. Eng. 2019, 46, 1314–1322+1333. [Google Scholar]
- Qiu, X.Y.; Liu, J.Q.; Gao, Q.; Song, Y.M.; Feng, X.J. Optimization design of frame structure parameters of orchard operating machine based on Kriging approximate model. Chin. J. Agric. Mech. 2023, 44, 93–101. [Google Scholar]
- Zheng, M.J.; Zhao, C.L.; Wu, W.J.; Yang, S. Analysis and Optimization of All-terrain Mobile Robot Body Structure. Chin. J. Eng. Des. 2021, 28, 195–202. [Google Scholar]
- Tang, P.; Yang, R.; Ni, X.; Zhao, H.; Xu, F. Research on a lightweight unmanned sightseeing vehicle frame based on multi-condition and multi-objective optimization. Adv. Mech. Eng. 2022, 14, 16878132221131748. [Google Scholar] [CrossRef]
- Wang, C.; Li, M.; Cheng, A.G.; He, Z.C.; Yu, W.Y. Lightweight Design of Material-Structure for Steel-Aluminum Hybrid Cab. Automot. Eng. 2019, 46, 735–744. [Google Scholar]
- Zhao, X.; Liu, Y.; Hua, L.; Mao, H. Structural Analysis and Size Optimization of a Fine-Blanking Press Frame Based on Sensitivity Analysis. J. Mech. Eng. Stroj. Vestn. 2020, 66, 408. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, X.; Zuo, W. Analytical sensitivity analysis method of cross-sectional shape for thin-walled automobile frame considering global performances. Int. J. Automot. Technol. 2020, 21, 1207–1216. [Google Scholar] [CrossRef]
- Wu, J.; Yang, Y.; Hu, J. Optimization of Pile Driver Frame Based on Sensitivity Analysis. Appl. Sci. 2023, 13, 4774. [Google Scholar] [CrossRef]
- Ma, W.; Lu, Y.; Wang, P.; Wang, Y.; Wang, J. Double optimization design of the formula racing car frame based on the variable density method and the joint variable method. Appl. Sci. 2023, 13, 10155. [Google Scholar] [CrossRef]
- Medeiros, G.; Florindo, T.; Talamini, E.; Fett Neto, A.; Ruviaro, C. Optimising tree plantation land use in Brazil by analysing trade-offs between economic and environmental factors using multi-objective programming. Forests 2020, 11, 723. [Google Scholar] [CrossRef]
- Wu, B.; Zheng, H.; Xu, Z.; Wu, Z.; Zhao, Y. Forest burned area detection using a novel spectral index based on multi-objective optimization. Forests 2022, 13, 1787. [Google Scholar] [CrossRef]
- Ru, S.; Zhao, C.; Yang, S. Multi-objective optimization and analysis of mechanical properties of coir fiber from coconut forest waste. Forests 2022, 13, 2033. [Google Scholar] [CrossRef]
- Qiu, H.; Zhang, H.; Lei, K.; Hu, X.; Yang, T.; Jiang, X. A New Tree-Level Multi-Objective Forest Harvest Model (MO-PSO): Integrating Neighborhood Indices and PSO Algorithm to Improve the Optimization Effect of Spatial Structure. Forests 2023, 14, 441. [Google Scholar] [CrossRef]
- Jia, N.; Guo, L.; Wang, R.; Liu, J. Design of Vibration and Noise Reduction for Ultra-Thin Cemented Carbide Circular Saw Blades in Woodworking Based on Multi-Objective Optimization. Forests 2024, 15, 1554. [Google Scholar] [CrossRef]
- Tong, H. Distributed least squares prediction for functional linear regression. Inverse Probl. 2021, 38, 025002. [Google Scholar] [CrossRef]
- Esposito, R.; Cerrato, M.; Locatelli, M. Partitioned least squares. Mach. Learn. 2024, 113, 6839–6869. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, R.C.; Li, X.; Song, F.J.; Liu, D.W. Multi-objective optimization of the low-speed electric vehicle frame based on the surrogate model. J. Mach. Des. 2020, 37, 105–109. [Google Scholar]
- Wang, T.; Wang, L.; Wang, C.; Zou, X. Crashworthiness analysis and multi-objective optimization of a commercial vehicle frame: A mixed meta-modeling-based method. Adv. Mech. Eng. 2018, 10, 1687814018778480. [Google Scholar] [CrossRef]
- Bao, X.; Han, F.; Ling, Q.H.; Ren, Y.Q. A multi-instance multi-label learning algorithm based on radial basis functions and multi-objective particle swarm optimization. Intell. Data Anal. 2023, 27, 1681–1698. [Google Scholar] [CrossRef]
- Kien, D.N.; Zhuang, X. Radial basis function based finite element method: Formulation and applications. Eng. Anal. Bound. Elem. 2023, 152, 455–472. [Google Scholar] [CrossRef]
- Chen, C.H.; Zhu, Y.F.; Yao, Y.; Huang, Y. The finite element model research of the pre-twisted thin-walled beam. Struct. Eng. Mech. Int. J. 2016, 57, 389–402. [Google Scholar] [CrossRef]
- Lewiński, J.; Magnucki, K. Optimization of anti-symmetrical open cross-sections of cold-formed thin-walled beams. J. Theor. Appl. Mech. 2009, 47, 553–571. [Google Scholar]
- Griso, G. Decomposition of the displacements of thin-walled beams with rectangular cross-section. Math. Methods Appl. Sci. 2024, 47, 5975–5998. [Google Scholar] [CrossRef]
- Kim, S.W.; Song, J.W.; Hong, J.P.; Kim, H.J.; Kang, J.H. Finite Element Analysis and Validation of Wind Turbine Bearings. Energies 2024, 17, 692. [Google Scholar] [CrossRef]
- Fröhlich, B.; Gade, J.; Geiger, F.; Bischoff, M.; Eberhard, P. Geometric element parameterization and parametric model order reduction in finite element based shape optimization. Comput. Mech. 2019, 63, 853–868. [Google Scholar] [CrossRef]
- Wang, F.; Li, Y.; Han, K.; Feng, Y.T. A general finite element model for numerical simulation of structure dynamics. Sci. China Ser. G Phys. Mech. Astron. 2006, 49, 440–450. [Google Scholar] [CrossRef]
- He, R. Lightweight Design of Frame Structure Based on Multi-discipline and Multi-Objective. Noise Vib. Control 2022, 42, 173. [Google Scholar]
- Liu, W.W.; Liu, J. Mechanical Analysis and Experiment on Frame of Wide-body Dump Truck under the Conditions of Starting and Braking. J. Beihua Univ. (Nat. Sci. Ed.) 2022, 23, 403–407. [Google Scholar]
- Zhao, H.J. Research on Lightweight of Pure Electric Unmanned Collector Vehicle Frame Based on Sensitivity Analysis. Master’s Thesis, Yancheng Institute of Technology, Yancheng, China, 2023. [Google Scholar]
- Hou, J.J.; Wang, Y.; Zhong, Y.D.; Zhao, D.F.; He, W.B.; Zhou, F. Lightweight design of body in white structure based on adaptive response surface method. Sci. Technol. Eng. 2019, 24, 3416–3425. [Google Scholar]
- Shi, H.; Zhang, X.; Gao, Y.; Wang, S.; Ning, Y. Robust Total Least Squares Estimation Method for Uncertain Linear Regression Model. Mathematics 2023, 11, 4354. [Google Scholar] [CrossRef]
- Xiao, J.; Wang, Y.D.; Liu, X.M.; Zhang, Z.P. Multi-Condition Aerodynamic Optimization of the Air Compressor Impeller Used in Fuel-Cell Vehicles. J. Xi’an Jiaotong Univ. 2021, 55, 39–48. [Google Scholar]
- Sun, X.L.; Wang, D.F.; Rong, B.; Li, B. Applying Response Surface Method to Multi-objective Optimization of Automobile′s Side Structure. Mech. Sci. Technol. Aerosp. Eng. 2022, 41, 1039–1047. [Google Scholar]
- Ren, W.X.; Chen, H.B. Finite element model updating in structural dynamics by using the response surface method. Eng. Struct. 2010, 32, 2455–2465. [Google Scholar] [CrossRef]
- Mohan, S.C.; Maiti, D.K. Structural optimization of rotating disk using response surface equation and genetic algorithm. Int. J. Comput. Methods Eng. Sci. Mech. 2013, 14, 124–132. [Google Scholar] [CrossRef]
- Wang, S.; Wang, D. Crashworthiness-based multi-objective integrated optimization of electric vehicle chassis frame. Arch. Civ. Mech. Eng. 2021, 21, 103. [Google Scholar] [CrossRef]
- Nazerian, M.; Naderi, F.; Partovinia, A.; Papadopoulos, A.N.; Younesi-Kordkheili, H. Modeling the bending strength of MDF faced, polyurethane foam-cored sandwich panels using response surface methodology (RSM) and artificial neural network (ANN). Forests 2021, 12, 1514. [Google Scholar] [CrossRef]
- Xu, M.; Wang, Z.; Li, Z.; Sun, Z.; Shang, L.; Tian, G.; Ma, J.; Liu, X.E. The Optimization of the Steam-Heat-Treated Process of Rattan (Calamus simplicifolius) Based on the Response Surface Analysis and Its Chemical Changes. Forests 2024, 15, 615. [Google Scholar] [CrossRef]
- Li, Y.H.; Li, D.M.; Gong, Q.; Wu, Y.X. Multi-objective reliability optimization design of motor hanger for EMU. Mech. Sci. Technol. Mach. 2021, 40, 1100–1105. [Google Scholar]
- Ke, J.; Zu, H.F.; Shi, W.K. Multi-objective Optimization Method of thrust rod ball Joint Based on Finite Element Method and Genetic Algorithm. Automot. Eng. 2019, 42, 178–183. [Google Scholar]













| Materials | Density (g/cm3) | Modulus of Elasticity (E/GPa) | Poisson’s Ratio μ | Yield Strength (MPa) |
|---|---|---|---|---|
| 7A58AL | 2.78 | 68.9 | 0.33 | 345 |
| Inspection Item | Inspection Standard | Weighting Ratio (%) |
|---|---|---|
| Aspect Ratio | <5 | 100.0% |
| Jacobin | >0.7 | 99.9% |
| Taper | <0.5 | 99.9% |
| Warpage | <5 | 100.0% |
| Skew | <60 | 100.0% |
| Angle | 45–135 | 99.9% |
| Modal Order | Frequency | Mode Shape |
|---|---|---|
| First-Order Mode | 80.9 Hz | Torsional Mode |
| Second-Order Mode | 89.5 Hz | Combined Bending and Local Swing Mode |
| Third-Order Mode | 112.5 Hz | Local Swing Mode |
| Fourth-Order Mode | 121.1 Hz | Bending Mode |
| Fifth-Order Mode | 137.9 Hz | Combined Torsional and Local Swing Mode |
| Sixth-Order Mode | 145.7 Hz | Combined Bending and Torsional Mode |
| Bending Condition | Measurement Point 1 | Measurement Point 2 | Measurement Point 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Simulated Value | True Value | Error Rate | Simulated Value | True Value | Error Rate | Simulated Value | True Value | Error Rate | |
| 500 N | 1.09 | 0.99 | 3.8% | 1.06 | 1.01 | 5.0% | 0.98 | 0.93 | 5.4% |
| 1000 N | 2.17 | 2.08 | 4.3% | 2.12 | 2.05 | 3.4% | 1.96 | 1.9 | 3.2% |
| 1500 N | 3.26 | 3.17 | 2.8% | 3.19 | 3.15 | 1.3% | 2.95 | 2.88 | 2.4% |
| 2000 N | 4.35 | 4.22 | 3.1% | 4.25 | 4.17 | 1.9% | 3.93 | 3.81 | 3.1% |
| 2500 N | 5.43 | 5.28 | 2.8% | 5.31 | 5.18 | 2.5% | 4.91 | 4.82 | 1.9% |
| Torsion Condition | Measurement Point 1 | Measurement Point 2 | Measurement Point 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Simulated Value | True Value | Error Rate | Simulated Value | True Value | Error Rate | Simulated Value | True Value | Error Rate | |
| 500 N mm | 2.96 | 2.83 | 4.6% | 3.31 | 3.15 | 5.1% | 2.61 | 2.49 | 4.8% |
| 1000 N mm | 5.91 | 5.71 | 3.5% | 6.63 | 6.49 | 2.2% | 5.22 | 4.96 | 5.2% |
| 1500 N mm | 8.87 | 8.57 | 3.5% | 9.94 | 9.68 | 2.7% | 7.83 | 7.63 | 2.6% |
| 2000 N mm | 11.82 | 11.37 | 4.0% | 13.25 | 12.93 | 2.5% | 10.44 | 10.27 | 1.7% |
| 2500 N mm | 14.78 | 14.29 | 3.4% | 16.57 | 16.18 | 2.4% | 13.06 | 12.76 | 2.4% |
| Modal Order | Simulated Frequency/Hz | Experimental Frequency/Hz | Relative Error |
|---|---|---|---|
| First-Order Mode | 80.9 | 78.5 | 3.1% |
| Second-Order Mode | 89.5 | 92.2 | 2.9% |
| Third-Order Mode | 112.5 | 114.2 | 1.5% |
| Fourth-Order Mode | 121.1 | 125.2 | 3.3% |
| Fifth-Order Mode | 137.9 | 136.0 | 1.4% |
| Sixth-Order Mode | 145.7 | 147.0 | 0.9% |
| Serial Number | Quality | Bending Stiffness | Torsional Stiffness | First-Order Frequency | Serial Number | Quality | Bending Stiffness | Torsional Stiffness | First-Order Frequency |
|---|---|---|---|---|---|---|---|---|---|
| num1 | 5.67 × 10−4 | −1.58 × 10−4 | 1.09 × 10−2 | 3.79 × 10−8 | num24 | 3.89 × 10−4 | −5.98 × 10−4 | −1.16 × 10−2 | −1.22 × 10−6 |
| num2 | 5.67 × 10−4 | −5.47 × 10−7 | 3.32 × 10−2 | 4.85 × 10−8 | num25 | 7.94 × 10−4 | −1.69 × 10−3 | −1.25 × 10−2 | −1.02 × 10−7 |
| num3 | 5.67 × 10−4 | −8.34 × 10−5 | 1.67 × 10−2 | 3.24 × 10−8 | num26 | 7.94 × 10−4 | −1.58 × 10−3 | −2.22 × 10−2 | 4.89 × 10−8 |
| num4 | 5.22 × 10−4 | −1.63 × 10−5 | 2.35 × 10−2 | −1.16 × 10−6 | num27 | 4.16 × 10−4 | −1.24 × 10−5 | −1.21 × 10−2 | −1.23 × 10−6 |
| num5 | 5.22 × 10−4 | −1.58 × 10−6 | 3.62 × 10−2 | −1.53 × 10−6 | num28 | 9.06 × 10−4 | −9.35 × 10−2 | −3.00 × 10−3 | −2.44 × 10−6 |
| num6 | 1.85 × 10−3 | −1.89 × 10−2 | −1.46 × 10−1 | 1.18 × 10−7 | num29 | 4.20 × 10−4 | −3.05 × 10−2 | 8.24 × 10−4 | −1.14 × 10−6 |
| num7 | 1.85 × 10−3 | −1.88 × 10−2 | −6.84 × 10−2 | −1.68 × 10−7 | num30 | 4.20 × 10−4 | −3.51 × 10−2 | −8.05 × 10−4 | −1.26 × 10−6 |
| num8 | 4.79 × 10−4 | −4.93 × 10−4 | −8.33 × 10−2 | −8.58 × 10−7 | num31 | 5.22 × 10−4 | −3.20 × 10−4 | −1.27 × 10−2 | −2.00 × 10−6 |
| num9 | 4.79 × 10−4 | −3.93 × 10−4 | −3.91 × 10−2 | −7.27 × 10−7 | num32 | 7.94 × 10−4 | −3.89 × 10−3 | −4.32 × 10−3 | 5.83 × 10−8 |
| num10 | 4.73 × 10−4 | −7.37 × 10−6 | −1.11 × 10−2 | −8.68 × 10−7 | num33 | 4.16 × 10−4 | −1.79 × 10−2 | −6.36 × 10−5 | −1.90 × 10−6 |
| num11 | 4.73 × 10−4 | −6.25 × 10−6 | −5.65 × 10−3 | −8.54 × 10−7 | num34 | 7.94 × 10−4 | −4.09 × 10−3 | −3.68 × 10−3 | 2.47 × 10−8 |
| num12 | 4.86 × 10−4 | −6.86 × 10−6 | −1.63 × 10−2 | −6.57 × 10−7 | num35 | 4.59 × 10−4 | −3.83 × 10−4 | −1.54 × 10−3 | −9.78 × 10−7 |
| num13 | 4.86 × 10−4 | −6.29 × 10−6 | −1.59 × 10−2 | −7.56 × 10−7 | num36 | 4.59 × 10−4 | −3.84 × 10−4 | −1.59 × 10−3 | −1.11 × 10−6 |
| num14 | 2.37 × 10−4 | 2.08 × 10−4 | −9.79 × 10−4 | −3.97 × 10−7 | num37 | 4.59 × 10−4 | −1.83 × 10−3 | −3.51 × 10−3 | −1.46 × 10−6 |
| num15 | 5.11 × 10−4 | −2.29 × 10−3 | −1.33 × 10−2 | −9.09 × 10−7 | num38 | 4.59 × 10−4 | −1.86 × 10−3 | −3.40 × 10−3 | −1.59 × 10−6 |
| num16 | 2.37 × 10−4 | −2.39 × 10−3 | −6.22 × 10−3 | −4.12 × 10−7 | num39 | 5.22 × 10−4 | −5.87 × 10−4 | −3.86 × 10−3 | −2.66 × 10−6 |
| num17 | 5.22 × 10−4 | −7.13 × 10−5 | −5.27 × 10−2 | −1.35 × 10−6 | num40 | 5.67 × 10−4 | −5.90 × 10−4 | −1.11 × 10−3 | 4.47 × 10−8 |
| num18 | 7.94 × 10−4 | −1.88 × 10−3 | −6.79 × 10−2 | 6.26 × 10−8 | num41 | 5.22 × 10−4 | −1.82 × 10−4 | −9.62 × 10−4 | −3.03 × 10−6 |
| num19 | 7.94 × 10−4 | −1.54 × 10−3 | −4.83 × 10−2 | −2.94 × 10−8 | num42 | 5.67 × 10−4 | −5.75 × 10−4 | −1.07 × 10−3 | 5.64 × 10−8 |
| num20 | 4.16 × 10−4 | −2.33 × 10−2 | −6.54 × 10−3 | −1.31 × 10−6 | num43 | 5.67 × 10−4 | −4.16 × 10−5 | −1.11 × 10−3 | −5.30 × 10−8 |
| num21 | 8.69 × 10−4 | −1.51 × 10−4 | −2.03 × 10−2 | −6.87 × 10−8 | num44 | 4.97 × 10−4 | −1.70 × 10−3 | −7.46 × 10−5 | −1.75 × 10−6 |
| num22 | 8.69 × 10−4 | −1.56 × 10−4 | −2.13 × 10−2 | 4.59 × 10−8 | num45 | 2.30 × 10−4 | −1.86 × 10−3 | −9.58 × 10−5 | −7.47 × 10−7 |
| num23 | 3.89 × 10−4 | −5.29 × 10−4 | −1.68 × 10−2 | −1.24 × 10−6 | num46 | 2.30 × 10−4 | 1.81 × 10−4 | −1.14 × 10−4 | −8.30 × 10−7 |
| Unit: mm | |||||||
|---|---|---|---|---|---|---|---|
| Design Variable | Initial Value | Lower Limit | Upper Limit | Design Variable | Initial Value | Lower Limit | Upper Limit |
| num1 | 5 | 3 | 7 | num25 | 5 | 3 | 7 |
| num2 | 5 | 3 | 7 | num26 | 5 | 3 | 7 |
| num3 | 5 | 3 | 7 | num28 | 5 | 3 | 7 |
| num6 | 5 | 3 | 7 | num29 | 5 | 3 | 7 |
| num7 | 5 | 3 | 7 | num30 | 5 | 3 | 7 |
| num8 | 5 | 3 | 7 | num32 | 5 | 3 | 7 |
| num9 | 5 | 3 | 7 | num34 | 5 | 3 | 7 |
| num10 | 5 | 3 | 7 | num40 | 5 | 3 | 7 |
| num11 | 5 | 3 | 7 | num41 | 5 | 3 | 7 |
| num14 | 5 | 3 | 7 | num42 | 5 | 3 | 7 |
| num21 | 5 | 3 | 7 | num43 | 5 | 3 | 7 |
| num22 | 5 | 3 | 7 | ||||
| Design Variable | Response Type | R2 |
|---|---|---|
| RBF | 0.9962576 | |
| RBF | 0.9795060 | |
| LSR | 0.9936960 | |
| LSR | 0.9600508 |
| Unit: mm | |||||
|---|---|---|---|---|---|
| Design Variable | Initial Value | Optimized Value | Design Variable | Initial Value | Optimized Value |
| num1 | 5 | 4.7 | num25 | 5 | 3.7 |
| num2 | 5 | 4.4 | num26 | 5 | 3.2 |
| num3 | 5 | 4.2 | num28 | 5 | 5.0 |
| num6 | 5 | 4.1 | num29 | 5 | 4.7 |
| num7 | 5 | 4.0 | num30 | 5 | 3.9 |
| num8 | 5 | 5.6 | num32 | 5 | 3.3 |
| num9 | 5 | 6.2 | num34 | 5 | 3.4 |
| num10 | 5 | 3.6 | num40 | 5 | 3.0 |
| num11 | 5 | 6.2 | num41 | 5 | 4.9 |
| num14 | 5 | 3.1 | num42 | 5 | 5.6 |
| num21 | 5 | 3.0 | num43 | 5 | 4.5 |
| num22 | 5 | 3.2 | |||
| Design Variable | Before Optimization | After Optimization |
|---|---|---|
| /kg | 135.8 kg | 125.7 kg |
| 1st Mode Frequency /Hz | 80.8 Hz | 76.3 Hz |
| Bending /MPa | 69.30 MPa | 73.69 MPa |
| Torsion /MPa | 189.2 MPa | 194.0 MPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; Zhao, Y.; Wang, D.; Chen, Z.; Wang, Q.; Yuan, X. Multi-Level Matching Optimization Design of Thin-Walled Beam Cross-Section for Tri-Axle Unmanned Forestry Vehicle Frame. Forests 2025, 16, 69. https://doi.org/10.3390/f16010069
Chen Q, Zhao Y, Wang D, Chen Z, Wang Q, Yuan X. Multi-Level Matching Optimization Design of Thin-Walled Beam Cross-Section for Tri-Axle Unmanned Forestry Vehicle Frame. Forests. 2025; 16(1):69. https://doi.org/10.3390/f16010069
Chicago/Turabian StyleChen, Qiang, Yilu Zhao, Dequan Wang, Zhongjia Chen, Qingchun Wang, and Xiangyue Yuan. 2025. "Multi-Level Matching Optimization Design of Thin-Walled Beam Cross-Section for Tri-Axle Unmanned Forestry Vehicle Frame" Forests 16, no. 1: 69. https://doi.org/10.3390/f16010069
APA StyleChen, Q., Zhao, Y., Wang, D., Chen, Z., Wang, Q., & Yuan, X. (2025). Multi-Level Matching Optimization Design of Thin-Walled Beam Cross-Section for Tri-Axle Unmanned Forestry Vehicle Frame. Forests, 16(1), 69. https://doi.org/10.3390/f16010069





