Next Article in Journal
Whole-Genome Identification and Expression Profiles of WRKY Genes Related to the Leaf Expansion Period in the Camphor Tree
Previous Article in Journal
Ecological Traits of Three Species of Xiphydria Woodwasps from Japan: Host Tree Species and Eggs, Symbiotic Fungi, and Mucus in Their Bodies
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 16
Issue 2
10.3390/f16020265
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Assessment of the Modulus of Rupture and Modulus of Elasticity in Static Bending of Yellow Pine Earlywood and Latewood

by
Piotr Mańkowski
,
Zbigniew Karwat
and
Agnieszka Laskowska
*
Institute of Wood Sciences and Furniture, Warsaw University of Life Sciences, 159 Nowoursynowska St., 02-776 Warsaw, Poland
*
Author to whom correspondence should be addressed.
Forests 2025, 16(2), 265; https://doi.org/10.3390/f16020265
Submission received: 9 November 2024 / Revised: 26 January 2025 / Accepted: 28 January 2025 / Published: 2 February 2025
(This article belongs to the Section Wood Science and Forest Products)
Browse Figures
Versions Notes

Abstract

:
The purpose of this research was to investigate the modulus of rupture (MOR) and modulus of elasticity (MOE) in the static bending of yellow pine (Pinus ponderosa Douglas ex C. Lawson) earlywood and latewood. The relationship between the properties of these wood zones and the MOR and MOE of yellow pine wood tested was determined with the methodology specified in the standards. An important element of the research was to verify the suitability of the developed method for testing the MOR and MOE of small wood samples obtained from the earlywood and latewood zone. The MOR of the earlywood was about 6% higher than the MOR of the pine wood determined using standard samples, and these differences were not statistically significant. However, the MOR of the latewood was approximately three times higher than the MOR of the pine wood determined using standard samples, and these differences were statistically significant. The MOR of the latewood was found to be 2.5 times higher than the MOR of the earlywood. The MOE of the latewood was found to be two times higher than the MOE of the earlywood. This was due to the density of particular wood zones and the dimensions of structural elements—tracheids. The maximum load (Fmax) transferred by latewood zones was four times higher than the Fmax transferred by earlywood zones. The deflection at the Fmax of the earlywood zone was 20% smaller than the deflection at the Fmax of the latewood zone.

1. Introduction

Despite competition from other construction materials, wood is still commonly used in many branches of industry, mainly in construction and furniture. Thanks to the development of computational techniques, it is possible to perform an accurate strength analysis of wooden structures, but the condition for its correctness is, among others, knowledge of the wood elastic properties. For this reason, elastic properties are the subject of constant analysis. The issues related to the study of the wood mechanical properties are more complex compared to most other construction materials. This is due to the wood anisotropic structure. In addition, due to the wood hygroscopicity, these properties depend on the parameters of air, and consequently on the wood moisture content. Wood defects also play a significant role [1,2,3].
Due to its high strength and, at the same time, low density, wood is a widely used material, e.g., for girders and roof truss elements. In European and North American countries, softwood is most often used for the production of structural elements [4,5]. This is due to the availability of the raw material and the lower price compared to hardwood [6,7,8]. Static bending strength is, apart from the compressive strength parallel to the fibers, the most frequently analyzed strength test [5,9,10]. The bending strength of wood shows intermediate values between the compressive strength and the tensile strength [11]. Low safety factors can be used under compressive and bending stresses of wood. The range of tensile strength values is very wide, and in this respect, wood is an uncertain material requiring a high safety factor. The use of wood for the prefabrication of glued-laminated house construction elements requires testing the physical and mechanical properties of the raw material for the production of these elements, as well as the joints [12,13].
The static bending strength of wood depends on a number of factors. It results from the structure and wood properties [9], as well as the method of testing. The influence of wood origin [10,14,15], type of forest from which the wood was harvested [14], tree age [16,17,18,19,20], chemical composition [21,22,23], anatomical structure [15,20,24,25,26], wood defects [27,28,29], and moisture content [30,31,32] on wood properties are significant. Static bending strength is one of the criteria for classifying structural timber in accordance with European standards [12].
Wood is an anisotropic material. Structure inhomogeneity can be observed organoleptically. The profile of annual rings expressed by latewood ratio, width of latewood, and microfibril angle has a significant effect on mechanical properties of softwood [33,34]. The differences in structure between earlywood and latewood within a single annual growth ring are significant [5]. This translates into differences in the chemical, physical, mechanical properties of wood [25]. The determination of intra-ring mechanical properties is crucial for a complete, hierarchical characterization of wood [35]. The mechanical properties are tested on full-size sawn timber, often containing defects [10], as well as on small samples without defects [36,37,38], and also on a micro scale [39,40,41,42,43,44,45]. Krauss et al. [17] determined the differences in the mechanical properties of earlywood and latewood of pine tree (Pinus sylvestris L.). Cramer et al. [39] evaluated the elastic properties and variability of earlywood and latewood in specimens from six loblolly pine trees in a commercial plantation. Lanvermann et al. [40] evaluated the intra-ring variation and generic behavior of Norway spruce earlywood and latewood until failure. Büyüksarı et al. [41] determined the relationship between the calculated and measured values of bending strength, modulus of elasticity in bending, and tensile strength of earlywood and latewood for Scots pine (Pinus sylvestris L.). In another study, Büyüksarı et al. [42] also investigated the bending strength, modulus of elasticity in bending, compression strength, and tensile strength of oak (Quercus petraea) wood using micro- and standard-size mechanical test samples. Groom et al. [43] evaluated the mechanical properties of individual southern pine fibers. Wimmer et al. [44] researched the Young’s modulus of spruce tracheid secondary walls using nanoindentation technique. Bergander and Salmén [45] analyzed cell wall properties and their effects on fiber mechanical properties.
The aim of the study was to determine the relationship between the modulus of rupture (MOR) of yellow pine (Pinus ponderosa Douglas ex C. Lawson) earlywood and latewood. This also concerned the modulus of elasticity (MOE) in the static bending of earlywood and latewood of yellow pine wood. The relationship between the properties of these wood zones and the MOR and MOE of the yellow pine wood tested with the methodology specified in the standards was important part of the study. Tests on very small samples make it possible to determine the influence of the annual ring structure on the properties of wood. An important issue was to verify the extent to which a particular wood zone (earlywood, latewood) determines the MOR and MOE of the tested raw material. There is a lack of data on the MOR and MOE of earlywood and latewood, and the determinations carried out mainly concern the tensile strength of earlywood and latewood [39,40,41,42,43,44,45]. This is an important aspect from a scientific and utilitarian point of view [35]. There is not sufficient data about the relationship between the mechanical properties of yellow pine at the micro- and macro-scale. Therefore, the aim of this study was to determine the relationship between the mechanical properties of annual ring zones and the raw material tested with the methodology specified in the standards. The study constitutes an important contribution to the development of methods for testing wood properties using very small samples.

2. Materials and Methods

2.1. Yellow Pine Wood Samples

Yellow pine wood (Pinus ponderosa Douglas ex C. Lawson), 70 years old, was used for the study. The wood was obtained from the western part of the USA. A planing operation was used to prepare the sample surfaces. The samples were obtained from a sapwood area, a knot-free butt-end part. Based on previously conducted research by Mańkowski and Laskowska [5], it was determined that in the sapwood area, the width of annual growth rings was 5.73 mm (±0.38 mm), and the share of latewood was 38% (±4%). The moisture content and density of yellow pine wood were determined according to ISO 13061-1:2014 [46] and ISO 13061-2:2014 [47], respectively. Twenty samples were used to determine the yellow pine wood properties.

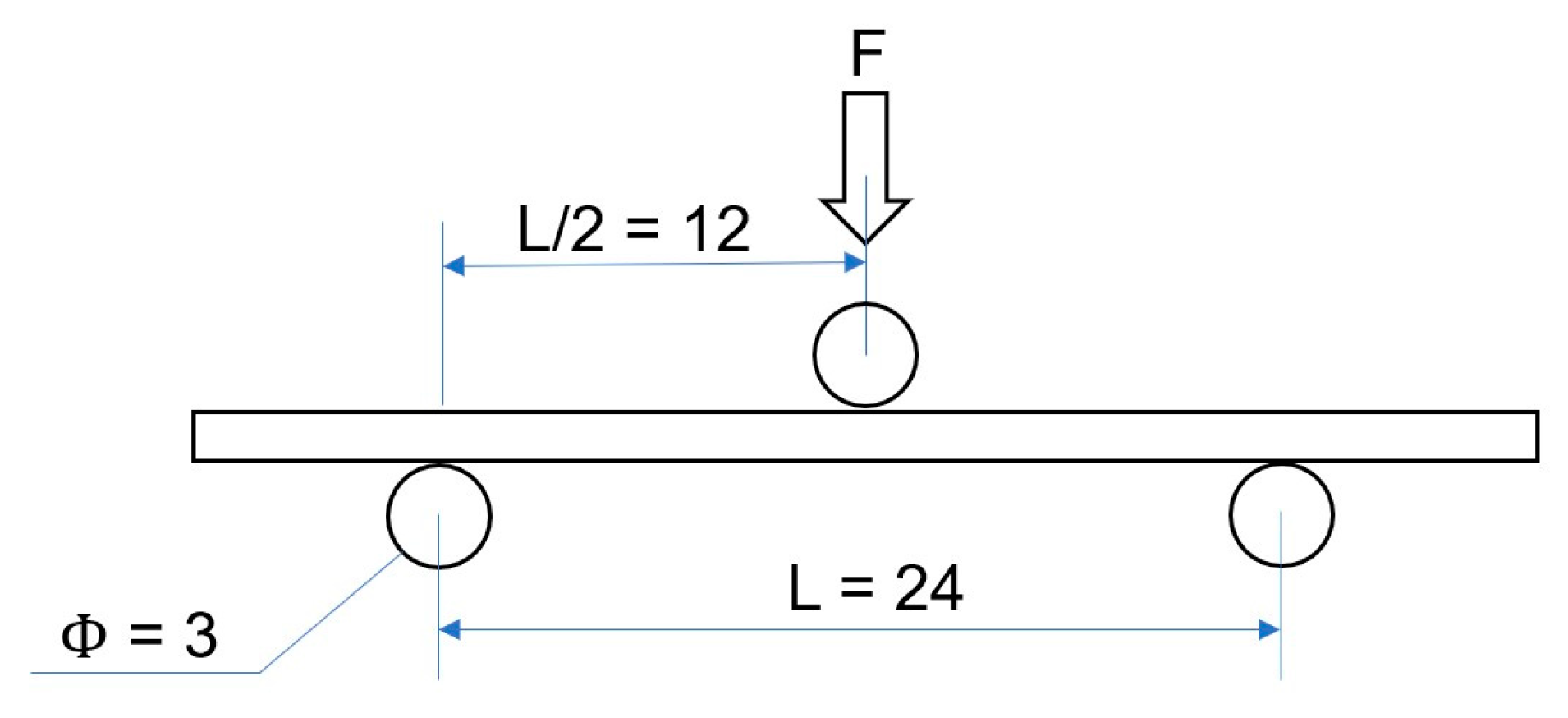
2.2. Determination of Modulus of Rupture and Modulus of Elasticity in Static Bending Using Standard Wood Samples

The determination of the modulus of rupture (MOR) and modulus of elasticity in bending (MOE) were provided according to ISO 13061-3:2014 [48] and ISO 13061-4:2014 [49], respectively. Standard wood samples (ST) were used. The MOR and MOE of yellow pine was carried out using an Instron® testing machine, model 3369 (Instron®, Norwood, MA, USA). The span length in the bending test for standard samples was 240 mm, the load speed was 5 mm × min−1. Twenty samples were used to determine the yellow pine wood properties.

2.3. Determination of Modulus of Rupture and Modulus of Elasticity in Static Bending of Earlywood (EW) and Latewood (LW) from the Yellow Pine Sapwood Area

The MOR and MOE of the earlywood (EW) and latewood (LW) samples of the yellow pine were determined. The samples had the following dimensions: 2 mm (radial) × 2 mm (tangential) × 55 mm (longitudinal). Twenty samples of the yellow pine were used to determine the MOR and MOE of each wood zone (earlywood, latewood). The scheme for samples preparation for the MOR and MOE of earlywood and latewood determination is presented in Figure 1. The annual ring of solid wood gradually varies in one year. Therefore, the boundary between the earlywood and latewood was determined based on density criterion. The MOR and MOE of earlywood and latewood were determined according to ISO 13061-3:2014 [48] and ISO 13061-4:2014 [49] standards, with minor alterations. It resulted from the size of the wood samples obtained from the annual growth ring zone. For the samples of earlywood and latewood, the spacing of supports was 24 mm. The load speed in the bending test for earlywood and latewood samples was 1 mm × min−1. The samples were tested according to test arrangement for the three-point bending (Figure 2). Shimadzu AG-X Plus testing machine (Shimadzu Analytical & Measuring Instruments Division, Tokyo, Japan) was used to examine wood samples. A different testing machine was used to determine the MOR and MOE of earlywood and latewood than to determine the standard samples of yellow pine wood. This resulted from the need to select the appropriate range of loading forces and load speed in relation to the size of the tested samples.

2.4. Statistical Analysis

The statistical analysis of test results was carried out based on the STATISTICA (version-13.3) software of StatSoft, Inc. (TIBCO Software Inc., Palo Alto, CA, USA). The t-test and the Fischer’s F-test, with a significance level (p) of 0.050, were used.

3. Results

The average density of yellow pine sapwood (standard samples—ST) with the determined moisture content of 8–10% was 467 ± 48 kg × m−3 (Figure 3a). This density was in the range of 340–500 kg × m−3 for pine wood with a moisture content of 12–15% that given by Wagenführ [11]. The density of earlywood (EW) was 366 ± 57 kg × m−3, whilst the density of latewood (LW) was 699 ± 39 kg × m−3, and these differences were statistically significant (t-test, p ≤ 0.050).
The modulus of rupture (MOR) determined using the standard samples (ST) of yellow pine wood was 68.3 ± 24.9 MPa (Figure 3b). The MOR was in the range of 41–71 MPa for the yellow pine, as given by Wagenführ [11]. The MOR of the standard samples was from the lower range for the MOR of the Scots pine (Pinus sylvestris L.), estimated in the range of 41–205 MPa [11]. The MOR of the earlywood (EW) was 72.2 ± 14.6 MPa, and thus, it was about 6% higher than the MOR of the pine wood determined using standard samples, and these differences were not statistically significant (t-test, p > 0.050). However, the MOR of the latewood (LW) was 187.7 ± 18.4 MPa. It was approximately three times higher than the MOR of the pine wood determined using standard samples, and these differences were statistically significant (t-test, p ≤ 0.050). The MOR of the latewood was 2.5 times higher than the MOR of the earlywood. These relationships result from the higher density of latewood compared to earlywood (Figure 3a). Based on previously conducted research by Mańkowski and Laskowska [5], it was determined that the latewood tracheids had a 1.5-times-greater thickness than the earlywood tracheids. These dependencies concerned the thickness of tangential and radial walls of tracheids. The diameter of earlywood tracheids in the radial direction was greater than the diameter in the tangential direction. It was the opposite in latewood tracheids. Latewood tracheids were flattened in the radial direction, which is characteristic of softwood [11,50]. Mańkowski and Laskowska [5] concluded that in the radial direction, the diameter of the earlywood tracheids in yellow pine was twice as large compared to the diameter of the latewood tracheids. The earlywood tracheid diameter in the tangential direction was similar to the latewood tracheid diameter in this direction. This resulted in a two-times-lower density of the earlywood compared to the latewood. The observation confirms that wood density cannot be treated as the only factor shaping wood mechanical properties [26,51].
The modulus of elasticity in bending (MOE) determined using the standard samples (ST) of pine wood was 7520 ± 2552 MPa (Figure 3c). According to the literature data [11], the MOE of yellow pine wood ranges from 8270 MPa to 11,350 MPa. The MOE determined for standard samples of yellow pine was in the lower range of values determined for Scots pine (Pinus sylvestris L.), estimated in the range of 6900–20,100 MPa [11]. The MOE of earlywood (EW) was 5107 ± 927 MPa, and thus, it was about 32% lower compared to the MOE determined for standard samples of pine wood, and these differences were statistically significant (t-test, p ≤ 0.050). The MOE of latewood (LW) was 10,385 ± 1185 MPa. It was about 38% higher than the MOE of the pine wood determined using standard samples, and these differences were statistically significant (t-test, p ≤ 0.050). The MOE of latewood was 2 times higher than the MOE of earlywood. This was influenced by the density of the individual wood zones and the dimensions of the tracheids [5,52,53]. Moliński and Krauss [26] studied the radial gradients of the density and wood elasticity modulus in a tensile test. Microtome samples were obtained from earlywood and latewood in annual growth rings of pine wood. The authors stated that the elasticity modulus of earlywood was independent of the cambial age of annual rings, whereas the elasticity modulus of latewood increases with increasing cambial age of annual rings. The changes in the elastic modulus resulted from changes in wood density and microfibril angle (MFA) in tracheid walls.
Load–deflection curves of yellow pine wood under bending test are presented in Figure 4. These curves are characteristic for wood when subjected to a three-point bending load [54,55,56]. The direction of the changes in the deflection was the same regardless of the wood zone and sample type (earlywood, latewood, standard samples). The differences were visible in the size of these changes, i.e., load and deflection values. The destructive force increases until the earlywood and latewood samples are destroyed. In the case of standard samples, the weakest zones of wood crack in the sample, which is visible in the figure as the local maxima. The load–deflection curves indicate that the failure mode of the latewood was ductile, and that of the earlywood was nearly brittle. This translated into different failure patterns and on the values of MOR and MOE. The samples of earlywood and latewood of yellow pine wood after bending test are presented in Figure 5. The failure type of the earlywood (Figure 5a) and latewood (Figure 5b) in the bending test with the span parallel to the grain can be described as splintering tension. The same type of failure is exhibited by the standard samples (Figure 5c).
The maximum load (Fmax) transferred by latewood zones was 65 ± 9 N, which was four times higher than the Fmax (16 ± 5 N) transferred by the earlywood zones. The deflection at the Fmax of the earlywood zone was 1.21 ± 0.21 mm, and it was about 20% smaller than the deflection (1.47 ± 0.24 mm) at the Fmax of the latewood zone. The load-carrying capacity depends on the size of the samples [57,58]. The standard samples of yellow pine wood carried a maximum load of 1525 ± 478 N, and the deflection at the maximum load was 6.75 ± 1.13 mm.
The relationship between the density and MOR of yellow pine wood was shown in Figure 6a. The linear approximation of the relationship is presented. The R2 ratio for the standard samples (ST) was 0.81. Much lower values of the R2 ratio were recorded for the density–MOR relationship for “small” samples, i.e., latewood (LW) samples (R2 at 0.44) and earlywood (EW) samples (R2 at 0.24). This showed that the MOR of the earlywood and latewood was slightly determined by density. Similar dependencies were noted for the density–MOE relationship (Figure 6b). The R2 ratio for MOE determined for standard samples was 0.87. Much lower values of the R2 ratio were recorded for the density–MOE relationship for “small” samples, i.e., latewood samples (R2 at 0.42) and earlywood (R2 at 0.15). This confirms that regardless of the type of samples or wood zone, the wood mechanical properties do not depend solely on wood density. Büyüksarı et al. [41] stated that the difference in the mechanical properties, i.e., earlywood (EW) and latewood (LW) of Scots pine could be attributed to the differences in the density and microfibril angle (MFA) of EW and LW. Roszyk [59] indicated that the density of the EW and LW of Scots pine was, respectively, 235 kg × m−3 and 665 kg × m−3, whereas the MFA was, respectively, 16.4° and 9.0°. Some authors [41,45,60,61] stated that the cellulose determined the wood properties for small MFA values. However, for higher MFA values, the mechanical properties of cell walls depend mainly on the matrix hemicelluloses and lignin incrusting the cellulose skeleton. Among the determined properties, the greatest variability was recorded for the MOE (Figure 6b), and the smallest in the case of the MOR (Figure 6a). The wood density changes in the radial direction and is accompanied in particular by changes in the elastic modulus [26]. Fitted curves predicting the MOR and MOE of the yellow pine earlywood (EW) samples, latewood (LW) samples, and standard samples (ST) depending on density (WD) are presented in Table 1. The statistical results for the linear regression lines showed that only the linear regression for the density—MOE of earlywood is not significant (p > 0.050).
High R2 values were recorded for the relationship between the modulus of rupture (MOR) and modulus of elasticity in bending (MOE) of yellow pine wood (Figure 7). This confirms a strong dependence of MOR on the value of the yellow pine MOE regardless of the type of samples and wood zone. These relationships can be described by the equations: MOREW = 0.011 MOE + 13.531 for earlywood, MORLW = 0.013 MOE + 49.695 for latewood, and MORST = 0.009 MOE + 1.015 for the standard samples.

4. Conclusions

The research conducted indicates the differences in the properties of yellow pine wood regardless of the wood zone and sample type (earlywood, latewood, standard samples):
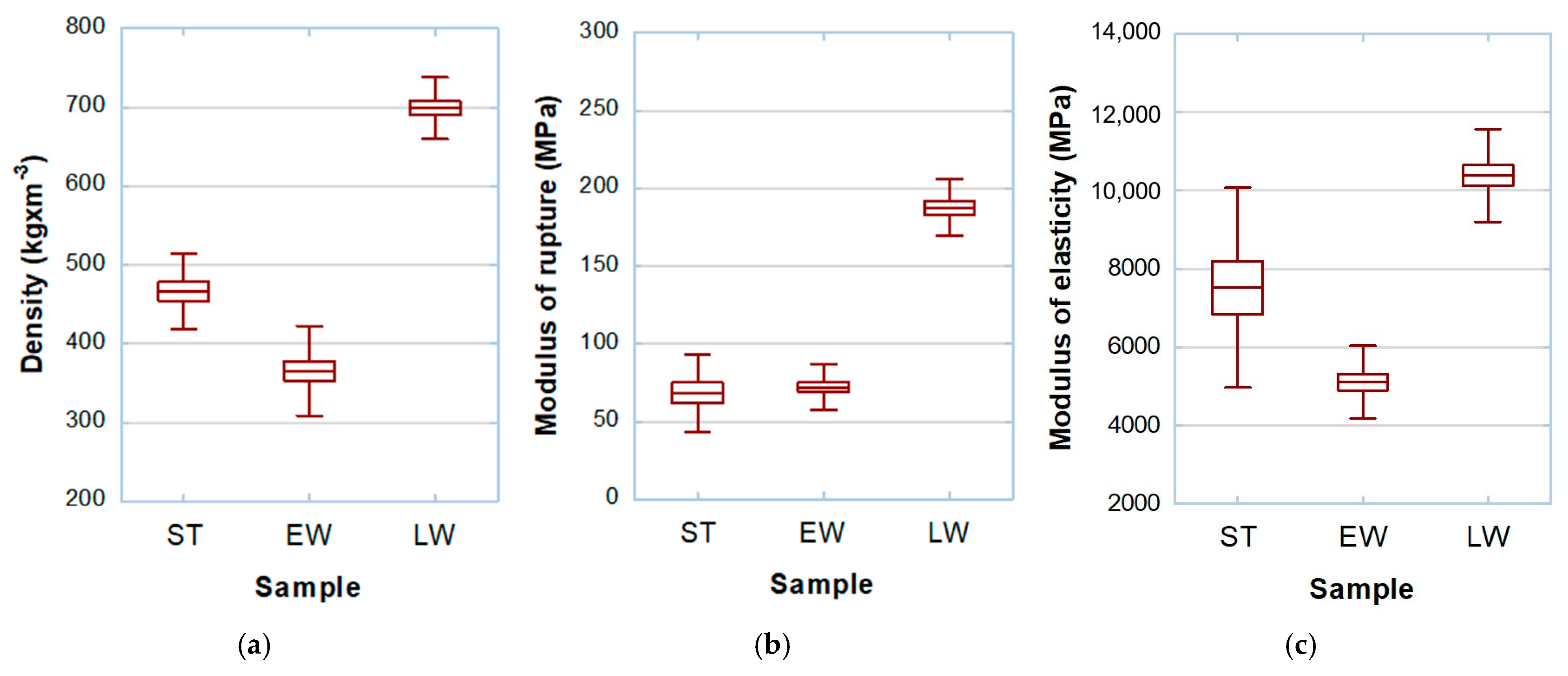
  • The density of the yellow pine earlywood was 22% lower than the density of sapwood. The density of the latewood was 50% higher than the density of the sapwood. In general, it should be stated that the density of the latewood was twice as high as the density of the earlywood of yellow pine.
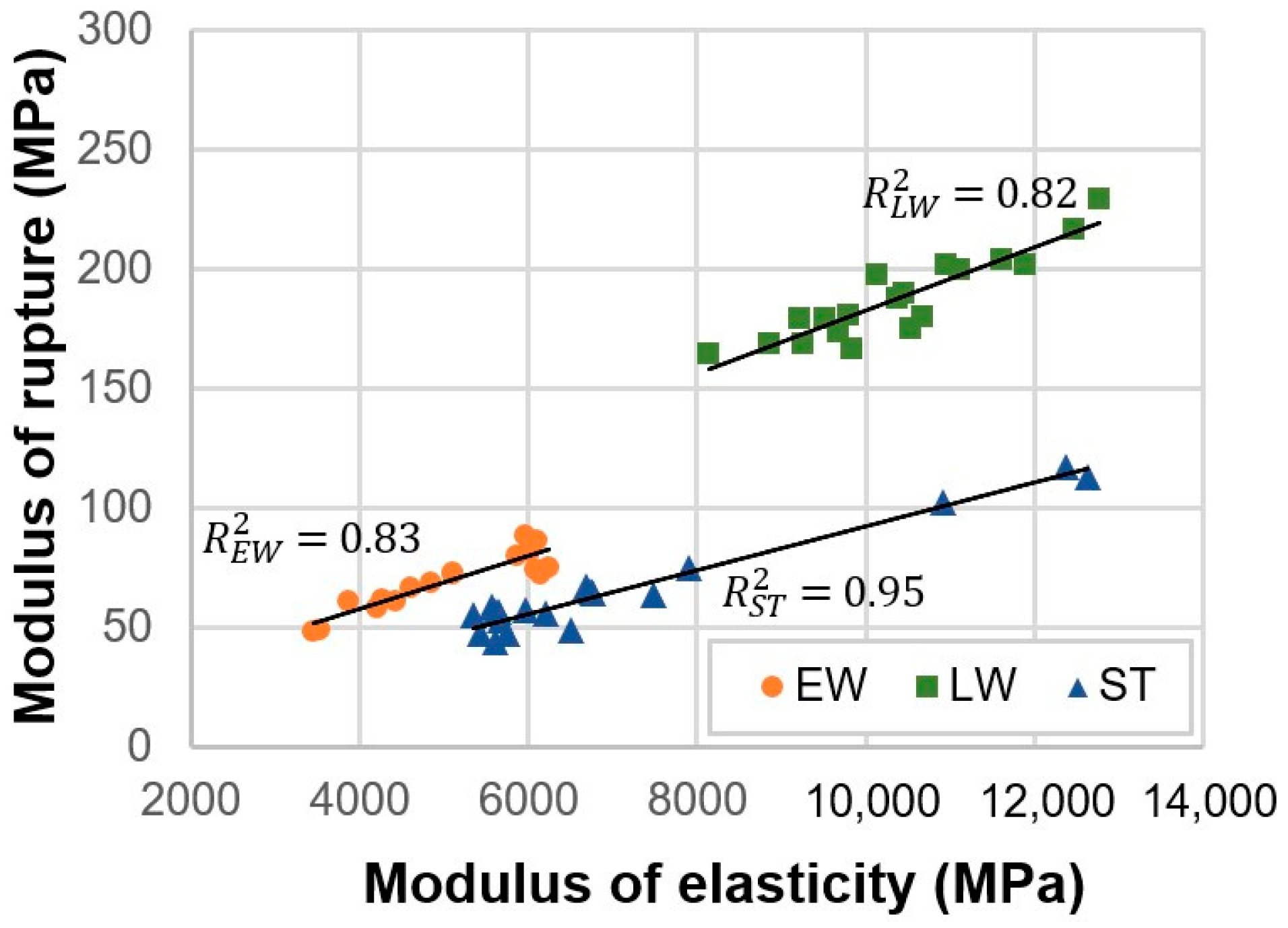
  • The modulus of rupture of the yellow pine earlywood was about 6% higher than the modulus of rupture of the pine wood, determined using standard samples, and these differences were not statistically significant. The modulus of rupture of the latewood was approximately three times higher than the modulus of rupture of the pine wood determined using standard samples, and these differences were statistically significant. The modulus of rupture of latewood was 2.5 times higher than the modulus of rupture of the earlywood.
  • The modulus of elasticity of the earlywood was about 32% lower than the modulus of elasticity of the pine wood determined using standard samples, and these differences were statistically significant. The modulus of elasticity of the latewood was about 38% higher than the modulus of elasticity of the pine wood determined using standard samples, and these differences were statistically significant. The modulus of elasticity of the latewood was found to be two times higher than the modulus of elasticity of the earlywood.
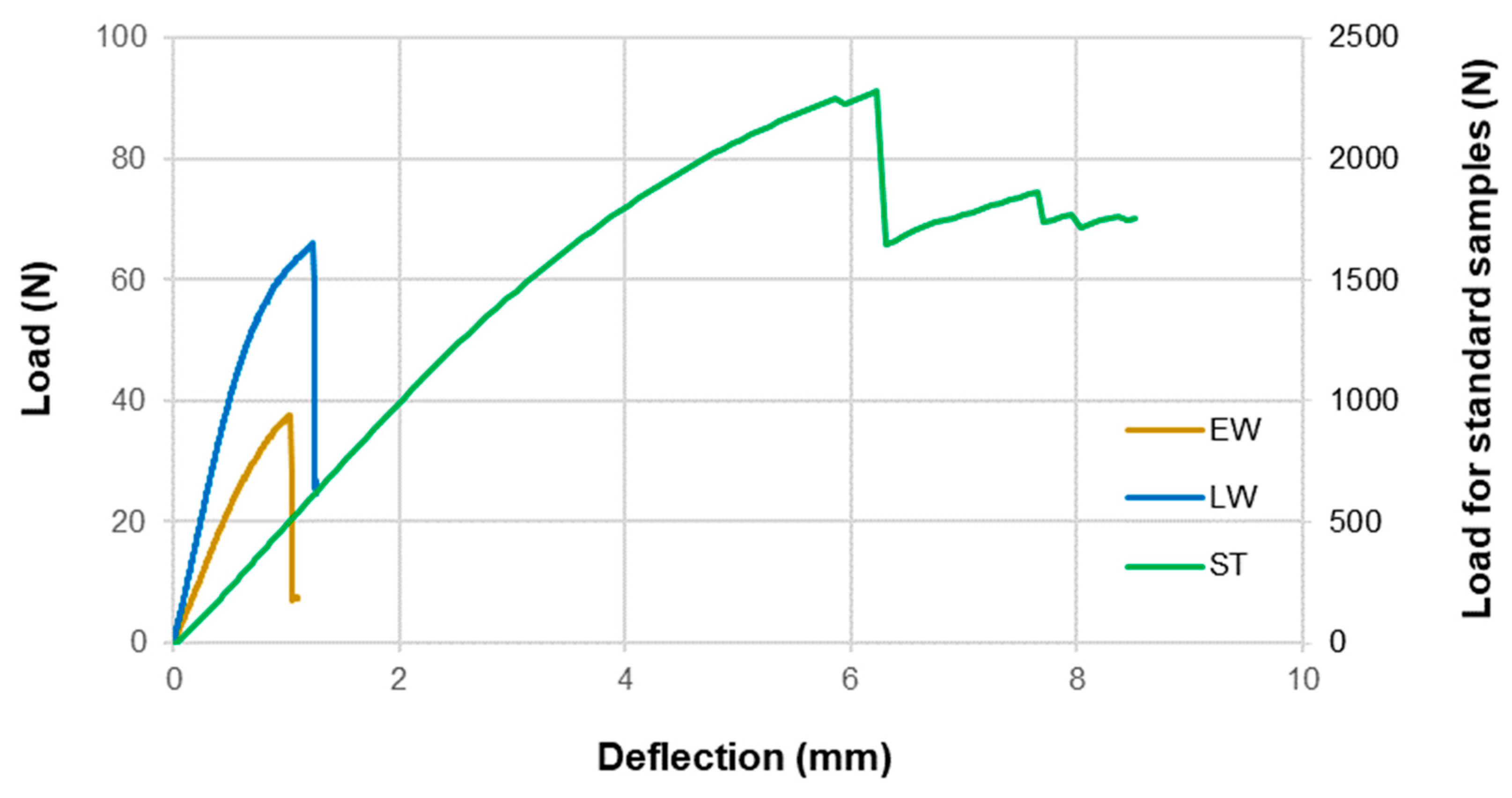
  • The maximum load transferred by latewood zones was four times higher than the maximum load transferred by earlywood zones. The deflection at the maximum load of earlywood zones was 20% smaller than the deflection at the maximum load of latewood zones.

Author Contributions

Conceptualization, Z.K., P.M. and A.L.; methodology, Z.K., P.M. and A.L.; formal analysis, A.L. and P.M.; investigation, A.L. and P.M.; resources, A.L. and P.M.; data curation, A.L.; writing—original draft preparation, A.L.; writing—review and editing, A.L. and P.M; visualization, A.L.; supervision, A.L. and P.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Goodman, J.R.; Bodig, J. Orthotropic elastic properties of wood. J. Struct. Div. 1970, 96, 2301–2319. [Google Scholar] [CrossRef]
  2. Wilczyński, A.; Gogolin, M. Badanie Właściwości Sprężystych Drewna Sosny, Buka i Dębu [Investigation of the Elastic Properties of Pine, Beech and Oak Wood]; Zeszyty Naukowe Wyższej Szkoły Pedagogicznej w Bydgoszczy: Studia Techniczne, 15; Biblioteka Uniwersytetu Kazimierza Wielkiego: Bydgoszcz, Poland, 1989. [Google Scholar]
  3. Bergander, A.; Salmén, L. Variations in transverse fibre wall properties: Relations between elastic properties and structure. Holzforschung 2000, 54, 654–660. [Google Scholar] [CrossRef]
  4. Andersson, F.A. (Ed.) Coniferous Forests, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2005; Volume 6, ISBN 9780444816276. [Google Scholar]
  5. Mańkowski, P.; Laskowska, A. Compressive strength parallel to grain of earlywood and latewood of yellow pine. Maderas-Cienc. Tecnol. 2021, 23, 1–12. [Google Scholar] [CrossRef]
  6. Paschalis-Jakubowicz, P.; Kulik, P.; Lachowicz, H. Kształtowanie cen oraz metody sprzedaży surowca cennego w Polsce [Prices and sales methods of the valuable timber in Poland]. Sylwan 2015, 159, 267–277. [Google Scholar]
  7. Mikołajczak, E.; Wieruszewski, M.; Wanat, L. A sustainable roundwood pricing strategy as an opportunity or a threat for the development of wood-based industry in Poland. In Proceedings of the 13th International Scientific Conference WoodEMA 2020 and the 31st International Scientfic Conference ICWST 2020, Vinkovci, Croatia, 28–30 September 2020; pp. 245–250. [Google Scholar]
  8. Zastocki, D.; Oktaba, J.; Lachowicz, H. Changes in the Market of Precious Wood: A Case Study of Submission System in Poland. Forests 2021, 12, 421. [Google Scholar] [CrossRef]
  9. Kollmann, F.; Côté, W. Principles of Wood Science and Technology; Springer: Berlin/Heidelberg, Germany, 1968; Volume 1: Solid Wood. [Google Scholar]
  10. Burawska-Kupniewska, I.; Mańkowski, P.; Krzosek, S. Mechanical Properties of Machine Stress Graded Sawn Timber Depending on the Log Type. Forests 2021, 12, 532. [Google Scholar] [CrossRef]
  11. Wagenführ, R. Holzatlas [The Atlas of Wood]; Fachbuchverlag Leipzig: München, Germany, 2007. [Google Scholar]
  12. EN 408:2010+A1:2012; Timber Structures—Structural Timber and Glued Laminated Timber—Determination of Some Physical and Mechanical Properties. European Committee for Standardization: Brussels, Belgium, 2012.
  13. EN 384:2016+A2:2022; Structural Timber—Determination of Characteristic Values of Mechanical Properties and Density. European Committee for Standardization: Brussels, Belgium, 2022.
  14. Šilinskas, B.; Varnagiryte-Kabašinskiene, I.; Aleinikovas, M.; Beniušiene, L.; Aleinikoviene, J.; Škema, M. Scots pine and Norway spruce wood properties at sites with different stand densities. Forests 2020, 11, 587. [Google Scholar] [CrossRef]
  15. Vega, M.; Hamilton, M.; Downes, G.; Harrison, P.A.; Potts, B. Radial variation in modulus of elasticity, microfibril angle and wood density of veneer logs from plantation-grown Eucalyptus nitens. Ann. For. Sci. 2020, 77, 65. [Google Scholar] [CrossRef]
  16. Alteyrac, J.; Cloutier, A.; Zhang, S.Y. Characterization of juvenile wood to mature wood transition age in black spruce (Picea mariana (Mill.) B.S.P.) at different stand densities and sampling heights. Wood Sci. Technol. 2006, 40, 124–138. [Google Scholar] [CrossRef]
  17. Krauss, A.; Moliński, W.; Kúdela, J.; Čunderlík, I. Differences in the mechanical properties of early and latewood within individual annual rings in dominant pine tree (Pinus sylvestris L.). Wood Res. 2011, 56, 1–12. [Google Scholar]
  18. Huang, Y.; Fei, B.; Yu, Y.; Wang, S.; Shi, Z.; Zhao, R. Modulus of elasticity and hardness of compression and opposite wood cell walls of masson pine. BioResources 2012, 7, 3028–3037. [Google Scholar] [CrossRef]
  19. Moya, L.; Laguarda, M.F.; Cagno, M.; Cardoso, A.; Gatto, F.; O’Neill, H. Physical and Mechanical Properties of Loblolly and Slash Pine Wood from Uruguayan Plantations. For. Prod. J. 2013, 63, 128–137. [Google Scholar] [CrossRef]
  20. Mania, P.; Nowicki, M. Nanohardness and elasticity of cell walls of Scots pine (Pinus sylvestris L.) juvenile and mature wood. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 1237–1241. [Google Scholar] [CrossRef]
  21. Prosiński, S. Chemia Drewna [Chemistry of Wood]; PWRiL: Warsaw, Poland, 1984. [Google Scholar]
  22. Kacik, F.; Solár, R. Analyticka Chemia Dreva [Analitical Chemistry of Wood]; Technicka Univerzita vo Zwolene: Zwolen, Slowak, 1999. [Google Scholar]
  23. Solár, R. Chémia Dreva [Chemistry of Wood]; Technicka Univerzita vo Zwolene: Zwolen, Slowak, 2004. [Google Scholar]
  24. Grotta, A.T.; Leichti, R.J.; Gartner, B.L.; Johnson, G.R. Effect of growth ring orientation and placement of earlywood and latewood on MOE and MOR of very-small clear Douglas-Fir beams. Wood Fiber Sci. 2005, 37, 207–212. [Google Scholar]
  25. Kretschmann, D.E.; Cramer, S.M. The role of earlywood and latewood properties on dimensional stability of loblolly pine. In Proceedings of the Compromised Wood Workshop, Christchurch, New Zealand, 29–30 January 2007; Wood Technology Research Centre, School of Forestry, University of Canterbury: Christchurch, New Zealand, 2007; pp. 215–236, ISBN 978-0-473-12768-8. [Google Scholar]
  26. Moliński, W.; Krauss, A. Radial gradient of modulus of elasticity of wood and tracheid cell walls in dominant pine trees (Pinus sylvestris L.). Folia Forestalia Polonica. Ser. B Drzew. 2008, 39, 19–29. [Google Scholar]
  27. Rocha, M.F.V.; Costa, L.R.; Costa, L.J.; De Araújo, A.C.C.; Soares, B.C.D.; Hein, P.R.G. Wood knots influence the modulus of elasticity and resistance to compression. Floresta e Ambiente 2018, 25, e20170906. [Google Scholar] [CrossRef]
  28. Ruel, J.J.; Ayres, M.P.; Lorio, P.L. Loblolly pine responds to mechanical wounding with increased resin flow. Can. J. Bot. 1998, 28, 596–602. [Google Scholar] [CrossRef]
  29. Wieruszewski, M.; Trociński, A.; Kawalerczyk, J.; Derkowski, A.; Mirski, R. The Strength of Pine (Pinus sylvestris L.) Sawn Timber in Correlation with Selected Wood Defects. Materials 2022, 15, 3974. [Google Scholar] [CrossRef] [PubMed]
  30. Green, D.W.; Gorman, T.M.; Murphy, J.F.; Wheeler, M.B. Moisture Content and the Properties of Lodgepole Pine Logs in Bending and Compression Parallel to the Grain; Research Paper FPL-RP-639; Forest Products Laboratory, U.S. Department of Agriculture, Forest Service: Madison, WI, USA, 2007. [Google Scholar] [CrossRef]
  31. Glass, S.V.; Zelinka, S.L. Moisture Relations and Physical Properties of Wood. In Wood Handbook; General Technical Report FPL-GTR-190; Forest Products Laboratory, U.S. Department of Agriculture, Forest Service: Madison, WI, USA, 2010; Chapter 4; pp. 1–19. [Google Scholar]
  32. Ishimaru, Y.; Arai, K.; Mizutani, M.; Oshima, K.; Iida, I. Physical and mechanical properties of wood after moisture conditioning. J. Wood Sci. 2001, 47, 185–191. [Google Scholar] [CrossRef]
  33. Li, W.; Zhang, Y.; Wang, X.; Wang, J. Relationship between structural characteristics of growth rings and strain accumulation in thermally modified Douglas fir wood during compressive test. Wood Mater. Sci. Eng. 2024, 1–10. [Google Scholar] [CrossRef]
  34. Li, W.; Yang, K.; Zhang, Y.; Shi, J.; Van den Buckle, J.; Acker, J.V. The effect of growth-ring orientation on the compressive performance of Douglas fir. Wood Mater. Sci. Eng. 2024, 19, 131–142. [Google Scholar] [CrossRef]
  35. Zink-Sharp, A.; Price, C. Intra-ring compression strength of low density hardwoods. Maderas-Cienc. Tecnol. 2006, 8, 117–126. [Google Scholar] [CrossRef]
  36. Auty, D.; Achim, A.; MacDonald, E.; Cameron, A.; Gardiner, B. Models for Predicting Clearwood Mechanical Properties of Scots Pine. For. Sci. 2016, 62, 403–413. [Google Scholar] [CrossRef]
  37. Verkasalo, E.; Leban, J.M. MOE and MOR in static bending of small clear specimens of Scots pine, Norway spruce and European fir from Finland and France and their prediction for the comparison of wood quality. Pap. Timber J. Finish For. Ind. 2002, 84, 332–340. [Google Scholar]
  38. Bytner, O.; Drożdżek, M.; Laskowska, A.; Zawadzki, J. Influence of Thermal Modification in Nitrogen Atmosphere on the Selected Mechanical Properties of Black Poplar Wood (Populus nigra L.). Materials 2022, 15, 7949. [Google Scholar] [CrossRef]
  39. Cramer, S.; Kretschmann, D.; Lakes, R.; Schmidt, T. Earlywood and latewood elastic properties in loblolly pine. Holzforschung 2005, 59, 531–538. [Google Scholar] [CrossRef]
  40. Lanvermann, C.H.; Hass, P.H.; Wittel, F.K.; Niemz, P. Mechanical Properties of Norway Spruce: Intra-Ring Variation and Generic Behavior of Earlywood and Latewood until Failure. BioResources 2014, 9, 105–119. [Google Scholar] [CrossRef]
  41. Büyüksarı, Ü.; As, N.; Dündar, T. Mechanical Properties of Earlywood and Latewood Sections of Scots Pine Wood. BioResources 2017, 12, 4004–4012. [Google Scholar] [CrossRef]
  42. Büyüksarı, Ü.; As, N.; Dündar, T. Intra-Ring Properties of Earlywood and Latewood Sections of Sessile Oak (Quercus petraea). BioResources 2018, 13, 836–845. [Google Scholar] [CrossRef]
  43. Groom, L.; Shaler, S.; Mott, L. Mechanical properties of individual southern pine fibers. Part III. Global relationships between fiber properties and fiber location within an individual tree. Wood Fiber Sci. 2002, 34, 238–250. [Google Scholar]
  44. Wimmer, R.; Lucas, B.N.; Tsui, T.Y.; Oliver, W.C. Longitudinal hardness and Young’s modulus of spruce tracheid secondary walls using nanoindentation technique. Wood Sci. Technol. 1997, 31, 131–141. [Google Scholar] [CrossRef]
  45. Bergander, A.; Salmén, L. Cell wall properties and their effects on the mechanical properties of fibers. J. Mater. Sci. Lett. 2002, 37, 151–156. [Google Scholar] [CrossRef]
  46. ISO 13061-1:2014; Physical and Mechanical Properties of Wood—Test Methods for Small Clear Wood Specimens—Part 1: Determination of Moisture Content for Physical and Mechanical Tests. International Organization of Standardization: Geneva, Switzerland, 2014.
  47. ISO 13061-2:2014; Physical and Mechanical Properties of Wood—Test Methods for Small Clear Wood Specimens—Part 2: Determination of Density for Physical and Mechanical Tests. International Organization of Standardization: Geneva, Switzerland, 2014.
  48. ISO 13061-3:2014; Physical and Mechanical Properties of Wood—Test Methods for Small Clear Wood Specimens—Part 3: Determination of Ultimate Strength in Static Bending. International Organization of Standardization: Geneva, Switzerland, 2014.
  49. ISO 13061-4:2014; Physical and Mechanical Properties of Wood—Test Methods for Small Clear Wood Specimens—Part 4: Determination of Modulus of Elasticity in Static Bending. International Organization of Standardization: Geneva, Switzerland, 2014.
  50. Kozakiewicz, P.; Życzkowski, W. Physical and mechanical properties and anatomy of common juniper (Juniperus communis L.) wood. Sylwan 2015, 159, 151–159. [Google Scholar] [CrossRef]
  51. Cave, I.D.; Walker, J.C.F. Stiffness of wood in fast-grown plantation softwoods: The influence of microfibril angle. For. Prod. J. 1994, 44, 43–48. [Google Scholar]
  52. Peltola, H.; Gort, J.; Pulkkinen, P.; Zubizarreta Gerendiain, A.; Karppinen, J.; Ikonen, V.P. Differences in growth and wood density traits in Scots pine (Pinus sylvestris L.) genetic entries grown at different spacing and sites. Silva Fenn. 2009, 43, 339–354. [Google Scholar] [CrossRef]
  53. Traoré, M.; Kaal, J.; Martínez Cortizas, A. Differentiation between pine woods according to species and growing location using FTIR-ATR. Wood Sci. Technol. 2018, 52, 487–504. [Google Scholar] [CrossRef]
  54. Danawade, B.A.; Malagi, R.R.; Patil, B.S.; Hanamapure, R.S. Effect of finger joint on flexural strength of teak wood. Int. J. Eng. Technol. 2014, 5, 4929–4937. [Google Scholar]
  55. Souppez, J.B.R. Timber construction: An experimental assessment of the strength of scarf joints and the effectiveness of various adhesives for laminated wood. In Historic Ships; The Royal Institution of Naval Architects (RINA): London, UK, 2020; pp. 53–60. [Google Scholar]
  56. Hu, W.; Yu, R. Mechanical and acoustic characteristics of four wood species subjected to bending load. Maderas. Cienc. Tecnol. 2023, 25, 1–12. [Google Scholar] [CrossRef]
  57. Sokołowski, P.K.; Kossakowski, P.G. Static Analysis of Wooden Beams Strengthened with FRCM-PBO Composite in Bending. Materials 2023, 16, 1870. [Google Scholar] [CrossRef]
  58. Bakalarz, M.M. Mechanical Properties of Full-Scale Wooden Beams Strengthened with Carbon-Fibre-Reinforced Polymer Sheets. Materials 2024, 17, 4917. [Google Scholar] [CrossRef]
  59. Roszyk, E. The effect of ultrastructure and moisture content on mechanical parameters of pine wood (Pinus sylvestris L.) upon tensile stress along the grains. Turk. J. Agric. For. 2014, 38, 413–419. [Google Scholar] [CrossRef]
  60. Roszyk, E.; Moliński, W.; Kamiński, M. Tensile properties along the grains of earlywood and latewood of Scots pine (Pinus sylvestris L.) in dry and wet state. BioResources 2016, 11, 3027–3037. [Google Scholar] [CrossRef]
  61. Barnett, J.R.; Bonham, V.A. Cellulose microfibril angle in the cell wall of wood fibres. Biol. Rev. 2004, 79, 461–472. [Google Scholar] [CrossRef] [PubMed]
Forests 16 00265 g001
Figure 1. Scheme of preparation of the test specimens of yellow pine earlywood (EW) and latewood (LW).
Figure 1. Scheme of preparation of the test specimens of yellow pine earlywood (EW) and latewood (LW).
Forests 16 00265 g001
Forests 16 00265 g002
Figure 2. Test arrangement for the three-point bending to measure modulus of rupture (MOR) and modulus of elasticity in bending (MOE) of earlywood (EW) and latewood (LW) of yellow pine.
Figure 2. Test arrangement for the three-point bending to measure modulus of rupture (MOR) and modulus of elasticity in bending (MOE) of earlywood (EW) and latewood (LW) of yellow pine.
Forests 16 00265 g002
Forests 16 00265 g003
Figure 3. (a) Density, (b) modulus of rupture (MOR), (c) modulus of elasticity in bending (MOE) of yellow pine wood (ST—standard samples; EW—earlywood; LW—latewood).
Figure 3. (a) Density, (b) modulus of rupture (MOR), (c) modulus of elasticity in bending (MOE) of yellow pine wood (ST—standard samples; EW—earlywood; LW—latewood).
Forests 16 00265 g003
Forests 16 00265 g004
Figure 4. Load–deflection curves of yellow pine wood under bending test (EW—earlywood; LW—latewood; ST—standard samples).
Figure 4. Load–deflection curves of yellow pine wood under bending test (EW—earlywood; LW—latewood; ST—standard samples).
Forests 16 00265 g004
Forests 16 00265 g005
Figure 5. The (a) earlywood (EW), (b) latewood (LW), and (c) standard samples (ST) of yellow pine wood after bending test.
Figure 5. The (a) earlywood (EW), (b) latewood (LW), and (c) standard samples (ST) of yellow pine wood after bending test.
Forests 16 00265 g005
Forests 16 00265 g006
Figure 6. (a) The relationship between the density and modulus of rupture (MOR); (b) the relationship between the density and modulus of elasticity in bending (MOE) of yellow pine wood (EW—earlywood; LW—latewood; ST—standard samples).
Figure 6. (a) The relationship between the density and modulus of rupture (MOR); (b) the relationship between the density and modulus of elasticity in bending (MOE) of yellow pine wood (EW—earlywood; LW—latewood; ST—standard samples).
Forests 16 00265 g006
Forests 16 00265 g007
Figure 7. The relationship between the modulus of rupture (MOR) and modulus of elasticity in bending (MOE) of yellow pine wood (EW—earlywood; LW—latewood; ST—standard samples).
Figure 7. The relationship between the modulus of rupture (MOR) and modulus of elasticity in bending (MOE) of yellow pine wood (EW—earlywood; LW—latewood; ST—standard samples).
Forests 16 00265 g007
Table 1. Fitted curves predicting the modulus of rupture (MOR) and modulus of elasticity in bending (MOE) of yellow pine earlywood (EW) samples, latewood (LW) samples, and standard samples (ST) depending on density (WD). Statistical results of the linear regression line.
Table 1. Fitted curves predicting the modulus of rupture (MOR) and modulus of elasticity in bending (MOE) of yellow pine earlywood (EW) samples, latewood (LW) samples, and standard samples (ST) depending on density (WD). Statistical results of the linear regression line.
Wood SamplePropertyStatistical Parameters
MORF-ValueSignificance Level p
EWMOREW = 0.118 WD + 28.9935.566p < 0.050
LWMORLW = 0.295 WD − 18.81914.265p < 0.050
STMORST = 0.419 WD − 124.49174.430p < 0.050
MOEF-ValueSignificance Level p
EWMOEEW = 6.343 WD + 27883.202p > 0.050
LWMOELW = 19.64 WD − 334512.999p < 0.050
STMOEST = 46.18 WD − 13,866116.37p < 0.050
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Mańkowski, P.; Karwat, Z.; Laskowska, A. Assessment of the Modulus of Rupture and Modulus of Elasticity in Static Bending of Yellow Pine Earlywood and Latewood. Forests 2025, 16, 265. https://doi.org/10.3390/f16020265

AMA Style

Mańkowski P, Karwat Z, Laskowska A. Assessment of the Modulus of Rupture and Modulus of Elasticity in Static Bending of Yellow Pine Earlywood and Latewood. Forests. 2025; 16(2):265. https://doi.org/10.3390/f16020265

Chicago/Turabian Style

Mańkowski, Piotr, Zbigniew Karwat, and Agnieszka Laskowska. 2025. "Assessment of the Modulus of Rupture and Modulus of Elasticity in Static Bending of Yellow Pine Earlywood and Latewood" Forests 16, no. 2: 265. https://doi.org/10.3390/f16020265

APA Style

Mańkowski, P., Karwat, Z., & Laskowska, A. (2025). Assessment of the Modulus of Rupture and Modulus of Elasticity in Static Bending of Yellow Pine Earlywood and Latewood. Forests, 16(2), 265. https://doi.org/10.3390/f16020265

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop