Genetics of Growth and Stem Straightness Traits in Pinus taeda in Argentina: Exploring Genetic Competition Across Ages and Sites
Abstract
:1. Introduction
2. Materials and Methods
2.1. Genetic Material, Trial Description, and Trait Evaluated
2.2. Modeling Environmental Heterogeneity and/or Competition Effects
- Spatial (Spa) Mixed Model
- 2.
- Spatial-Competition (Spa-Comp) mixed model
2.3. Parameter Estimation and Model Comparison
3. Results
3.1. Survival, Growth, and Stem Straightness Across Ages and Sites
3.2. Model Convergence and Statistical Significance
3.3. Competition Genetic Effects Across Traits, Ages, and Sites
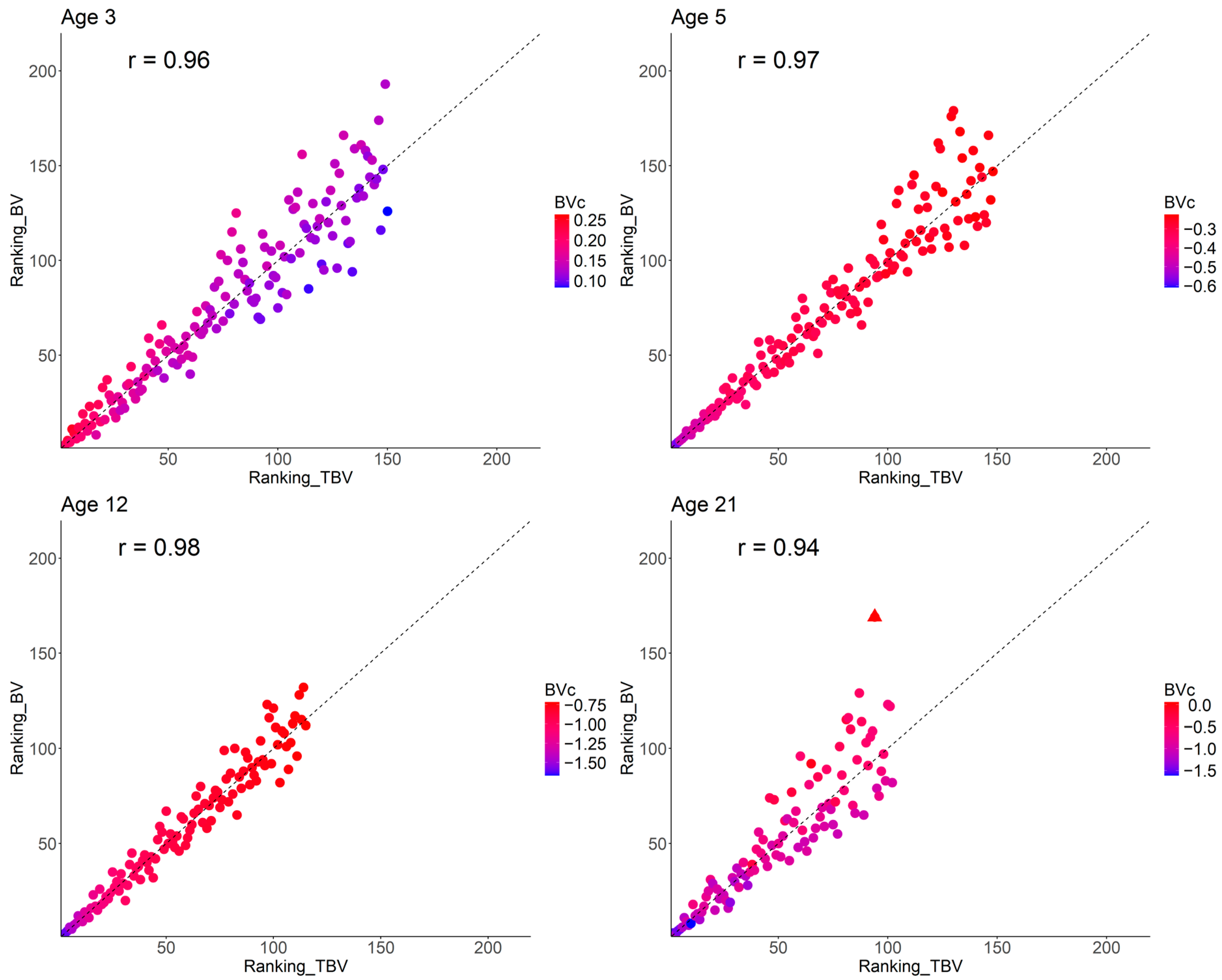
3.4. Breeding Values Accuracy, Response to Selection, and Ranking Changes
4. Discussion
4.1. Dynamics of Genetic Competition Across Traits, Ages, and Sites
4.2. Impact of Competition Genetic Effects on Theoretical Accuracy, Response to Selection, and Ranking
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cappa, E.P.; Cantet, R.J.C. Direct and Competition Additive Effects in Tree Breeding: Bayesian Estimation From an Individual Tree Mixed Model. Silvae Genet. 2008, 57, 45–56. [Google Scholar] [CrossRef]
- Shalizi, M.N.; McKeand, S.E.; Walker, T.D. Age Affects Genetic Gain Estimates in Pinus taeda L. Progeny Tests. Silvae Genet. 2024, 73, 149–159. [Google Scholar] [CrossRef]
- Brotherstone, S.; White, I.M.S.; Sykes, R.; Thompson, R.; Connolly, T.; Lee, S.; Woolliams, J. Competition Effects in a Young Sitka Spruce (Picea sitchensis, Bong. Carr) Clonal Trial. Silvae Genet. 2011, 60, 149–155. [Google Scholar] [CrossRef]
- Dong, L.; Xie, Y.; Wu, H.X.; Sun, X. Spatial and Competition Models Increase the Progeny Testing Efficiency of Japanese Larch. Can. J. For. Res. 2020, 50, 1373–1382. [Google Scholar] [CrossRef]
- Costa e Silva, J.; Potts, B.M.; Gilmour, A.R.; Kerr, R.J. Genetic-Based Interactions among Tree Neighbors: Identification of the Most Influential Neighbors, and Estimation of Correlations among Direct and Indirect Genetic Effects for Leaf Disease and Growth in Eucalyptus Globulus. Heredity 2017, 119, 125–135. [Google Scholar] [CrossRef]
- Ferreira, F.M.; Chaves, S.F.S.; Bhering, L.L.; Alves, R.S.; Takahashi, E.K.; Sousa, J.E.; Resende, M.D.V.; Leite, F.P.; Gezan, S.A.; Viana, J.M.S.; et al. A Novel Strategy to Predict Clonal Composites by Jointly Modeling Spatial Variation and Genetic Competition. For. Ecol. Manag. 2023, 548, 121393. [Google Scholar] [CrossRef]
- Jansson, G.; Kerr, R.; Dutkowski, G.; Kroon, J. Competition Effects in Breeding Value Prediction of Forest Trees. Can. J. For. Res. 2021, 51, 1002–1014. [Google Scholar] [CrossRef]
- Ferreira, F.M.; Chaves, S.F.D.S.; Dos Santos, O.P.; Nunes, A.C.P.; Tambarussi, E.V.; Pereira, G.D.S.; Dos Santos, G.A.; Bhering, L.L.; Dias, K.O.D.G. Competition Effects Can Mislead Selection in Eucalypt Breeding Trials. For. Ecol. Manag. 2024, 561, 121892. [Google Scholar] [CrossRef]
- Cappa, E.P.; Stoehr, M.U.; Xie, C.-Y.; Yanchuk, A.D. Identification and Joint Modeling of Competition Effects and Environmental Heterogeneity in Three Douglas-Fir (Pseudotsuga menziesii Var. Menziesii) Trials. Tree Genet. Genomes 2016, 12, 102. [Google Scholar] [CrossRef]
- Costa e Silva, J.; Potts, B.M.; Bijma, P.; Kerr, R.J.; Pilbeam, D.J. Genetic Control of Interactions among Individuals: Contrasting Outcomes of Indirect Genetic Effects Arising from Neighbour Disease Infection and Competition in a Forest Tree. New Phytol. 2013, 197, 631–641. [Google Scholar] [CrossRef]
- Hernández, M.A.; López, J.A.; Cappa, E.P. Improving Genetic Analysis of Corymbia Citriodora Subsp. Variegata with Single- and Multiple-Trait Spatial-Competition Models. For. Sci. 2019, 65, 570–580. [Google Scholar] [CrossRef]
- Belaber, E.C.; Gauchat, M.E.; Schoffen, C.D.; Muñoz, F.; Borralho, N.M.; Sanchez, L.; Cappa, E.P. Accounting for Competition in Multi-Environment Tree Genetic Evaluations: A Case Study with Hybrid Pines. Ann. For. Sci. 2021, 78, 2. [Google Scholar] [CrossRef]
- de Araujo, M.J.; da Rocha, G.N.; Estopa, R.A.; Oberschelp, J.; da Silva, P.H.M. Conservative or Non-Conservative Strategy to Advance Breeding Generation? A Case Study in Eucalyptus benthamii Using Spatial Variation and Competition Model. Silvae Genet. 2023, 72, 1–10. [Google Scholar] [CrossRef]
- Baud, A.; McPeek, S.; Chen, N.; Hughes, K.A. Indirect Genetic Effects: A Cross-Disciplinary Perspective on Empirical Studies. J. Hered. 2022, 113, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Flores Junior, P.C.; Ishibashi, V.; Matos, J.L.M.D.; Martinez, D.T.; Higa, A.R. Effect of Competition in Different Ages in a Progeny Test of Pinus taeda L. Sci. For. 2020, 48, e3290. [Google Scholar] [CrossRef]
- Ishibashi, V.; Martinez, D.T.; Higa, A.R. Phenotypic Models of Competition for Pinus taeda L Genetic Parameters Estimation. CERNE 2017, 23, 349–358. [Google Scholar] [CrossRef]
- Bijma, P. A General Definition of the Heritable Variation That Determines the Potential of a Population to Respond to Selection. Genetics 2011, 189, 1347–1359. [Google Scholar] [CrossRef]
- Costa e Silva, J.; Kerr, R.J. Accounting for Competition in Genetic Analysis, with Particular Emphasis on Forest Genetic Trials. Tree Genet. Genomes 2013, 9, 1–17. [Google Scholar] [CrossRef]
- Cadena de Valor Foresto Industrial–Producción Foresto Industrial. Available online: https://www.magyp.gob.ar/desarrollo-foresto-industrial/cadena-valor.php (accessed on 21 March 2025).
- Gianola, D.; Norton, H.W. Scaling Threshold Characters. Genetics 1981, 99, 357–364. [Google Scholar] [CrossRef]
- Henderson, C.R. Applications of Linear Models in Animal Breeding; University of Guelph: Guelph, ON, Canada, 1984. [Google Scholar]
- Gilmour, A.R.; Cullis, B.R.; Verbyla, A.P.; Verbyla, A.P. Accounting for Natural and Extraneous Variation in the Analysis of Field Experiments. J. Agric. Biol. Environ. Stat. 1997, 2, 269. [Google Scholar] [CrossRef]
- Dutkowski, G.W.; Silva, J.C.E.; Gilmour, A.R.; Lopez, G.A. Spatial Analysis Methods for Forest Genetic Trials. Can. J. For. Res. 2002, 32, 2201–2214. [Google Scholar] [CrossRef]
- Gilmour, A.R.; Thompson, R.; Cullis, B.R. Average Information REML: An Efficient Algorithm for Variance Parameter Estimation in Linear Mixed Models. Biometrics 1995, 51, 1440–1450. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.bibsonomy.org/bibtex/7469ffee3b07f9167cf47e7555041ee7 (accessed on 24 March 2025).
- Butler, D.G.; Cullis, B.R.; Gilmour, A.R.; Gogel, B.J.; Thompson, R. ASReml-R Reference Manual Version 4.2; VSN International Ltd.: Hemel Hempstead, UK, 2023. [Google Scholar]
- Wickham, H. Ggplot2: Elegant Graphics for Data Analysis, Use R! 2nd ed.; Springer International Publishing: Cham, Switzerland, 2016; ISBN 978-3-319-24275-0. [Google Scholar]
- Stram, D.O.; Lee, J.W. Variance Components Testing in the Longitudinal Mixed Effects Model. Biometrics 1994, 50, 1171. [Google Scholar] [CrossRef]
- de Araujo, M.J.; de Paula, R.C.; de Moraes, C.B.; Pieroni, G.; da Silva, P.H.M. Thinning Strategies for Eucalyptus Dunnii Population: Balance between Breeding and Conservation Using Spatial Variation and Competition Model. Tree Genet. Genomes 2021, 17, 42. [Google Scholar] [CrossRef]
- Nagashima, H.; Hikosaka, K. Plants in a Crowded Stand Regulate Their Height Growth so as to Maintain Similar Heights to Neighbours Even When They Have Potential Advantages in Height Growth. Ann. Bot. 2011, 108, 207–214. [Google Scholar] [CrossRef]
- Bergmüller, K.O.; Vanderwel, M.C. Evaluating Effects of Remotely Sensed Neighborhood Crowding and Depth-to-Water on Tree Height Growth. Forests 2023, 14, 242. [Google Scholar] [CrossRef]
- Meng, S.X.; Lieffers, V.J.; Reid, D.E.B.; Rudnicki, M.; Silins, U.; Jin, M. Reducing Stem Bending Increases the Height Growth of Tall Pines. J. Exp. Bot. 2006, 57, 3175–3182. [Google Scholar] [CrossRef]
- von Euler, F.; Baradat, P.; Lemoine, B. Effects of Plantation Density and Spacing on Competitive Interactions among Half-Sib Families of Maritime Pine. Can. J. For. Res. 1992, 22, 482–489. [Google Scholar] [CrossRef]
- Gould, P.J.; Clair, J.B.S.; Anderson, P.D. Performance of Full-Sib Families of Douglas-Fir in Pure-Family and Mixed-Family Deployments. For. Ecol. Manag. 2011, 262, 1417–1425. [Google Scholar] [CrossRef]
- Ye, T.Z.; Jayawickrama, K.J.S. Efficiency of Using Spatial Analysis in First-Generation Coastal Douglas-Fir Progeny Tests in the US Pacific Northwest. Tree Genet. Genomes 2008, 4, 677–692. [Google Scholar] [CrossRef]
- Chen, Z.; Helmersson, A.; Westin, J.; Karlsson, B.; Wu, H.X. Efficiency of Using Spatial Analysis for Norway Spruce Progeny Tests in Sweden. Ann. For. Sci. 2018, 75, 2. [Google Scholar] [CrossRef]
- White, T.L.; Adams, W.T.; Neale, D.B. Forest Genetics, 1st ed.; CABI: Wallingford, UK, 2007; ISBN 978-0-85199-348-5. [Google Scholar]
- Chaves, S.F.S.; Ferreira, F.M.; Ferreira, G.C.; Gezan, S.A.; Dias, K.O.G. Incorporating Spatial and Genetic Competition into Breeding Pipelines with the R Package Gencomp. Heredity 2025, 134, 129–141. [Google Scholar] [CrossRef] [PubMed]
- Binkley, D. A Hypothesis about the Interaction of Tree Dominance and Stand Production through Stand Development. For. Ecol. Manag. 2004, 190, 265–271. [Google Scholar] [CrossRef]
- Fernández, M.E.; Gyenge, J. Testing Binkley’s Hypothesis about the Interaction of Individual Tree Water Use Efficiency and Growth Efficiency with Dominance Patterns in Open and Close Canopy Stands. For. Ecol. Manag. 2009, 257, 1859–1865. [Google Scholar] [CrossRef]
- West, P.W. Quantifying Effects on Tree Growth Rates of Symmetric and Asymmetric Inter-Tree Competition in Even-Aged, Monoculture Eucalyptus Pilularis Forests. Trees 2023, 37, 239–254. [Google Scholar] [CrossRef]

| Series Number | Test Number | Test Type 1 | Local Name | Generation | Planting Date | Spacing (m) | Latitude (S) | Longitude (W) | Elevation (m) | Soil Texture | Drainage Class | Number of Trees |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | HS | San Antonio | First | September 2002 | 3 × 3 | 26°02′ | 53°46′ | 540 | Clay | Good | 2959 |
| 2 | HS | Wanda | First | July 2002 | 2.4 × 2.4 | 25°58′ | 54°23′ | 305 | Clay | Good | 2782 | |
| 3 | HS | Cerro Azul | First | October 2002 | 3 × 3 | 27°39′ | 55°25′ | 252 | Rocky | Good | 1647 | |
| 4 | HS | Ituzaingó | First | July 2002 | 4 × 2.25 | 27°37′ | 56°13′ | 108 | Clay | Good | 1910 | |
| 5 | HS | Virasoro | First | October 2002 | 3 × 3 | 28°08′ | 55°58′ | 140 | Clay | Good | 2749 | |
| 6 | HS | Concepción | First | August 2002 | 3 × 3 | 28°29′ | 57°55′ | 68 | Sandy | Good | 2260 | |
| 7 | HS | Paso de los Libres | First | August 2002 | 3 × 3 | 29°31′ | 57° 04′ | 88 | Sandy-Loam | Poor | 2871 | |
| 2 | 8 | FS | Wanda | First | June 2012 | 3 × 2.5 | 26° 00′ | 54°23′ | 256 | Clay | Good | 1613 |
| 9 | FS | Mado | First | June 2012 | 3 × 3 | 26°15′ | 54°31′ | 218 | Rocky | Good | 1744 | |
| 3 | 11 | FS | Wanda | First | June 2013 | 4 × 1.8 | 26° 06′ | 54°23′ | 291 | Clay | Good | 2393 |
| 14 | FS | San Miguel | First | July 2013 | 2.5 × 5 | 28° 06′ | 57°34 | 74 | Sandy | Poor | 2074 | |
| 4 | 10 | HS | Wanda | First-Second | June 2013 | 2.5 × 3 | 25°58′ | 54°31′ | 237 | Rocky | Good | 3524 |
| 12 | HS | Montecarlo | First-Second | August 2013 | 4 × 2.5 | 26° 32′ | 54°44′ | 239 | Clay | Good | 2319 | |
| 13 | HS | San Miguel | First-Second | July 2013 | 2.5 × 5 | 28° 05′ | 57°22′ | 74 | Sandy | Poor | 1930 |
| Test | Age | Model | () | ρr | ρc | logL | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | Spa | 1.02 (0.13) | 0.30 (0.07) | 0.98 (0.15) | 0.94 | 0.91 | −2557.44 | ||||
| 1 | 3 | Spa-Comp | 1.02 (0.15) | 0.34 (0.16) | 1.02 (0.15) | 0.03 (0.05) | 0.03 | 0.51 (0.44) | 0.98 | 0.95 | −2552.63 * | |
| 3 | 3 | Spa | 0.68 (0.09) | 0.59 (0.17) | 0.37 (0.09) | 0.98 | 0.96 | −945.90 | ||||
| 3 | 3 | Spa-Comp | 0.63 (0.09) | 0.70 (0.30) | 0.39 (0.09) | 0.07 (0.04) | 0.18 | 0.10 (0.17) | 0.94 | 0.97 | −943.77 * | |
| 4 | 3 | Spa | 0.71 (0.13) | 0.11 (0.04) | 1.10 (0.15) | 0.86 | 0.98 | −2302.12 | ||||
| 4 | 3 | Spa-Comp | 0.69 (0.13) | 0.12 (0.03) | 1.08 (0.15) | 0.01 (0.04) | 0.01 | 0.14 (0.04) | 0.74 | 0.95 | −2298.10 * | |
| 5 | 3 | Spa | 0.93 (0.11) | 0.51 (0.06) | 0.63 (0.20) | 0.72 | 0.73 | −2224.14 | ||||
| 5 | 3 | Spa-Comp | 0.99 (0.10) | 0.21 (0.07) | 0.66 (0.11) | 0.06 (0.07) | 0.09 | 0.85 (0.53) | 0.94 | 0.91 | −2208.59 * | |
| 6 | 3 | Spa | 1.08 (0.10) | 0.14 (0.05) | 0.58 (0.11) | 0.93 | 0.94 | −1750.35 | ||||
| 6 | 3 | Spa-Comp | 0.99 (0.11) | 0.19 (0.16) | 0.58 (0.11) | 0.11 (0.05) | 0.19 | −0.09 (0.12) | 0.97 | 0.98 | −1746.85 * | |
| 10 | 3 | Spa | 2.19 (0.25) | 0.57 (0.16) | 2.04 (0.31) | 0.93 | 0.96 | −4326.63 | ||||
| 10 | 3 | Spa-Comp | 2.11 (0.26) | 0.57 (0.16) | 2.01 (0.30) | 0.10 (0.08) | 0.05 | −0.30 (0.13) | 0.94 | 0.96 | −4324.04 * | |
| 1 | 5 | Spa | 1.92 (0.36) | 0.25 (0.08) | 3.18 (0.44) | 0.97 | 0.90 | −3815.95 | ||||
| 1 | 5 | Spa-Comp | 1.79 (0.37) | 0.46 (0.16) | 3.25 (0.44) | 0.05 (0.09) | 0.02 | −0.81 (0.57) | 0.98 | 0.97 | −3803.58 * | |
| 2 | 5 | Spa | 2.65 (0.44) | 0.07 (0.06) | 3.69 (0.54) | 0.98 | 0.98 | −3879.73 | ||||
| 2 | 5 | Spa-Comp | 2.33 (0.43) | 0.17 (0.06) | 3.75 (0.50) | 0.13 (0.11) | 0.03 | −0.99 (0.34) | 0.98 | 0.55 | −3845.85 * | |
| 4 | 5 | Spa | 1.39 (0.32) | 0.14 (0.06) | 2.90 (0.40) | 0.91 | 0.98 | −3477.39 | ||||
| 4 | 5 | Spa-Comp | 1.10 (0.31) | 0.18 (0.05) | 3.05 (0.38) | 0.11 (0.07) | 0.04 | −0.90 (0.25) | 0.75 | 0.95 | −3447.52 * | |
| 6 | 5 | Spa | 1.65 (0.19) | 0.19 (0.08) | 1.17 (0.22) | 0.98 | 0.98 | −2285.03 | ||||
| 6 | 5 | Spa-Comp | 1.57 (0.20) | 0.19 (0.09) | 1.17 (0.22) | 0.09 (0.07) | 0.08 | −0.31 (0.14) | 0.98 | 0.98 | −2283.20 * | |
| 7 | 5 | Spa | 1.40 (0.11) | 0.48 (0.09) | 0.62 (0.12) | 0.69 | 0.98 | −2539.22 | ||||
| 7 | 5 | Spa-Comp | 1.32 (0.12) | 0.52 (0.11) | 0.65 (0.12) | 0.04 (0.04) | 0.06 | −0.79 (0.37) | 0.70 | 0.98 | −2532.87 * | |
| 11 | 5 | Spa | 6.70 (0.64) | 0.54 (0.24) | 0.36 (0.12) | 3.09 (1.17) | 0.98 | 0.93 | −3745.06 | |||
| 11 | 5 | Spa-Comp | 7.40 (0.32) | 0.48 (0.16) | 0.41 (0.13) | 1.11 (0.36) | 0.22 (0.15) | 0.20 | −0.72 (0.33) | 0.94 | 0.91 | −3738.89 * |
| 13 | 5 | Spa | 2.89 (0.60) | 3.73 (0.89) | 3.76 (0.73) | 0.85 | 0.97 | −2753.89 | ||||
| 13 | 5 | Spa-Comp | 2.28 (0.64) | 3.81 (0.84) | 4.02 (0.76) | 0.29 (0.20) | 0.07 | −0.47 (0.16) | 0.84 | 0.97 | −2748.18 * | |
| 1 | 12 | Spa | 8.48 (1.23) | 0.56 (0.30) | 8.72 (1.44) | 0.98 | 0.97 | −4361.82 | ||||
| 1 | 12 | Spa-Comp | 7.33 (1.31) | 0.80 (0.36) | 9.66 (1.47) | 0.28 (0.38) | 0.03 | −0.98 (0.56) | 0.98 | 0.98 | −4345.23 * | |
| 1 | 21 | Spa | 16.74 (1.92) | 0.12 (0.04) | 10.69 (2.10) | 0.66 | 0.98 | −4379.15 | ||||
| 1 | 21 | Spa-Comp | 16.69 (2.02) | 0.13 (0.15) | 10.25 (2.05) | 1.07 (0.75) | 0.10 | −0.52 (0.16) | 0.43 | 0.47 | −4372.37 * |
| Test | Age | Model | () | ρr | ρc | logL | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | Spa | 0.19 (0.02) | 0.08 (0.01) | 0.17 (0.03) | 0.77 | 0.80 | −128.14 | ||||
| 1 | 3 | Spa-Comp | 0.20 (0.02) | 0.06 (0.01) | 0.18 (0.03) | 0.01 (0.01) | 0.06 | 0.07 (0.02) | 0.88 | 0.89 | −124.69 * | |
| 3 | 3 | Spa | 0.18 (0.02) | 0.18 (0.06) | 0.08 (0.02) | 0.94 | 0.97 | 165.64 | ||||
| 3 | 3 | Spa-Comp | 0.18 (0.02) | 0.20 (0.09) | 0.09 (0.02) | 0.01 (0.01) | 0.11 | 0.26 (0.27) | 0.96 | 0.98 | 167.69 * | |
| 5 | 3 | Spa | 0.15 (0.01) | 0.09 (0.01) | 0.08 (0.02) | 0.79 | 0.77 | 391.51 | ||||
| 5 | 3 | Spa-Comp | 0.16 (0.01) | 0.06 (0.01) | 0.08 (0.02) | 0.02 (0.01) | 0.25 | 0.61 (0.15) | 0.93 | 0.90 | 405.25 * | |
| 8 | 3 | Spa | 0.38 (0.04) | 0.32 (0.10) | 0.01 (0.01) | 0.15 (0.06) | 0.98 | 0.71 | −326.05 | |||
| 8 | 3 | Spa-Comp | 0.36 (0.03) | 0.17 (0.04) | 0.01 (0.01) | 0.18 (0.06) | 0.03 (0.01) | 0.17 | 0.81 (0.18) | 0.98 | 0.43 | −318.66 * |
| 12 | 3 | Spa | 0.44 (0.04) | 0.19 (0.02) | 0.27 (0.05) | 0.95 | 0.32 | −1263.98 | ||||
| 12 | 3 | Spa-Comp | 0.43 (0.04) | 0.16 (0.02) | 0.28 (0.03) | 0.03 (0.01) | 0.11 | 0.27 (0.17) | 0.96 | 0.23 | −1260.29 * | |
| 1 | 5 | Spa | 0.35 (0.07) | 0.94 (0.02) | 0.61 (0.09) | 0.93 | 0.85 | −1434.14 | ||||
| 1 | 5 | Spa-Comp | 0.36 (0.07) | 0.16 (0.05) | 0.63 (0.09) | 0.004 (0.02) | 0.01 | 0.17 (0.05) | 0.97 | 0.91 | −1429.17 * | |
| 5 | 5 | Spa | 0.23 (0.04) | 0.23 (0.04) | 0.32 (0.05) | 0.98 | 0.57 | −642.06 | ||||
| 5 | 5 | Spa-Comp | 0.22 (0.04) | 0.20 (0.03) | 0.31 (0.05) | 0.02 (0.01) | 0.06 | 0.22 (0.19) | 0.98 | 0.53 | −637.77 * | |
| 8 | 5 | Spa | 0.77 (0.08) | 0.35 (0.07) | 0.04 (0.01) | 0.30 (0.13) | 0.98 | 0.10 | −888.24 | |||
| 8 | 5 | Spa-Comp | 0.66 (0.09) | 0.30 (0.06) | 0.04 (0.02) | 0.46 (0.18) | 0.06 (0.03) | 0.13 | 0.60 (0.18) | 0.98 | −0.09 | −878.58 * |
| 9 | 5 | Spa | 0.78 (0.06) | 0.58 (0.11) | 0.03 (0.01) | 0.24 (0.11) | 0.97 | 0.27 | −975.73 | |||
| 9 | 5 | Spa-Comp | 0.75 (0.08) | 0.48 (0.09) | 0.03 (0.01) | 0.33 (0.13) | 0.02 (0.01) | 0.06 | 0.90 (0.28) | 0.97 | 0.05 | −971.81 * |
| Test | Age | Model | () | ρr | ρc | logL | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 | Spa | 0.64 (0.04) | 0.02 (0.01) | 0.14 (0.04) | 0.21 | −0.95 | −1158.39 | |||
| 1 | 5 | Spa-Comp | 0.62 (0.04) | 0.03 (0.02) | 0.15 (0.04) | 0.01 (0.02) | 0.07 | 0.73 (1.26) | 0.20 | −0.83 | −1156.12 * |
| 1 | 12 | Spa | 0.53 (0.04) | 0.02 (0.01) | 0.13 (0.04) | 0.90 | 0.98 | −704.29 | |||
| 1 | 12 | Spa-Comp | 0.52 (0.04) | 0.02 (0.01) | 0.13 (0.04) | 0.02 (0.02) | 0.15 | −0.56 (0.29) | 0.88 | 0.98 | −701.81 * |
| 1 | 21 | Spa | 0.15 (2.36) | 0.51 (2.36) | 0.22 (0.06) | 0.09 | −0.04 | −893.53 | |||
| 1 | 21 | Spa-Comp | 0.45 (0.26) | 0.15 (0.24) | 0.23 (0.06) | 0.06 (0.03) | 0.26 | −0.03 (0.17) | 0.17 | −0.29 | −890.27 * |
| Age | 3 | 5 | 12 | 21 |
|---|---|---|---|---|
| 3 | - | 0.86 | 0.60 | 0.54 |
| 5 | −0.75 | - | 0.72 | 0.65 |
| 12 | −0.54 | 0.72 | - | 0.95 |
| 21 | −0.36 | 0.56 | 0.81 | - |
| Trait | Age | Model | Parent | Offspring | Parent | Offspring |
|---|---|---|---|---|---|---|
| 3 | Spa | 0.79 | 0.72 | - | - | |
| Spa-Comp | 0.79 | 0.72 | 0.26 | 0.15 | ||
| 5 | Spa | 0.82 | 0.80 | - | - | |
| Spa-Comp | 0.83 | 0.81 | 0.64 | 0.62 | ||
| DBH | 12 | Spa | 0.75 | 0.73 | - | - |
| Spa-Comp | 0.76 | 0.76 | 0.75 | 0.75 | ||
| 21 | Spa | 0.68 | 0.65 | - | - | |
| Spa-Comp | 0.67 | 0.64 | 0.33 | 0.27 | ||
| 3 | Spa | 0.77 | 0.68 | - | - | |
| Spa-Comp | 0.77 | 0.69 | 0.65 | 0.62 | ||
| TH | 5 | Spa | 0.82 | 0.79 | - | - |
| Spa-Comp | 0.82 | 0.79 | 0.65 | 0.64 | ||
| 5 | Spa | 0.60 | 0.48 | - | - | |
| Spa-Comp | 0.62 | 0.51 | 0.74 | 0.71 | ||
| 12 | Spa | 0.56 | 0.48 | - | - | |
| NSTR | Spa-Comp | 0.57 | 0.49 | 0.60 | 0.57 | |
| 21 | Spa | 0.59 | 0.54 | - | - | |
| Spa-Comp | 0.61 | 0.56 | 0.38 | 0.35 | ||
| Trait | Age | Model | Criteria | CT% | |
|---|---|---|---|---|---|
| 3 | Spa | BV | 18.42 | ||
| Spa-Comp | TBV | 22.67 | 93% | ||
| 5 | Spa | BV | 18.62 | ||
| DBH | Spa-Comp | TBV | 14.79 | 94% | |
| 12 | Spa | BV | 19.32 | ||
| Spa-Comp | TBV | 16.26 | 95% | ||
| 21 | Spa | BV | 16.85 | ||
| Spa-Comp | TBV | 13.13 | 89% | ||
| 3 | Spa | BV | 14.15 | ||
| Spa-Comp | TBV | 13.97 | 91% | ||
| TH | 5 | Spa | BV | 14.15 | |
| Spa-Comp | TBV | 15.51 | 93% | ||
| 5 | Spa | BV | 14.50 | ||
| Spa-Comp | TBV | 19.52 | 78% | ||
| NSTR | 12 | Spa | BV | 10.60 | |
| Spa-Comp | TBV | 7.67 | 100% | ||
| 21 | Spa | BV | 23.25 | ||
| Spa-Comp | TBV | 24.48 | 79% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belaber, E.C.; Borralho, N.M.; Cappa, E.P. Genetics of Growth and Stem Straightness Traits in Pinus taeda in Argentina: Exploring Genetic Competition Across Ages and Sites. Forests 2025, 16, 675. https://doi.org/10.3390/f16040675
Belaber EC, Borralho NM, Cappa EP. Genetics of Growth and Stem Straightness Traits in Pinus taeda in Argentina: Exploring Genetic Competition Across Ages and Sites. Forests. 2025; 16(4):675. https://doi.org/10.3390/f16040675
Chicago/Turabian StyleBelaber, Ector C., Nuno M. Borralho, and Eduardo P. Cappa. 2025. "Genetics of Growth and Stem Straightness Traits in Pinus taeda in Argentina: Exploring Genetic Competition Across Ages and Sites" Forests 16, no. 4: 675. https://doi.org/10.3390/f16040675
APA StyleBelaber, E. C., Borralho, N. M., & Cappa, E. P. (2025). Genetics of Growth and Stem Straightness Traits in Pinus taeda in Argentina: Exploring Genetic Competition Across Ages and Sites. Forests, 16(4), 675. https://doi.org/10.3390/f16040675





