Moisture-Dependent Transverse Isotropic Elastic Constants of Wood S2 Secondary Cell Wall Layers Determined Using Nanoindentation
Abstract
1. Introduction
2. Materials and Methods
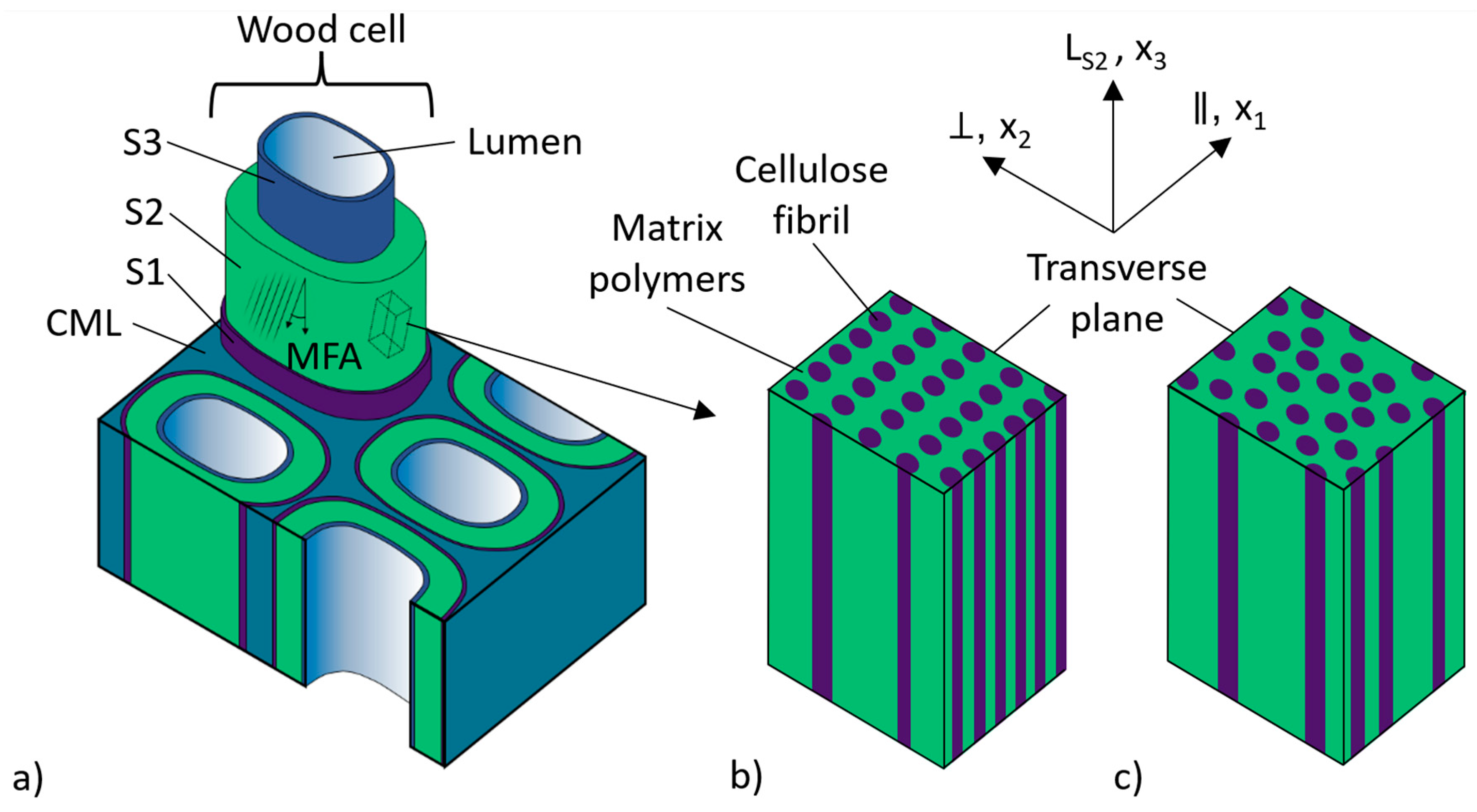
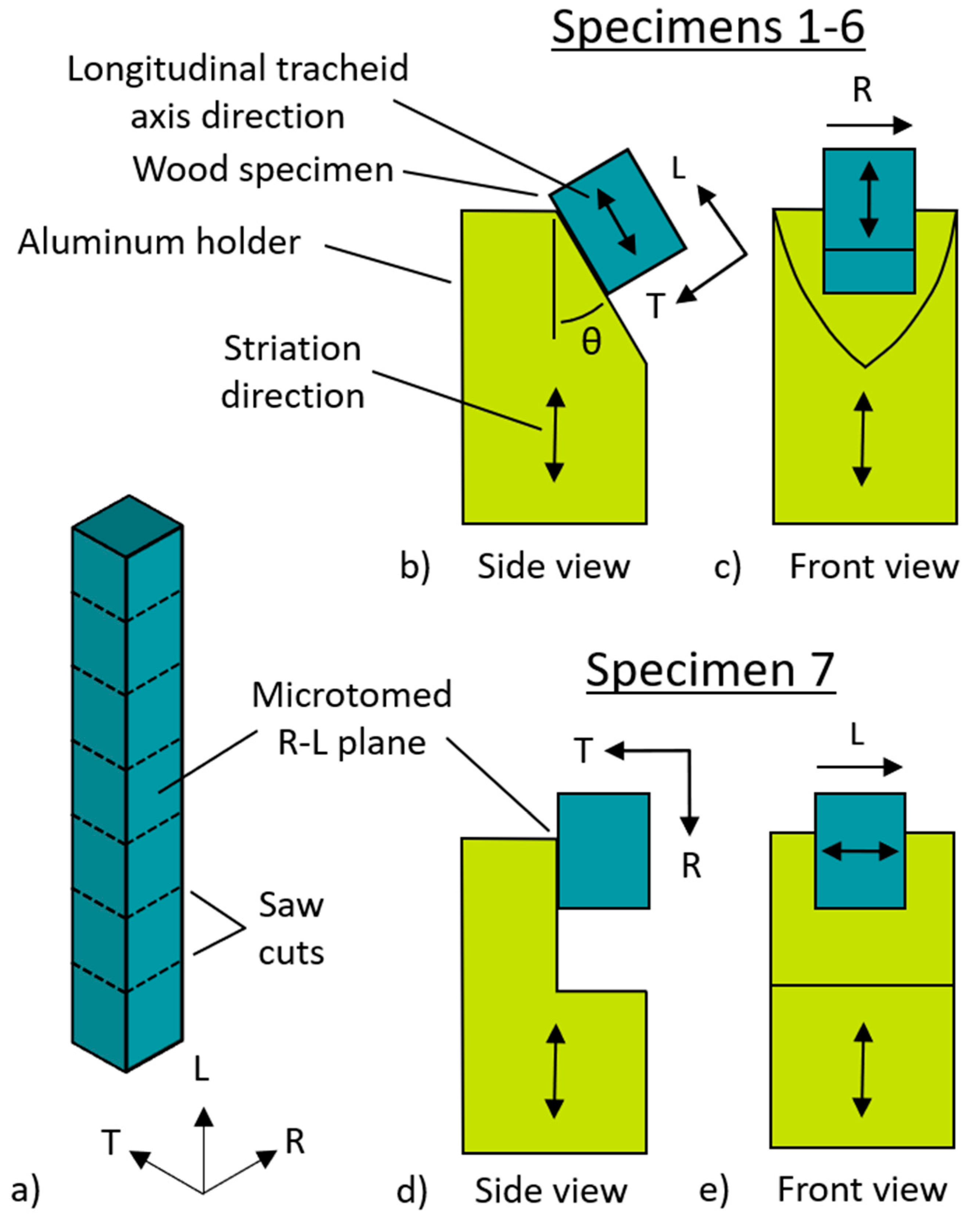
2.1. Materials
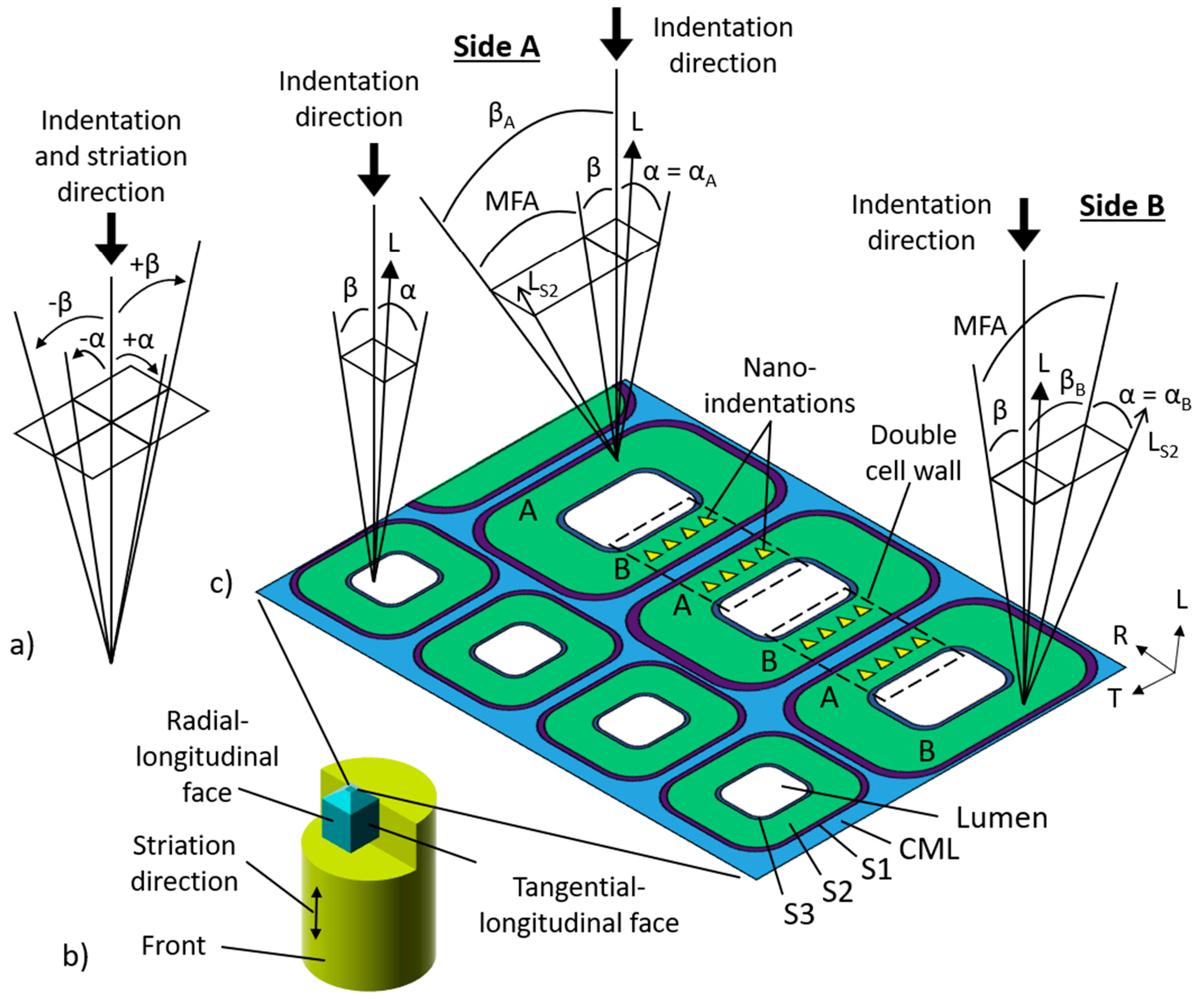
2.2. Nanoindentation
2.3. Wide Angle X-Ray Diffraction Measurements
3. Results and Discussion
3.1. Microfibril Angle (MFA) Measurement
3.2. Calculation of δ
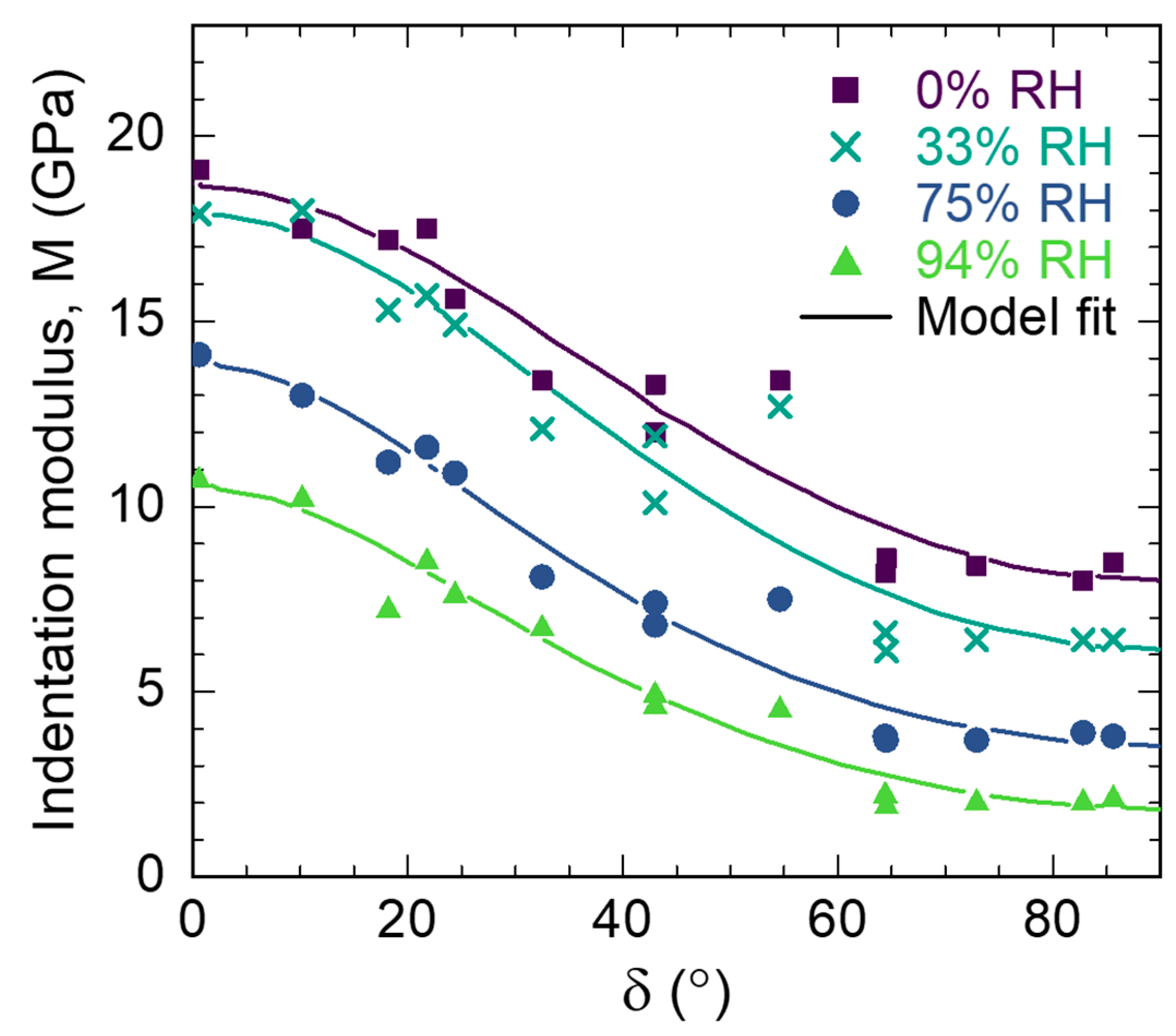
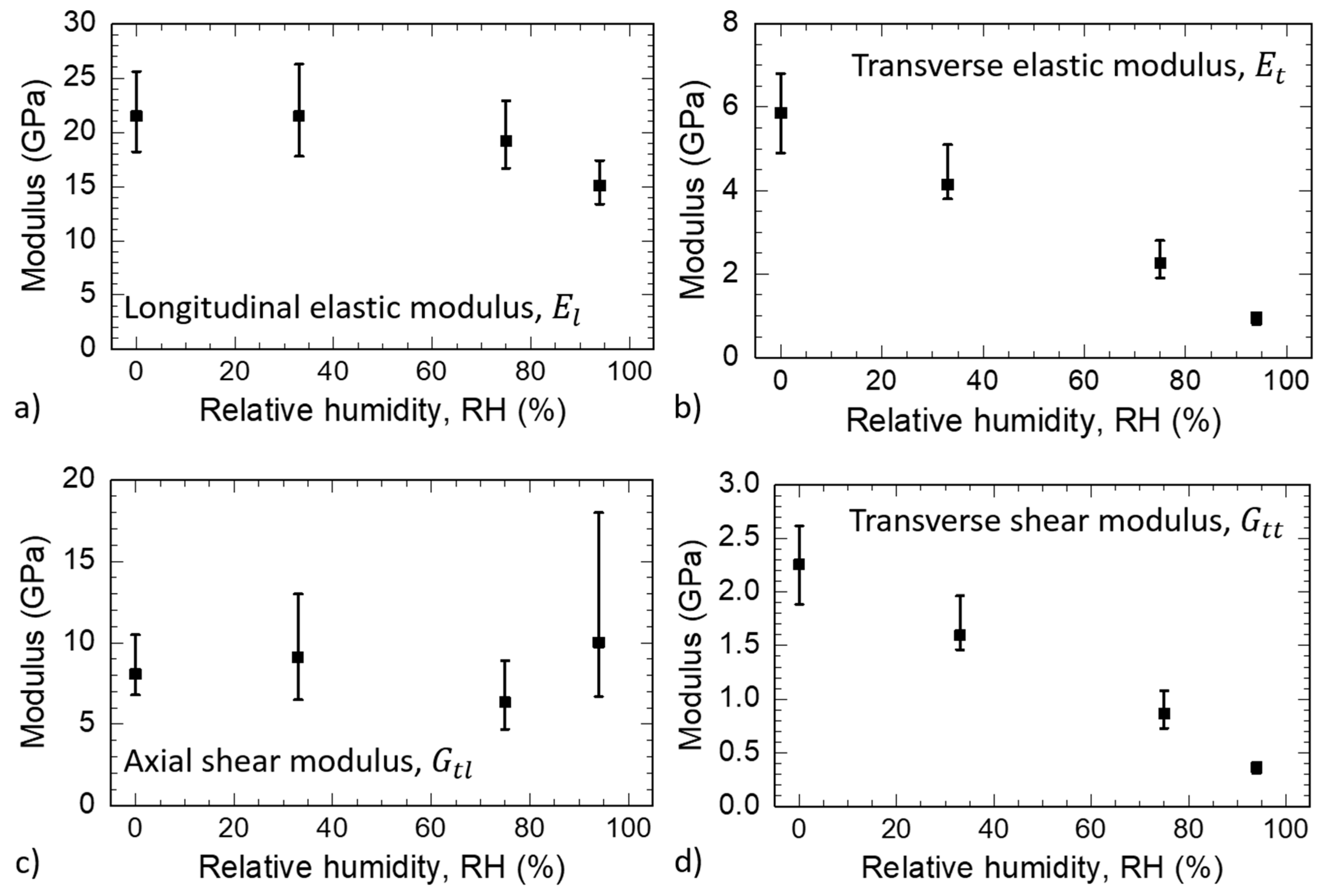
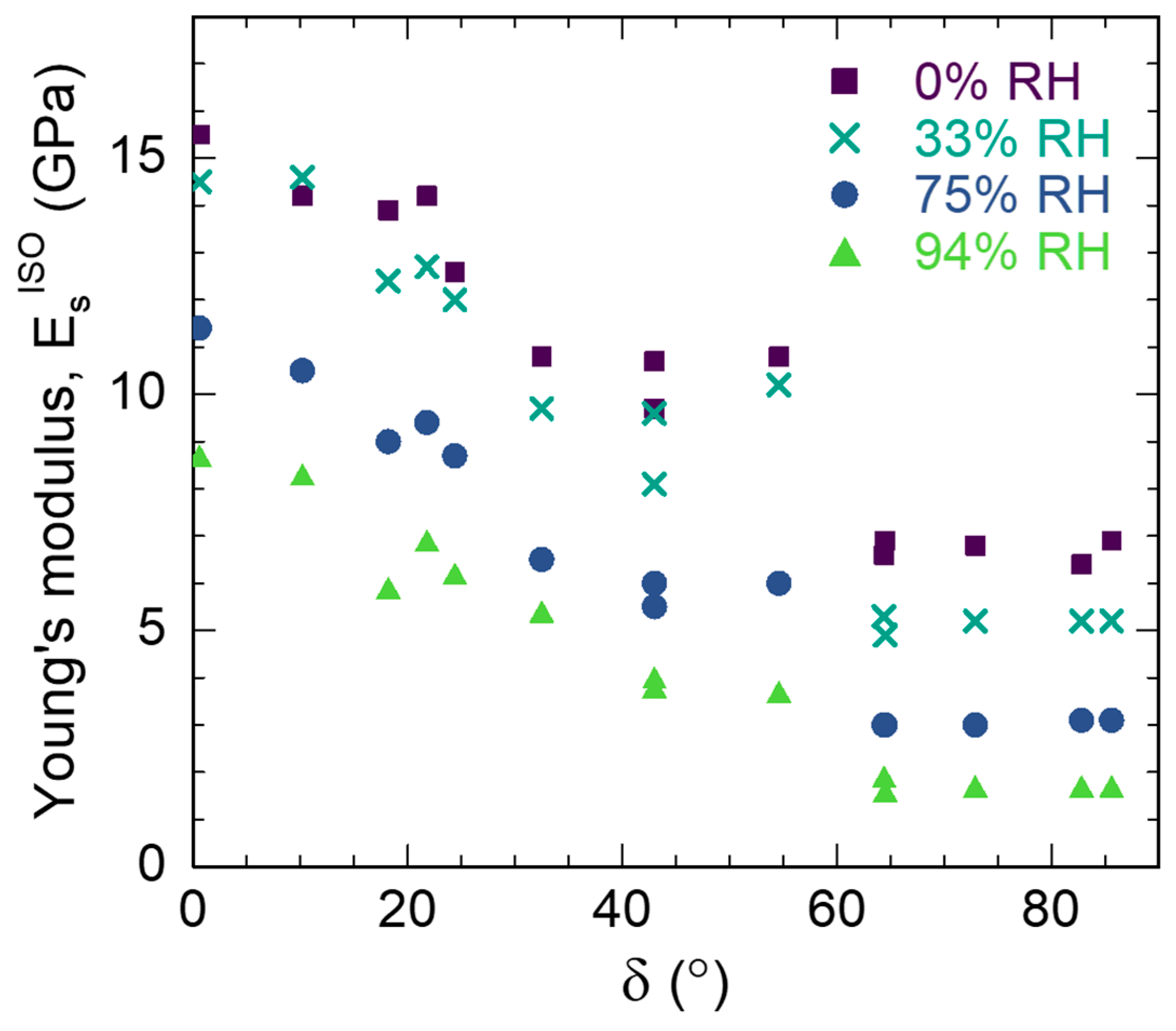
3.3. S2 Layer Elastic Properties
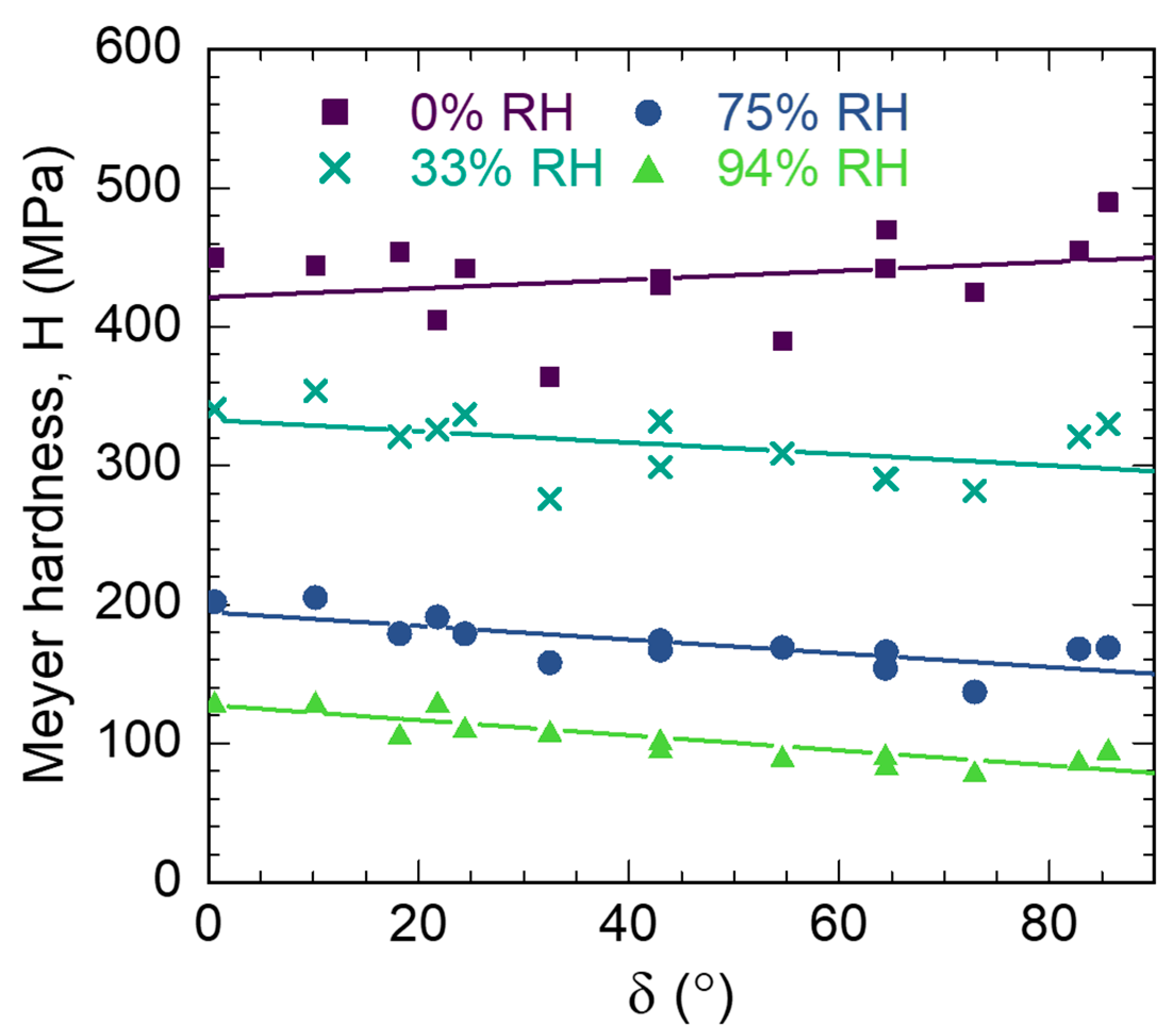
3.4. S2 Layer Hardness Properties
3.5. Coefficient of Variation Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CML | Compound middle lamella |
| L | Bulk wood longitudinal direction |
| LS2 | S2 layer longitudinal direction |
| MFA | Microfibril angle |
| R | Bulk wood radial direction |
| RH | Relative humidity |
| SPM | Scanning probe microscopy |
| T | S2 layer tangential direction |
| WAXD | Wide angle X-ray Diffraction |
References
- Hofstetter, K.; Gamstedt, E.K. Hierarchical modelling of microstructural effects on mechanical properties of wood. A review COST Action E35 2004–2008: Wood machining—Micromechanics and fracture. Holzforschung 2009, 63, 130–138. [Google Scholar] [CrossRef]
- Salmen, L.; Burgert, I. Cell wall features with regard to mechanical performance. A review. COST Action E35 2004-2008: Wood machining—Micromechanics and fracture. Holzforschung 2009, 63, 121–129. [Google Scholar] [CrossRef]
- Terashima, N.; Kitano, K.; Kojima, M.; Yoshida, M.; Yamamoto, H.; Westermark, U. Nanostructural assembly of cellulose, hemicellulose, and lignin in the middle layer of secondary wall of ginkgo tracheid. J. Wood Sci. 2009, 55, 409–416. [Google Scholar] [CrossRef]
- Cramer, S.; Kretschmann, D.; Lakes, R.; Schmidt, T. Earlywood and latewood elastic properties in loblolly pine. Holzforschung 2005, 59, 531–538. [Google Scholar] [CrossRef]
- Mott, L.; Groom, L.; Shaler, S. Mechanical Properties Of Individual Southern Pine Fibers. Part II. Comparison Of Earlywood And Latewood Fibers With Respect To Tree Height And Juvenility. Wood Fiber Sci. 2002, 34, 221–237. [Google Scholar]
- Salmén, L. Wood morphology and properties from molecular perspectives. Ann. For. Sci. 2015, 72, 679–684. [Google Scholar] [CrossRef]
- Fahlén, J.; Salmén, L. On the Lamellar Structure of the Tracheid Cell Wall. Plant Biol. 2002, 4, 339–345. [Google Scholar] [CrossRef]
- Green, D.W.; Kretschmann, D.E. Moisture Content and the Properties of Clear Southern Pine; Forest Products Laboratory Research Paper; FPL–RP–531-FPL–RP–531; U.S. Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 1994.
- Kretschmann, D. Mechanical Properties of Wood. In Wood Handbook—Wood as an Engineering Material; GTR-190; USDA: Washington, DC, USA, 2010; pp. 1–46. Available online: https://research.fs.usda.gov/treesearch/37427 (accessed on 21 April 2025).
- Bertinetti, L.; Hangen, U.D.; Eder, M.; Leibner, P.; Fratzl, P.; Zlotnikov, I. Characterizing moisture-dependent mechanical properties of organic materials: Humidity-controlled static and dynamic nanoindentation of wood cell walls. Philos. Mag. 2015, 95, 1992–1998. [Google Scholar] [CrossRef][Green Version]
- Youssefian, S.; Jakes, J.E.; Rahbar, N. Variation of Nanostructures, Molecular Interactions, and Anisotropic Elastic Moduli of Lignocellulosic Cell Walls with Moisture. Sci. Rep. 2017, 7, 2054. [Google Scholar] [CrossRef]
- Yu, Y.; Fei, B.; Wang, H.; Tian, G. Longitudinal mechanical properties of cell wall of Masson pine (Pinus massoniana Lamb) as related to moisture content: A nanoindentation study. Holzforschung 2011, 65, 121–126. [Google Scholar] [CrossRef]
- Meng, Y.; Xia, Y.; Young, T.M.; Cai, Z.; Wang, S. Viscoelasticity of wood cell walls with different moisture content as measured by nanoindentation. RSC Adv. 2015, 5, 47538–47547. [Google Scholar] [CrossRef]
- Wanju, L.; Wang, H.; Hao, W.; Yu, Y. Moisture dependence of indentation deformation and mechanical properties of Masson pine (Pinus massoniana lamb) cell walls as related to microfibril angle. Wood Fiber Sci. 2014, 46, 228–236. [Google Scholar]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 1997. [Google Scholar]
- Hunt, C.G.; Frihart, C.R.; Dunky, M.; Rohumaa, A. Understanding Wood Bonds–Going Beyond What Meets the Eye: A Critical Review. Rev. Adhes. Adhes. 2018, 6, 369–440. [Google Scholar] [CrossRef]
- Esteves, B.; Pereira, H. Wood Modification by Heat Treatment: A Review. BioResources 2008, 4, 370–404. [Google Scholar] [CrossRef]
- Jäger, A.; Bader, T.; Hofstetter, K.; Eberhardsteiner, J. The relation between indentation modulus, microfibril angle, and elastic properties of wood cell walls. Compos. Part A Appl. Sci. Manuf. 2011, 42, 677–685. [Google Scholar] [CrossRef]
- Jäger, A.; Hofstetter, K.; Buksnowitz, C.; Gindl-Altmutter, W.; Konnerth, J. Identification of stiffness tensor components of wood cell walls by means of nanoindentation. Compos. Part A Appl. Sci. Manuf. 2011, 42, 2101–2109. [Google Scholar] [CrossRef]
- Fischer-Cripps, A.C. Nanoindentation, 2nd ed.; Springer: New York, NY, USA, 2004; p. 264. [Google Scholar]
- Vlassak, J.J.; Ciavarella, M.; Barber, J.R.; Wang, X. The indentation modulus of elastically anisotropic materials for indenters of arbitrary shape. J. Mech. Phys. Solids 2003, 51, 1701–1721. [Google Scholar] [CrossRef]
- Kim, J.-W.; Harper, D.P.; Taylor, A.M. Technical Note: Effect of Epoxy Embedment on Micromechanical Properties of Brown-Rot-Decayed Wood Cell Walls Assessed with Nanoindentation. Wood Fiber Sci. 2012, 44, 103–107. [Google Scholar]
- Meng, Y.; Wang, S.; Cai, Z.; Young, T.M.; Du, G.; Li, Y. A novel sample preparation method to avoid influence of embedding medium during nano-indentation. Appl. Phys. A 2012, 110, 361–369. [Google Scholar] [CrossRef]
- Majstorović, F.; Hirschmann, E.; Butterling, M.; Attallah, A.G.; Wagner, A.; Jakes, J.E. Positrons as microprobes to study water-dependent free volume of wood cell walls: A preliminary study. Cellulose 2025, 32, 2779–2791. [Google Scholar] [CrossRef]
- Arzola-Villegas, X.; Báez, C.; Lakes, R.; Stone, D.S.; O’Dell, J.; Shevchenko, P.; Xiao, X.; De Carlo, F.; Jakes, J.E. Convolutional Neural Network for Segmenting Micro-X-ray Computed Tomography Images of Wood Cellular Structures. Appl. Sci. 2023, 13, 8146. [Google Scholar] [CrossRef]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef]
- Jakes, J.E.; Stone, D.S. Best Practices for Quasistatic Berkovich Nanoindentation of Wood Cell Walls. Forests 2021, 12, 1696. [Google Scholar] [CrossRef]
- Jakes, J.E. Improved methods for nanoindentation Berkovich probe calibrations using fused silica. J. Mater. Sci. 2018, 53, 4814–4827. [Google Scholar] [CrossRef]
- Stone, D.S.; Yoder, K.B.; Sproul, W.D. Hardness and elastic modulus of TiN based on continuous indentation technique and new correlation. J. Vac. Sci. Technol. A (Vac. Surf. Film.) 1991, 9, 2543–2547. [Google Scholar] [CrossRef]
- Jakes, J.E.; Hunt, C.G.; Yelle, D.J.; Lorenz, L.F.; Hirth, K.; Gleber, S.-C.; Vogt, S.; Grigsby, W.; Frihart, C.R. Synchrotron-based X-ray fluorescence microscopy in conjunction with nanoindentation to study molecular-scale interactions of phenol-formaldehyde in wood cell walls. ACS Appl. Mater. Interfaces 2015, 7, 6584–6589. [Google Scholar] [CrossRef]
- Jakes, J.E.; Frihart, C.R.; Beecher, J.F.; Moon, R.J.; Stone, D.S. Experimental method to account for structural compliance in nanoindentation measurements. J. Mater. Res. 2008, 23, 1113–1127. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. Improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1580. [Google Scholar] [CrossRef]
- SRM 640e; Line Position and Line Shape Standard for Powder Diffraction (Silicon Powder). National Institute of Standards and Technology; U.S. Department of Commerce: Gaithersburg, MD, USA, 2015.
- Knudsen, E.B.; Sørensen, H.O.; Wright, J.P.; Goret, G.; Kieffer, J. FabIO: Easy access to two-dimensional X-ray detector images in Python. J. Appl. Crystallogr. 2013, 46, 537–539. [Google Scholar] [CrossRef]
- Newville, M.; Stensitzki, T.; Allen, D.B.; Ingargiola, A. Non-Linear Least-Square Minimization and Curve-Fitting for Python. Version 1.0.3 Zenodo. Switzerland. 14 October 2021. Available online: https://zenodo.org/records/5570790 (accessed on 21 April 2025).
- Plaza, N. Automated Python Script for the Microfibril Angle Calculation from 2D Wide-Angle X-Ray Diffraction Data from Wood. Zenodo. Switzerland. 6 March 2020. Available online: https://zenodo.org/records/3699590 (accessed on 21 April 2025).
- Lichtenegger, H.C.; Reiterer, A.; Stanzl-Tschegg, S.E.; Fratzl, P. Comment about “The measurement of the micro-fibril angle in soft-wood” by K. M. Entwistle and N. J. Terrill. J. Mater. Sci. Lett. 2001, 20, 2245–2247. [Google Scholar] [CrossRef]
- Penttilä, P.A.; Altgen, M.; Carl, N.; van der Linden, P.; Morfin, I.; Österberg, M.; Schweins, R.; Rautkari, L. Moisture-related changes in the nanostructure of woods studied with X-ray and neutron scattering. Cellulose 2020, 27, 71–87. [Google Scholar] [CrossRef]
- Leppänen, K.; Bjurhager, I.; Peura, M.; Kallonen, A.; Suuronen, J.-P.; Penttilä, P.; Love, J.; Fagerstedt, K.; Serimaa, R. X-ray scattering and microtomography study on the structural changes of never-dried silver birch, European aspen and hybrid aspen during drying. Holzforschung 2011, 65, 865–873. [Google Scholar] [CrossRef]
- Lube, V.; Lazarescu, C.; Mansfield, S.D.; Avramidis, S. Wood microfibril angle variation after drying. Holzforschung 2016, 70, 485–488. [Google Scholar] [CrossRef]
- Harrington, J.J.; Astley, R.J.; Booker, R. Modelling the elastic properties of softwood. Eur. J. Wood Wood Prod. 1998, 56, 37–41. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; John Wiley & Sons Inc.: New York, NY, USA, 1980; p. 641. [Google Scholar]
- Apicella, A.; Tessieri, R.; de Cataldis, C. Sorption modes of water in glassy epoxies. J. Membr. Sci. 1984, 18, 211–225. [Google Scholar] [CrossRef]
- Frisch, H.L. Sorption and transport in glassy polymers-a review. Polym. Eng. Sci. 1980, 20, 2–13. [Google Scholar] [CrossRef]
- Hodge, R.M.; Bastow, T.J.; Edward, G.H.; Simon, G.P.; Hill, A.J. Free volume and the mechanism of plasticization in water-swollen poly(vinyl alcohol). Macromolecules 1996, 29, 8137–8143. [Google Scholar] [CrossRef]
- Fernandes, A.N.; Thomas, L.H.; Altaner, C.M.; Callow, P.; Forsyth, V.T.; Apperley, D.C.; Kennedy, C.J.; Jarvis, M.C. Nanostructure of cellulose microfibrils in spruce wood. Proc. Natl. Acad. Sci. USA 2011, 108, E1195–E1203. [Google Scholar] [CrossRef]
- Cousins, W.J. Elastic modulus of lignin as related to moisture content. Wood Sci. Technol. 1976, 10, 9–17. [Google Scholar] [CrossRef]
- Cousins, W.J. Young’s modulus of hemicellulose as related to moisture content. Wood Sci. Technol. 1978, 12, 161–167. [Google Scholar] [CrossRef]
- Salmén, L. Micromechanical understanding of the cell-wall structure. Comptes Rendus Biol. 2004, 327, 873–880. [Google Scholar] [CrossRef] [PubMed]
- Horvath, L.; Peralta, P.; Peszlen, I.; Csoka, L.; Horvath, B.; Jakes, J. Modeling hygroelastic properties of genetically modified aspen. Wood Fiber Sci. 2012, 44, 22–35. [Google Scholar]
- Müller, U.; Sretenovic, A.; Gindl, W.; Teischinger, A. Longitudinal shear properties of European larch wood related to cell-wall structure. Wood Fiber Sci. 2004, 36, 143–151. [Google Scholar]
- Gindl, W.; Schoberl, T. The significance of the elastic modulus of wood cell walls obtained from nanoindentation measurements. Compos. Part A Appl. Sci. Manuf. 2004, 35, 1345–1349. [Google Scholar] [CrossRef]
- Kulasinski, K.; Derome, D.; Carmeliet, J. Impact of hydration on the micromechanical properties of the polymer composite structure of wood investigated with atomistic simulations. J. Mech. Phys. Solids 2017, 103, 221–235. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, M.; Keten, S.; Coasne, B.; Derome, D.; Carmeliet, J. Hygromechanical mechanisms of wood cell wall revealed by molecular modeling and mixture rule analysis. Sci. Adv. 2021, 7, eabi8919. [Google Scholar] [CrossRef]
- Bondeson, D.; Mathew, A.; Oksman, K. Optimization of the isolation of nanocrystals from microcrystalline cellulose by acid hydrolysis. Cellulose 2006, 13, 171–180. [Google Scholar] [CrossRef]
- Moon, R.J.; Martini, A.; Nairn, J.; Simonsen, J.; Youngblood, J. Cellulose nanomaterials review: Structure, properties and nanocomposites. Chem. Soc. Rev. 2011, 40, 3941–3994. [Google Scholar] [CrossRef]
- Nishiyama, Y. Structure and properties of the cellulose microfibril. J. Wood Sci. 2009, 55, 241–249. [Google Scholar] [CrossRef]
- Gindl, W.; Gupta, H.S.; Schoberl, T.; Lichtenegger, H.C.; Fratzl, P. Mechanical properties of spruce wood cell walls by nanoindentation. Appl. Phys. A Mater. Sci. Process. 2004, A79, 2069–2073. [Google Scholar] [CrossRef]
- Fratzl, P.; Burgert, I.; Keckes, J. Mechanical model for the deformation of the wood cell wall. Z. Für Met. 2004, 95, 579–584. [Google Scholar] [CrossRef]
- Hofstetter, K.; Hellmich, C.; Eberhardsteiner, J.; Mang, H.A. Micromechanical Estimates for Elastic Limit States in Wood Materials, Revealing Nanostructural Failure Mechanisms. Mech. Adv. Mater. Struct. 2008, 15, 474–484. [Google Scholar] [CrossRef]
- Keckes, J.; Burgert, I.; Fruhmann, K.; Muller, M.; Kolln, K.; Hamilton, M.; Burghammer, M.; Roth, S.V.; Stanzl-Tschegg, S.; Fratzl, P. Cell-wall recovery after irreversible deformation of wood. Nat. Mater. 2003, 2, 810–813. [Google Scholar] [CrossRef] [PubMed]

| Relative Humidity (%) | MFA (°) |
|---|---|
| 1 | 21.2 ± 1.3 |
| 33 | 21.8 ± 0.6 |
| 73 | 20.9 ± 1.5 |
| 93 | 21.4 ± 1.2 |
| Specimen | Cylinder Angle (θ) (°) | Side | (°) | (°) | (°) | (°) | (°) |
|---|---|---|---|---|---|---|---|
| 1 | 0 | A | −1.4 | −1.4 | −3.1 | −24.4 | 24.4 |
| B | −1.4 | −1.4 | −3.1 | 18.2 | 18.2 | ||
| 2 | 11 | A | 1.7 | 1.7 | 11.2 | −10.1 | 10.2 |
| B | 1.7 | 1.7 | 11.2 | 32.5 | 32.5 | ||
| 3 | 22.5 | A | −0.5 | −0.5 | 21.7 | 0.4 | 0.6 |
| B | −0.5 | −0.5 | 21.7 | 43 | 43.0 | ||
| 4 | 45 | A | 1.6 | 1.6 | 43.1 | 21.8 | 21.8 |
| B | 1.6 | 1.6 | 43.1 | 64.4 | 64.4 | ||
| 5 | 67.5 | A | 0 | 0 | 64.3 | 43 | 43.0 |
| B | 0 | 0 | 64.3 | 85.6 | 85.6 | ||
| 6 | 79 | A | 0 | 0 | 75.9 | 54.6 | 54.6 |
| B | 0 | 0 | 75.9 | 97.2 | 82.8 | ||
| 7 | 0 | A | 85.8 | 107.1 | 0 | 0 | 72.9 |
| B | 85.8 | 64.5 | 0 | 0 | 64.5 |
| (°) | 0% RH | 33% RH | 75% RH | 94% RH | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (GPa) | (GPa) | (GPa) | (GPa) | |||||||||
| n 1 | Ave 2 | Std 3 | n | Ave | Std | n | Ave | Std | n | Ave | Std | |
| 0.6 | 64 | 19.1 | 2.3 | 48 | 17.9 | 1.4 | 60 | 14.1 | 3.4 | 52 | 10.8 | 1.2 |
| 10.2 | 64 | 17.5 | 1.7 | 56 | 18.0 | 2.4 | 67 | 13.0 | 1.1 | 50 | 10.3 | 1.1 |
| 18.2 | 64 | 17.2 | 1.5 | 48 | 15.3 | 1.5 | 62 | 11.2 | 1.5 | 63 | 7.3 | 1.3 |
| 21.8 | 56 | 17.5 | 1.9 | 48 | 15.7 | 1.8 | 86 | 11.6 | 2.3 | 71 | 8.6 | 1.3 |
| 24.4 | 88 | 15.6 | 1.6 | 48 | 14.9 | 1.4 | 60 | 10.9 | 1.7 | 61 | 7.7 | 1.0 |
| 32.5 | 64 | 13.4 | 2.2 | 64 | 12.1 | 2.1 | 67 | 8.1 | 1.3 | 71 | 6.8 | 1.2 |
| 43.0 | 56 | 13.3 | 1.0 | 40 | 11.9 | 0.6 | 70 | 7.4 | 0.7 | 36 | 5.0 | 0.4 |
| 43.0 | 56 | 12.0 | 1.2 | 65 | 10.1 | 1.2 | 61 | 6.8 | 1.7 | 45 | 4.7 | 0.5 |
| 54.6 | 64 | 13.4 | 1.4 | 72 | 12.7 | 2.3 | 69 | 7.5 | 0.5 | 54 | 4.6 | 0.9 |
| 64.4 | 64 | 8.2 | 0.4 | 65 | 6.6 | 0.5 | 90 | 3.8 | 0.2 | 54 | 2.3 | 0.2 |
| 64.5 | 64 | 8.6 | 0.6 | 58 | 6.1 | 0.3 | 71 | 3.7 | 0.2 | 45 | 2.0 | 0.2 |
| 72.9 | 32 | 8.4 | 0.6 | 32 | 6.4 | 0.5 | 36 | 3.7 | 0.3 | 18 | 2.1 | 0.1 |
| 82.8 | 64 | 8.0 | 0.5 | 72 | 6.4 | 0.3 | 72 | 3.9 | 0.2 | 63 | 2.1 | 0.2 |
| 85.6 | 56 | 8.5 | 0.5 | 56 | 6.4 | 0.2 | 61 | 3.8 | 0.2 | 90 | 2.2 | 0.1 |
| Relative Humidity (%) | (GPa) | (GPa) | (GPa) | (GPa) | R |
|---|---|---|---|---|---|
| 0 | 21.5 | 5.9 | 8.1 | 2.3 | 0.074 |
| 33 | 21.5 | 4.1 | 9.1 | 1.6 | 0.101 |
| 75 | 19.2 | 2.3 | 6.3 | 0.9 | 0.082 |
| 94 | 15.1 | 1.0 | 10.0 | 0.4 | 0.093 |
| (°) | 0% RH | 33% RH | 75% RH | 94% RH | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (GPa) | (GPa) | (GPa) | (GPa) | |||||||||
| n 1 | Ave 2 | Std 3 | n | Ave | Std | n | Ave | Std | n | Ave | Std | |
| 0.6 | 64 | 15.5 | 1.8 | 48 | 14.5 | 1.1 | 60 | 11.4 | 2.7 | 52 | 8.7 | 1.0 |
| 10.2 | 64 | 14.2 | 1.4 | 56 | 14.6 | 1.9 | 67 | 10.5 | 0.9 | 50 | 8.3 | 0.8 |
| 18.2 | 64 | 13.9 | 1.2 | 48 | 12.4 | 1.2 | 62 | 9.0 | 1.2 | 63 | 5.9 | 1.0 |
| 21.8 | 56 | 14.2 | 1.5 | 48 | 12.7 | 1.5 | 86 | 9.4 | 1.8 | 71 | 6.9 | 1.1 |
| 24.4 | 88 | 12.6 | 1.3 | 48 | 12.0 | 1.2 | 60 | 8.7 | 1.3 | 61 | 6.2 | 0.8 |
| 32.5 | 64 | 10.8 | 1.8 | 64 | 9.7 | 1.7 | 67 | 6.5 | 1.0 | 71 | 5.4 | 1.0 |
| 43.0 | 56 | 10.7 | 0.8 | 40 | 9.6 | 0.5 | 70 | 6.0 | 0.6 | 36 | 4.0 | 0.3 |
| 43.0 | 56 | 9.7 | 0.9 | 65 | 8.1 | 1.0 | 61 | 5.5 | 1.3 | 45 | 3.8 | 0.4 |
| 54.6 | 64 | 10.8 | 1.1 | 72 | 10.2 | 1.8 | 69 | 6.0 | 0.4 | 54 | 3.7 | 0.7 |
| 64.4 | 64 | 6.6 | 0.3 | 65 | 5.3 | 0.4 | 90 | 3.0 | 0.2 | 54 | 1.9 | 0.2 |
| 64.5 | 64 | 6.9 | 0.4 | 58 | 4.9 | 0.2 | 71 | 3.0 | 0.2 | 45 | 1.6 | 0.1 |
| 72.9 | 32 | 6.8 | 0.5 | 32 | 5.2 | 0.4 | 36 | 3.0 | 0.2 | 18 | 1.7 | 0.1 |
| 82.8 | 64 | 6.4 | 0.4 | 72 | 5.2 | 0.3 | 72 | 3.1 | 0.2 | 63 | 1.7 | 0.1 |
| 85.6 | 56 | 6.9 | 0.4 | 56 | 5.2 | 0.1 | 61 | 3.1 | 0.2 | 90 | 1.7 | 0.1 |
| (°) | 0% RH | 33% RH | 75% RH | 94% RH | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (MPa) | (MPa) | (MPa) | (MPa) | |||||||||
| n 1 | Ave 2 | Std 3 | n | Ave | Std | n | Ave | Std | n | Ave | Std | |
| 0.6 | 64 | 450 | 39 | 48 | 341 | 20 | 60 | 202 | 35 | 52 | 130 | 23 |
| 10.2 | 64 | 444 | 19 | 56 | 354 | 30 | 67 | 205 | 21 | 50 | 130 | 17 |
| 18.2 | 64 | 454 | 27 | 48 | 321 | 19 | 62 | 179 | 23 | 63 | 107 | 14 |
| 21.8 | 56 | 405 | 43 | 48 | 326 | 28 | 86 | 191 | 26 | 71 | 130 | 18 |
| 24.4 | 88 | 442 | 28 | 48 | 337 | 23 | 60 | 179 | 22 | 61 | 112 | 11 |
| 32.5 | 64 | 364 | 54 | 64 | 276 | 33 | 67 | 158 | 19 | 71 | 109 | 17 |
| 43.0 | 56 | 435 | 25 | 40 | 332 | 16 | 70 | 174 | 13 | 36 | 103 | 8 |
| 43.0 | 56 | 430 | 25 | 65 | 299 | 23 | 61 | 167 | 24 | 45 | 97 | 9 |
| 54.6 | 64 | 390 | 45 | 72 | 309 | 44 | 69 | 169 | 9 | 54 | 91 | 8 |
| 64.4 | 64 | 442 | 14 | 65 | 291 | 18 | 90 | 154 | 9 | 54 | 92 | 5 |
| 64.5 | 64 | 470 | 40 | 58 | 290 | 23 | 71 | 166 | 8 | 45 | 85 | 9 |
| 72.9 | 32 | 425 | 18 | 32 | 282 | 15 | 36 | 137 | 6 | 18 | 80 | 3 |
| 82.8 | 64 | 455 | 30 | 72 | 321 | 12 | 72 | 168 | 7 | 63 | 88 | 7 |
| 85.6 | 56 | 490 | 25 | 56 | 330 | 11 | 61 | 169 | 14 | 90 | 96 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arzola-Villegas, X.; Plaza, N.Z.; Bechle, N.J.; Wang, Y.; Lakes, R.; Stone, D.S.; Jakes, J.E. Moisture-Dependent Transverse Isotropic Elastic Constants of Wood S2 Secondary Cell Wall Layers Determined Using Nanoindentation. Forests 2025, 16, 712. https://doi.org/10.3390/f16050712
Arzola-Villegas X, Plaza NZ, Bechle NJ, Wang Y, Lakes R, Stone DS, Jakes JE. Moisture-Dependent Transverse Isotropic Elastic Constants of Wood S2 Secondary Cell Wall Layers Determined Using Nanoindentation. Forests. 2025; 16(5):712. https://doi.org/10.3390/f16050712
Chicago/Turabian StyleArzola-Villegas, Xavier, Nayomi Z. Plaza, Nathan J. Bechle, Yikai Wang, Roderic Lakes, Donald S. Stone, and Joseph E. Jakes. 2025. "Moisture-Dependent Transverse Isotropic Elastic Constants of Wood S2 Secondary Cell Wall Layers Determined Using Nanoindentation" Forests 16, no. 5: 712. https://doi.org/10.3390/f16050712
APA StyleArzola-Villegas, X., Plaza, N. Z., Bechle, N. J., Wang, Y., Lakes, R., Stone, D. S., & Jakes, J. E. (2025). Moisture-Dependent Transverse Isotropic Elastic Constants of Wood S2 Secondary Cell Wall Layers Determined Using Nanoindentation. Forests, 16(5), 712. https://doi.org/10.3390/f16050712








