Assessing the Impact of Forest Change and Climate Variability on Dry Season Runoff by an Improved Single Watershed Approach: A Comparative Study in Two Large Watersheds, China

Abstract

Extensive studies on hydrological responses to forest change have been published for centuries, yet partitioning the hydrological effects of forest change, climate variability and other factors in a large watershed remains a challenge. In this study, we developed a single watershed approach combining the modified double mass curve (MDMC) and the time series multivariate autoregressive integrated moving average model (ARIMAX) to separate the impact of forest change, climate variability and other factors on dry season runoff variation in two large watersheds in China. The Zagunao watershed was examined for the deforestation effect, while the Meijiang watershed was examined to study the hydrological impact of reforestation. The key findings are: (1) both deforestation and reforestation led to significant reductions in dry season runoff, while climate variability yielded positive effects in the studied watersheds; (2) the hydrological response to forest change varied over time due to changes in soil infiltration and evapotranspiration after vegetation regeneration; (3) changes of subalpine natural forests produced greater impact on dry season runoff than alteration of planted forests. These findings are beneficial to water resource and forest management under climate change and highlight a better planning of forest operations and management incorporated trade-off between carbon and water in different forests.

1. Introduction

In spite of numerous studies on the hydrological responses of dry season runoff to forest change (forest harvesting, reforestation, etc.) [1,2,3,4,5], consistent conclusions can hardly be drawn [6,7]. The effect of forest change on dry season flows can be positive, negative or insignificant [8]. Some studies have demonstrated that forest loss can increase dry season runoff since the removal or death of forests can reduce evapotranspiration and canopy interception in disturbed sites and ultimately increase soil moisture and groundwater recharge [9]. Meanwhile, other studies have reported that fast vegetation regrowth and soil disturbances after forest harvesting may offset the water increment or even decrease dry season runoff [6,8,10]. Similarly, variable responses of dry season flow to afforestation or reforestation have also been found, which are mainly determined by the changes in soil properties caused by forest regrowth and forest practices [11,12]. However, most studies are conducted in small watersheds (<10 km²), and the impact of forest change on dry season runoff in large watersheds (>1000 km²) has been less investigated due to limitations such as the lack of efficient and commonly-accepted methods and complexity in ecological and hydrological processes at a larger spatial scale [13,14,15,16].

In the past few years, researchers have applied various approaches in large watershed studies. The experimental paired watersheds, physical hydrological models, sensitivity analysis, elasticity analysis and statistical test-hydrograph combined method are commonly used to evaluate the hydrological effect resulting from forest change, but they still have several limitations [17,18,19,20,21]. The experimental paired watershed approach requires long-term commitment and expensive cost. In addition, it is often constrained by the great difficulty in finding two watersheds with similarities in climate patterns, land use, forest, soil, morphology and geology at a larger spatial scale [5]. Hydrological models, especially distributed models (e.g., MIKE-SHE, Distributed Hydrology Soil Vegetation Model (DHSVM) and Soil and Water Assessment Tool (SWAT)) need long-term hydrological and climatic data, as well as detailed information on watershed properties (e.g., forest, soil and topography), which are often absent in many watersheds [22,23]. Despite their ability to provide an efficient assessment, the sensitivity analysis, elasticity analysis or statistical test and hydrograph combined method may fail to remove the hydrological effect of non-forest drivers completely given that most of them only consider climate variability and forest change or land cover change as two dominating drivers, and neglect other factors [21,24].

Wei and Zhang (2010b) developed a single watershed approach, the “modified double mass curve” (MDMC), to estimate the hydrological effect of forest change in a large watershed [25]. Despite its successful application in both China and Canada [26,27,28,29,30], this approach can only be used in watersheds with limited human activities since it cannot differentiate the hydrological impact of other confounding factors including urbanization and agricultural activities from that of forest change. As a matter of fact, few forested watersheds worldwide are exempt from human impact. This calls for the development of a new efficient method that can be widely applied to separate the impact of climate variability, forest change and other confounding factors on hydrology. In order to address this problem, we improved the MDMC approach by introducing the multivariate autoregressive integrated moving average (ARIMAX) model to differentiate the effects of forest change, climate variability and other factors (e.g., human activities) on runoff. The MDMC was firstly used to exclude the climatic effect on runoff variation and then to estimate runoff variation attributed to non-climatic factors (forest change and other factors). Finally, the ARIMAX model was used to quantify the runoff variation attributed to forest change by establishing a quantitative relationship between accumulated runoff variation due to non-climatic factors and forest coverage data. We provided two examples (the Zagunao and Meijiang watersheds) demonstrating the application of this method to separate the effects of forest change and climate variability on dry season runoff. The Zagunao watershed dominated by subalpine natural coniferous forest suffered from deforestation due to forest harvesting lasting from the 1950s–1980s (about 15% reduction of forest coverage). The Meijiang watershed is mainly covered by subtropical coniferous plantations due to a large-scale reforestation program launched since 1980s (about a 44% increase of forest coverage). Understanding the responses of dry season runoff to forest change is essential for the strategy design of forest practices and forest ecosystem protection in these watersheds.

2. Materials and Methods

2.1. Study Watersheds

The Zagunao River originates from the Zhegu Mountain and enters the Minjiang River, the largest tributary of the Upper Yangtze River at Weizhou County in the northwest of Sichuan Province, China (Figure 1). The Zagunao watershed is situated in the transitional zone from the Qinghai-Tibet Plateau to the Sichuan Basin, covering an area of 2441.77 km². The Meijiang River flows into the Ganjiang River, the headwaters of the Poyang Lake in Jiangxi Province of China. The Meijiang River watershed covers an area of 6310.13 km².

The Zagunao watershed is situated in a typical alpine climate zone mainly controlled by the Southwest Monsoon from the Indian Ocean in summer, resulting in wet season precipitation (May–October) accounting for about 80% of the annual total. The Meijiang watershed belongs to the humid subtropical monsoon climate, with mild climate and abundant precipitation. The mean annual precipitation and dry season (September–February) precipitation were 1735.5 mm and 447.8 mm, respectively. More information on watershed properties can be found in

Table 1. A summary of watershed characteristics.

Metrics	Zagunao	Meijiang
Drainage area	2441.77 km²	6310.13 km²
Climate type	Alpine climate	Subtropical monsoon climate
Hydrological year	November–October	March–February
Dry season	November–April	September–February
T (°C)	11.2	18.4
Td (°C)	5.5	14.0
P (mm)	999.7	1735.5
Pd (mm)	184.4	447.8
Q (mm)	773.4	857.7
Qd (mm)	160.4	233.0

Note: T_d, P_d and Q_d refer to dry season temperature, dry season precipitation and dry season runoff.

.

The major vegetation types in the Zagunao watershed include alpine meadow and subalpine coniferous forest, covering 46% and 32% of the total watershed area, respectively. The dominant tree species are Abies faxoniana Rehder & E.H.Wilson and Picea purpurea Mast. [27]. Forest land, orchard and farmland are major land cover types in the Meijiang watershed (

Table 2. Land use/cover in the study watersheds.

Land Use Types	% of Total Watershed Area
	Zagunao	Meijiang
Forest land	37.00	68.75
Orchard	12.00	8.48
Farmland	0.49	20.39
Urban or built-up land	0.01	1.01
Grassland	47.00	1.37
Snow and Ice	3.50	0.00

). The natural forests consist of subtropical evergreen broad-leaved species such as Castanopsis fabri Hance and Castanopsis fissa (Champ. ex Benth.) Rehd. & Wils., while planted forests are dominated by Pinus massoniana Lamb., Cunninghamia lanceolata (Lamb.) Hook. and moso bamboo (Phyllostachys edulis (Carrière) J.Houz.) [30].

The Zagunao watershed was originally covered by a large area of natural subalpine coniferous forests, which were destroyed by continuous forest harvesting during the 1950s–1990s. Intensive logging of the old-growth coniferous forests started from 1955–1962, then gradually declined after 1965 and finally stopped in 1998 due to the Natural Forest Protection Plan. From 1950–2004, forest coverage in the Zagunao watershed dropped from 52.5%–36.9% (Figure 2). The Meijiang watershed maintained a low level of forest coverage around 25% from the 1960s–1970s due to large-scale logging since the 1940s. Large-scale reforestation was continuously conducted watershed-wide since the 1980s, leading to a significant increase in forest coverage from 27.6% in 1980 to 71.4% in 2005 (Figure 2).

2.2. Data

Daily hydrological records between 1959 and 2004 were collected from the Zagunao hydrological station, located at the outlet of the Zagunao watershed. Daily flow data from 1958–2005 were from Fenkeng hydrometric station situated at the outlet of the Meijiang watershed (Figure 1). Daily records were used to calculate monthly runoff, dry season runoff and annual runoff in this study (Table 1).

Climate data are very limited within or around the Zagunao watershed. There are only one active weather station (Li) and one rain gauge station (Miyaluo) situated within the Zagunao watershed. Monthly mean/min/max temperature data (1958–2004) from the Li County national weather station were used in the analysis. In order to capture the high spatial variability of precipitation in the Zagunao watershed, monthly precipitation data from 51 rain gauge and weather stations in the Minjiang River watershed were collected to generate spatially-interpolated monthly precipitation data from 1958–2004 by use of the ANUSPIN model. Then, monthly precipitation data from 1958–2004 for the Zagunao watershed were derived and calculated accordingly. For the Meijiang watershed, more weather stations are available. There are six active weather stations (Ningdu, Shicheng, Guangchang, Ruijin, Xingguo, Yudu) within or near the Meijiang watershed. Monthly mean/min/max temperature and precipitation during 1961 and 2005 from these weather stations were also applied in the ANUSPIN model to generate spatially-interpolated monthly climate data for the Meijiang watershed over the study period.

Forest coverage data used in the Zagunao and Meijiang watersheds were provided by the Miyaluo Forest Station of Sichuan Province and Ganzhou Regional Forestry Bureaus of Jiangxi Province, respectively.

2.3. Methods

Hydrological processes in the study watersheds can be influenced by climate variability, forest change (e.g., harvesting or reforestation) and other factors. The following methods including MDMC and ARIMAX were applied to separate and quantify the effects of climate variability, forest change and other factors on dry season runoff.

2.3.1. Trend Analysis

Trend analysis was first used to detect possible significant trends in hydrology, climate and forest coverage variables [31]. Kendall tau and Spearman rho tests were employed to identify the statistical significance of trends in dry season precipitation, temperature, evapotranspiration, runoff and forest coverage. These tests can eliminate the impacts of outliers and have no requirement for data distribution [32,33,34].

2.3.2. Excluding the Effect of Climate Variability on Dry Season Runoff

Wei and Zhang (2010b) developed the modified double mass curve (MDMC) to exclude the influence of climate variability on runoff in a single watershed successfully (Figure 3). The traditional double mass curve (DMC), which plots the accumulated runoff from the disturbed watershed against the accumulated runoff from the undisturbed one, is frequently used in paired watershed studies to detect the consistency in the runoff relationship between the disturbed watershed and the control watershed [35,36]. Unlike the traditional DMC, MDMC is for a single watershed study, by plotting accumulated runoff versus accumulated effective precipitation (the difference between precipitation and evapotranspiration). In this way, the climatic effects on runoff variation can be eliminated. In this study, the modified double mass curve was firstly plotted by accumulated dry season effective precipitation versus accumulated dry season runoff. The effective dry season precipitation refers to the difference between dry season precipitation and dry season evapotranspiration. Watershed-scale evapotranspiration can be computed according to land cover types and their corresponding proportions [27]. Evapotranspiration for each land cover type was calculated by Zhang’s equation, a revised version of Budyko’s evaporation (Equation (1)), by introducing a vegetation factor ω [37]. The Hargreaves equation was used to estimate potential evapotranspiration (Equation (2)) [38]:

$$E=P\left(1+\omega \left(E_0/P\right)\right)/\left(1+\omega \left(E_0/P\right)+P/E_0\right)$$

(1)

$$E_0=0.0023\times R_a\times \left(\left(T_{\max }+T_{\max }\right)/2+17.8\right)\times {\left(T_{\max }-T_{\max }\right)}^{0.5}$$

(2)

where E stands for the dry season actual evapotranspiration for each type; E₀ and P are potential evapotranspiration and precipitation in the dry season; ω is the plant-available water coefficient, which for forest, grassland and shrub land are 2.0, 0.5 and 1.0, respectively [38]. T_min and T_max are the minimum and maximum temperature in °C.

According to Wei and Zhang’s illustration, MDMC of a given watershed is featured by a straight line during a less disturbed or undisturbed period, indicating a stable water balance relationship between forest and runoff. A breakpoint can be found in the MDMC if non-climatic factors significantly affect runoff (Figure 3). ARIMA intervention analysis (autoregressive integrate moving average) was used to detect whether the change point in the slope of MDMC was statistically significant [39]. Once the change point in the MDMC is statistically significant (α = 0.05), the period before breakpoint is defined as the reference period, while the period after the breakpoint is named as the disturbed period. The Wilcoxon test and sign test were further applied to confirm the statistical significance of the change point detected by the ARIMA intervention analysis. If both tests illustrate that the medians of the observed and the predicted data are statistically insignificant (α = 0.05) in the reference period and significant (α = 0.05) in disturbed periods, the change point is statistically significant. Then, a linear regression model established by observed accumulated dry season effective precipitation and accumulated dry season runoff without disturbances during the reference period can be used to predict the accumulated dry season runoff during the disturbed period. The differences between the observed accumulated dry season runoff and the predicted accumulated dry season runoff during the disturbed period can be viewed as the cumulative effect of non-climatic factors on runoff.

The cumulative effect of non-climatic factors (∆Q_anc) and climate variability (∆Q_ac) on dry season runoff can be computed by Equations (3) and (4).

$$\Delta Q_{anc}(t)=\Delta Q_a(t)-\Delta Q_{a0}(t)$$

(3)

where ∆Q_a(t) and ∆Q_a0(t) are observed accumulated dry season runoff for the t-th year and predicted accumulated dry season runoff without disturbances for the t-th year; ∆Q_anc(t) represents accumulated dry season runoff variation attributed to non-climatic factors for the t-th year.

$$\Delta Q_{ac}(t)=\Delta Q_a(t)-\Delta Q_{anc}(t)$$

(4)

where ∆Q_ac(t) stands for accumulated dry season runoff variation attributed to climate variability for the t-th year.

2.3.3. Quantifying the Effect of Forest Change on Dry Season Runoff

As mentioned before, the MDMC method can only separate runoff variation due to climate variability from that caused by non-climatic factors, and the hydrological effect of forest change and other factors cannot be quantified directly. We improved the MDMC method by introducing a multivariate ARIMA (ARIMAX) model that established a quantitative relationship between accumulated dry season runoff variation attributed to non-climatic factors (∆Q_anc) and forest coverage over the disturbed period.

The ARIMAX, an extension of the ARIMA model with external regressors to improve model performance, has been widely used to predict auto-correlated data series in natural and social sciences [40,41,42]. An ARIMAX model fitted by ∆Q_anc data series was established first. The accumulated forest coverage data series were pre-whitened to eliminate autocorrelations by fitting an ARIMA model [39,40,43]. Then, the pre-whitened accumulated forest coverage time series was added as a dynamic regressor in the established ARIMAX model. The selected ARIMAX model with forest coverage as the dynamic regressor can eventually be used to predict ∆Q_anc. The predicted ∆Q_anc can be defined as ∆Q_anc0. Given that forest coverage serves as a predictor, the differences between ∆Q_anc0 and ∆Q_anc (∆Q_ad, Equations (5) and (6)), can express statistical errors (∆Q_se) and dry season runoff variation from other factors (∆Q_o). Here, we used the 95% confidence interval (CI) of predicted values as a standard to evaluate statistical errors of the selected ARIMAX model. Therefore, ∆Q_d located beyond 95% CI are viewed as data points affected by both of the other factors and statistical errors, while ∆Q_d within 95% CI are viewed as data points with statistical errors only (Figure 4). Once data points affected by both of the other factors and statistical errors are identified, runoff variation attributed to other factors (∆Q_o) can be estimated for these data points (Equation (7)), and eventually, dry season runoff variation due to forest change can be computed accordingly (Equation (8)). All the statistical analyses were accomplished in R Studio Version 1.0.136, and free and open tools for R (the R Project for Statistical Computing) and the package “TSA” were used to establish the ARIMAX model. More detailed instruction on ARIMAX modelling can be found in the user manual of the TSA package in R.

$$\Delta Q_{ad}(t)=\Delta Q_{anc}(t)-\Delta Q_{anc0}(t)$$

(5)

$$\Delta Q_{ad}(t)=\Delta Q_d(1)+\Delta Q_d(2)+\dots \dots +\Delta Q_d(\mathrm{t})$$

(6)

$$\Delta Q_o(t)=\Delta Q_d(t)-\Delta Q_{se}(t)$$

(7)

$$\Delta Q_f(t)=\Delta Q_{nc}(t)-\Delta Q_o(t)$$

(8)

where ∆Q_anc(t), ∆Q_anc0(t) and ∆Q_ad(t) are observed accumulated dry season runoff variation attributed to non-climatic factors, predicted accumulated dry season runoff variation attributed to non-climatic factors and accumulated dry season runoff variation from the others for the t-th year. ∆Q_o(t) and ∆Q_f(t) represent dry season variation attributed to other factors and forest change for the t-th year; ∆Q_se(t) is the statistical errors from the ARIMAX model for the t-th year.

3. Results

3.1. Trend Analysis

As shown in

Table 3. Results of trend analysis in the study watersheds.

Variables	Zagunao		Meijiang
	Kendall Tau	Spearman Rho	Kendall Tau	Spearman Rho
Annual runoff	0.32 *	0.46 *	0.01	0.00
Dry season runoff	0.40 *	0.57 *	−0.03	−0.06
Annual precipitation	0.14	0.23	0.10	0.10
Dry season precipitation	−0.13	−0.14	−0.15	−0.25
Annual mean temperature	0.09	0.15	0.47 *	0.65 *
Annual maximum temperature	0.22	0.32	0.54 *	0.71 *
Annual minimum temperature	−0.15	−0.22	0.44 *	0.61 *
Dry season mean temperature	0.07	0.09	0.39 *	0.53 *
Annual evapotranspiration	0.10	−0.12	0.12	0.16
Dry season evapotranspiration	−0.17	−0.23	−0.07	−0.13
Forest coverage	0.77 *	0.92 *	−0.98 *	−0.99 *

* Significant at α = 0.05.

, there was a significant (α = 0.05) upward trend in dry season runoff in the Zagunao watershed. In the Meijiang watershed, dry season temperature showed a significant rising tendency (α = 0.05). Forest coverage showed a significant (α = 0.05) downward trend in the Zagunao watershed, while in the Meijiang watershed, a significant (α = 0.05) increasing trend in forest coverage was detected (α = 0.05). Meanwhile, we failed to identify significant changes in other variables.

3.2. Dry Season Runoff Variation Caused by Non-Climate Factors

According to the modified double mass curves (Figure 5), the ARIMA intervention test (

Table 4. ARIMA Intervention models for the slope of MDMC.

Watershed	AP Part		Int Part	MA Part	Intervention Part				Change Type	Model Structure	MS
					CP1		CP2
	p(1)	p(2)	d(1)	q(1)	Ω(1)	△(1)	Ω(2)	△(2)
Zagunao	0	0	0	−0.98 (p = 0.00)	1.90 (p = 0.00)	−0.33 (p = 0.03)	0	0	GP	Ln(x) (0,0,1)	0.69
Meijiang	−0.95 (p = 0.00)	−0.68 (p = 0.00)	1	0	−0.78 (p = 0.03)	−0.95 (p = 0.00)	−0.94 (p = 0.03)	−0.98 (p = 0.00)	GP	Ln(x) (2,1,0)	0.16

Note: p, d and q are parameters for autoregression, differencing and moving average; Ω and △ are parameters for intervention; AR part, Int part and MA part refer to the autoregressive part, the integrated part and the moving average part, respectively; CP, GP and MS refer to the change point, gradual permanent change and model residual, respectively. ARIMA: autoregressive integrated moving average; MDMC: modified double mass curve.

) and the Wilcoxon and sign test (

Table 5. Wilcoxon test and Sign test for significance of differences in predicted dry season runoff and observed dry season runoff in reference and disturbed periods.

Watershed	Period	Wilcoxon Test	Sign Test
Zagunao	Reference period (1959–1975)	0.31 (p = 0.758)	0.22 (p = 0.737)
	Disturbed period (1976–2004)	4.00 * (p = 0.000)	2.97 * (p = 0.003)
Meijiang	Reference period (1961–1986)	0.65 (p = 0.517)	0.59 (p = 0.556)
	Disturbed period (1987–1994)	2.52 * (p = 0.011)	2.47 * (p = 0.013)
	Disturbed period (1995–2005)	2.93 * (p = 0.003)	3.02 * (p = 0.003)

* Significant at α = 0.05.

), we identified two significant change points in the Meijiang watershed (1987 and 1995), while only one breakpoint in the Zagunao watershed (1976). As estimated, accumulated dry season runoff variation attributed to non-climatic factors and climate variability during 1976–2004 in the Zagunao watershed was from −680.0 mm–2.3 mm and −76.2 mm–672.3 mm, respectively. In the Meijiang watershed, accumulated dry season runoff variation due to non-climatic factors and climate variability over 1987–2005 varied from −752.6 mm–−30.2 mm and 465.3 mm–1345.6 mm, respectively.

3.3. Hydrological Response to Forest Change and Other Factors

Table 6. ARIMAX models for accumulation of forest coverage and ∆Q_anc0.

Watershed	Model Structure	Parameter Estimation
		p(1)	q(1)	c	Forest Coverage
Zagunao	Accumulation of forest coverage: ARIMA(1,1,1)	0.59 (p < 0.001)	0.78 (p < 0.001)	/	/
	∆Qanc0: ARIMAX(0,0,1)	/	1.24 (p < 0.001)	−190.5 (p < 0.005)	−112.4 (p < 0.001)
Meijiang	Accumulation of forest coverage: ARIMA(1,1,1)	0.626 (p < 0.000)	0.795 (p < 0.001)	/	/
	∆Qanc0: ARIMAX(1,0,0)	0.601 (p < 0.001)	/	−1283.136 (p < 0.001)	509.451 (p < 0.001)

Note: p is autoregressive parameter; q is moving average parameter; c stands for constant.

shows the structure, parameters’ estimation and model performance for the best fitted factored ARIMAX model of accumulated dry season runoff variation attributed to non-climatic factors (∆Q_anc) with forest coverage data series as a dynamic regressor in the study watersheds. Figure 6 shows the predicted values of accumulated dry season runoff variation attributed to non-climatic factors by established ARIMAX models. There are significant differences between accumulated dry season runoff variation attributed to non-climatic factors and its predicted values in the Zagunao and Meijiang watersheds.

Figure 7 shows the estimated dry season runoff variation attributed to climate variability, forest change and other factors during the disturbed period in the study watersheds. Dry season runoff variation attributed to climate variability, forest change and other factors over the whole disturbed period (1976–2004) in the Zagunao watershed were 23.2 mm, −15.5 mm and −3.5 mm, respectively; and the relative contributions of climate variability, forest change and other factors to dry season runoff were 34.1%, 38.7% and 27.1%, respectively. In the Meijiang watershed, dry season runoff variation attributed to climate variability, forest change and other factors over the disturbed period was 58.0 mm, −6.3 mm and 4.6 mm, respectively, and their relative contributions were 45.8%, 25.7% and 28.5%, respectively (

Table 7. Dry season runoff variations to climate variability, forest change and other factors in the study watersheds.

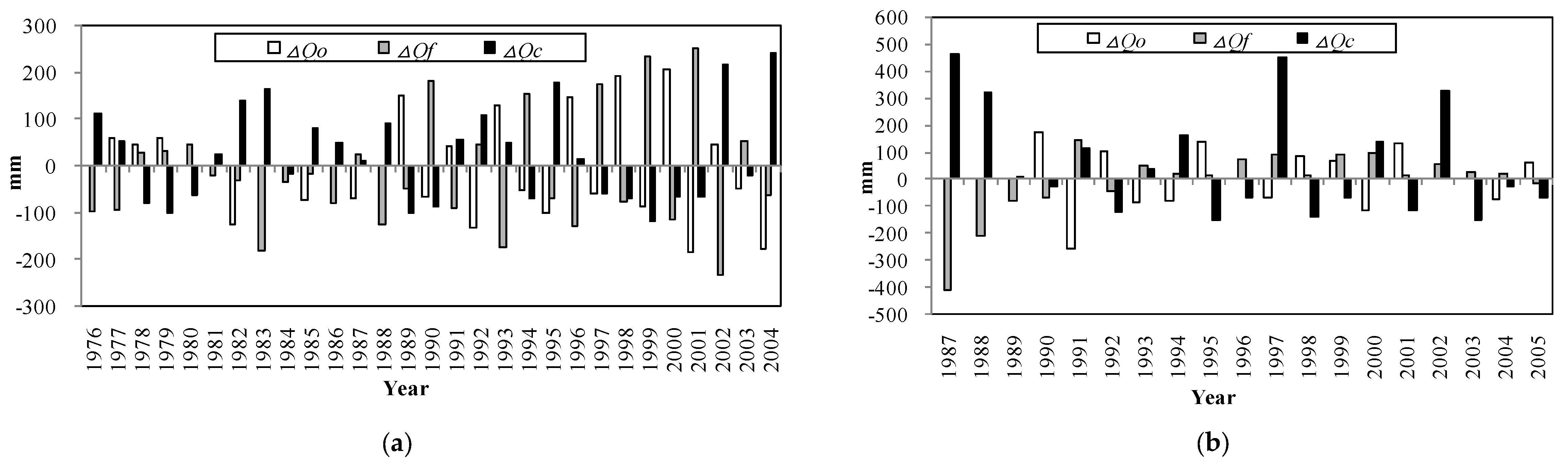
Watershed	Phase	∆Q (mm)	∆Qc (mm)	∆Qf (mm)	∆Qo (mm)	∆Qc (%)	∆Qf (%)	∆Qo (%)	∆Q (%)	Rc (%)	Rf (%)	Ro (%)	F (%)	Reference F (%)
Zagunao	1976–1994	−4.8 ± 5.2	22.0 ± 19.5	−25.0 ± 22.1	−1.8 ± 17.3	13.7 ± 12.2	−15.6 ± 13.8	−1.1 ± 10.8	−3.0 ± 3.2	38.2 ± 3.2	38.8 ± 4.3	23.1 ± 4.9	37.7	45.4
	1995–2004	21.3 ± 7.0	25.4 ± 42.4	2.6 ± 52.9	−6.7 ± 46.1	15.8 ± 26.4	1.6 ± 33.0	−4.2 ± 28.8	13.3 ± 4.3	26.4 ± 5.2	38.4 ± 5.0	35.2 ± 5.0	37.5
	1976–2004	4.2 ± 4.7	23.2 ± 19.0	−15.5 ± 22.8	−3.5 ± 19.0	14.5 ± 11.8	−9.7 ± 14.2	−2.2 ± 11.9	2.6 ± 2.9	34.1 ± 2.9	38.7 ± 3.3	27.2 ± 3.7	37.5
Meijiang	1987–1994	27.1 ± 24.9	121.2 ± 68.2	−76.1 ± 60.6	−18.0 ± 46.3	52.0 ± 29.3	−32.7 ± 26.0	−7.7 ± 19.9	11.6 ± 10.7	35.8 ± 7.7	35.1 ± 8.8	29.0 ± 9.2	47.1	30.0
	1995–2005	77.6 ± 56.5	12.1 ± 61.8	44.5 ± 11.7	21.0 ± 25.6	5.2 ± 26.5	19.1 ± 5.0	9.0 ± 11.0	33.3 ± 24.2	53.0 ± 6.3	18.9 ± 4.6	28.1 ± 6.7	69.2
	1987–2005	56.3 ± 34.1	58.0 ± 46.4	−6.3 ± 29.0	4.6 ± 24.1	24.9 ± 19.9	−2.7 ± 12.5	2.0 ± 10.4	24.2 ± 14.6	45.8 ± 5.2	25.7 ± 4.8	28.5 ± 5.3	59.9

Note: ∆Q%, ∆Q_f%, ∆Q_c% and ∆Q_o% are relative dry season mean flow variation (∆Q% = ∆Q/Q × 100%, Q is average dry season mean flow), relative dry season mean flow variation attributed to forest change (∆Q_f% = ΔQ_f/Q × 100%), relative dry season mean flow variation attributed to climate variability (∆Qc% = ΔQc/Q × 100%) and relative dry season mean flow variation attributed to other factors (∆Q_o% = ΔQ_o/Q × 100%). R_f, R_c, R_o, F are the relative contributions of forest change, climate variability, other factors and forest coverage, respectively. R_f = |∆Q_f|/(|ΔQ_f| + |ΔQ_c| + |ΔQ_o|) × 100%; R_c = 100 × |ΔQ_c|/(|ΔQ_f| + |ΔQ_c| + |ΔQ_o|) × 100%; R_o = |ΔQ_o|/(|ΔQ_f| + |ΔQ_c| + |ΔQ_o|) × 100%.

).

In addition, the impact of forest change on dry season runoff changed over time with forest recovery or regrowth. Over the period of 1976–1994, with mean forest coverage 37.7% less than the reference period, dry season runoff was reduced by 25 mm/year on average in the Zagunao watershed. During the period of 1995–2004, with limited forest harvesting, dry season runoff was averagely increased by 2.6 mm/year in this watershed. In the Meijiang watershed, dry season runoff decreased by 76.1 mm/year with increasing forest coverage over the period of 1987–1994, while during the period of 1995–2005, dry season runoff increased by 44.5 mm/year due to continuing forest cover gain.

4. Discussion

4.1. Dry Season Runoff Response to Forest Change

In the Zagunao watershed, dry season runoff reduced by 15.5 mm (9.7%) on average as a result of a 15.6% forest reduction due to forest harvesting from 1976–2004. This result was consistent with a qualitative study that detected a significant, positive correlation between forest harvesting rate and dry season runoff in the Zagunao watershed [29]. An experimental study in this watershed also showed that dry season runoff in a clear-cut site was lower than an undisturbed site [44]. However, the response of dry season runoff to forest harvesting varied over time as suggested by Figure 7. In the first few years after the breakpoint (1976–1982), dry season runoff was increased by forest harvesting due to the decrease in forest canopy interception and transpiration, resulting in more soil infiltration and soil water for the generation of dry season runoff. Several years later with the fast regeneration of understory vegetation and secondary broad-leaved forests such as birch, the effect of forest harvesting on dry season runoff became negative. The natural coniferous forests feature lower evaporation and transpiration and higher water conservation capacity, while the regenerated young broad-leaved trees were found to transpire more water than previous old-growth coniferous trees, resulting in a reduction of soil moisture [45]. In addition, given that natural forests are normally distributed on steep slopes in the Zagunao watershed, summer storms can cause severe soil loss and erosion without forest cover, leading to less soil water storage and recharge for groundwater in the wet season [46]. Since dry season runoff is mostly sustained by groundwater and soil water, reduced soil infiltration, water storage and groundwater caused by forest harvesting consequently yielded a negative effect on dry season runoff [27]. From 1995–2004, the negative effect of forest harvesting on dry season runoff diminished. Forest change increased dry season runoff by 1.6% (2.6 mm). This is due to the fact that forest harvesting gradually ceased and early plantation of Picea asperata Mast at the clear-cut sites started to mature in the late 1980s, which led to a gradual recovery of the water conservation capacity of forests in the Zagunao watershed.

Interestingly, large-scale plantation in the Meijiang watershed also yielded a negative effect on dry season runoff over the whole study period, but about a 40% increment in forest coverage only resulted in a 6.3 mm/year reduction in dry season runoff. The plantation in the early years was especially associated with a significant reduction of dry season runoff. During 1987–1994, dry season runoff was decreased by 76.1 mm/year (32.7%) as a result of the 17.1% forest increment. This is likely because the planted trees were mainly Cunninghamia lanceolata and Pinus massoniana, which featured high transpiration and soil evaporation, poorly developed understory vegetation and low litter cover, particularly for immature stands [47]. Therefore, high water consumption by planted young trees coupled with poorly-developed water conservation capacity greatly reduced dry season runoff during the early development of forest stands. However, as reforestation proceeded along with early planted trees being mature, the sponge effect of forests emerged when forest coverage reached about 60%. Over the period of 1995–2005, dry season runoff was increased by 44.5 mm/year (19.1%). The mature stands tended to have lower evapotranspiration than young stands, but more developed understory and forest litter to conserve soil water, thus more infiltration for groundwater and more water available for dry season runoff generation [48].

Obviously, with a disproportionate relationship to forest coverage rate, the response of dry season runoff to forest change is mainly determined by soil conditions, soil disturbances, tree species and vegetation regeneration after disturbances, as well as watershed topography. The integrated effects of these factors can lead to the highly variable response of dry season runoff to forest change over time and among watersheds. These findings are of great importance for watershed managers to make strategies to sustain both water resources and forest ecosystems in forest watersheds.

4.2. Relative Contributions of Forest Change and Climate Variability on Dry Season Runoff

The relative contributions of forest change and climate variability to runoff variation can imply their impact strength [49,50,51]. As suggested by our calculation, the relative contributions of forest change and climate variability can be different among watersheds. In the Zagunao watershed, forest change is more influential on dry season runoff than climate variability. The relative contribution of forest change to dry season runoff variation was 38.7%, while that of climate variability was 34.1%. On the contrary, climate variability was the major driver for dry season runoff variation in the Meijiang watershed. The relative contribution of climate variability was up to 45.8%, much greater than that of forest change (25.7%), in this watershed. The different result in these two watersheds clearly demonstrated that forests play a more important role in the water cycle in the Zagunao watershed than in the Meijiang watershed. In other words, dry season runoff in the Zagunao watershed can be more sensitive to forest change than that in the Meijiang watershed. Subalpine old-growth coniferous forests in the Zagunao watershed characterized by low transpiration and evaporation, high canopy interception and soil water storage are crucial for sustaining a stable water supply in the dry season [52,53]. Once they are harvested, it will take a long time to reach a full hydrological recovery. This highlights the importance of protection of subalpine natural forests in the upper streams of the Yangtze River. In spite of large-scale plantation with a forest coverage increment of 40% in the Meijiang watershed, its contribution to dry season runoff was relatively low. This suggests that planted forests in this watershed are poorly managed, especially for understory vegetation and forest litter [12]. This calls for a better design of forest operations and plantation management, for example site preparation, establishment, thinning, management of understory and litter. A sound plantation strategy should not only aim to increase biomass, but also recover the hydrological function of forests to ensure a stable water supply in dry seasons.

4.3. Limitations and Future Studies

Our improved single watershed approach combining MDMC and ARIMAX can successfully separate the impact of forest change, climate variability and other factor on dry season runoff over a watershed scale. It can yield a quick assessment of the relative contributions of climate variability, land cover/land use change and other factors (human activities such as urbanization, agricultural activities, infrastructure and road construction) on runoff variations and can be widely applied in any watershed with fewer data requirements. Nevertheless, this single watershed approach fails to identify the impact of climate variability and forest change on other hydrological processes such as soil water and evapotranspiration, as well as low flows and peak flows. In addition, it cannot quantify the spatial differences in hydrological response to forest change at a watershed scale. Therefore, a physically-based hydrological model should also be used in future studies to quantify responses of various hydrological processes to forest change and climate variability and to investigate their feedback mechanism over a large spatial scale.

5. Conclusions

Forest loss caused by harvesting generally yielded a negative effect on dry season runoff in the Zagunao watershed. In the Meijiang watershed, forest gains due to large-scale planation also produced a negative impact on dry season runoff over the disturbed period. However, the hydrological response to forest change varied over time due to vegetation regeneration-associated changes in soil infiltration and evapotranspiration. In addition, dry season runoff in the Zagunao watershed can be more sensitive to forest change than that in the Meijiang watershed. This highlights the protection of the subalpine natural forest ecosystem in the Zagunao River and better planning of forest operations and management incorporated trade-off between carbon and water.