Lightweight Design of Front Suspension Upright of Electric Formula Car Based on Topology Optimization Method
Abstract
:1. Introduction
2. Topology Optimization Method
3. Topology Optimization of Front Upright of Racing Suspension
3.1. Front Upright Topology Optimization Process
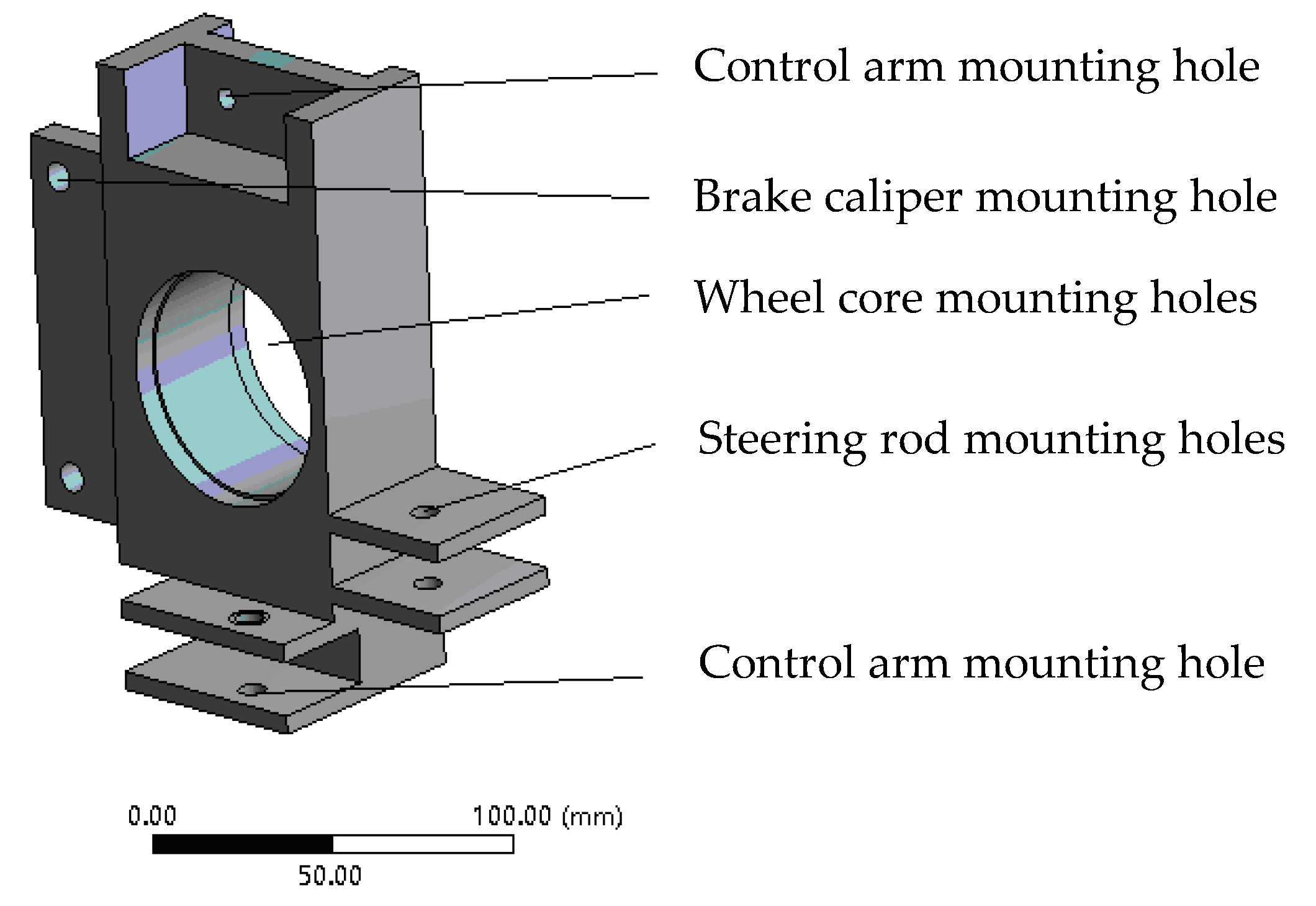
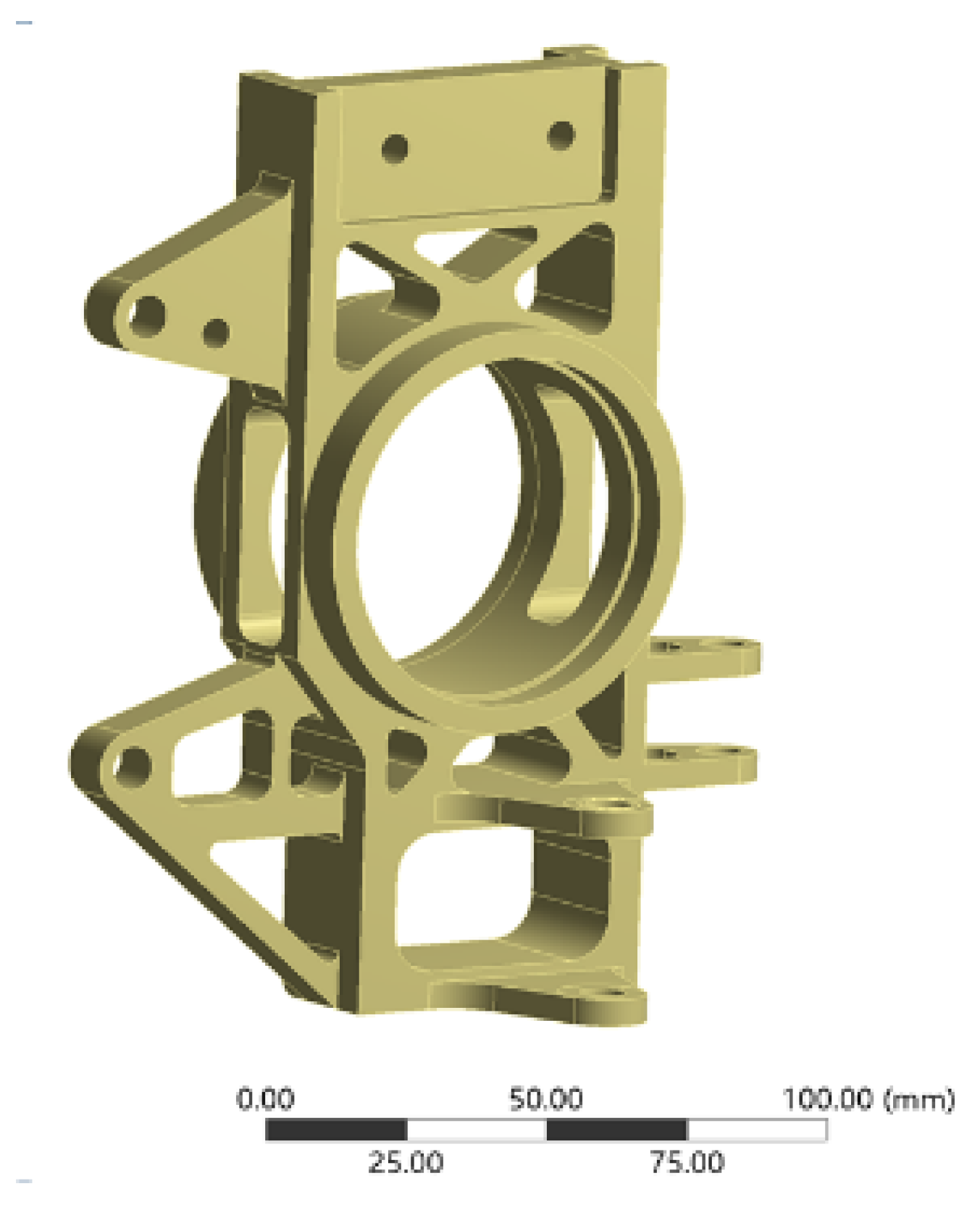
3.2. Determination of Initial Geometric Space and Establishment of Analytical Model
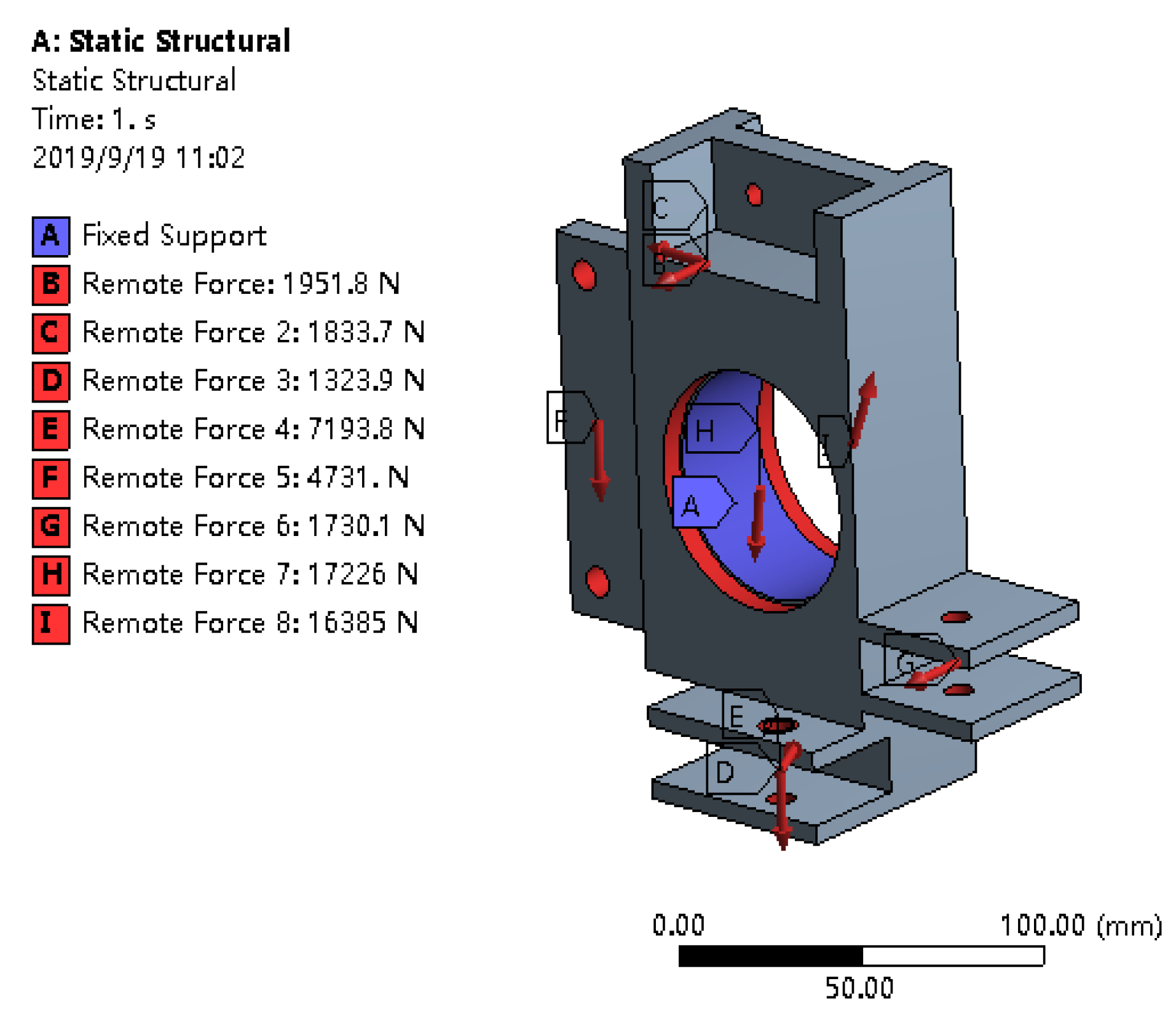
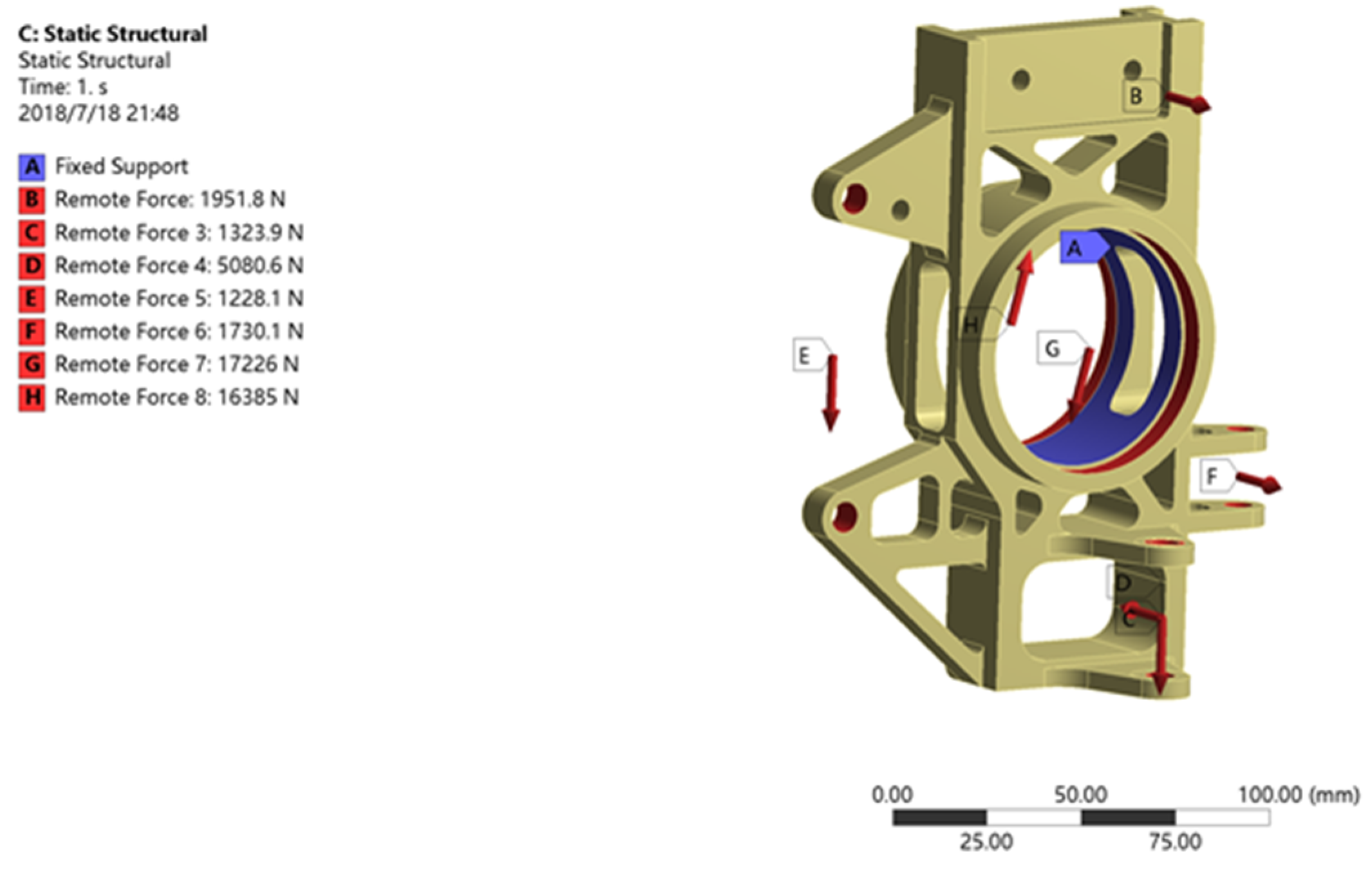
3.3. Strength Analysis of Initial Model
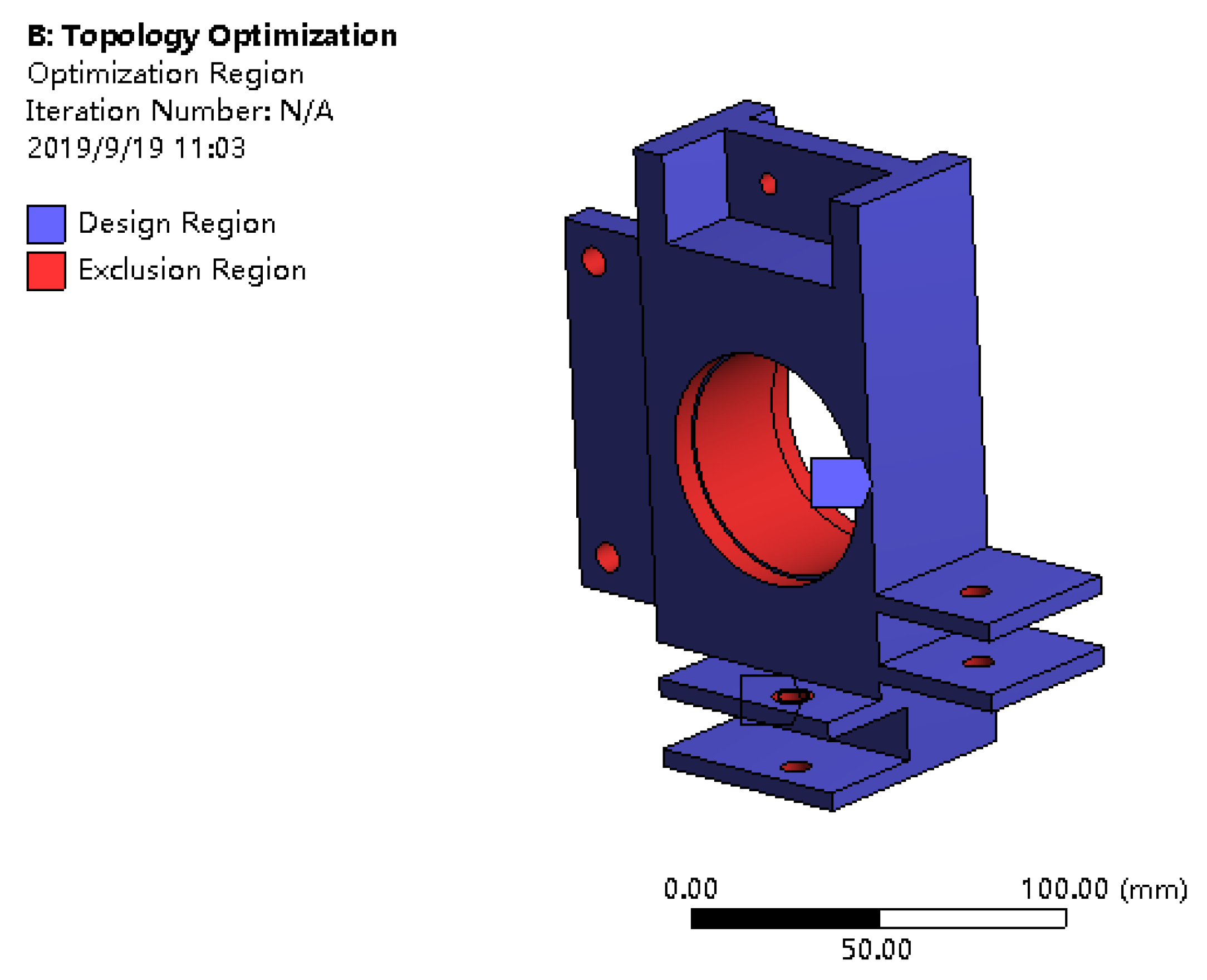
3.4. Topological Optimization of Front Upright
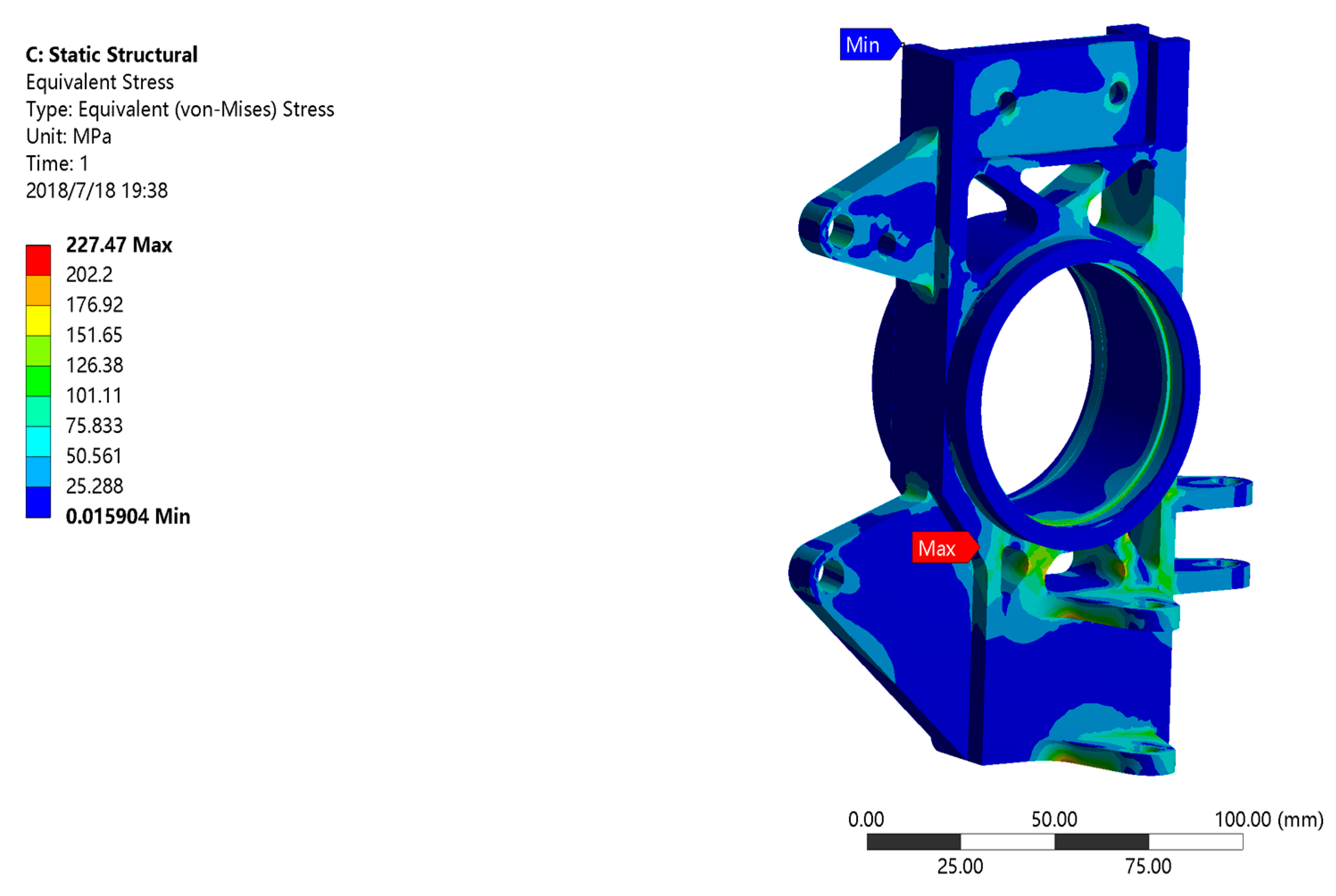
3.5. Optimization Results Analysis and Simulation Verification
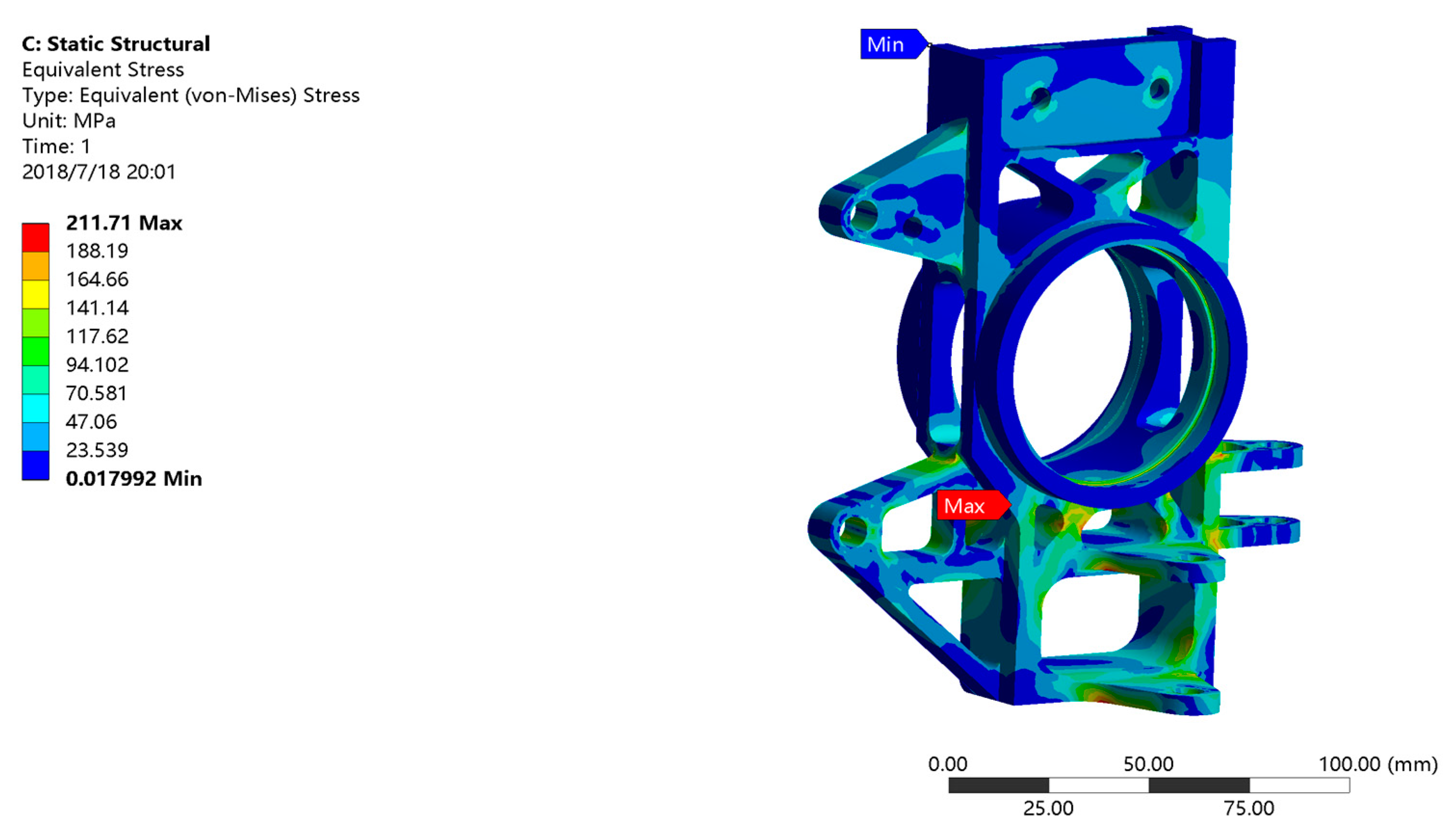
3.5.1. Analysis and Verification under Turning Brake Conditions
3.5.2. Analysis and Verification under Emergency Braking Conditions
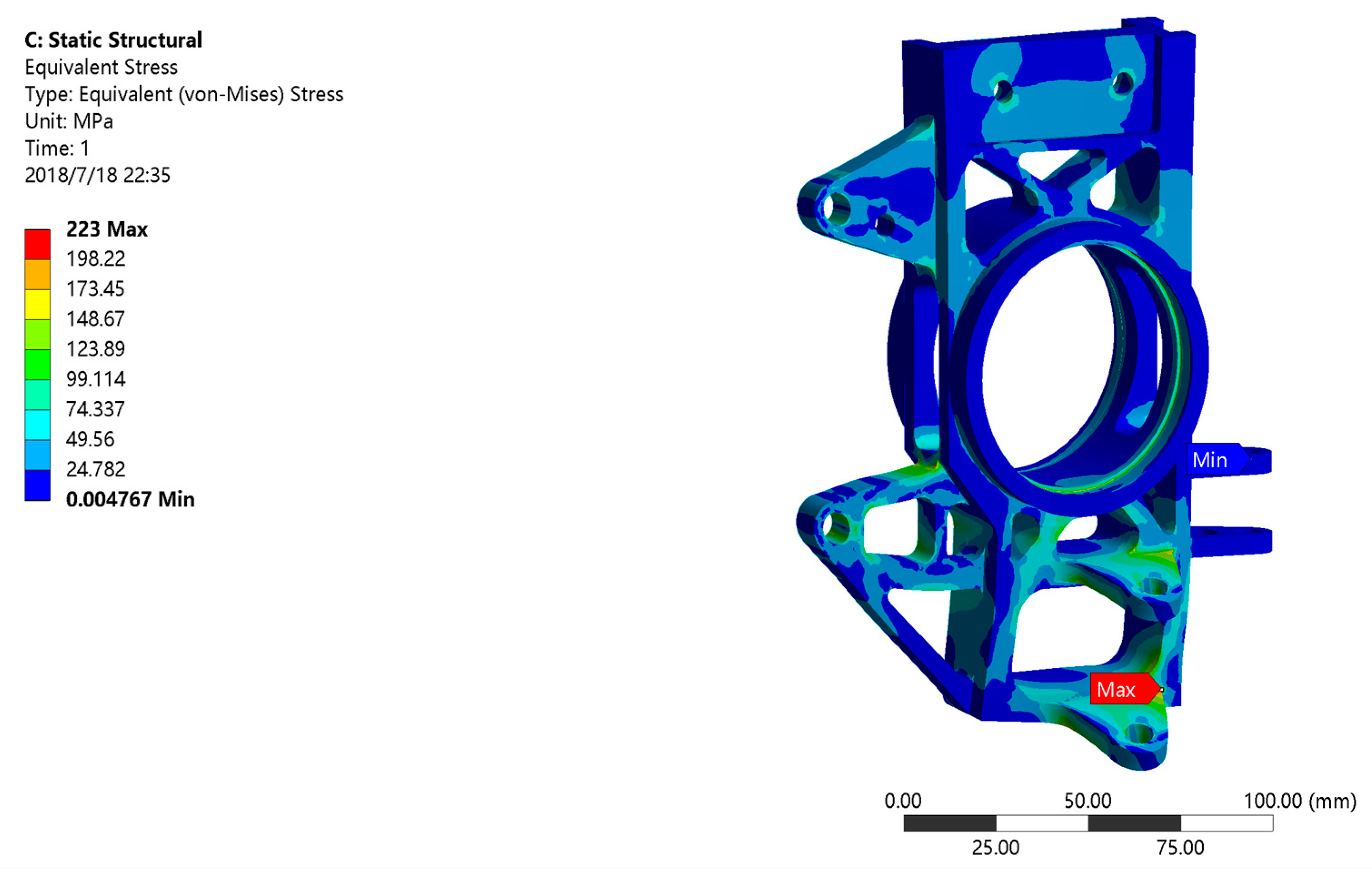
3.5.3. Analysis and Verification under Emergency Turning Conditions
4. Experiment Verification of Front Upright
5. Conclusions
- (1)
- By analyzing the structural topology optimization method, the mathematical model for the topology optimization of the front suspension of the racing suspension is established, and the initial geometry of the front upright is designed according to the suspension requirements provided by the 2018 Chinese University Formula Competition.
- (2)
- Then, using the established topology optimization mathematical model, the initial geometry model of the suspension front upright is optimized for the purpose of weight reduction, and the lightweight front upright with the mass reduction of 60.43% is obtained; the turning brake condition, emergency braking, and emergency turning are adopted. The strength, stiffness, and safety factor of the front upright are simulated under three extreme conditions. The results show that the lightweight front upright of the virtual design meets the requirements of the work.
- (3)
- The processing route of the front upright racing suspension is designed, the physical prototype is manufactured, and the assembly is integrated into a racing car. An experiment using the vehicle is conducted. The experimental result shows that the designed and manufactured lightweight suspension front upright meets the basic requirements of performance.
Author Contributions
Funding
Conflicts of Interest
References
- Wangyu, W. Automotive Design; Mechanical Industry Press: Beijing, China, 2017. [Google Scholar]
- China University Formula Vehicles Rules Committee. 2018 Chinese University Formula Competition Rules, 3rd ed.; Society of Automotive Engineers of China: Beijing, China, 2018. [Google Scholar]
- Li, F.; Tingting, H. Topology optimization of FSAE car frame. Zhejiang Univ. Technol. 2016, 44, 369–374. [Google Scholar]
- Shouli, Y.; Jiahui, L. The Design of FSAE Formula Frame with Light Weight. J. Zhengzhou Univ. 2018, 39, 18–24. [Google Scholar]
- Tongyao, H.; Xin, T.; Zhanfeng, H.; Zhongkai, T. Design and Topology Optimization for Suspension Bellcrank of a Formula Racing Car. Agric. Equip. Vehicle Eng. 2017, 55, 55–57. [Google Scholar]
- Renren, L.; Kai, X.; Shunan, H. The Topological Optimization Design of Differential Brackets for FSC Racing Car. J. Changshu Inst. Technol. 2019, 33, 57–59. [Google Scholar]
- Qing, Z.; Hongbiao, L.; Qia, Z. Topology Optimization Design of Transmission Case Housing Used in Electric Vehicle. J. Mech. Transm. 2017, 41, 75–79. [Google Scholar]
- Dongfeng, T.; Shihui, Y. Reliability-based Structural Dynamic Topology Optimization Method. J. Hunan Univ. 2017, 44, 62–67. [Google Scholar]
- Lijie, Z.; Chao, D.; Kai, L. Topology optimization for the compliant wing’s leading edge based on the multi-phase materials. J. Mach. Design 2019, 36, 86–90. [Google Scholar]
- Lanchun, Z.; Qinghai, Z.; Hongxin, Z. Multi-objective Topology Optimization for the Mount Bracket of Vehicle Powertrain. Automot. Eng. 2017, 39, 551–555. [Google Scholar]
- Qiping, W. Mechanical Manufacturing Technology; Harbin Institute of Technology Press: Harbin, China, 1997. [Google Scholar]















© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Tan, J.; Dong, J. Lightweight Design of Front Suspension Upright of Electric Formula Car Based on Topology Optimization Method. World Electr. Veh. J. 2020, 11, 15. https://doi.org/10.3390/wevj11010015
Li J, Tan J, Dong J. Lightweight Design of Front Suspension Upright of Electric Formula Car Based on Topology Optimization Method. World Electric Vehicle Journal. 2020; 11(1):15. https://doi.org/10.3390/wevj11010015
Chicago/Turabian StyleLi, Jixiong, Jianliang Tan, and Jianbin Dong. 2020. "Lightweight Design of Front Suspension Upright of Electric Formula Car Based on Topology Optimization Method" World Electric Vehicle Journal 11, no. 1: 15. https://doi.org/10.3390/wevj11010015
APA StyleLi, J., Tan, J., & Dong, J. (2020). Lightweight Design of Front Suspension Upright of Electric Formula Car Based on Topology Optimization Method. World Electric Vehicle Journal, 11(1), 15. https://doi.org/10.3390/wevj11010015




