Discontinuous Space Vector PWM Strategy for Three-Phase Three-Level Electric Vehicle Traction Inverter Fed Two-Phase Load

Abstract

Discontinuous pulse width modulation (DPWM) strategies are usually adopted to reduce the switching loss and output current ripple of three-phase three-level traction inverters under three-phase load conditions. However, if there is a short circuit in any arbitrary phase or the inverter is used to feed a two-phase load, the output performance of conventional DPWM strategies will be deteriorated. Here, four improved DPWM (IDPWM) strategies for three-phase three-level neutral-point-clamped (NPC) traction inverter fed two-phase load are proposed. Unlike three-phase load conditions, the phase angle and the amplitude of each basic voltage vector in the space vector diagram are modified under two-phase load conditions. Consequently, sectors are re-divided and duty cycles of basic vectors during synthesis are recalculated. Clamping intervals of each phase for the four type discontinuous PWM (DPWM) strategies are rearranged according to the modified space vector diagram; then, the proposed DPWM strategies can be obtained. Compared with the conventional DPWM strategies, the output current waveform quality of the proposed strategy is significantly improved. Meanwhile, the amplitude of the neutral-point voltage ripple is also reduced.

1. Introduction

Multilevel inverters are more and more widely being used for not only high-voltage and medium-voltage applications, but also low-voltage applications because of significantly high output waveform quality and low dV/dt [1,2,3]. Due to the low stress to switching devices, switching loss and switching noise are reduced. Electric vehicles (EVs) and plug-in hybrid EVs are put forward to replace the traditional fuel vehicle due to the unpredictable crude oil futures prices and increasingly stringent vehicle emission standards all over the world. In EV applications, the standard two-level six-switch inverter is usually used as the traction inverter [4]. On one hand, the switching frequency of the inverter needs to be increased so as to reduce the size of passive component. Correspondingly, the switching loss of the inverter is relatively high. Furthermore, with the increase of power and voltage level, the switching frequency is limited. A three-level inverter could effectively reduce the switching loss without loss of output waveform quality. On the other hand, conventional two-level inverters do not have any fault-tolerant ability; instead, the vehicle’s powertrain loses controllability and might have to stall. Thus, additional switches need to be paralleled to mitigate this, which increases the overall cost of the electric vehicle. Three-level inverters can realize fault-tolerant operation with additional advantages of lower common mode voltage, higher power density enhancement, and lower stress of the switches. Thus, three-level inverters could be under consideration for vehicle traction applications.

There are three main types of topology for three-level inverters: cascade H-bridge (CHB) [5], flying capacitor (FC) [6], and neutral-point-clamped (NPC) [7]. Among them, NPC three-level inverters play a dominant role in industrial applications. The modulation strategies of three-level inverters can be divided into continuous pulse width modulation (CPWM) and discontinuous pulse width modulation (DPWM), in accordance with the following condition, that is, whether there are discontinuous intervals in the modulation signal. The switching loss of three-level traction inverters can be considerably reduced by the use of DPWM. For this reason, DPWM is one of the preferred modulation strategies applied in EV applications. Moreover, the output performance of DPWM is better than CPWM under higher modulation index condition [8].

The traditional DPWM strategies (namely, DPWM0–DPWM3) for three-phase NPC three-level inverters were first proposed in [9]. According to the power factor, the appropriate strategy can be selected from DPWM0–DPWM3 to reduce the switching loss. In recent years, DPWM strategies have gradually shown their advantages against conventional CPWM strategies. A sector subdivision DPWM strategy was proposed in [8], and the discontinuous intervals are arranged according to the evaluation index of average current ripple vector. The output waveform quality of the proposed strategy is better than the conventional CPWM and DPWM0–DPWM3. In [10], a DPWM strategy was proposed to control the neutral-point voltage ripple and reduce the switching loss; the discontinuous intervals are distributed according to the polarity of neutral-point voltage. An adjustable DPWM strategy was presented in [11]; the discontinuous intervals are changed with the variation of power factor so as to reduce the switching loss in the whole power factor range. However, these strategies are only suitable for three-phase inverter fed three-phase load. If any arbitrary phase of three-phase load is short-circuited or the three-phase inverter is adopted to feed a two-phase load, the output current harmonic distortion and the amplitude of neutral-point voltage ripple will be increased significantly [12]. For EV application, it is necessary for the vehicle to keep driving stably in the short period when the motor experiences a single phase fault, therefore the modulation strategy needs to be reconsidered to adapt the operation conditions mentioned above.

The continuous modulation strategy for analog and digital implementation for a three-phase two-level inverter fed two-phase induction motor can be found in [13,14,15]. Discontinuous modulation strategy for three-phase two-level inverter fed two-phase load was first proposed by Tomaselli et al. [12]. Based on the analysis above, a discontinuous modulation strategy for three-phase two-level inverter fed two-phase load was proposed to reduce the switching loss and current ripple [16]. A generalized discontinuous modulation strategy for unbalanced two-phase loads was proposed in [17]. The switching loss could be effectively reduced for the full power factor range. A discontinuous modulation strategy for both balanced and unbalanced two-phase loads is proposed in [18]. Duty cycles of three-phase were recalculated to optimize the switching sequences. The switching loss could be significantly reduced in both situations. Although the discontinuous modulation strategy for three-phase two-level inverter fed two-phase load has been well established, the strategy for a three-phase three-level inverter has not been discussed yet.

In this paper, the amplitude and phase angle of basic voltage vectors of three-level inverter fed two-phase load are modified, the sectors are re-divided, and duty cycles of basic vectors during synthesis are recalculated. Clamping intervals of each phase for the four types of DPWM strategies are rearranged according to the modified space vector diagram; then, the improved DPWM strategies can be obtained. The principle of DPWM under three-phase load condition is explained in detail in Section 2. The modification process of basic vectors and the expressions of duty cycle of basic vectors synthesizing the reference vector under two-phase load condition are presented in Section 3. In Section 4, the proposed improved DPWMs (IDPWM)s are validated through extensive experimental results in the whole modulation index range, with a constant voltage to frequency (V/f) control. The conclusions are presented in Section 5.

2. Discontinuous Pulse Width Modulation (DPWM) under Three-Phase Load Condition

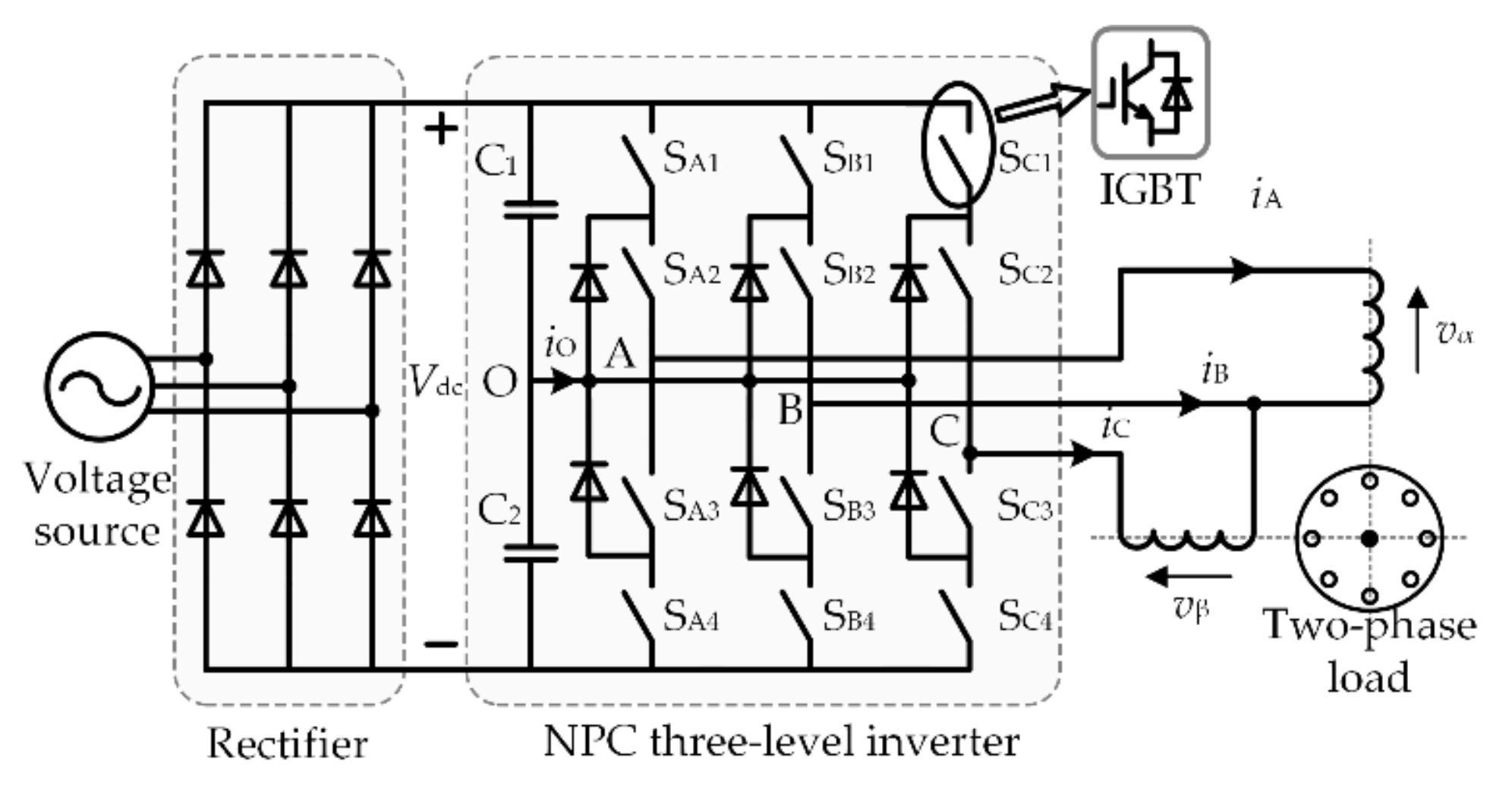
For a three-phase NPC three-level inverter (as shown in Figure 1), the four switching devices of each phase-leg can generate three switching states, namely P, O, and N (

Table 1. Definition of switching states for phase A.

Switching State	SA1	SA2	SA3	SA4
P	1	1	0	0
O	0	1	1	0
N	0	0	1	1

); so there are altogether 3³ = 27 switching state combinations for a three-phase three-level inverter. According to Equation (1), each switching state combination corresponds to one basic vector in the space vector diagram:

$${\mathit{V}}_n=v_A{e}^{j0}+v_B{e}^{j\frac{2\pi }{3}}+v_C{e}^{j\frac{4\pi }{3}},n=0,1,2,\dots ,18.$$

(1)

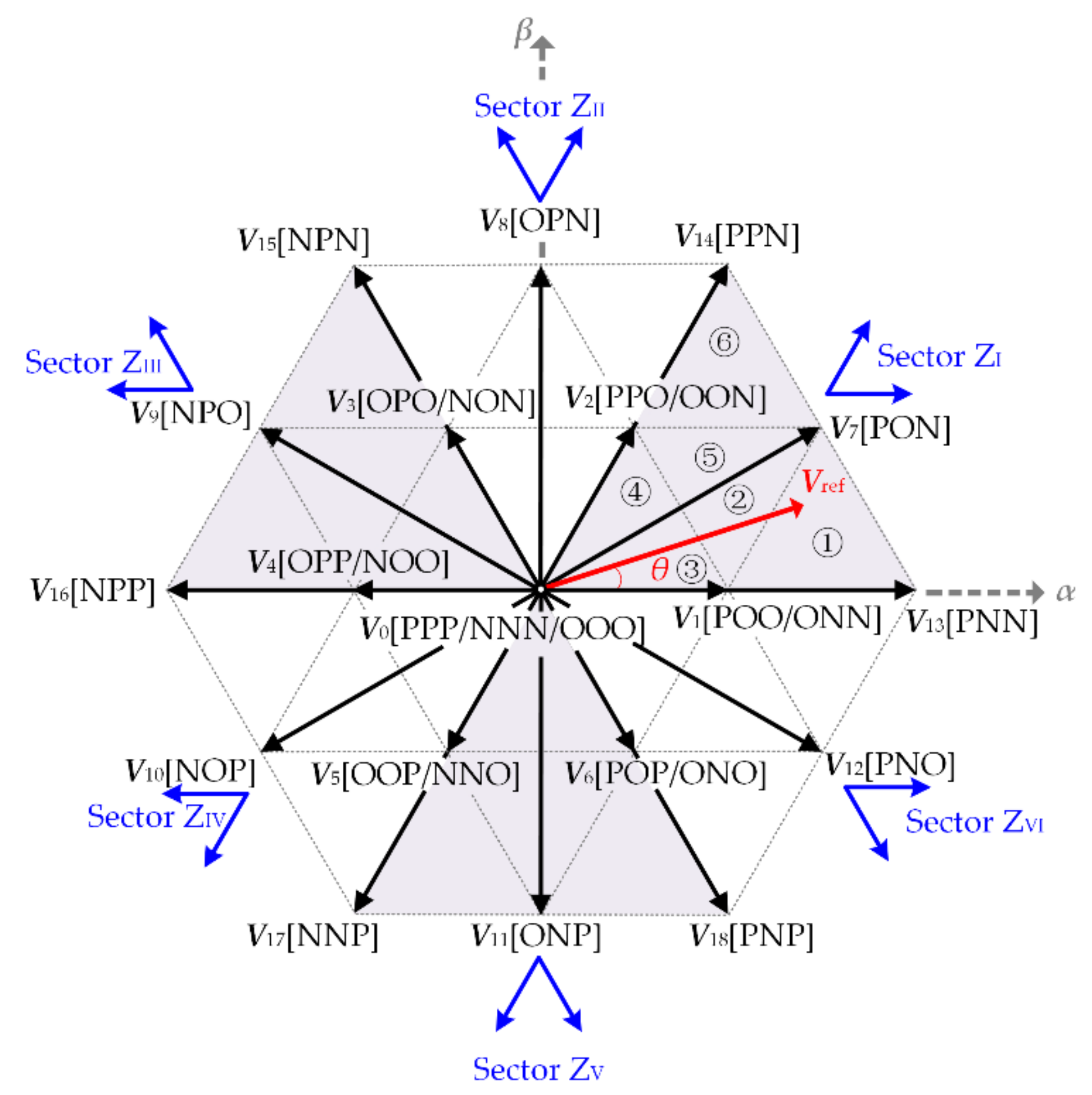
As shown in Figure 2, basic vectors can be categorized into four types (zero vector V₀, small vector V₁–V₆, medium vector V₇–V₁₂ and large vector V₁₃–V₁₈) according to their amplitudes. There are three switching state combinations corresponding to zero vector, and there are two switching state combinations corresponding to each small vector. Taking large vectors as the boundaries, the space vector diagram can be divided into six sectors Z_I–Z_VI, and each sector can be further divided into six small triangles ①–⑥. The nearest three basic vectors are usually used to synthesize the reference vector V_ref. Basic vectors used to synthesize V_ref in each triangle of sector Z_I are listed in

Table 2. Basic vectors used to synthesize V_ref in each triangle of sector Z_I.

Small Triangle	Basic Voltage Vector
①	V1 [POO/ONN], V7 [PON], V13 [PNN]
② and ⑤	V1 [POO/ONN], V2 [PPO/OON], V7 [PON]
③ and ④	V0 [PPP/OOO/NNN], V1 [POO/ONN], V2 [PPO/OON]
⑥	V2 [PPO/OON], V7 [PON], V14 [PPN]

. The situation in other sectors can be obtained in the same manner.

For four basic types of conventional DPWMs, that is DPWM0–DPWM3 [9], switching sequences used to synthesize V_ref in sector Z_I are shown in

Table 3. Switching sequences of discontinuous pulse width modulation (DPWM): DPWM0–DPWM3 in sector Z_I Reproduced with permission from [19].

θ	Triangle	DPWM0	DPWM1	DPWM2	DPWM3
[0, π/6)	①	POO↔PON↔PNN	POO↔PON↔PNN	ONN↔PNN↔PON	ONN↔PNN↔PON
	②	PPO↔POO↔PON	PPO↔POO↔PON	ONN↔OON↔PON	ONN↔OON↔PON
	③	POO↔PPO↔PPP	POO↔PPO↔PPP	OON↔ONN↔NNN	OON↔ONN↔NNN
[π/6, π/3)	④	OON↔ONN↔NNN	POO→PPO→PPP	OON↔ONN↔NNN	POO→PPO→PPP
	⑤	ONN↔OON↔PON	PPO↔POO↔PON	ONN↔OON↔PON	PPO↔POO↔PON
	⑥	OON↔PON↔PPN	PPO→PPN→PON	OON↔PON↔PPN	PPO→PPN→PON

. The switching sequences of other sectors can be obtained according to sector and vector symmetry. By the use of the volt-second balance principle, the duty cycles of the basic vectors synthesizing the reference vector can be achieved. If the reference vector V_ref is located in triangle ① of sector Z_I, then V₁, V₇, and V₁₃ will be used to synthesize V_ref, yielding:

$$\left\{\begin{array}{l}{\mathit{V}}_{ref}={\mathit{V}}_{13}{d}_1+{\mathit{V}}_7{d}_2+{\mathit{V}}_1{d}_0\\ 1=d_1+d_2+d_0\end{array}\right.,$$

(2)

where d₁, d₂, and d₀ are duty cycles of basic vectors V₁, V₇, and V₁₃, respectively. The duty cycles of the nearest three vectors used to synthesize V_ref in each triangle of sector Z_I are shown in

Table 4. Duty cycles of basic voltage vectors used to synthesize the reference voltage vector.

Triangle	d1	d2	d0
①	V13: 2msin (π/3 − θ) − 1	V7: 2msinθ	V1: 2[1 – msin (π/3 + θ)]
② and ⑤	V1: 1 − 2msinθ	V2: 2msin (θ − π/3)+1	V7: 2msin (π/3 + θ) − 1
③ and ④	V1: 2msin (π/3 − θ)	V2: 2msinθ	V0: 1 − 2msin (π/3 + θ)
⑥	V14: 2msinθ − 1	V7: 2msin (π/3 − θ)	V2: 2[1 – msin (π/3 + θ)]

.

In Table 4, m is the modulation index and m = $\sqrt{,3}$V_ref/V_dc. As shown in Table 3, in the first half or the second half of sector Z_I, the switching state of one of the three phases is always P or N. This phase is defined as the clamping phase and the switching state is defined as the clamping state. For example, the switching state of phase A is P in sector Z_I when DPWM1 is adopted, therefore the clamping phase is phase A and the clamping state is P in Z_I. The clamping phase and clamping state of DPWM0–DPWM3 are listed in

Table 5. Clamping phase and clamping state of DPWM0–DPWM3.

Sector	θ	DPWM0	DPWM1	DPWM2	DPWM3
ZI	[0, π/6)	A [P]	A [P]	C [N]	C [N]
	[π/6, π/3)	C [N]	A [P]	C [N]	A [P]
ZII	[π/3, π/2)	C [N]	C [N]	B [P]	B [P]
	[π/2, 2π/3)	B [P]	C [N]	B [P]	C [N]
ZIII	[2π/3, 5π/6)	B [P]	B [P]	A [N]	A [N]
	[5π/6, π)	A [N]	B [P]	A [N]	B [P]
ZIV	[π, 7π/6)	A [N]	A [N]	C [P]	C [P]
	[7π/6, 4π/3)	C [P]	A [N]	C [P]	A [N]
ZV	[4π/3, 3π/2)	C [P]	C [P]	B [N]	B [N]
	[3π/2, 5π/3)	B [N]	C [P]	B [N]	C [P]
ZVI	[5π/3, 11π/6)	B [N]	B [N]	A [P]	A [P]
	[11π/6, 2π)	A [P]	B [N]	A [P]	B [N]

. For example, A [P] means that the clamping phase is A and the clamping state is P, and C [N] means that the clamping phase is C and the clamping state is N.

3. DPWM under Two-Phase Load Condition

When three-level inverters are used to drive two-phase loads, the amplitude and the phase angle of the basic vector are changed. If the switching sequence and the duty cycle of DPWMs under three-phase load conditions are still adopted, the output performance of the inverter will be deteriorated. Thus, the space vector diagram under two-load conditions needs to be modified. Taking the output of phase B directly connecting to the neutral-point O as an example (as shown in Figure 3), the expression of the basic voltage vector ${\mathit{V}}_n^{\prime }$ is shown in Equation (3):

$${\mathit{V}}_n^{\prime }=v_{\alpha }+v_{\beta }{e}^{j\frac{\pi }{2}},n=0,1,2,\dots ,18.$$

(3)

According to Equation (3), the space vector diagram of the three-level inverter under two-phase load condition can be obtained, as shown in Figure 4. As can be seen, the amplitude and phase angle of each basic vector are both changed. The whole space vector diagram can still be divided into six sectors. Unlike three-phase load conditions, sectors are no longer equally divided. As can be seen in Figure 4, intervals of sector Z_I and Z_IV are π/2, while intervals of sector Z_II, Z_III, Z_V, and Z_VI are π/4. Each sector can also be divided into six triangles.

The reference vector is still synthesized by the nearest three vectors, so that Equation (2) is still stable. However, the amplitude and the phase angle of basic vectors are changed, so that duty cycles of the nearest three vectors used to synthesize V_ref in each triangle of sector Z_I need to be recalculated, which are listed in

Table 6. Duty cycles of basic voltage vectors used to synthesize the reference voltage vector.

Triangle	d1	d2	d0
①	V13: $\sqrt{\mathrm{,2}}$m’cosθ − 1	V7: $\sqrt{\mathrm{,2}}$m’sinθ	V1: 2 − 2m’cos (θ − π/4)
② and ⑤	V1: 1 − $\sqrt{\mathrm{,2}}$m’sinθ	V2: 1 − $\sqrt{\mathrm{,2}}$m’cosθ	V7: 2m’cos (θ − π/4) − 1
③ and ④	V1: $\sqrt{\mathrm{,2}}$m’cosθ	V2: $\sqrt{\mathrm{,2}}$m’sinθ	V0: 1 − 2m’cos (θ − π/4)
⑥	V14: $\sqrt{\mathrm{,2}}$m’sinθ − 1	V7: $\sqrt{\mathrm{,2}}$m’cosθ	V2: 2 − 2m’cos (θ − π/4)

.

In Table 6, m’ = $\sqrt{\mathrm{,2}}$V_ref/V_dc. The four types of discontinuous modulation strategies under two-phase load conditions are named as IDPWM0–IDPWM3. The switching sequences of IDPWM0–IDPWM3 are consistent with DPWM0–DPWM3 (Table 3). However, clamping intervals are changed with the variation of basic vectors. The modulation waves of phase A for DPWM0–DPWM3 and IDPWM0–IDPWM3 are shown in Figure 5a,b, respectively.

The realization of IDPWM0–IDPWM3 can be divided into the following steps:

1)

Sector and triangle judgement: m’ and θ are used to determine in which sector (Z_I–Z_VI) and triangle (①–⑥) the reference vector V_ref is located.

2)

Switching sequence selection: The switching sequence used to synthesize reference vector V_ref can be selected according to Table 3.

3)

Duty cycle calculation: According to Equation (2), the duty cycles d₁, d₂, and d₀ corresponding to three basic vectors can be determined.

4)

PWM generation: The switching signal of each phase could be generated according to the switching sequence and duty cycles.

4. Experimental Verification

DPWM0–DPWM3 and IDPWM0–IDPWM3 are tested on the experimental prototype of the neutral-point-clamped three-level inverter fed two-phase load shown in Figure 6. Parameters of the experimental prototype are list in

Table 7. Parameters of the experimental prototype.

Parameter	Unit	Value
dc-link voltage Vdc	V	80
dc-link capacitor C1,C2	μF	1000
switching frequency fsw	kHz	2
Load resistance R	Ω	10
Load inductance L	mH	40

. The model of the proposed IDPWM is built using MATLAB/Simulink. The input and output signals of the model are then connected to the I/O block of the Real Time Interface (RTI) blockset embedded in Simulink. Next, code generation is used to generate the C code of the proposed IDPWM. The code is then debugged and downloaded into DS1007 through dSPACE ControlDesk. Then, the switch signals of the power switches of three-level inverter can be generated by the digital output interface of DS1007.

It is worth mentioning that the DC-link of the inverter is powered by two series connected DC regulated power supplies (rated output voltage: 60 V, rated output current: 15 A), so the DC-link voltage is set to 80 V. For conventional two-level inverters adopted in EV applications, the range of switching frequency is 4–15 kHz, while for three-level inverters, the switching frequency could be even lower than that of two-level inverters to maintain the same output performance, so the switching frequency is set to 2 kHz in the experiment.

4.1. Output Waveform Quality

Experimental waveforms of output phase voltage v_AO, output line voltage v_AB, output current i_A and neutral-point voltage ripple v_O for DPWM0–DPWM3 and IDPWM0–IDPWM3 under two-phase load conditions when m’ = 0.3 and m’ = 0.8 are presented in Figure 7, Figure 8, Figure 9 and Figure 10, respectively.

As can be seen from Figure 7 and Figure 8, due to the low frequency oscillation in the neutral-point, the output voltages of DPWM0–DPWM3 are deteriorated under two-phase load conditions. As a result, the performance of the output current is poor. By the use of IDPWM0–IDPWM3, the basic vectors are modified and the duty cycles are recalculated so that the distortion of output voltage is reduced. Consequently, the performance of the output current is improved, as shown in Figure 9 and Figure 10.

By using the fast fourier transformation (FFT) analysis tool in MATLAB, the total harmonic distortion of the output current (I_THD) in the whole modulation range can be calculated on the basis of experimental results. Then variations of I_THD with the change of modulation index m’ for DPWM0–DPWM3 and IDPWM0–IDPWM3 can be obtained, which are illustrated in Figure 11. For IDPWM1, I_THD is always considerably lower than that of DPWM1 in the whole modulation range, and I_THD is decreased by about 50% at most. While for IDPWM0, IDPWM2, and IDPWM3, the improvement is significant in the lower (m’ ≤ 0.5) and higher (m’ ≥ 0.8) modulation range.

4.2. Neutral-Point Voltage Ripple

From Figure 7 and Figure 9, when m’ = 0.3, the amplitude of the neutral-point voltage ripple for DPWM0–DPWM3 is 20–30 V. While for IDPWM0–IDPWM3, the amplitude is 10 V, the neutral-point voltage ripple is reduced by about 33–50% so that the suppression effect of neutral-point voltage ripple is obvious under lower modulation index conditions. As can be seen in Figure 8 and Figure 10, when m’ = 0.8, the amplitude of the neutral-point voltage ripple for DPWM0–DPWM3 is 12–15 V. While for IDPWM0–IDPWM3, the amplitude is 7–10 V. The suppression of neutral-point voltage ripple still works.

In conclusion, the output waveform quality of the inverter can be improved by IDPWM0–IDPWM3 under two-phase loads conditions, and the improvement is significant in lower and higher modulation range. Moreover, the neutral-point voltage ripple can also be suppressed by IDPWM0–IDPWM3 in the whole modulation range, and the suppression effect is remarkable under the lower modulation condition.

5. Conclusions

Based on the conventional discontinuous PWM strategies for three-level traction inverter fed three-phase load, four improved discontinuous strategies under two-phase load conditions are proposed in this paper. The basic voltage vectors are modified and the duty cycles are re-calculated. Experimental results show that the output performance of the proposed strategies are better than that of the conventional strategies. Meanwhile, amplitudes of neutral-point voltage ripple for the proposed strategies are also lower than those of the conventional strategies.