1. Introduction
Permanent magnet synchronous motors (PMSM) have a lot of merits, such as high reliability, high efficiency, simple construction, and good control performance, thus, it is being increasingly applied on hybrid electrical vehicle (HEV)/electrical vehicle (EV) [
1,
2]. The normal operations of a PMSM need the support of high-performance control strategies. Field-oriented control (FOC) and direct torque control (DTC) are two well-established control strategies for the PMSM. When compared to FOC, DTC has better dynamic performance since it aims at the control of stator flux linkage and torque directly [
3]. The use of hysteresis controllers of conventional DTC (CDTC) will cause significant torque and flux linkage ripple [
4]. Many researchers have attempted to reduce these ripples through different schemes. Duty ratio modulation and space vector pulse width modulation (SVPWM) are two of the most popular schemes that have been widely accepted.
When compared to CDTC, duty ratio modulation for DTC (DDTC) is capable of regulating the applied time of the active vector in one period. There are different methods for the calculation of duty ratio [
5]. Yuan et al. determine the applied time of the active vector by the active angle between flux linkage and the active voltage vector and the impact angle between flux linkage and the zero vector [
6]. Mohan et al. propose a duty ratio calculation method that can reduce the flux dropping phenomenon in the low speed range [
7]. DDTC could maintain the dynamic performance of CDTC without complex calculation and reduce the torque and flux ripple of CDTC. However, the introduction of the duty ratio could only regulate the amplitude of active vector. Consequently, the ability to mitigate the torque ripple is limited.
SVPWM can make the switching frequency of the controller stable and output the voltage vectors of arbitrary amplitude and phase angle. Therefore, it has been widely used in DTC and it can effectively suppress the torque ripple that is caused by hysteresis controllers [
8,
9]. SVPWM-DTC requires complex calculations and coordinate transformations, and it cannot maintain the good dynamic response performance of CDTC [
10]. However, with the development of the control chip, the advantages of SVPWM-DTC will stand out, so this paper is based on the framework of SVPWM-DTC. However, SVPWM-DTC can only reduce the torque ripple that is introduced by hysteresis controller, not including the torque ripple caused by the spatial harmonics and magnetic saturation characteristics of PMSM.
The torque ripple that is caused by nonlinear characteristics of the motor could be suppressed by machine optimization [
11,
12] or active control of current harmonics [
13,
14,
15,
16,
17]. For active control of current harmonics, the methods applied include PI control in multiple synchronous frames [
14], proportional resonant (PR) [
15], and repetitive control [
16]. However, these methods are mainly focusing on eliminating the current harmonics, for the injection of current harmonics, the feedforward controller is a commonly used method [
17,
18]. The feedforward controller can effectively make up for the shortcomings of the insufficient bandwidth of the feedback closed-loop controller, but it requires an accurate motor model as a prerequisite [
19]. A harmonic voltage model in a multi-synchronous coordinate system was derived and a feedforward harmonic voltage controller is designed in [
17]. Zhong et al. proposed an accurate motor model that is based on magnetic common energy reconstruction, on this basis; a feedforward controller is designed to suppress the torque ripple [
18]. These researches have achieved significant results in suppressing the torque ripple that is caused by the harmonic and magnetic saturation characteristics of the motor. However, these researches mainly focus on the framework of FOC, being rarely involved in DTC.
This paper proposed a novel feedforward controller for realizing the active suppression of torque ripple caused by non-linear characteristic of PMSM under the framework of SVPWM-DTC. When compared to FOC, the control object is converted from current harmonics into flux linkage harmonics. The basic principle of SVPWM-DTC was introduced firstly and then analytical model of PMSM was derived. After that, the calculation of the optimal flux linkage was demonstrated and a feedforward controller was then designed and applied in the SVPWM-DTC framework. Finally, the simulations and experiments were carried out and the results were analyzed. The results show that the proposed method is effective in the suppression of torque ripple.
3. Feedforward Controller Based on Analytical Model of PMSM
3.1. Analytical Model of PMSM
The variation in magnetic co-energy (MCE) can clearly reflect the spatial harmonic and magnetic saturation characteristics of motor. Therefore, the numerical solution of MCE under several operating conditions was obtained from finite element analysis (FEA). It is a discrete data table with three dimensions that determine the MCE based on amplitude of the stator current vector , torque angle β, and rotor position .
The reconstruction of MCE is to transform the discrete numerical solution into a continuous analytic solution. The MCE exhibits periodicity in both
and
β dimensions. Therefore, a two-dimensional (2D) Fourier series decomposition can be applied to describe the MCE in
and
β dimensions. Subsequently, the MCE can be expressed as:
where
and
denote the highest Fourier series order of
and
β, respectively;
is the Fourier coefficients with corresponding orders
and
;
k represents the different values of MCE and coefficients of different current amplitude
.
The polynomial fitting method was used to establish the relationship between
and
in order to further describe the changing law of
with respect to
, which can be expressed as:
where
denotes the highest order of polynomial and
is the
nth order of the polynomial coefficients. Combining all of the
into one matrix, we have:
Finally, the MCE is illustrated with matrix form:
where
and
is the vector form of Fourier series in
and
dimension, respectively, which can be expressed as:
Here, the discrete numerical of MCE is transformed into a continuous analytic solution (9). The key of the model is the matrix
, which can describe the relationship of MCE with respect to rotor position
and stator current
. The analytical model of flux linkage and torque can be derived from the relationship of MCE with respect to the flux linkage and torque, which can be expressed as:
The main difference between the analytical model and the traditional model is that the flux linkage and torque fluctuate with the rotor position at a given current, that is, the spatial harmonics of PMSM can be reflected by . In addition, the relationship of the flux linkage and torque with respect to the current is obtained by fitting polynomials. It is no longer a simple linear relationship, and the magnetic saturation characteristics of the inductance can also be considered. The flux linkage and torque observers in this paper are constructed based on (12) and (13). The calculation of the optimal stator flux linkage is based on the analytical model.
3.2. Calculation of Optimal Stator Flux Linkage
The relationship between torque and current is linear over a wide range. Therefore, the cogging torque of PMSM could be balanced by the injection of current harmonics, which generates the torque harmonics of the same amplitude and opposite phase angle. The torque equation can be expressed as the first-order Taylor expansion at a specific operating point (
):
where
and
is the difference between real current and fundamental current (
). The first term on the right side of (14) is the torque under the excitation of fundamental current; this part of torque includes cogging torque that can be described by the analytical torque model (13). Additionally it can be compensated by the last two terms of (14), so we need to find the appropriate current harmonics
and
. The stator current could be illustrated by vector
or
and
, the relationship between them is:
Afterwards,
and
can be derived by (13) and (15). Let the left term of (14) equal 0, which means that the torque ripple is minimized, and then we can obtain the optimal current harmonics
and
under the specific operating point (
), which is the function of rotor position
:
where
x represents the
d or
q and
represents the amplitude of the
kth harmonic in
dimension. In FOC, we can directly inject the current harmonics above, but in DTC we must convert it into flux linkage harmonics.
The first-order Taylor expansion of the
d- and
q-axis flux linkage at the operating point (
) can be illustrated as:
where
L represents the self-inductance and mutual inductance of the
d- and
q-axis, which can be expressed as:
From (17), we can see that the flux harmonics are mainly composed of two parts, the first one is the flux linkage spatial harmonic under the excitation of the fundamental current wave and the other is the flux linkage harmonic that is generated by the current harmonics. The former can be obtained by the analytical flux linkage model (12), and for the latter, ,,, and could be derived from (12) and (15) and are already obtained in (16). The sum of the two parts is the required optimal stator flux linkage vector.
3.3. Feedword Controller
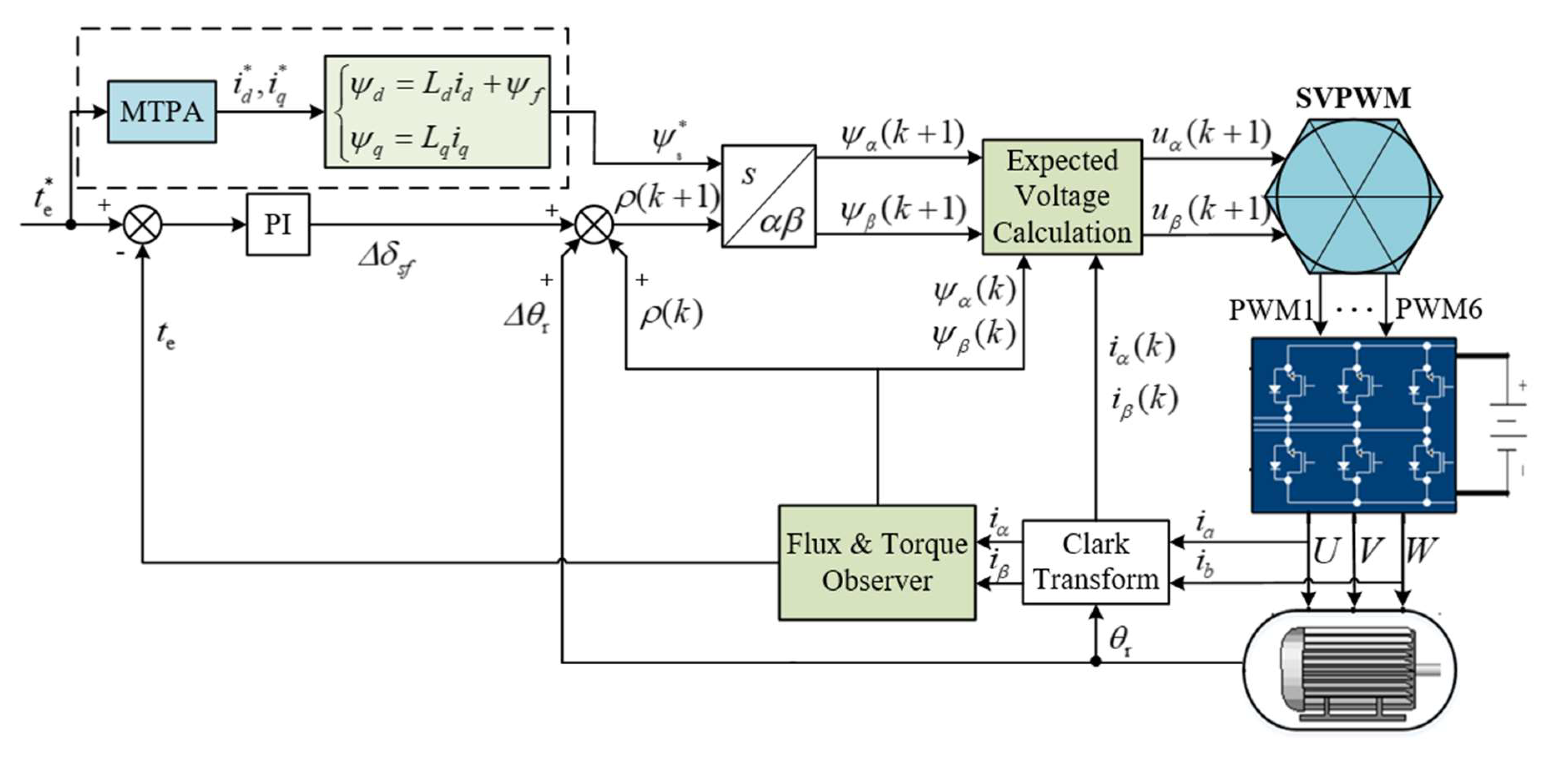
Figure 2 shows the calculation process of the optimal flux linkage. The reference torque
is converted into reference current
and
by MTPA. From the analytical flux linkage model (12) the first part of flux linkage harmonics
in (17) can be obtained and from the analytical torque model (13) the torque harmonics
can be obtained. According to (14), the current harmonics
to balance the torque harmonics can be obtained and the second part of flux linkage harmonics
in (17) can then be obtained. The sum of the two parts is the optimal flux linkage, which is the function of rotor position
. The rotor position of the present control cycle
could be obtained by the sensor and rotor position of next control cycle
is the cumulative values of
and
, which could be represented by the product of angular speed
and control period
T approximately. Subsequently, the load angle increment
required for the suppression of torque disturbance that is caused by cogging and magnetic saturation of PMSM is calculated and added to PI controller. The dashed box part in
Figure 1 could be replaced by
Figure 2 and the feedforward controller of optimal flux linkage is established.
4. Simulation and Experiment Result
4.1. Simulation Result
The simulation of the control algorithm above was carried out with the FEA PMSM model that takes the non-linear characteristics into account, whose parameters are shown in
Table 1. It is a motor designed for hybrid electric vehicle (HEV) with three pole pairs and 36 slots, which will result in 12
th torque harmonic. The SVPWM-DTC with and without feedforward controller was built in Simulink and
Table 2 shows the simulation parameters. The torque wave of the motor model was observed and the fast Fourier transform (FFT) analysis of it was conducted.
From
Figure 3a and
Figure 4a, it can be intuitively seen that the torque pulsation of the SVPWM-DTC control algorithm with the feed forward controller is reduced from 1.5 Nm to 0.8 Nm, with a decrement of 46.7%. It can be seen from the FFT analysis that this is mainly due to the suppression of 12th torque harmonic. The optimal stator flux linkage harmonic that was obtained according to the analytical PMSM model was added to the PI controller and the bandwidth problem of the PI controller was effectively solved. The torque disturbance caused by the spatial harmonics and magnetic saturation characteristics of the motor was suppressed.
4.2. Applicability Analysis
We set the motor speed to 100 rpm and 2000 rpm, respectively, in order to verify the applicability of the improved algorithm under other conditions. Other simulation conditions are the same as in
Table 2.
Figure 5 shows the torque response.
It can be seen that the control of torque ripple deteriorates with the increase of rotational speed. Voltage harmonics ultimately achieve the injection of flux linkage harmonics. When the mechanical motor speed is 2000 rpm, the number of pole pairs is 3, and the frequency of 12th voltage harmonic is 1.2 kHz. At this time, it is difficult to output the voltage vector by the inverter whose switching frequency is 10 kHz, which results in poor control of the torque.
To verify The reference torque is set to 30 Nm and other simulation conditions are the same as in
Table 2 to verify the torque ripple suppression effect under high load.
Figure 6 shows the torque response. It can be seen that the algorithm can maintain a good torque ripple suppression effect under high load.
4.3. Experiment Result
Based on the simulation, experiments further verified the feedforward controller. The experiments were carried out on the motor test bench shown in
Figure 7. It is mainly composed of a dynamometer and the motor under test. The control algorithm is implemented by the motor controller, Semikron, whose inverter is IGBT and its maximum switching frequency is 10 kHz, so the period of the control cycle was set as 1 × 10
−4. CAN realized the communication between the controller and the computer. The working point is the same as the simulation. The control algorithms with and without feedforward controller are separately tested under the same condition. The torque response was measured by the torque transducer and
Figure 8 and
Figure 9 show the results.
It can be seen from results that the torque ripple is larger than the simulation. From the FFT analysis of torque wave, it can be found that other than 6th, 12th, 18th harmonics caused by the slot of the motor itself, the torque ripple contains many harmonics of other orders that are introduced by factors, like dynamometer and the test bench, whose amplitude is not negligible. However, after the introduction of the feedforward controller, the torque ripple is greatly reduced and, from FFT analysis, we can see that the 12th torque harmonic is reduced by 60.28%. The test results are consistent with the simulation.
In conclusion, the experimental results are consistent with the simulation results and the SVPWM-DTC that is based on distributed parameter model has achieved remarkable results in torque ripple reduction.