State of Charge Estimation of Lithium-Ion Battery for Electric Vehicles Using Machine Learning Algorithms
Abstract
:1. Introduction
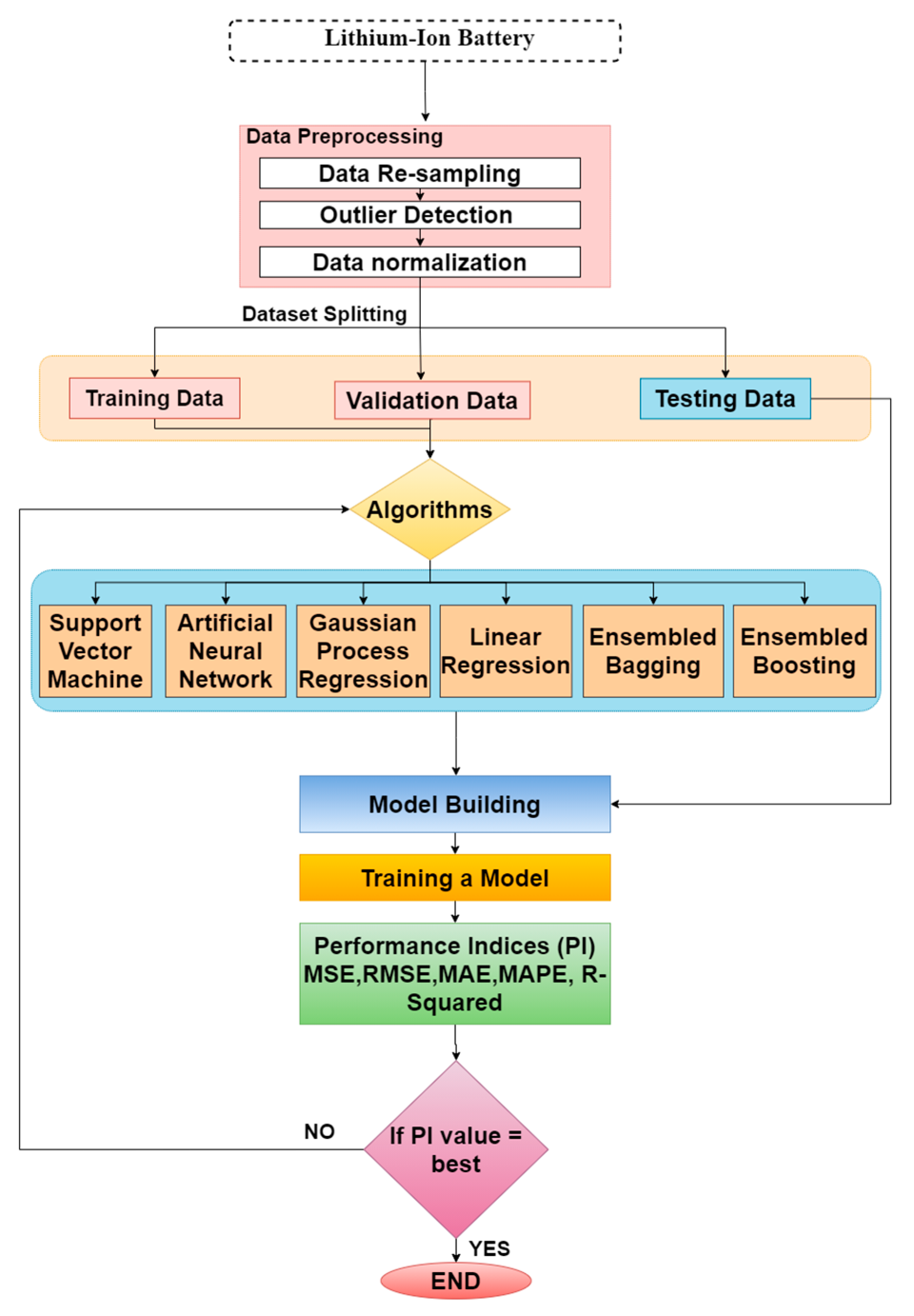
2. Materials and Method
2.1. Batteries State of Charge Estimation
2.2. Artificial Neural Network (ANN)
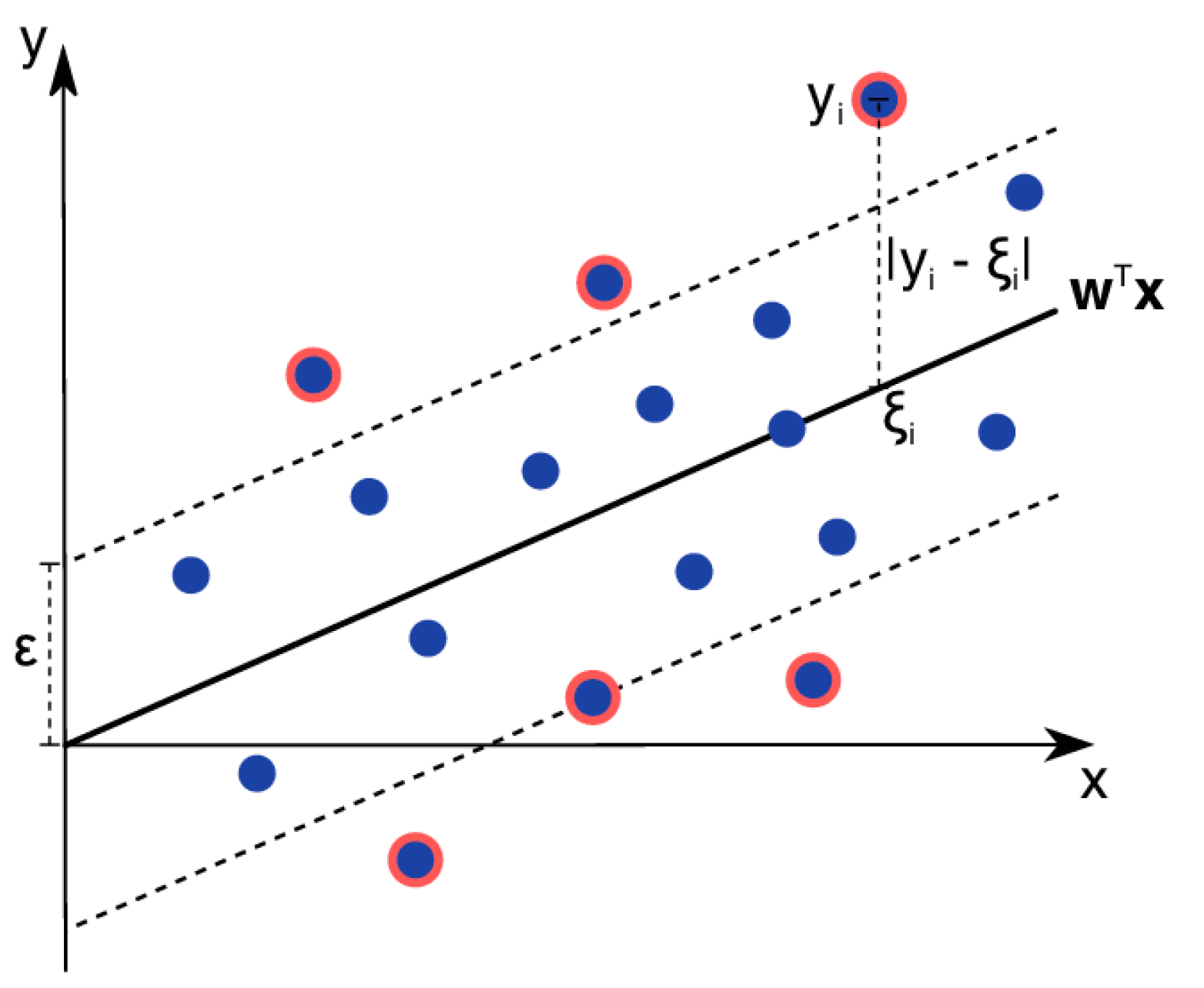
2.3. Support Vector Machine (SVM)
- Step 1.
- Import the input features
- Step 2.
- Analyze the correlation and directivity of the data
- Step 3.
- Split the dataset into the train and validation test
- Step 4.
- Choose the kernel function out of (linear, polynomial, sigmoid, radial basis)
- Step 5.
- Train the model with training data
- Step 6.
- Evaluate the model performance
- Step 7.
- Test the model with testing data
- Step 8.
- Calculate the performance metrics for the tested data
2.4. Linear Regression (LR)
- Step 1.
- Get the input features
- Step 2.
- Analyze the correlation and directivity of the data
- Step 3.
- Estimate the model
- Step 4.
- Fit the best fitting line
- Step 5.
- Evaluate the model and
- Step 6.
- Test the model with testing data
- Step 7.
- Calculate the performance metrics for the tested data
2.5. Gaussian Process Regression (GPR)
- Step 1.
- Import the input features
- Step 2.
- Analyze the correlation and directivity of the data
- Step 3.
- Split the dataset into the train and validation test
- Step 4.
- Build the model for the Gaussian process regression model
- Step 5.
- Train the model with training data
- Step 6.
- Evaluate the model performance
2.6. Ensemble Bagging (EBa)
- Step 1.
- for i = 1 to K, do
- Step 2.
- Generate a bootstrap sample of the original data
- Step 3.
- Train an unpruned tree model on this sample
- Step 4.
- End
2.7. Ensemble Boosting (EBo)
- Step 1.
- Set (x) = 0 and = for all i in the training set
- Step 2.
- Compute the average response, , and use this as the initial predicted value sample
- Step 3.
- for i = 1 to K, do
- Step 4.
- Fit a tree with D splits (d + 1 terminal nodes) to the training data
- Step 5.
- Update (x) by adding in a shrunken version of the new tree:
- Step 6.
- Step 7.
- Update the residuals, -
- Step 8.
- End
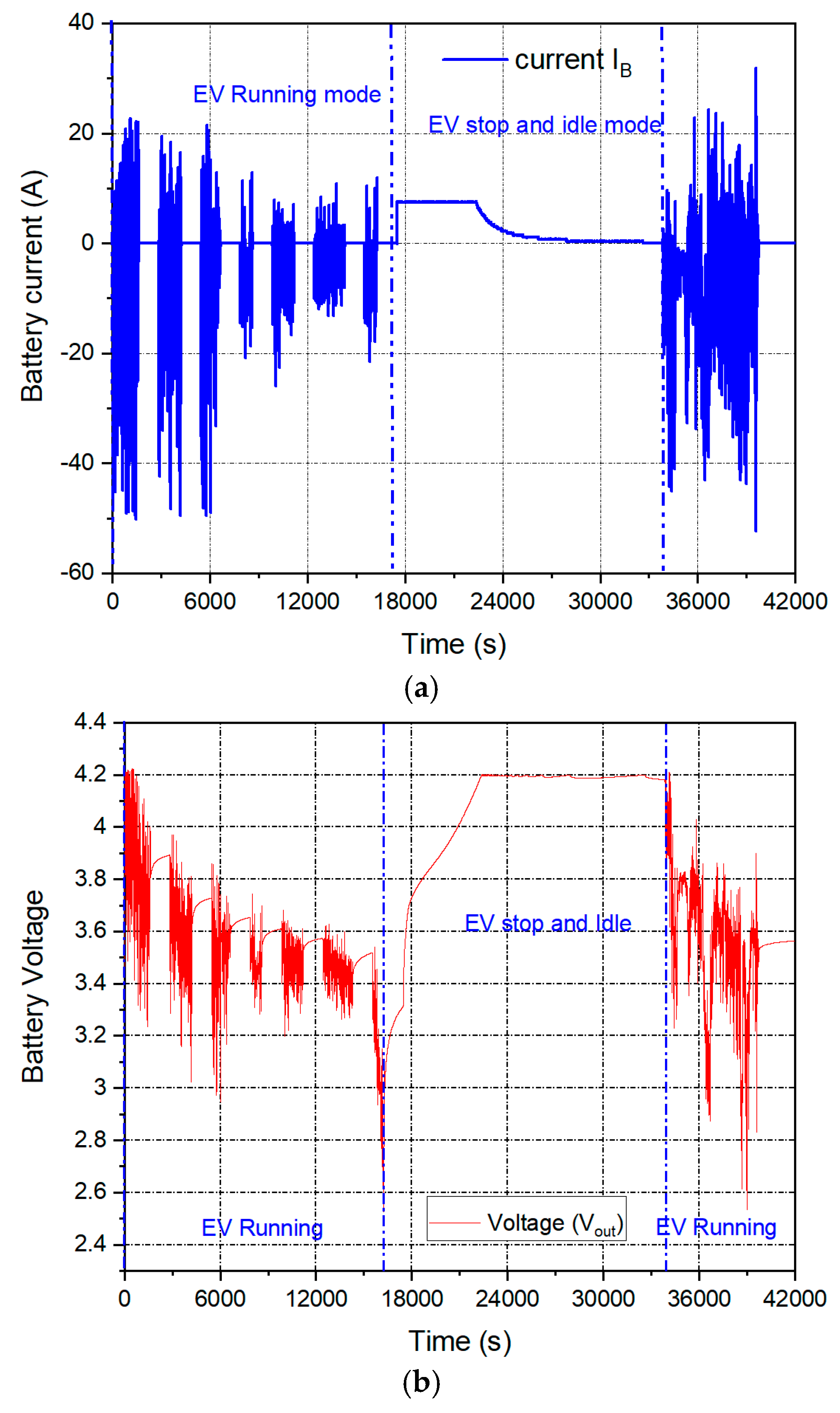
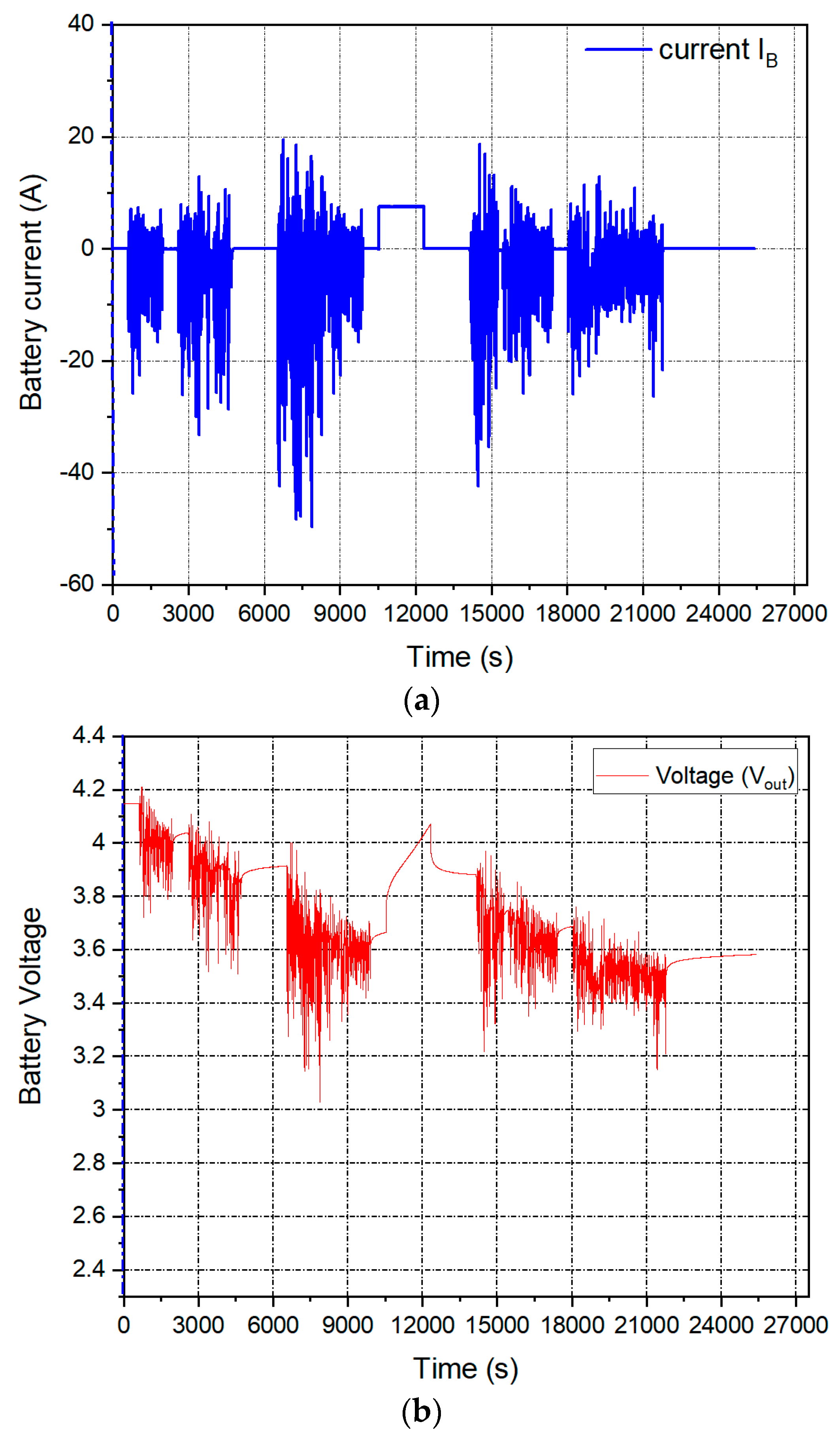
3. Training and Testing Datasets
4. Performance Metrics
4.1. Root Mean Square Error (RMSE)
4.2. R2 Square
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ghosh, A. Possibilities and Challenges for the Inclusion of the Electric Vehicle ( EV ) to Reduce the Carbon Footprint in the Transport Sector: A Review. Energies 2020, 13, 2602. [Google Scholar] [CrossRef]
- Tang, X.; Gao, F.; Zou, C.; Yao, K.; Hu, W.; Wik, T. Load-responsive model switching estimation for state of charge of lithium-ion batteries. Appl. Energy 2019, 238, 423–434. [Google Scholar] [CrossRef]
- Świerczyński, M.; Stroe, D.I.; Laerke, R.; Stan, A.I.; Kjaer, P.C.; Teodorescu, R.; Kaer, S.K. Field Experience from Li-Ion BESS Delivering Primary Frequency Regulation in the Danish Energy Market. ECS Trans. 2014, 61, 1–14. [Google Scholar] [CrossRef]
- Rahimi-Eichi, H.; Ojha, U.; Baronti, F.; Chow, M.Y. Battery management system: An overview of its application in the smart grid and electric vehicles. IEEE Ind. Electron. Mag. 2013, 7, 4–16. [Google Scholar] [CrossRef]
- Ramanan, P.; Kalidasa Murugavel, K.; Karthick, A.; Sudhakar, K. Performance evaluation of building-integrated photovoltaic systems for residential buildings in southern India. Build. Serv. Eng. Res. Technol. 2019, 41, 492–506. [Google Scholar] [CrossRef]
- Karthick, A.; Athikesavan, M.M.; Pasupathi, M.K.; Kumar, N.M.; Chopra, S.S.; Ghosh, A. Investigation of inorganic phase change material for a semi-transparent photovoltaic (STPV) module. Energies 2020, 13, 3582. [Google Scholar] [CrossRef]
- Chandrika, V.S.; Thalib, M.M.; Karthick, A.; Sathyamurthy, R.; Manokar, A.M.; Subramaniam, U.; Stalin, B. Performance assessment of free standing and building integrated grid connected photovoltaic system for southern part of India. Build. Serv. Eng. Res. Technol. 2020. [Google Scholar] [CrossRef]
- Berecibar, M.; Gandiaga, I.; Villarreal, I.; Omar, N.; Van Mierlo, J.; Van Den Bossche, P. Critical review of state of health estimation methods of Li-ion batteries for real applications. Renew. Sustain. Energy Rev. 2016, 56, 572–587. [Google Scholar] [CrossRef]
- Cadini, F.; Sbarufatti, C.; Cancelliere, F.; Giglio, M. State-of-life prognosis and diagnosis of lithium-ion batteries by data-driven particle filters. Appl. Energy 2019, 235, 661–672. [Google Scholar] [CrossRef]
- Bhattacharjee, A.; Mohanty, R.K.; Ghosh, A. Design of an Optimized Thermal Management System for Li-Ion Batteries under Different Discharging Conditions. Energies 2020, 13, 5695. [Google Scholar] [CrossRef]
- Karthick, A.; Kalidasa Murugavel, K.; Ghosh, A.; Sudhakar, K.; Ramanan, P. Investigation of a binary eutectic mixture of phase change material for building integrated photovoltaic (BIPV) system. Sol. Energy Mater. Sol. Cells 2020, 207. [Google Scholar] [CrossRef]
- Pagani, M.; Korosec, W.; Chokani, N.; Abhari, R.S. User behaviour and electric vehicle charging infrastructure: An agent-based model assessment. Appl. Energy 2019, 254. [Google Scholar] [CrossRef]
- Karthick, A.; Kalidasa Murugavel, K.; Suse Raja Prabhakaran, D. Energy analysis of building integrated photovoltaic modules. In Proceedings of the International Conference on Power and Embedded Drive Control, ICPEDC 2017, Chennai, India, 16–18 March 2017; pp. 307–311. [Google Scholar]
- Ghosh, A. Potential of building integrated and attached/applied photovoltaic (BIPV/BAPV) for adaptive less energy-hungry building’s skin: A comprehensive Review. J. Clean. Prod. 2020, 123343. [Google Scholar] [CrossRef]
- Reddy, P.; Gupta, M.V.N.S.; Nundy, S.; Karthick, A. Status of BIPV and BAPV System for Less Energy-Hungry Building in India—A Review. Appl. Sci. 2020, 10, 2337. [Google Scholar] [CrossRef] [Green Version]
- Khalid, M.; Shanks, K.; Ghosh, A.; Tahir, A.; Sundaram, S.; Mallick, T.K. Temperature regulation of concentrating photovoltaic window using argon gas and polymer dispersed liquid crystal fi lms. Renew. Energy 2021, 164, 96–108. [Google Scholar] [CrossRef]
- Mesloub, A.; Ghosh, A. Daylighting performance of light shelf photovoltaics (LSPV) for office buildings in hot desert-like regions. Appl. Sci. 2020, 10, 7959. [Google Scholar] [CrossRef]
- Mesloub, A.; Ghosh, A.; Touahmia, M. Performance Analysis of Photovoltaic Integrated Shading Devices (PVSDs) and Semi-Transparent Photovoltaic ( STPV ) Devices Retrofitted to a Prototype O ffi ce Building in a Hot Desert Climate. Sustainability 2020, 12, 10145. [Google Scholar] [CrossRef]
- Kotia, A.; Borkakoti, S.; Ghosh, S.K. Wear and performance analysis of a 4-stroke diesel engine employing nanolubricants. Particuology 2018, 37, 54–63. [Google Scholar] [CrossRef]
- Ramanan, P.; Karthick, A. Performance analysis and energy metrics of grid-connected photovoltaic systems. Energy Sustain. Dev. 2019, 52, 104–115. [Google Scholar] [CrossRef]
- Amjad, M.; Ahmad, A.; Rehmani, M.H.; Umer, T. A review of EVs charging: From the perspective of energy optimization, optimization approaches, and charging techniques. Transp. Res. Part D Transp. Environ. 2018, 62, 386–417. [Google Scholar] [CrossRef]
- Sathyamurthy, R.; Kabeel, A.E.; Chamkha, A.; Karthick, A.; Muthu Manokar, A.; Sumithra, M.G. Experimental investigation on cooling the photovoltaic panel using hybrid nanofluids. Appl. Nanosci. 2020. [Google Scholar] [CrossRef]
- Ghosh, A.; Norton, B.; Duffy, A. First outdoor characterisation of a PV powered suspended particle device switchable glazing. Sol. Energy Mater. Sol. Cells 2016, 157, 1–9. [Google Scholar] [CrossRef]
- Ghosh, A.; Norton, B. Optimization of PV powered SPD switchable glazing to minimise probability of loss of power supply. Renew. Energy 2019, 131, 993–1001. [Google Scholar] [CrossRef]
- Liu, K.; Shang, Y.; Ouyang, Q.; Widanage, W.D. A Data-driven Approach with Uncertainty Quantification for Predicting Future Capacities and Remaining Useful Life of Lithium-ion Battery. IEEE Trans. Ind. Electron. 2020, 1. [Google Scholar] [CrossRef]
- Bonfitto, A.; Ezemobi, E.; Amati, N.; Feraco, S.; Tonoli, A.; Hegde, S. State of health estimation of lithium batteries for automotive applications with artificial neural networks. In Proceedings of the 2019 AEIT International Conference of Electrical and Electronic Technologies for Automotive (AEIT AUTOMOTIVE), Turin, Italy, 2–4 July 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Dang, X.; Yan, L.; Xu, K.; Wu, X.; Jiang, H.; Sun, H. Open-Circuit Voltage-Based State of Charge Estimation of Lithium-ion Battery Using Dual Neural Network Fusion Battery Model. Electrochim. Acta 2016, 188, 356–366. [Google Scholar] [CrossRef]
- Chang, Y.; Fang, H.; Zhang, Y. A new hybrid method for the prediction of the remaining useful life of a lithium-ion battery. Appl. Energy 2017, 206, 1564–1578. [Google Scholar] [CrossRef]
- Nuhic, A.; Terzimehic, T.; Soczka-Guth, T.; Buchholz, M.; Dietmayer, K. Health diagnosis and remaining useful life prognostics of lithium-ion batteries using data-driven methods. J. Power Sources 2013, 239, 680–688. [Google Scholar] [CrossRef]
- Dai, H.; Zhao, G.; Lin, M.; Wu, J.; Zheng, G. A novel estimation method for the state of health of lithium-ion battery using prior knowledge-based neural network and markov chain. IEEE Trans. Ind. Electron. 2019, 66, 7706–7716. [Google Scholar] [CrossRef]
- Feng, X.; Weng, C.; He, X.; Han, X.; Lu, L.; Ren, D.; Ouyang, M. Online State-of-Health Estimation for Li-Ion Battery Using Partial Charging Segment Based on Support Vector Machine. IEEE Trans. Veh. Technol. 2019, 68, 8583–8592. [Google Scholar] [CrossRef]
- Liu, K.; Li, Y.; Hu, X.; Lucu, M.; Widanage, W.D. Gaussian Process Regression with Automatic Relevance Determination Kernel for Calendar Aging Prediction of Lithium-Ion Batteries. IEEE Trans. Ind. Inform. 2020, 16, 3767–3777. [Google Scholar] [CrossRef] [Green Version]
- Liu, K.; Hu, X.; Wei, Z.; Li, Y.; Jiang, Y. Modified Gaussian Process Regression Models for Cyclic Capacity Prediction of Lithium-Ion Batteries. IEEE Trans. Transp. Electrif. 2019, 5, 1225–1236. [Google Scholar] [CrossRef]
- Richardson, R.R.; Osborne, M.A.; Howey, D.A. Gaussian process regression for forecasting battery state of health. arXiv 2017, 357, 209–219. [Google Scholar] [CrossRef]
- Malkhandi, S. Fuzzy logic-based learning system and estimation of state-of-charge of lead-acid battery. Eng. Appl. Artif. Intell. 2006, 19, 479–485. [Google Scholar] [CrossRef]
- Burgos, C.; Sáez, D.; Orchard, M.E.; Cárdenas, R. Fuzzy modelling for the state-of-charge estimation of lead-acid batteries. J. Power Sources 2015, 274, 355–366. [Google Scholar] [CrossRef]
- Lee, D.T.; Shiah, S.J.; Lee, C.M.; Wang, Y.C. State-of-charge estimation for electric scooters by using learning mechanisms. IEEE Trans. Veh. Technol. 2007, 56, 544–556. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Emadi, A. State-of-charge estimation of Li-ion batteries using deep neural networks: A machine learning approach. J. Power Sources 2018, 400, 242–255. [Google Scholar] [CrossRef]
- Ting, T.O.; Man, K.L.; Lim, E.G.; Leach, M. Tuning of Kalman filter parameters via genetic algorithm for state-of-charge estimation in battery management system. Sci. World J. 2014, 2014. [Google Scholar] [CrossRef] [Green Version]
- Li, I.H.; Wang, W.Y.; Su, S.F.; Lee, Y.S. A merged fuzzy neural network and its applications in battery state-of-charge estimation. IEEE Trans. Energy Convers. 2007, 22, 697–708. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Z.; Lu, Z.; Li, J.; Ji, B.; Wei, H.; Pan, H. A novel state-of-charge estimation method of lithium-ion batteries combining the grey model and genetic algorithms. IEEE Trans. Power Electron. 2018, 33, 8797–8807. [Google Scholar] [CrossRef] [Green Version]
- Bonfitto, A.; Feraco, S.; Tonoli, A.; Amati, N.; Monti, F. Estimation accuracy and computational cost analysis of artificial neural networks for state of charge estimation in lithium batteries. Batteries 2019, 5, 47. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.; Wang, J.; Fan, Q.; Lund, P.D.; Hong, J. Improving the state of charge estimation of reused lithium-ion batteries by abating hysteresis using machine learning technique. J. Energy Storage 2020, 32. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, B.; Zou, X.; Li, Y.; Shi, S. Machine learning assisted materials design and discovery for rechargeable batteries. Energy Storage Mater. 2020, 31, 434–450. [Google Scholar] [CrossRef]
- Kim, S.; Lim, H. Reinforcement learning based energy management algorithm for smart energy buildings. Energies 2018, 11, 2010. [Google Scholar] [CrossRef] [Green Version]
- Attia, M.E.H.; Karthick, A.; Manokar, A.M.; Driss, Z.; Kabeel, A.E.; Sathyamurthy, R.; Sharifpur, M. Sustainable potable water production from conventional solar still during the winter season at Algerian dry areas: Energy and exergy analysis. J. Therm. Anal. Calorim. 2020. [Google Scholar] [CrossRef]
- Dhanalakshmi, C.S.; Madhu, P.; Karthick, A.; Mathew, M.; Vignesh Kumar, R. A comprehensive MCDM-based approach using TOPSIS and EDAS as an auxiliary tool for pyrolysis material selection and its application. Biomass Convers. Biorefinery 2020. [Google Scholar] [CrossRef]
- Karthick, A.; Ramanan, P.; Ghosh, A.; Stalin, B.; Vignesh Kumar, R.; Baranilingesan, I. Performance enhancement of copper indium diselenide photovoltaic module using inorganic phase change material. Asia-Pac. J. Chem. Eng. 2020, 15. [Google Scholar] [CrossRef]
- Shepero, M.; Munkhammar, J.; Widén, J.; Bishop, J.D.K.; Boström, T. Modeling of photovoltaic power generation and electric vehicles charging on city-scale: A review. Renew. Sustain. Energy Rev. 2018, 89, 61–71. [Google Scholar] [CrossRef] [Green Version]
- Hoarau, Q.; Perez, Y. Interactions between electric mobility and photovoltaic generation: A review. Renew. Sustain. Energy Rev. 2018, 94, 510–522. [Google Scholar] [CrossRef] [Green Version]
- Karthick, A.; Kalidasa Murugavel, K.; Sudalaiyandi, K.; Muthu Manokar, A. Building integrated photovoltaic modules and the integration of phase change materials for equatorial applications. Build. Serv. Eng. Res. Technol. 2020, 41, 634–652. [Google Scholar] [CrossRef]
- Sudalaiyandi, K.; Alagar, K.; VJ, M.P.; Madhu, P. Performance and emission characteristics of diesel engine fueled with ternary blends of linseed and rubber seed oil biodiesel. Fuel 2021, 285, 119255. [Google Scholar] [CrossRef]
- Li, Y.; Sheng, H.; Cheng, Y.; Stroe, D.I.; Teodorescu, R. State-of-health estimation of lithium-ion batteries based on semi-supervised transfer component analysis. Appl. Energy 2020, 277. [Google Scholar] [CrossRef]
- Mawonou, K.S.R.; Eddahech, A.; Dumur, D.; Beauvois, D.; Godoy, E. State-of-health estimators coupled to a random forest approach for lithium-ion battery aging factor ranking. J. Power Sources 2020. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, X.; Pan, R.; Wang, Y.; Chen, Z. A novel Gaussian process regression model for state-of-health estimation of lithium-ion battery using charging curve. J. Power Sources 2018, 384, 387–395. [Google Scholar] [CrossRef]
- Lu, C.; Tao, L.; Fan, H. Li-ion battery capacity estimation: A geometrical approach. J. Power Sources 2014, 261, 141–147. [Google Scholar] [CrossRef]
- Shu, X.; Li, G.; Zhang, Y.; Shen, J.; Chen, Z.; Liu, Y. Online diagnosis of state of health for lithium-ion batteries based on short-term charging profiles. J. Power Sources 2020, 471. [Google Scholar] [CrossRef]
- Li, W.; Jiao, Z.; Du, L.; Fan, W.; Zhu, Y. An indirect RUL prognosis for lithium-ion battery under vibration stress using Elman neural network. Int. J. Hydrogen Energy 2019, 44, 12270–12276. [Google Scholar] [CrossRef]
- Stroe, D.I.; Schaltz, E. Lithium-Ion Battery State-of-Health Estimation Using the Incremental Capacity Analysis Technique. IEEE Trans. Ind. Appl. 2020, 56, 678–685. [Google Scholar] [CrossRef]
- Li, Y.; Zou, C.; Berecibar, M.; Nanini-Maury, E.; Chan, J.C.W.; van den Bossche, P.; Van Mierlo, J.; Omar, N. Random forest regression for online capacity estimation of lithium-ion batteries. Appl. Energy 2018, 232, 197–210. [Google Scholar] [CrossRef]









| Feature Parameter | Battery | Performance Index and Precision | Reference | |
|---|---|---|---|---|
| The energy of the signal (current, voltage) | NASA 18650 | MAE | <1.29% | [53] |
| Temperature (min, max, average, area) | NASA 18650 | RMSE | <3.58% | [54] |
| The slope of the charging voltage curve | NASA 18650 | RMSE | <3.45% | [55] |
| The slope of the discharging voltage curve | NASA 18650 | RMSE | <3.84% | [56] |
| Equal voltage drops in charging curve | NCM/ graphite | RMSE | 2% | [57] |
| Equal voltage drops in discharging curve | NASA 18650 | MAE | <1.29% | [58] |
| The characteristic of I.C. curves (peak, valley) | Prismatic Li-ion Battery | RMSE | 2.99% | [59] |
| Algorithms Model | Empirical Equation |
|---|---|
| Artificial Neural Network | weight to neuron i from neuron j bias input vectors |
| Support Vector Machine | = predicted output W = weights K = kernel trick support vectors B = bias |
| Gaussian Process Regression | Test the model with testing data calculate the performance metrics for the tested data noise variance coefficient vector observtion |
| Linear Regression | bias value input feature values |
| Ensemble Bagging | Output the bagging model: |
| Ensemble Boosting | The output of boosting tree: |
| Dataset Splitting | ||
|---|---|---|
| Total Training Set = 43,355 | Testing Set | |
| Training set (80%) | Validation set (20 %) | |
| 34,684 | 8671 | 25,416 |
| Algorithm | MSE | RMSE | NRMSE | MAE | MAPE | Scatter Index | Variance | R2 |
|---|---|---|---|---|---|---|---|---|
| SVM | 0.01505 | 0.12266 | 0.17517 | 0.00752 | 0.000052 | 0.21 | 81.63 | 0.999 |
| ANN | 0.00054 | 0.02329 | 0.03126 | 0.00027 | 0.000002 | 0.040 | 99.99 | 0.999 |
| Linear | 0.00130 | 0.03610 | 0.04829 | 0.00065 | 0.000004 | 0.062 | 99.95 | 0.979 |
| GPR | 0.00170 | 0.04118 | 0.05507 | 0.00085 | 0.000006 | 0.071 | 99.83 | 1.000 |
| Ensemble boosting | 0.05245 | 0.22902 | 0.32122 | 0.02623 | 0.000186 | 0.39 | 90.32 | 1.000 |
| Ensemble bagging | 0.04231 | 0.04118 | 0.28576 | 0.02115 | 0.000149 | 0.35 | 85.25 | 0.979 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chandran, V.; Patil, C.K.; Karthick, A.; Ganeshaperumal, D.; Rahim, R.; Ghosh, A. State of Charge Estimation of Lithium-Ion Battery for Electric Vehicles Using Machine Learning Algorithms. World Electr. Veh. J. 2021, 12, 38. https://doi.org/10.3390/wevj12010038
Chandran V, Patil CK, Karthick A, Ganeshaperumal D, Rahim R, Ghosh A. State of Charge Estimation of Lithium-Ion Battery for Electric Vehicles Using Machine Learning Algorithms. World Electric Vehicle Journal. 2021; 12(1):38. https://doi.org/10.3390/wevj12010038
Chicago/Turabian StyleChandran, Venkatesan, Chandrashekhar K. Patil, Alagar Karthick, Dharmaraj Ganeshaperumal, Robbi Rahim, and Aritra Ghosh. 2021. "State of Charge Estimation of Lithium-Ion Battery for Electric Vehicles Using Machine Learning Algorithms" World Electric Vehicle Journal 12, no. 1: 38. https://doi.org/10.3390/wevj12010038







