Box–Jenkins Black-Box Modeling of a Lithium-Ion Battery Cell Based on Automotive Drive Cycle Data
Abstract
:1. Introduction
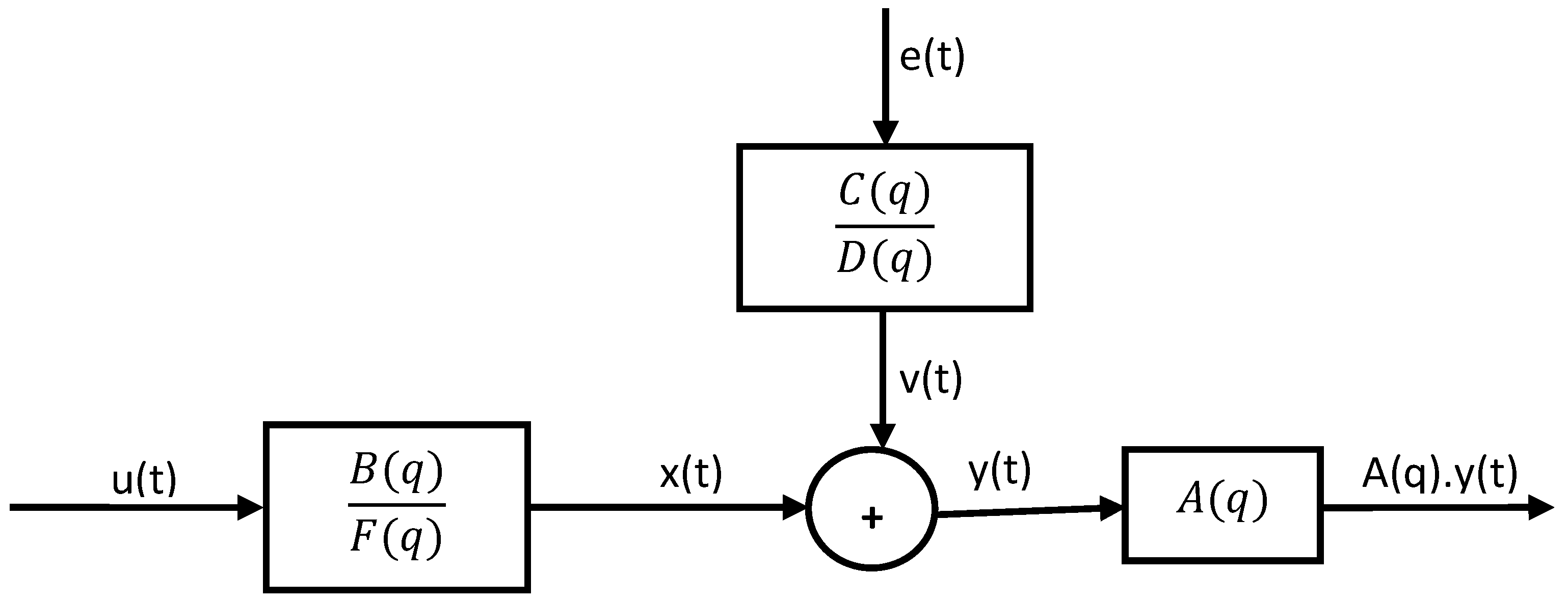
2. Box–Jenkins Polynomial Model Structure
Box–Jenkins Model Structure
- is the polynomial order plus 1 ()
- is the polynomial order plus 1 ()
- is the polynomial order plus 1 ()
- is the polynomial order plus 1 ()
- is the input delay (in number of samples, matrix) where is the input number and is the output number.
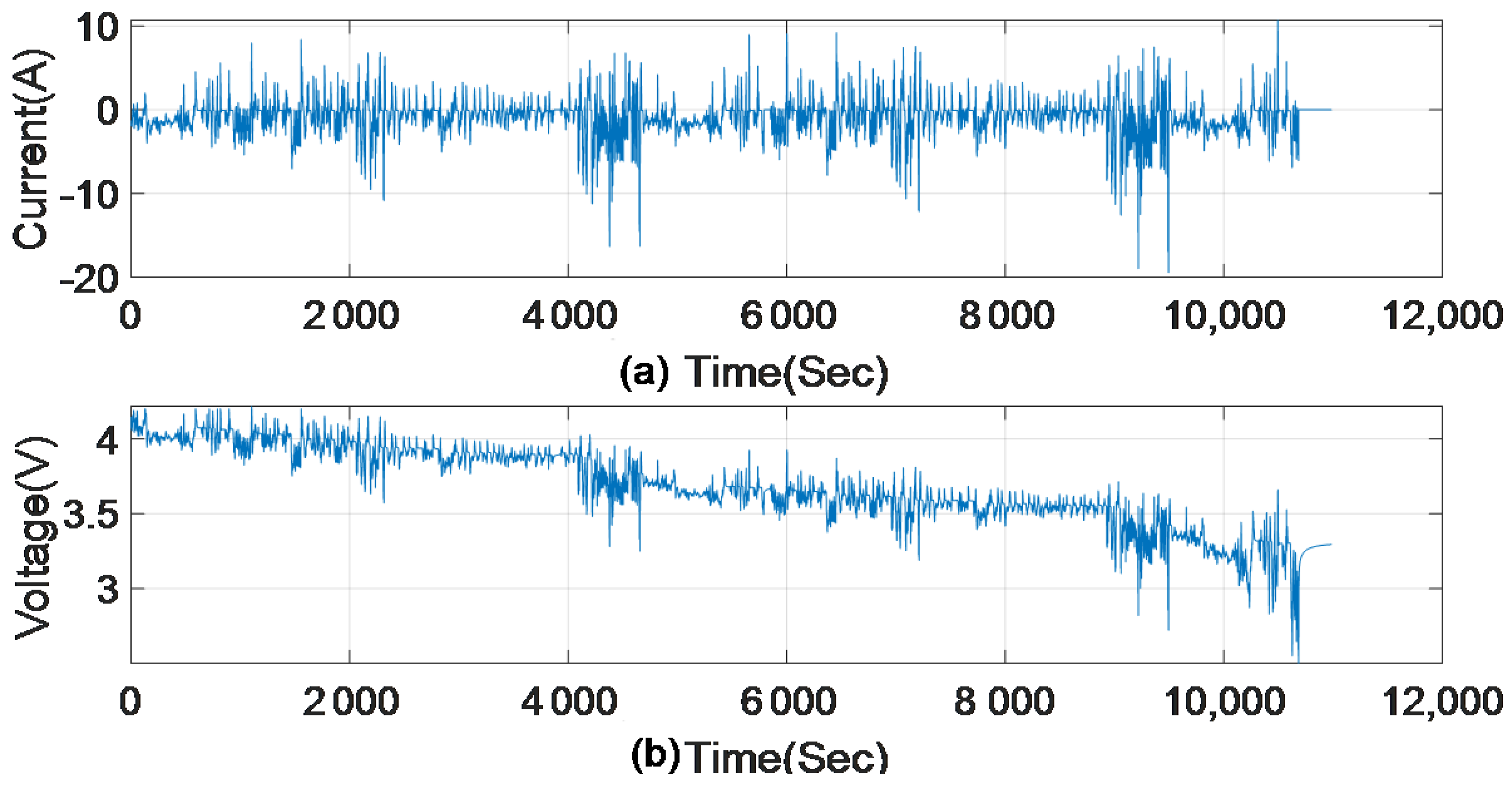
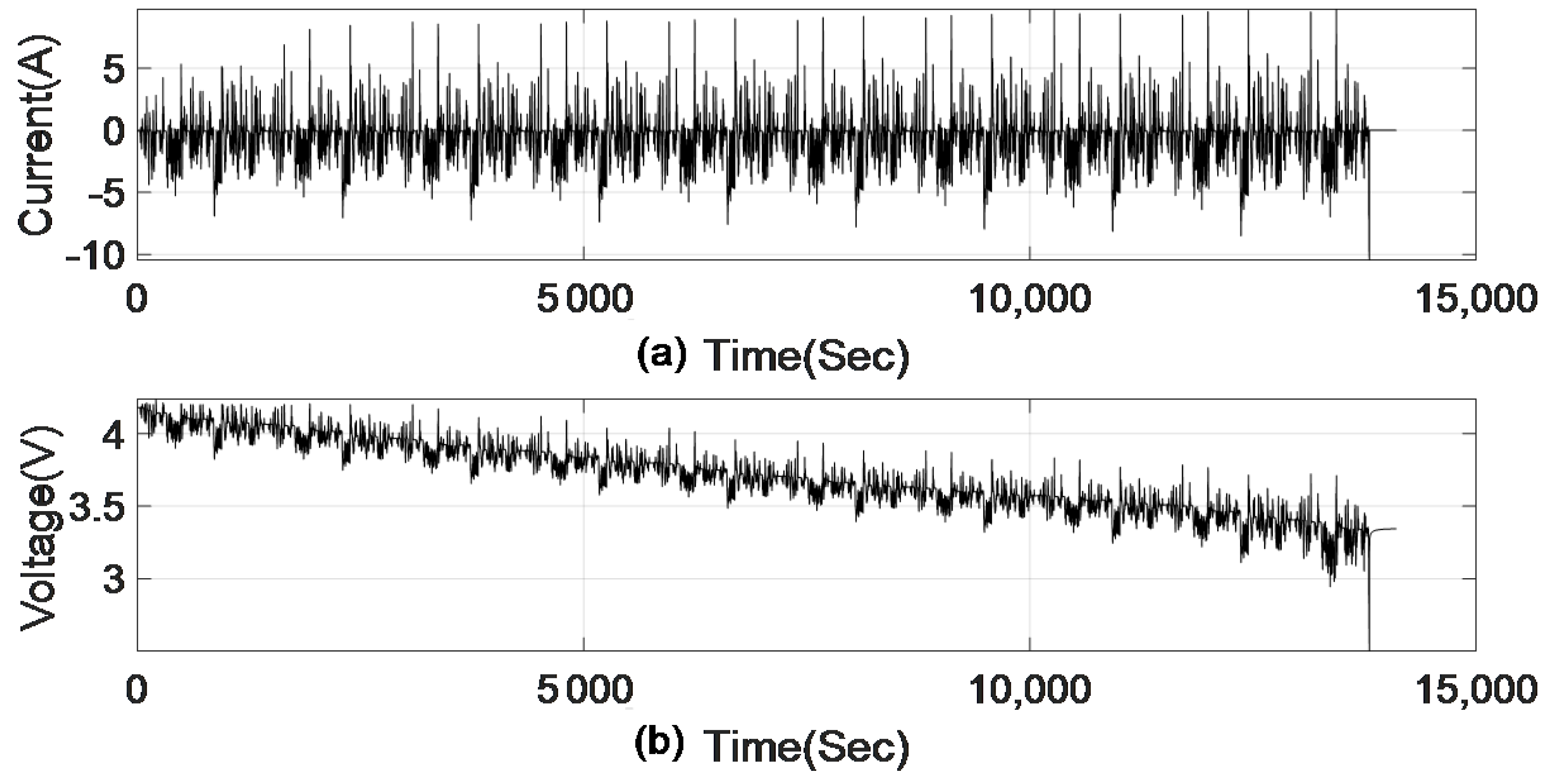
3. Experimental Data
- UDDS: In the early 70s, this cycle was developed to describe an urban route. The cycle consists of a cold start step. This step is followed by a transient step with many speed peaks that start from rest.
- LA-92: This cycle represents, similar to the UDDS, an urban route and it has a higher average speed. LA-92 is a chassis-dynamometer driving schedule for light-duty vehicles developed in 1992 by the CARB (California Air Resources Board).
- US06: This test addresses the need for aggressive, high-acceleration and/or high-speed driving behavior, rapid speed fluctuations, and driving behavior following startup.
- HWFET: This drive cycle is the Highway Fuel Economy Test developed in 1974. Overall, it simulates interstate rural and highway driving conditions.
- Neural Network: This drive cycle consists of a combination of portions of the US06 and LA92 drive cycles, and it was designed to have some additional dynamics that may be useful for training neural networks.
- MIX: This drive cycle represents a random mix of the five driving cycles presented previously (LA-92, HWFET, NN, US06, HWFET, and UDDS).
- -
- The measured voltage at the terminal of the battery cell in (V).
- -
- The measured current applied to the battery cell in (A).
- -
- The time of the test measured in (s), which starts from 0 s at the beginning of each data set.
- -
- The ambient temperature of the test chamber where the battery cell is located in degC, which remains fixed at 25 degC during the test.
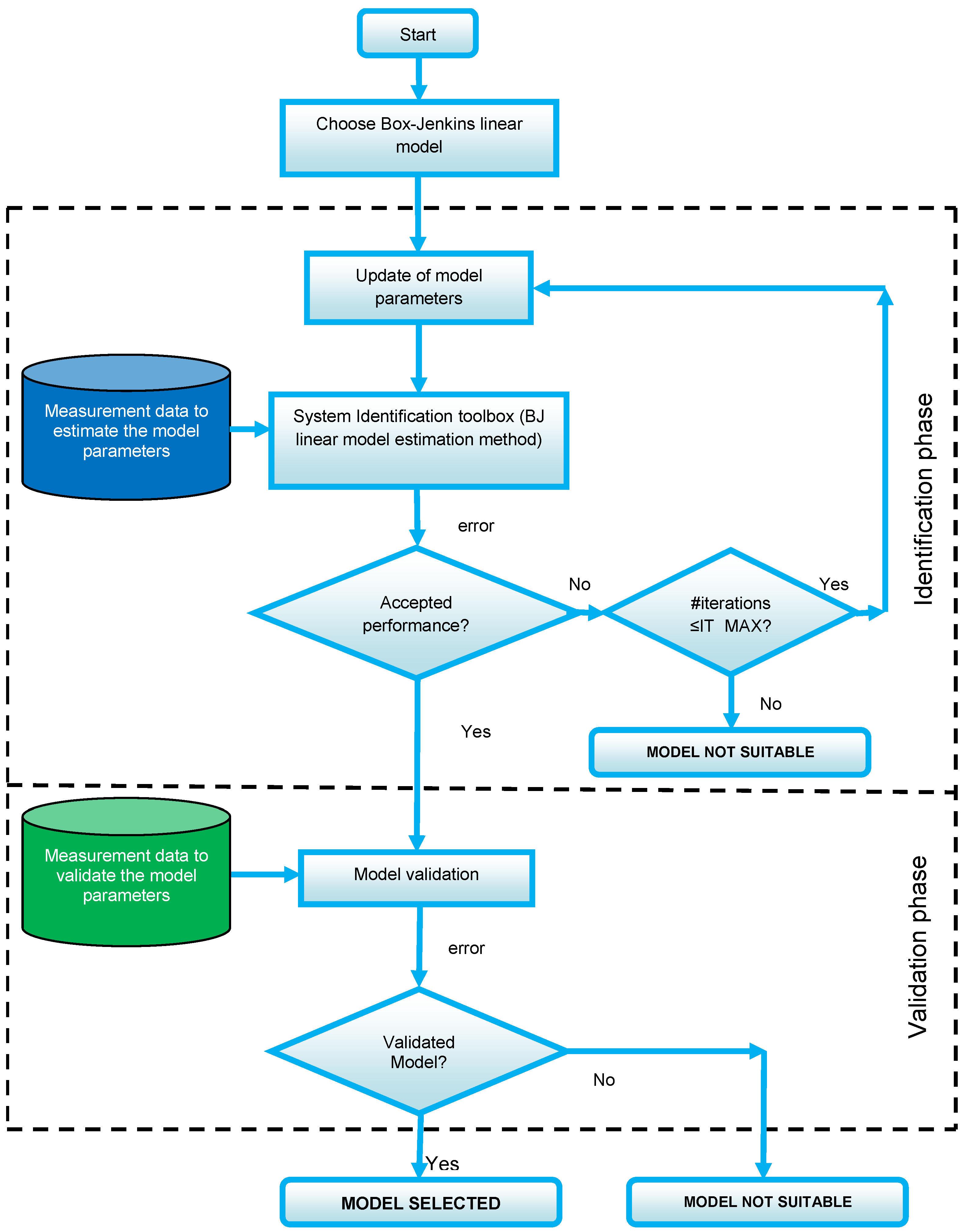
4. Battery Cell Identification Procedure
- Acquire experimental data sampled from the actual battery cell during a driving cycle of an electric vehicle to estimate the Box–Jenkins polynomial model. For this step, we used data from experimental tests available in [37].
- Import the experimental data in MATLAB toolbox “System Identification”.
- Choose the Box–Jenkins polynomial model structure that can approximate the operation of this cell.
- Specify the BJ model orders and delays in the orders field.
- Choose a search method for iterative minimization in the iteration option.
- Start the system identification process to add to the model board in the system identification toolbox. If the model quality metrics are not acceptable and the number of iterations is less than or equal to the maximum allowed value IT_MAX, update the BJ model and move to the next iteration, as the battery cell BJ model is not suitable.
- Validate the estimated BJ model by comparing the BJ model response with the battery cell measured response. To validate the estimated model, it is necessary to use a dataset different from that used to estimate the BJ model. For this step, we used data from another experimental test available in [37]. If the model quality metrics are not acceptable, the battery cell BJ model is not suitable.
- -
- is a vector representing the difference between the model predicted output and the battery cell measured output
- -
- is the cost function
- -
- is the data size
5. Results and Discussion
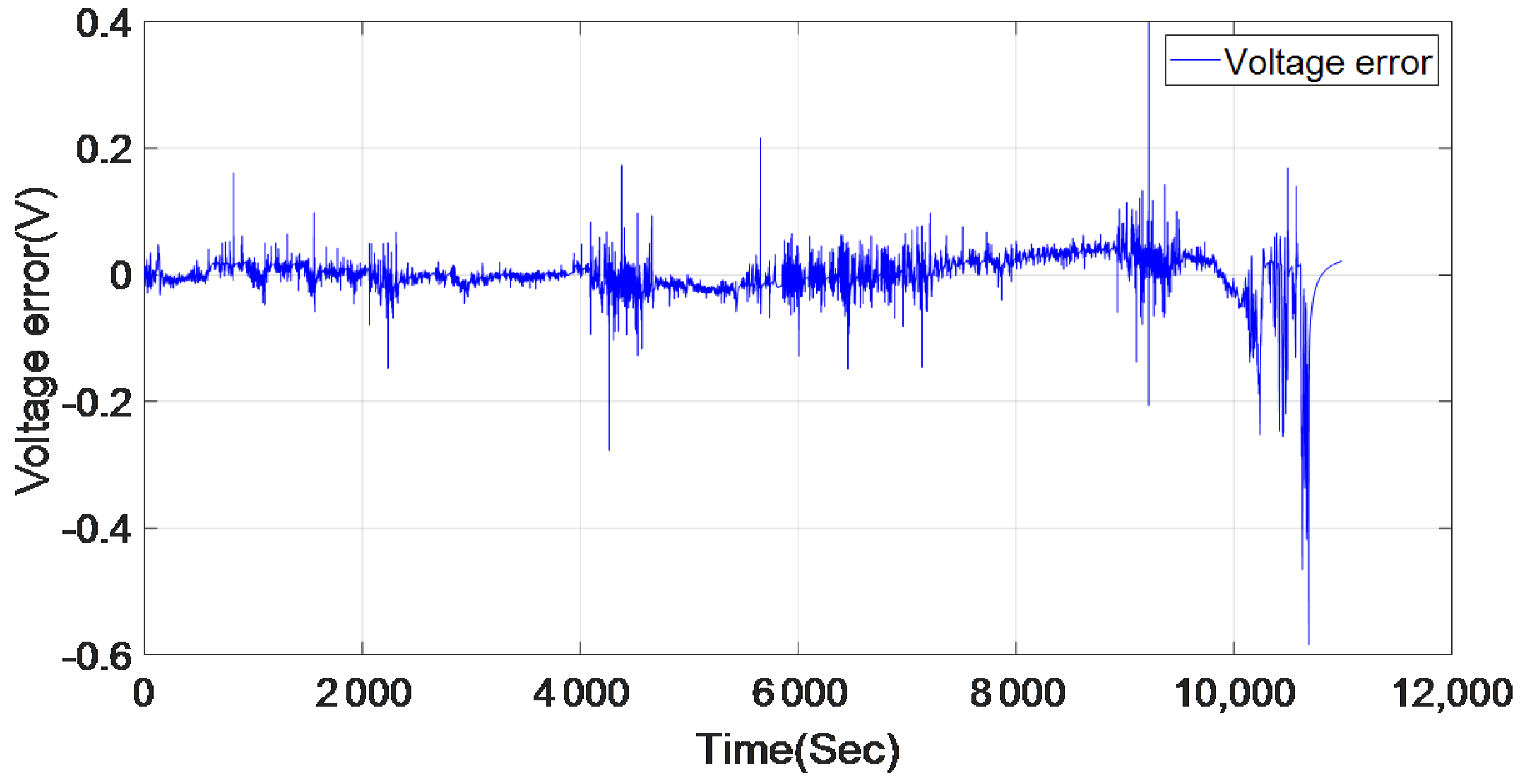
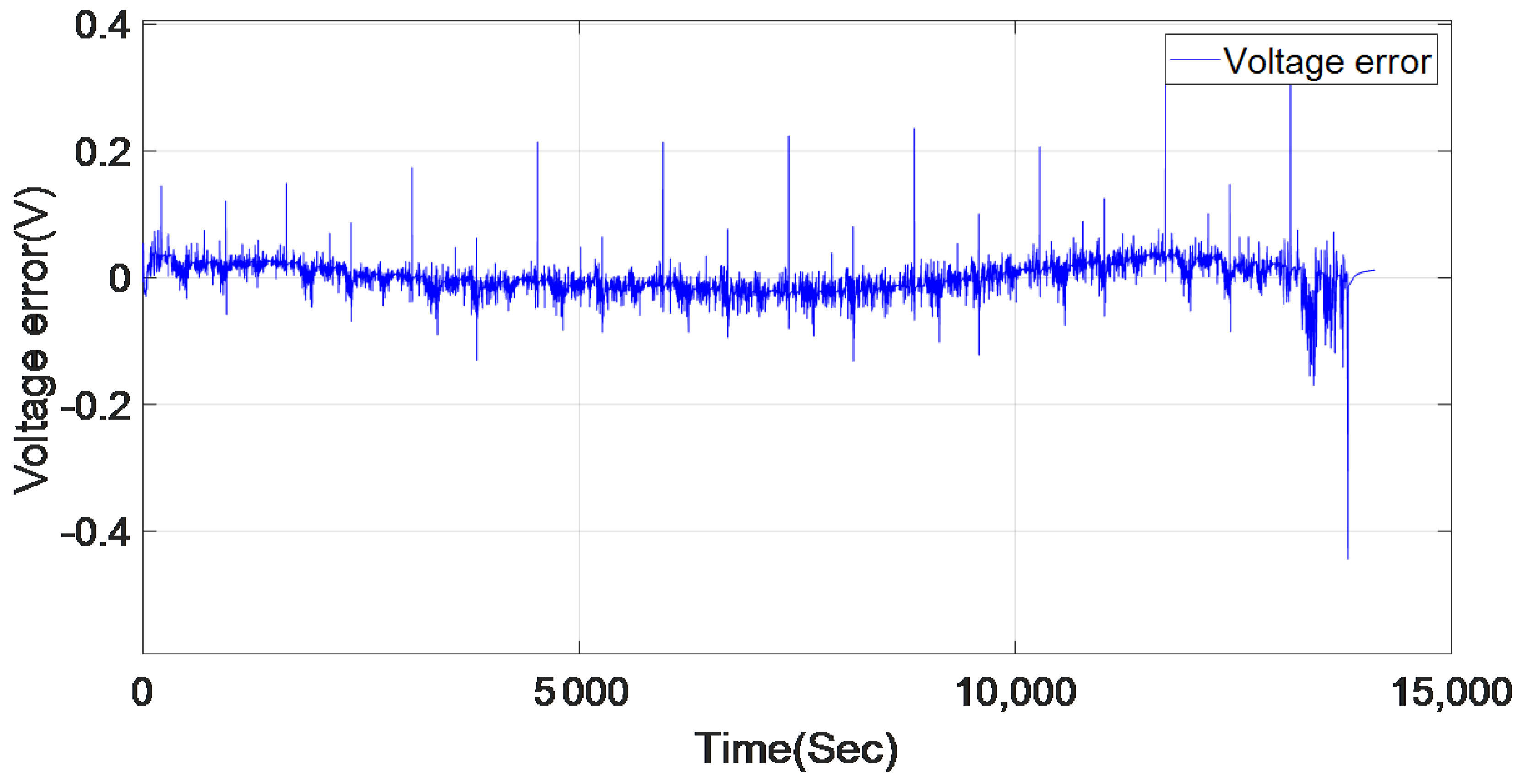
5.1. BJ Black-Box Model Estimation
- -
- the battery cell input, the battery cell output, and the noise
- -
- The polynomials variable are expressed in the time-shift operator as follows:
5.2. BJ Black-Box Model Validation
5.3. Comparison between the BJ Model (BJ7) and Two Other Models
- -
- Equivalent electrical circuit model (EECM): a second-order model that consists of an internal resistance R0 in series with an ideal voltage source Uoc and two RC dipoles parallel circuit pairs to capture double-layer capacitance and charge transfer resistance effects.
- -
- Neural network model: a simple neural network model that was developed based on neural network fitting.
5.4. Discussion
- -
- In most cases, the selected battery cell model BJ7 provides the minimum error between measured and simulated output, which is based on the low MSE value and the high goodness of fit value compared to other models presented previously in Table 4. For the LA-92 driving cycle, the goodness of fit was 86.85% with the estimation data and 90.83% for the validation data, which shows that BJ7 model successfully represents the dynamic behavior of the battery cell for an electric vehicle driving cycle.
- -
- Furthermore, if a simple and basic battery cell model has to be used, the best option is the BJ3 model for its simplicity and linearity.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations and Notations
| ARMAX | Autoregressive moving average with exogenous inputs |
| ARX | Autoregressive with Extra Input |
| BJ | Box–Jenkins |
| BMS | Battery Management System |
| EECM | Equivalent electrical circuit model |
| Fit | Goodness-of-fit |
| IT_MAX | Maximum iteration |
| GN | Gauss-Newton |
| HWFET | Highway Fuel Economy Test |
| MSE | Mean squared error |
| NARX | Nonlinear Auto-Regressive with eXogene input |
| NN | Neural Network |
| OE | Output-Error |
| UDDS | Urban Dynamometer Driving Schedule |
| US06 | or (SFTP) Supplemental Federal Test Procedure |
| A, B, C, D, and F | polynomials variables |
| Vmes | measured battery cell terminal voltage |
| Vmod | model battery cell voltage |
| t | time |
| VN | cost function |
| N | data size |
| Nu | input number |
| Ny | output number |
| nb | B polynomial order plus 1 |
| nc | C polynomial order plus 1 |
| nd | D polynomial order plus 1 |
| nf | F polynomial order plus 1 |
| nk | input delay |
| λ | variance of the white noise e(t) |
| u(t) | input |
| e(t) | noise |
| y(t) | output |
| ui | ith input |
| nki | ith input delay |
| LiNiCoAlO2 or NCA | lithium nickel cobalt aluminum oxide |
| MIX | random mix of the five driving cycles (LA-92, HWFET, NN, US06, HWFET, and UDDS) |
| V | voltage unity |
| A | current unity |
| S | time unity |
| degC | temperature unity |
References
- Ghosh, A. Possibilities and Challenges for the Inclusion of the Electric Vehicle (EV) to Reduce the Carbon Footprint in the Transport Sector: A Review. Energies 2020, 13, 2602. [Google Scholar] [CrossRef]
- Chandran, V.; Patil, C.K.; Karthick, A.; Ganeshaperumal, D.; Rahim, R.; Ghosh, A. State of Charge Estimation of Lithium-Ion Battery for Electric Vehicles Using Machine Learning Algorithms. World Electr. Veh. J. 2021, 12, 38. [Google Scholar] [CrossRef]
- Bhattacharjee, A.; Mohanty, R.K.; Ghosh, A. Design of an Optimized Thermal Management System for Li-Ion Batteries under Different Discharging Conditions. Energies 2020, 13, 5695. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, M.; Zheng, J.; Sun, X.; Zhao, M.; Wang, X. Life cycle greenhouse gas emission reduction potential of battery electric vehicle. J. Clean. Prod. 2018, 190, 462–470. [Google Scholar] [CrossRef]
- Wang, D.; Zamel, N.; Jiao, K.; Zhou, Y.; Yu, S.; Du, Q.; Yin, Y. Life cycle analysis of internal combustion engine, electric and fuel cell vehicles for China. Energy 2013, 59, 402–412. [Google Scholar] [CrossRef]
- Hu, X.; Zou, C.; Zhang, C.; Li, Y. Technological Developments in Batteries: A Survey of Principal Roles, Types, and Management Needs. IEEE Power Energy Mag. 2017, 15, 20–31. [Google Scholar] [CrossRef]
- Emadi, A. Advanced Electric Drive Vehicles; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar] [CrossRef]
- Chemali, E.; Preindl, M.; Malysz, P.; Emadi, A. Electrochemical and Electrostatic Energy Storage and Management Systems for Electric Drive Vehicles: State-of-the-Art Review and Future Trends. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1117–1134. [Google Scholar] [CrossRef]
- Dorn, R.; Schwartz, R.; et Steurich, B. Battery management system. In Lithium-Ion Batteries: Basics and Applications; Springer: Berlin/Heidelberg, Germany, 2018; pp. 165–175. [Google Scholar]
- Slanina, Z.; Dedek, J.; Golembiovsky, M. Low cost battery management system. J. Telecommun. Electron. Comput. Eng. (JTEC) 2017, 9, 87–90. [Google Scholar]
- Gabbar, H.A.; Othman, A.M.; Abdussami, M.R. Review of Battery Management Systems (BMS) Development and Industrial Standards. Technologies 2021, 9, 28. [Google Scholar] [CrossRef]
- Xiao, F.; Li, C.; Fan, Y.; Yang, G.; Tang, X. State of charge estimation for lithium-ion battery based on Gaussian process regression with deep recurrent kernel. Int. J. Electr. Power Energy Syst. 2021, 124, 106369. [Google Scholar] [CrossRef]
- Naguib, M.; Kollmeyer, P.; et Emadi, A. Lithium-Ion Battery Pack Robust State of Charge Estimation, Cell Inconsistency, and Balancing. IEEE Access 2021, 9, 50570–50582. [Google Scholar]
- El Mehdi Laadissi, J.K.; Belhora, F.; Ennawaoui, C.; El Ballouti, A. Aging study of a lead-acid storage bank in a multi-source hybrid system. Indones. J. Electr. Eng. Comput. Sci. 2020, 20, 1109–1117. [Google Scholar] [CrossRef]
- El Mehdi Laadissi, A.E.; Zazi, M.; El Ballouti, A. Comparative study of lead acid battery modelling. ARPN J. Eng. Appl. Sci. 2018, 13, 4448–4452. [Google Scholar]
- Khalfi, J.; Boumaaz, N.; Soulmani, A. Review on Lithium-Ion battery modeling for different applications. Int. J. Eng. Appl. Phys. 2021, 1, 38–47. [Google Scholar]
- Marwane, E.R. Lithium-ion battery modeling using equivalent circuit model. Int. J. Eng. Appl. Phys. 2021, 1, 48–60. [Google Scholar]
- Laadissi, E.M.; Anas, E.F.; Zazi, M.; Jaouad, K. Parameter identification of a lithium-ion battery model using Levenberg-Marquardt algorithm. J. Eng. Appl. Sci. 2019, 14, 1267–1273. [Google Scholar] [CrossRef] [Green Version]
- Khalfi, J.; Boumaaz, N.; Soulmani, A.; Laadissi, E.M. An electric circuit model for a lithium-ion battery cell based on automotive drive cycles measurements. Int. J. Electr. Comput. Eng. (2088–8708) 2021, 11, 2798–2810. [Google Scholar]
- Zazi, M. Nonlinear black box modeling of a lead acid battery using Hammerstein-Wiener model. J. Theor. Appl. Inf. Technol. 2016, 89, 476. [Google Scholar]
- Khalfi, J.; Boumaaz, N.; Soulmani, A. Nonlinear Modeling of Lithium-Ion Battery Cells for Electric Vehicles using a Hammerstein–Wiener Model. J. Electr. Eng. Technol. 2021, 16, 659–669. [Google Scholar] [CrossRef]
- El Mehdi, L.; El Filali, A.; Zazi, M. A Nonlinear TSNN Based Model of a Lead Acid Battery. Bull. Electr. Eng. Inform. 2018, 7, 169–175. [Google Scholar]
- Tran, N.T.; Khan, A.B.; Choi, W. State of charge and state of health estimation of AGM VRLA batteries by employing a dual extended kalman filter and an ARX model for online parameter estimation. Energies 2017, 10, 137. [Google Scholar] [CrossRef] [Green Version]
- Yuan, S.; Wu, H.; et Yin, C. State of charge estimation using the extended Kalman filter for battery management systems based on the ARX battery model. Energies 2013, 6, 444–470. [Google Scholar] [CrossRef]
- Dostal, L.; Grossert, H.; Duecker, D.A.; Grube, M.; Kreuter, D.C.; Sandmann, K.; Zillmann, B.; Seifried, R. Predictability of vibration loads from experimental data by means of reduced vehicle models and machine learning. IEEE Access 2020, 8, 177180–177194. [Google Scholar] [CrossRef]
- Frausto, H.U.; Pieters, J.G.; Deltour, J.M. Modelling greenhouse temperature by means of auto regressive models. Biosyst. Eng. 2003, 84, 147–157. [Google Scholar] [CrossRef]
- Naseri, F.; Schaltz, E.; Stroe, D.; Gismero, A.; Farjah, E. An Enhanced Equivalent Circuit Model with Real-Time Parameter Identification for Battery State-of-Charge Estimation. IEEE Trans. Ind. Electron. 2021. [Google Scholar] [CrossRef]
- Sekhar, R.; Singh, T.P.; et Shah, P. Machine learning based predictive modeling and control of surface roughness generation while machining micro boron carbide and carbon nanotube particle reinforced Al-Mg matrix composites. Part. Sci. Technol. 2021, 1–18. [Google Scholar] [CrossRef]
- Mechaqrane, A.; Zouak, M. A comparison of linear and neural network ARX models applied to a prediction of the indoor temperature of a building. Neural Comput. Appl. 2004, 13, 32–37. [Google Scholar]
- Ljung, L. System identification toolbox. In Matlab User’s Guide; The MathWorks, Inc.: Natick, MA, USA, 1988. [Google Scholar]
- Panasonic. Panasonic NCR18650PF Lithium-Ion Battery Datasheet. 2016. Available online: https://actec.dk/media/documents/70FC46554038.pdf (accessed on 1 June 2021).
- Panasonic. Introduction of NCR18650PF, Panasonic. 2013. Available online: https://voltaplex.com/media/whitepapers/specification-sheet/Panasonic_PF_Specification_Sheet.pdf (accessed on 1 June 2021).
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Ahmed, R.; Emadi, A. Long Short-Term Memory Networks for Accurate State-of-Charge Estimation of Li-ion Batteries. IEEE Trans. Ind. Electron. 2018, 65, 6730–6739. [Google Scholar] [CrossRef]
- Kollmeyer, P.; Hackl, A.; Emadi, A. Li-ion battery model performance for automotive drive cycles with current pulse and EIS parameterization. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo (ITEC), Chicago, IL, USA; 2017; pp. 486–492. [Google Scholar] [CrossRef]
- Lu, W.; Jian, M.; Xuan, Z.; Xuebo, L. Development of a Typical Urban Driving Cycle for Battery Electric Vehicles Based on Kernel Principal Component Analysis and Random Forest. IEEE Access 2021, 9, 15053–15065. [Google Scholar]
- Giakoumis, E.G. Driving and Engine Cycles; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Phillip, K. Panasonic 18650PF Li-ion Battery Data. Mendeley Data. 2018. Available online: http://dx.doi.org/10.17632/wykht8y7tg.1#file-57a2002f-d618-4dd8-96e3-37ffb6bc26c5; http://dx.doi.org/10.17632/wykht8y7tg.1#file-3adfe076-1b29-4002-a145-b736adf830ca; http://dx.doi.org/10.17632/wykht8y7tg.1#file-cd43ca76-7e05-401f-b6de-84a783a3b1f3; http://dx.doi.org/10.17632/wykht8y7tg.1#file-49c96285-4765-454e-853a-3c86bffa2e42; http://dx.doi.org/10.17632/wykht8y7tg.1#file-0e344811-7e34-4fd6-bbef-bc4bfe901800; http://dx.doi.org/10.17632/wykht8y7tg.1#file-048adbe6-fc81-4295-91c9-5b483509d7c6 (accessed on 1 June 2021).



| Battery Cell Parameters | Value |
|---|---|
| Nominal Open Circuit Voltage Capacity | 3.6 V Min. 2.75 Ah/Typ. 2.9 Ah |
| Min/Max Voltage | 2.5 V/4.2 V |
| Mass/Energy Storage | 48 g/9.9 Wh |
| Minimum Charging Temperature | 10 °C |
| Cycles to 80% Capacity | 500 (100% DOD, 25 °C) |
| Model | Polynomial Orders | Input Delay | Model Properties | ||||
|---|---|---|---|---|---|---|---|
| nb | nc | nd | nf | nk | MSE | Fit (%) | |
| BJ1 | 0 | 1 | 2 | 1 | 1 | 0.009718 | 62.23 |
| BJ2 | 1 | 1 | 2 | 2 | 1 | 0.006826 | 68.35 |
| BJ3 | 2 | 1 | 2 | 3 | 1 | 0.001406 | 85.64 |
| BJ4 | 3 | 1 | 2 | 4 | 1 | 0.001923 | 83.2 |
| BJ5 | 4 | 1 | 2 | 5 | 1 | 0.001364 | 85.85 |
| BJ6 | 5 | 1 | 2 | 6 | 1 | 0.001193 | 86.77 |
| BJ7 | 6 | 1 | 2 | 7 | 1 | 0.001176 | 86.86 |
| BJ8 | 7 | 1 | 2 | 8 | 1 | 0.001267 | 86.36 |
| BJ9 | 8 | 1 | 2 | 9 | 1 | 0.001207 | 86.69 |
| BJ10 | 9 | 1 | 2 | 10 | 1 | 0.001351 | 85.92 |
| Drive Cycle Type | Fit (%) |
|---|---|
| LA-92 | 90.83 |
| HWFET | 81.85 |
| NN | 90.55 |
| US06 | 89.6 |
| UDDS | 90.35 |
| Model Type | MSE |
|---|---|
| Neural network model | 0.00514245 |
| Box–Jenkins model (BJ7) | 0.001177 |
| Equivalent electrical circuit model | 0.0013 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalfi, J.; Boumaaz, N.; Soulmani, A.; Laadissi, E.M. Box–Jenkins Black-Box Modeling of a Lithium-Ion Battery Cell Based on Automotive Drive Cycle Data. World Electr. Veh. J. 2021, 12, 102. https://doi.org/10.3390/wevj12030102
Khalfi J, Boumaaz N, Soulmani A, Laadissi EM. Box–Jenkins Black-Box Modeling of a Lithium-Ion Battery Cell Based on Automotive Drive Cycle Data. World Electric Vehicle Journal. 2021; 12(3):102. https://doi.org/10.3390/wevj12030102
Chicago/Turabian StyleKhalfi, Jaouad, Najib Boumaaz, Abdallah Soulmani, and El Mehdi Laadissi. 2021. "Box–Jenkins Black-Box Modeling of a Lithium-Ion Battery Cell Based on Automotive Drive Cycle Data" World Electric Vehicle Journal 12, no. 3: 102. https://doi.org/10.3390/wevj12030102
APA StyleKhalfi, J., Boumaaz, N., Soulmani, A., & Laadissi, E. M. (2021). Box–Jenkins Black-Box Modeling of a Lithium-Ion Battery Cell Based on Automotive Drive Cycle Data. World Electric Vehicle Journal, 12(3), 102. https://doi.org/10.3390/wevj12030102







