Modelling of Humidity Dynamics for Open-Cathode Proton Exchange Membrane Fuel Cell
Abstract
:1. Introduction
2. Modelling
2.1. Electrochemical Model
2.2. Mass Flow Model
2.2.1. Air Delivery System
2.2.2. Cathode Flow Channel
2.2.3. Anode Flow Channel
2.2.4. Cathode Gas Diffusion Layer
2.2.5. Cathode Catalyst Layer
2.2.6. Membrane
2.3. Thermal Model
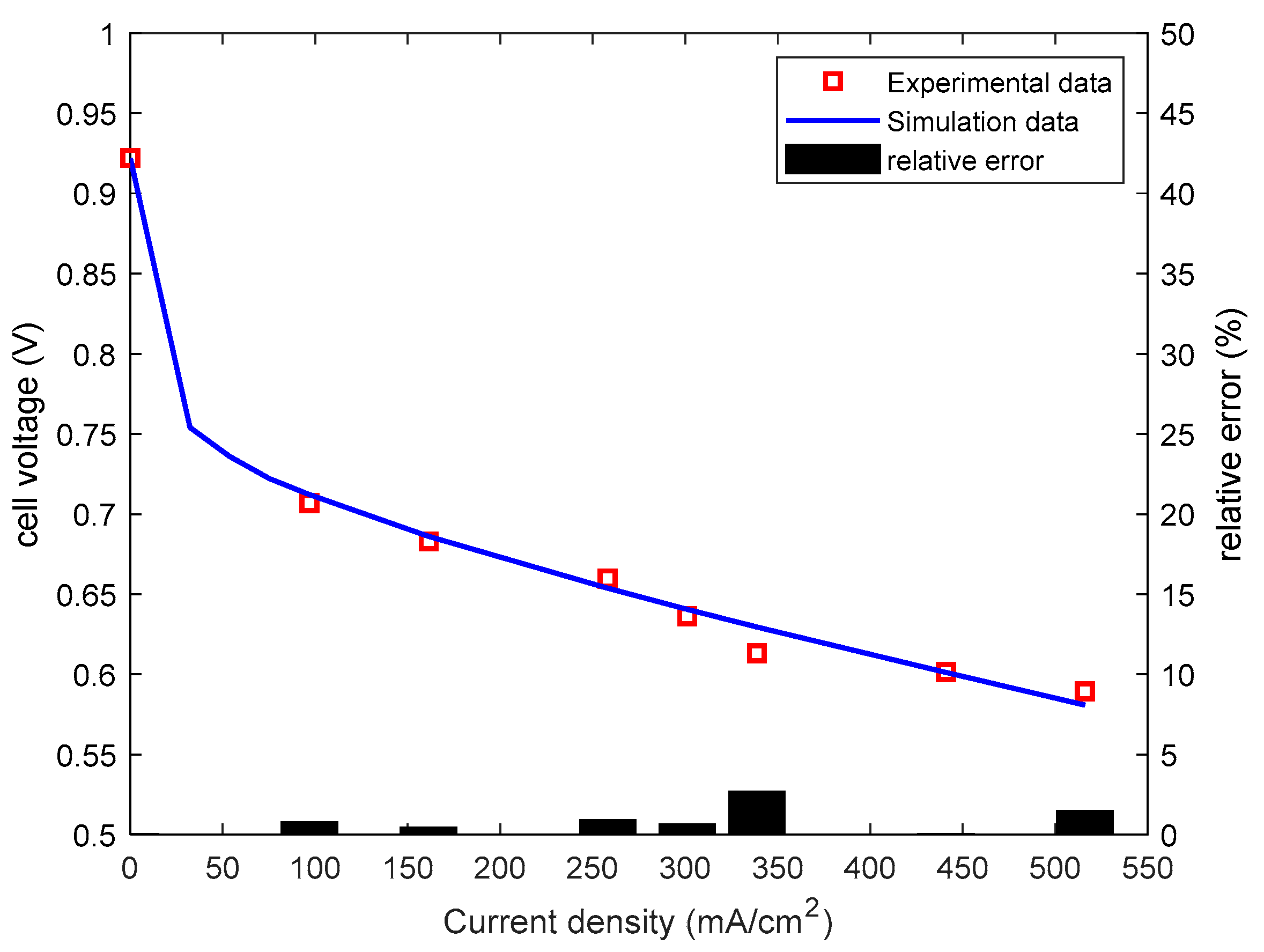
3. Results and Discussion
- Firstly, this is because the water flow rate caused by electro-osmotic drag suddenly increases in response to the step of current. Therefore, more water moves from the anode to cathode, which leads to the decrease of the water content in the anode. However, the humidity at the cathode catalyst layer is already in saturation state. Hence, the water content at the membrane cathode side remains nearly unchanged. According to the dynamic model of membrane, with unchanged water content at the membrane cathode side and a decreased water content at the anode, a drop of membrane water content occurs.
- Secondly, in order to ensure the output performance and efficiency of the stack, the operation temperature of the stack is higher with the increase of stack current, which leads to a rise in saturated vapor pressure. Hence, the relative humidity within the stack is decreased, so that there is a decline in membrane water content. In this respect, the relationship between temperature and humidity dynamics is illustrated.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Saleh, I.M.M.; Ali, R.; Hongwei, Z. Simplified mathematical model of proton exchange membrane fuel cell based on horizon fuel cell stack. J. Mod. Power Syst. Clean Energy 2016, 4, 668–679. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Han, K.; Song, Y. Dynamic behaviors of PEM fuel cells under load changes. Int. J. Hydrogen Energy 2020, 45, 20312–20320. [Google Scholar] [CrossRef]
- Hao, W.; Xianguo, L.; Berg, P. Numerical analysis of dynamic processes in fully humidified PEM fuel cells. Int. J. Hydrogen Energy 2007, 32, 2022–2031. [Google Scholar] [CrossRef]
- Dong Gyun, K.; Chanyeong, P.; In Seop, L.; Sung Hoon, C.; Dong Keun, L.; Min Soo, K. Performance enhancement of air-cooled open cathode polymer electrolyte membrane fuel cell with inserting metal foam in the cathode side. Int. J. Hydrogen Energy 2020, 45, 27622–27631. [Google Scholar] [CrossRef]
- Sagar, A.; Chugh, S.; Sonkar, K.; Sharma, A.; Kjeang, E. A computational analysis on the operational behaviour of open-cathode polymer electrolyte membrane fuel cells. Int. J. Hydrogen Energy 2020, 45, 34125–34138. [Google Scholar] [CrossRef]
- Bidoggia, B.; Kaer, S.K. Estimation of membrane hydration status for standby proton exchange membrane fuel cell systems by complex impedance measurement: Constant temperature stack characterization. Int. J. Hydrogen Energy 2013, 38, 4054–4066. [Google Scholar] [CrossRef]
- Santa Rosa, D.T.; Pinto, D.G.; Silva, V.S.; Silva, R.A.; Rangel, C.M. High performance PEMFC stack with open-cathode at ambient pressure and temperature conditions. Int. J. Hydrogen Energy 2007, 32, 4350–4357. [Google Scholar] [CrossRef]
- Lopez-Sabiron, A.M.; Barroso, J.; Roda, V.; Barranco, J.; Lozano, A.; Barreras, F. Design and development of the cooling system of a 2 kW nominal power open-cathode polymer electrolyte fuel cell stack. Int. J. Hydrogen Energy 2012, 37, 7289–7298. [Google Scholar] [CrossRef]
- Fu, H.; Shen, J.; Sun, L.; Lee, K.Y. Fuel cell humidity modeling and control using cathode internal water content. Int. J. Hydrogen Energy 2021, 46, 9905–9917. [Google Scholar] [CrossRef]
- Fengxiang, C.; Jieran, J.; Zhongjun, H.; Wei, C.; Jun, C.; Zenggang, X.; Jie, C. Robust polymer electrolyte membrane fuel cell temperature tracking control based on cascade internal model control. J. Power Sources 2020, 479, 229008. [Google Scholar] [CrossRef]
- Headley, A.; Yu, V.; Borduin, R.; Dongmei, C.; Wei, L. Development and experimental validation of a physics-based PEM fuel cell model for cathode humidity control design. IEEE/ASME Trans. Mechatron. 2016, 21, 1775–1782. [Google Scholar] [CrossRef]
- Hong, P.; Xu, L.; Li, J.; Ouyang, M. Modeling of membrane electrode assembly of PEM fuel cell to analyze voltage losses inside. Energy 2017, 139, 277–288. [Google Scholar] [CrossRef]
- Dongmei, C.; Huei, P. Modeling and simulation of a PEM fuel cell humidification system. In Proceedings of the 2004 American Control Conference, Piscataway, NJ, USA, 30 June–2 July 2004; pp. 822–827. [Google Scholar]
- Pukrushpan, J.T.; Peng, H.; Stefanopoulou, A.G. Control-oriented modeling and analysis for automotive fuel cell systems. J. Dyn. Syst. Meas. Control. Trans. ASME 2004, 126, 14–25. [Google Scholar] [CrossRef]
- Strahl, S.; Husar, A.; Serra, M. Development and experimental validation of a dynamic thermal and water distribution model of an open cathode proton exchange membrane fuel cell. J. Power Sources 2011, 196, 4251–4263. [Google Scholar] [CrossRef] [Green Version]
- Strahl, S.; Costa-Castello, R. Model-based analysis for the thermal management of open-cathode proton exchange membrane fuel cell systems concerning efficiency and stability. J. Process. Control. 2016, 47, 201–212. [Google Scholar] [CrossRef] [Green Version]
- Mahjoubi, C.; Olivier, J.C.; Skander-mustapha, S.; Machmoum, M.; Slama-belkhodja, I. An improved thermal control of open cathode proton exchange membrane fuel cell. Int. J. Hydrogen Energy 2019, 44, 11332–11345. [Google Scholar] [CrossRef]
- Zhang, B.; Lin, F.; Zhang, C.; Liao, R.; Wang, Y.-X. Design and implementation of model predictive control for an open-cathode fuel cell thermal management system. Renew. Energy 2020, 154, 1014–1024. [Google Scholar] [CrossRef]
- Yan, Z.; Biao, Z. Modeling and control of a portable proton exchange membrane fuel cell-battery power system. J. Power Sources 2011, 196, 8413–8423. [Google Scholar] [CrossRef]
- Lu, L.; Liangzhen, Y.; Qi, L.; Weirong, C. Control-oriented temperature dynamic modeling of open-cathode PEM fuel cell via on-line T-S fuzzy identification method. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Piscataway, NJ, USA, 7–10 August 2017; p. 5. [Google Scholar]
- Sun, L.; Jin, Y.; You, F. Active disturbance rejection temperature control of open-cathode proton exchange membrane fuel cell. Appl. Energy 2020, 261, 114381. [Google Scholar] [CrossRef]
- Ismail, M.S.; Ingham, D.B.; Hughes, K.J.; Ma, L.; Pourkashanian, M. An efficient mathematical model for air-breathing PEM fuel cells. Appl. Energy 2014, 135, 490–503. [Google Scholar] [CrossRef]
- O’Hayre, R.; Fabian, T.; Litster, S.; Prinz, F.B.; Santiago, J.G. Engineering model of a passive planar air breathing fuel cell cathode. J. Power Sources 2007, 167, 118–129. [Google Scholar] [CrossRef]
- Yalcinoz, T.; Alam, M.S. Dynamic modeling and simulation of air-breathing proton exchange membrane fuel cell. J. Power Sources 2008, 182, 168–174. [Google Scholar] [CrossRef]
- Liso, V.; Araya, S.S.; Olesen, A.C.; Nielsen, M.P.; Kaer, S.K. Modeling and experimental validation of water mass balance in a PEM fuel cell stack. Int. J. Hydrogen Energy 2016, 41, 3079–3092. [Google Scholar] [CrossRef]
- Shang-Wen, T.; Yong-Song, C. A mathematical model to study the energy efficiency of a proton exchange membrane fuel cell with a dead-ended anode. Appl. Energy 2017, 188, 151–159. [Google Scholar] [CrossRef]



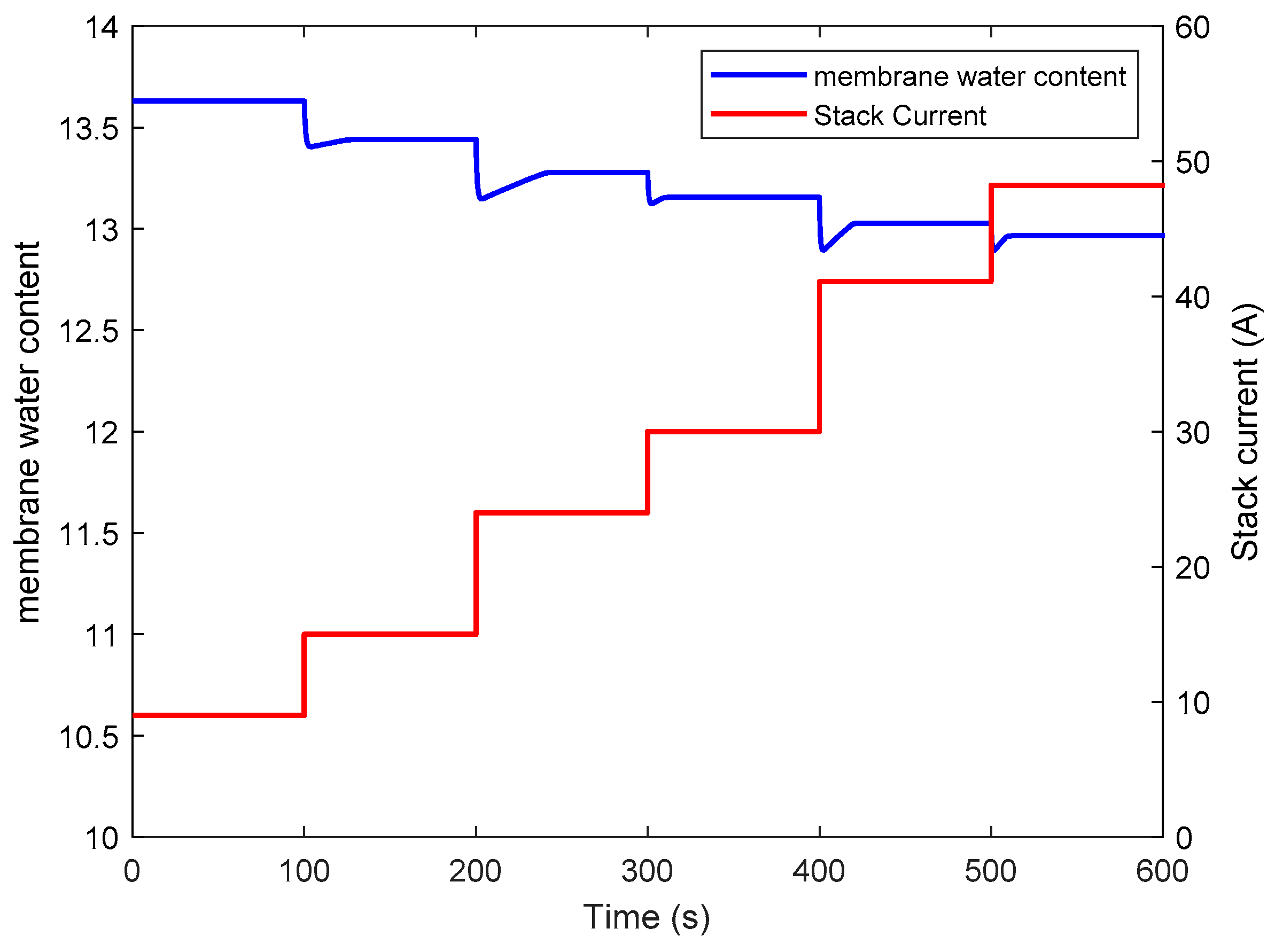

| Current Step Test | Settling Time(s) |
|---|---|
| 9 A to 15 A | 22.5 |
| 15 A to 24 A | 39.4 |
| 24 A to 30 A | 8.5 |
| 30 A to 41 A | 18.9 |
| 41 A to 48 A | 9.8 |
| Stack Current (A) | Current Density (mA/cm2) | Operation Temperature (°C) |
|---|---|---|
| 9 A | 96.8 | 33 |
| 15 A | 161.3 | 36 |
| 24 A | 258.1 | 44 |
| 30 A | 322.6 | 46 |
| 41 A | 440.9 | 53 |
| 48 A | 516.1 | 57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, F.; Zhang, L.; Jiao, J. Modelling of Humidity Dynamics for Open-Cathode Proton Exchange Membrane Fuel Cell. World Electr. Veh. J. 2021, 12, 106. https://doi.org/10.3390/wevj12030106
Chen F, Zhang L, Jiao J. Modelling of Humidity Dynamics for Open-Cathode Proton Exchange Membrane Fuel Cell. World Electric Vehicle Journal. 2021; 12(3):106. https://doi.org/10.3390/wevj12030106
Chicago/Turabian StyleChen, Fengxiang, Liming Zhang, and Jieran Jiao. 2021. "Modelling of Humidity Dynamics for Open-Cathode Proton Exchange Membrane Fuel Cell" World Electric Vehicle Journal 12, no. 3: 106. https://doi.org/10.3390/wevj12030106
APA StyleChen, F., Zhang, L., & Jiao, J. (2021). Modelling of Humidity Dynamics for Open-Cathode Proton Exchange Membrane Fuel Cell. World Electric Vehicle Journal, 12(3), 106. https://doi.org/10.3390/wevj12030106





