Numerical Simulation of Hydrogen Leakage and Diffusion Process of Fuel Cell Vehicle
Abstract
:1. Introduction
2. Numerical Simulation Model
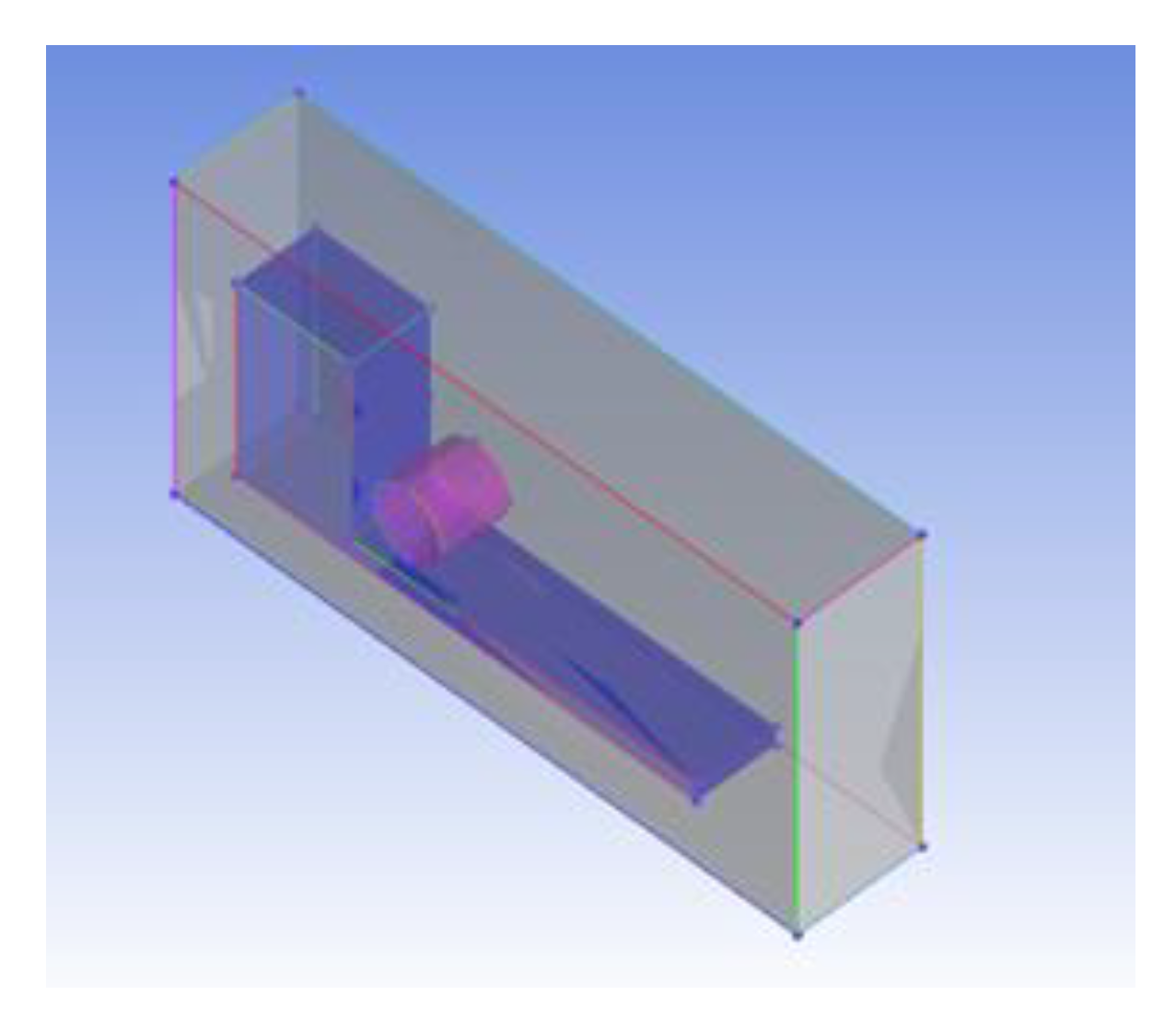
2.1. Physical Model
2.2. Boundary Conditions
2.3. Mathematical Model
2.4. Model Validation
3. Results
3.1. Hydrogen Leakage and Diffusion Process HFCV Open Space and Influencing Factors
3.1.1. Location of Leakage
3.1.2. Rate of Leakage
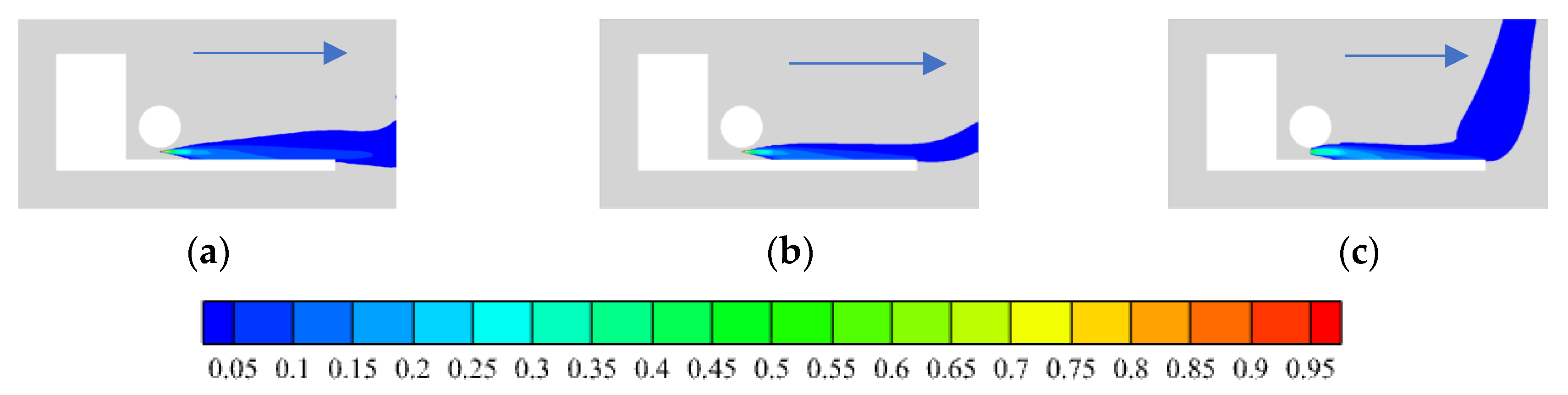
3.1.3. Wind Speed
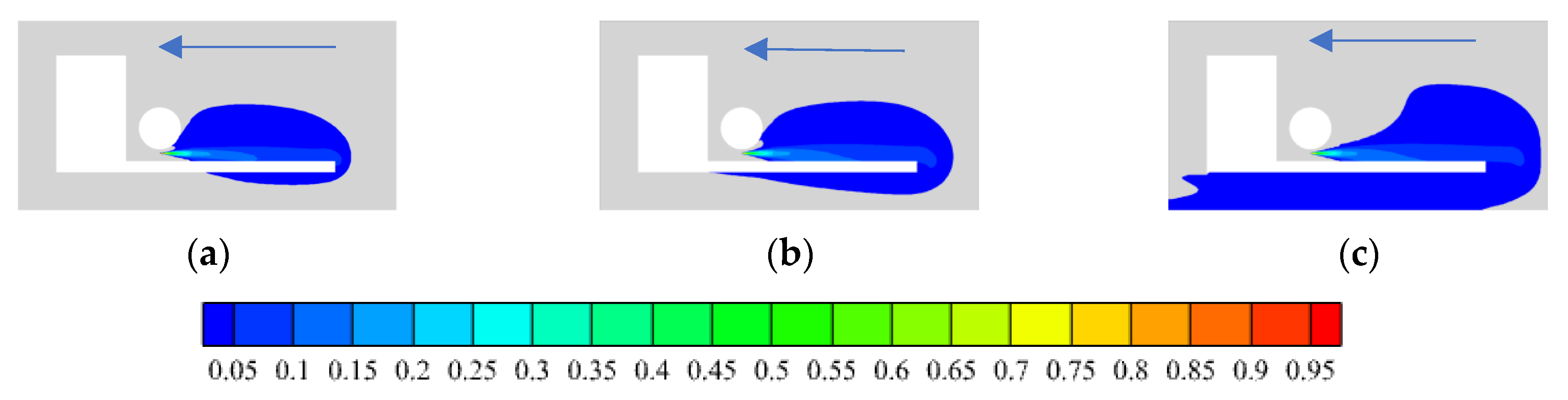
3.1.4. Wind Direction
3.2. Analysis of the Influencing Factors of the Airway in Closed Space
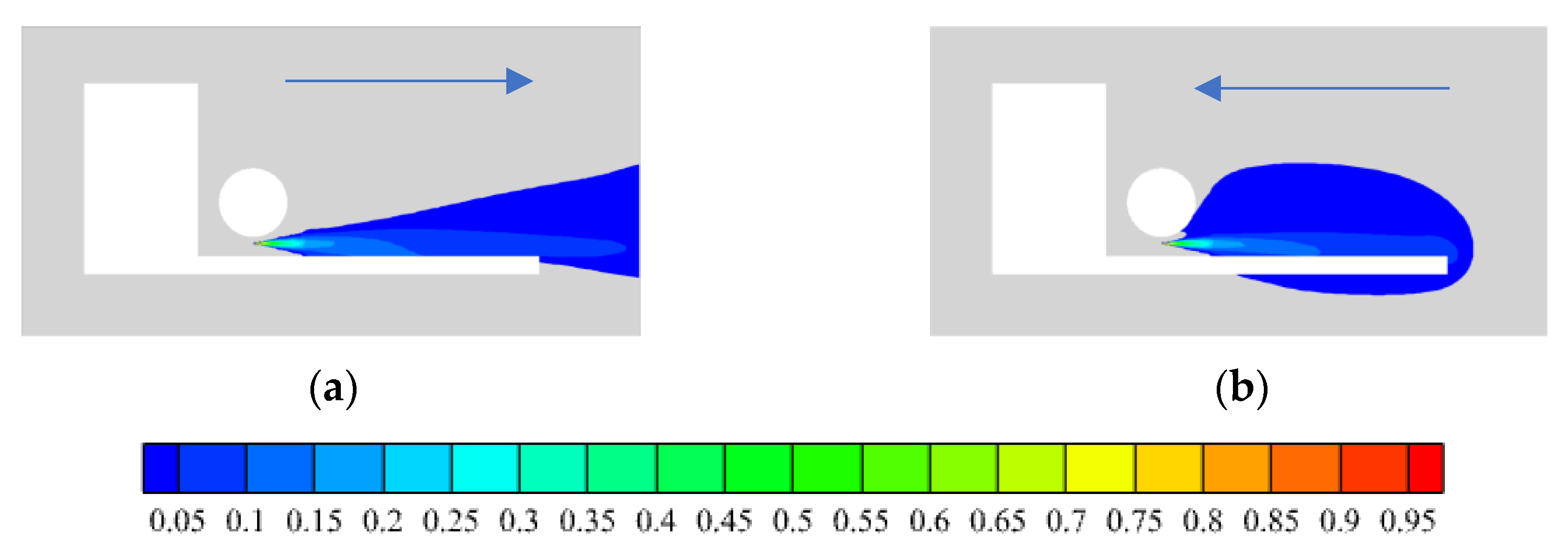
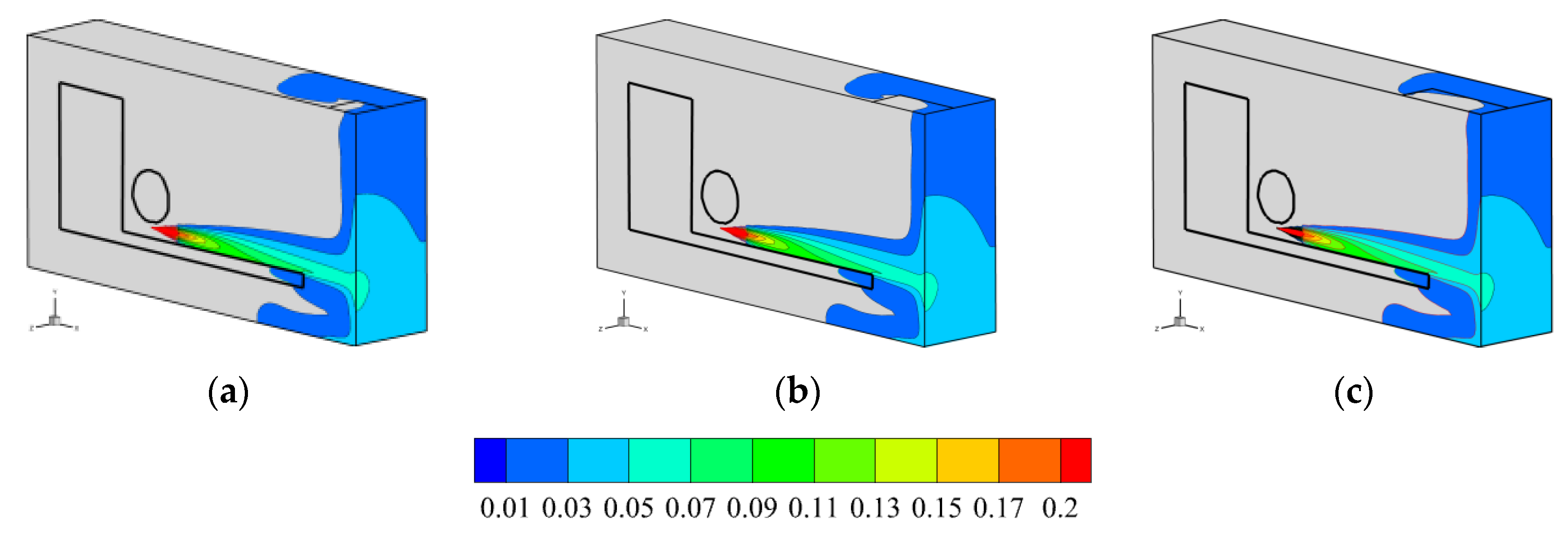
3.2.1. Area of Vent
3.2.2. Location of Vent
4. Conclusions
- The hydrogen leakage and diffusion process in open space is divided into three stages: leakage and diffusion, concentration dilution and stable balance. At the beginning of the leakage, when the air can dilute hydrogen, the distribution range is reduced. After the hydrogen leakage, diffusion and dilution, the hydrogen distribution range never changes. When the distribution is stable, the hydrogen concentration is characterized by a conical stratified distribution structure, the hydrogen concentration and concentrated gradient near the leakage port. The width increases with the diffusion distance and with the inclined straight line characteristics.
- In open space, the leakage rate greatly effects the hydrogen distribution range. The greater the leakage rate, the greater the hydrogen concentration range. Environmental wind affects the hydrogen distribution range and the diffusion direction. When hydrogen leaks to the rear of the car, the smaller the wind speed under different adverse wind speeds, the larger the hydrogen distribution range, and more hydrogen is distributed under the chassis, which is not conducive to the safety of HFCV. Under different wind directions, the 90-degree side wind significantly changes the hydrogen diffusion direction of hydrogen, with the fastest diffusion and the minimum concentration distribution range, the most conducive to hydrogen diffusion. However, the maximum distribution range and the highest risk are under the reverse wind.
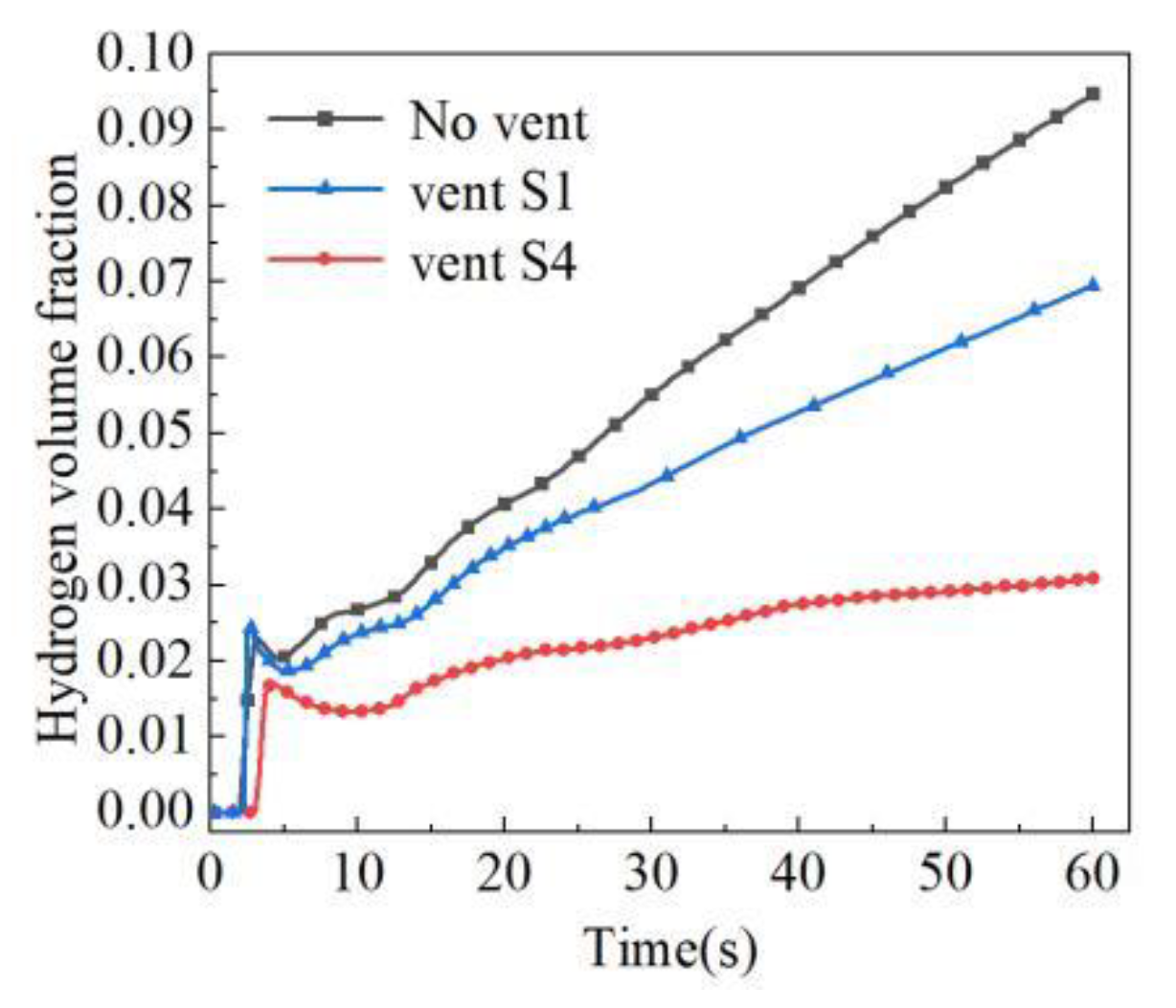
- The air outlet in closed space has an effect on the rising rate and size of hydrogen concentration. In the case of hydrogen backward leakage, the influence of the top vent is slight. Under different top vent areas, the overall diffusion process of hydrogen in space never changes, and the effect is limited to the vicinity of the vent. Compared with the top vent, opening the vent at the back of the space can make hydrogen diffuse to the external environment faster and significantly reduce the rising rate and concentration of hydrogen concentration in this space. Therefore, after hydrogen leakage, the best effect is to open the vent in the position where hydrogen first diffuses.
Author Contributions
Funding
Conflicts of Interest
References
- Lacome, J.; Jamois, D.; Perrette, L. Large-scale hydrogen release in an isothermal confined area. Int. J. Hydrogen Energy 2011, 36, 2302–2312. [Google Scholar] [CrossRef] [Green Version]
- Prabhakar, A.; Agrawal, N.; Raghavan, V. Experimental investigation onhelium distribution and stratification in unventilated vertical cylindrical enclosure effect of jet release rates and total release volume. Int. J. Hydrogen Energy 2016, 48, 23131–23228. [Google Scholar]
- Shu, Z.; Liang, W.; Zheng, X. Dispersion characteristics of hydrogen leakage: Comparing the prediction model with the experiment. Energy 2021, 236, 121420. [Google Scholar] [CrossRef]
- Venetsanos, A.; Papanikolaou, E.; Delichatsios, M. An inter-comparison exercise on the capabilities of CFD models to predict the short- and long-term distribution and mixing of hydrogen in a garage. Int. J. Hydrogen Energy 2009, 34, 5912–5923. [Google Scholar] [CrossRef]
- Zou, Q.; Tian, Y.; Han, F. Prediction of state property during hydrogen leaks from high-pressure hydrogen storage systems. Int. J. Hydrogen Energy 2019, 44, 22394–22404. [Google Scholar] [CrossRef]
- Abohamzeh, E.; Salehi, F.; Sheikholeslami, M. Review of hydrogen safety during storage, transmission, and applications processes. J. Loss Prev. Process Ind. 2021, 72, 104569. [Google Scholar] [CrossRef]
- Yu, Z. Numerical simulation of hydrogen leakage and diffusion [D]. Natl. Univ. Def. Sci. Technol. 2008. [Google Scholar]
- Liu, Y. High pressure hydrogen rapid charge temperature rise control and leakage diffusion law. Study Zhejiang Univ. 2009. [Google Scholar]
- Xu, P.; Liu, P.; Liu, Y. Numerical simulation of leakage and diffusion at different positions of high pressure hydrogen storage tank. J. Chem./Eng. 2008, 22, 921–926. [Google Scholar]
- Zheng, J.; Liu, Y.; Xu, P. Numerical simulation of influence of obstacles on leakage and diffusion of high pressure hydrogen storage tank. J. Zhejiang Univ. 2008, 42, 2177–2180. [Google Scholar]
- Choi, J.; Hur, N.; Kang, S. A CFD simulation of hydrogen dispersion for the hydrogen leakage from a fuel cell vehicle in an underground parking garage. Int. J. Hydrogen Energy 2013, 19, 8084–8091. [Google Scholar] [CrossRef]
- Hajjia, Y.; Jouinia, B.; Bouteraaa, M. Numerical study of hydrogen release accidents in a residential garage. Int. J. Hydrogen Energy 2015, 31, 9747–9759. [Google Scholar] [CrossRef]
- Hajji, Y.; Bouteraa, M.; Cafsi, A. Dispersion and behavior of hydrogen during a leak in a prismatic cavity. Int. J. Hydrogen Energy 2014, 11, 6111–6119. [Google Scholar] [CrossRef]
- Hajji, Y.; Bouteraa, M.; ELCafsi, A. Natural ventilation of hydrogen during a leak in a residential garage. Renew. Sust. Energy Rev. 2015, 50, 810–818. [Google Scholar] [CrossRef]
- Prasad, K.; Pitts, W.; Yang, J. Effect of wind and buoyancy on hydrogen release and dispersion in a compartment with vents at multiple levels. Int. J. Hydrogen Energy 2010, 35, 9218–9231. [Google Scholar] [CrossRef]
- Kazuo, M.; Masami, N.; Jun, I. Forced ventilation for sensing-based risk mitigation of leaking hydrogen in a partially open space. Int. J. Hydrogen Energy 2010, 35, 980–8578. [Google Scholar]
- Matsuura, K.; Nakano, M.; Ishimoto, J. Acceleration of hydrogen forced ventilation after leakage ceases in a partially open space. Int. J. Hydrogen Energy 2012, 9, 7940–7949. [Google Scholar] [CrossRef]
- Matsuura, K.; Nakano, M.; Ishimoto, J. Sensing-based risk mitigation control of hydrogen dispersion and accumulation in a partially open space with low-height openings by forced ventilation. Int. J. Hydrogen Energy 2012, 37, 1972–1984. [Google Scholar] [CrossRef]
- Papanikolaou, E.; Venetsanos, A.; Heitsch, M.; Baraldi, D.; Huser, A.; Pujol, J.; Garcia, J.; Markatos, N. HySafe SBEP-V20: Numerical studies of release experiments inside a naturally ventilated residential garage. Int. J. Hydrogen Energy 2010, 35, 4747–4757. [Google Scholar] [CrossRef] [Green Version]
- Kazuo, M.; Hiroshi, K.; Hisayoshi, T. Numerical simulation of leaking hydrogen dispersion behavior in a partially open space. Int. J. Hydrogen Energy 2007, 33, 240–247. [Google Scholar]
- Barley, C.D.; Gawlik, K. Buoyancy-driven ventilation of hydrogen from buildings: Laboratory test and model validation. Int. J. Hydrogen Energy 2009, 34, 5592–5603. [Google Scholar] [CrossRef] [Green Version]
- Cariteau, B.; Tkatschenko, I. Experimental study of the effects of vent geometry on the dispersion of a buoyant gas in a small enclosure. Int. J. Hydrogen Energy 2013, 38, 8030–8038. [Google Scholar] [CrossRef]
- Isaac, W.E.; William, G.H.; Greg, H.E.; Merilo, E.G.; Groethe, M.A. Experimental investigation of hydrogen release and ignition from fuel cell powered forklifts in enclosed spaces. Int. J. Hydrogen Energy 2012, 37, 17446–17456. [Google Scholar]
- Giannissi, S.G.; Shentsov, V.; Melideo, D.; Cariteau, B.; Baraldi, D.; Venetsanos, A.G.; Molkov, V. CFD benchmark on hydrogen release and dispersion in confined, naturally ventilated space with one vent. Int. J. Hydrogen Energy 2015, 40, 2415–2429. [Google Scholar] [CrossRef]
- Giannissi, S.G.; Venetsanos, A.G.; Markatos, N. CFD modeling of hydrogen dispersion under cryogenic release conditions. Int. J. Hydrogen Energy 2014, 39, 15851–15863. [Google Scholar] [CrossRef]
- Gupta, S.; Brinster, J.; Studer, E. Hydrogen related risks within aprivate garage: Concentration measurements in a realistic full-scale experimental facility. Int. J. Hydrogen Energy 2009, 34, 5902–5911. [Google Scholar] [CrossRef]
- Pitts, W.M.; Yang, J.C.; Blais, M.; Joyce, A. Dispersion and burning behavior of hydrogen released in a full-scale residential garage in the presence and absence of conventional automobiles. Int. J. Hydrogen Energy 2012, 37, 17457–17469. [Google Scholar] [CrossRef]

















| Nomenclature | |||
|---|---|---|---|
| velocity (m/s) | E | total energy of micro element (J) | |
| t | time (s) | thermal conductivity | |
| gas density (kg/m3) | h | enthalpy | |
| viscous stress (N) | mass concentration | ||
| P | gas pressure (Pa) | c | volume concentration |
| J | diffusion flux | D | diffusion coefficient |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, M.; Zhu, H.; Huang, J.; Zhang, X. Numerical Simulation of Hydrogen Leakage and Diffusion Process of Fuel Cell Vehicle. World Electr. Veh. J. 2021, 12, 193. https://doi.org/10.3390/wevj12040193
Jiao M, Zhu H, Huang J, Zhang X. Numerical Simulation of Hydrogen Leakage and Diffusion Process of Fuel Cell Vehicle. World Electric Vehicle Journal. 2021; 12(4):193. https://doi.org/10.3390/wevj12040193
Chicago/Turabian StyleJiao, Mingyu, Haoran Zhu, Jinglong Huang, and Xin Zhang. 2021. "Numerical Simulation of Hydrogen Leakage and Diffusion Process of Fuel Cell Vehicle" World Electric Vehicle Journal 12, no. 4: 193. https://doi.org/10.3390/wevj12040193
APA StyleJiao, M., Zhu, H., Huang, J., & Zhang, X. (2021). Numerical Simulation of Hydrogen Leakage and Diffusion Process of Fuel Cell Vehicle. World Electric Vehicle Journal, 12(4), 193. https://doi.org/10.3390/wevj12040193





