Implementation of Equilibrium Strategy Aiming at Throughput Maximization of Series Battery Pack
Abstract
:1. Introduction
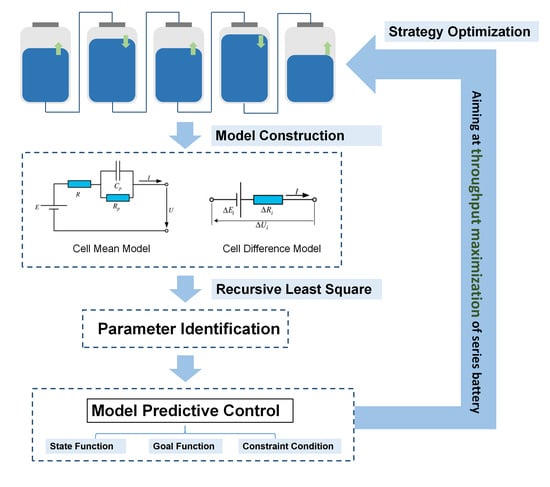
2. Parameter Identification for Series Batteries
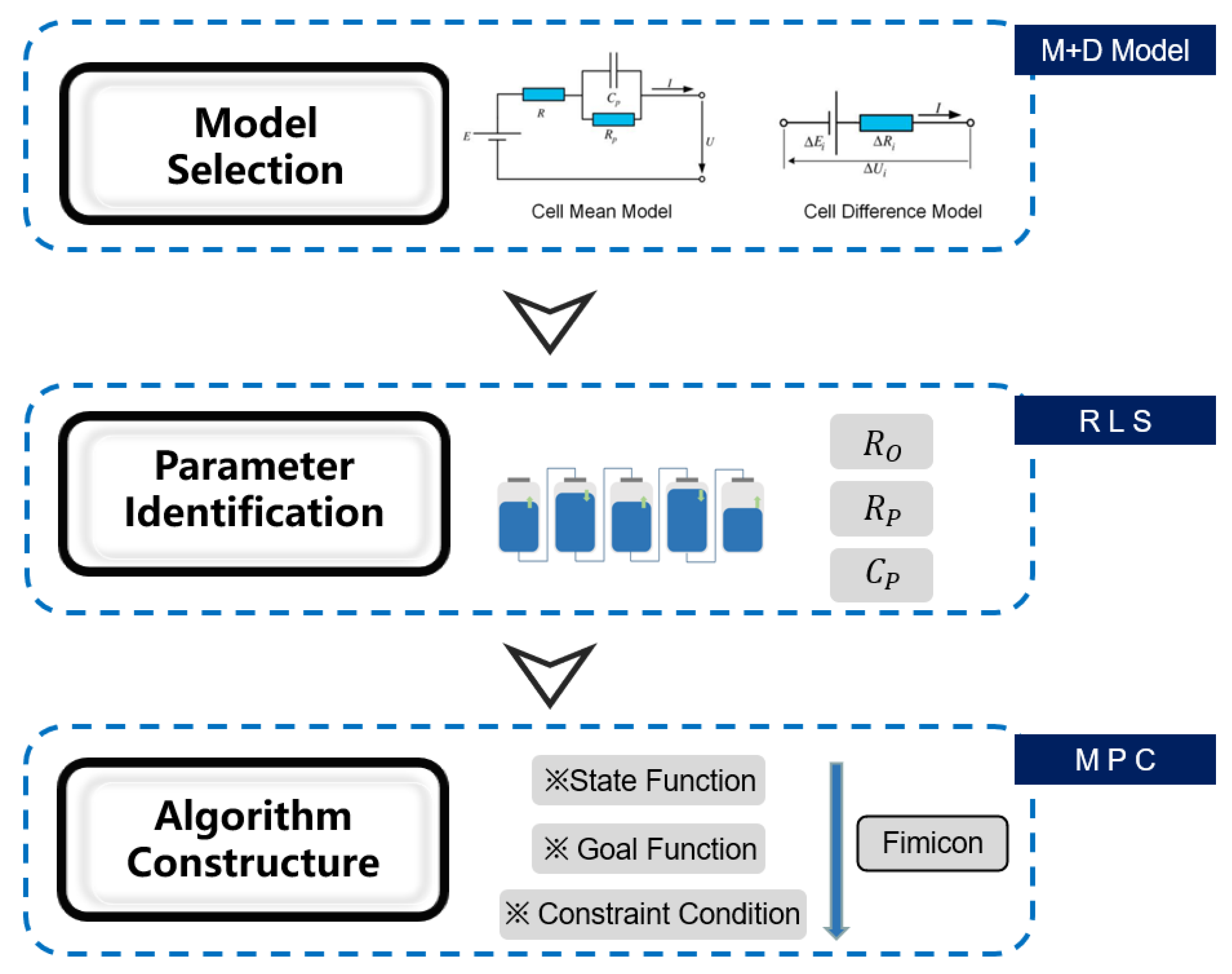
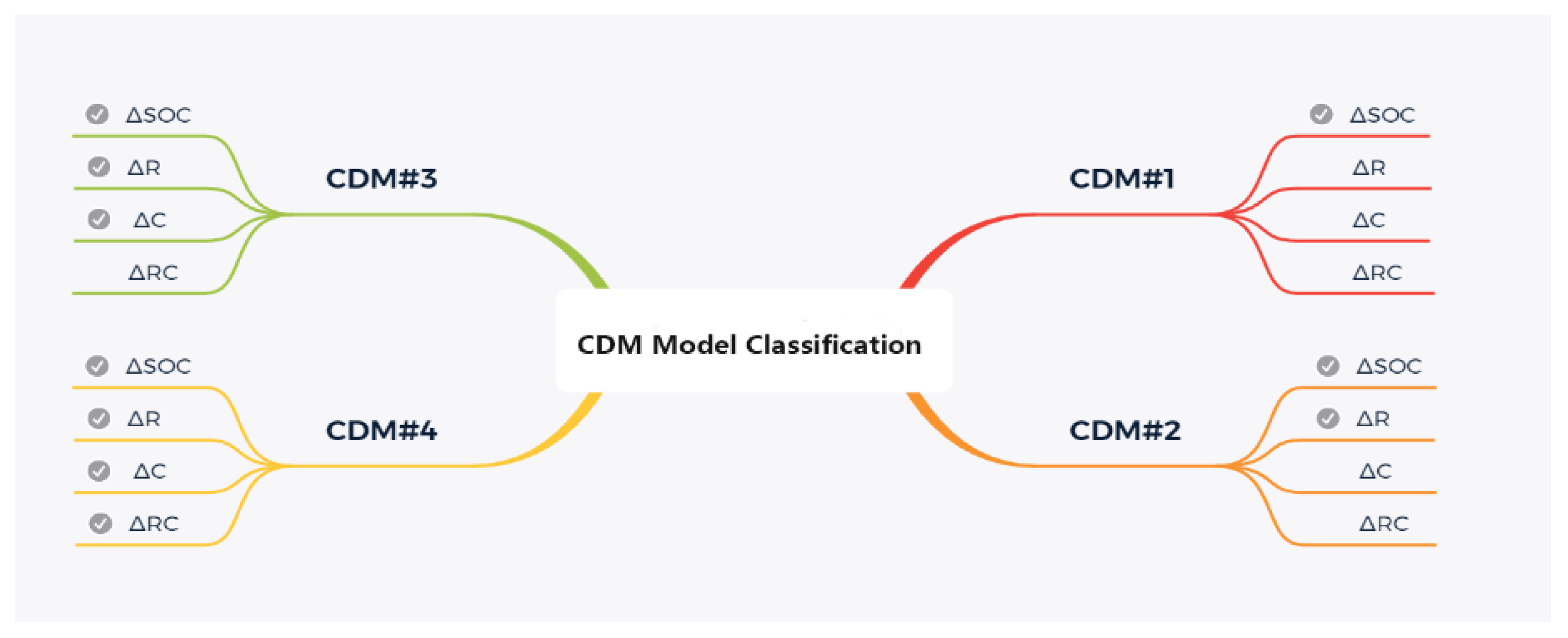
2.1. M+D Model
2.2. Parameter Identification Based on RLS
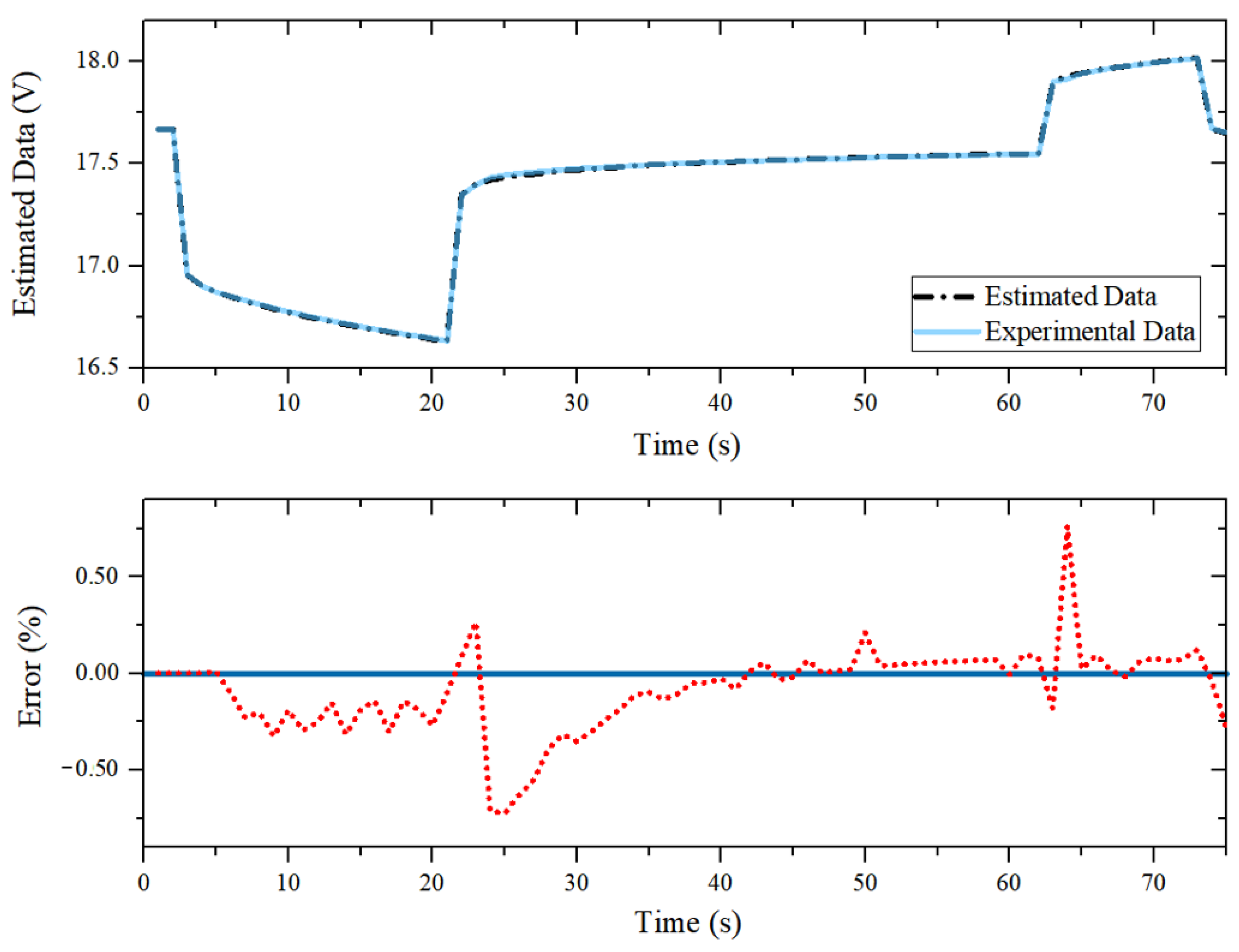
2.3. Parameter Identification Results
3. Equalization Strategy Design Based on Model Predictive Control
3.1. State Space Model of Series Batteries
3.2. Objective Function and Solution Method of Equilibrium Strategy
4. Simulation Result
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feng, F.; Hu, X.; Liu, K.; Che, Y.; Lin, X.; Jin, G.; Liu, B. A practical and comprehensive evaluation method for series-connected battery pack models. IEEE Trans. Transp. Electrif. 2020, 6, 391–416. [Google Scholar] [CrossRef]
- Liu, X.; Ai, W.; Naylor, M.; Patel, Y.; Wu, B. The effect of cell-to-cell variations and thermal gradients on the performance and degradation of lithium-ion battery packs. Appl. Energy 2019, 248, 489–499. [Google Scholar] [CrossRef]
- Schmalstieg, J.; Käbitz, S.; Ecker, M.; Sauer, D.U. A holistic aging model for Li(NiMnCo)O2 based 18650 lithium-ion batteries. J. Power Sources 2014, 257, 325–334. [Google Scholar] [CrossRef]
- Yang, S.; He, R.; Zhang, Z.; Cao, Y.; Gao, X.; Liu, X. CHAIN: Cyber hierarchy and interactional network enabling digital solution for battery full-lifespan management. Matter 2020, 3, 27–41. [Google Scholar] [CrossRef]
- Weng, C.; Feng, X.; Sun, J.; Peng, H. State-of-health monitoring of lithium-ion battery modules and packs via incremental capacity peak tracking. Appl. Energy 2016, 180, 360–368. [Google Scholar] [CrossRef] [Green Version]
- Gao, X.; Liu, X.; He, R.; Wang, M.; Xie, W.; Brandon, N.P.; Wu, B.; Ling, H.; Zang, S. Designed high-performance lithium-ion battery electrodes using a novel hybrid model-data driven approach. Energy Storage Mater. 2021, 36, 435–458. [Google Scholar] [CrossRef]
- Wu, B.; Widanage, W.D.; Yang, S.; Liu, X. Battery digital twins: Perspectives on the fusion of models, data and artificial intelligence for smart battery management systems. Energy AI 2020, 1, 100016. [Google Scholar] [CrossRef]
- Che, Y.; Deng, Z.; Lin, X.; Hu, L. Learning and online model Correction. IEEE Trans. Veh. Technol. 2021, 70, 1269–1277. [Google Scholar] [CrossRef]
- Yang, S.; Gao, X.; Li, Y.; Xie, W.; Guo, B.; Zhang, L.; Liu, X. Minimum lithium plating overpotential control based charging strategy for parallel battery module prevents side reactions. J. Power Sources 2021, 494, 229772. [Google Scholar] [CrossRef]
- Feng, F.; Hu, X.; Liu, J.; Lin, X.; Liu, B. A review of equalization strategies for series battery packs: Variables, objectives, and algorithms. Renew. Sustain. Energy Rev. 2019, 116, 109464. [Google Scholar] [CrossRef]
- Li, W.; Sengupta, N.; Dechent, P.; Howey, D.; Annaswamy, A.; Sauer, D.U. Online capacity estimation of lithium-ion batteries with deep long short-term memory networks. J. Power Sources 2021, 482, 228863. [Google Scholar] [CrossRef]
- Nguyen, N.; Oruganti, S.K.; Na, K.; Bien, F. An adaptive backward control battery equalization system for serially connected lithium-ion battery packs. IEEE Trans. Veh. Technol. 2014, 63, 3651–3660. [Google Scholar] [CrossRef]
- Ugle, R.; Li, Y.; Dhingra, A. Equalization integrated online monitoring of health map and worthiness of replacement for battery pack of electric vehicles. J. Power Sources 2013, 223, 293–305. [Google Scholar] [CrossRef]
- Zheng, Y.; Ouyang, M.; Lu, L.; Li, J.; Han, X.; Xu, L. On-line equalization for lithium-ion battery packs based on charging cell voltages: Part 1. Equalization based on remaining charging capacity estimation. J. Power Sources 2014, 247, 676–686. [Google Scholar] [CrossRef]
- Zou, C.; Manzie, C.; Ne, D. Multi-time-scale observer design for state-of-charge and state-of- health of a lithium-ion battery. J. Power Sources 2016, 335, 121–130. [Google Scholar] [CrossRef]
- Dai, H.; Wei, X.; Sun, Z.; Wang, J.; Gu, W. Online cell SOC estimation of Li-ion battery packs using a dual time-scale Kalman filtering for EV applications. Appl. Energy 2012, 95, 227–237. [Google Scholar] [CrossRef]
- Wu, T.; Qi, Y.; Liao, L.; Ji, F.; Chen, H. Research on equalization strategy of lithium-ion batteries based on fuzzy logic control. J. Energy Storage 2021, 40, 102722. [Google Scholar] [CrossRef]
- Crespo, M.; Georgious, R.; Garcia, P.; Villa, G. Active equalization of series/parallel Li-ion battery modules including no-load conditions. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Detroit, MI, USA, 11–15 October 2020; pp. 4431–4437. [Google Scholar]
- Li, K.; Zong, X.; Liu, Q.; Sun, Y.; Xue, F. Design of an active battery equalization circuit with DC-DC converter. In Proceedings of the 3rd Asia Energy and Electrical Engineering Symposium, Chengdu, China, 26–29 March 2021; pp. 863–866. [Google Scholar]
- Xiong, H.; Song, D.; Shi, F.; Wei, Y.; Jinzhen, L. Novel voltage equalisation circuit of the lithium battery pack based on bidirectional flyback converter. IET Power Electron. 2020, 13, 2194–2200. [Google Scholar] [CrossRef]
- Zhang, S.; Qiang, J.; Yang, L.; Zhao, X. Prior-knowledge-independent equalization to improve battery uniformity with energy efficiency and time efficiency for lithium-ion battery. Energy 2016, 94, 1–12. [Google Scholar] [CrossRef]
- Diao, W.; Xue, N.; Bhattacharjee, V.; Jiang, J.; Karabasoglu, O. Active battery cell equalization based on residual available energy maximization. Appl. Energy 2018, 210, 690–698. [Google Scholar] [CrossRef]
- Wang, B.; Qin, F.; Zhao, X.; Ni, X.; Xuan, D. Equalization of series connected lithium-ion batteries based on back propagation neural network and fuzzy logic control. Int. J. Energy Res. 2020, 44, 4812–4826. [Google Scholar] [CrossRef]
- Song, L.; Liang, T.; Lu, L.; Ouyang, M. Lithium-ion battery pack equalization based on charging voltage curves. Int. J. Electr. Power Energy Syst. 2020, 115, 105516. [Google Scholar] [CrossRef]
- Lin, Y.; Xu, X.; Wang, F.; Xu, Q. Active equalization control strategy of Li-ion battery based on state of charge estimation of an electrochemical-thermal coupling model. Int. J. Energy Res. 2020, 44, 3778–3789. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, L.; Zhao, X.; Qiang, J. Electrical power and energy systems a GA optimization for lithium-ion battery equalization based on SOC estimation by NN and FLC. Int. J. Electr. Power Energy Syst. 2015, 73, 318–328. [Google Scholar] [CrossRef]
- Einhorn, M.; Guertlschmid, W.; Blochberger, T.; Kumpusch, R.; Permann, R.; Conte, F.V.; Kral, C.; Fleig, J. A current equalization method for serially connected battery cells using a single power converter for each cell. IEEE Trans. Veh. Technol. 2011, 60, 4227–4237. [Google Scholar] [CrossRef]
- Zheng, Y.; Ouyang, M.; Lu, L.; Li, J.; Han, X.; Xu, L.; Ma, H.; Dollmeyer, T.A.; Freyermuth, V. Cell state-of-charge inconsistency estimation for LiFePO4 battery pack in hybrid electric vehicles using mean-difference model. Appl. Energy 2013, 111, 571–580. [Google Scholar] [CrossRef]
- Hu, L.; Hu, X.; Che, Y.; Feng, F.; Lin, X.; Zhang, Z. Reliable state of charge estimation of battery packs using fuzzy adaptive federated filtering. Appl. Energy 2020, 262, 114569. [Google Scholar] [CrossRef]
- Feng, T.; Yang, L.; Zhao, X.; Zhang, H.; Qiang, J. Online identification of lithium-ion battery parameters based on an improved equivalent-circuit model and its implementation on battery state-of-power prediction. J. Power Sources 2015, 281, 192–203. [Google Scholar] [CrossRef]
- Altaf, F.; Egardt, B. Gain-scheduled control of modular battery for thermal and SOC balancing. Engineering 2016, 49, 62–69. [Google Scholar]
- Liu, J.; Chen, Y.; Fathy, H.K.; Chen, Y. Nonlinear model-predictive optimal control of an active cell-to-cell lithium-ion battery pack balancing circuit. IFAC 2017, 50, 14483–14488. [Google Scholar] [CrossRef]
- Liu, J.; Duan, Q.; Chen, H.; Sun, J.; Wang, Q. An optimal multistage charge strategy for commercial lithium ion batteries. Sustain. Energy Fuels 2018, 2, 1726–1736. [Google Scholar]
- Han, W.; Zhang, L. Battery cell reconfiguration to expedite charge equalization in series-connected battery systems. IEEE Robot. Autom. Lett. 2018, 3, 22–28. [Google Scholar] [CrossRef]
- Burgos-Mellado, C.; Orchard, M.E.; Kazerani, M.; Cárdenas, R.; Sáez, D. Particle-filtering-based estimation of maximum available power state in Lithium-Ion batteries. Appl. Energy 2016, 161, 349–363. [Google Scholar] [CrossRef]
- Birkl, C.R.; Roberts, M.R.; McTurk, E.; Bruce, P.G.; Howey, D.A. Degradation diagnostics for lithium ion cells. J. Power Sources 2017, 341, 373–386. [Google Scholar] [CrossRef]

| M+D Model | State Equations |
|---|---|
CMM 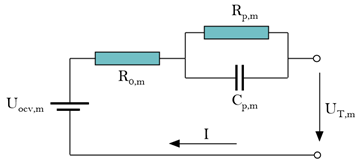 | where represents the mean terminal voltage of the battery pack, and are the polarization internal resistance and polarization capacitance. is the polarization voltage, represents the ohm internal resistance, and is the instantaneous current in the circuit. represents the OCV. |
CDM#2 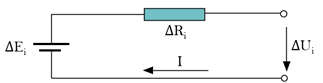 | where represents difference between ohmic resistance and mean ohmic resistance of each cell and is the instantaneous current in the circuit |
| CMM: (i) Initialization: , , , , (ii) Calculate and measure the mean voltage: (iii) Calculate of mean cell gain matrix: (iv) Calculate the mean cell error covariance matrix: (v) Update mean cell parameter matrix: (vi) Update estimated voltage: CDM#2: where represents the terminal voltage value of the cell k at sampling point i, represents the terminal voltage value of the battery pack at time i. In addition The forgetting factor = 0.95 |
| Parameter | Cell #1 | Cell #2 | Cell #3 | Cell #4 | Cell #5 | CMM |
|---|---|---|---|---|---|---|
| (mΩ) | 1.3626 | 1.3652 | 1.3679 | 1.3706 | 1.3701 | 1.3676 |
| (mΩ) | 0.6017 | |||||
| (104 F) | 1.1969 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, R.; Liu, X.; Zhang, Z.; Wang, M.; Cheng, H.; Gao, X.; Yan, X.; Yang, S. Implementation of Equilibrium Strategy Aiming at Throughput Maximization of Series Battery Pack. World Electr. Veh. J. 2021, 12, 208. https://doi.org/10.3390/wevj12040208
Cao R, Liu X, Zhang Z, Wang M, Cheng H, Gao X, Yan X, Yang S. Implementation of Equilibrium Strategy Aiming at Throughput Maximization of Series Battery Pack. World Electric Vehicle Journal. 2021; 12(4):208. https://doi.org/10.3390/wevj12040208
Chicago/Turabian StyleCao, Rui, Xinhua Liu, Zhengjie Zhang, Mingyue Wang, Hanchao Cheng, Xinlei Gao, Xiaoyu Yan, and Shichun Yang. 2021. "Implementation of Equilibrium Strategy Aiming at Throughput Maximization of Series Battery Pack" World Electric Vehicle Journal 12, no. 4: 208. https://doi.org/10.3390/wevj12040208
APA StyleCao, R., Liu, X., Zhang, Z., Wang, M., Cheng, H., Gao, X., Yan, X., & Yang, S. (2021). Implementation of Equilibrium Strategy Aiming at Throughput Maximization of Series Battery Pack. World Electric Vehicle Journal, 12(4), 208. https://doi.org/10.3390/wevj12040208