Optimization Approach for Long-Term Planning of Charging Infrastructure for Fixed-Route Transportation Systems

Abstract

As the electrification of the transportation sector advances, fleet operators have to rethink their approach regarding fleet management against the background of limiting factors, such as a reduced range or extended recharging times. Charging infrastructure plays a critical role, and it is worthwhile to consider its planning as an integral part for the long-term operation of an electric vehicle fleet. In the category of fixed route transportation systems, the predictable character of the routes can be exploited when planning charging infrastructure. After a prior categorization of stakeholders and their respective optimization objectives in the sector coupling domain, a cost optimization framework for fixed route transportation systems is presented as the main contribution of this work. We confirm previous literature in that there is no one-fits-all optimization method for this kind of problem. The method is tested on seven scenarios for the public transport operator of Darmstadt, Germany. The core optimization is formulated as a mixed integer linear programming (MILP) problem. All scenarios are terminated by the criterion of a maximum solving time of 48 h and provide feasible solutions with a relative MIP-gap between 7 and 24%.

1. Introduction

The electrification process is shaping the mobility of future generations. Environmental concerns; technological enablers, such as higher battery energy densities; and political agendas are advancing the process of electrifying different sectors across society. The motivation ranges from pure economic considerations over social welfare reasons to combating climate change for environmental causes. Commitments like the Paris Agreement underline the momentum of this process [1]. With the advancement of the energy transition in Germany towards a carbon neutral society in 2050, as envisioned by the German government [2], incentives for consuming more renewable energies come along. In the transportation and the energy sector, minimizing carbon emissions is a major goal. During this process, maintaining the stability of the electricity grid is of high importance. The fluctuating character of renewable energies needs to be compensated. One way to achieve this is by using energy storage systems that accumulate excess energy and feed it back into the grid when demand increases. Charging infrastructure plays a crucial role here because it enables the flow of energy and information between the energy and the transportation sector. Thanks to vehicle to grid (V2G) technology, the storage capacities of electric vehicles can be used as energy storage and thereby alleviate fluctuations in the grid [3]. The benefits of charging infrastructure at a macroscopic level are clear. However, when breaking it down to individual stakeholders, the question remains: What is the most cost-effective way for constructing charging infrastructure and operating the vehicle fleet? To find an answer to this question, we will review previous literature in this chapter and present an optimization framework in Section 2. Against the background of a rapid pace of technological advancements, it is worthwhile to regularly check and update the assumptions made in previous literature contributions regarding charging infrastructure. As an example, Kunith et al. assumed a battery capacity for electric buses of 150 kWh in their paper from 2016 regarding the optimization of fast-charging infrastructure of an electric bus fleet [4]. This represented a perfectly reasonable assumption at the time. However, the current relevance of their outcomes has to be questioned since electric buses with a battery capacity of up to 441 kWh are available in 2021 [5]. Since the battery capacity of individual vehicles highly influences their range, it can impact the whole operation of, e.g., a bus fleet. The use-case of electric buses is, in fact, analyzed by many researchers and will serve as reference use-case in the present paper. Lajunen et al. highlighted that the main challenges in adopting electric buses are related to charging infrastructure [6] (p. 57).

In 2014, Wang et al. concluded that the payback period of the charging infrastructure investment for electric fleets is very long. Additionally, cost calculation models among academia were not yet very developed [6] (p. 57). As Lajunen et al. pointed out, Wang and González and Mahmoud et al. found that the successful implementation of electric buses is highly sensitive to the operational context and energy profile. Lajunen et al. also pointed out that when evaluating individual electric buses, the lifecycle costs during the fleet operation have rarely been considered in literature. However, they have a great impact on individual vehicles, which motivates a holistic approach [6].

Lin et al. touched upon large-scale fast-charging infrastructure from a broader perspective. They hinted at its influence on the power grid network and the fact that power grid restrictions may constrain the charging network. Their suggestion is that these interactions should be modeled from the start, which motivates a holistic approach [7] (p. 425). Generally, when analyzing the behavior of a technology, integrating it in its real-world, interaction-driven context results in more meaningful outcomes as compared to a use-case independent one-fits-all analysis.

Different interdisciplinary studies have pursued holistic approaches for analyzing or optimizing charging infrastructure. They go beyond the exclusive consideration of a single technological domain or perspective. As the system boundaries of these studies get wider, the number of variables used to describe the system behavior increases. This increased complexity can be dealt with by pursuing the following:

• A clear definition of the purpose of the analysis or optimization, which implies clarifying the use-case, its system boundaries, the stakeholder perspective, and the stakeholder objective.
• A careful a-priori selection of a reduced number of important influence factors—variables or parameters—depending on the use-case definition, the perspective, and the ultimate objective.

1.1. Literature Overview of Stakeholder Perspectives and Objective Formulation

As just pointed out, researchers from different disciplines have developed comprehensive, holistic models targeting charging infrastructure. This has led to an increasing number of different modeling methodologies, which hinders a straightforward comparison of their results. However, every contribution adds value to the academic field by taking different perspectives and pursuing different objectives. Handling the arising complexity and number of interactions becomes very difficult. Therefore, we want to introduce a brief literature overview related to the planning of charging infrastructure for vehicles. For ease of comprehension, we proceed with a top-down structure starting with the energy and the transportation sector (first column of

Table 1. Overview of stakeholders in the energy and transportation sectors and their different optimization objectives from economic, environmental, and social welfare perspectives.

Sector	Stakeholder	Perspective	Objective	Reference
Energy	Electricity Producers	Economical	Minimize electricity production costs	Authors.
	Electricity Producers	Environmental	Minimize greenhouse-gas emissions	Authors.
	Electricity Producers	Environmental	Minimize resource utilization	Authors.
	Grid Operators	Economical	Maximize voltage stability	[3]
	Grid Operators	Economical	Minimize cost of infrastructure	Authors.
	Grid Operators	Economical	Minimize transmission losses	[3]
	Grid Operators	Economical	Minimize resource utilization	Authors.
Transportation	End-user/Client	Social Welfare	Minimize individual agent’s travel time	Authors.
	End-user/Client	Social Welfare	Minimize cumulative travel time	Authors.
	End-user/Client	Social Welfare	Minimize delivery times	Authors.
	End-user/Client	Social Welfare	Minimize discomfort of drivers	[8]
	End-user/Client	Social Welfare	Maximize social welfare	[9]
	End-user/Client	Social Welfare	Maximize number of reached households	[10]
	End-user/Client	Environmental	Minimize energy consumption	Authors.
	End-user/Client	Environmental	Minimize greenhouse-gas emissions	Authors.
	End-user/Client	Environmental	Maximize share of electric vehicle-kilometers traveled	[11] (p. 166)
	Fleet Operator	Economical	Minimize infrastructure cost	Authors.
	Fleet Operator	Economical	Minimize investment cost including vehicles	Authors.
	Fleet Operator	Economical	Minimize number of charging stations	Authors.
	Fleet Operator	Economical	Maximize schedule length of buses	[12]
	Fleet Operator	Economical	Maximize the share of distance traveled electrically	[13]
	Fleet Operator	Economical	Minimize operation cost	Authors.
	Fleet Operator	Economical	Minimize total cost of ownership	[12]
	Fleet Operator	Environmental	Minimize greenhouse-gas emissions	Authors.
	Fleet Operator	Environmental	Minimize noise pollution	Authors.
	Fleet Operator	Environmental	Maximize electrically traveled range	[11]
	Vehicle Manufacturer	Economical	Minimize production costs	Authors.
	Vehicle Manufacturer	Environmental	Minimize resource utilization	Authors.

). Subsequently, we break it down to a list of stakeholders complemented by perspectives, objectives, and literature references if applicable. Some entries in Table 1 have been assumed as plausible by the authors and are marked correspondingly as authors’ contributions in the last column. As Table 1 suggests, there is a variety of possible objectives depending on what aspect of which stakeholder is considered. Each stakeholder can have one or more optimization objectives assigned. In reality, some optimization objectives might apply to several stakeholders at once. For the sake of simplicity, Table 1 shows only the most straightforward objective allocation in the author’s opinion. In addition, it is worth noting that objectives from different perspectives, e.g., social welfare, economic, and environmental, can exhibit correlating or negatively correlating character to other objectives.

One example of partly correlating objectives are reduced costs and reduced greenhouse-gas emissions. Up to a certain point, they go hand in hand due to the proportional character of the fuel consumed and the cost of fuel. When stakeholder objectives stop correlating or negatively correlate, common procedure dictates identifying the Pareto-Frontier, which represents a set of optimality points for a given problem. Yi et al., for example, optimized for maximizing the number of reachable households and minimizing the overall energy cost with charging infrastructure by identifying the Pareto optimal solution [10]. This bi objective optimization falls into the category of multi objective optimization. Abdalrahman et al. suggested a few procedures for dealing with multi-objective planning associated with transportation and power systems. They highlighted the following possibilities [3] (p. 14):

• converting different objectives to one via weighted sum of objectives,
• a hierarchical optimization model with layers, and
• a cross-entropy method.

Liu Z. et al. characterized the problem of planning charging infrastructure taking into account geographical information, construction, and running cost as a non-convex, non-linear, combinatorial optimization problem [14]. These types of problems become difficult to solve at a certain size. There is not much literature that tries to compensate this problem complexity by narrowing down to the application domain of fixed-route transportation systems. Therefore, this paper focuses on the optimization of a single objective: minimizing the monetary cost related to the operation of a vehicle fleet, including the construction of charging infrastructure where the fleet operation exhibits the character of a fixed-route transportation system. After presenting several modeling methodologies in Section 1.2, we explain the method in detail in Section 2.

1.2. Literature Overview of Modeling Methodologies

Before delving into the details of the optimization approach, we want to briefly address similar optimization methods in order to clarify differences between fixed-route Transportation Systems (frTS) and transportation systems that are not characterized by fixed routes.

He et al. analyzed the deployment of public charging stations on urban road networks. Their approach considers several routes performed by a single driver with the objective of minimizing travel time. They assumed different starting states-of-charge (SoC) of the vehicles and different risk aversions by the drivers. A minimum SoC was implemented as a hard constraint [15]. This approach makes sense for transportation systems without fixed routes, as the network utilization—manifested as traffic—is influenced by random behavior. In frTS with a private charging infrastructure, however, it is safe to assume that the risk of not finding a charging point is limited once the scheduling has been performed.

An early study regarding the planning of charging infrastructure was done by Hisatomo Hanabusa and Ryota Horiguchi in 2012. They formulated their problem so that the location planning of charging stations could be solved analytically based on a stochastic user equilibrium. However, they assumed a fixed number of charging stations with a given charging power. This approach can provide quick results but overly simplifies a real-case planning scenario where there are many question marks at the beginning [16].

In the use-case of electric buses, when analyzing if bus networks are suited for electrification, Rogge et al. argued that the focus needs to be on entire vehicle schedules rather than individual trips. This is because required battery capacity of the vehicles and charging power of the charging stations are heavily dependent on the operating schedule [17]. This can be analyzed with several methods stemming from the fields of logistics and operations research. One of the more general problem formulations is the facility location problem. Many demand coverage models developed for determining charging infrastructure construction are derived from the facility location problem. Abdalrahman et al. listed a few ways of approximating the demand for charging: estimation of stationary demand density at system nodes, estimation of spatial demand and mobility of battery electric vehicles (BEV), estimation of spatial-temporal demand, and considering uncertainty [3] (p. 10). Stemming from the flow-capturing location model, which tries to capture as many routes as possible by placing charging points along them, several more variants can be derived, for example, the multipath-refueling location model, which allows drivers to deviate from their original path to refuel more than once along the way [3] (p. 14). This optionality is not required in a frTS. In Table 2, we summarize a few of the methodologies from the literature. Deb et al. gave a good overview of modeling techniques: those considering the transportation network, the distribution network, and those considering both [18].

Table 2. Overview of modeling methodologies for vehicle fleets with the purpose of identifying suitable charging infrastructure.

Methodology	Remarks	Reference
Facility Location Problem	Generic problem in transportation research
Estimation of Stationary Demand Density at System Nodes	Estimates charging demand at homes, stores, working places	[3]
Estimation of Spatial Demand and Mobility of BEVs	Estimation is based on traffic flow models; demand can be covered along the routes	[3]
Estimation of Spatial-temporal Demand	Real-world GPS data or fleet schedules extend demand estimation to the time domain	[3]
Flow-Capturing Location Model	Captures as many routes as possible by placing charging points along them	[3]
Multipath-Refueling Location Model	Allows drivers to deviate from their original path and to refuel more than once along the way	[3]
Spatial-Temporal Model: Multistage Infrastructure Planning	Budgeted multistage planning	[7]
Queuing Model	Implemented for a taxi fleet with waiting areas	[19]
Bi Level Stochastic Queuing Models
Graph Theoretic Model

Table 2. Overview of modeling methodologies for vehicle fleets with the purpose of identifying suitable charging infrastructure.

Methodology	Remarks	Reference
Facility Location Problem	Generic problem in transportation research
Estimation of Stationary Demand Density at System Nodes	Estimates charging demand at homes, stores, working places	[3]
Estimation of Spatial Demand and Mobility of BEVs	Estimation is based on traffic flow models; demand can be covered along the routes	[3]
Estimation of Spatial-temporal Demand	Real-world GPS data or fleet schedules extend demand estimation to the time domain	[3]
Flow-Capturing Location Model	Captures as many routes as possible by placing charging points along them	[3]
Multipath-Refueling Location Model	Allows drivers to deviate from their original path and to refuel more than once along the way	[3]
Spatial-Temporal Model: Multistage Infrastructure Planning	Budgeted multistage planning	[7]
Queuing Model	Implemented for a taxi fleet with waiting areas	[19]
Bi Level Stochastic Queuing Models
Graph Theoretic Model

In a recent approach published in 2020, Jefferies et al. presented a charging infrastructure optimization framework for the purpose of a total cost of ownership evaluation of bus systems. Their work includes a greedy scheduling algorithm and relies on a genetic algorithm for finding a cost-optimized charging infrastructure solution. In most cases analyzed in their case study, opportunity charging resulted favorably compared to depot charging. Nevertheless, they emphasized the importance of a dedicated analysis of local bus systems in order to provide meaningful results. Jefferies et al. compared several bus scheduling methods for electric vehicle fleets from the literature. This comparison shows that there is no single method that considers all aspects listed by the authors, e.g., vehicle type restrictions per trip. The latter is actually oftentimes omitted in research approaches but represents an important constraint. Jefferies et al.’s contribution to this academic field is comprehensive. However, readers have to be conscious about some of their algorithmic approaches when assessing their results. The great problem complexity leads them to trim the problem formulation at some parts. Here, we will touch upon a few: In their scheduling approach, the dwell time at end of trip bus stops with a charging point is forced to be sufficiently long in order to potentially fully charge a respective bus after its previous trip. This seems like a rather strict constraint to be applied for all trips given that some will probably not require a charging process. This constraint is related to one of the objectives of maximizing bus schedule length. While this seems a good approach in order to minimize the number of buses required for the whole fleet operation, ultimately, it does not fulfill this goal. As Jefferies et al. correctly identified, a decrease in transportation demand during midday is responsible for this counterintuitive result. When maximizing schedule length, many vehicles remain idle during their scheduled midday service time. Further, in an attempt to foster electrification in the optimization, a constraint is implemented, which penalizes results where there is not at least one charging location per bus route. This type of constraint can accelerate the solving procedure. However, it favors an electrification of the transportation system and should be carefully implemented for not falsely discarding otherwise feasible results [12].

A very extensive literature review on mathematically and data-driven approaches regarding charging station planning was conducted by Lin et al. (see Chapter 2 of their work) [7] (p. 426). Phase-wise budget availability for the construction of charging infrastructure influenced the optimal long-term cost solution. As Lin et al. explained regarding their budget-based approach, increasing the individual budgets available in each stage can never worsen the optimization results. Contrarily, the additional degree of freedom of having increased budget availability in an early period allows for a potential early investment, which in turn benefits an electrified transportation system. Since it is just an optionality, a solver will not choose an early investment if it does not reduce overall costs. This further motivates the long-term character when planning optimization approaches [7] (p. 434).

Another very interesting result of Lin et al. is that optimal results can comprise charging stations that are intended only for a limited time period and in later stages remain unused. At first, this is counterintuitive and seems like a bad investment. Nonetheless, certain constellations, such as a specific rate of fleet electrification, render this a viable solution [7] (p. 441). Consequently, simply pursuing the objective of maximizing charging station usage is not a reasonable approach when attempting to minimize costs.

Xiang et al. introduced a methodology for economically planning charging stations. They pointed out that in previous studies, when planning on the basis of operation behavior, uncertainty was dealt with in an overly simplified manner. Traffic networks were planned for the worst-case scenario, which rarely would yield an optimal solution. In their framework, they model user patience, one attribute of driver behavior, to enable better results. In addition, they forced a minimum distance between two charging stations. In the author’s view, there should not be any necessity to implement this type of constraint beforehand; if any, the distance between charging stations should be an implicit result of the optimization [20] (p. 649).

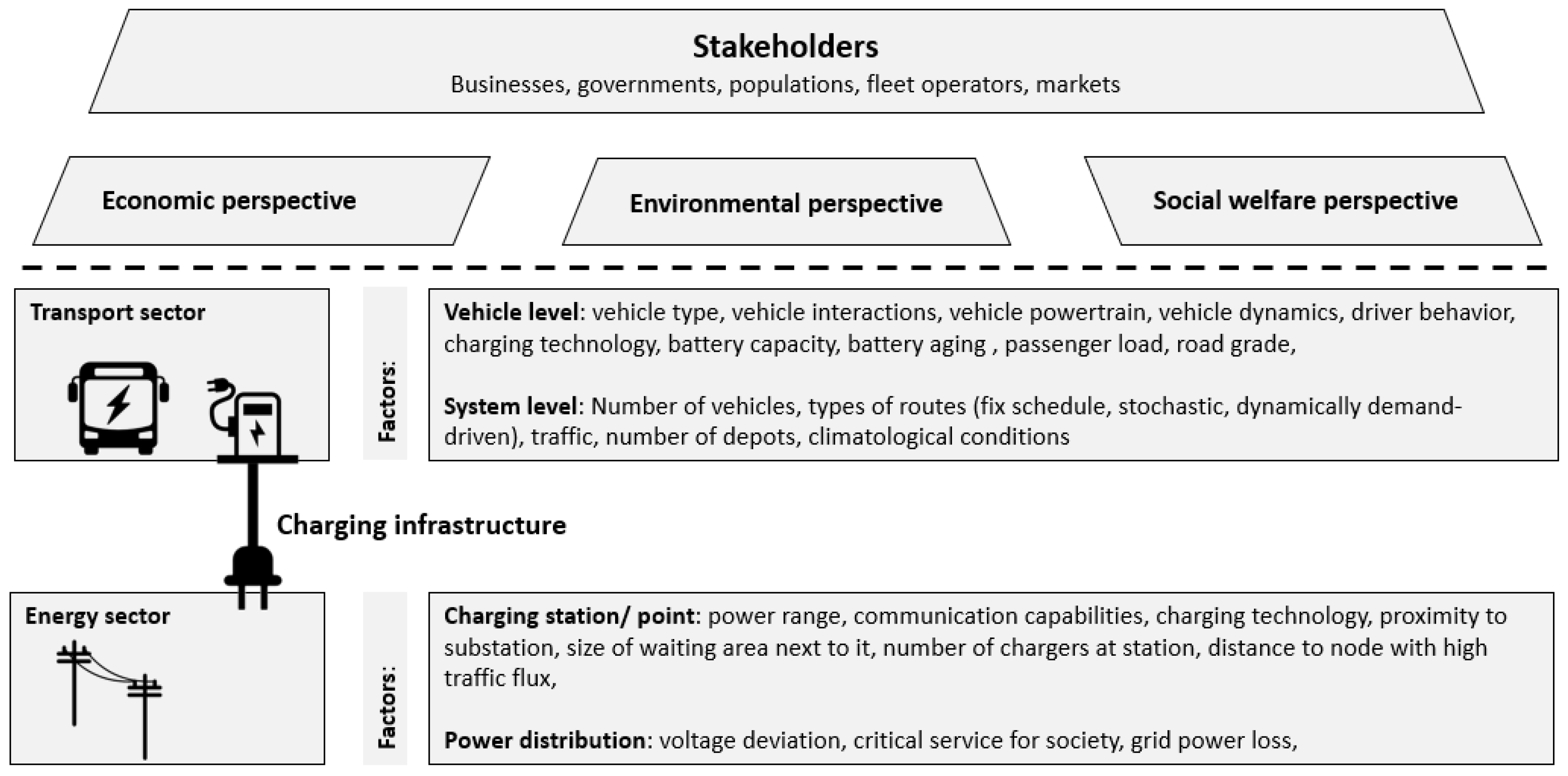
1.3. Impact Factors for the Planning of Charging Infrastructure

After discussing a few modeling methodologies, in the following, we highlight a few of the most influential impact factors for this type of problem. The factors taken into account—explicitly or implicitly—vary depending on the methodology. Mostly, they are implemented as constraints in the problem formulation. Figure 1 displays a collection of impact factors fitted in the bigger scope of stakeholders and their perspectives. Similar to Deb et al., we make a distinction between the transportation sector and the energy sector [18]. Alternatively, one can categorize influence factors according to Kunith et al. [4] (p. 2) into the following:

• infrastructure,
• technology related,
• operational planning,
• bus network, and
• energy consumption.

The relevance of the individual influence factors is strongly related to the modeling methodology. For example, the size of the waiting stations at stops, as cited by Abdalrahman et al., only has an impact on the result if queuing for charging facilities is modeled in the first place [3]. To expand a little further on some aspects of Figure 1, here are a few known relations from the literature regarding the transportation sector domain:

• In their comprehensive comparative investigation of heavy-duty vehicles performance, Giakoumis et al. found that vehicle velocity was the most influential parameter affecting performance and the whole operation of it. Further, the indicators stops-per-kilometer and relative positive acceleration correlate very well with fuel or energy consumption [21] (p. 16). Eßer et al. confirmed that vehicle consumption profiles strongly depend on the driving profiles [22].
• Impact factors on the consumption were also sorted in a graph by Gallet et al. in their study regarding a bus fleet [23] (p. 14). The three most influential parameters in decreasing order are: curb mass, auxiliary power, and rolling resistance.
• Regarding the fleet charging strategy, if overnight charging is chosen, this requires bigger battery capacities for the electric vehicles, according to Gallet et al. [23].
• Short distances between bus stops favor the use of electric buses because they are better suited for driving profiles with frequent start and stop situations than conventional buses [24] (p. 191).
• Kunith et al. stated that, in general, as concluded by previous studies, maximum charging power has a significant influence on the number of charging stations needed [4] (p. 9).
• Xylia et al. stated that the availability of higher charging powers favors the electrification of more bus routes [24] (p. 191), and shorter charging processes are required in inner-city areas because trips are shorter [25] (p. 780).
• Kunith et al. found that the extension of dwell time requires the adaptation of the operational schedule or the increase of the number of vehicles but relaxes the infrastructure requirements [4] (p. 9).
• Battery aging over time becomes a more restrictive constraint for the fleet management because with it the range of the vehicles decreases. These stricter constraints result in a higher fleet management effort for the fleet operator. However, it is seldom considered.

Regarding charging technologies, Lin et al. compared several technologies: wireless charging (stationary charging, quasi-dynamic wireless charging, dynamic wireless charging), plug in charging (fast charging, slow charging), and battery-swapping models. Dynamic wireless charging alleviates drawbacks, such as limited driving range and long charging times. However, Lin et al. stated that conductive plug-in technology is more suitable because this technology is more mature and has established itself in the market [7].

1.4. The Fixed-Route Transportation System Problem of Fleet Operators

We now want to narrow down to one specific application domain: fixed-route Transportation Systems (frTS). We think that, among published research papers, the charging infrastructure planning problem for this use-case has not yet been sufficiently analyzed in detail given the potential that can be drawn from its specific characteristics—mainly predictability. Therefore, it can be considered a research gap in this domain. Further, optimizing the charging infrastructure dedicatedly for a single fleet operator is an approach that adapts to business reality.

An issue regarding fleet electrification is the legal or ownership perspective. Assets like electric buses and depots are sometimes owned by several and different stakeholders, some public and some private. Optimization results for total cost of ownership cannot be directly translated into reality for most use-cases, as argued by Lin et al. [7] (p. 424).

One of the first questions for a fleet operator is if he wants to build a privately owned charging infrastructure or rely on public charging infrastructure. Kullman et al. stated that, when given the option, an EV fleet operator strategically preferred a private charging strategy due to uncertainty concerns. However, in their study, they developed policies which, theoretically, enable savings of up to 23% when using a combined public-private charging strategy. Therefore, where fleet operations allow it, a joint public utilization of charging infrastructure should be analyzed in order to reduce costs [26]. Their software tool is available online: [27]. Further, when considering the fixed-route vehicle charging problem, they claim their policies outperform the industry-standard routing strategy of depot charging (2020) [26].

Our focus, however, lies on conceiving a dedicated charging infrastructure for frTS. This means that the routes that have to be served by the vehicles are to be served periodically. Vazifeh et al. argued that human mobility in aggregate shows regularity, and therefore, near optimum solutions for single days of their genetic optimization approach are sufficiently robust and representative for other days as well [8]. This emergent regularity is exploited by fleet operators, e.g., a public transport company. For ease of planning, fixed, repeating bus schedules are determined for longer periods of time. The predictability of mobility demand renders the transportation systems themselves more predictable. Since many public transportation enterprises, distribution center operators, and waste management companies fall into the frTS category, we further investigate them. Additionally, we suppose there are many more use cases in the domain of supply chain management where recurring routes emerge because of business operations. This qualifies them as well for frTS charging infrastructure optimization.

To further expand on the implications when modeling frTS, Xylia et al. stated that bus networks are subject to more constraints in terms of where charging points can be placed when compared to general transportation systems [24] (p. 185). While additional constraints can either increase the computation time of optimizations because more mathematical operations have to be performed or decrease it because the solution space is narrowed down earlier, the fact that a transportation system is predictable allows for a simpler problem formulation and consequently reduces computation time.

As we will see in Section 2, we leverage the fact of knowing a great deal about fleet operation in advance. Exploiting the data we know in advance requires a versatile optimization framework. Pre-processing and pre-allocating consumption values derived from digital twins is a key step for reducing the problem size of the optimization.

The approach presented in the following chapter is dedicated for the long-term planning of charging infrastructure and fills the aforementioned research gap in the frTS domain. Emphasis lies on the gradual character of the charging infrastructure expansion, which mimics a real-world and continuous fleet electrification. This way, the transition itself to full electrification is not overlooked. This distinguishes our multi-period approach from a simpler one in which charging points can either be built once or not at all. This paper falls into the category of phase-wise optimization, like Lin et al.’s [7]. It is reasonable to pursue this kind of optimization since vehicle fleets composed of BEVs as well as internal combustion engine vehicles (ICEV) will be present for many years to decades or even permanently if a specific set of routes requires it.

2. Materials and Methods

The method presented in the following jointly considers the macroscopic and the microscopic view of frTS: the fleet management and the consumption profiles of individual vehicles respectively.

We rely on the optimization module Pyomo, which is written in Python. It enables an abstract problem formulation, which means that the same software architecture can be used for different use-cases.

The optimization method provides the possibility to define sequential periods. They are logically linked and emulate a real-world fleet electrification process. Lin et al. confirmed that the deployment of charging infrastructure is a step-by-step rollout process [7] (p. 425). Past studies perform the scheduling of electric bus fleets based on an a-priori agreed-upon charging strategy, mostly depot charging or end-terminus charging [7] (p. 426). The present approach is agnostic of any charging strategy. This means, fleet operators are not forced to prematurely constrain themselves to one charging strategy only. Rather, unique charging-point candidates (CPC) are defined in the depot and along routes. This leaves enough degrees of freedom for the optimization to choose individual charging points adequately. The charging strategy will emerge as part of the solution and might be different from period to period. Xylia et al. listed literature concerned with infrastructure optimization and found that many rely on a mixed-integer problem (MILP) formulation [24] (p. 185). Further, many of the methods listed in Table 2 rely on a MILP structure. This is because this type of problem formulation is well-suited for resource allocation problems.

In Section 2.1, we briefly elaborate on the overall structure of the optimization process. Section 2.2 focuses on the preparation steps for the charging infrastructure optimization comprising the consumption profiles and the activation of CPC. From here on, the activation of a CPC means that it is chosen by the optimization framework and actually constructed in the respective scenario. Then, in Section 2.3, the core optimization structure and process are explained in outline highlighting the general traits of the optimization framework implemented in Pyomo.

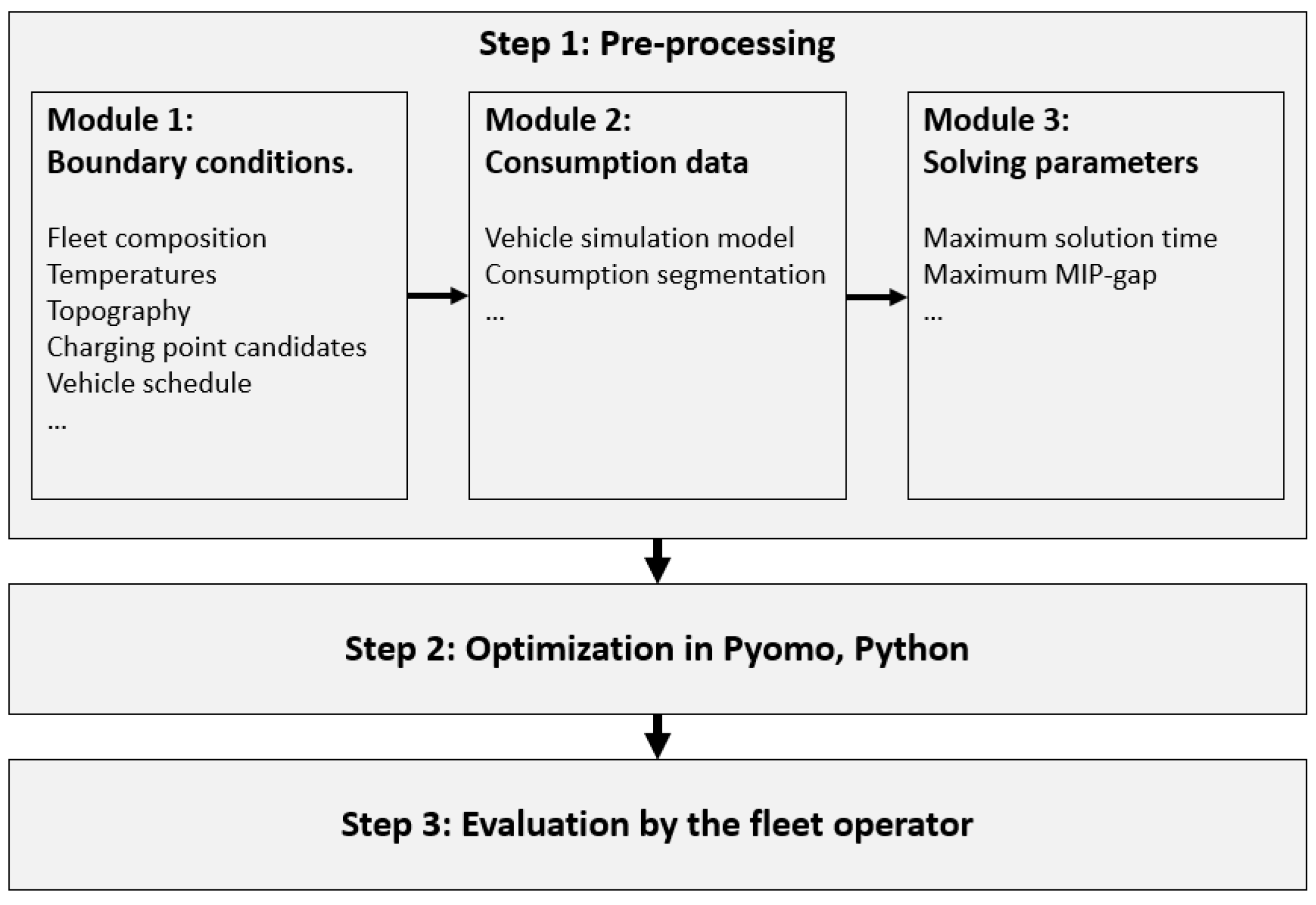
2.1. Optimization Framework Structure

The optimization framework structures the process into three steps. In step one, the pre-processing takes place. In step two, the optimization takes place, and in step three the results are evaluated by the fleet operator. Figure 2 shows the structure.

The first step is compartmentalized into three modules. In the first module, given a specific use-case, periodically recurring boundary conditions are aggregated. This includes yearly temperature values, topography, the schedule of the fleet in consideration, the fleet composition, and vehicle parameters. In each period, a number of representative days is chosen. Apart from considering the varying fleet operation of different days, different climatological boundary conditions can be simulated this way. Further, the CPC are defined. To avoid an overly large problem formulation, CPC have to be explicitly chosen. All other bus stops will be disregarded for the purpose of the charging infrastructure optimization. A similar procedure was implemented by Yi et al. A-priori reducing the size of the set of all CPC has a direct impact on the problem size. It can be done by taking into account power grid infrastructure constraints or the popularity of sites, they argued [10] (p. 29). This selection process strongly benefits from the knowledge of fleet operators about the sites and the schedules. A key criterion for defining a CPC is if at least one route passing it comprises a long enough dwell time at the respective bus stop. In terms of minutes, this is use-case specific and, therefore, is variable in the optimization framework. Mostly, end-terminus bus stops represent CPC because the dwell time at these stops is often longer. When choosing CPC, highly frequented bus stops should accommodate a substantial share of them, potentially allowing more electrified traffic to pass through an electrified transportation node. This is supported by Xylia et al.’s result that major public transport hubs show a higher concentration of chargers in their optimization of charging infrastructure [25] (p. 780). In the second module, GPS-velocity data are gathered in order to determine consumption profiles for all trips that are considered for the fleet operation. The velocity profiles are enhanced with elevation data, adhering to the methodology presented by Eßer et al. in [28]. This increases the accuracy of the consumption profiles. In longitudinal vehicle dynamics models—one for each vehicle type present in the fleet—the velocity profiles serve as input for determining the consumption profiles for the trips. Baouche et al. pursued a similar approach for characterizing energy needs of urban driving cycles in the Lyon Metropolitan Area [29]. As Xylia et al. stated, Khan and Clark confirmed that considering road grade and the type of driving cycle impacts the energy consumption by up to 30%. Further, considering traffic conditions can increase the energy consumption by up to 14%, which motivates a detailed analysis of consumption profiles [24] (p. 195). In their paper regarding driving cycle synthesis methods for city buses, Liu et al. concluded that considering the passenger load was of high importance when assessing the energy consumption [30] (p. 19). For now, we have not taken this into account in the second module since the data gathering in this issue involves great effort. All electric consumption profiles are segmented according to the bus stops along the trips. This allows determining the SoC drop of the battery of an electric bus between each pair of bus stops along a route. Then, the consumption profiles are discretized into equally long time windows for feeding them into the optimization. Depending on the problem complexity and the available hardware performance, different lengths for the discrete time steps can be tested. Adopting smaller time steps increases the problem size and negatively impacts the duration of the solving process. In the third module of step one, parameters regarding the solving process are to be defined. This comprises the type of solver, the maximum solving time, and others.

Adhering to the schematic in Figure 2, the second step of the optimization framework is where the optimization takes place. After concluding the solving process, in step three, the fleet operator can evaluate the results. In Section 2.4, a more detailed explanation of this step is given.

2.2. Preparing the Optimization: Pre-Processing

The optimization framework is fed with consumption data that are previously computed. This computation takes place for every trip a fleet operator serves. Further, all computations are performed once for every representative day for reproducing the impact of differing climate conditions. Route length alone as indicator for the estimation of energy demand is not enough, as concluded by Gallet et al. [23] (p. 11). The a-priori computation of the consumption values takes place for all types of vehicles that are available to a fleet operator. The optimization will then determine which vehicle is serving which trip. The underlying computation of the consumption values is implemented as a longitudinal vehicle dynamics simulation. Alternatively, energy consumption could be calculated according to DIN 70030, as done by Kunith et al. Using a standardized method ensures comparability. Nevertheless, our approach enables a much more detailed, real-world data-based optimization adjusted to specific use-cases [4] (p. 4).

For this study, a comprehensive set of trip data has been recorded for the use-case of the public transport fleet operator of Darmstadt, Germany. Before the GPS data—comprising the velocity profile among others—are fed to the optimization framework, the computed consumption values of electrified buses need to be assigned to the respective segments between the bus stops. Due to the incompleteness of vehicle parameters for the longitudinal vehicle dynamics models and real-world implications like delays, this process of consumption allocation to trip segments is currently not performed. Instead, the optimization framework operates based on specific consumption values for every vehicle type, e.g., kWh/km for BEVs and l/km for ICEVs. This is similar to the approach of Jefferies et al. since they computed their consumption profiles in a similar way [12].

The selection of CPC is jointly performed with the fleet operator. The cumulative dwell time at bus stops over one period serves as indicator for the eligibility as a CPC. This analysis is based on the bus schedule available in Darmstadt at the time. After this process, it becomes clear that the charging strategy will be strongly characterized by depot charging and end-terminus charging. This is due to the current fleet management: bus stops that are not at the end of a route are usually not intended for longer dwell times. Adhering to the research outcome of Lin et al. regarding the choice of charging technology, we stick to stationary plug-in conductive charging. Xylia et al. supported this argument, stating that wireless charging infrastructure leads to higher costs [25] (p. 779). Consequently, on-road charging technologies that would enable a dynamic charging process during a trip have not been considered.

2.3. Core Optimization Process

At this point, we want to highlight central aspects of the optimization problem. It has been formulated in Pyomo. As stated earlier, this framework pursues minimizing a single objective: the costs C_total related to the operation of a fleet, including the cost for its charging infrastructure. The total cost is the sum of the costs that arise in each period j over all periods considered, as can be seen in Equation (1):

$$C_{\mathrm{total}}={\displaystyle \sum }_{j=1}^{N_{\mathrm{periods}}}{C}_j$$

(1)

To reproduce the periodicity of the fleet operation, we set the duration of one period to one calendric year. The cost in any given period j is the sum of operation costs C_j,operation and investment costs C_j,investment.

$$C_{\mathrm{total}}={\displaystyle \sum }_{j=1}^{N_{\mathrm{periods}}}{C}_{j,\mathrm{operation}}+C_{j,\mathrm{investment}}$$

(2)

Investment costs are only incurred if charging infrastructure is constructed. The cost of charging infrastructure in a period is composed of the costs for activating CPC. These binary decisions of whether constructing a charging point p with a certain maximum charging power q are represented by the variable X_p, as can be seen in Equation (3). The potential costs are approximated a priori uniquely for every CPC p in the frTS. Since a detailed cost estimation considering the cost for charging modules, inverters, cables, etc., might be very time consuming, basing the cost on the maximum available charging power q is a reasonable first approach. In a real planning scenario, fleet operators and distribution system operators should be consulted because their knowledge in this regard is central for the estimation of potential costs. In Equation (3), α_p represents the monetary cost for activating CPC p. Note that, in the following, the index of the period j is omitted.

$$C_{\mathrm{investment}}={\displaystyle \sum }_{p=1}^{N_{\mathrm{charging}\mathrm{points}}}{X}_p·{\alpha }_p$$

(3)

Operational costs are computed once for every representative day t in a period j and then multiplied by its occurrence frequency f_t in that period. Additionally, the costs for the electricity contract for every charging point are added. Considering that a fleet operator is likely to sign a general agreement with a distribution system operator rather than separately doing so for each charging point, we consider the maximum aggregate power which is drawn in a certain period as the proxy for this share of the cost C_{power contract}.

$$C_{\mathrm{operation}}=C_{\mathrm{power}\mathrm{contract}}+{\displaystyle \sum }_{t=1}^{N_{\mathrm{representative}\mathrm{days}}}{C}_t·f_t$$

(4)

The cost C_{power contract} is determined via the decision variable Z_c that chooses exclusively one power contract from a set of available ones. Z_c determines the cost as in Equation (5) based on the price for a respective power contract δ_c. Further, Z_c constrains the maximum aggregate power that can be drawn in a single time step.

$$C_{\mathrm{power}\mathrm{contract}}={\displaystyle \sum }_{c=1}^{N_{\mathrm{power}\mathrm{contracts}}}{Z}_c·{\delta }_c$$

(5)

Since the routes are a result of the passenger transportation demand and, therefore, remain unchanged, they are not influenced by the optimization. Consequently, we are not considering the cost for personnel explicitly because it remains the same regardless of which type of vehicle is serving each trip. Maintenance costs are not considered because they usually represent only a fraction of total operation costs. Hence, the operation cost C_t on representative day t can be written as shown in Equations (6)–(8). The trip-dependent fuel consumption is given by Ω_k,v,r, where k references a trip, v a specific vehicle, and r the respective fuel consumed, e.g., diesel. The fuel price β_r is different for each fuel r. Y_v,k is a binary decision variable indicating if vehicle v serves trip k. It is worth noting that hybrid vehicles can be considered as well. In such a case, Ω_k,v,r will only represent a share of the total energy required for the vehicle operation. The electric energy is considered separately in Equation (8). Note that the index of the representative day t is omitted in Equations (7) and (8).

$$C_t=C_{t,\mathrm{fuel}}+C_{t,\mathrm{electricity}}$$

(6)

$$C_{\mathrm{fuel}}={\displaystyle \sum }_{v=1}^{N_{\mathrm{vehicles}}}{\displaystyle \sum }_{k=1}^{N_{\mathrm{trip}}}{\displaystyle \sum }_{r=1}^{N_{\mathrm{fuels}}}{Y}_{v,k}·{\Omega }_{k,v,r}·{\beta }_r$$

(7)

$$C_{\mathrm{electricity}}=\gamma ·{\displaystyle \sum }_{p=1}^{N_{\mathrm{charging}\mathrm{points}}}{\displaystyle \sum }_{ts=1}^{N_{\mathrm{time}\mathrm{step}}}{\displaystyle \sum }_{v=1}^{N_{\mathrm{vehicles}}}{\theta }_{p,ts,v}$$

(8)

θ_p,ts,v stands for the amount of energy charged to vehicle v at charging point p in time step ts. Summing up over all vehicles, time steps, and charging points, one gets the total amount of electric energy necessary for the fleet operation. The electricity price is assumed to remain constant over one representative day and is given by γ_t. The starting SoC is set by the fleet operator, and a constraint makes sure that the cumulative amount of electric energy stored in all the vehicles at the end of a representative day is equal to the one at the start of the day. This makes sure that vehicles are not completely drawn of their power, which would render them unprepared for the next day. One alternative is the implementation of vehicle-specific SoC constraints at the end of a representative day. However, this is too restrictive. We illustrate this with the following example: It might be the case that some vehicles arrive late and with a low SoC at the depot. Nonetheless, the fleet operation of the next day is not jeopardized because other sufficient vehicles are ready and charged.

After introducing the objective function formulation, now, we address some of the key constraints present in the optimization framework. Naturally, every trip encompassed in the bus schedule must be served. It follows that the number of vehicles serving a trip has to be equal to 1. The fleet composition itself is a fix input parameter provided by the fleet operator and has to be entered a priori for every period j. The SoC constraint during operation plays a critical role for the optimization. It is the core motivation for developing this framework. For ensuring the fleet operation, in every time step ts, there is a set of constraints for all electric vehicles limiting their SoC by a lower and upper bound, SoC_min and SoC_max, respectively. Additionally, the maximum SoC in each period is influenced by the battery aging. In every period, a percentage capacity loss is implemented to account for the battery aging. This effect propagates over the whole optimization time horizon and has a direct impact on the fleet operation. Depending on the battery cell technology, the user can set a suitable aging factor. Farmann et al. suggested coulomb counting as a simple method for estimating battery aging [31]. Implementing this renders the optimization problem very time consuming for the use-case of Darmstadt. Darmstadt represents a rather small problem compared to bigger cities. In fact, when implementing coulomb counting, the solving process had to be stopped because the RAM on the mid-end solving computer was exhausted. In order to not completely omit the influence of battery aging—especially long-term—a constant aging factor of 2% capacity loss per year is implemented. Equation (9) shows the SoC constraint for an electric vehicle ev in time step ts. This is valid on all representative days t and for all time-steps belonging to t, which we summarize in the set I_ts. The set of electric vehicles is denoted by I_ev.

$$So{C}_{\min }\le So{C}_{ts}\le So{C}_{\max }\forall ts\in I_{\mathrm{ts}}$$

(9)

SoC_min and SoC_max are percentage values entered prior to optimizing. The SoC_ts at time-step ts for an electric vehicle ev on a specific day is computed as follows:

$$So{C}_{ts}=So{C}_{\mathrm{Start}}-{\displaystyle \sum }_{cts=1}^{N_{\mathrm{cum}.\mathrm{time}\mathrm{steps}}}\left({\displaystyle \sum }_{k=1}^{N_{\mathrm{trip}}}{Y}_{ev,k}·{\epsilon }_{k,ev,cts}+{\displaystyle \sum }_{p=1}^{N_{\mathrm{charging}\mathrm{points}}}{\theta }_{p,cts,ev}\right)\forall ev\in I_{\mathrm{ev}}$$

(10)

where ε_k,ev,cts denotes the electric consumption that vehicle ev would have on trip k in each time-step cts, and N_{cum. time steps} denotes the highest number in the set of time-steps I_cts. The latter is comprised of ts and all previous time-steps on that representative day; e.g., in time step 3, the set becomes I_cts = [1, 2, 3]. As can be seen, the electric consumption is only considered if Y_ev,k is set to 1. As above, θ_p,cts,ev is the variable representing the electric energy throughput from charging point p to vehicle ev in time step cts.

Other constraints not stated here represent rather trivial logical conditions, e.g., a maximum number of one vehicle charging at a time at a charging point.

2.4. Evaluation of Optimization Results: Post Processing

Every solution to the charging infrastructure planning problem is comprised of the decisions of where and when CPC are activated and the corresponding fleet management for the representative days. These outcomes go hand in hand. A-posteriori changing the fleet management given a certain set of charging points will most likely not lead to minimum costs and eventually be infeasible. Figure 3 shows what the fleet management for a selection of vehicles on an exemplary representative day might look like. Note that the earliest time of departure is right after 3:30 in the morning, and the time discretization is 30 min.

As can be seen in the set of Equations (1)–(8), the costs are dependent on the fleet management. The solution set comprises the following information:

• at what point in time does there have to be an infrastructure expansion,
• with what maximum charging capacity should charging points be equipped, and
• what is the fleet management like on every single representative day?

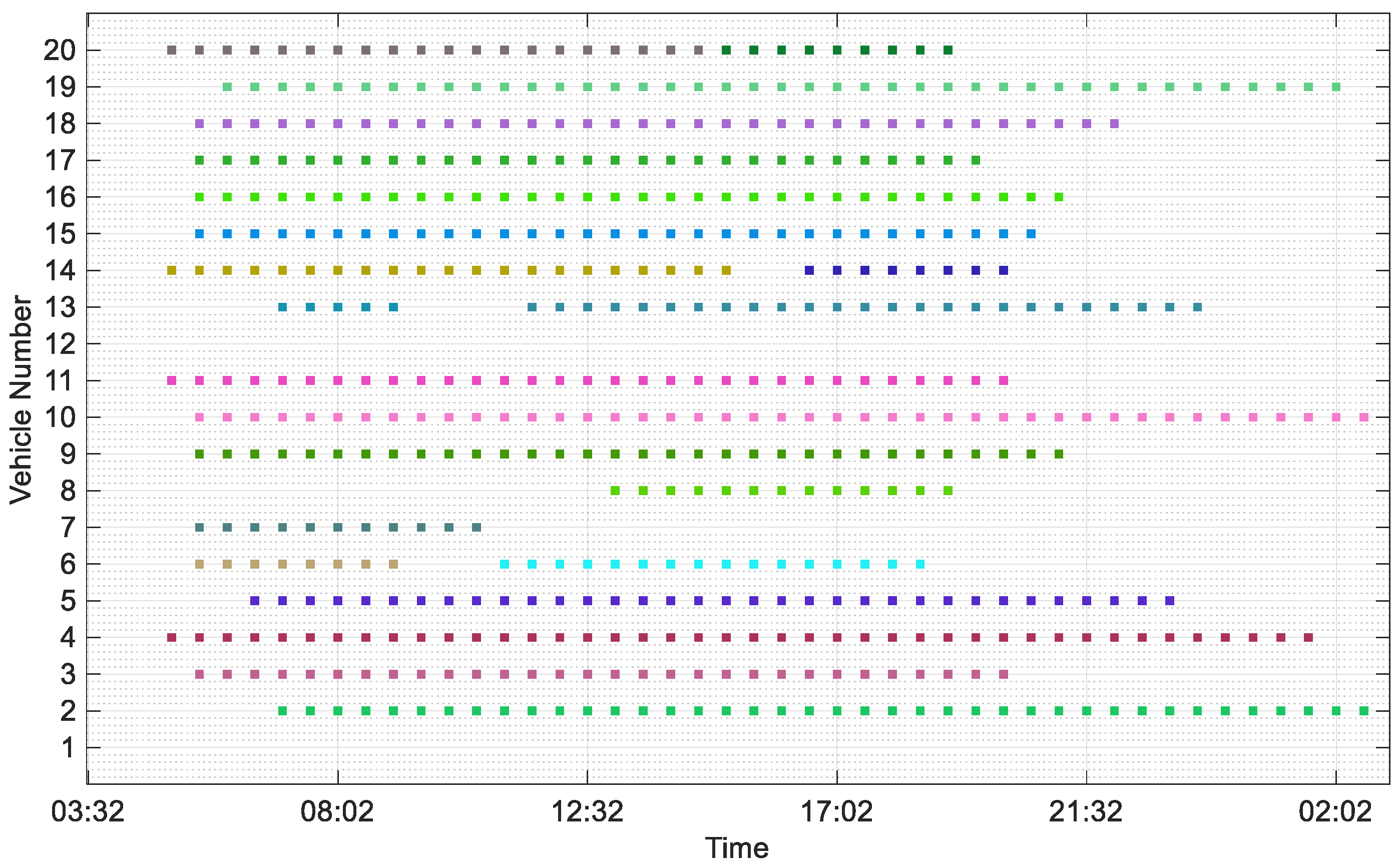
3. Results

Given the difficulty of comparing different use-cases due to their specificity, we compare different scenarios regarding one use-case only. The focus lies on the performance of the optimization process. The number of variables and constraints as well as the objective value for the different scenarios are compared as well. Processes are performed on a mid-end computer (16 GB RAM, i5 with 6 cores).

Even inside the scope of one use-case, the solution process duration can vary strongly. The reference data for our use-case are stated in

Table 3. Reference data for the optimization of the use-case of the public transport operator of Darmstadt.

Description	Unit	Value
Time horizon	Years	2
Number of reference days	-	4
Total number of vehicles	-	76
Number of unique trips	-	240
Underlying time discretization for the optimization	Minutes	30
Cost for electricity	€ per kWh	0.12
Cost for diesel fuel	€ per liter	1.05
Cost for activation of a CPC with 50 kW maximum charging power	€	7500
Cost for activation of a CPC with 150 kW maximum charging power	€	11,500
Annual cost for a power contract with 1 MW aggregate power	€	10,000
Annual cost for a power contract with 2 MW aggregate power	€	20,000

. Note that one unique trip can only be assigned to one representative day. On this basis, we analyze the effects of the fleet composition and the number of CPC on the overall problem size. Note that we have chosen an underlying time discretization of 30 min because higher time resolutions of 10- or 20-min intervals led to heavily increased problem complexities, which were not solvable in a reasonable amount of time with the given hardware.

The solution process is constituted by two subsequent phases: the model instantiation and the model solving process. In the status-quo scenario, all 76 vehicles are conventional diesel ICEVs, either standard or articulated ones. Obviously, there is no need for CPC. Instantiating the model takes 17 s, and solving it takes 6 s. The fleet management task is very simple in this case. Due to their lower specific consumption, standard diesel buses are assigned to the longest trips wherever possible rather than articulated buses that are heavier. The only constraint is that some trips require articulated buses to serve them because of a higher passenger transportation demand. This solution corresponds to the classical fleet management of conventional diesel buses. In the present use-case—as per past experience—a total number of 76 vehicles is required for the fleet operation. In Figure 4, scenarios 1 to 7 all represent a continuous electrification of the fleet from 5 out of 76 vehicles being electric in the first period to 25 in the second period. Five standard-length electric buses with a specific consumption of 100 kWh/100 km are complemented by 20 articulated electric buses with a specific consumption of 150 kWh/100 km. Figure 4 provides an overview of the scenarios in which the number of CPC initially selected in and outside the depot are varied. The CPC in the depot have a maximum power of 150 kW. On-route CPC are chosen from a set of 165 available bus stops based on the method mentioned in Section 2.2 and have either 50 kW or 150 kW maximum charging power. The five on-route CPC selected in scenarios 2, 4, and 6 are the same in all three scenarios. In scenario 7, the respective on-route bus stops are assigned two CPC instead of one. The time limit for solving the problem is set to 48 h and has been exhausted in scenarios 1 to 7 with the exception of the status-quo scenario.

As can be seen in Figure 4, increasing the number of CPC clearly increases the problem size, as expected. Conversely, a-priori reducing the problem size is, in fact, an important step for this type of problem. Therefore, holistic optimization approaches should always capitalize on this procedure. Additionally, one can observe that CPC outside of the depot have a much higher impact on the problem size as compared to CPC in the depot. In fact, scenarios 1 and 2 have the same total number of CPC, but scenario 2 generates nearly fourfold the number of variables and constraints because five CPC are on-route. Interestingly, scenarios 6 and 7 have the same number of variables and constraints. It appears that on-route CPC, which replace CPC of the depot, do only increase the overall problem size if they are placed at new bus stops. Since on-route CPC in scenarios 6 and 7 are assigned to the same five bus stops in both cases, it does not increase the problem size.

The optimization framework is tested with exemplary data of the public transport operator of Darmstadt. Since the gathering of real-world velocity data has not been performed for all trips, specific consumption values multiplied by trip distances are used on all trips to maintain overall consistency.

As stated earlier, battery aging is considered during the optimization. A constant aging factor of 2% annual capacity loss is implemented. This is a rough estimation because operation and consequentially battery cycling are not explicitly considered. The aging factor can be adapted depending on the battery technology and data availability in respective use-cases. The objective values found are in the range of 4.1 million € to 5 million €. However, these results are not indicative for which is the best solution among the scenarios. The relative mixed integer problem gap (MIP-gap) provides an indication of how far the optimization process is from finding an optimal solution (for more details, refer to the documentation of CPLEX [32]). As can be seen in Figure 4, the MIP-gaps of scenarios 1 to 7 increase from 7% to 24% with increasing problem size. Only in the status-quo scenario can we be certain of having found the actual optimal solution with an MIP-gap of 0%. The objective values of scenarios 3 to 7 are higher than scenarios 1 and 2. This is because of the limited solving time. Supposing a long enough solving time, it is safe to assume that the optimal objective values of scenarios 3 to 7 would be equally low or lower than in scenarios 1 and 2. This is because scenarios 3 to 7 expand on the optionality of scenarios 1 and 2, and therefore, optimal solutions of scenarios 1 and 2 are also possible solutions to scenarios 3 to 7.

4. Discussion

In this chapter, we first discuss general aspects of the optimization of charging infrastructure previously introduced in Section 1. Then, we highlight aspects of the present optimization framework that require further discussion.

The difficulty of allocating costs for power grid expansions to single stakeholders is seldom addressed in the literature. The fact that power grid expansions benefit many stakeholders in society raises the question of who should bear which share of the costs. When constructing private charging facilities, this becomes easier. The costs for the construction of a charging point can be directly allocated to the fleet operator issuing it. However, it might be the case that this construction involves laying cables over longer distances to reach the nearest substation of the grid. Then, other stakeholders can benefit from this power grid expansion in the future without having to pay for it, as only the first mover has to do so. In this context, it should be noted that the availability of electricity grid infrastructure suitable for powering electric vehicle fleets is strongly use-case dependent. Darmstadt, for example, has good prerequisites, so, in general, construction costs are lower, and allocating them solely to one fleet operator is more reasonable than in other use-cases.

In previous literature, many of the optimization approaches rely on non-essential constraints whose purpose is to speed up the optimization or force the electrification process. This has to be seen very critically. In some cases, it is difficult to assess to what extent this acceleration of the solution time influences the outcome of the optimization. Regarding the different charging strategies, one argument against a premature agreement on end-terminus charging is that end stops are usually not shared by many routes, so not many electric vehicles would profit from it [25] (p. 780). This is avoided by enabling the activation of each CPC individually. Further, the design of platform stations allows for degrees of freedom that are sometimes difficult to account for, as argued by Xylia et al. The ratio of layover zone to passenger-load zone and the number of charging connectors at a bus hub are just two examples [25] (p. 781). This requires a great effort if performed for all CPC. The importance of the design of the charging facilities is also highlighted by Dong et al. With their optimization for the siting and sizing of charging stations for taxis, which in part relies on a queuing model, they came to the conclusion that additional parking lots for queuing increases the usage ratio of single charging stations. In turn, this reduces the number of required charging stations in the overall system. It should be noted that this is not a frTS. However, the approach is based on the dwell pattern of a taxi fleet, which at a large scale is similar to schedule-based frTS [19]. Considering dynamic wireless charging processes would require a new optimization concept since it is currently not possible to fit this technology in the framework.

Regarding the scheduling of the vehicles and the underlying trips, the present optimization approach does not provide the possibility of adapting the routing of the vehicles. Theoretically, one could slightly adapt certain trips so that they pass by a charging point. This would increase the use-to-idle ratio of the charging points and alleviate infrastructure costs, as suggested by Xylia et al. in 2017 [25] (p. 780). Sticking to the domain of frTS has the advantage that the impact of the optimization results on other operations of a fleet operator is minimized; e.g., driver shifts do not have to be modified if routes stay the same. In fact, the planning of personnel represents a separate problem instance.

An aspect that can be improved in future works is a more detailed consideration of the charging process. The currently implemented linearization of charging processes ignores important effects. For example, the simplified charging processes do not account for power losses depending on the charging power, which would favor lower currents due to lower power losses. In this context, considering voltage curves when charging can be implemented as piece-wise linear functions. In addition, a discounting factor applied to the costs in every period can be useful for increasing the meaningfulness of the results by taking into account inflationary effects, similar to the approach of Xylia et al. [24]. Volume discounts that apply when reaching certain thresholds of charging points constructed can also be implemented. Further, electricity prices can be considered as price-vectors containing variable electricity prices for different times of the day. For the present paper, a time horizon of two periods has been set as reference parameter in Section 4. For a long-term consideration, the number of periods should be increased. The expected increase in the problem size should therefore be reduced by lowering the problem complexity or switching to a high-performance hardware.

In a final note regarding the discussion of the present optimization framework, it should be mentioned that it is currently not apt for bigger cities that have multiple depots.

5. Conclusions

We have presented an infrastructure optimization approach for frTS, which conceptually is capable of taking into account very detailed information of a fleet operator, including the degradation of the batteries of their vehicles.

The abstract problem formulation renders the framework very versatile for the application in different use-cases. The framework is conceived to allow maximum planning flexibility by enabling the activation of individual CPCs in any period, without having to follow a restrictive strategy, such as depot charging or opportunity charging only. Additional flexibility is granted thanks to different choices regarding the time discretization, e.g., 10-, 20-, or 30 min intervals. Unlike other comprehensive approaches in the literature that comprise a sequential combination of different methods and optimizations, the present paper integrates the whole planning procedure into one holistic optimization. We hereby avoid an empiric or rule based transfer of intermediate results between several separate sub optimizations. Additionally, the framework is not reliant on artificial constraints that might favor a specific outcome. As we have seen in Section 3, a cumulative solving time on a mid end computer of two weeks for seven scenarios has provided solutions with MIP gaps varying between 7% and 24%. We conclude that the method is reliable and functional. In order to find meaningful results that are indicative of best solutions with a higher confidence, computation time can be further increased.

The increased effort for gathering vehicle parametrizations and real-world velocity profiles and then pre-processing them were beyond the research time horizon. Consequently, similar to the optimization approach in [12], we assumed specific consumption values for the vehicles. The selection of CPC also implies great effort if performed thoroughly, for which the time horizon of this research was not sufficient. Nevertheless, at this point, we want to highlight the importance of the experiential knowledge of the respective fleet operators. One example is the regulatory environment regarding the modification of bus stops. This might impact the cost and, in some cases, render them unavailable for placing a charging point. Mostly, fleet operators will have an information basis regarding their set of bus stops. Additionally, when it comes to estimating the costs for constructing single charging points, the knowledge of distribution system operators plays a crucial role. The cost can be based on proxies like the distance to the next substation.

The question of how individual expansions of the electricity grid benefit society as a whole and how this should impact cost allocation in the use-cases remains unanswered. However, this consideration should play a role in every use-case, especially those where public funding is an option. A first step for giving fleet operators some perspective in this issue would be a sensitivity analysis on different constellations of shared costs. The financing counterpart might be a public institution or a private company.

Another option for reducing the impact of costs related to charging infrastructure is by leveraging it for providing grid balancing services or similar services that require an interface to otherwise disconnected batteries. Adhering to the use-case of a public transport operator, especially during the night, many idle vehicles can provide V2G services in aggregate. The monetary return for this service relativizes the upfront investment cost.

Parting from the reference use-case of this paper—a public fleet operator—the optimization framework can be integrated into a bigger enterprise optimization framework. In an iterative manner, different sets of routes can be assessed subsequently regarding their optimal complementary charging infrastructure.