Adaptive Model Predictive Control Including Battery Thermal Limitations for Fuel Consumption Reduction in P2 Hybrid Electric Vehicles
Abstract
:1. Introduction
2. Methodology
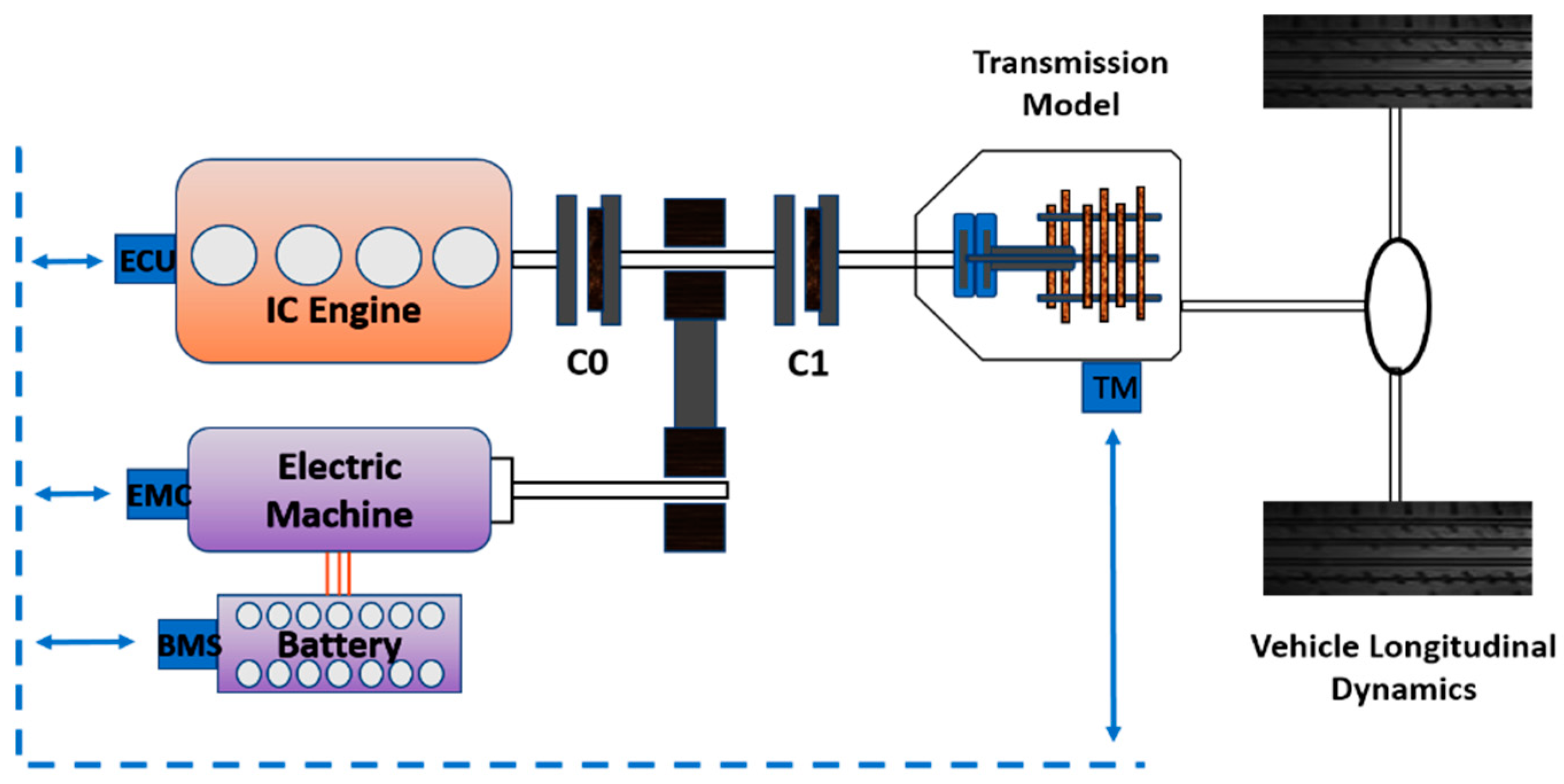
2.1. The Hybrid Electric Vehicle (HEV)
2.2. Vehicle Longitudinal Dynamic Model
2.3. Vehicle Transmission Model (Gearbox)
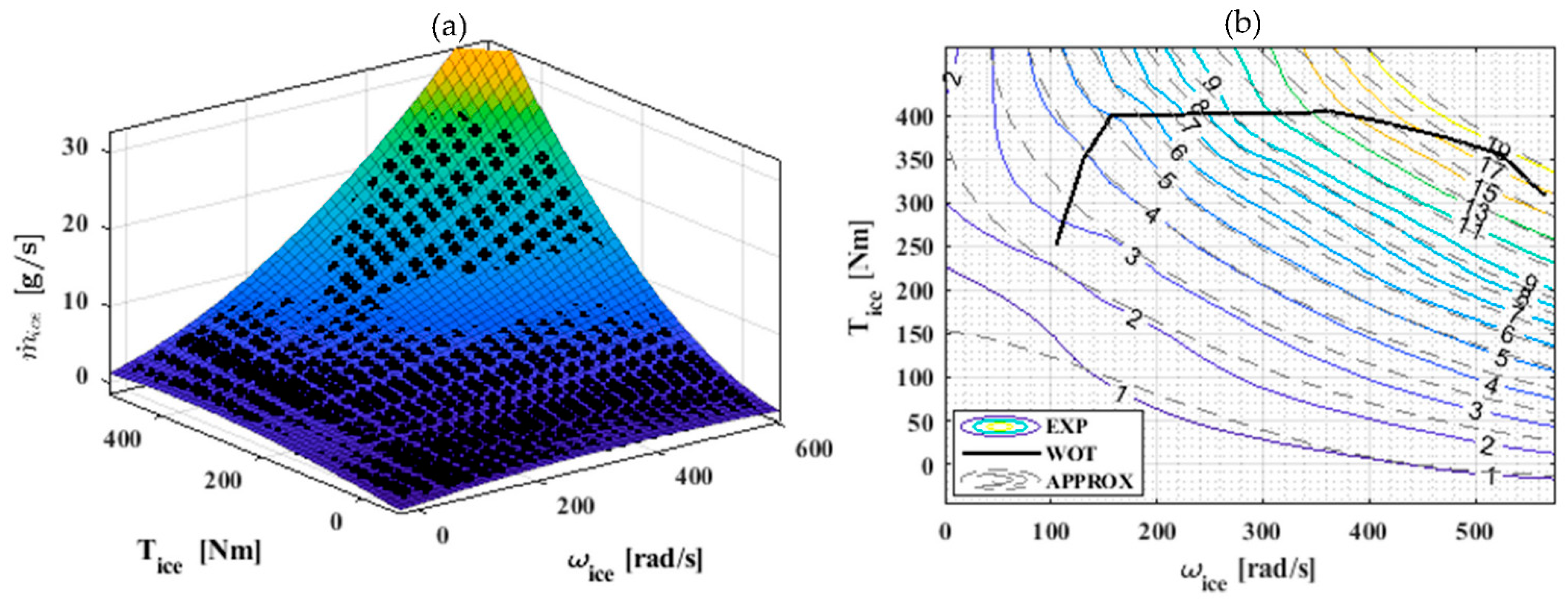
2.4. The Internal Combustion Engine
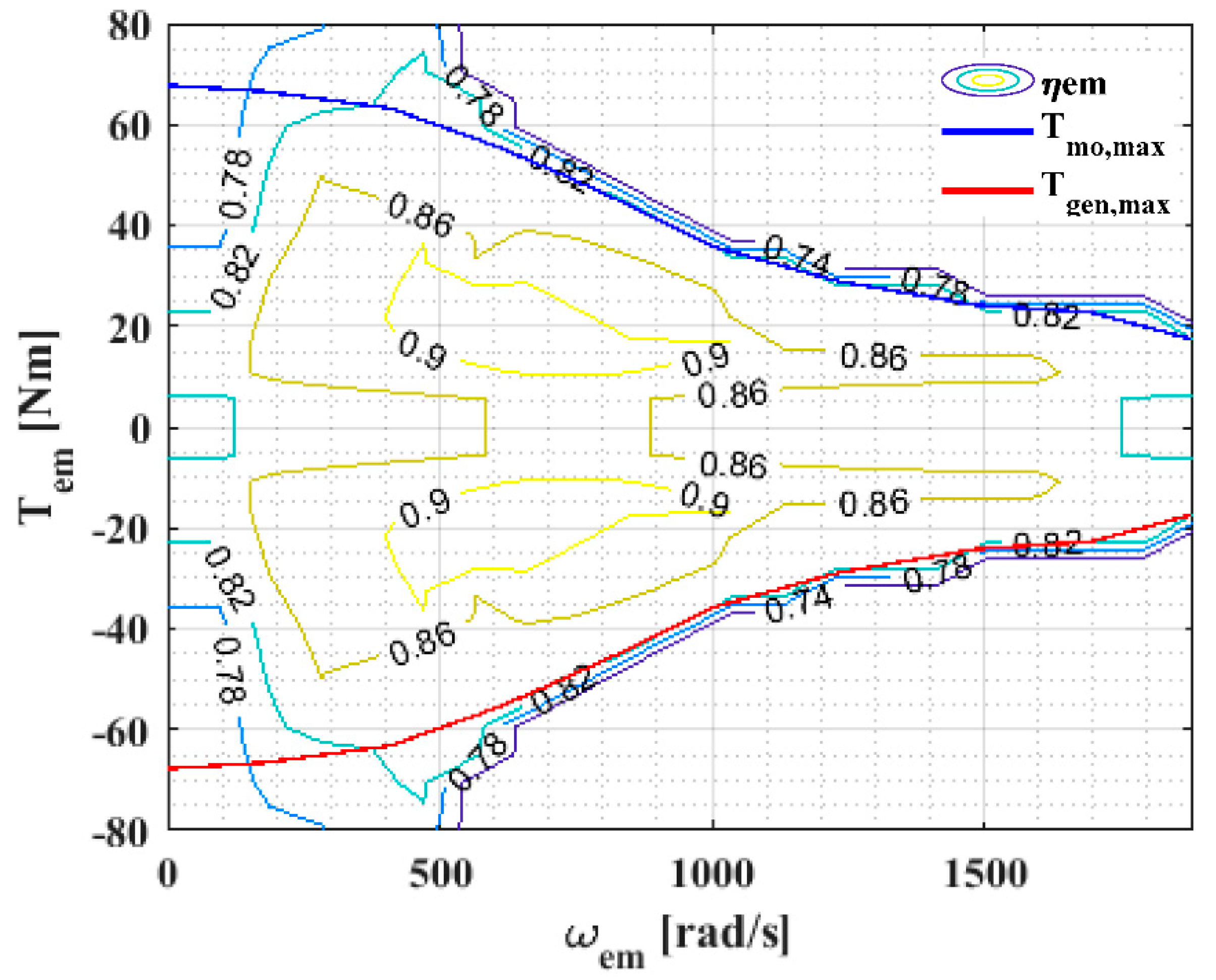
2.5. Electric Machine (EM)
2.6. Battery and Electro-Thermal Model
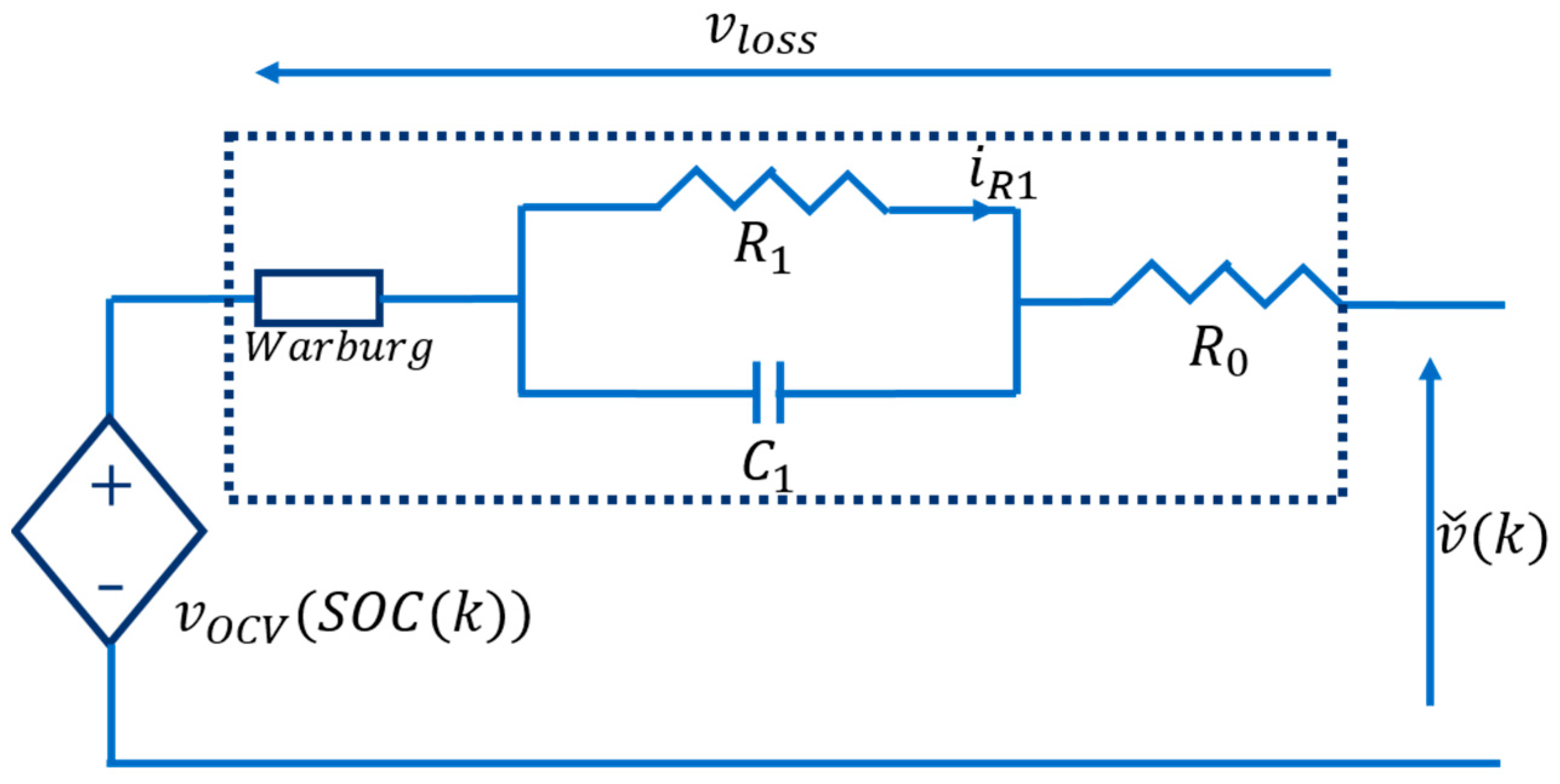
2.6.1. Cell Electric Model
2.6.2. Cell Thermal Model
2.7. Energy Management System (EMS) Strategy with Adaptive MPC
2.7.1. Design of an MPC Internal Prediction Model
2.7.2. Design of Standard MPC
2.7.3. Adaptive MPC
3. Results and Discussion
3.1. Fuel Consumption Computation Based on On/Off Model
3.2. Adaptive MPC Strategy Results
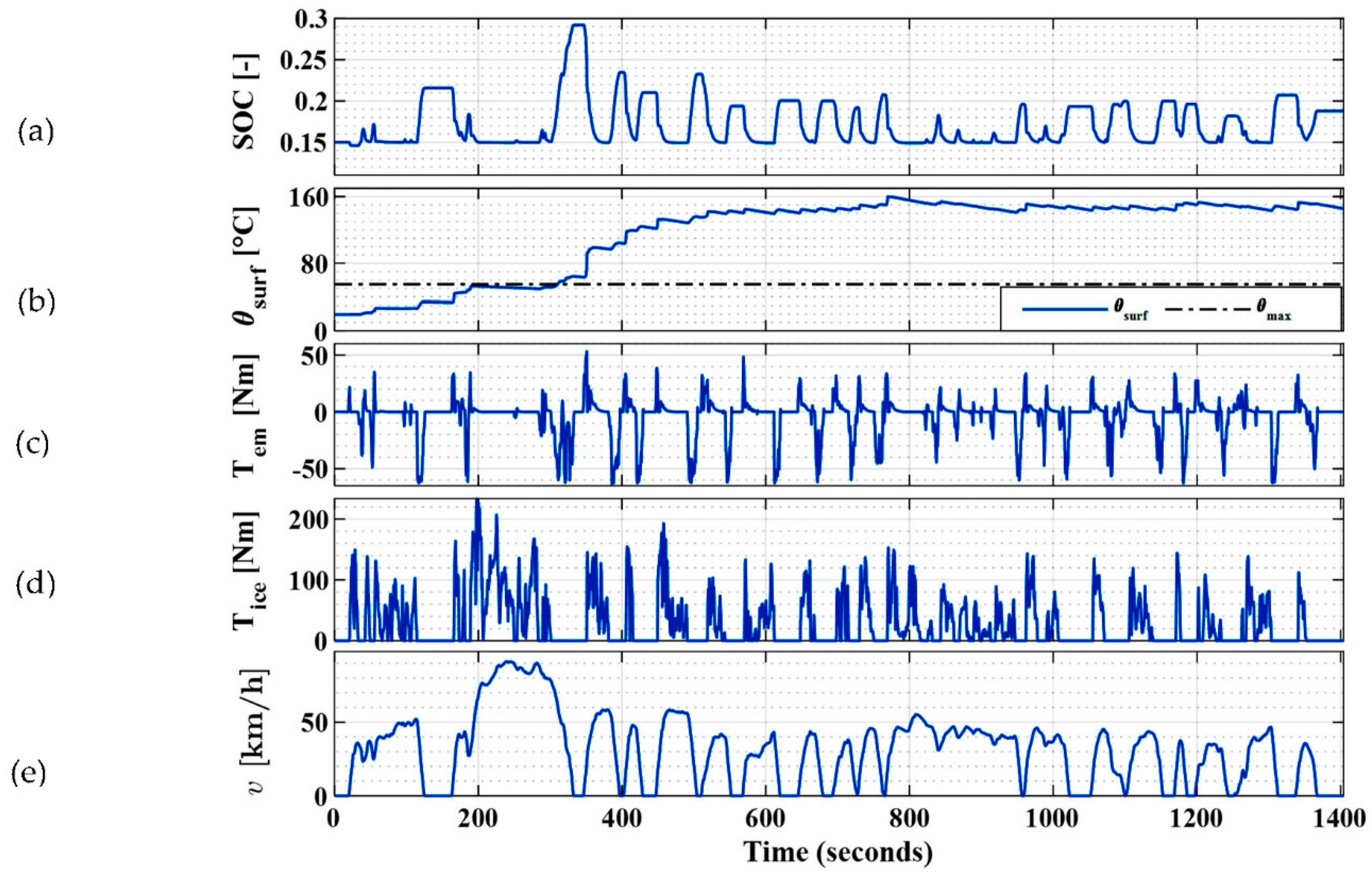
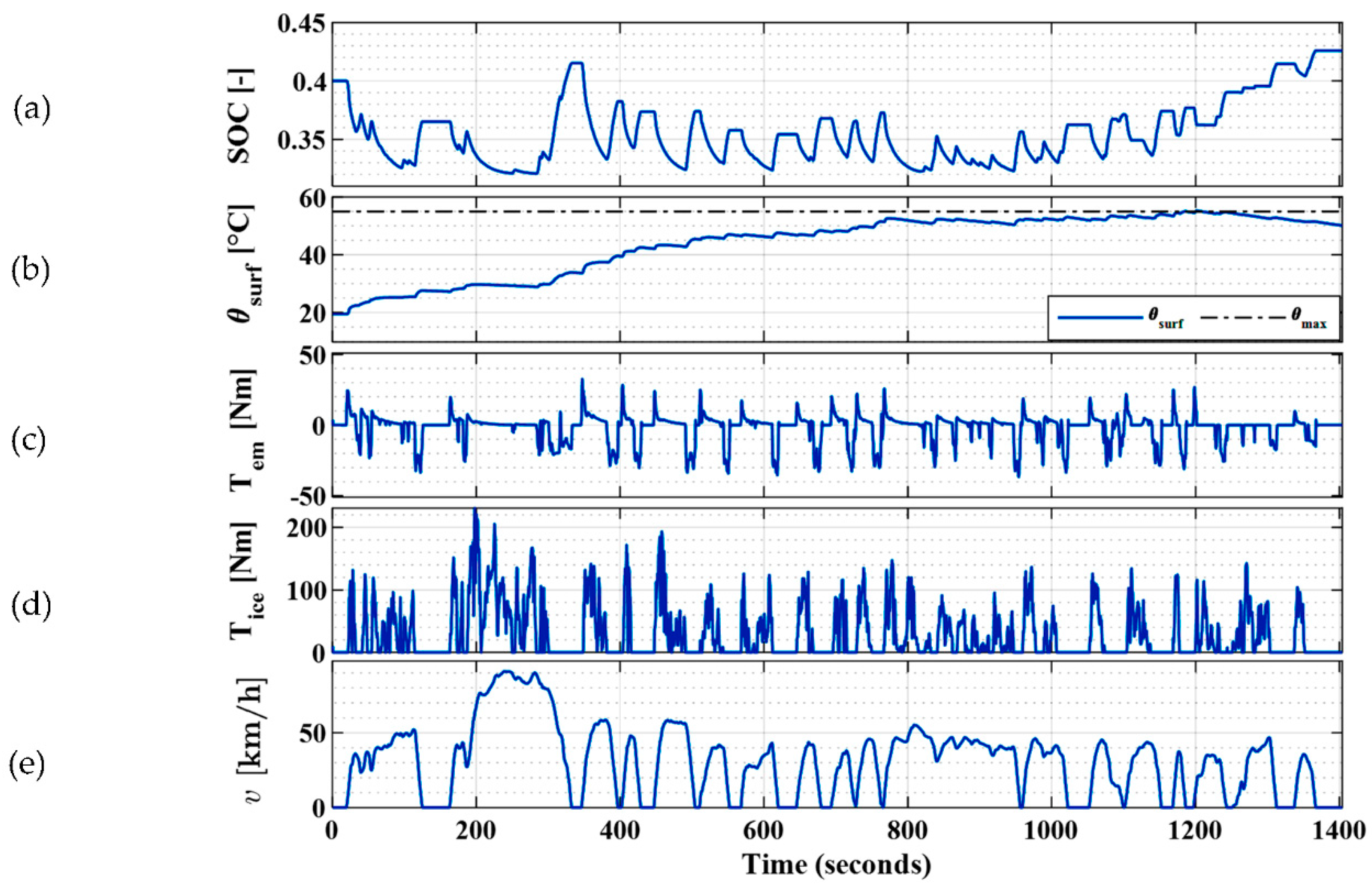
3.2.1. No Thermal Limitation Constraint
3.2.2. Increased Prediction Horizon with No Thermal Limitation Constraint
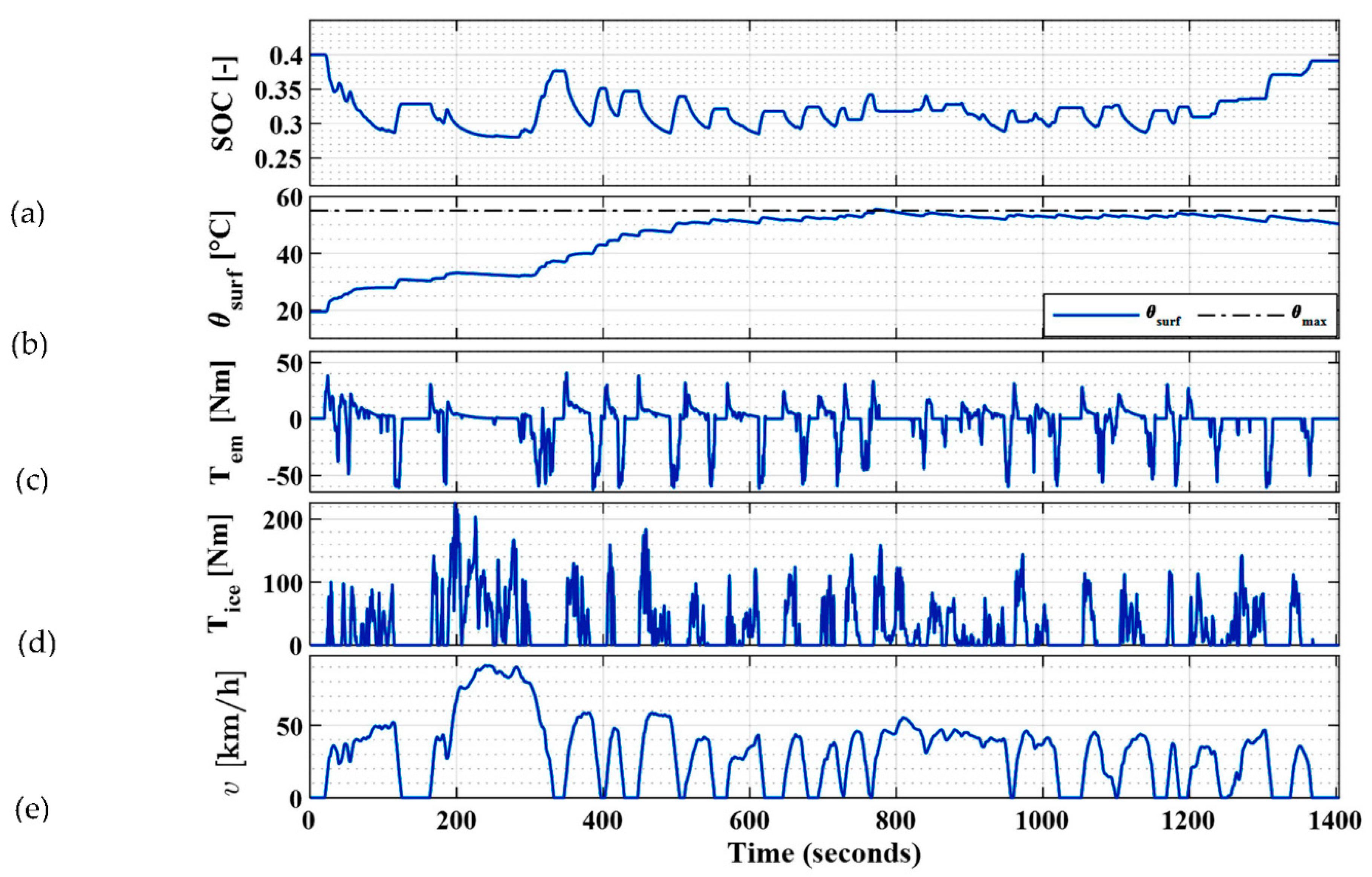
3.2.3. Introducing Thermal Limitation Constraint
3.2.4. Battery Thermal Enhancement with Battery Sizing
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chung, I.; Kang, H.; Park, J.; Lee, J. Fuel Economy Improvement Analysis of Hybrid Electric Vehicle. Int. J. Automot. Technol. 2019, 20, 531–537. [Google Scholar] [CrossRef]
- de Almeida, S.C.A.; Kruczan, R. Effects of Drivetrain Hybridization on Fuel Economy, Performance and Costs of a Fuel Cell Hybrid Electric Vehicle. Int. J. Hydrog. Energy 2021, 46, 39404–39414. [Google Scholar] [CrossRef]
- Ehsani, M.; Gao, Y.; Emadi, A. (Eds.) Modern Electric, Hybrid Electric, and Fuel Cell Vehicles: Fundamentals, Theory, and Design, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017; ISBN 9781315219400. [Google Scholar]
- Emadi, A. (Ed.) Advanced Electric Drive Vehicles; CRC Press: Boca Raton, FL, USA, 2014; ISBN 9781315215570. [Google Scholar]
- Zhuang, W.; Li (Eben), S.; Zhang, X.; Kum, D.; Song, Z.; Yin, G.; Ju, F. A Survey of Powertrain Configuration Studies on Hybrid Electric Vehicles. Appl. Energy 2020, 262, 114553. [Google Scholar] [CrossRef]
- Tran, D.-D.; Vafaeipour, M.; El Baghdadi, M.; Barrero, R.; Van Mierlo, J.; Hegazy, O. Thorough State-of-the-Art Analysis of Electric and Hybrid Vehicle Powertrains: Topologies and Integrated Energy Management Strategies. Renew. Sustain. Energy Rev. 2020, 119, 109596. [Google Scholar] [CrossRef]
- García, A.; Monsalve-Serrano, J.; Martínez-Boggio, S.; Wittek, K. Potential of Hybrid Powertrains in a Variable Compression Ratio Downsized Turbocharged VVA Spark Ignition Engine. Energy 2020, 195, 117039. [Google Scholar] [CrossRef]
- Sieg, C.; Küçükay, F. Benchmarking of Dedicated Hybrid Transmissions. Vehicles 2020, 2, 100–125. [Google Scholar] [CrossRef] [Green Version]
- Castellazzi, L.; Ruzimov, S.; Bonfitto, A.; Tonoli, A.; Amati, N. A Method for Battery Sizing in Parallel P4 Mild Hybrid Electric Vehicles. SAE Int. J. Electrified Veh. 2021, 11, 14-11-01-0008. [Google Scholar] [CrossRef]
- Whittingham, M.S. Materials Challenges Facing Electrical Energy Storage. MRS Bull. 2008, 33, 411–419. [Google Scholar] [CrossRef] [Green Version]
- Nitta, N.; Wu, F.; Lee, J.T.; Yushin, G. Li-Ion Battery Materials: Present and Future. Mater. Today 2015, 18, 252–264. [Google Scholar] [CrossRef]
- Sanjarbek, R.; Mavlonov, J.; Mukhitdinov, A. Analysis of the Powertrain Component Size of Electrified Vehicles Commercially Available on the Market. Commun. Sci. Lett. Univ. Zilina 2022, 24, B74–B86. [Google Scholar] [CrossRef]
- Wang, Q.; Jiang, B.; Li, B.; Yan, Y. A Critical Review of Thermal Management Models and Solutions of Lithium-Ion Batteries for the Development of Pure Electric Vehicles. Renew. Sustain. Energy Rev. 2016, 64, 106–128. [Google Scholar] [CrossRef]
- An, Z.; Jia, L.; Ding, Y.; Dang, C.; Li, X. A Review on Lithium-Ion Power Battery Thermal Management Technologies and Thermal Safety. J. Therm. Sci. 2017, 26, 391–412. [Google Scholar] [CrossRef]
- Zhou, B.; Rezaei, A.; Burl, J. Effect of Battery Temperature on Fuel Economy and Battery Aging When Using the Equivalent Consumption Minimization Strategy for Hybrid Electric Vehicles; SAE Technical Paper. No. 2020-01-1188; SAE International: Warrendale, PA, USA, 2020. [Google Scholar] [CrossRef]
- Du, R.; Hu, X.; Xie, S.; Hu, L.; Zhang, Z.; Lin, X. Battery Aging- and Temperature-Aware Predictive Energy Management for Hybrid Electric Vehicles. J. Power Sources 2020, 473, 228568. [Google Scholar] [CrossRef]
- Yakhshilikova, G.; Ezemobi, E.; Ruzimov, S.; Tonoli, A. Battery Sizing for Mild P2 HEVs Considering the Battery Pack Thermal Limitations. Appl. Sci. 2022, 12, 226. [Google Scholar] [CrossRef]
- Conte, F.V. Battery and Battery Management for Hybrid Electric Vehicles: A Review. Elektrotech. Inftech. 2006, 123, 424–431. [Google Scholar] [CrossRef]
- Sundström, O.; Guzzella, L.; Soltic, P. Optimal Hybridization in Two Parallel Hybrid Electric Vehicles Using Dynamic Programming. IFAC Proc. Vol. 2008, 41, 4642–4647. [Google Scholar] [CrossRef] [Green Version]
- Neffati, A.; Caux, S.; Fadel, M. Fuzzy switching of fuzzy rules for energy management in HEV. IFAC Proc. Vol. 2012, 45, 663–668. [Google Scholar] [CrossRef]
- Tie, S.F.; Tan, C.W. A Review of Energy Sources and Energy Management System in Electric Vehicles. Renew. Sustain. Energy Rev. 2013, 20, 82–102. [Google Scholar] [CrossRef]
- Ahmadi, S.; Hosseinpour, A.; Bathaee, S.M. Improving Fuel Economy and Performance of a Fuel-Cell Hybrid Electric Vehicle (Fuel-Cell, Battery, and Ultra-Capacitor) Using Optimized Energy Management Strategy. Energy Convers. Manag. 2018, 160, 74–84. [Google Scholar] [CrossRef]
- Geng, B.; Mills, J.K.; Sun, D. Energy Management Control of Microturbine-Powered Plug-In Hybrid Electric Vehicles Using the Telemetry Equivalent Consumption Minimization Strategy. IEEE Trans. Veh. Technol. 2011, 60, 4238–4248. [Google Scholar] [CrossRef]
- Rezaei, A.; Burl, J.B.; Zhou, B. Estimation of the ECMS Equivalent Factor Bounds for Hybrid Electric Vehicles. IEEE Trans. Control. Syst. Technol. 2018, 26, 2198–2205. [Google Scholar] [CrossRef]
- Sciarretta, A.; Back, M.; Guzzella, L. Optimal Control of Parallel Hybrid Electric Vehicles. IEEE Trans. Control. Syst. Technol. 2004, 12, 352–363. [Google Scholar] [CrossRef]
- Musardo, C.; Rizzoni, G.; Guezennec, Y.; Staccia, B. A-ECMS: An Adaptive Algorithm for Hybrid Electric Vehicle Energy Management. Eur. J. Control. 2005, 11, 509–524. [Google Scholar] [CrossRef]
- Rahmeh, H.; Bonfitto, A.; Ruzimov, S. Fuzzy Logic vs Equivalent Consumption Minimization Strategy for Energy Management in P2 Hybrid Electric Vehicles. In Proceedings of the ASME 2020 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Virtual, Online, 17–19 August 2020. [Google Scholar]
- Paganelli, G.; Delprat, S.; Guerra, T.M.; Rimaux, J.; Santin, J.J. Equivalent Consumption Minimization Strategy for Parallel Hybrid Powertrains. In Proceedings of the Vehicular Technology Conference IEEE 55th Vehicular Technology Conference. VTC Spring 2002 (Cat. No.02CH37367), Birmingham, AL, USA, 6–9 May 2002; Volume 4, pp. 2076–2081. [Google Scholar]
- Xie, S.; Sun, F.; He, H.; Peng, J. Plug-In Hybrid Electric Bus Energy Management Based on Dynamic Programming. Energy Procedia 2016, 104, 378–383. [Google Scholar] [CrossRef]
- Tribioli, L.; Cozzolino, R.; Chiappini, D.; Iora, P. Energy Management of a Plug-in Fuel Cell/Battery Hybrid Vehicle with on-Board Fuel Processing. Appl. Energy 2016, 184, 140–154. [Google Scholar] [CrossRef]
- Chen, Z.; Mi, C.C.; Xiong, R.; Xu, J.; You, C. Energy Management of a Power-Split Plug-in Hybrid Electric Vehicle Based on Genetic Algorithm and Quadratic Programming. J. Power Sources 2014, 248, 416–426. [Google Scholar] [CrossRef]
- He, H.; Zhang, J.; Li, G. Model Predictive Control for Energy Management of a Plug-in Hybrid Electric Bus. Energy Procedia 2016, 88, 901–907. [Google Scholar] [CrossRef] [Green Version]
- Borhan, H.; Vahidi, A.; Phillips, A.M.; Kuang, M.L.; Kolmanovsky, I.V.; Di Cairano, S. MPC-Based Energy Management of a Power-Split Hybrid Electric Vehicle. IEEE Trans. Control. Syst. Technol. 2012, 20, 593–603. [Google Scholar] [CrossRef]
- He, H.; Wang, Y.; Han, R.; Han, M.; Bai, Y.; Liu, Q. An Improved MPC-Based Energy Management Strategy for Hybrid Vehicles Using V2V and V2I Communications. Energy 2021, 225, 120273. [Google Scholar] [CrossRef]
- Nüesch, T.; Elbert, P.; Flankl, M.; Onder, C.; Guzzella, L. Convex Optimization for the Energy Management of Hybrid Electric Vehicles Considering Engine Start and Gearshift Costs. Energies 2014, 7, 834–856. [Google Scholar] [CrossRef] [Green Version]
- Cairano, S.D.; Bernardini, D.; Bemporad, A.; Kolmanovsky, I. Stochastic MPC With Learning for Driver-Predictive Vehicle Control and Its Application to HEV Energy Management. IEEE Trans. Control. Syst. Technol. 2014, 22, 1018–1031. [Google Scholar] [CrossRef]
- Vadamalu, R.S.; Beidl, C. Explicit MPC PHEV Energy Management Using Markov Chain Based Predictor: Development and Validation at Engine-In-The-Loop Testbed. In Proceedings of the 2016 European Control Conference (ECC), Aalborg, Denmark, 29 June–1 July 2016; pp. 453–458. [Google Scholar] [CrossRef]
- Kvasnica, M. Implicit vs Explicit MPC—Similarities, Differences, and a Path Owards a Unified Method. In Proceedings of the 2016 European Control Conference (ECC), Aalborg, Denmark, 29 June–1 July 2016; p. 603. [Google Scholar]
- Borhan, H.A.; Zhang, C.; Vahidi, A.; Phillips, A.M.; Kuang, M.L.; Di Cairano, S. Nonlinear Model Predictive Control for Power-Split Hybrid Electric Vehicles. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; pp. 4890–4895. [Google Scholar]
- Non-Linear Model Predictive Control of a Power-Split Hybrid Electric Vehicle Influence of Conclusion of Powertrain Dynamics. Available online: https://www.esteco.com/modefrontier/non-linear-model-predictive-control-power-split-hybrid-electric-vehicle-influence-concl (accessed on 25 November 2021).
- Dhar, A.; Bhasin, S. Adaptive MPC for Uncertain Discrete-Time LTI MIMO Systems with Incremental Input Constraints. IFAC-PapersOnLine 2018, 51, 329–334. [Google Scholar] [CrossRef]
- Bujarbaruah, M.; Zhang, X.; Rosolia, U.; Borrelli, F. Adaptive MPC for Iterative Tasks. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami, FL, USA, 17–19 December 2018; pp. 6322–6327. [Google Scholar]
- Wipke, K.B.; Cuddy, M.R.; Burch, S.D. ADVISOR 2.1: A User-Friendly Advanced Powertrain Simulation Using a Combined Backward/Forward Approach. IEEE Trans. Veh. Technol. 1999, 48, 1751–1761. [Google Scholar] [CrossRef]
- Energy Systems D3 2016 Mazda CX9 | Argonne National Laboratory. Available online: https://www.anl.gov/es/energy-systems-d3-2016-mazda-cx9 (accessed on 5 January 2022).
- US EPA. Combining Data into Complete Engine ALPHA Maps. Available online: https://www.epa.gov/vehicle-and-fuel-emissions-testing/combining-data-complete-engine-alpha-maps (accessed on 5 January 2022).
- Specifications for NCR 18650 GA Sanyo Lithium-Ion Battery. Available online: https://www.hurt.com.pl/prods/bat/_li_ion/ncr18650ga.pdf (accessed on 5 January 2022).
- Battery Management Systems, Volume 2: Equivalent-Circuit Methods. Available online: http://mocha-java.uccs.edu/BMS2/ (accessed on 8 January 2022).
- Variable-Order Equivalent Circuit Modeling and State of Charge Estimation of Lithium-Ion Battery Based on Electrochemical Impedance Spectroscopy. Available online: https://www.researchgate.net/publication/348950509_Variable-Order_Equivalent_Circuit_Modeling_and_State_of_Charge_Estimation_of_Lithium-Ion_Battery_Based_on_Electrochemical_Impedance_Spectroscopy (accessed on 16 November 2021).
- Dahbi, M.; Komaba, S. Chapter 16—Fluorine Chemistry for Negative Electrode in Sodium and Lithium Ion Batteries. In Advanced Fluoride-Based Materials for Energy Conversion; Nakajima, T., Groult, H., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 387–414. ISBN 9780128006795. [Google Scholar]
- Wang, W.; Wei, X.; Choi, D.; Lu, X.; Yang, G.; Sun, C. Chapter 1—Electrochemical Cells for Medium- and Large-Scale Energy Storage: Fundamentals. In Advances in Batteries for Medium and Large-Scale Energy Storage; Woodhead Publishing Series in Energy; Menictas, C., Skyllas-Kazacos, M., Lim, T.M., Eds.; Woodhead Publishing: Thorston, UK, 2015; pp. 3–28. ISBN 978-1-78242-013-2. [Google Scholar]
- Cui, X.; Zeng, J.; Zhang, H.; Yang, J.; Qiao, J.; Li, J.; Li, W. Optimization of the Lumped Parameter Thermal Model for Hard-Cased Li-Ion Batteries. J. Energy Storage 2020, 32, 101758. [Google Scholar] [CrossRef]
- Moradi, M.H. Predictive Control with Constraints, J.M. Maciejowski; Pearson Education Limited, Prentice Hall, London, 2002, Pp. IX+331, Price £35.99, ISBN 0-201-39823-0. Int. J. Adapt. Control. Signal Process. 2003, 17, 261–262. [Google Scholar] [CrossRef]
- Camacho, E.F. Constrained Control and Estimation: An Optimization Approach, G. C. Goodwin, M. M. Seron and J. A. de Dona, Springer, Berlin. No. of Pages: 411. ISBN: 1852335483. Int. J. Robust Nonlinear Control. 2007, 17, 347–348. [Google Scholar] [CrossRef]
- Falcone, P.; Borrelli, F.; Tseng, H.E.; Asgari, J.; Hrovat, D. Linear Time-Varying Model Predictive Control and Its Application to Active Steering Systems: Stability Analysis and Experimental Validation. Int. J. Robust Nonlinear Control. 2008, 18, 862–875. [Google Scholar] [CrossRef]
- Wan, Z.; Kothare, M.V. Efficient Scheduled Stabilizing Output Feedback Model Predictive Control for Constrained Nonlinear Systems. IEEE Trans. Autom. Control. 2004, 49, 1172–1177. [Google Scholar] [CrossRef]
- Technical Guidelines for the Preparation of Applications for the Approval of Innovative Technologies Pursuant to Regulation (EC) No 443/2009 of The European Parliament and of the Council. European Commission: Brussels, Belgium, February 2013. Available online: https://circabc.europa.eu/sd/a/a19b42c8-8e87-4b24-a78b-9b70760f82a9/July%202018%20Technical%20Guidelines.pdf (accessed on 5 January 2022).




| Parameter | Unit | Variable | Value | |
|---|---|---|---|---|
| Vehicle Description | Nominal mass | kg | 2041 | |
| Frontal Area | m2 | 2.4207 | ||
| Aerodynamic drag coefficient | - | 0.316 | ||
| Gear ratios | - | 6-speed gear shift | ||
| Final Drive Ratio | - | 4.41 | ||
| Tire size | - | P255/50VR20 | ||
| Passenger Capacity | 7 | |||
| Internal Combustion Engine | SAE Net Torque @ rpm | Nm | 310 @ 2000 | |
| Fuel System | - | Gasoline Direct Injection | ||
| SAE net power @ rpm | kW | 169 @ 5000 | ||
| Displacement | L | 2.5 | ||
| Electric Motor | Maximum power | kW | 27 | |
| Maximum torque @ rpm | Nm | 65 @ 4000 | ||
| Battery (Sanyo NCR 18650 GA Lithium-ion cell) | Single-cell nominal voltage | V | 3.6 | |
| Single-cell nominal capacity | Ah | 3.2 | ||
| Minimum battery SOC | % | 0 | ||
| Maximum battery SOC | % | 100 | ||
| Operating temperature | °C | −20~60 | ||
| Ambient temperature | °C | 20 | ||
| Battery Pack Configurations | - | 14s6p and 14s10p |
| Variable | Units | Value | |
|---|---|---|---|
| Electric Model | - | 0.017 | |
| - | negligible | ||
| Ohms | 0.024 | ||
| Ohm | 0.018 | ||
| Thermal Model | 1200 | ||
| 14.6 | |||
| kg |
| Input | States Variable | Nominal Eigenvalue | Output |
|---|---|---|---|
| State of charge (SOC) | 0 | SOC | |
| Diffusion-resistant current | −0.002 | ||
| −0.0282 | |||
| ) | 0 |
| SOC | (°C) | ||||
|---|---|---|---|---|---|
| min | 0 | 0 | 0.1 | 0 | |
| max | 0 | 0.9 | 50 |
| Operating Condition | Prediction Horizon | Pack Configuration | Maximum Temperature [°C] | Fuel Consumption [L/100 km] | Fuel Consumed [g] | Fuel Saving [%] | CO2 Consumption [g/km] |
|---|---|---|---|---|---|---|---|
| Conventional vehicle | - | - | - | 8.03 | 699.9 | 0 | 187.1 |
| On/Off | - | 14s6p | 55 | 7.54 | 672 | 4 | 175.7 |
| No. Temp Limit | 2 | 160 | 6.94 | 618.5 | 11.6 | 161.8 | |
| No. Temp Limit | 20 | 111 | 6.85 | 610 | 12.8 | 159.5 | |
| Temp. Limited | 20 | 55 | 6.98 | 621.5 | 11.3 | 162.6 | |
| Increased battery capacity | 20 | 14s10p | 55 | 6.63 | 590.4 | 15.7 | 154.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ezemobi, E.; Yakhshilikova, G.; Ruzimov, S.; Castellanos, L.M.; Tonoli, A. Adaptive Model Predictive Control Including Battery Thermal Limitations for Fuel Consumption Reduction in P2 Hybrid Electric Vehicles. World Electr. Veh. J. 2022, 13, 33. https://doi.org/10.3390/wevj13020033
Ezemobi E, Yakhshilikova G, Ruzimov S, Castellanos LM, Tonoli A. Adaptive Model Predictive Control Including Battery Thermal Limitations for Fuel Consumption Reduction in P2 Hybrid Electric Vehicles. World Electric Vehicle Journal. 2022; 13(2):33. https://doi.org/10.3390/wevj13020033
Chicago/Turabian StyleEzemobi, Ethelbert, Gulnora Yakhshilikova, Sanjarbek Ruzimov, Luis Miguel Castellanos, and Andrea Tonoli. 2022. "Adaptive Model Predictive Control Including Battery Thermal Limitations for Fuel Consumption Reduction in P2 Hybrid Electric Vehicles" World Electric Vehicle Journal 13, no. 2: 33. https://doi.org/10.3390/wevj13020033
APA StyleEzemobi, E., Yakhshilikova, G., Ruzimov, S., Castellanos, L. M., & Tonoli, A. (2022). Adaptive Model Predictive Control Including Battery Thermal Limitations for Fuel Consumption Reduction in P2 Hybrid Electric Vehicles. World Electric Vehicle Journal, 13(2), 33. https://doi.org/10.3390/wevj13020033








