A Smart Battery Management System for Electric Vehicles Using Deep Learning-Based Sensor Fault Detection
Abstract
1. Introduction
2. Related Works
Problem Statement
3. Methodology
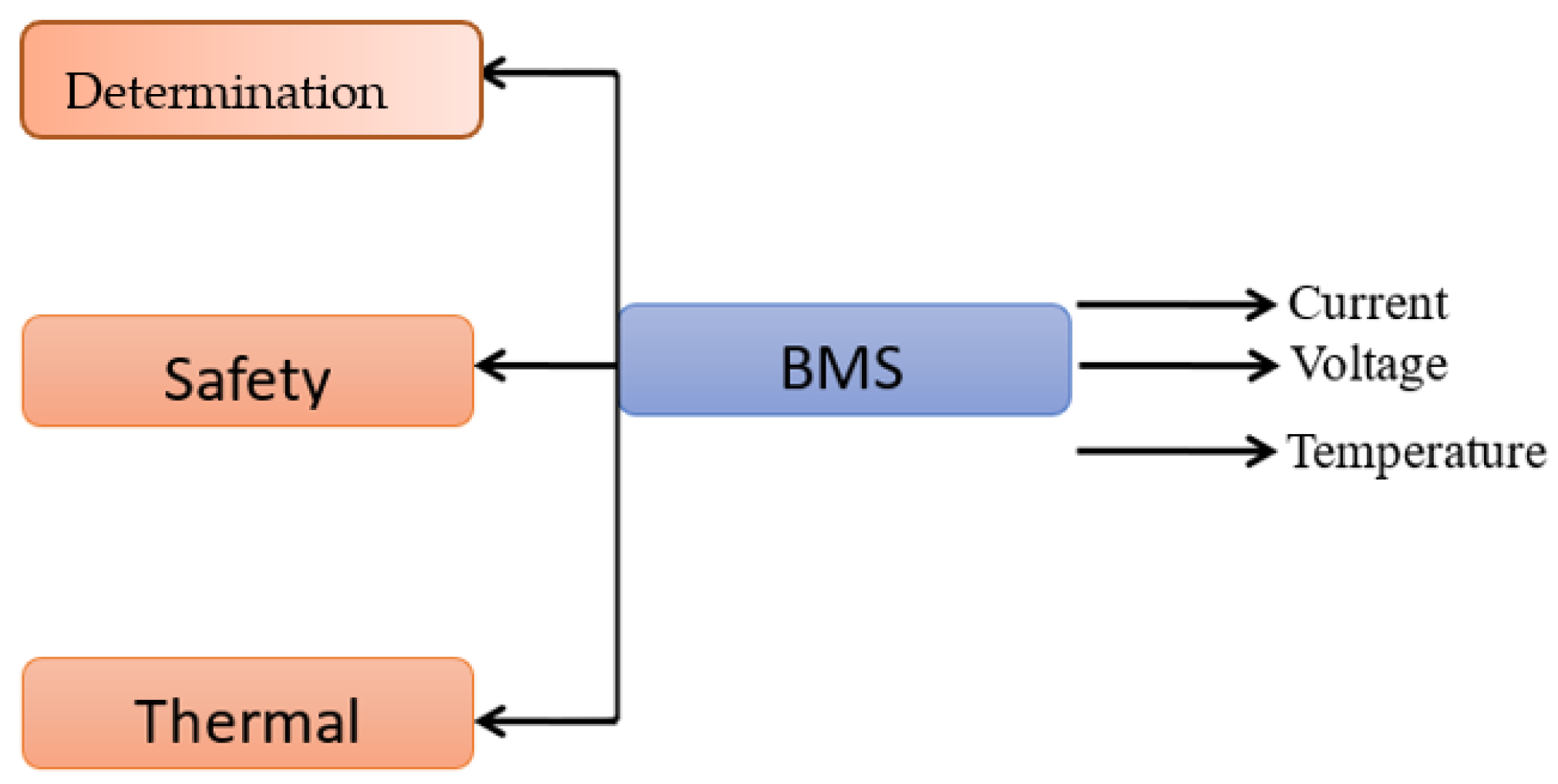
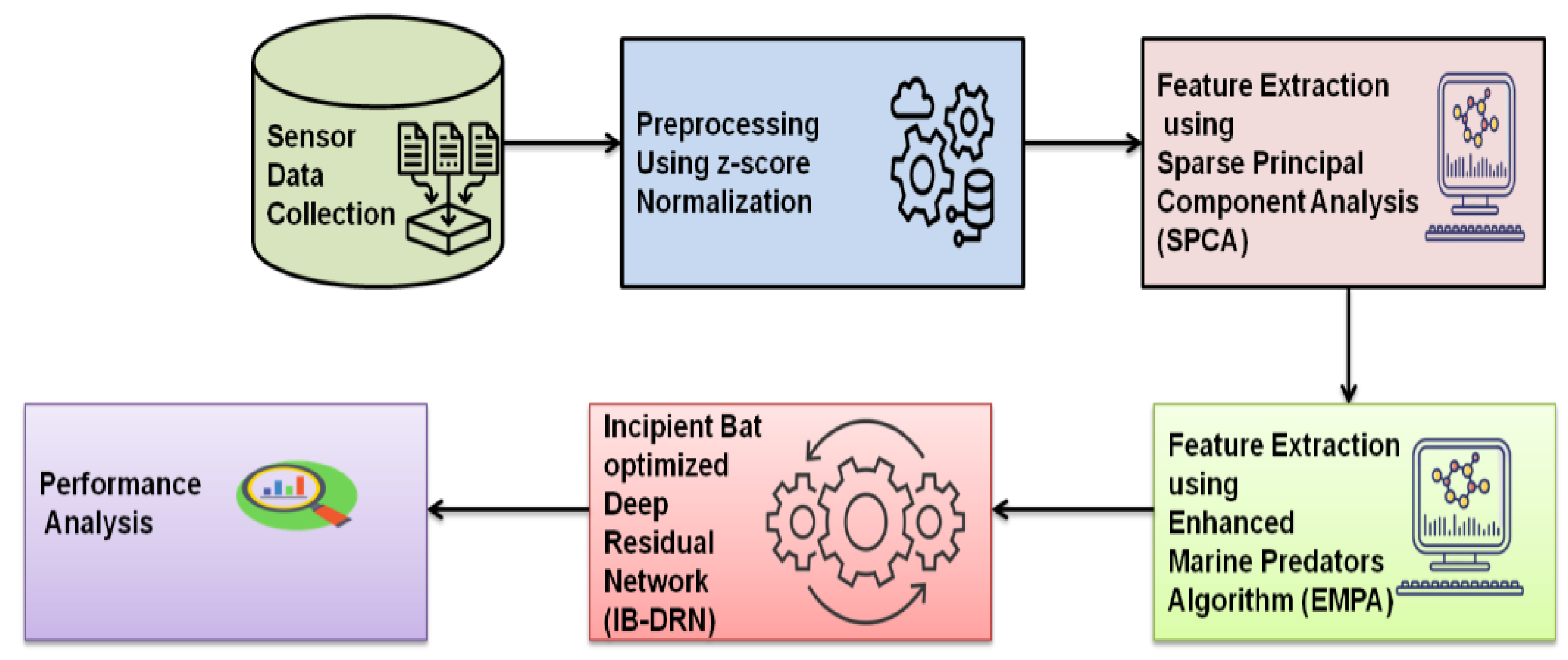
3.1. Process Overview
3.2. Sensor Data Collection
3.3. Preprocessing Using Z-Score Normalization
3.4. Feature Extraction
Feature Extraction Using Sparse Principal Component Analysis
3.5. Feature Selection Using Enhanced Marine Predators’ Algorithm
3.6. Incipient Bat-Optimized Deep Residual Network
- Each bat employs the advantages of echolocation to look for prey and avoid obstacles.
- Each bat searches for food by flying at a velocity vi, location xi, constant frequency fmin, variable wavelength, and loudness L0. Depending on how close the target is, bats may automatically change the frequency of their produced pulses and the rate of pulse emission r in the range [0, 1].
- A minimal constant value Lmin and a large positive number L0 represent the range of loudness Lm.
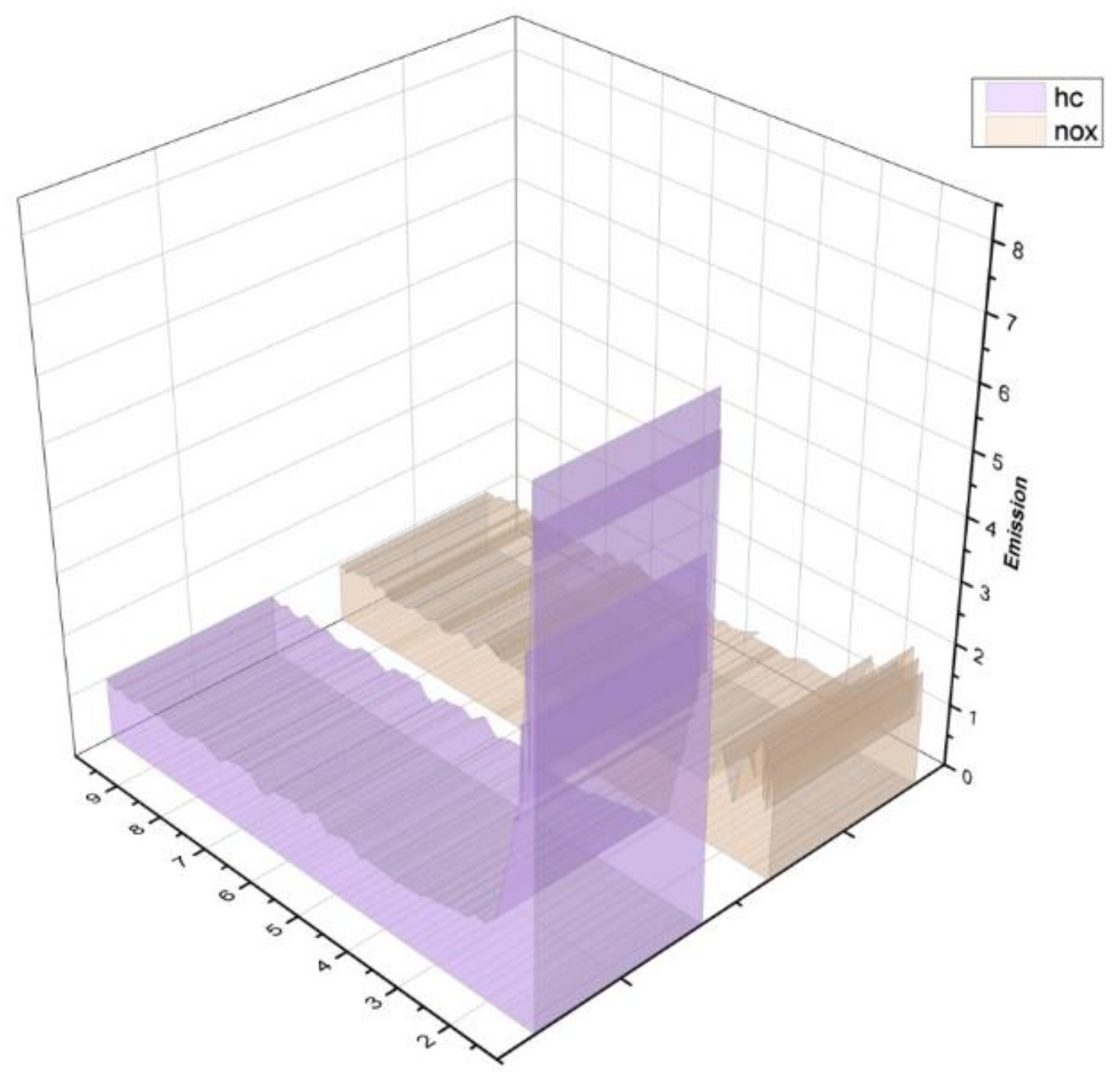
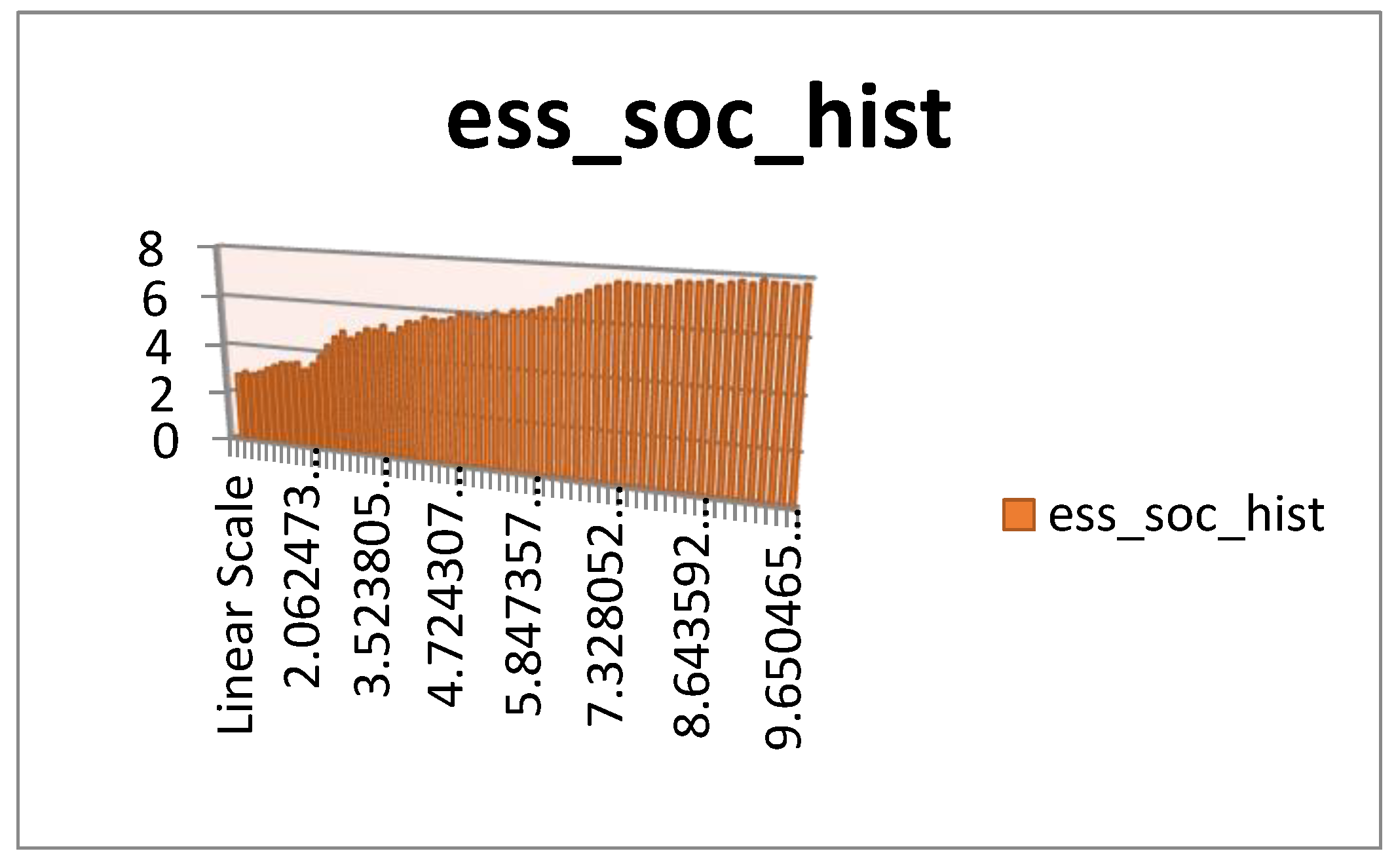
4. Performance Analysis
5. Discussions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chandran, V.; Patil, C.; Karthick, A.; Ganeshaperumal, D.; Rahim, R.; Ghosh, A. State of Charge Estimation of Lithium-Ion Battery for Electric Vehicles Using Machine Learning Algorithms. World Electr. Veh. J. 2021, 12, 38. [Google Scholar] [CrossRef]
- Duraisamy, T.; Kaliyaperumal, D. Machine Learning-Based Optimal Cell Balancing Mechanism for Electric Vehicle Battery Management System. IEEE Access 2021, 9, 132846–132861. [Google Scholar] [CrossRef]
- Yu, Q.; Wan, C.; Li, J.; Xiong, R.; Chen, Z. A Model-Based Sensor Fault Diagnosis Scheme for Batteries in Electric Vehicles. Energies 2021, 14, 829. [Google Scholar] [CrossRef]
- Xiong, R.; Yu, Q.; Shen, W.; Lin, C.; Sun, F. A Sensor Fault Diagnosis Method for a Lithium-Ion Battery Pack in Electric Vehicles. IEEE Trans. Power Electron. 2019, 34, 9709–9718. [Google Scholar] [CrossRef]
- Lipu, M.H.; Hannan, M.; Karim, T.F.; Hussain, A.; Saad, M.H.M.; Ayob, A.; Miah, S.; Mahlia, T.I. Intelligent algorithms and control strategies for battery management system in electric vehicles: Progress, challenges and future outlook. J. Clean. Prod. 2021, 292, 126044. [Google Scholar] [CrossRef]
- Liu, K.; Li, K.; Peng, Q.; Zhang, C. A brief review on key technologies in the battery management system of electric vehicles. Front. Mech. Eng. 2018, 14, 47–64. [Google Scholar] [CrossRef]
- Rajalakshmi, M.; Sultana, W.R. Intelligent Hybrid Battery Management System for Electric Vehicle. Artificial Intelligent Techniques for Electric and Hybrid Electric Vehicles; Wiley Online Library: New York, NY, USA, 2020; pp. 179–206. [Google Scholar] [CrossRef]
- Lelie, M.; Braun, T.; Knips, M.; Nordmann, H.; Ringbeck, F.; Zappen, H.; Sauer, D.U. Battery Management System Hardware Concepts: An Overview. Appl. Sci. 2018, 8, 534. [Google Scholar] [CrossRef]
- Sanguesa, J.; Torres-Sanz, V.; Garrido, P.; Martinez, F.; Marquez-Barja, J. A Review on Electric Vehicles: Technologies and Challenges. Smart Cities 2021, 4, 372–404. [Google Scholar] [CrossRef]
- Suarez, C.; Martinez, W. Fast and Ultra-Fast Charging for Battery Electric Vehicles—A Review. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019. [Google Scholar] [CrossRef]
- Tran, M.-K.; Bhatti, A.; Vrolyk, R.; Wong, D.; Panchal, S.; Fowler, M.; Fraser, R. A Review of Range Extenders in Battery Electric Vehicles: Current Progress and Future Perspectives. World Electr. Veh. J. 2021, 12, 54. [Google Scholar] [CrossRef]
- Sun, P.; Bisschop, R.; Niu, H.; Huang, X. A Review of Battery Fires in Electric Vehicles. Fire Technol. 2020, 56, 1361–1410. [Google Scholar] [CrossRef]
- Chen, H.-C.; Li, S.-S.; Wu, S.-L.; Lee, C.-Y. Design of a Modular Battery Management System for Electric Motorcycle. Energies 2021, 14, 3532. [Google Scholar] [CrossRef]
- Ma, J.; Sun, Y.; Zhang, S.; Li, J.; Li, S. Experimental study on the performance of vehicle integrated thermal management system for pure electric vehicles. Energy Convers. Manag. 2022, 253, 115183. [Google Scholar] [CrossRef]
- Balasingam, B.; Ahmed, M.; Pattipati, K. Battery Management Systems—Challenges and Some Solutions. Energies 2020, 13, 2825. [Google Scholar] [CrossRef]
- Lopez, K.L.; Gagne, C.; Gardner, M.-A. Demand-Side Management Using Deep Learning for Smart Charging of Electric Vehicles. IEEE Trans. Smart Grid 2018, 10, 2683–2691. [Google Scholar] [CrossRef]
- Trivedi, M.; Kakkar, R.; Gupta, R.; Agrawal, S.; Tanwar, S.; Niculescu, V.-C.; Raboaca, M.S.; Alqahtani, F.; Saad, A.; Tolba, A. Blockchain and Deep Learning-Based Fault Detection Framework for Electric Vehicles. Mathematics 2022, 10, 3626. [Google Scholar] [CrossRef]
- Aguilera, F.; de la Barrera, P.M.; De Angelo, C.H. Speed and current sensor fault-tolerant induction motor drive for electric vehicles based on virtual sensors. Electr. Eng. 2022, 104, 3157–3171. [Google Scholar] [CrossRef]
- Liu, P.; Sun, Z.; Wang, Z.; Zhang, J. Entropy-Based Voltage Fault Diagnosis of Battery Systems for Electric Vehicles. Energies 2018, 11, 136. [Google Scholar] [CrossRef]
- Li, X.; Dai, K.; Wang, Z.; Han, W. Lithium-ion batteries fault diagnostic for electric vehicles using sample entropy analysis method. J. Energy Storage 2020, 27, 101121. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z. A novel fault diagnosis method for lithium-Ion battery packs of electric vehicles. Measurement 2018, 116, 402–411. [Google Scholar] [CrossRef]
- Gabbar, H.A.; Othman, A.M.; Abdussami, M.R. Review of Battery Management Systems (BMS) Development and Industrial Standards. Technologies 2021, 9, 28. [Google Scholar] [CrossRef]
- Li, Y.; Sun, Z.; Wang, J. Design for battery management system hardware-in-loop test platform. In Proceedings of the 2009 9th International Conference on Electronic Measurement & Instruments, Beijing, China, 16–19 August 2009; pp. 3-399–3-402. [Google Scholar] [CrossRef]
- Mishra, R.K.; Kim, K.H. Role of Li-Ion Battery Energy Storage System in Renewable-Based Microgrid: A Review. Energies 2019, 12, 446. [Google Scholar] [CrossRef]
- Vivas, F.J.; Segura, F.; Andújar, J.M. Fuzzy logic-based energy management system for grid-connected residential DC microgrids with multi-stack fuel cell systems: A multi-objective approach. Sustain. Energy Grids Netw. 2022, 32, 100909. [Google Scholar] [CrossRef]
- Moulik, B.; Söffker, D. Battery Management System for Future Electric Vehicles. Appl. Sci. 2020, 10, 5095. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, W.; Yu, Q.; Sun, F. Research progress, challenges and prospects of fault diagnosis on battery system of electric vehicles. Appl. Energy 2020, 279, 115855. [Google Scholar] [CrossRef]
- Bonfitto, A.; Ezemobi, E.; Amati, N.; Feraco, S.; Tonoli, A.; Hegde, S. State of health estimation of lithium batteries for automotive applications with artificial neural networks. In Proceedings of the 2019 AEIT International Conference of Electrical and Electronic Technologies for Automotive (AEIT AUTOMOTIVE), IEEE, Turin, Italy, 2–4 July 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Xuan, L.; Qian, L.; Chen, J.; Bai, X.; Wu, B. State-of-Charge Prediction of Battery Management System Based on Principal Component Analysis and Improved Support Vector Machine for Regression. IEEE Access 2020, 8, 164693–164704. [Google Scholar] [CrossRef]
- Hong, J.; Wang, Z.; Chen, W.; Wang, L.-Y.; Qu, C. Online joint-prediction of multi-forward-step battery SOC using LSTM neural networks and multiple linear regression for real-world electric vehicles. J. Energy Storage 2020, 30, 101459. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T.; Tibshirani, R. Sparse Principal Component Analysis. J. Comput. Graph. Stat. 2006, 15, 265–286. [Google Scholar] [CrossRef]
| Abbreviations | Definitions |
|---|---|
| EV | Electric Vehicles |
| BEV | Battery Electric Vehicles |
| BMS | Battery Management System |
| SOC | State of Charge |
| SOH | State of Health |
| ECU | Vehicle or Electronic Controller Units |
| OSMC-EV | Operation Service and Management Center for Electric Vehicle |
| ML | Machine Learning |
| FTA | Fault Tree Analysis |
| IB-DRN | Incipient Bat optimized Deep Residual Network |
| ICC | Interclass Correlation Coefficient |
| SPCA | Sparse Principal Component Analysis |
| PCA | Principle Component Analysis |
| SVD | Singular Value Decomposition |
| PCs | Principal Components |
| QR decomposition | QR factorization | Q is orthonormal, and R is higher triangular |
| SPCs | Sparse Principal Component |
| PVE | Proportion of Explained Variation |
| EMPA | Enhanced Marine Predators Algorithm |
| ANN | Artificial Neural Network |
| SVM | Support Vector Machine |
| LR | Linear Regression |
| GPR | Gaussian Process Regression |
| UDDS | Urban Dynamometer Driving Schedule |
| TP | True Positives |
| FP | False Positives |
| FN | False Negatives |
| MSE | Mean Squared Error |
| RMSE | Root Mean Square Error |
| Battery Voltage (V) | Battery Current (A) | Battery Temperature (°C) | State of Charge (%) | State of Health (%) | Charge/Discharge Status | Charging Power (kW) | Charging Time (h) | Cell Voltage (V)—Cell 1 | Cell Voltage (V)—Cell 2 | Cell Voltage (V)—Cell 3 | Cell Voltage (V)—Cell 4 | Cell Voltage (V)—Cell 5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 385 | 80 | 35 | 75 | 95 | Charging | 10 | 2 | 3.8 | 3.9 | 3.7 | 3.6 | 3.5 |
| 386 | 82 | 35.2 | 75.2 | 94.9 | Discharging | 10 | 2.01 | 3.9 | 3.8 | 3.6 | 3.7 | 3.4 |
| 387 | 85 | 35.4 | 75.4 | 94.8 | Charging | 10 | 2.02 | 3.7 | 3.9 | 3.5 | 3.6 | 3.3 |
| 388 | 88 | 35.6 | 75.6 | 94.6 | Discharging | 10 | 2.03 | 3.8 | 3.7 | 3.6 | 3.5 | 3.4 |
| 389 | 90 | 35.8 | 75.8 | 94.4 | Charging | 10 | 2.04 | 3.9 | 3.8 | 3.7 | 3.6 | 3.5 |
| Algorithm: The Enhanced MPA |
|---|
| Initialize search agents or the prey population i = 1,⋯,N |
| t = 1 |
| while (t < Max T) |
| Calculate the fitness and create the Elite matrix |
| Update prey using Equation (11) |
| else if |
| for |
| Update prey based on Equation (14) |
| for |
| Update prey based on Equation (19) |
| else if |
| Update prey based on Equation (22) |
| End if |
| Achieve memory saving and update Elite matrix |
| Apply the effect and update using Equation (24) |
| Accomplish memory saving and update Elite matrix |
| end while |
| Algorithm: Incipient Bat Algorithm |
|---|
| 1 Define the objective function ; |
| 2 Initialize the bat population ; |
| 3 for each bat in the population do |
| 4 Initialize the velocity the pulse rate and loudness ; |
| 5 Define the frequency at position ; |
| 6 while termination criterion not reached do |
| 7 for each bat in the population do |
| 8 if rand then |
| 9 Select one solution among the best ones. |
| 10 Generate local solution around the best one. |
| 11 Generate a new solution by flying randomly. |
| 12 if then |
| 13 Accept the new solutions. |
| 14 Increase the and reduce ; |
| 15 Rank bats and find current best solution |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kosuru, V.S.R.; Kavasseri Venkitaraman, A. A Smart Battery Management System for Electric Vehicles Using Deep Learning-Based Sensor Fault Detection. World Electr. Veh. J. 2023, 14, 101. https://doi.org/10.3390/wevj14040101
Kosuru VSR, Kavasseri Venkitaraman A. A Smart Battery Management System for Electric Vehicles Using Deep Learning-Based Sensor Fault Detection. World Electric Vehicle Journal. 2023; 14(4):101. https://doi.org/10.3390/wevj14040101
Chicago/Turabian StyleKosuru, Venkata Satya Rahul, and Ashwin Kavasseri Venkitaraman. 2023. "A Smart Battery Management System for Electric Vehicles Using Deep Learning-Based Sensor Fault Detection" World Electric Vehicle Journal 14, no. 4: 101. https://doi.org/10.3390/wevj14040101
APA StyleKosuru, V. S. R., & Kavasseri Venkitaraman, A. (2023). A Smart Battery Management System for Electric Vehicles Using Deep Learning-Based Sensor Fault Detection. World Electric Vehicle Journal, 14(4), 101. https://doi.org/10.3390/wevj14040101












