Design of Auto-Tuning Nonlinear PID Tracking Speed Control for Electric Vehicle with Uncertainty Consideration
Abstract
1. Introduction
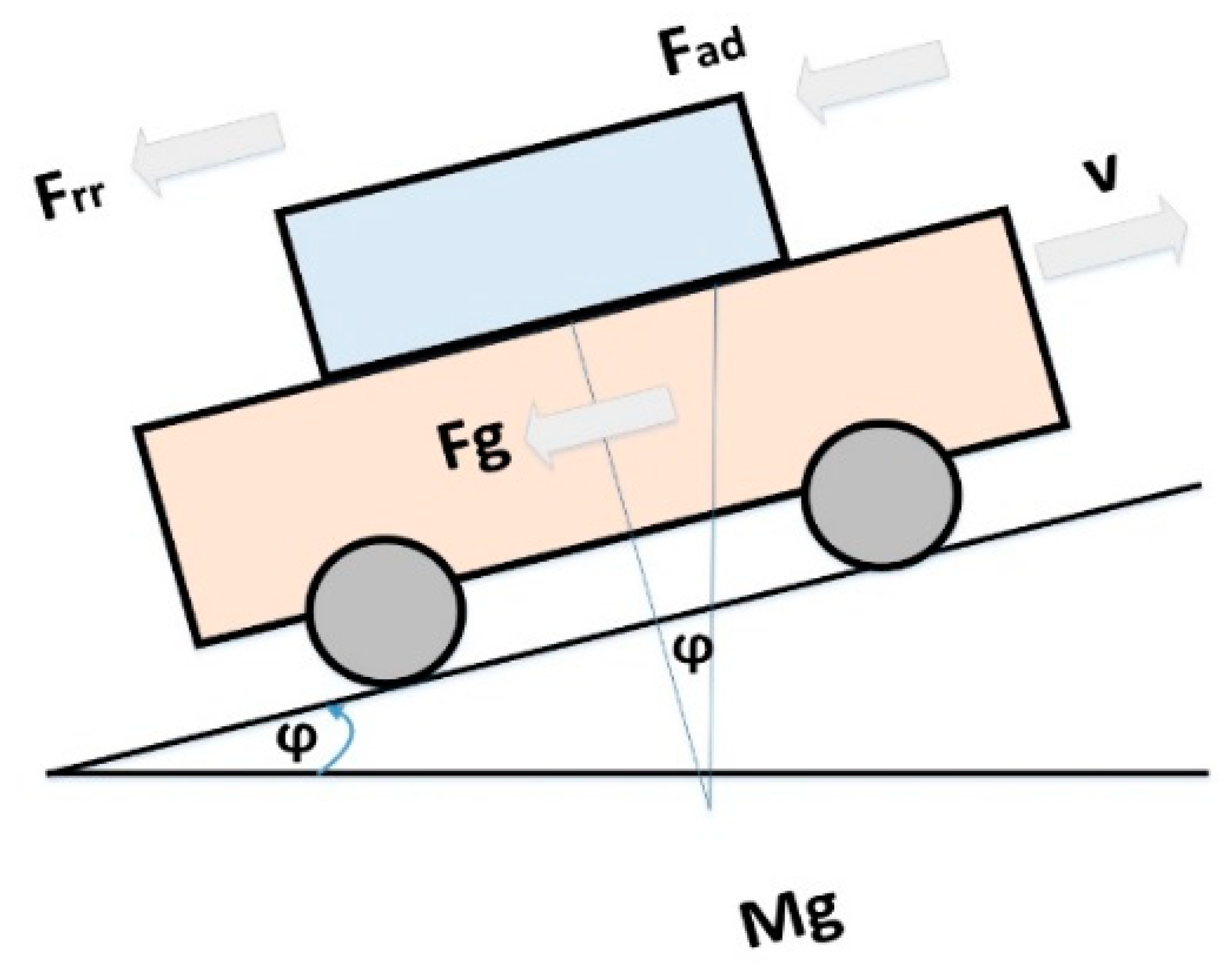
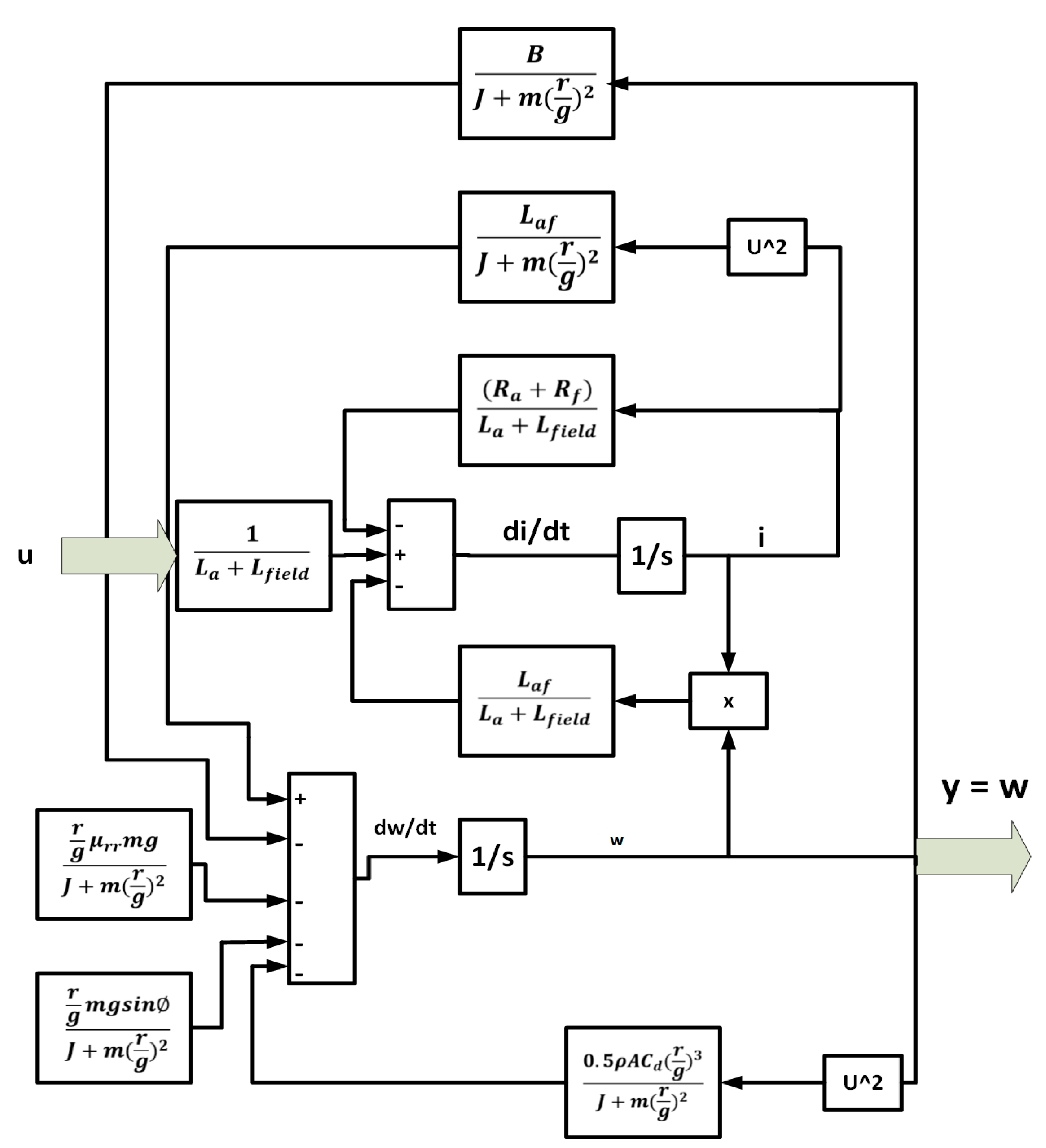
2. System Modeling
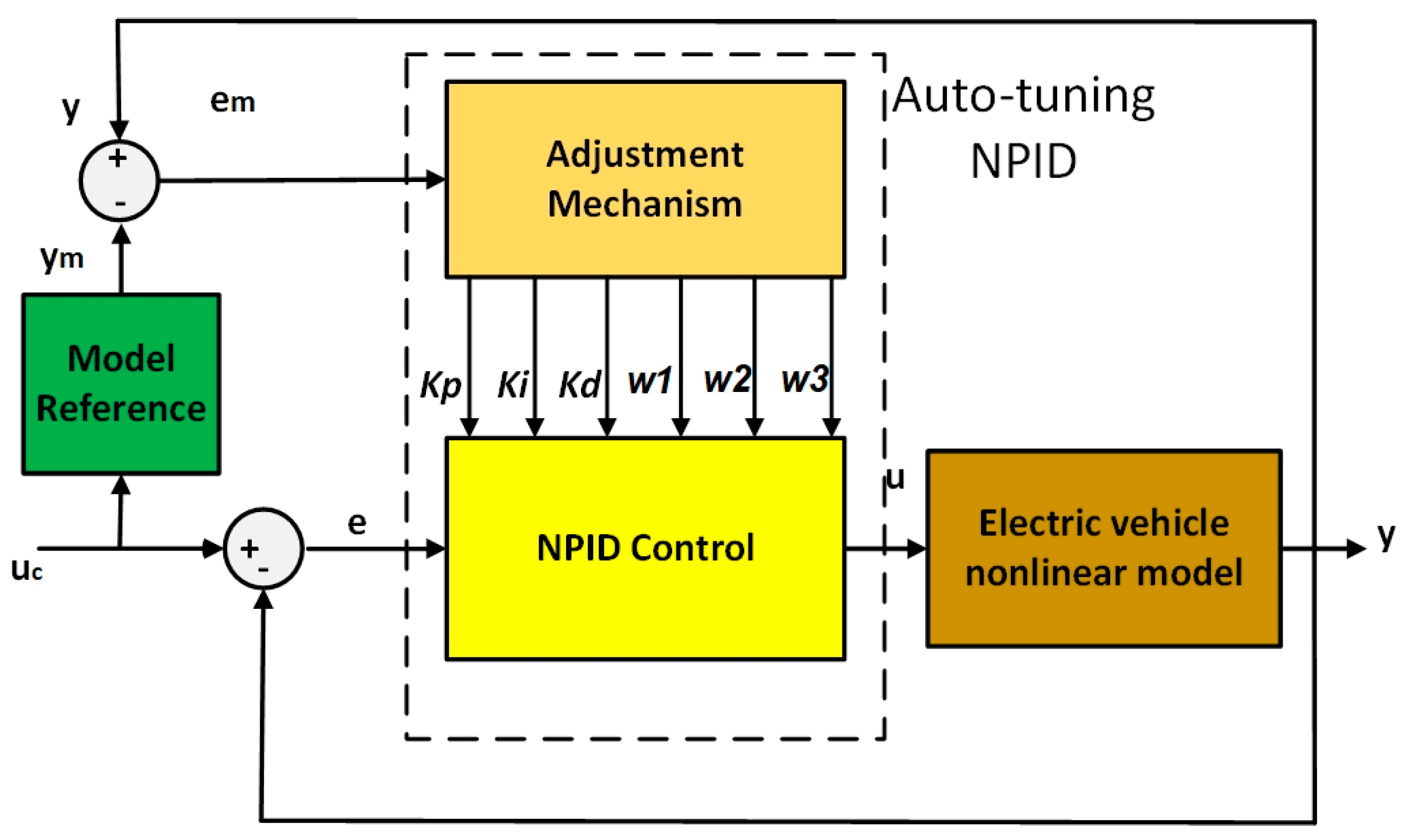
3. Auto-Tuning Nonlinear PID Control
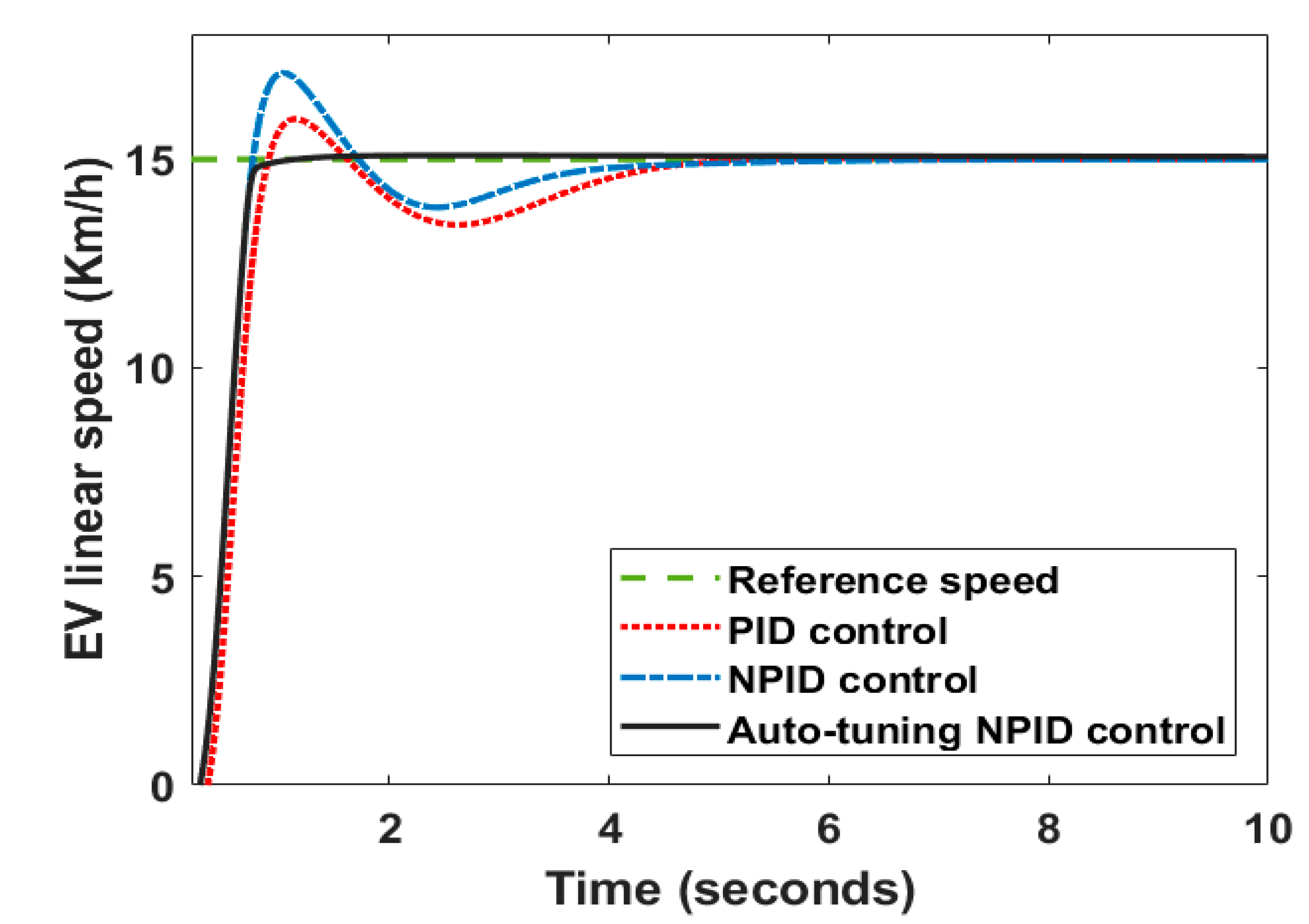
4. Results and Discussion
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Potnuru, D.; Ayyarao, T.S.L.V.; Kumar, L.V.S.; Kumar, Y.V.P.; Pradeep, D.J.; Reddy, C.P. Salp Swarm Algorithm Based Optimal Speed Control for Electric Vehicles. Int. J. Power Electron. Drive Syst. 2022, 13, 755–763. [Google Scholar] [CrossRef]
- Nguefack, C.F.; Fotso, B.M.; Talawo, R.C.; Fogue, M. Aerodynamic Analysis of an Electric Vehicle Equipped With Horizontal Axis Savonius Wind Turbines. Int. J. Recent Trends Eng. Res. 2019, 05, 17–26. [Google Scholar] [CrossRef]
- Dinc, A.; Otkur, M. Optimization of Electric Vehicle Battery Size and Reduction Ratio Using Genetic Algorithm. In Proceedings of the 2020 11th International Conference on Mechanical and Aerospace Engineering, Athens, Greece, 14–17 July 2020; pp. 281–285. [Google Scholar] [CrossRef]
- Ouda, A.; Mohamed, A. Autonomous Fuzzy Heading Control for a Multi-Wheeled Combat Vehicle. Int. J. Robot. Control Syst. 2021, 1, 90–101. [Google Scholar] [CrossRef]
- He, R.; Yan, Y.; Hu, D. Optimised Adaptive Control Methodology for Mode Transition of Hybrid Electric Vehicle Based on the Dynamic Characteristics Analysis. Veh. Syst. Dyn. 2021, 59, 1282–1303. [Google Scholar] [CrossRef]
- Hossain, M.F.; Fara, N. Integration of Wind Into Running Vehicles to meet its Total Energy Demand. Energy Ecol. Environ. 2017, 2, 35–48. [Google Scholar] [CrossRef]
- Shamseldin, M.A. An Efficient Single Neuron PID—Sliding Mode Tracking Control for Simple Electric Vehicle Model. J. Appl. Nonlinear Dyn. 2022, 11, 1–15. [Google Scholar] [CrossRef]
- Alkhafaji, A.S.; Al-Hayder, A.A.; Hassooni, A.S. Hybrid IWOPSO Optimization Based Marine Engine Rotational Speed Control Automatic System. Int. J. Electr. Comput. Eng. 2020, 10, 840–848. [Google Scholar] [CrossRef]
- Holst, T.L. Genetic Algorithms Applied to Multi-Objective Aerospace Shape Optimization. J. Aerosp. Comput. Inf. Commun. 2005, 2, 217–235. [Google Scholar] [CrossRef]
- Bitar, Z.; Al Jabi, S.; Khamis, I. Modeling and Simulation of Series DC Motors in Electric Car. Energy Procedia 2014, 50, 460–470. [Google Scholar] [CrossRef]
- Karuppannan, A.; Muthusamy, M. Wavelet Neural Learning-Based Type-2 Fuzzy PID Controller for Speed Regulation in BLDC motor. Neural Comput. Appl. 2021, 33, 13481–13503. [Google Scholar] [CrossRef]
- Shamseldin, M.A.; Sallam, M.; Bassiuny, A.M.; Abdel Ghany, A.M. A Novel Self-Tuning Fractional Order PID Control Based on Optimal Model Reference Adaptive System. Int. J. Power Electron. Drive Syst. 2018, 10, 230–241. [Google Scholar] [CrossRef]
- Shamseldin, M.A.; Ghany, M.A.A.; Ghany, A.M.A. Performance Study of Enhanced Non-Linear PID Control Applied on Brushless DC Motor. Int. J. Power Electron. Drive Syst. 2018, 9, 536–545. [Google Scholar] [CrossRef]
- Martínez-Álvarez, F.; Asencio-Cortés, G.; Torres, J.F.; Gutiérrez-Avilés, D.; Melgar-García, L.; Pérez-Chacón, R.; Rubio-Escudero, C.; Riquelme, J.C.; Troncoso, A. Coronavirus Optimization Algorithm: A Bioinspired Metaheuristic Based on the COVID-19 Propagation Model. Big Data 2020, 8, 308–322. [Google Scholar] [CrossRef]
- Shamseldin, M.A. Optimal Covid-19 Based PD/PID Cascaded Tracking Control for Robot Arm driven by BLDC Motor. Wseas Trans. Syst. 2021, 20, 217–227. [Google Scholar] [CrossRef]
- Omar, M.; Soliman, M.; Ghany, A.M.A.; Bendary, F. Optimal Tuning of PID Controllers for Hydrothermal Load Frequency Control Using Ant Colony Optimization. Int. J. Electr. Eng. Inform. 2013, 5, 348–360. [Google Scholar] [CrossRef]
- Shamseldin, M.A. Optimal Coronavirus Optimization Algorithm Based PID Controller for High Performance Brushless DC Motor. Algorithms Artic. 2021, 14, 17. [Google Scholar] [CrossRef]
- Shamseldin, M.A.; Sallam, M.; Bassiuny, A.M.; Ghany, A.M.A. A New Model Reference Self-Tuning Fractional Order PD Control for One Stage Servomechanism System. WSEAS Trans. Syst. Control 2019, 14, 8–18. [Google Scholar]
- Zhang, Y.; Wang, W.; Xiang, C.; Yang, C.; Peng, H.; Wei, C. A Swarm Intelligence-Based Predictive Regenerative Braking Control Strategy for Hybrid Electric Vehicle. Veh. Syst. Dyn. 2022, 60, 973–997. [Google Scholar] [CrossRef]
- Purwadi, A.; Dozeno, J.; Heryana, N. Testing Performance of 10 kW BLDC Motor and LiFePO 4 Battery on ITB-1 Electric Car Prototype. Procedia Technol. 2013, 11, 1074–1082. [Google Scholar] [CrossRef]
- Chaleshtari, M.H.B.; Norouzi, E.; Ahmadi, H. Optimizing Control Motion of a Human Arm with PSO-PID Controller. J. Comput. Appl. Res. Mech. Eng. 2017, 7, 23–34. [Google Scholar] [CrossRef]
- Shamseldin, M.A.; Sallam, M.; Bassiuny, A.M.; Abdel Ghany, A.M. LabVIEW Implementation of an Enhanced Nonlinear PID Controller Based on Harmony Search for One-Stage Servomechanism System. J. Comput. Appl. Res. Mech. Eng. 2019, 12, 4161–4179. [Google Scholar] [CrossRef]
- Kumar, P.; Gupta, M.; Kunar, V. Multi-Objective Particle Swarm Optimization of WEDM Process Parameters for Inconel 825. J. Comput. Appl. Res. Mech. Eng 2021, 10, 291–309. [Google Scholar] [CrossRef]
- Shamseldin, M.A. Adaptive Controller with PID, FOPID, and NPID Compensators for Tracking Control of Electric–Wind Vehicle. J. Robot. Control 2022, 3, 546–565. [Google Scholar]
- Shamseldin, M.A.; Khaled, E.; Youssef, A.; Mohamed, D.; Ahmed, S.; Hesham, A.; Elkodama, A.; Badran, M. A New Design Identification and Control Based on GA Optimization for An Autonomous Wheelchair. Robotics 2022, 11, 101. [Google Scholar] [CrossRef]
- EL-Tehewy, L.M.; Shamseldin, M.A.; Sallam, M.; Abdel Ghany, A.M.A.G. Optimal Flower Pollination Based Nonlinear PID Controller for Pantograph Robot Mechanism. Int. J. Mech. Eng. Robot. Res. 2022, 11. [Google Scholar] [CrossRef]
- Tahmasebi, M.; Gohari, M.; Emami, A. An Autonomous Pesticide Sprayer Robot with a Color-based Vision System. Int. J. Robot. Control Syst. 2022, 2, 115–123. [Google Scholar] [CrossRef]
- Chen, T.; Zheng, M.; Zhang, N.; Luo, L.; Liu, P.; Zhong, W. Study on a Novel Configuration Switchable Hydraulically Interconnected Suspension System Under Nonlinear Model Predictive Control. Veh. Syst. Dyn. 2022, 60, 3440–3461. [Google Scholar] [CrossRef]
- Ma, C.; Xu, M.; Wang, H. Dynamic Emulation of Road/Tyre Longitudinal Interaction for Developing Electric Vehicle Control Systems. Veh. Syst. Dyn. 2011, 49, 433–447. [Google Scholar] [CrossRef]
- Raksincharoensak, P.; Nagai, M.; Shino, M. Lane Keeping Control Strategy with Direct Yaw Moment Control Input by Considering Dynamics of Electric Vehicle. Veh. Syst. Dyn. 2006, 44, 192–201. [Google Scholar] [CrossRef]
- Shamseldin, M.; Ghany, M.A.; Hendawey, Y. Optimal Nonlinear PID Speed Control Based on Harmony Search for an Electric Vehicle Optimal Nonlinear PID Speed Control Based on Harmony Search for An Electric Vehicle. Future Eng. J. 2021, 2, 4. [Google Scholar]
- El-Τehewy, L.M.; Shamseldin, M.A.; Sallam, M.; Abdel Ghany, A.M. A Modified Model Reference Adaptive Control for High-Performance Pantograph Robot Mechanism. WSEAS Trans. Appl. Theor. Mech. 2021, 16, 193–203. [Google Scholar] [CrossRef]
- Ngarambe, J.; Yun, G.Y.; Santamouris, M. The use of Artificial Intelligence (AI) Methods in the Prediction of Thermal Comfort in Buildings: Energy Implications of AI-Based Thermal Comfort Controls. Energy Build. 2020, 211, 109807. [Google Scholar] [CrossRef]
- Borkowski, P. Inference Engine in an Intelligent Ship Course-Keeping System. Comput. Intell. Neurosci. 2017, 2017, 2561383. [Google Scholar] [CrossRef] [PubMed]
- Sudheer, H.; Kodad, S.F.; Sarvesh, B. Improved Fuzzy Logic Based DTC Of Induction Machine for Wide Range of Speed Control Using AI Based Controllers. J. Electr. Syst. 2016, 12, 301–314. [Google Scholar]
- Williams, J.G.; Liu, G.-P.; Thanapalan, K.; Rees, D. Design and Implementation of On-Line Self-Tuning Control for PEM Fuel Cells. World Electr. Veh. J. 2008, 2, 242–252. [Google Scholar] [CrossRef]
- Chu, L.; Li, H.; Xu, Y.; Zhao, D.; Sun, C. Research on Longitudinal Control Algorithm of Adaptive Cruise Control System for Pure Electric Vehicles. World Electr. Veh. J. 2023, 14, 32. [Google Scholar] [CrossRef]
- Du, P.P.; Su, H.; Tang, G.Y. Friction Compensation Control for Electric Power Steering Systems. In Proceedings of the 2018 IEEE International Conference on Industrial Electrononics for Sustainaibale Energy Systems (IESES 2018), Hamilton, New Zealand, 31 January–2 February 2018; pp. 212–217. [Google Scholar] [CrossRef]
- Maharajan, M.P.; Xavier, S.A.E. Design of Speed Control and Reduction of Torque Ripple Factor in BLdc Motor Using Spider Based Controller. IEEE Trans. Power Electron. 2019, 34, 7826–7837. [Google Scholar] [CrossRef]
- Kim, T.Y.; Lee, S.H. Combustion and Emission Characteristics of Wood Pyrolysis Oil-Butanol Blended Fuels in a Di Diesel Engine. Int. J. Automot. Technol. 2012, 13, 293–300. [Google Scholar] [CrossRef]
- Niu, J.; Wang, Y.; Liu, F.; Li, R. Numerical Study on Comparison of Detailed Flow Field and Aerodynamic Performance of Bogies of Stationary Train and Moving Train. Veh. Syst. Dyn. 2021, 59, 1844–1866. [Google Scholar] [CrossRef]
- Pilecki, J.; Bednarczyk, M.A.; Jamroga, W. Model Checking Properties of Multi-Agent Systems with Imperfect Information and Imperfect Recall. In Intelligent Systems’2014; Angelov, P., Atanassov, K.T., Doukovska, L., Hadjiski, M., Jotsov, V., Kacprzyk, J., Kasabov, N., Sotirov, S., Szmidt, E., Zadrożny, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 322, pp. 415–426. [Google Scholar]
- Mo, J.; Yang, R.; Zhang, S.; Zhou, Y.; Huang, W. TD3-Based EMS Using Action Mask and Considering Battery Aging for Hybrid Electric Dump Trucks. World Electr. Veh. J. 2023, 14, 74. [Google Scholar] [CrossRef]
- Kozioł, K.; Stanisławski, R.; Bialic, G. Fractional-Order Sir Epidemic Model for Transmission Prediction of COVID-19 Disease. Appl. Sci. 2020, 10, 8316. [Google Scholar] [CrossRef]
- Yao, A.W.L.; Chen, H.C. An Intelligent Color Image Recognition and Mobile Control System for Robotic Arm. Int. J. Robot. Control Syst. 2022, 2, 97–104. [Google Scholar] [CrossRef]

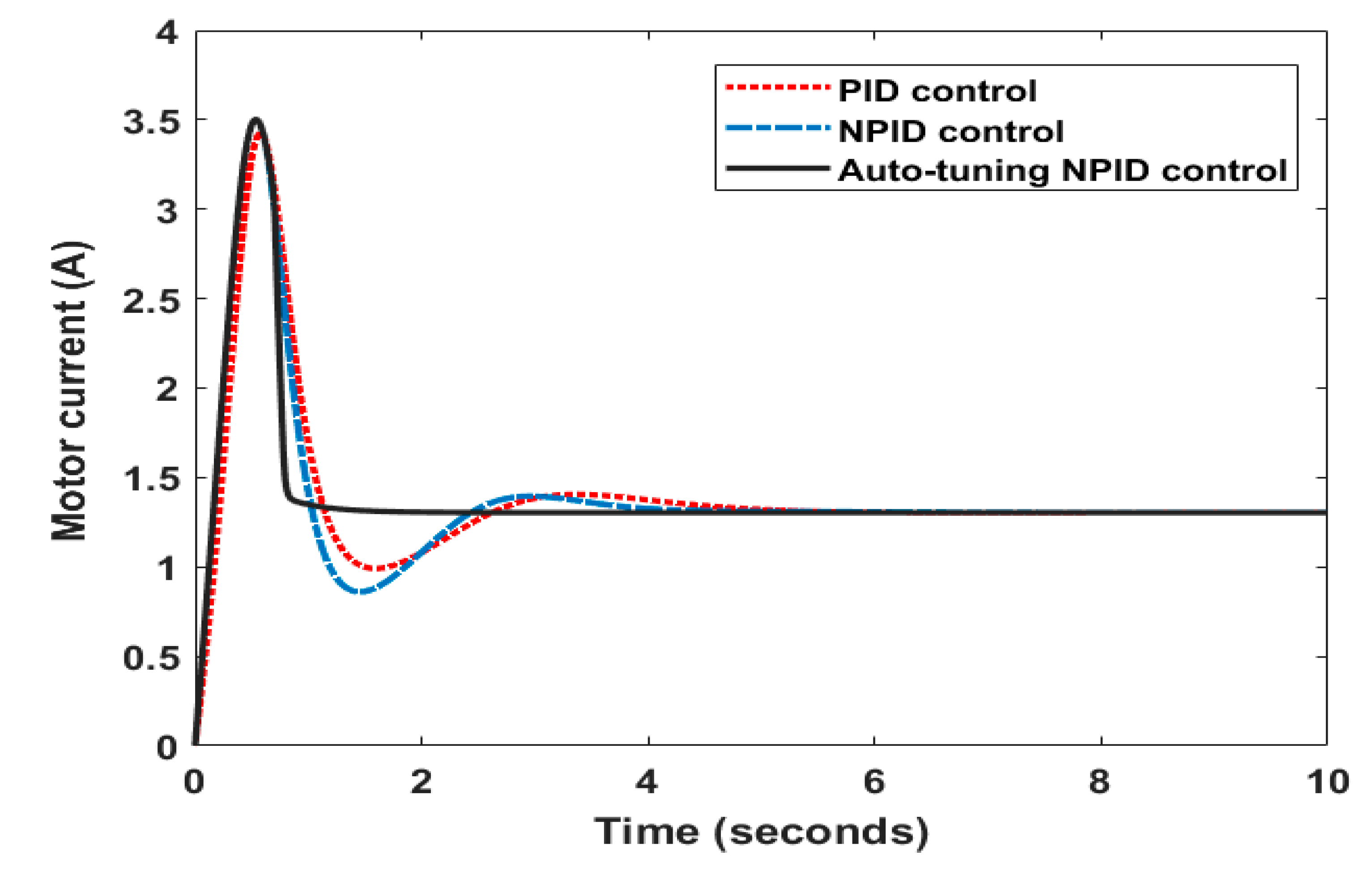
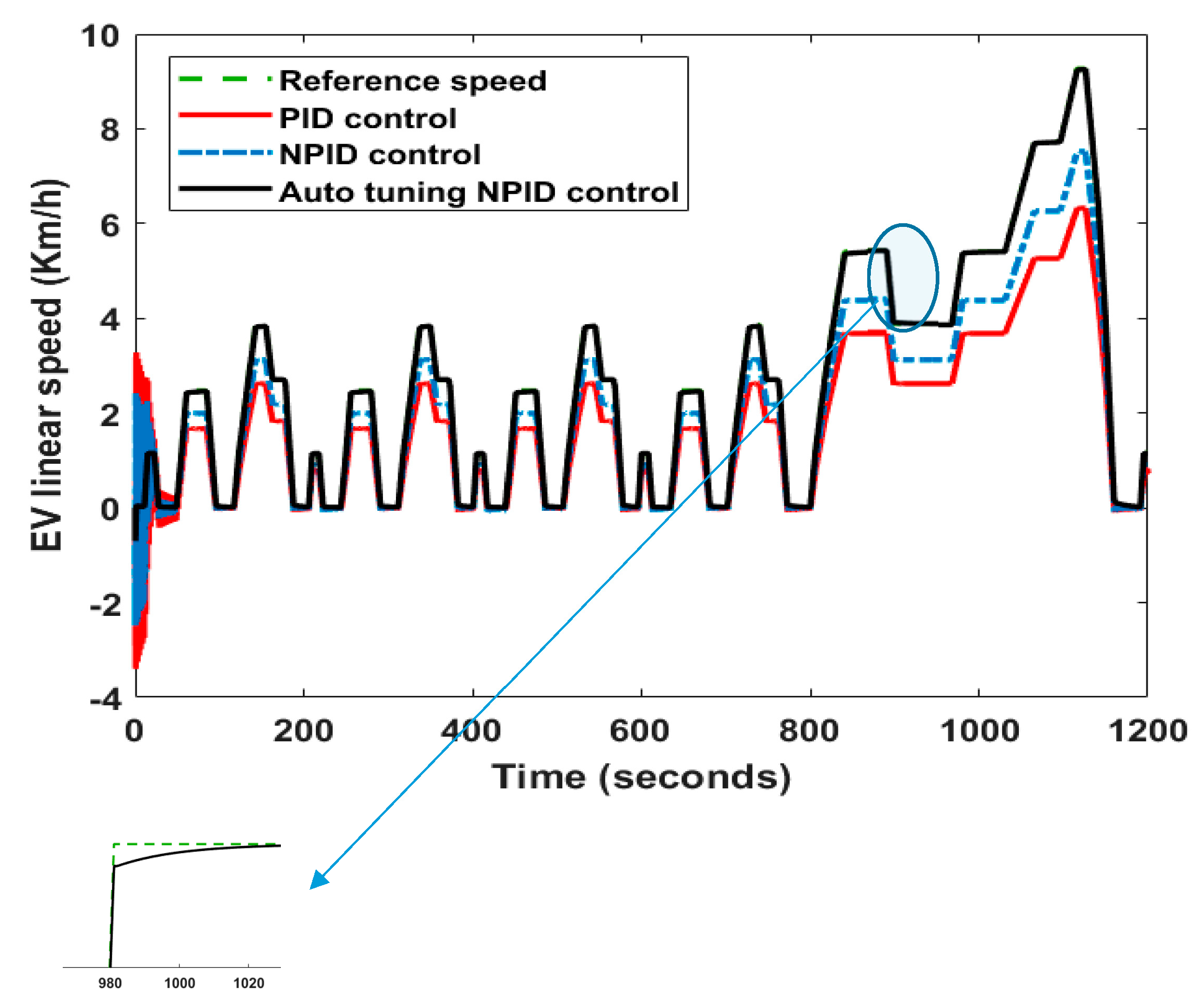

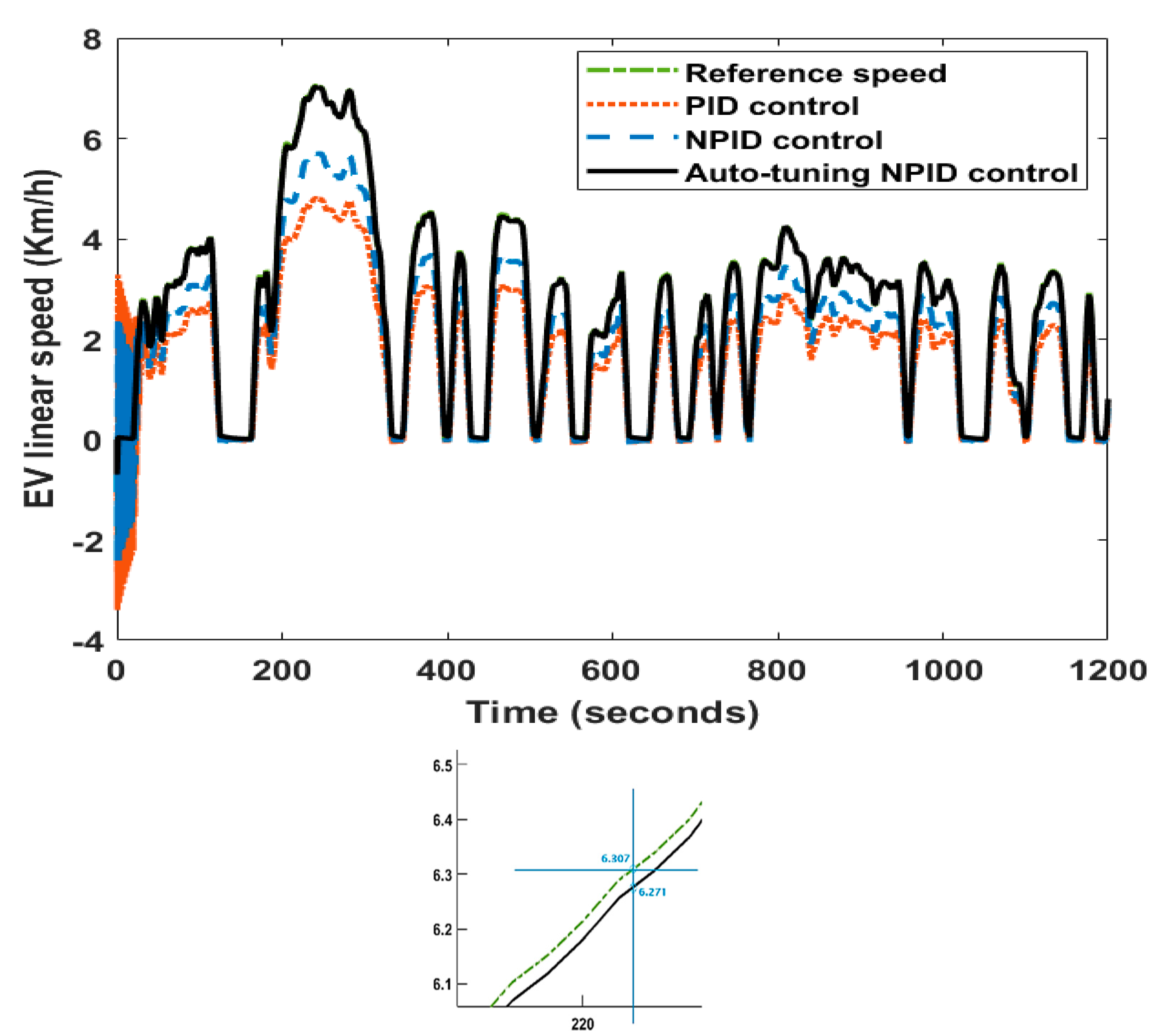
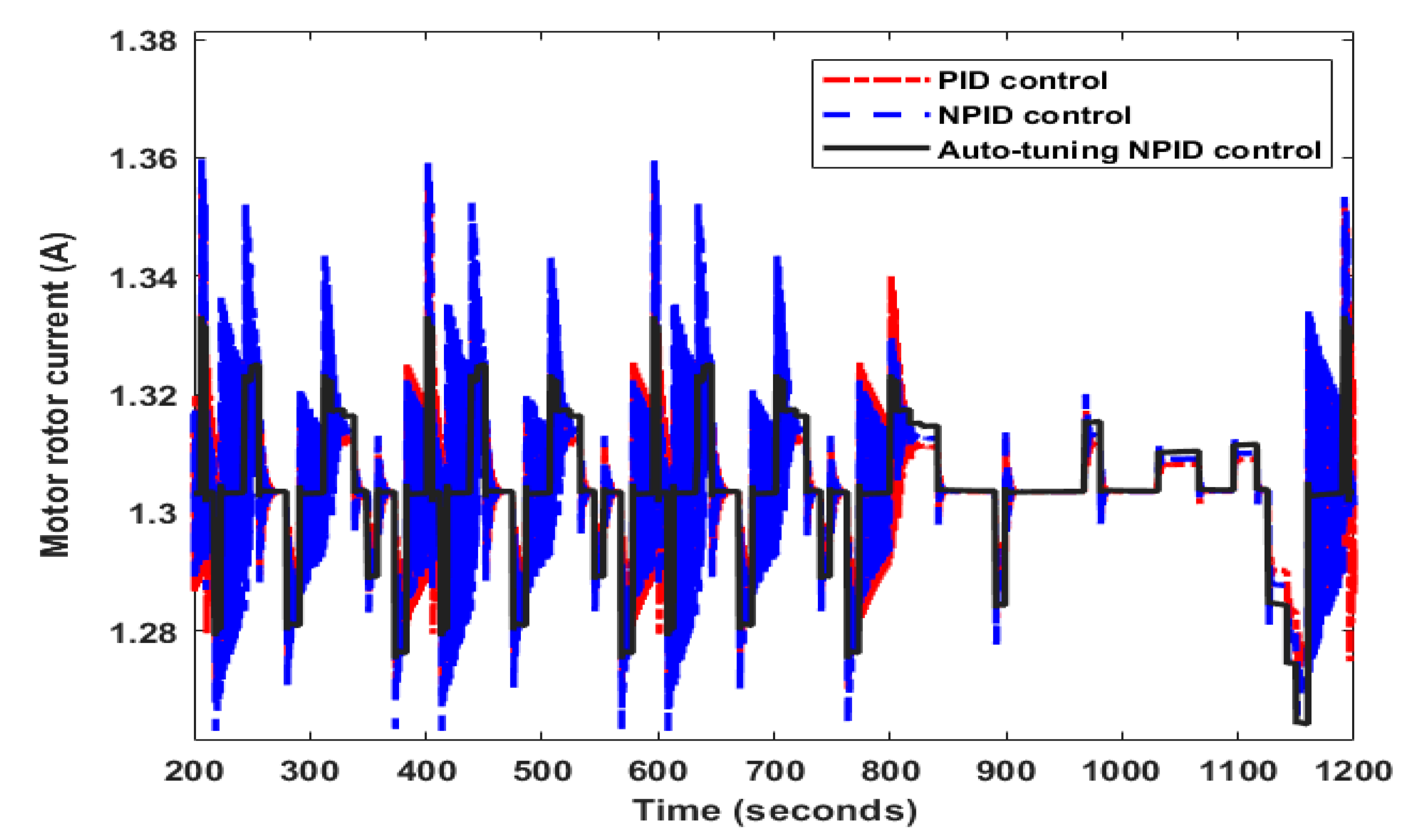
| Symbol | Value | Symbol | Value |
|---|---|---|---|
| + | 6.008 mH | 800 kg | |
| + | 0.12 | 1.8 m2 | |
| 0.001 mH | 1.25 (kg/m3) | ||
| 78 A (250 max) | 0 | ||
| 0:48 V | 0.3 | ||
| 0.0002 N.M.s | 0.015 | ||
| 0.05 Kg.m2 | 11 | ||
| 25 Km/h | r | 0.25 m |
| Parameter | Variation % |
|---|---|
| Ra + Rf | +10 |
| La + Lf | −20 |
| r | +25 |
| J | −20 |
| m | +30 |
| Cd | −20 |
| μrr | +30 |
| Controller Type | Parameter | Value |
|---|---|---|
| PID control | 5.254 | |
| 0.05 | ||
| 0.02 | ||
| NPID Control | 10.23 | |
| 2.23 | ||
| 1.58 | ||
| 0.25 | ||
| 0.34 | ||
| 0.01 | ||
| Auto-Tuning NPID Control | (0) | 6.35 |
| 0.125 | ||
| 2.31 | ||
| 0.45 | ||
| 0.69 | ||
| 0.78 |
| Controller Type | Peak Current (A) | Average Current (A) |
|---|---|---|
| PID controller | 1.35 | 0.912 |
| NPID controller | 1.36 | 0.851 |
| Auto-tuning NPID controller | 1.33 | 0.712 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shamseldin, M.A. Design of Auto-Tuning Nonlinear PID Tracking Speed Control for Electric Vehicle with Uncertainty Consideration. World Electr. Veh. J. 2023, 14, 78. https://doi.org/10.3390/wevj14040078
Shamseldin MA. Design of Auto-Tuning Nonlinear PID Tracking Speed Control for Electric Vehicle with Uncertainty Consideration. World Electric Vehicle Journal. 2023; 14(4):78. https://doi.org/10.3390/wevj14040078
Chicago/Turabian StyleShamseldin, Mohamed A. 2023. "Design of Auto-Tuning Nonlinear PID Tracking Speed Control for Electric Vehicle with Uncertainty Consideration" World Electric Vehicle Journal 14, no. 4: 78. https://doi.org/10.3390/wevj14040078
APA StyleShamseldin, M. A. (2023). Design of Auto-Tuning Nonlinear PID Tracking Speed Control for Electric Vehicle with Uncertainty Consideration. World Electric Vehicle Journal, 14(4), 78. https://doi.org/10.3390/wevj14040078







