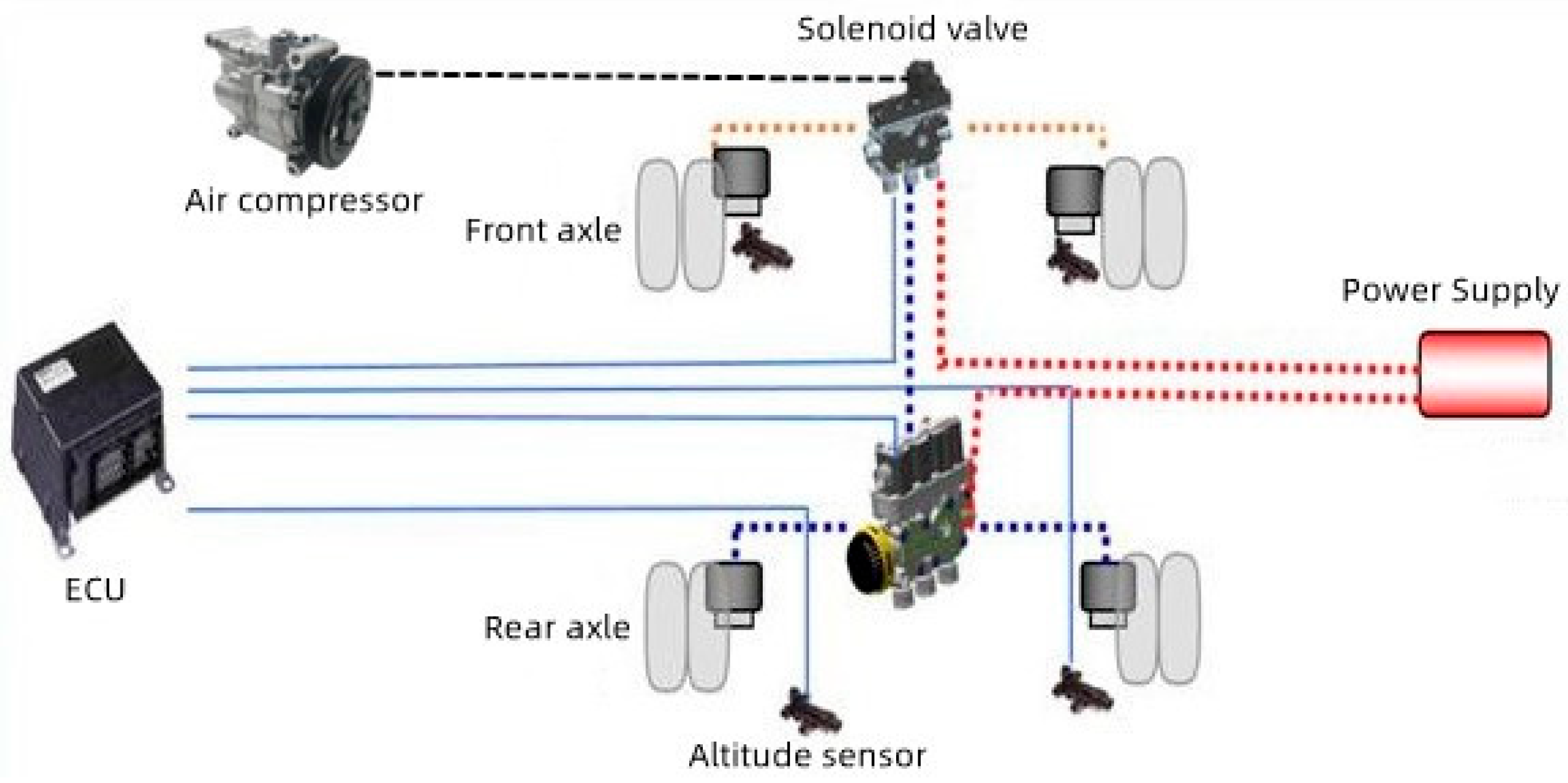
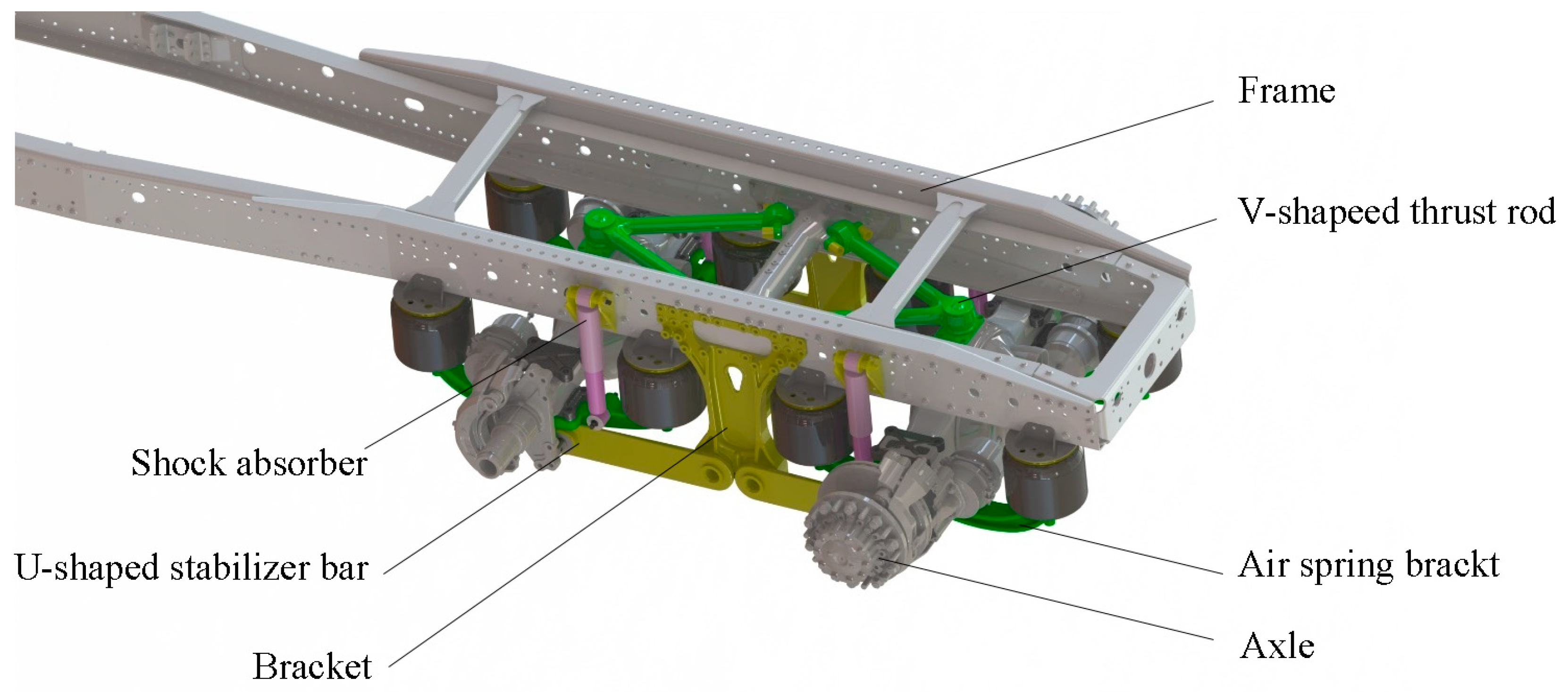
The suspension system is a crucial component of a heavy vehicle’s chassis, as it greatly impacts the ride comfort. An active air suspension system adjusts its stiffness and damping in real time, based on the uneven and bumpy road conditions, enabling the vehicle to achieve optimal driving conditions. The active air suspension system possesses excellent shock absorption performance and stability, significantly reducing the cab’s heaving and the trailer’s shaking during heavy vehicle driving, minimizing cargo damage and reducing driver fatigue. The use of air suspension in heavy trucks, especially heavy truck traction vehicles, is widespread in countries with developed automotive industries such as Europe, America, and Japan. It is predicted that in the next few years, air suspension systems will become the mainstream configuration of heavy vehicles [
1,
2,
3,
4].
Researchers from various countries have conducted extensive studies on active air suspension systems, including control strategies and other related aspects. For instance, Christian Graf et al. designed a force-controlled air spring for active suspension in commercial vehicle cockpits, whereby the damping forces of the air spring are generated by varying the air mass within its volume [
5]. Nguyen Van Tuan et al. aimed to improve the performance of the semi-trailer air suspension system by taking the dynamic load coefficient (DLC) as the objective function, discussing the optimization design method of the geometric parameters of the air spring suspension system [
6]. Wang Shaohua et al. from Jiangsu University completed the vehicle modeling of the air suspension of a bus and established a complete multibody dynamic model of the vehicle. They analyzed the matching damping of the air spring suspension, selecting body vertical acceleration, suspension working space, and dynamic tire load as performance indices in four typical working conditions [
7]. Cheng Yue, a doctoral student at Jilin University, conducted an optimization and experimental study on the parameter matching of the bus air suspension system, and the results proved the correctness and practicality of the optimal control method [
8,
9,
10,
11,
12,
13]. Yan Tianyi et al. conducted comprehensive testing on the air suspension system, including stiffness testing, damping testing, and on-road vehicle testing. Through in-depth analysis and experimentation on the stiffness characteristics of the air suspension system, they fitted the relationship curve between the stiffness of the air spring and the inflation/deflation time. In the damping testing, they compared and evaluated different testing methods, finding that using the basic excitation method yielded more realistic damping characteristics of the air spring. The real vehicle testing validated the authenticity and effectiveness of the control strategy, providing valuable insights for the control strategy of the electronic-controlled air suspension system [
14,
15,
16,
17]. Li Hailin et al. conducted an analysis and research on the air suspension of heavy-duty tractor trucks using the multibody dynamics software ADAMS. They optimized the layout and basic parameters of the guiding rod system in the air suspension and further performed vehicle optimization using ADAMS/Insight, resulting in a more rational arrangement of the air suspension guiding rod system. Additionally, they conducted theoretical analysis and utilized the orthogonal experimental method to study the design and performance of the air springs, providing solutions for improving aspects such as the vehicle’s brake nodding, acceleration squat, and lateral stability [
18,
19,
20,
21,
22,
23]. To evaluate the performance of control damping (CD) and control air spring (CAS) of the vehicle air suspension system regarding driving comfort and road friendliness, Nguyen V. et al. proposed a three-dimensional (3D), nonlinear dynamic model of heavy trucks with 14 degrees of freedom (DOF) and an optimal fuzzy control (OFC) with control rules optimized by genetic algorithms (GAs) [
24]. Yang Chen et al. designed the traditional air suspension to improve the dynamic response of the suspension body to body roll, enhancing the vehicle’s handling and stability [
25]. Lastly, Ma Xinbo et al. considered the vehicle dynamics as a highly nonlinear model, proposing a new nonlinear predictive controller to deal with the multi-objective control requirements of the vehicle system [
26]. Tuan Anh Nguyen et al. conducted research on methods for controlling active suspension system operation, namely the AFSPIDF algorithm, OSMC algorithm, and integrated pneumatic suspension system. The AFSPIDF algorithm combines PID, SMC, and Fuzzy algorithms, significantly reducing vehicle vibration displacement and acceleration, thereby enhancing vehicle stability and comfort. The OSMC algorithm controls vehicle vibration using a quarter-dynamic model, maintaining stable interaction between the wheels and the road surface. The integrated pneumatic suspension system integrates pneumatic suspension and hydraulic actuators, resulting in a significant reduction in displacement and acceleration of the sprung mass under random excitation. These research findings demonstrate the advantages of these methods over traditional approaches, substantially improving vehicle performance and comfort [
27,
28,
29]. These studies mainly focused on the structural design, control strategies, modeling, and simulation of air suspension or active suspension, with less involvement in the control system design and control strategy research for active air suspension in heavy-duty vehicles.
This paper presents the design of an active air suspension system for a 6 × 4 heavy vehicle, along with a detailed study and analysis of the height regulation control strategy of the active air suspension. It not only addresses the key issue of customizing an active air suspension system for heavy vehicles but also introduces an advanced fuzzy PID control strategy, setting a new standard for enhancing ride comfort and overall driving performance. The innovative combination of fuzzy logic and PID control bestows adaptability and intelligence upon the suspension system, paving the way for the continuous evolution of heavy vehicle technology towards a safer, more efficient, and comfortable future. The structure of this paper will unfold as follows. Firstly,
Section 1 provided an introduction, introducing the background and objectives of this study, emphasizing the significance and necessity of active air suspension systems in the field of automotive engineering. Next,
Section 2 will comprehensively describe the design of the active air suspension system, including its working principles, structural design, and the design of the air suspension height adjustment controller. In
Section 3, we will elucidate the modeling process of the active air suspension system, encompassing the establishment of the pavement excitation model and the air suspension model, along with an introduction to the design method of the fuzzy PID controller. Subsequently,
Section 4 will present the simulation results and in-depth analysis, evaluating the performance of the active air suspension system under various operating conditions. Lastly,
Section 5 will summarize the research findings, provide conclusions and discussions, highlighting the research contributions of this paper and potential directions for future expansion. Through the aforementioned chapter arrangement, we aim to systematically present the research content and outcomes of this study, offering readers a clear guide to the paper’s structure.