Quad-Rotor Unmanned Aerial Vehicle Path Planning Based on the Target Bias Extension and Dynamic Step Size RRT* Algorithm
Abstract
1. Introduction
- When the path is planned, the RRT* algorithm suffers from slow convergence speed and poor target orientation;
- In a complex terrain environment, due to the fixed expansion step size, the path of the quad-rotor UAVs cannot be dynamically adjusted, resulting in the failure of the RRT* algorithm to determine the optimal path, and the path planning will be sustainably inefficient;
- The flight path is tortuous during path planning, and it must meet the kinematic constraints for the quad-rotor UAVs to fly smoothly.
- During path searches, the probability threshold should be changed, and the range areas near the target point should be set as the target bias, thus allowing the algorithm to adapt to different environments while strengthening its target-oriented nature.
- We adjust the step size of the quad-rotor UAVs through obstacles in a complex terrain environment in real-time. When path searching begins, the UAV is far away from the target point and the obstacles. A large step size and a fixed step size are used to search the path in order to improve the path-searching efficiency of the algorithm. When the UAV is close to the target point and the obstacles, the search expansion is carried out in small steps, guaranteeing that the UAV will not collide with any obstacles and arrive at the target point exactly.
- For the polyline path, the B-spline curve interpolation method was used to smooth the path, allowing for the determination of the optimal flight path for quad-rotor UAVs.
2. Fundamentals of the RRT* Algorithm
3. TD-RRT* Algorithm
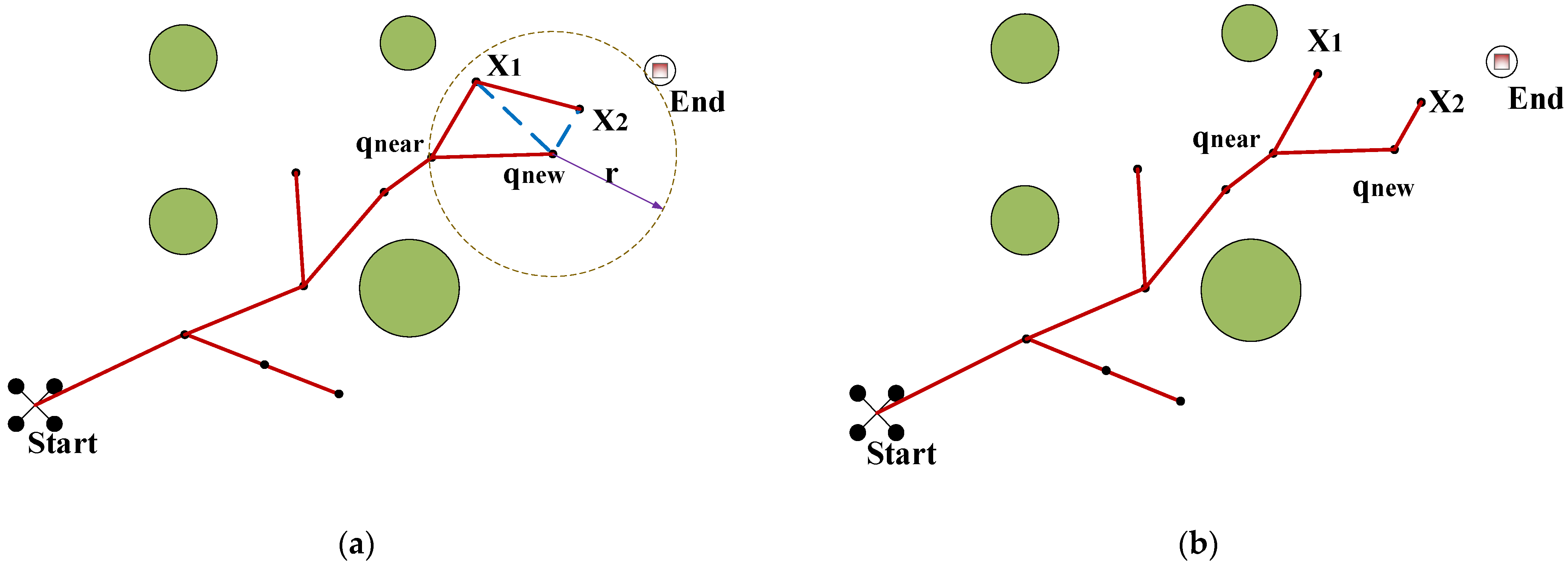
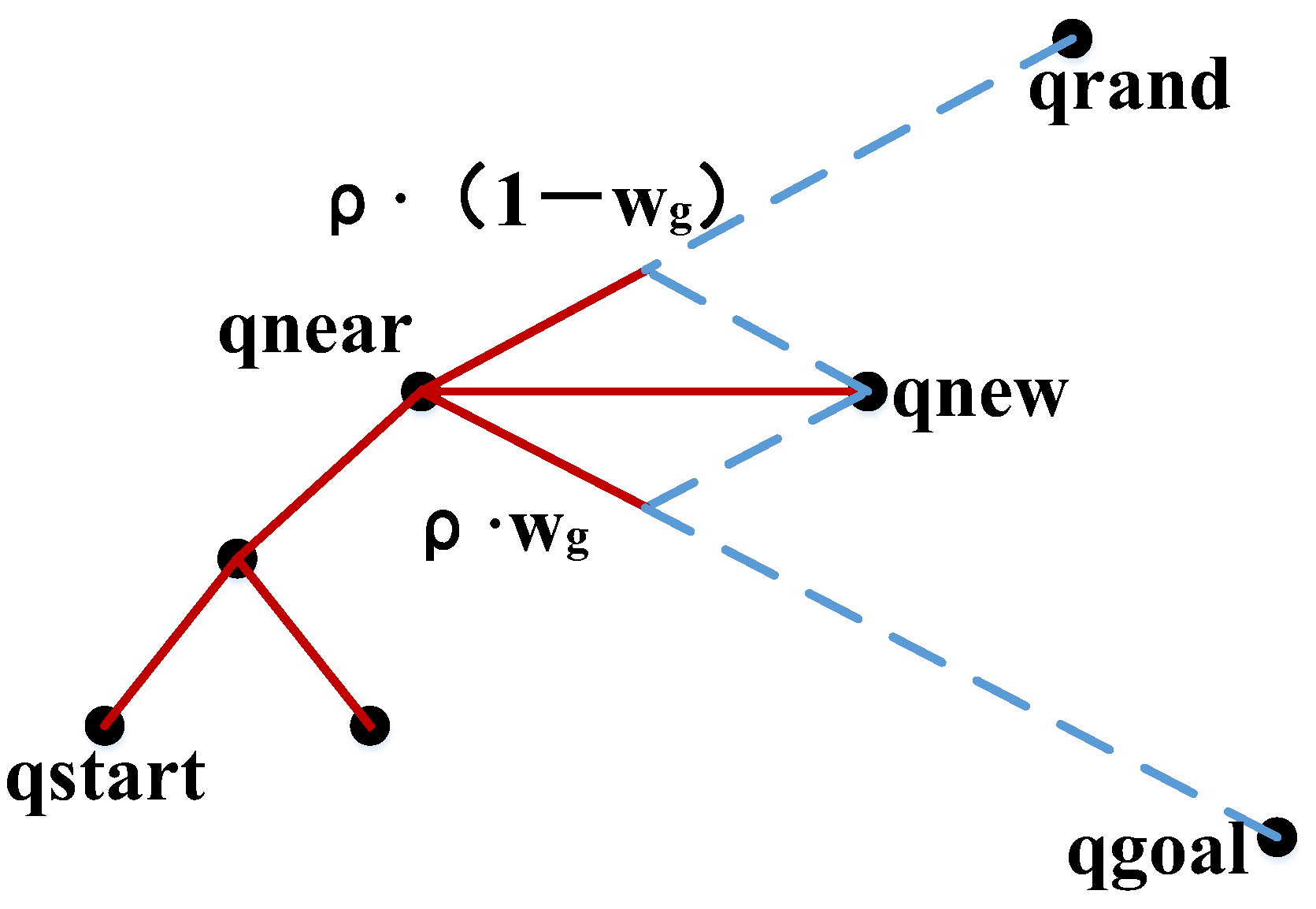
3.1. Target Bias Expansion
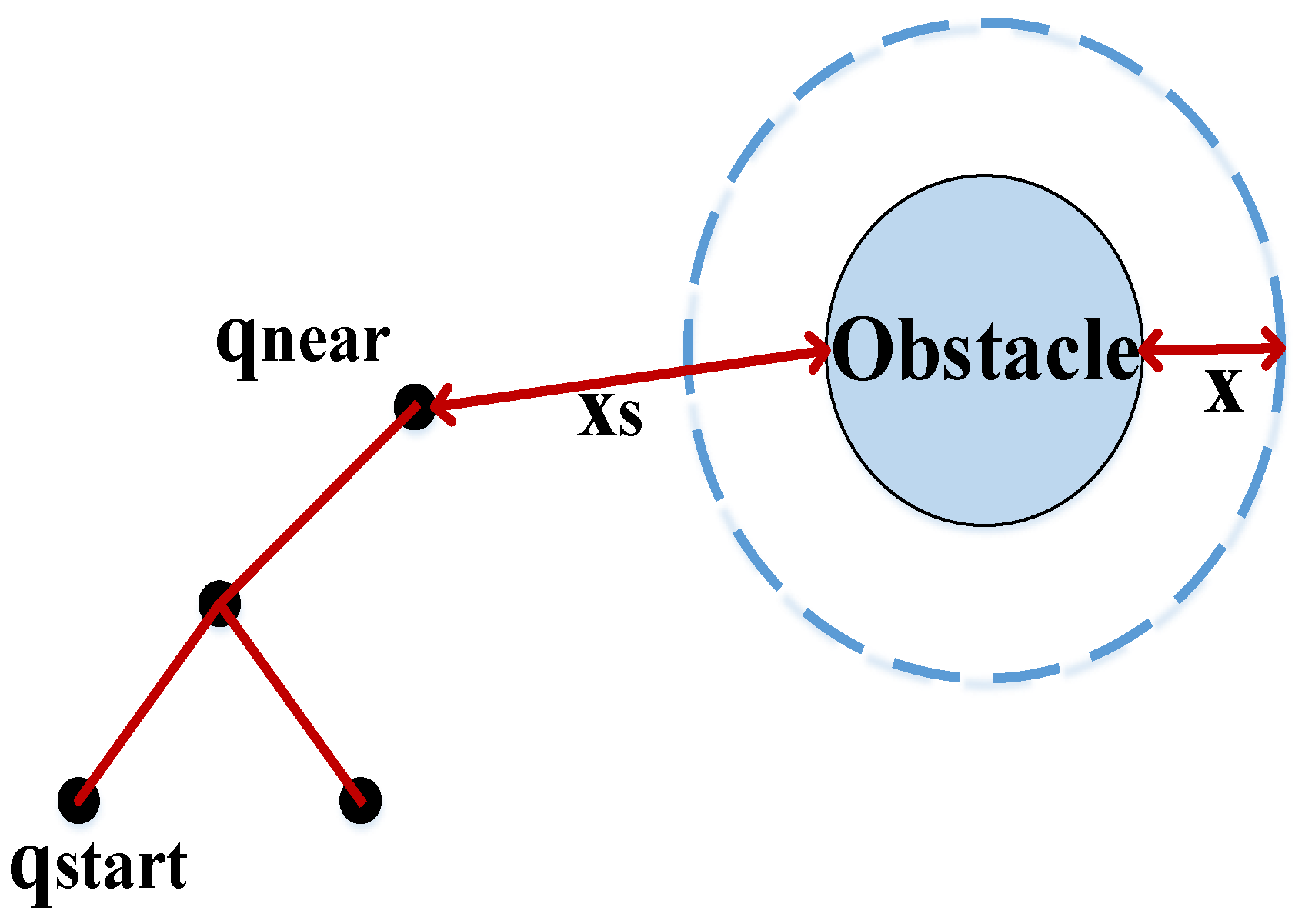
3.2. Dynamic Step Size
3.3. Path-Smoothing Processing
3.4. Flowchart of the TD-RRT* Algorithm
4. Simulation Experiments
4.1. Experimental Environment
- Operating System—Windows10 (64 bits);
- Computer graphics cards—NVIDIA GeForce GTX 1650;
- Processor (CPU)—Intel (R) Core (TM) i5-10400F CPU @ 2.90 GHz.
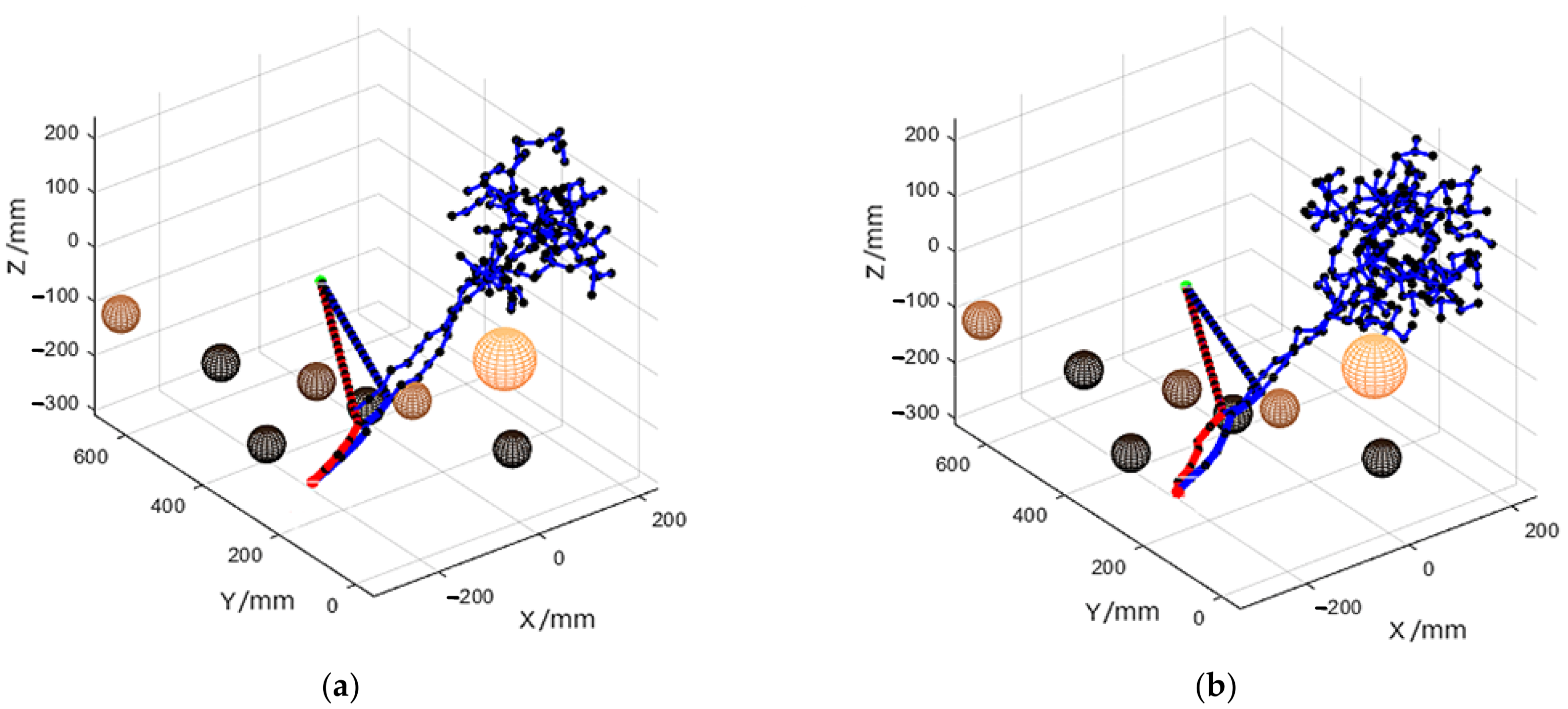
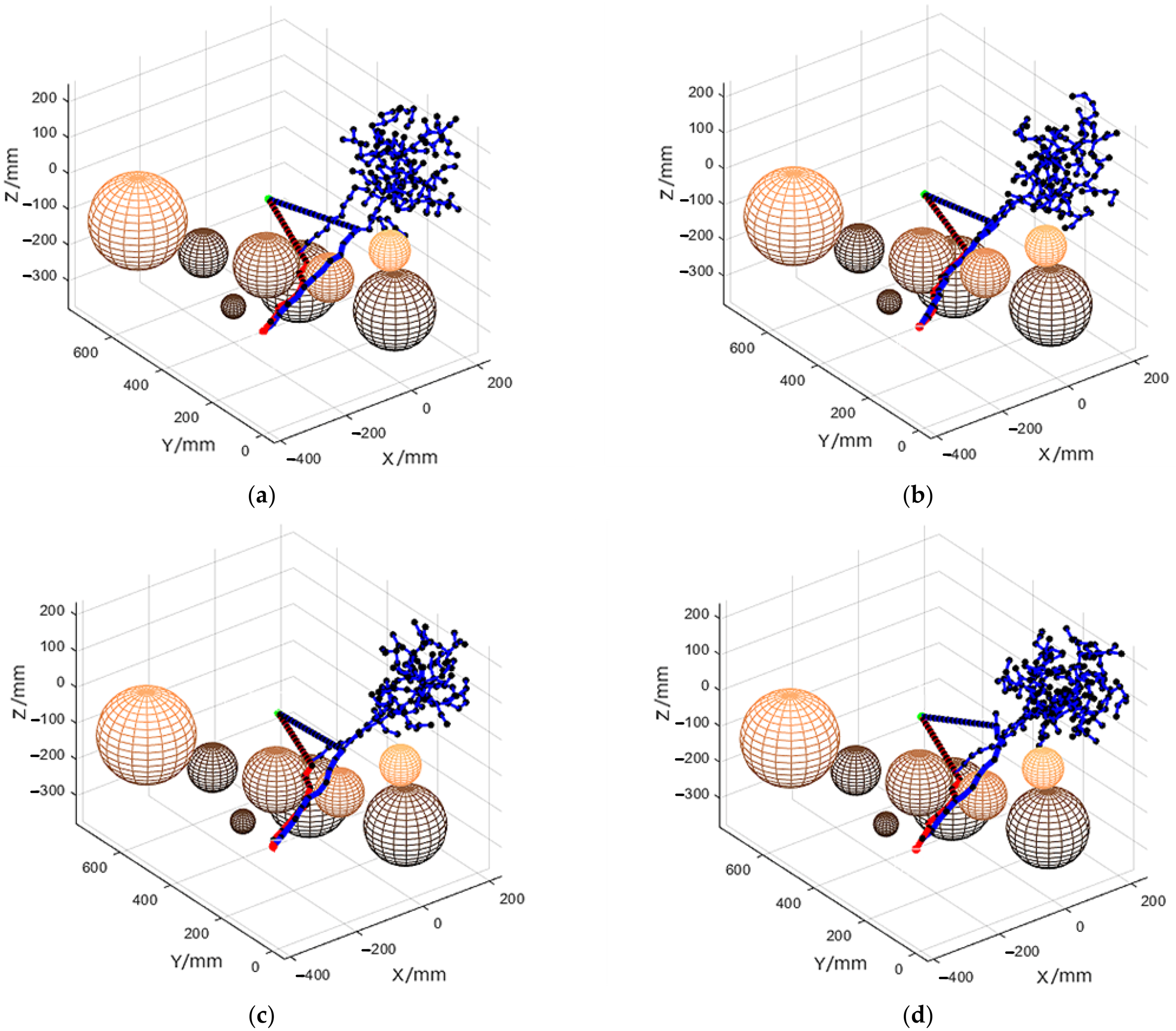
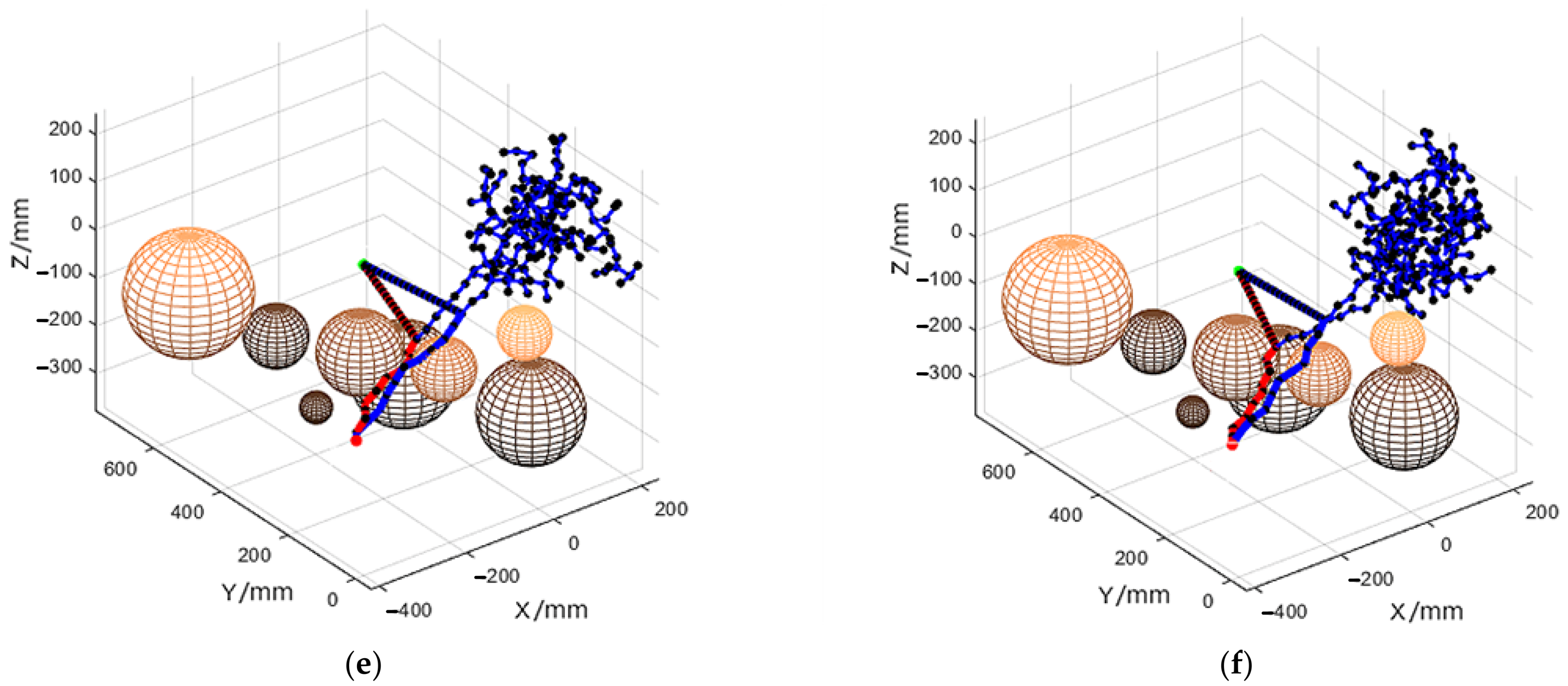
4.2. Simulation Experiment
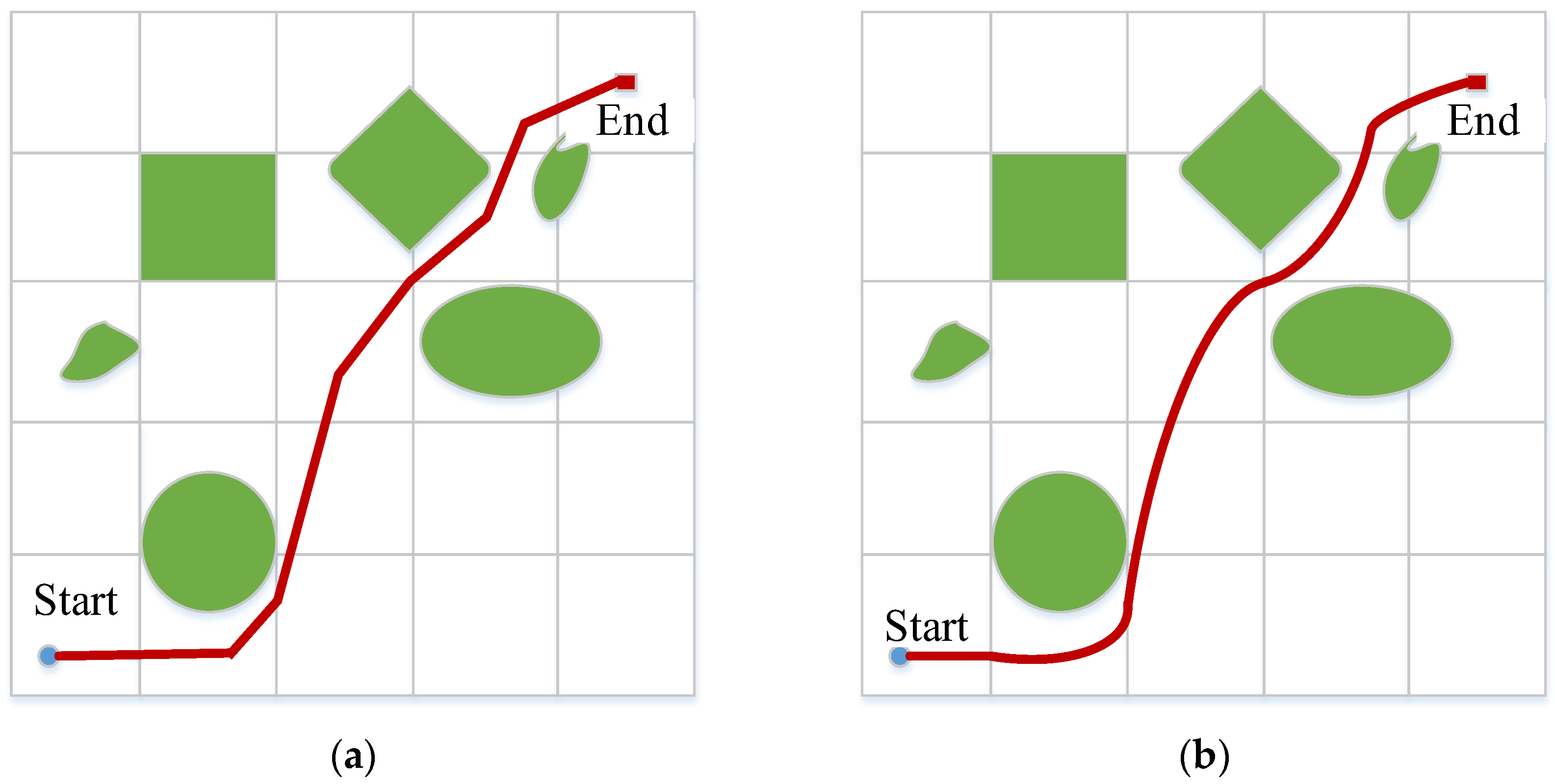
4.3. Path-Planning Efficiency Analysis
4.4. Analysis of Path Optimization Effect
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lyu, X.M.; Zhou, J.N.; Gu, H.W.; Li, Z.X.; Shen, S.J.; Zhang, F. Disturbance Observer Based Hovering Control of Quadrotor Tail-Sitter VTOL UAV Using Synthesis. IEEE Robot. Autom. Lett. 2018, 14, 2910–2917. [Google Scholar] [CrossRef]
- Yunes, A.; Murat, M.; Ayman, K.; Gamal, E. A numerically-stable trajectory generation and optimization algorithm for autonomous quadrotor UAV. Robot. Auton. Syst. 2023, 170, 104532. [Google Scholar]
- Liu, Y.Q.; Xu, D.; Cheng, G.; Chen, G. UAV fast trajectory planning method based on improved A~* algorithm. Flight Mech. 2020, 38, 40–46. [Google Scholar]
- Diao, Q.F.; Zhang, J.F.; Liu, M.; Yang, J.X. A Disaster Relief UAV Path Planning Based on APF-IRRT* Fusion Algorithm. Drones 2023, 7, 323. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Z.Q.; Sun, X.H.; Sun, Q.L.; Sun, M.W. Dynamic surface attitude control of quadrotor UAV based on disturbance rejection. J. Jilin Univ. Eng. Ed. 2019, 49, 562–569. [Google Scholar]
- Qi, G.Y.; Huang, D.H. Modeling and dynamical analysis of a small-scale unmanned helirotor. Nonlinear Dyn. Int. J. Nonlinear Dyn. Chaos Eng. Syst. 2019, 98, 2131–2145. [Google Scholar]
- Zhou, L.H.; Zhang, J.Q.; Dou, J.X.; Wen, B.C. A fuzzy adaptive backstepping control based on mass observer for trajectory tracking of a quadrotor UAV. Int. J. Adapt. Control Signal Process. 2018, 32, 1675–1693. [Google Scholar] [CrossRef]
- Sun, W.Z.; Liu, X.C.; Wu, S.; Cai, C.W. Design of fixed-point multi-rotor UAV wireless charging system for border patrol. J. Electr. Mach. Control 2023, in press.
- Wei, T.; Long, C. Path planning of mobile robot based on improved genetic algorithm. J. Beihang Univ. 2020, 46, 703–711. [Google Scholar] [CrossRef]
- Chen, Q.L.; He, Q.; Zhang, D.M. UAV Path Planning Based on an Improved Chimp Optimization Algorithm. Axioms 2023, 12, 702. [Google Scholar] [CrossRef]
- Gong, H.; Ni, C.; Wang, P.; Cheng, N. Smooth path planning method based on Dijkstra algorithm. J. Beihang Univ. 2023, in press.
- Sun, H.; Yuan, Y.; Zhang, Q.; Zhang, X.B. Aviation cable path planning method based on improved A~* algorithm. China Mech. Eng. 2023, 34, 1958–1966, 1974. [Google Scholar]
- Fransen, K.; van Eekelen, J. Efficient path planning for automated guided vehicles using a* (astar) algorithm incorporating turning costs in search heuristic. Int. J. Prod. Res. 2023, 61, 707–725. [Google Scholar] [CrossRef]
- Bai, X.; Jiang, H.; Cui, J.; Lu, K.; Chen, P.; Zhang, M. UAV Path Planning Based on Improved A and DWA Algorithms. Int. J. Aerosp. Eng. 2021, 2021, 4511252. [Google Scholar] [CrossRef]
- Xin, P.; Wang, Y.H.; Liu, X.L.; Ma, X.Q.; Xu, D. Optimize and improve the path planning algorithm of RRT and artificial potential field method. Comput. Integr. Manuf. Syst. 2023, 29, 2899–2907. [Google Scholar]
- Tamoor, A.K.; Shuai, L.; Seifedine, K.; Yunyoung, N. Control Framework for Trajectory Planning of Soft Manipulator Using Optimized RRT Algorithm. IEEE Access 2020, 8, 171730–171743. [Google Scholar]
- Yu, F.J.; Shang, H.Q.; Zhu, Q.L.; Zhang, H.S.; Chen, Y. An efficient RRT-based motion planning algorithm for autonomous underwater vehicles under cylindrical sampling constraints. Auton. Robot. 2023, 47, 281–297. [Google Scholar] [CrossRef]
- Huang, G.; Ma, Q. Research on path planning algorithm of autonomous vehicles based on improved RRT algorithm. Int. J. Intell. Transp. Syst. Res. 2022, 20, 170–180. [Google Scholar] [CrossRef]
- Li, J.; Liu, H.; Lai, K.K.; Ram, B. Vehicle and UAV Collaborative Delivery Path Optimization Model. Mathematics 2022, 10, 3744. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, T.; Du, L.; Hu, Y.; Liu, H. Local path planning of autonomous vehicle based on an improved heuristic bi-rrt algorithm in dynamic obstacle avoidance environment. Sensors 2022, 22, 7968. [Google Scholar] [CrossRef]
- Meng, B.H.; Godage, I.S.; Kanj, I. RRT*-based Path Planning for Continuum Arms. IEEE Robot. Autom. Lett. 2022, 7, 6830–6837. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Liu, X.; Jiang, W.; Zhang, W. Collision-Free 4D Dynamic Path Planning for Multiple UAVs Based on Dynamic Priority RRT* and Artificial Potential Field. Drones 2023, 7, 180. [Google Scholar] [CrossRef]
- Wan, X.; Ye, Y.; Leitao, Y.; Zhu, L. A global path planning algorithm based on improved RRT*. Control Decis. 2022, 37, 829–838. [Google Scholar]
- Li, Y.; Wei, W.; Gao, Y.; Wang, D.; Fan, Z. PQ-RRT*: An improved path planning algorithm for mobile robots. Expert Syst. Appl. 2020, 152, 113425. [Google Scholar] [CrossRef]
- Fan, J.; Chen, X.; Liang, X. UAV trajectory planning based on bi-directional APF-RRT* algorithm with goal-biased. Expert Syst. Appl. 2023, 213, 119137. [Google Scholar] [CrossRef]
- Nayagam, R.D.; Selvathi, D.; Geeta, R.; Gopinath, D.; Sivakumar, G. Mobile Application based Indoor Positioning and Navigational System using Dijkstra’s Algorithm. J. Phys. Conf. Ser. 2023, 2466, 012007. [Google Scholar] [CrossRef]
- Du, Y.W. Multi-UAV Search and Rescue with Enhanced A* Algorithm Path Planning in 3D Environment. Int. J. Aerosp. Eng. 2023, 2023, 8614117. [Google Scholar] [CrossRef]
- Melchiorre, M.; Salamina, L.; Scimmi, S.L.; Pastorelli, S. Experiments on the Artificial Potential Field with Local Attractors for Mobile Robot Navigation. Robotics 2023, 12, 81. [Google Scholar] [CrossRef]
- Luo, H.; Jiang, T.; Zhou, N.; Xu, L.; Tan, X.M.; Cheng, Y.J. Improved two-stage smooth search algorithm for RRT. Comput. Eng. Appl. 2022, 58, 74–84. [Google Scholar]
- Gu, Z.L.; Liu, Y.; Sun, W.B.; Yue, G.; Sun, S.W. UAV dynamic route planning algorithm based on RRT. Comput. Sci. 2023, 50, 65–69. [Google Scholar]
- Chen, D.; Diao, X.Y.; Chen, W.; Gao, P.; Ge, L.Q. Online rolling path planning of UAV based on AI-RRT* algorithm. Flight Mech. 2023, 41, 54–60. [Google Scholar]
- Yang, X.C.; Du, Y.L.; Bu, Y.N.; Liu, Y.B.; Gao, C. Online three-dimensional RRT~* collaborative route planning based on hierarchical decomposition. Syst. Eng. Electron. Technol. 2023, 45, 1409–1419. [Google Scholar]
- Chen, J.T.; Li, H.Y.; Ren, H.R.; Lu, R.Q. Indoor collaborative path planning of high-rise firefighting UAV based on RRT forest algorithm. Acta Autom. Sin. 2021, 45, 1–12. [Google Scholar]
- Wang, F.B.; Gao, Y.F.; Chen, Z.; Gong, X.; Zhu, D.R.; Cong, W.L. A Path Planning Algorithm of Inspection Robots for Solar Power Plants Based on Improved RRT*. Electronics 2023, 12, 4455. [Google Scholar] [CrossRef]
- Long, H.Y.; Li, G.; Zhou, F.L.; Chen, T.F. Cooperative Dynamic Motion Planning for Dual Manipulator Arms Based on RRT*Smart-AD Algorithm. Sensors 2023, 23, 7759. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Gao, F.; Zhao, F.K. Research on Path Planning and Tracking Control of Autonomous Vehicles Based on Improved RRT* and PSO-LQR. Processes 2023, 11, 1841. [Google Scholar] [CrossRef]
- Fan, J.M.; Chen, X.; Wang, Y.; Chen, X.M. UAV trajectory planning in cluttered environments based on PF-RRT* algorithm with goal-biased strategy. Eng. Appl. Artif. Intell. 2022, 114, 105182. [Google Scholar] [CrossRef]
- Liao, B.; Wan, F.Y.; Hua, Y.; Ma, R.R.; Zhu, S.R.; Qing, X.L. F-RRT*: An improved path planning algorithm with improved initial solution and convergence rate. Expert Syst. Appl. 2021, 184, 115457. [Google Scholar] [CrossRef]
- Guo, Y.C.; Liu, X.X.; Jiang, W.; Zhang, W.G. HDP-TSRRT*: A Time-Space Cooperative Path Planning Algorithm for Multiple UAVs. Drones 2023, 7, 170. [Google Scholar] [CrossRef]
- Zhang, W.M.; Fu, Z.X. Path Planning of Mobile Robot Based on Improved RRT~* Algorithm. J. Huazhong Univ. Sci. Technol. Nat. Sci. Ed. 2021, 49, 31–36. [Google Scholar]
- Yi, H.W. Three-dimensional operation path planning of manipulator based on improved ant colony algorithm. Comput. Appl. Softw. 2014, 31, 302–304+307. [Google Scholar]
- Cengiz, B.; Sitki, O.; Melih, K.; Ismet, K. Dynamic Centripetal Parameterization Method for B-Spline Curve Interpolation. IEEE Access 2020, 8, 589–598. [Google Scholar]
- Chiaravalli, D.; Califano, F.; Biagiotti, L.; De, D.G. Physical-consistent behavior embodied in B-spline curves for robot path planning. IFAC Pap. 2018, 51, 306–311. [Google Scholar] [CrossRef]
- Zhou, D. Parametric path generation method for agricultural machinery harvesting operation. Agric. Eng. 2022, 12, 13–21. [Google Scholar]
- Xu, J.; Ren, C.F.; Zhang, X.N. Robot Time-Optimal Trajectory Planning Based on Quintic Polynomial Interpolation and Improved Harris Hawks Algorithm. Axioms 2023, 12, 245. [Google Scholar] [CrossRef]
- Wang, H.F.; Zhang, Y.; Zhu, Y.K.; Chen, X.B. Path Planning Algorithm for Mobile Robot Based on Improved Bidirectional RRT~*. J. Northeast. Univ. Nat. Sci. Ed. 2021, 42, 1065–1070, 1142. [Google Scholar]



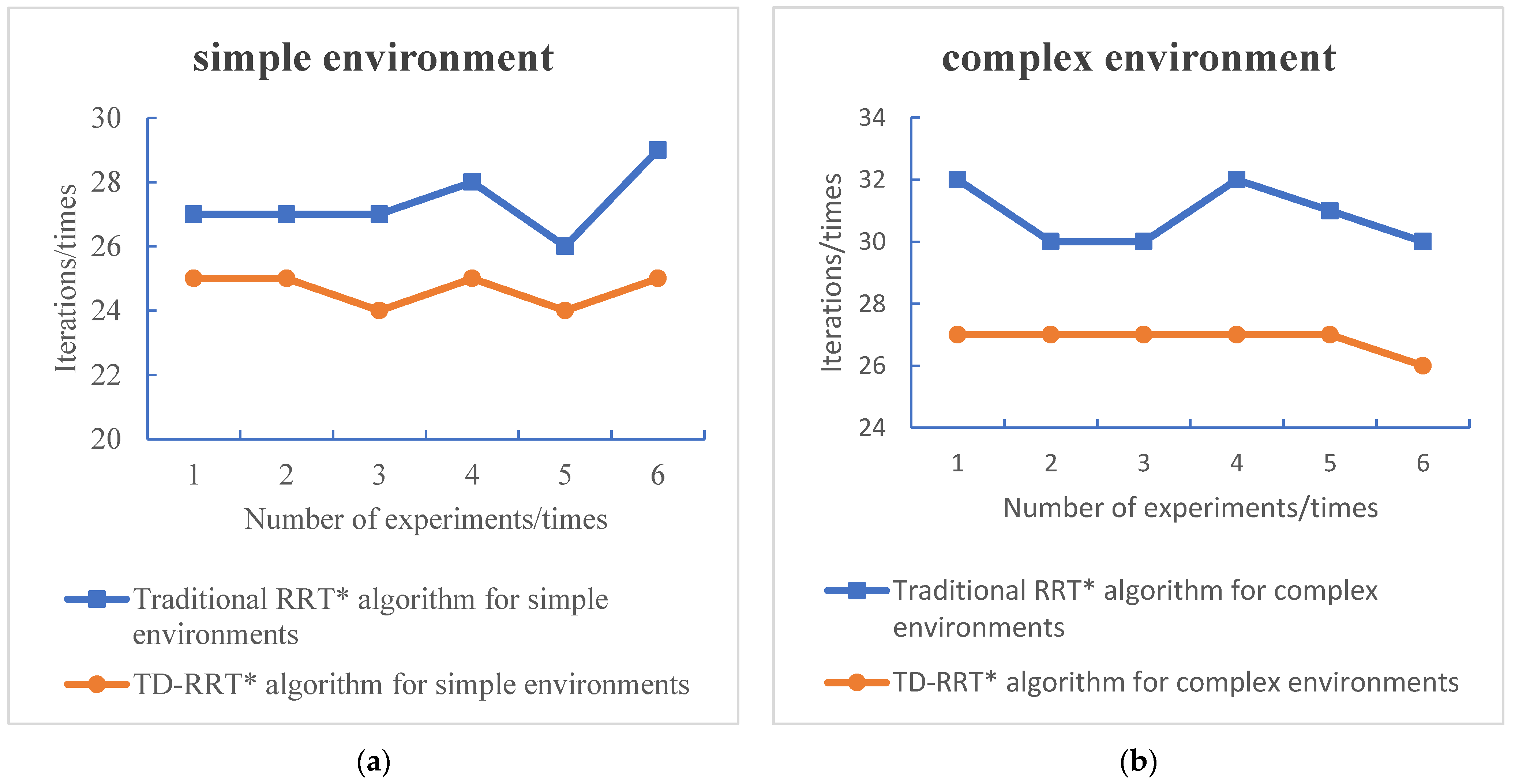
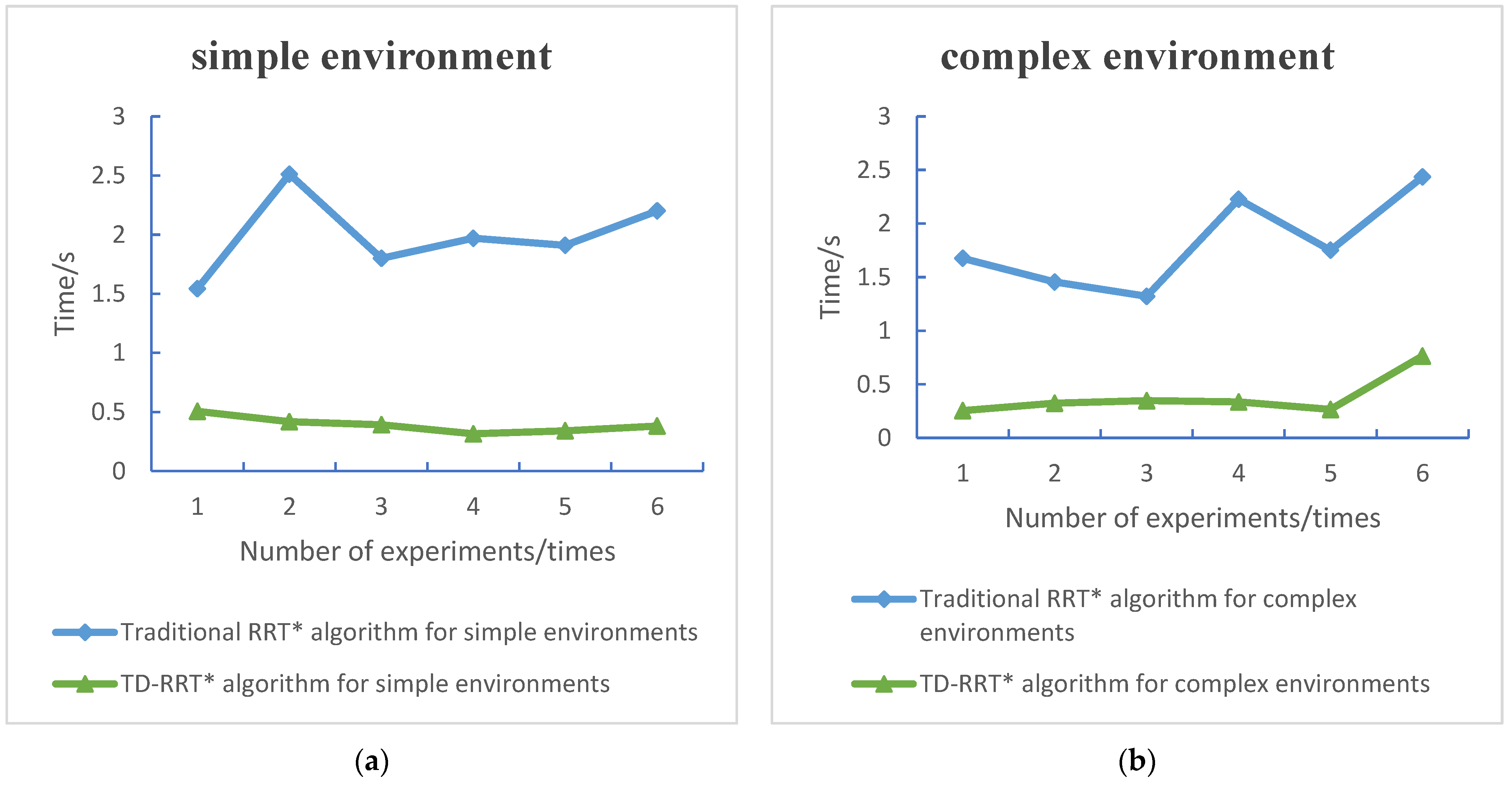
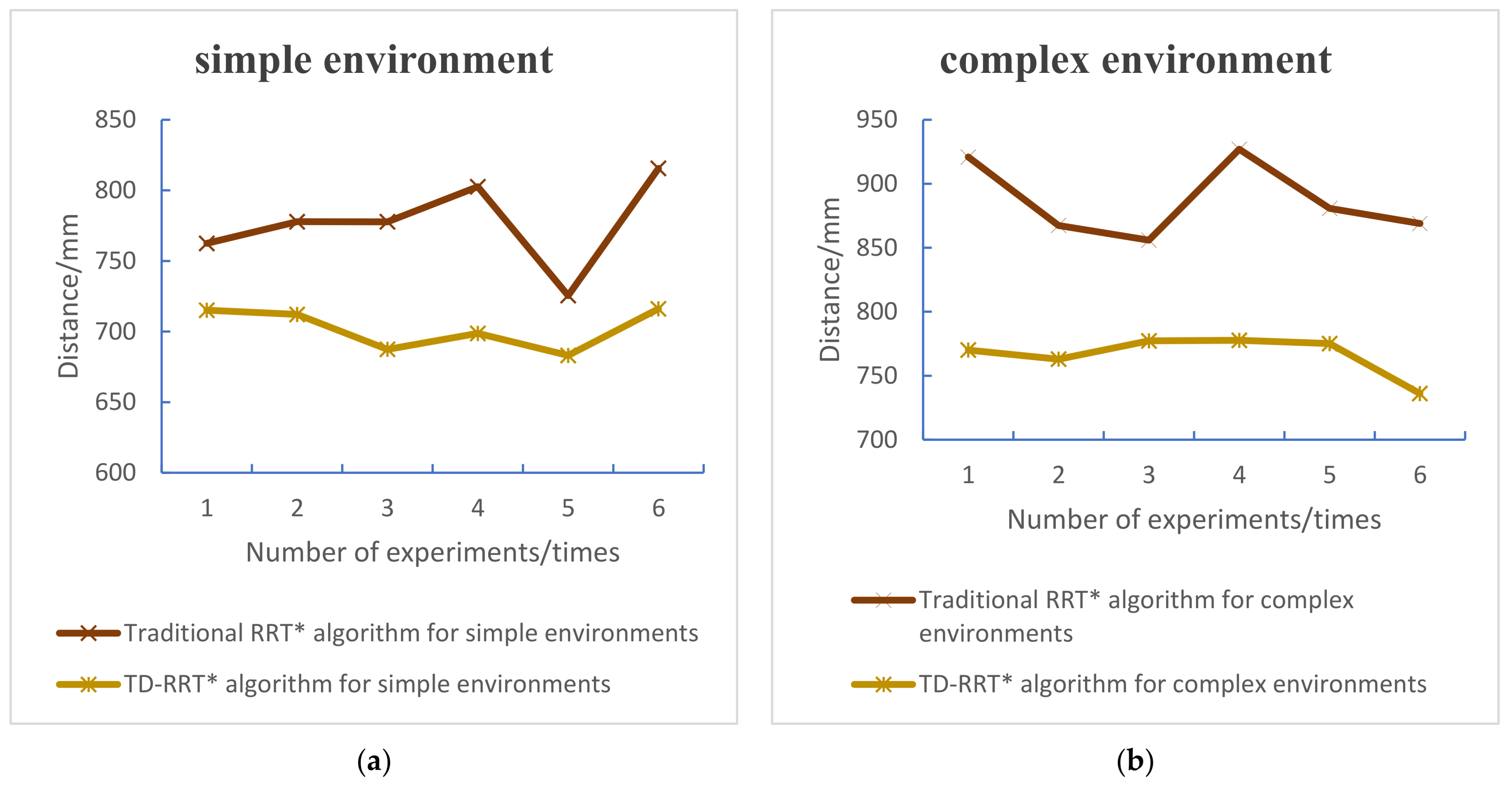
| Environments | Number of Experimental Groups | Algorithms | Travel Distance/mm | Number of Iterations | Timing/s |
|---|---|---|---|---|---|
| Simple environment | Group 1 | Traditional RRT* algorithm | 762.4299 | 27 | 1.5437 |
| TD-RRT* algorithm | 715.1080 | 25 | 0.5055 | ||
| Group 2 | Traditional RRT* algorithm | 777.7699 | 27 | 2.5113 | |
| TD-RRT* algorithm | 712.1347 | 25 | 0.4176 | ||
| Group 3 | Traditional RRT* algorithm | 777.7230 | 27 | 1.7996 | |
| TD-RRT* algorithm | 687.4352 | 24 | 0.3927 | ||
| Group 4 | Traditional RRT* algorithm | 802.5991 | 28 | 1.9696 | |
| TD-RRT* algorithm | 698.6941 | 25 | 0.3158 | ||
| Group 5 | Traditional RRT* algorithm | 725.4604 | 26 | 1.9095 | |
| TD-RRT* algorithm | 683.1005 | 24 | 0.3412 | ||
| Group 6 | Traditional RRT* algorithm | 815.5573 | 29 | 2.2013 | |
| TD-RRT* algorithm | 716.1098 | 25 | 0.3815 |
| Environments | Number of Experimental Groups | Algorithms | Travel Distance/mm | Number of Iterations | Timing/s |
|---|---|---|---|---|---|
| Complex environment | Group 1 | Traditional RRT* algorithm | 920.8943 | 32 | 1.6757 |
| TD-RRT* algorithm | 770.0329 | 27 | 0.2548 | ||
| Group 2 | Traditional RRT* algorithm | 867.4032 | 30 | 1.4547 | |
| TD-RRT* algorithm | 762.9468 | 27 | 0.3240 | ||
| Group 3 | Traditional RRT* algorithm | 855.9435 | 30 | 1.3218 | |
| TD-RRT* algorithm | 777.2276 | 27 | 0.3476 | ||
| Group 4 | Traditional RRT* algorithm | 926.9955 | 32 | 2.2267 | |
| TD-RRT* algorithm | 777.6863 | 27 | 0.3358 | ||
| Group 5 | Traditional RRT* algorithm | 880.7327 | 31 | 1.7511 | |
| TD-RRT* algorithm | 775.1276 | 27 | 0.2661 | ||
| Group 6 | Traditional RRT* algorithm | 868.9602 | 30 | 2.4354 | |
| TD-RRT* algorithm | 736.0981 | 26 | 0.7648 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, H.; Hou, X.; Xu, J.; Guan, B. Quad-Rotor Unmanned Aerial Vehicle Path Planning Based on the Target Bias Extension and Dynamic Step Size RRT* Algorithm. World Electr. Veh. J. 2024, 15, 29. https://doi.org/10.3390/wevj15010029
Gao H, Hou X, Xu J, Guan B. Quad-Rotor Unmanned Aerial Vehicle Path Planning Based on the Target Bias Extension and Dynamic Step Size RRT* Algorithm. World Electric Vehicle Journal. 2024; 15(1):29. https://doi.org/10.3390/wevj15010029
Chicago/Turabian StyleGao, Haitao, Xiaozhu Hou, Jiangpeng Xu, and Banggui Guan. 2024. "Quad-Rotor Unmanned Aerial Vehicle Path Planning Based on the Target Bias Extension and Dynamic Step Size RRT* Algorithm" World Electric Vehicle Journal 15, no. 1: 29. https://doi.org/10.3390/wevj15010029
APA StyleGao, H., Hou, X., Xu, J., & Guan, B. (2024). Quad-Rotor Unmanned Aerial Vehicle Path Planning Based on the Target Bias Extension and Dynamic Step Size RRT* Algorithm. World Electric Vehicle Journal, 15(1), 29. https://doi.org/10.3390/wevj15010029






