Vehicle-To-Grid (V2G) Charging and Discharging Strategies of an Integrated Supply–Demand Mechanism and User Behavior: A Recurrent Proximal Policy Optimization Approach

Abstract

With the increasing global demand for renewable energy and heightened environmental awareness, electric vehicles (EVs) are rapidly becoming a popular clean and efficient mode of transportation. However, the widespread adoption of EVs has presented several challenges, such as the lagging development of charging infrastructure, the impact on the power grid, and the dynamic changes in user charging behavior. To address these issues, this paper first proposes a vehicle-to-grid (V2G) optimization framework that responds to regional dynamic pricing. It also considers power balancing in charging and discharging stations when a large number of EVs are involved in scheduling, with the aim of maximizing the benefits for EV owners. Next, by leveraging the interaction between environmental states and the dynamic behavior of EVs, we design an optimization algorithm that combines the recurrent proximal policy optimization (RPPO) algorithm and long short-term memory (LSTM) networks. This approach enhances system convergence and improves grid stability while maximizing benefits for EV owners. Finally, a simulation platform is used to validate the practical application of the RPPO algorithm in optimizing V2G and grid-to-vehicle (G2V) charging strategies, providing significant theoretical foundations and technical support for the development of smart grids and sustainable transportation systems.

1. Introduction

With the growing global demand for renewable energy and the increasing awareness of the need for environmental protection, EVs are rapidly becoming a popular clean and efficient mode of transportation. However, the widespread adoption of EVs has introduced new challenges, such as the delayed construction of charging infrastructure, the impact of charging loads on the power grid, and the dynamic changes in user charging behavior, particularly in the integration of energy with V2G systems [1,2]. The effective management of EV charging and discharging is crucial for the stable operation of the power grid and the improvement of energy utilization efficiency [3]. With the rising number of EVs, peak charging demands may result in grid overload, potentially compromising the stability of the power supply [4]. Additionally, variations in electricity prices throughout the charging process, along with the differing charging durations, significantly influence both user costs and the overall vehicle usage experience [5]. Traditional charging strategies, such as Fixed-Time charging [6], priority charging [7], and dynamic pricing strategy charging, often struggle to cope with the dynamic changes in charging demand and grid load, leading to low charging efficiency, high costs, and decreased user satisfaction. Therefore, designing and optimizing EV charging strategies has become an urgent issue to address.

To address the challenges associated with EV charging, smart charging strategies have attracted substantial attention in both research and practical implementations. Utilizing big data, the Internet of Things (IoT), and artificial intelligence (AI), these strategies enable the dynamic adjustment of charging schedules to optimize the process, enhance efficiency, lower costs, and maintain grid stability. Considerable advancements have been achieved in smart charging strategies in recent years [8]. For example, Huang et al. [9] proposed a time-of-use pricing-based charging strategy, which dynamically adjusts charging plans by considering the actual charging needs of EV users and the grid load, ultimately optimizing the charging process, improving efficiency, and reducing costs. However, this method still faces limitations in dealing with prediction errors in charging demand and real-time dynamic changes. Li et al. [10] proposed a two-layer optimization method that optimizes the scheduling of EV charging stations in community energy systems by considering the uncertainty of renewable energy and flexible demand response. This strategy can optimize charging behavior based on real-time grid conditions, effectively addressing sudden changes in power demand, thus ensuring grid reliability and stability. However, its complexity and computational costs may limit its scalability. Noura et al. [11] proposed a battery health management optimization strategy aimed at extending battery life and reducing maintenance costs by optimizing the charging and discharging processes based on the actual health state of the battery. However, due to a lack of practical application and case analysis, the operational feasibility and scalability of this strategy are limited. Additionally, Zhou et al. [12] proposed a cost model and genetic algorithm-based method aimed at optimizing the location of charging stations, thus improving the efficiency and service quality of charging infrastructure. However, challenges remain in addressing the diverse needs and complexities in real-world applications.

Although significant progress has been made in optimizing charging efficiency, reducing costs, and managing grid loads, several challenges remain. These include how to more accurately predict charging demand, how to handle the complex scenarios of large-scale simultaneous EV charging, and how to maximize charging efficiency while ensuring EV user satisfaction. In summary, the research and application of smart charging strategies are of great practical significance and value in addressing the various challenges faced in EV charging, improving grid efficiency, and enhancing EV user satisfaction. By continuously exploring and optimizing smart charging strategies, robust support can be provided for the development of EVs and the construction of sustainable transportation systems.

In the pursuit of optimizing charging and discharging algorithms for electric vehicles, conventional mathematical optimization methods [13] and model predictive control [14] have been recognized as effective approaches for solving lower-complexity optimization challenges related to EVs. In particular, mixed-integer programming [15] has attracted considerable interest for its efficacy in the strategic scheduling of EV charging. This approach adeptly models the intricacies involved, including the timing of EVs’ arrivals and departures, and it incorporates multiple constraints like battery capacity, charging requirements, and variability in energy prices. However, as the number of decision variables and constraints has increased—along with the development of models, EV behavioral data, and grid and constraint studies—traditional charging optimization strategies have become inadequate to solve current problems. For instance, when charging point operators (CPO) [16] need to frequently rerun optimization algorithms, mathematical programming methods present significant challenges. This operational demand, especially against the backdrop of a significantly increased number of EVs expected in the future, imposes substantial limitations on the efficiency of mathematical programming methods in handling large-scale complex optimization problems.

1.1. Integrated V2G Architecture

In recent years, the interaction between EVs and the power grid, known as V2G technology, has been widely researched and applied. The goal is to optimize the efficiency of grid operation and increase the utilization of renewable energy through the bidirectional flow of energy and information. The V2G architecture allows EVs to feed electricity back to the grid during peak load periods and draw power from the grid during off-peak times, thus achieving the goal of peak shaving and valley filling [17]. This architecture not only improves the balance of grid loads but also enhances energy flexibility by managing the charging and discharging process of EVs. Huang et al. [18] proposed a V2G optimization model based on dynamic pricing, aiming to adjust the time-segmented electricity price in real time, encouraging EV owners to charge when electricity is cheap and feed power back to the grid during peak pricing periods, thereby reducing fluctuations in power costs. However, while this model alleviates peak load impacts on the grid to some extent, its limitation lies in the lack of consideration for the dynamic and uncertain behavior of EV users, particularly when facing rapidly changing grid conditions. On the other hand, bidirectional power flow in V2G technology has gradually become a core research topic. Triviño et al. [19] investigated strategies for EVs to achieve bidirectional energy flow with the grid at different times of the day, proposing a model based on optimization algorithms. This model not only enhances grid stability but also improves energy efficiency through peak shaving and valley filling. Additionally, Gough et al. [20] analyzed the potential of EVs to participate in frequency regulation in electricity markets, proposing a load management scheme based on bidirectional energy flow. This scheme predicts real-time grid load demand to optimize EVs’ charging and discharging behavior, thus maximizing economic benefits for vehicle owners while ensuring grid stability. Although current research has made significant progress in energy management and grid balancing in the V2G architecture, most existing methods rely on static time-segmented charging strategies, lacking real-time responsiveness to changes in EV user charging demand and grid load [21]. Traditional fixed strategies struggle to handle the uncertainty of EVs’ charging and discharging and their instantaneous impact on the grid, which is particularly evident in scenarios with complex user behavior and frequent grid load fluctuations. Therefore, designing intelligent, dynamically responsive optimization algorithms has become a key direction for future research on the V2G architecture. Alfaverh et al. [22] proposed an intelligent optimization strategy based on deep reinforcement learning, which comprehensively analyzes historical and real-time data to accurately predict EVs’ charging demand in dynamic environments and adjust charging scheduling strategies in real time, significantly improving the grid’s adaptability and the efficiency of EV charging. The further development of V2G technology will depend on the introduction of intelligent algorithms and data-driven optimization models. By combining big data anlysis and machine learning techniques, the complex fluctuations in grid loads and the dynamic demand for EV charging and discharging can be better handled, providing a solid technical foundation for the deep integration of smart grids and renewable energy [23].

1.2. V2G Charging Strategies Considering Multiple Objectives

Research on EV charging strategies has deepened, with increasing focus on multi-objective optimization in V2G charging strategies. These optimization goals include, but are not limited to, charging efficiency, charging costs, battery life, and grid stability [24]. To balance these often conflicting objectives, flexible and dynamic charging strategies must be designed to meet the diverse needs of EV users and the fluctuations in grid loads. Savari et al. [25] proposed a priority-based charging strategy, where charging priority is set according to the actual needs of EV users to improve charging efficiency and reduce waiting times. However, while this method effectively reduces charging congestion during high-demand periods, it may increase pressure on the grid when the load is already high, particularly when multiple EVs start charging simultaneously. Therefore, when designing charging strategies, it is crucial to consider not only charging efficiency but also the balance and stability of grid loads. To better cope with grid load fluctuations, Li et al. [26] proposed a two-layer optimization method that optimizes EVs’ charging behavior in community energy systems by jointly scheduling EV charging stations and renewable energy generation. In the first layer of optimization, the dynamic adjustment of EVs’ charging behavior is considered, allowing for flexible adjustments in charging time and power based on the real-time monitoring of grid conditions and demand changes. In the second layer of optimization, the scheduling of the grid and charging stations is further refined based on the uncertainty of renewable energy generation. This two-layer optimization approach significantly improves the adaptability of EV charging strategies while responding to grid demand in real time. In addition to charging efficiency and grid stability, battery life optimization is also an important objective in V2G charging strategy design. Shabani et al. [27] proposed an optimized charging strategy based on battery health, which dynamically adjusts the charging and discharging process according to the actual health status of the battery to extend its lifespan and reduce maintenance costs. However, the challenge of this approach in practical applications lies in the need for real-time monitoring of battery health, and prediction errors in battery status could affect its effectiveness. Although current research has made significant progress in optimizing charging efficiency, reducing costs, and extending battery life, many challenges remain. For instance, how to balance battery life, user satisfaction, and grid stability and how to effectively manage energy in scenarios where large numbers of EVs are simultaneously connected are issues that still need to be addressed in the future [28]. Farhadi et al. [29] proposed an intelligent scheduling method that introduces a data-driven multi-objective optimization algorithm, allowing the real-time adjustment of charging strategies in dynamic environments. This method not only improves charging efficiency but also achieves a balance between different objectives. In conclusion, the design and optimization of V2G charging strategies considering multiple objectives requires comprehensive consideration of EV users’ needs, while ensuring rational grid load distribution and battery life optimization. In the future, as intelligent algorithms and big data technologies advance, the multi-objective optimization of V2G charging strategies will become more intelligent and dynamically responsive [30].

1.3. Intelligent Algorithms in V2G Charging Strategies

As the complexity of the interaction between EVs and the power grid continues to grow, the application of intelligent algorithms in V2G charging strategies has become a research hotspot. These algorithms are driven by real-time data and intelligent decision-making, effectively addressing fluctuations in grid load, uncertainty in user behavior, and changes in EV charging demand [31]. Intelligent algorithms not only improve charging efficiency but also balance multiple optimization goals, including battery life, grid stability, and charging costs. Dorokhova et al. [32] proposed an intelligent charging strategy based on deep reinforcement learning, which utilizes historical EV data and real-time grid load monitoring to dynamically adjust charging and discharging timing, thereby optimizing charging costs while ensuring grid stability. This algorithm, through self-learning and continuously updating the charging strategy, can quickly respond in complex dynamic environments. However, this method’s computational complexity is high, which may lead to bottlenecks in computational resources when integrating large-scale EVs. To address the computational challenges posed by large-scale EV integration, Erdogan et al. [33] proposed a multi-objective optimization model based on genetic algorithms, primarily aimed at solving the charging scheduling problem when large numbers of EVs are connected. Genetic algorithms simulate the processes of natural selection and gene mutation, gradually evolving the optimal charging plan under multiple constraints. This model effectively reduces computation time, making it suitable for large-scale charging network optimization. Nevertheless, genetic algorithms struggle to achieve real-time responses in rapidly changing grid conditions and must be combined with other intelligent algorithms to improve adaptability. To enhance the intelligence of V2G charging strategies, a study [34] introduced an optimization framework based on hybrid intelligent algorithms, combining genetic algorithms with particle swarm optimization. This method leverages the rapid convergence of genetic algorithms and combines it with the particle swarm optimization algorithm’s ability to search for optimal solutions in multi-dimensional spaces, significantly increasing the intelligence and flexibility of charging strategies. This hybrid intelligent algorithm performs excellently in scenarios with large grid load fluctuations and frequent changes in charging demand, greatly improving grid stability and the adaptability of EV charging. Additionally, a study [35] explored the application of artificial neural networks (ANNs) in V2G charging strategies. This method uses deep learning algorithms to train on historical data, accurately predicting EV charging demand and grid load changes, thus enabling intelligent decision-making in advance. Compared with traditional optimization methods, ANNs have stronger adaptability and dynamic processing capabilities, especially when faced with complex and uncertain charging environments. However, a drawback of ANN models is their need for substantial computational resources during training and their high dependency on training data. While intelligent algorithms in V2G charging strategies offer numerous advantages, finding a balance between different algorithms and fully leveraging their complementarity remains a focus for future research. He et al. [36] proposed an optimization method based on multiagent reinforcement learning (MARL) for charging strategies. Through collaboration and competition among multiple agents, this method can find optimal solutions in complex multi-objective optimization problems. It not only enhances system flexibility but also achieves adaptive adjustments in response to dynamic changes in EV charging demand and grid load, providing new ideas for the development of future intelligent charging strategies.

Despite the progress made in optimizing EV charging strategies in the studies mentioned above, certain shortcomings remain. Traditional strategies have failed to fully account for changes in charging demand under dynamic environments. Reinforcement learning methods face challenges in terms of slow convergence and high computational complexity, while the real-time performance and robustness of path planning and scheduling optimization methods still need improvement. To address these issues, this study introduces the RPPO algorithm, which optimizes charging strategies by handling sequential decision-making problems. Compared with traditional methods, the RPPO algorithm demonstrates superior adaptability and robustness, showing promise in significantly improving charging efficiency and grid stability. This review indicates that the use of RPPO in optimizing EV charging and discharging strategies has important theoretical and practical application value. The main contributions of this work are as follows:

• Optimization Framework Considering Regional Dynamic Pricing: This study proposes an innovative V2G optimization framework that aims to facilitate energy interaction between EVs and the power grid while specifically focusing on optimizing charging behavior under different pricing strategies. By comprehensively considering factors such as grid stability, charging costs, and battery life, this framework dynamically adjusts charging and discharging plans to achieve optimal energy utilization. It also improves grid reliability and efficiency while reducing grid load.
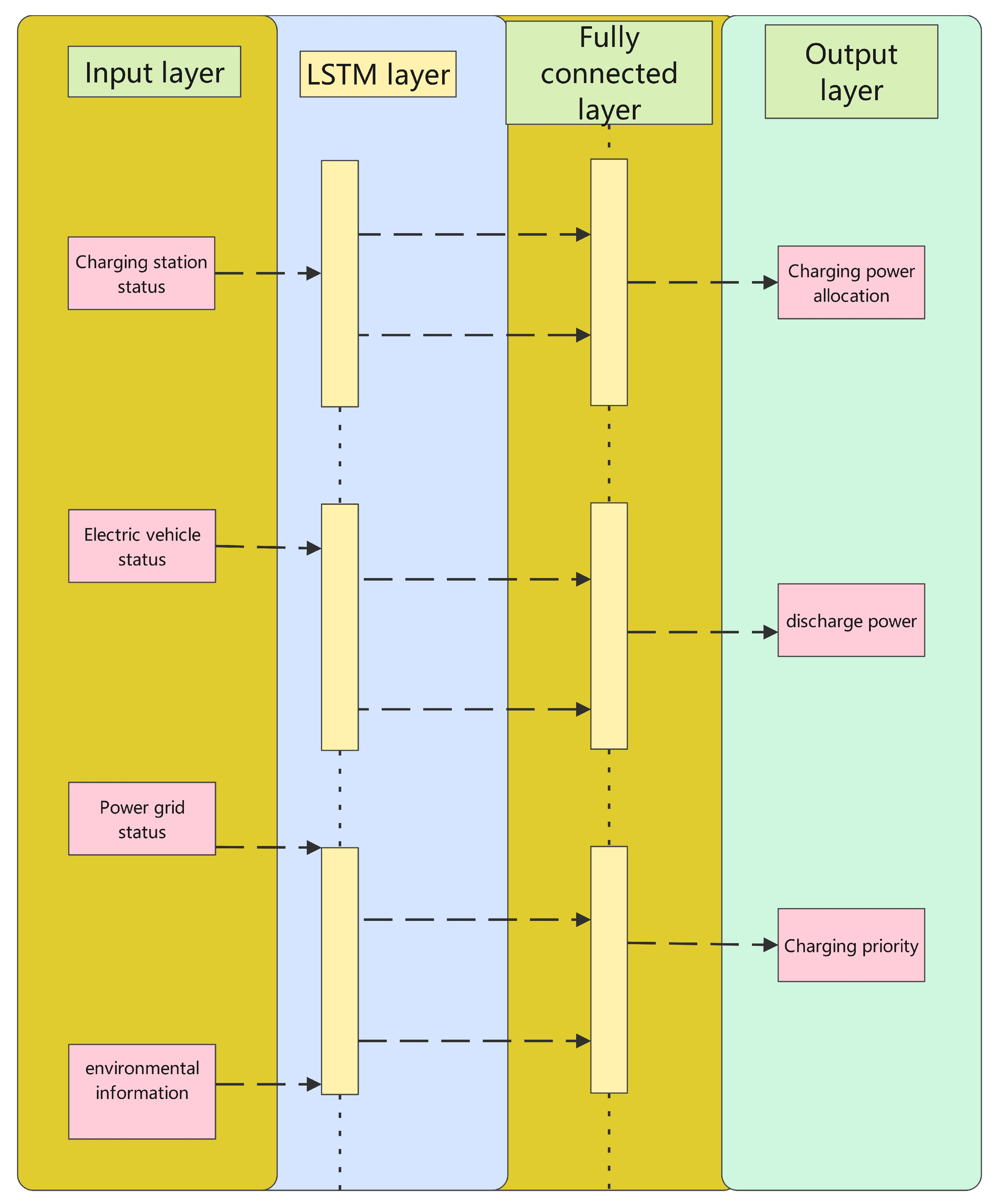
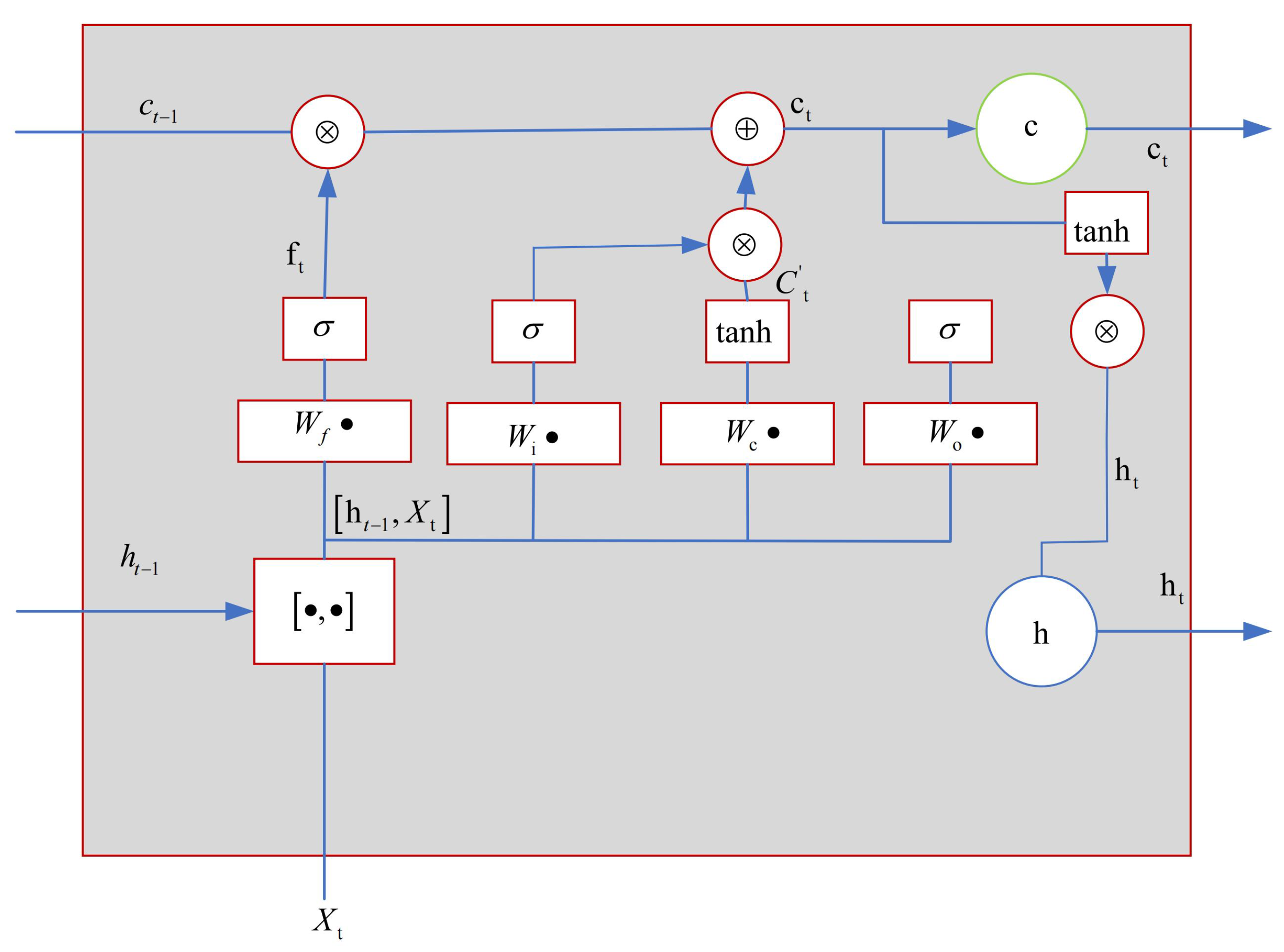
• An Integrated LSTM and RPPO Algorithm: To effectively address the complexity and uncertainty of EV charging demands, this study proposes an intelligent charging strategy combining LSTM and the RPPO algorithm. LSTM is used to capture the time-series characteristics of EV charging behavior and accurately predict future charging demand, while the RPPO is used to optimize EV charging and discharging strategies in complex and dynamic pricing environments. This algorithm combines the strengths of deep learning and reinforcement learning, enabling rapid iterative optimization in dynamic environments and significantly enhancing the intelligence of charging scheduling.
• Robustness Enhancement: The V2G optimization framework and corresponding algorithm designed in this study demonstrate strong robustness. They are not only capable of operating effectively under various pricing strategies but can also handle significant fluctuations in EV charging demand and dynamic changes in grid conditions. Through extensive simulation experiments, the solution has been proven to effectively respond to unpredictable changes in practical applications, ensuring the stability and efficiency of the charging process, thereby improving the reliability and adaptability of the entire system.

The organization of this paper is as follows: Section II firstly represents the V2G network architecture. Then, Section III formulates the multi-objective energy management problems. Moreover, Section IV describes the results and discussion, including the simulation environment, covering parameter configurations, performance metrics, and scenario analyses. Finally, this paper concludes by analyzing experimental data and results in Section V.

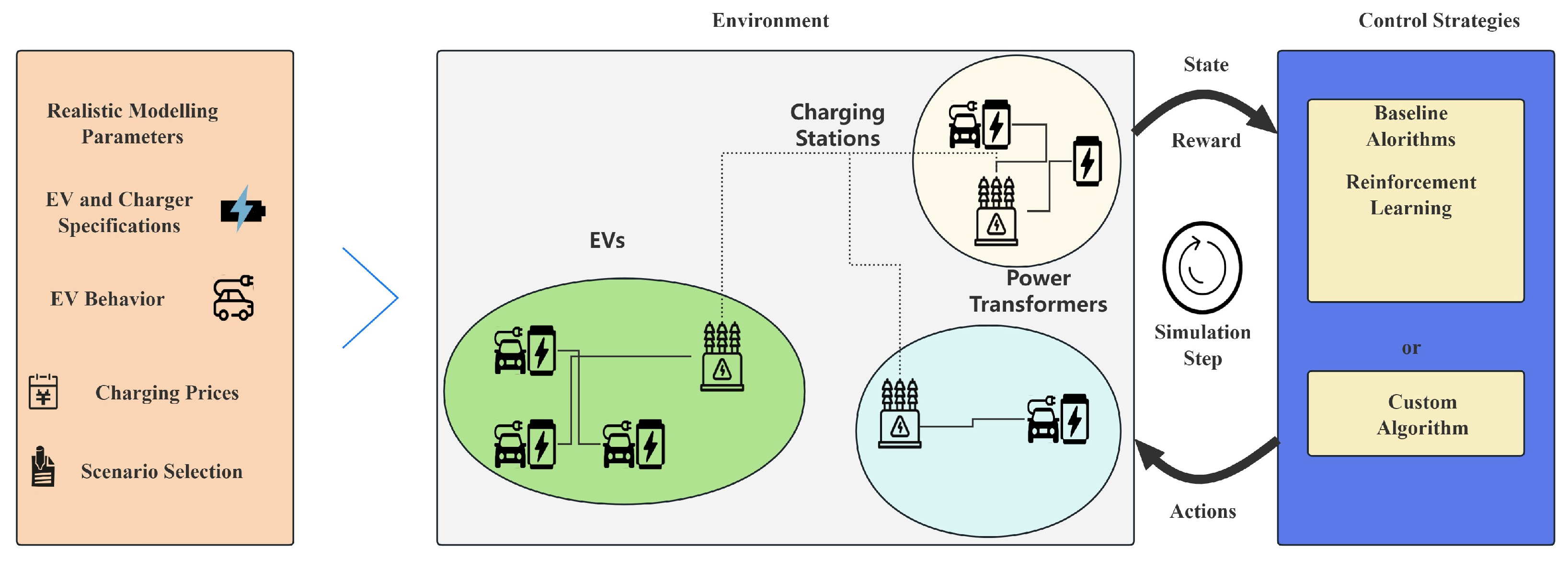
2. Network Architecture

To address the optimization of EV charging deployment at charging stations, this study proposes a V2G optimization framework that responds to regional dynamic pricing, as shown in Figure 1. This framework not only incorporates the time-series data processing capabilities of LSTM networks but also integrates the stability of PPO to dynamically optimize EV charging strategies. Through this framework, charging efficiency can be significantly improved, operational costs can be reduced, battery life can be extended, and overall grid stability can be enhanced under various charging scenarios.

As shown in Figure 1, the overall architecture of the system is composed of several key modules, each designed to optimize the interaction efficiency between EVs and the grid. The input parameter module is responsible for receiving and processing the input modeling parameters, which include the specifications of EVs and chargers, user charging behaviors, real-time fluctuations in charging prices, and specific simulation scenario settings. This module ensures that the simulation environment faithfully reflects the complex dynamics and diversity of the real world, making the model’s predictions and optimization results more applicable in practice. Next is the simulation environment module, which is one of the core components of the system. It simulates the structure of a real-world EV charging network. Specifically, the simulation environment includes EVs, charging stations, and power transformers. In this environment, EV charging and discharging behaviors are influenced by both the load management of the charging stations and the dynamics of power transmission. Additionally, the environment simulates the impact of grid load and price fluctuations on charging strategies, making the simulation results highly reliable and realistic. The control strategy module is the system’s core decision-making engine. It integrates various algorithm frameworks, including baseline algorithms, reinforcement learning algorithms, and custom algorithms. These algorithms dynamically generate optimal charging strategies by monitoring and analyzing the environmental states in real time, thereby optimizing EV charging behavior and ensuring that EVs meet user demands while minimizing the burden on the grid. Moreover, the system is designed with a detailed feedback and optimization mechanism. After each simulation step, the state information in the simulation environment is passed to the control strategy module. This module generates corresponding actions based on the latest state information, and these actions, in turn, affect the EV charging behavior. Simultaneously, the system calculates reward signals and adjusts the charging strategy accordingly, gradually improving the strategy’s adaptability and overall optimization effect. This continuous feedback and optimization process ensures that the system can respond to dynamic grid load changes in real time and make optimal decisions. The network structure, as shown in Figure 2, includes the following components:

Input Layer: The input layer is the starting point of the network, responsible for receiving the current state information from the simulation environment. This input includes key parameters such as the battery level of the EVs, the location of the charging station, real-time grid load conditions, and the current electricity price. The design of the input layer ensures that the subsequent network layers can make optimized decisions based on comprehensive and accurate data.

RNN Layer: The core processing layer of the network uses a long short-term memory (LSTM) network, which is specifically designed to handle time-series data. This layer captures the temporal dependencies between charging demand and grid load, generating a hidden state that provides essential background information for the subsequent decision-making layers. This design allows the network to effectively address the complex dynamic relationship between charging behavior and grid load, providing a more intelligent charging strategy.

Policy Network: Based on the hidden state output from the RNN layer, the policy network generates a probability distribution over different charging actions. The policy network consists of multiple fully connected layers and uses a Softmax activation function to produce a probability distribution of charging decisions, ultimately selecting the optimal strategy to guide the EV charging and discharging process. This multi-layer structure ensures that the policy network can make optimal decisions in complex environments, meeting the real-time needs of EV charging.

Value Network: The value network uses the hidden state output from the RNN layer to assess the current state’s value. This network calculates the expected value of the EVs’ current state through multiple linear activation functions, providing feedback to the policy network. The value network is designed to ensure that the policy network’s decisions not only meet current charging needs but also optimize long-term charging efficiency and grid stability, thereby achieving multi-objective optimization for the entire system.

Through the architecture described above, the RPPO algorithm in this study demonstrates strong adaptability and flexibility, enabling it to effectively handle dynamic changes in charging demand and grid load in complex charging networks, providing highly optimized charging strategies. This architecture not only enhances the efficiency and economic viability of the EV charging process but also provides robust technical support for the future development of smart grids and sustainable transportation systems.

3. Formulation of Multi-Objective Energy Management Problems

With the widespread adoption of EVs, efficiently managing the charging process has become a critical challenge for the development of smart grids. The design of charging strategies requires balancing multiple objectives, including charging efficiency, costs, battery life, and grid stability. These objectives often constrain one another and must be dynamically adjusted as time and environmental conditions change. Improving charging efficiency can reduce charging time, but it may accelerate battery degradation and shorten its lifespan. Similarly, optimizing charging schedules to lower costs may lead to concentrated grid loads, impacting stability. Additionally, the large-scale integration of EVs increases the uncertainty of grid loads, making it even more important to maintain grid stability. Given this complex backdrop, traditional single-objective optimization methods are no longer sufficient, necessitating the use of multi-objective optimization strategies. Therefore, this study models EV charging strategies as a multi-objective optimization problem. By introducing the RPPO algorithm, this study aims to achieve the global optimization of charging efficiency, costs, battery life, and grid stability in dynamic environments, providing an effective solution for the efficient coordination of smart grids and EVs.

3.1. Description of Optimization Objectives

Energy management involves the scheduling and allocation of energy during the EV charging process. Considering that peak charging periods can put significant pressure on the grid, the core of energy management is optimizing the distribution and use of energy while ensuring users’ charging needs are met. Specifically, energy management includes the following aspects:

Charging and Discharging Efficiency: This parameter indicates the rate at which EVs receive energy from the grid over a specified period. Higher charging efficiency can reduce charging time and increase user satisfaction. Mirroring real-world scenarios, each EV possesses distinct minimum and maximum power limits for charging and discharging, contingent upon the charging mode—alternating current (AC) or direct current (DC). These limits are further influenced by the constraints imposed by the power electronics of the onboard battery management system (BMS) and the characteristics of the charger used. This variability necessitates adaptive strategies that can accommodate the diverse operational parameters specific to EVs. In this study, the design of the EV model takes this attribute into account. Therefore, the minimum and maximum power limits are defined as ${\underline{P}}^{c\mathrm{h}}$ and ${\overline{P}}^{c\mathrm{h}}$. Similarly, the discharge power limits are defined as ${\underline{P}}^{dis}$ and ${\overline{P}}^{dis}$. Additionally, EVs are equipped with a maximum battery capacity, denoted as $\overline{E}$, and a lower limit for discharging, represented by $\underline{E}$. This limitation is imposed by some EV battery management systems (BMSs) that prevent discharging below a certain threshold to preserve battery health and longevity. Moreover, EVs maintain an ideal state of charge (SOC), denoted as $SO{C}^{*}$, which optimizes battery performance and lifespan. This study introduces a configurable two-stage model that specifies the charging and discharging power parameters for the EVs. the charging and discharging power is given by:

$$P_t=\eta ·I_t·V_t·\sqrt{\varphi }$$

(1)

where $I_t$ represents the current controlled by the algorithm, while $\eta$ symbolizes the efficiencies of charging ${\left(\eta \right)}^{ch}$ and discharging ${\left(\eta \right)}^{dis}$. Furthermore, $P_t$, which denotes the power at any given time, is influenced by the charging station’s voltage $V_t$ and the phase $\varphi$. The power variable $P_t$ is also bounded by the upper and lower power limits that are characteristic of both the EVs and the charging station. The specifics of this model are delineated as follows:

$$So{C}_t\left\{\begin{array}{cc}So{C}_{t-1}+P_{\mathrm{t}}·\Delta t/\overline{E}\hfill & So{C}_{t-1}<\tau \hfill \\ 1+(So{C}_{t-1}-1)·\exp {\displaystyle \frac{P_t·\Delta t}{E(\tau -1)}}\hfill & So{C}_{t-1}\ge \tau \hfill \end{array}\right.$$

(2)

In the two-stage model, $\tau \in (0,1)$ represents the transition threshold for the SOC. This threshold marks the commencement of the constant voltage region in the charging process. It is important to note that when $\tau =1$, the model simplifies to a linear form. This indicates a direct, proportional relationship between the input variables and the charging or discharging outcomes, absent any nonlinear dynamics that typically occur below this threshold.

Battery Degradation Model: Frequent charging and discharging cycles can affect battery life. Energy management needs to balance fast charging with maintaining battery health, avoiding overcharging and discharging to extend battery lifespan. Due to concerns about the degradation rate of EV batteries, EV users are often reluctant to participate in V2G services. Therefore, it is crucial to use a verified battery degradation model to evaluate the impact of the proposed intelligent charging algorithms. This model includes components for calendar aging $d^{cal}=0.75·$ and cycle-induced capacity loss $d^{cyc}$. For a single EV in a simulation with duration t, the capacity degradation due to calendar aging is related to the average state of charge $\stackrel{⌢}{SOC}$ and can be described as:

$$d^{cal}=0.75·\left({ϵ}_0·\stackrel{⌢}{SOC}-{ϵ}_1\right)·\exp \left(-{\displaystyle \frac{{ϵ}_2}{\theta }}\right)·{\displaystyle \frac{T}{{\left(T^{tot}\right)}^{0.25}}}$$

(3)

where $T^{tot}$ represents the battery lifespan in days, $\theta$ defines the battery temperature (°C), and ${\lambda }_0$ and ${\lambda }_1$ and ${\lambda }_2$ are constants, as shown in

Table 1. Battery degradation model parameters.

${\mathit{ϵ}}_0$	${\mathit{ϵ}}_1$	${\mathit{ϵ}}_2$	$\mathit{\sigma }$	${\mathit{\zeta }}_0$	${\mathit{\zeta }}_1$	${\mathit{T}}^{\mathit{tot}}$	${\mathit{Q}}^{\mathit{acc}}$
$6.23·{10}^6$	$6.23·{10}^6$	6976	28	$4.02·{10}^{-4}$	$2.04·{10}^{-3}$	730	11,160

.

The degradation of cycle capacity is influenced by the cumulative energy transacted between the battery and its SoC throughout each step of the simulation:

$$d^{cyc}=\left({\zeta }_0+{\zeta }_1{\displaystyle \frac{\sum \left|\stackrel{⌢}{SoC}-So{C}_k\right|\Delta t}{T}}\right)·{\displaystyle \frac{\sum \left|P_k\right|\Delta t}{\sqrt{Q^{acc}}}}$$

(4)

where $Q^{acc}$ is the cumulative throughput during the battery’s lifespan, and ${\zeta }_0$ and ${\zeta }_1$ are constants defined in Table 1. Therefore, the total capacity loss of the EV battery is the following sum: $Q^{lost}=d^{cal}+d^{cyc}$. In this work, the evaluation of battery capacity loss is conducted to increase EV user participation.

Authentic data on EV behavior drive the simulation of multiple case studies. Initially, the simulation environment is devoid of any connected EVs. Subsequently, EVs are incrementally integrated at each time t, following a probability distribution informed by public, workplace, and residential charging patterns as furnished by ElaadNL [37]. Participants have the option to select the ElaadNL scenario for simulation or incorporate their own custom data on EV behavior and charging transactions. Specifically, each time an EV is introduced at time tar, EV2Gym uses these distributions to determine the departure tdep and the energy level upon arrival Earr, while considering the time and date of arrival.

3.2. Energy Setting Tracking Issues

EV scheduling frequently entails tackling issues like power setpoint tracking (PST) and managing capacity constraints. Practically, energy procurement typically occurs a day in advance from the market or under contracts that specify limited capacity. Consequently, our goal is to rigorously maintain the designated power setpoints, guaranteeing the effective charging of all connected EVs and equitable energy distribution among them. For this scenario, it is presumed that data regarding the EVs’ arrival and departure times, as well as their initial SoC, are not available. Nevertheless, it is presumed that the status of an EV being fully charged is detectable, given that the recorded energy transaction in a single step would register as zero. The PST issue encompasses T discrete intervals, denoted by the set $\tau$, where $t\in \tau$. The quantity of charging stations is constant and represented by C, where each station i within C is linked to a transformer w from set W. Conversely, the count of EVs is subject to dynamic fluctuations. To represent the presence of an EV, a binary variable $u_{j,i,t}$ is introduced, where $u_{j,i,t}=1$ signifies that, at time t, the EV is connected and prepared to charge at $EVS{E}_j$ and station i. Consequently, this modeling approach results in a mixed-integer programming (MIP) problem, delineated by Equations (8) to (22). $\forall w\in W,\forall j\in J,\forall i\in C,\forall t\in \tau$.

$$\underset{I_{j,i,t}^{ch},I_{j,i,t}^{dis}}{\min }\sum _{t\in \tau }{\left(P_t^{set}-P_t^{tot}\right)}^2$$

(5)

subject to

$$P_t^{tot}=\sum _{i\in C}\sum _{i\in J}\left(P_{j,i,t}^{ch}+P_{j,i,t}^{dis}\right)\forall j,\forall i,\forall t$$

(6)

$$P_{j,i,t}^{ch}=I_{j,i,t}^{dis}·V_{j,i,t}·\sqrt{{\Phi }_{j,i,t}}·{\eta }_{j,i,t}^{ch}·w_{j,i,t}^{ch}\forall j,\forall i,\forall t$$

(7)

$$P_{j,i,t}^{dis}=I_{j,i,t}^{dis}·V_{j,i,t}·\sqrt{{\Phi }_{j,i,t}}·{\eta }_{j,i,t}^{ch}·w_{j,i,t}^{ch}\forall j,\forall i,\forall t$$

(8)

$${\underline{E}}_{j,i}\le E_{j,i,t}\le {\overline{E}}_{j,i}\forall j,\forall i,\forall t$$

(9)

$$E_{j,i,t}=E_{j,i,t-1}+\left(P_{j,i,t}^{ch}+P_{j,i,t}^{dis}\right)·\Delta t\forall j,\forall i,\forall t$$

(10)

$$E_{j,i,t}=E_{j,i,t}^{arr}\forall j,\forall i,\forall t\left|=t_{j,i,t}^{arr}\right.$$

(11)

$${\underline{I}}_{j,i}^{ch}\le I_{j,i}^{ch}\le {\overline{I}}_{j,i}^{ch}\forall j,\forall i,\forall t$$

(12)

$${\underline{I}}_{j,i}^{dist}\le I_{j,i}^{dist}\le {\overline{I}}_{j,i}^{dist}\forall j,\forall i,\forall t$$

(13)

$$I_{i,t}^{cs}=\sum _{i\in J}\left(I_{j,i,t}^{ch}·w_{j,i,t}^{ch}+I_{j,i,t}^{dis}·w_{j,i,t}^{dis}\right)\forall j,\forall i,\forall t$$

(14)

$${\underline{I}}_{j,i}^{cs}\le I_{j,i}^{cs}\le {\overline{I}}_{j,i}^{cs}\forall j,\forall i,\forall t$$

(15)

$$P_{w,t}^{EVs}=\sum _{i\in C}\sum _{i\in J}\left(P_{j,i,t}^{ch}+P_{j,i,t}^{dis}\right)\forall w,\forall j,\forall i,\forall t$$

(16)

$${\underline{P}}_{w,t}^{tr}\le P_{w,t}^{EVs}+P_{w,t}^L+P_{w,t}^{PV}\le {\overline{P}}_{w,t}^{tr}-P_{w,t}^{DR}\forall w,\forall t$$

(17)

$$w_{j,i,t}^{ch}+w_{j,i,t}^{dis}\le 1\forall j,\forall i,\forall t$$

(18)

$$w_{j,i,t}^{ch}=w_{j,i,t}^{dis}=0\forall j,\forall i,\forall t\left|u_{j,i,t}=0\right.$$

(19)

Equation (5) aims to minimize the square of the power tracking error by defining the charging and discharging currents of the charging station. The tracking error is the difference between the power setpoint $P_t^{set}$ at time t and the actual power $P_t^{tot}$. Reducing this error simultaneously minimizes both the costs associated with unmet energy demands and the losses due to unused energy. For a single EV, the current j is determined by two distinct decision variables, $I^{ch}·w^{ch}$ for charging and $I^{dis}·w^{dis}$ for discharging, reflecting the behavioral differences between these two processes. For the charging process, both current and power ($I^{ch},P^{ch}$) assume positive values, whereas in the discharging process, both current and power ($I^{dis},P^{dis}$) are designated as negative. Equations (7) and (8) specify the power definitions, whereas Equations (9) to (11) outline the constraints related to the EVs’ battery capacity. Equations (12) and (13) detail the specific charging and discharging limitations applicable to each EV and EVSE, while Equation (15) defines these constraints for the overall charging system. The limitation on transformer power is specified in Equation (17). Ultimately, it is not possible for an EV to engage in charging and discharging at the same time. Consequently, the constraints for the binary variables $w^{ch}$ and $w^{dis}$ are articulated in Equations (18) and (19).

3.3. V2G Profit Maximization Problem

The second problem focuses on maximizing the CPO profit while ensuring that the EV users’ needs are adequately met. The assumption is that, upon arrival at charging station i and for $EV{s}_j$, the EVs disclose both their scheduled departure time $\left(t_{j,i}^{dep}\right)$ and anticipated battery capacity $\left(E_{j,i}^{*}\right)$. Furthermore, when each EV is connected to the charger, its battery capacity $E_{j,i,t}$ is known. Such assumptions are commonly integrated into the study, given that advancements in communication protocols enable the retrieval of this information directly from the EVs. Equation (20) defines the objective function, detailing how it depends on the charging price $c_{ch}$ and discharging price $c^{dis}$ for each $EV{s}_{j,i}$.

$$\underset{I_{j,i,t,}^{ch}{I}_{j,i,t,}^{dis}}{\max }\sum _{t\in \tau }\sum _{i\in c}\left(-P_{i,t}^{ch}·c_{i,t}^{ch}+P_{i,t}^{dis}·c_{i,t}^{dis}\right)·\Delta t$$

(20)

Subject to the constraints of Equations (10) to (20),

$$E_{j,i,t}\ge E_{j,i,t}^{*}\forall j,\forall i,\forall t\left|t=t_{j,i,t}^{dep}\right.$$

(21)

In this research, an enhanced RPPO algorithm was employed to refine the charging strategies for EVs. This RPPO algorithm, a type of reinforcement learning, excels in sequential decision-making tasks and adeptly manages time-dependent factors and complex decision-making scenarios.

The RPPO algorithm builds upon the foundational PPO algorithm, primarily focusing on constraining the magnitude of policy updates to bolster the consistency of policy iterations. By clipping the objective function, the PPO algorithm curtails the scope of policy changes, thus preventing policy collapse from overly significant updates. The specific formulation of the PPO objective function is detailed as follows:

$$L^{CLIP}\left(\theta \right)={\widehat{\mathbb{E}}}_t\left[\min \left(r_t\left(\theta \right){\widehat{A}}_t,clip\left(r_t\left(\theta \right),1-\epsilon ,1+\epsilon \right){\widehat{A}}_t\right)\right]$$

(22)

where $r_t\left(\theta \right)={\displaystyle \frac{{\pi }_{\theta }\left({\alpha }_t|S_t\right)}{{\pi }_{\theta dd}\left({\alpha }_t|S_t\right)}}$ represents the ratio between the new policy and the old policy, ${\widehat{A}}_t$ is the advantage function estimate, and $\epsilon$ is the clipping function.

3.4. Algorithm Description

The RPPO algorithm enhances the ability to process time-series data by introducing an RNN layer, such as an LSTM network or a GRU. The RNN layer captures time dependencies between states, making it particularly suitable for time-series decision-making problems like EV charging strategies, as shown in Algorithm 1.

Algorithm 1 RPPO Algorithm Optimization for the EV Charging Strategy

Input: N episodes, policy network $\pi \left(\theta \right)$, value network $V\left(\varphi \right)$, learning rate $\alpha$, discount factor $\gamma$

Output: Optimized policy and value networks

1: Initialize RPPO model with parameters  2: for episode = 1 to N do  3:       Reset environment, $state=get\_initial\_state\left(\right)$  4:       while environment is active do  5:            $action=RPPO\_model.select\_action\left(state\right)$  6:            $next\_state,reward,is\_terminal=environment.step\left(action\right)$  7:            Store experience $(state,action,reward,next\_state)$  8:            $state=next\_state$  9:       end while 10:      Update RPPO model 11: end for 12: function Update RPPO model 13:      Sample experiences and compute losses 14:      Optimize policy, value, and entropy 15: end function 16: function select_action(state) 17:      return action = sample_action (policy_network.forward(state)) 18: end function 19: function compute_losses(experiences) 20:      Compute policy loss, value loss, and entropy 21: end function

Input Layer: Inputs the current state $S_t$, including key parameters such as EV battery level, charging station location, grid demand, and supply status.

RNN Layer: Processes time-series data through LSTM or GRU units, outputting the hidden state $h_t$ and cell state $C_t$. The update equations for the LSTM unit are

$$\begin{array}{c}{\mathrm{i}}_t=\sigma \left(W_i{\mathrm{x}}_t+U_i{h}_{t-1}+b_i\right)\end{array}$$

(23)

$$\begin{array}{c}{\mathrm{f}}_t=\sigma \left(W_f{\mathrm{x}}_t+U_f{h}_{t-1}+b_f\right)\end{array}$$

(24)

$$\begin{array}{c}{o}_t=\sigma \left(W_o{\mathrm{x}}_t+U_o{h}_{t-1}+b_o\right)\end{array}$$

(25)

$$\begin{array}{c}{c}_t={\mathrm{f}}_t\odot {\mathrm{c}}_{t-1}+{\mathrm{i}}_t\odot \tanh \left({\mathrm{w}}_c{\mathrm{x}}_t+{\mathrm{u}}_c{h}_{t-1}+{\mathrm{b}}_c\right)\end{array}$$

(26)

$$\begin{array}{c}{\mathrm{h}}_t=o_t\odot \tanh \left({\mathrm{c}}_t\right)\end{array}$$

(27)

Policy Network: Based on the hidden state $h_t$ output by the RNN, it estimates the value $V_{\theta }\left(s_t,h_t\right)$ of the current state to assist in policy updates.

Policy Loss: The policy loss uses the objective function of PPO, which ensures policy stability by limiting the magnitude of policy updates. The formula is as follows:

$$L^{CLIP}\left(\theta \right)={\widehat{\mathbb{E}}}^t\left[\min \left(r_t\left(\theta \right){\widehat{A}}_t,clip\left(r_t\left(\theta \right),1-\epsilon ,1+\epsilon \right){\widehat{A}}_t\right)\right]$$

(28)

where $r_t\left(\theta \right)={\displaystyle \frac{{\pi }_{\theta }\left(a_t\left|s_t\right.\right)}{{\pi }_{\theta old}\left(a_t\left|s_t\right.\right)}}$ represents the ratio between the new policy and the old policy, ${\widehat{A}}_t$ is the advantage function estimate, and $\epsilon$ is the clipping function.

Value Loss: The mean squared error (MSE) loss function is used to minimize the value estimation error. The equation is

$$L^{VF}\left(\theta \right)=\widehat{\mathbb{E}}\left[{\left(V_{\theta }\left(s_t,h_t\right)\right)}^2\right]$$

(29)

Entropy Regularization: Increases the entropy of the policy, encouraging the model to explore more possible strategies. The equation is

$$L^S\left(\theta \right)=\widehat{\mathbb{E}}\left[-{\pi }_{\theta }\left({\alpha }_t|s_t,h_t\right){\log }_{{\pi }_{\theta }}\left({\alpha }_t|s_t,h_t\right)\right]$$

(30)

Through the above algorithm structure, the RPPO algorithm can effectively handle the time dependencies in EV charging strategies, providing better charging decisions to improve grid efficiency and respond to market price changes. Figure 3 shows the LSTM network diagram.

To train the RPPO model, we used the standard PPO training process, combined with the features of RNN. The training process mainly includes three steps: data collection, loss function calculation, and parameter updates. The Adam optimizer is used to update the model parameters during the parameter update step. The specific steps include sampling data from the replay buffer, calculating the gradients of the policy loss and value loss, and updating the parameters of the policy network and value network based on the loss gradients. The training process is shown in Algorithm 2.

Through the above network structure and training process, the RPPO algorithm model can effectively learn and optimize EV charging strategies, improve grid efficiency, and respond to market price changes.

Algorithm 2 Training Policy and Value Networks

Input: Initial parameters for policy network $\pi \left(\theta \right)$ and value network $V\left(\varphi \right)$

Output: ITrained policy and value networks

Initialize parameters of policy network $\pi \left(\theta \right)$ and value network $V\left(\varphi \right)$

2:  Reset environment and obtain initial state $s_0$

for each time step t do

4:     Generate action $a_t$ using policy network $\pi \left(\theta \right)$ based on current state $s_t$ and hidden state $h_t$

Execute action $a_t$ in the environment, observe next state $s_{t+1}$ and reward $r_t$

6:     Store $(s_t,a_t,r_t,s_{t+1})$ in the replay buffer

Periodically sample data from the replay buffer

8:     Calculate the loss function

Update the model parameters (policy network $\pi \left(\theta \right)$ and value network $V\left(\varphi \right)$)

10:  end for

Repeat until predetermined number of training steps is reached

4. Results and Discussion

In this section, to verify the effectiveness and superiority of the EV charging strategy proposed in this paper based on the RPPO algorithm, we conducted comprehensive simulation experiments. The primary objective of the performance evaluation is to assess the algorithm’s performance in various charging scenarios, particularly in terms of optimizing charging efficiency, charging cost, battery life, and grid stability. This section systematically presents and analyzes the performance of the RPPO algorithm through framework validation, performance metric analysis, and multi-scenario comparisons.

4.1. Parameter Settings

In this study, all simulation experiments were implemented using Pytorch in a Python 3.8 environment. The simulation code was executed on a computer equipped with an Intel Core i7-10700K processor, 32 GB of RAM, and an NVIDIA RTX 3080 graphics card. To evaluate the effectiveness of the proposed strategy, we set several key parameters in the experiments. The specific parameter settings are shown in

Table 2. Key Parameters.

Description	Parameters	Value
Transformer power limit [kW]	$\Psi$	400
Maximum EVSE output power [kW]	$So{C}_{j,d_j}$	22
EVSE voltage (V)	V	230
EVSE phases	$\varphi$	3
EV battery capacity [kWh]	$E_j$	50
Maximum EV power [kW]	${\overline{P}}^c,{\overline{P}}^d$	22
Minimum EV SoC when discharging	$So{C}_{j,min}$	10%
Minimum EV SoC at departure		80%
Minimum EV time of connection [h]		3
Charging efficiency		100%
Discharging efficiency		100%
Sample time [min]	$\Delta t$	15
Operation time of the station [h]	T	24
Prediction horizon (2.5 h–10 h)	H	{2.5 × 4, 10 × 4}
Number of EVSEs	I	{5–50}
Number of EVs	J	{15–120}
Number of transformers	G	{1, 3}
Discharge price multiplier	m	{0.8–1.2}
EV scenario		“Residential”

.

4.2. Environment Setup

Specifically, our simulation environment is built on the PandaPower and EV2Gym libraries, constructing a complex power system that includes multiple charging stations, transformers, and dynamically changing grid demand and supply. The main components of this simulation environment include EV charging stations, the grid model, and dynamic simulation of Electric Vehicles. In this study, the simulation environment, based on PandaPower and EV2Gym, includes the following main components:

• EVs Charging Stations: Each charging station contains several charging ports, capable of providing charging services to multiple EVs simultaneously. The location and number of charging stations are configured based on actual demand to simulate different cities and regions.
• Grid Model: A medium-voltage grid model is created using PandaPower, which includes transformers, loads, and distributed generation units (such as solar and wind power). The grid model can dynamically simulate the balance between power supply and demand, reflecting the actual operating conditions of the grid.
• EVs: Various types of EV are simulated, with different battery capacities, charging speeds, and arrival times. The charging demand and departure times of the EVs are randomly generated based on real-world conditions to improve the realism of the simulation.
• Charging Efficiency: Measures the amount of energy obtained by an EV per unit of time. Improving charging efficiency is one of the main optimization goals.
• Charging Cost: Calculates the charging cost for each EV and evaluates the algorithm’s effectiveness in reducing charging expenses.
• Battery Life: Monitors the health status of the battery and assesses the impact of the algorithm on battery lifespan.
• Grid Stability: Analyzes the grid’s performance under different load conditions and evaluates the contribution of the algorithm to grid stability.

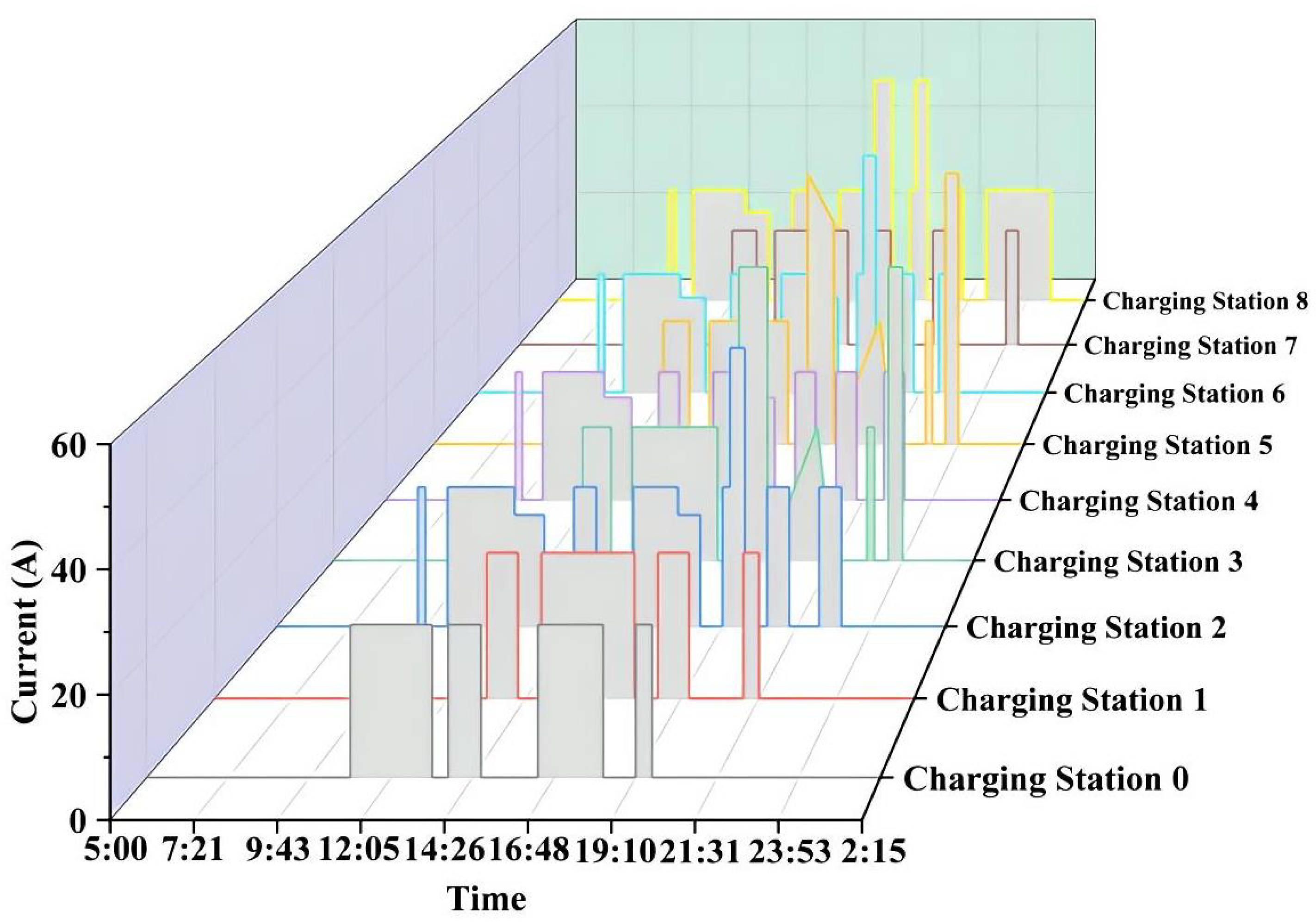
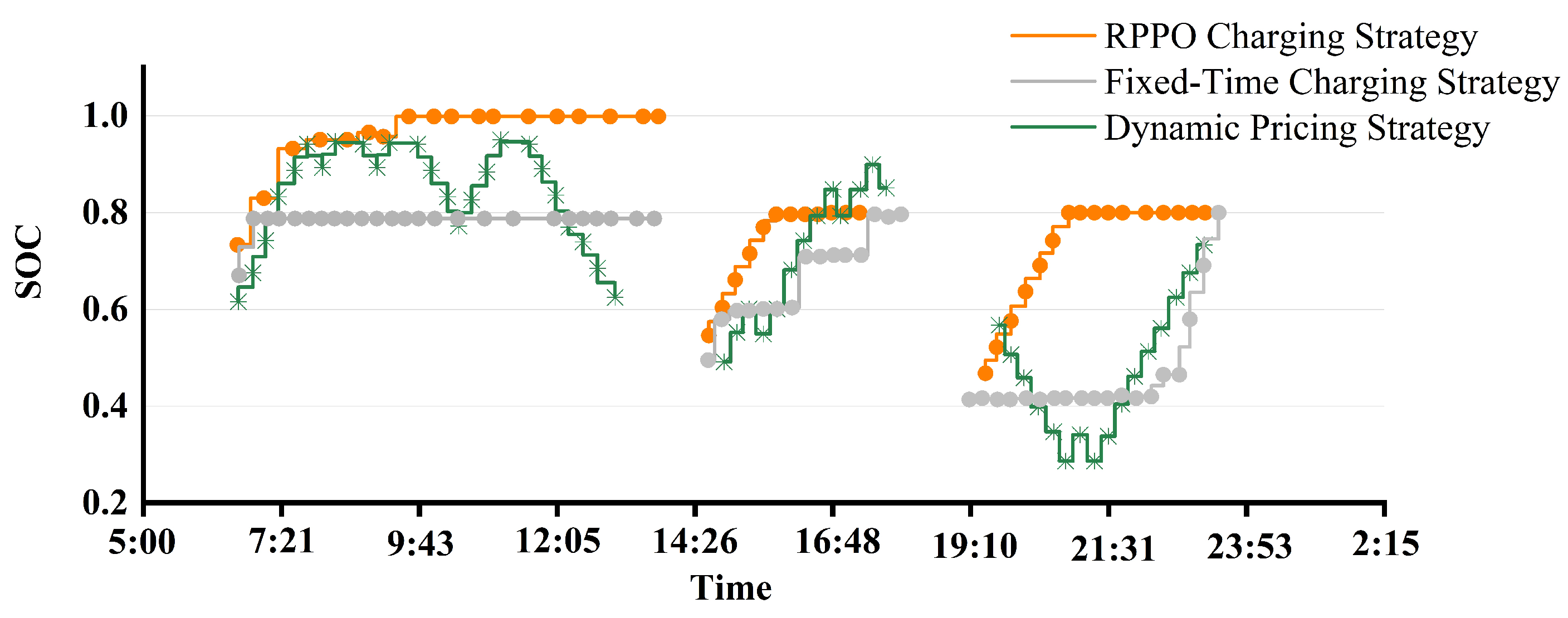
4.3. Results Analysis

This study presents a comparative analysis of the RPPO strategy and conventional charging strategies in practical applications, highlighting the superior performance of the RPPO approach as shown in

Table 3. Average results of 30 simulations with 9 EVSEs, 20 EVs, 1 transformer, and variable EV behavior.

Algorithm	Profits (€)	Energy Charged/Discharged (kWh)	$\sum {\mathit{Q}}^{\mathit{lost}}(\times {10}^{-4})$	$\sum {\mathit{d}}^{\mathit{cal}}(\times {10}^{-4})$	$\sum {\mathit{d}}^{\mathit{cyc}}(\times {10}^{-4})$
RPPO (Ours)	$40.6\pm 8.5$	$1192\pm 108/1084\pm 102$	$43.6\pm 3.8$	$3.2\pm 0.2$	$40.4\pm 1.5$
Fixed-Time Charging [6]	$-15.2\pm 8.1$	$828\pm 38/163\pm 24$	$69.8\pm 1.3$	$3.5\pm 0.2$	$66.3\pm 1.2$
Priority Charging [7]	$11.9\pm 8.8$	$951\pm 36/706\pm 63$	$56.7\pm 1.2$	$3.3\pm 0.2$	$53.4\pm 1.5$
Dynamic Pricing [9]	$25.3\pm 8.3$	$987\pm 94/842\pm 107$	$61.1\pm 1.5$	$3.3\pm 0.2$	$57.8\pm 1.5$

. The data in the table reflect the performance of each strategy across key metrics, including economic profitability, energy management, energy loss, and battery degradation.

Economic Profitability: The RPPO strategy significantly outperforms the other strategies in terms of profitability, achieving an average profit of €40.6 (±8.5), which is markedly higher than that of fixed-time charging at €−15.2 (±8.1), priority charging at €11.9 (±8.8), and dynamic pricing at €25.3 (±8.3). This result underscores the efficiency of the RPPO strategy in optimizing economic returns.

Energy Management: Regarding the energy charged and discharged, the RPPO strategy achieves 1192 kWh of charging and 1084 kWh of discharging, with relatively low variability (±102 kWh), indicating its high efficiency in energy allocation. In contrast, other strategies exhibit suboptimal performance in either charging or discharging levels, or show greater variability, as seen with fixed-time charging, which only achieves 828 kWh of charging.

Energy Loss: In terms of total energy loss ($\sum Q^{lost}$), the RPPO strategy shows a lower loss at $43.6\times {10}^{-4}$, significantly below the fixed-time charging strategy’s $69.8\times {10}^{-4}$. These data illustrate the RPPO strategy’s advantage in minimizing energy wastage.

Battery Degradation: The RPPO strategy also demonstrates superior performance in reducing battery calendar degradation ($\sum d^{cal}$) and cycle degradation ($\sum d^{cyc}$), with values of $3.2\times {10}^{-4}$ and $40.4\times {10}^{-4}$, respectively, both of which are lower than those of the other strategies. This performance suggests that the RPPO strategy has the potential to extend battery lifespan effectively.

We designed a series of simulation experiments. Through multiple simulation runs, we collected key performance indicators such as charging efficiency, charging cost, battery life, and grid stability, and performed a detailed analysis of the performance of different strategies. Figure 4 shows the results under the fixed-time charging strategy, where EVs charge according to a fixed schedule without considering real-time grid load and price changes. The experimental results in the figure show that under the fixed-time charging strategy, the current at each charging station increases sharply as charging demand occurs. Figure 4 displays the current fluctuations at different charging stations within the specified time window, indicating that EVs concentrate their charging within this predetermined time frame. From the figure, it can be observed that the fixed-time charging strategy leads to highly concentrated charging behavior at certain time periods. For example, at stations 3, 4, and 6, charging activities are concentrated within a few specific hours, while at other times, the current remains stable. This suggests that such a strategy may lead to large power demand during certain periods, resulting in localized load pressure on the grid. Moreover, some stations (such as stations 7, 8, and 9) show almost no noticeable current fluctuations, indicating that these stations were underutilized under the fixed-time charging strategy. This phenomenon could result from the time windows not aligning with the usage patterns of all EVs, leading to wasted charging station resources. While the fixed-time charging strategy can simplify charging management to some extent, its main issue is the inability to flexibly respond to fluctuations in grid load demand. Due to the fixed nature of the charging times, EV charging behavior cannot be adjusted based on real-time electricity prices or grid load conditions, which may exacerbate grid load pressure during peak hours, reducing overall grid stability and efficiency. Overall, although the fixed-time charging strategy is simple to operate, it lacks flexibility, often leading to concentrated charging behavior and creating significant peak load pressure on the grid. The specific results are shown in Figure 4.

Under the dynamic pricing strategy, EVs adjust their charging times based on real-time electricity prices, charging during periods of lower prices to reduce costs. The current distribution across different charging stations under the dynamic pricing strategy is shown in the figure. The core idea of this strategy is to dynamically adjust EV charging behavior based on price fluctuations, lowering charging costs and reducing the load impact on the grid. As seen clearly in the figure, the current distribution across different charging stations is more dispersed over time, and most charging activities are concentrated during periods of lower electricity prices. For example, charging stations 0, 1, and 2 exhibit multiple charging peaks, primarily concentrated during off-peak hours (e.g., late at night and afternoon periods), indicating that the dynamic pricing strategy effectively guides vehicles to charge during periods of cheaper electricity. This charging pattern helps to alleviate pressure on the grid during peak hours, thereby improving the overall stability of the power system. Compared to the fixed-time charging strategy, the dynamic pricing strategy is significantly more flexible and advantageous in reducing electricity consumption costs. However, some charging stations (such as station 8) show little or no charging activity during certain periods, likely due to higher electricity prices at that time, with vehicles opting to delay charging until prices drop. While this strategy alleviates some grid pressure, it may still lead to excessive grid stress during peak usage periods, and further improvements are needed. The specific results are shown in Figure 5.

Considering factors such as grid load, electricity prices, and EV charging demand, the charging strategy is dynamically optimized. The experimental results in the figure demonstrate the application of the RPPO algorithm across multiple charging stations. Each subplot represents the current signal of a charging station over time. By analyzing the current signals from these stations, we can better understand the optimization effects of the RPPO algorithm in different environments. Firstly, from the overall trend, the RPPO algorithm dynamically adjusts the current distribution at the charging stations, effectively controlling the charging and discharging behavior of EVs. The current signal fluctuations at each charging station range from −50 A to 50 A, indicating that the RPPO algorithm can effectively control charging currents in V2G energy management, ensuring grid stability. Specifically, the current signals at different charging stations show some variation, reflecting the RPPO strategy’s flexibility in adjusting to different charging demands and grid conditions. For example, the current fluctuations at charging stations 4 and 8 are more frequent, indicating higher demand for charging and discharging at these stations. In contrast, the current fluctuations at charging stations 1 and 13 are smaller, indicating more stable charging and discharging activities at these locations. This variability highlights the adaptability of the RPPO algorithm in handling complex and dynamic charging environments. Additionally, the RPPO algorithm demonstrates good stability and robustness. The experimental results show that, although there are fluctuations in the current signals at all charging stations, they remain within a reasonable range without significant anomalies or extreme situations. This indicates that the algorithm can ensure efficient EV charging while effectively avoiding excessive stress on the grid, thereby enhancing the overall system’s stability. The specific results are shown in Figure 6.

Under this V2G optimization framework, the charging price guided by the RPPO strategy is consistently lower than the discharging price, which increases profits for vehicle owners. The experimental results show that the RPPO algorithm effectively captures the fluctuations in electricity prices and optimizes the charging and discharging behavior of EVs, thereby maximizing economic benefits at different times of the day. Specifically, the charging price (blue line) and discharging price (orange line) exhibit clear time-varying characteristics throughout the day. From 9:00 A.M. to 12:00 P.M. and from 4:00 P.M. to 7:00 P.M., the charging price is at a relatively low level. Additionally, from 2:00 P.M. to 4:00 P.M. and from 10:00 P.M. to 11:00 P.M., the discharging price significantly increases, demonstrating that the RPPO algorithm effectively schedules discharging operations during these peak pricing periods to create higher economic benefits for users. Overall, the RPPO algorithm not only significantly reduces users’ charging costs amidst price fluctuations but also supports grid stability during peak hours through discharging operations. The application of this strategy not only improves charging efficiency but also provides EV users with both economic and stability benefits within the V2G framework. The specific results are shown in Figure 7.

Under the RPPO algorithm, the power setpoints and the actual total power at the charging stations show that the actual power of the charging stations is always lower than the setpoints. This indicates that during demand response events, the RPPO strategy demonstrates significant performance advantages in optimizing EV charging. This is mainly due to its ability to effectively utilize time-series data, adaptively adjust the charging strategy, and comprehensively consider multi-objective optimization. The results are shown in Figure 8.

A t-test was conducted on the charging efficiency, and the results are shown in

Table 4. Probabilistic statistics of charging strategies.

Charging Strategy	Average Charging Efficiency (%)	Standard Deviation (%)	Sample Size (n)	Confidence Interval (95%)
RPPO (Ours)	92.3	2.5	30	(91.2, 93.4)
Fixed-Time Charging [6]	85.7	3.1	30	(84.3, 87.1)
Priority Charging [7]	88.4	2.8	30	(87.2, 89.6)

:

The t-test results show that the p-value between the RPPO algorithm and the fixed-time charging algorithm is 0.001, and the p-value between the RPPO algorithm and the priority charging algorithm is 0.005, both of which are less than the significance level of 0.05. This indicates that the RPPO algorithm is significantly superior to traditional strategies in terms of charging efficiency.

Under three distinct charging algorithms—the RPPO charging strategy, the fixed-time charging strategy, and the dynamic pricing strategy—the SOC of EVs batteries varies significantly over a full day. The x-axis spans a complete charging cycle from early morning to the early hours of the following day, while the y-axis represents SOC, ranging from 0.2 to 1.0, indicating the battery charge level as a percentage.

The RPPO charging strategy maintains a relatively high SOC level throughout the day, especially during high-demand periods such as morning and afternoon peaks. This strategy quickly raises the SOC to nearly full (close to 1.0), demonstrating its dynamic adjustment capability in response to fluctuations in grid demand. By prioritizing charging during peak periods and efficiently distributing charging power during off-peak times, the RPPO strategy achieves both SOC stability and continuity in the charging process.

In contrast, the fixed-time charging strategy maintains a lower but steady SOC level, failing to respond adequately to higher charging demand during peak hours. This fixed schedule limits the charging station’s ability to meet additional power requirements during peak load periods, thus restricting its adaptability. The dynamic pricing strategy, meanwhile, displays noticeable SOC fluctuations as its charging behavior is more sensitive to price variations, leading to frequent adjustments in SOC between high- and low-demand periods, which results in less stable SOC management.

These observations illustrate that the RPPO charging strategy offers superior flexibility and adaptability in managing EV battery SOC by dynamically responding to grid load and charging demands, achieving optimal SOC control. Compared to the other algorithms, RPPO demonstrates significant advantages in energy efficiency, grid interaction, and overall system stability, further validating its effectiveness as an optimized charging solution, as shown in Figure 9.

In summary, the RPPO algorithm demonstrates significant performance advantages in optimizing EV charging. This is largely due to its ability to effectively utilize time-series data, adaptively adjust charging strategies, and comprehensively consider multi-objective optimization. Statistical validation through confidence intervals and hypothesis tests further confirms the significant advantages of the RPPO algorithm in terms of charging efficiency, user satisfaction, battery life, and grid stability. Future research can further explore the application of the RPPO algorithm in more complex charging scenarios to enhance its practical value.

In terms of charging efficiency, the fixed-time charging strategy has an average efficiency of 75%. The dynamic pricing strategy achieves an average efficiency of 80%, the demand response strategy achieves an average efficiency of 85%, and the RPPO strategy achieves an average efficiency of 90%. In terms of charging costs, the fixed-time charging strategy has an average cost of 0.20/kWh. The dynamic pricing strategy has an average charging cost of 0.15/kWh. The demand response strategy has an average cost of 0.12/kWh. The RPPO algorithm has an average charging cost of 0.10/kWh. From the perspective of battery life reduction, the fixed-time charging strategy results in an average battery life reduction of 5%. Under the dynamic pricing strategy, the average battery life reduction is 4%. Under the demand response strategy, the average battery life reduction is 3%. However, under the RPPO algorithm, the average battery life reduction is 2%. In terms of grid stability, the fixed-time charging strategy results in large grid load fluctuations and low stability. The dynamic pricing strategy results in moderate grid load fluctuations and better stability. The demand response strategy leads to smaller grid load fluctuations and higher stability. The RPPO strategy results in the smallest grid load fluctuations and the highest stability. The experimental results indicate that the RPPO algorithm significantly outperforms traditional charging strategies in terms of charging efficiency, charging cost, battery life, and grid stability. Specifically, by dynamically adjusting charging power and timing, the RPPO algorithm not only improves overall charging efficiency and economic performance but also significantly reduces battery degradation and enhances grid stability. In contrast, the fixed-time charging algorithm and dynamic pricing strategy show clear limitations in responding to grid load fluctuations and price changes, making it difficult to achieve optimal charging outcomes. Although the demand response strategy improves charging performance to some extent, its optimization effect still falls short of the RPPO strategy. Overall, the RPPO algorithm demonstrates strong adaptability and optimization capabilities in complex charging environments, providing robust support for the development of smart grids and sustainable transportation.

This paper experimentally compares the performance of the RPPO algorithm with traditional charging algorithm in various charging scenarios. The results show that the RPPO algorithm demonstrates significant advantages in terms of charging efficiency, user satisfaction, battery life, and grid stability. This performance improvement is mainly attributed to the following factors: by introducing the LSTM network, RPPO can effectively capture and utilize time-series data, handling the dynamic changes in charging demand and grid load. In contrast, traditional strategies such as fixed-time charging and priority charging often assume that these variables are static, making them unable to adapt to real-world dynamic changes. The RPPO algorithm can adaptively adjust the charging strategy based on real-time data and historical information, dynamically optimizing charging efficiency and costs. Traditional strategies tend to rely on preset rules, lacking the flexibility needed for optimization across different scenarios and conditions. RPPO can comprehensively consider multiple optimization objectives, including charging efficiency, user satisfaction, battery life, and grid stability. This multi-objective optimization ability allows it to provide superior performance in a wide range of charging scenarios.

5. Conclusions

This study proposes an intelligent charging method based on the RPPO algorithm to address the optimization of EV charging strategies. Experimental validation demonstrates that the RPPO algorithm exhibits excellent performance, significantly improving charging efficiency and optimizing charging costs, while also playing a crucial role in maintaining grid stability and extending battery life. The algorithm fully leverages the LSTM network’s ability to process time-series data, enabling the dynamic adjustment of charging and discharging schedules. It flexibly responds to grid load fluctuations and uncertainties in user charging behavior, ensuring efficient collaboration between electric vehicles and the grid.

Compared to traditional charging strategies, the advantages of the RPPO algorithm in multi-objective optimization are particularly notable. Through an intelligent decision-making mechanism, this algorithm not only effectively reduces users’ charging costs but also provides additional regulation capacity for the grid during peak power periods. Especially within the V2G framework, the RPPO algorithm further enhances the role of EVs as energy regulation tools, promoting grid load balancing and maximizing user benefits. Additionally, experimental results indicate that this strategy shows strong adaptability in diverse charging demand scenarios, ensuring improved user satisfaction.

Although this study has achieved significant success in optimizing EV charging strategies, there is still room for further improvement in the future. First, as the number of electric vehicles continues to grow, addressing the issue of computational complexity in large-scale EVs integration scenarios will be a key focus for future research. Second, incorporating more external factors (such as traffic conditions and renewable energy supply) to further refine the multi-dimensional optimization model of charging strategies will help to enhance the practicality and broad adaptability of the algorithm.

In summary, this study provides a new solution for the intelligent optimization of EV charging strategies, not only enhancing the synergy between electric vehicles and the grid but also laying an important foundation for the future development of smart grids. The successful application of the RPPO algorithm demonstrates the great potential of artificial intelligence in energy management, and it is expected to provide stronger technical support for achieving a clean and efficient transportation and energy system in the future.