Rolling Bearing Fault Diagnosis Based on Optimized VMD Combining Signal Features and Improved CNN
Abstract
:1. Introduction
2. Methods
2.1. Golden Jackal Optimization Algorithm
- (1)
- Initialization
- (2)
- Searching for prey:
- (3)
- Surrounding and attacking prey
2.2. Principle of Variational Modal Decomposition
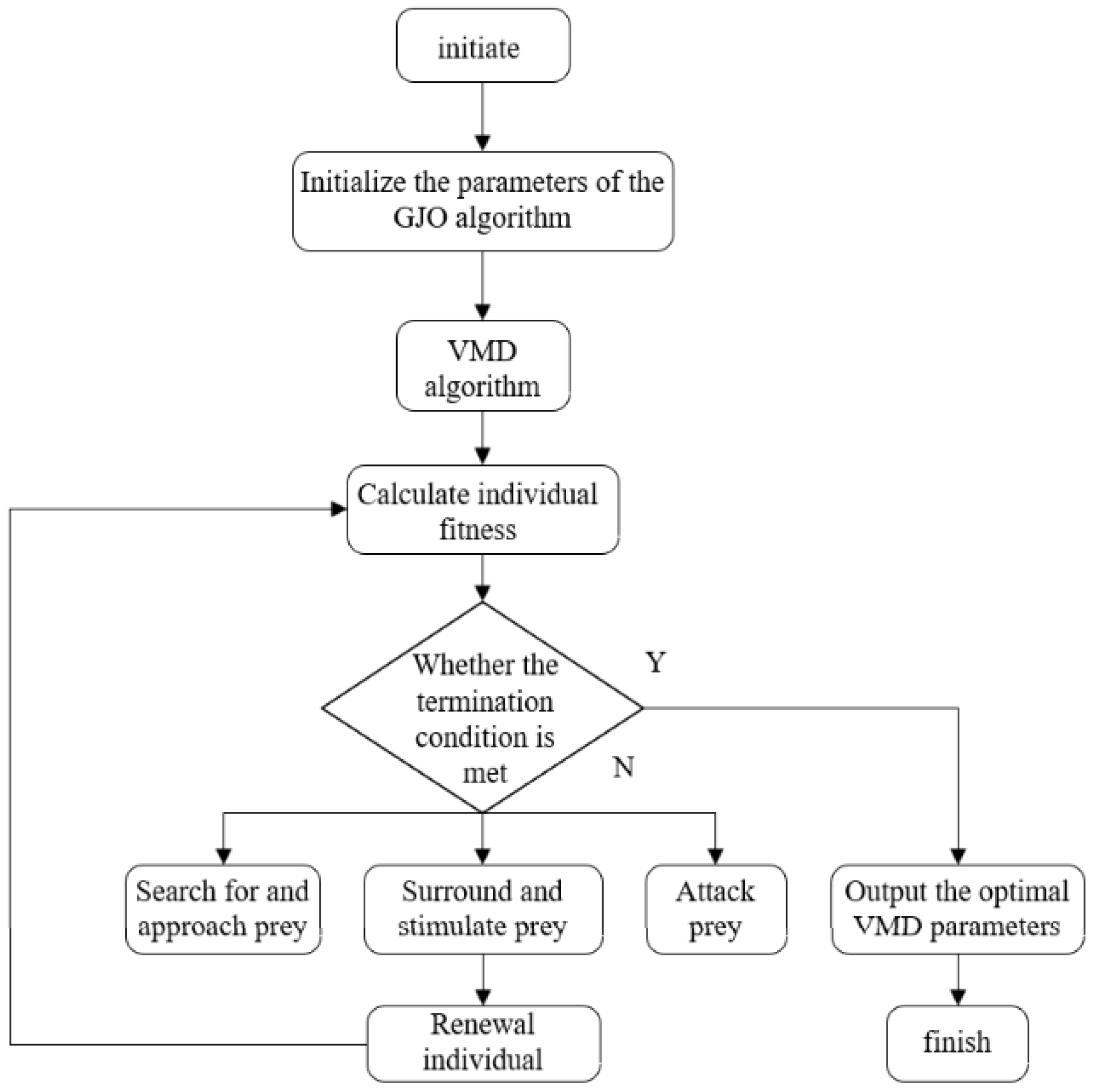
2.3. GJO Optimization VMD
- (1)
- Input the fault signal, given the relevant parameters in the GJO, and the range of (k, α) in the VMD.
- (2)
- The VMD decomposition of the fault signal is performed according to the given parameters, in which the value of the minimum envelope entropy in each iteration is solved and the current minimum envelope entropy and its corresponding local optimal solution are constantly updated and saved.
- (3)
- Repeat (2) to keep the values updated until the maximum number of iterations is given, thus stopping the loop and obtaining the optimal (k, α).
2.4. Kurtosis Criterion and Cross-Correlation Coefficient Criterion
2.4.1. Kurtosis Criterion
2.4.2. Cross-Correlation Coefficient Criterion
2.5. Time-Domain Indicators
2.6. CNN-SVM Combined Network Architecture
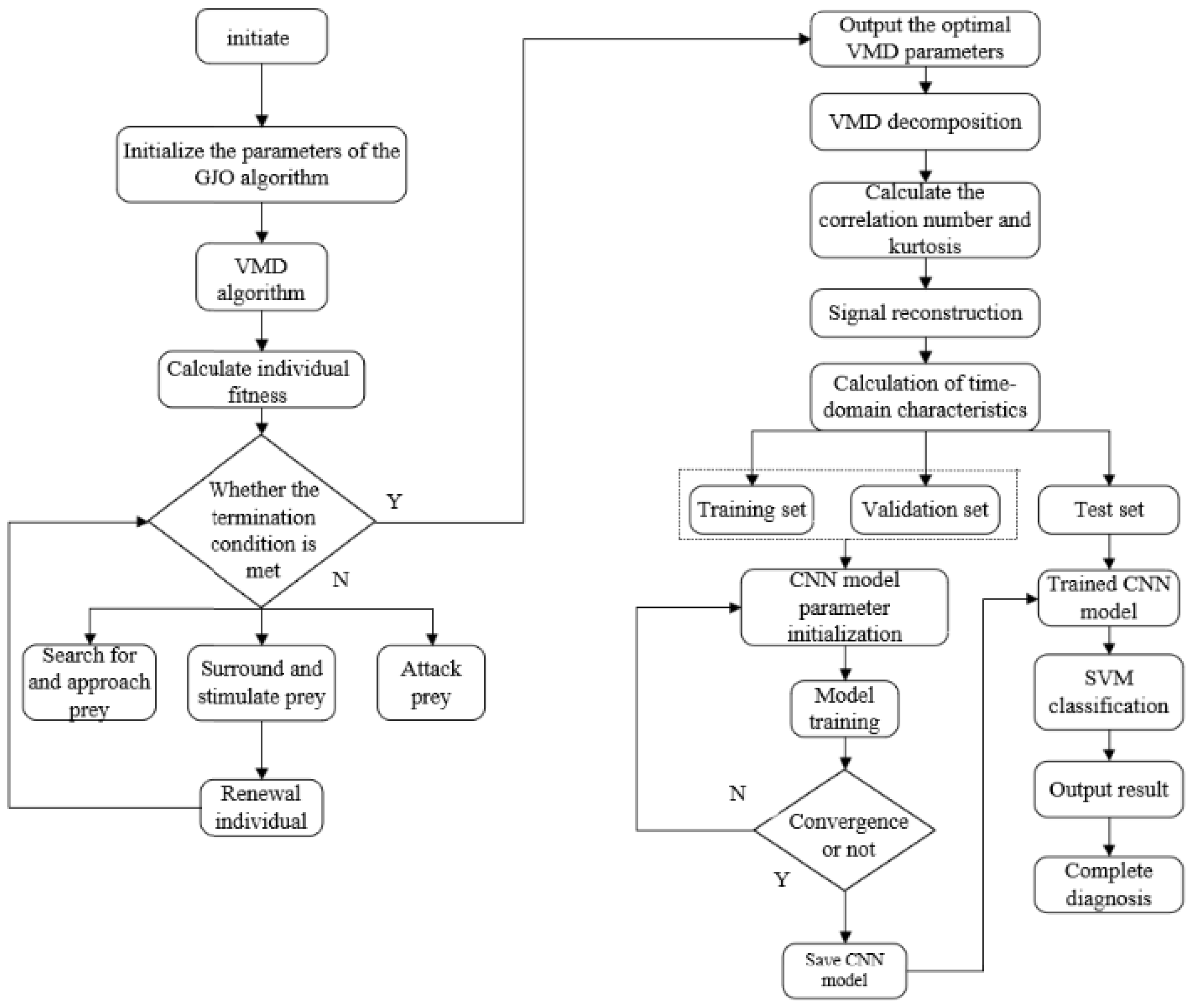
2.7. Diagnostic Process
- (1)
- The original data are subjected to data partitioning, the partitioned data are fed into the GJO algorithm, the fitness function of the algorithm is set as well as the various parameters, and the optimal parameters, k and α, that are most suitable for the VMD decomposition of each signal are determined based on the different characteristics of the different data.
- (2)
- The best parameters obtained are substituted into VMD for signal decomposition to obtain the respective decomposed IMF components.
- (3)
- The kurtosis value and cross-correlation coefficient value of each IMF component are calculated and the component that meets both the kurtosis criterion and the cross-correlation coefficient criterion for signal reconstruction is selected so as to obtain the signal after noise reduction.
- (4)
- The mean, variance, peak, magnitude, RMS, peak factor, pulse factor, waveform factor, and margin factor of the reconstructed signal are calculated to form the feature data.
- (5)
- The composed feature data are used as the input to the CNN-SVM network to realize the bearing fault diagnosis.
3. Results
3.1. Public Dataset Testing
- (1)
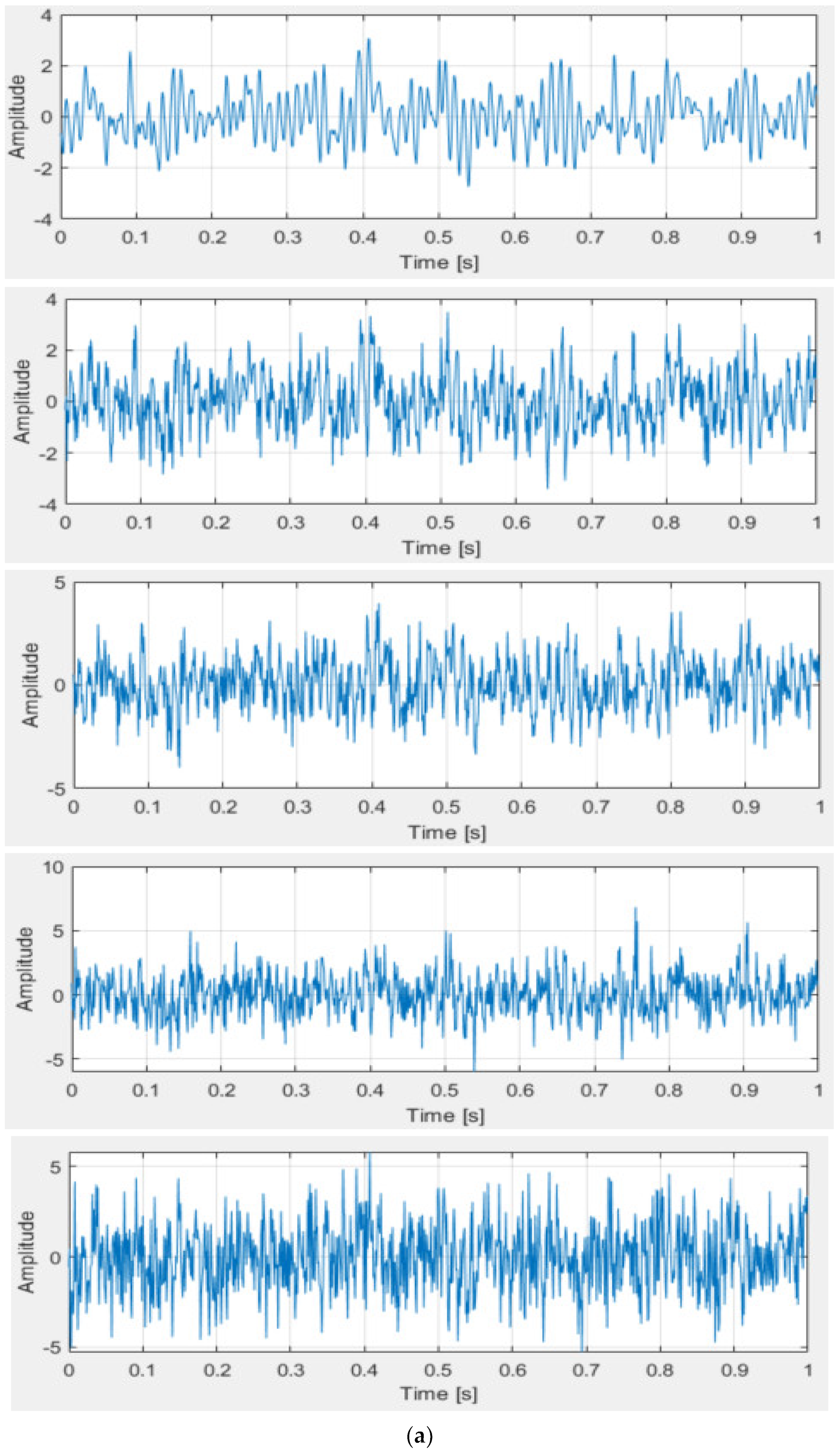
- Experimental data
- (2)
- Construct the feature data vector
- (3)
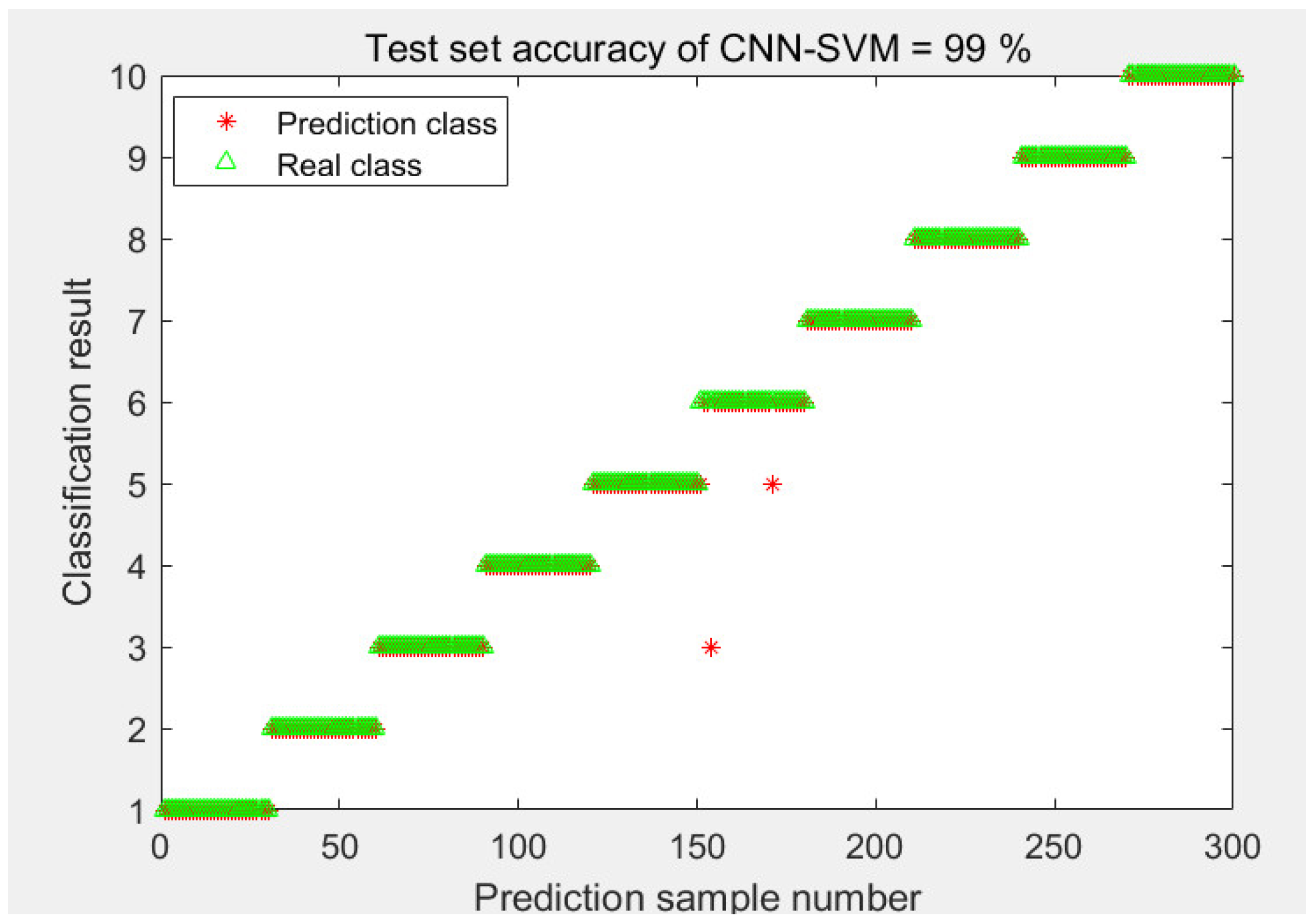
- Fault diagnosis
- (4)
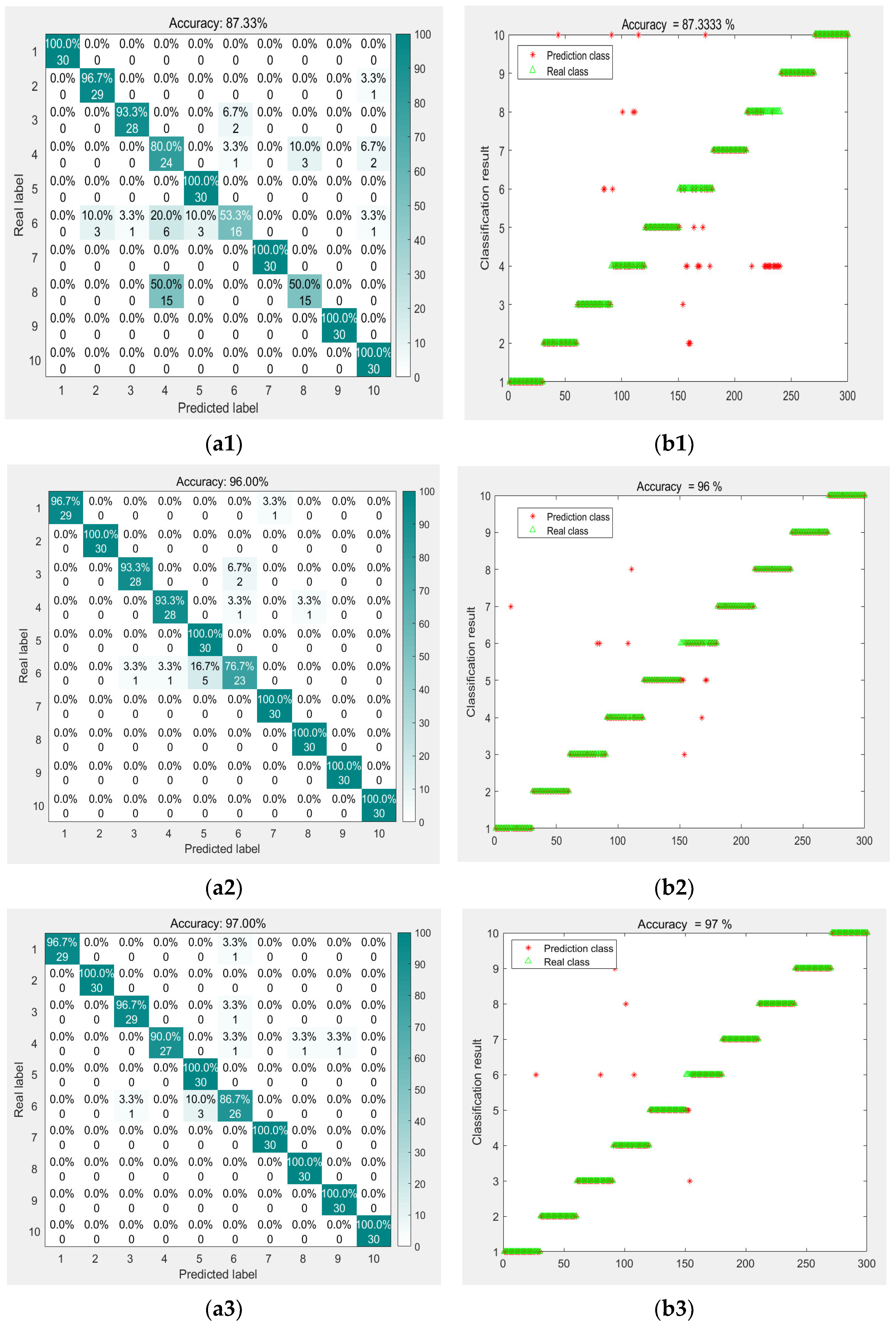
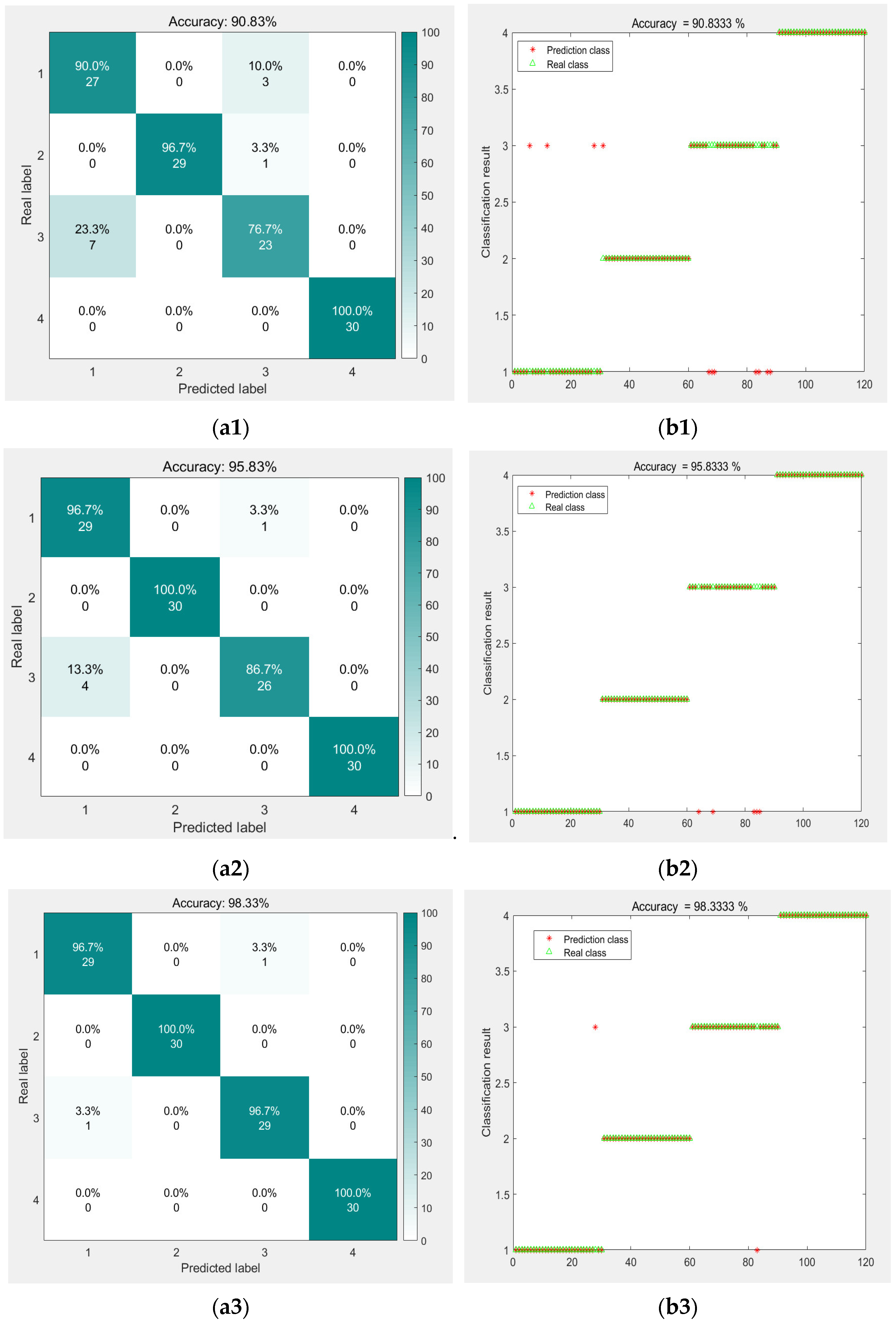
- Model Comparison
3.2. Experimental Verification
- (1)
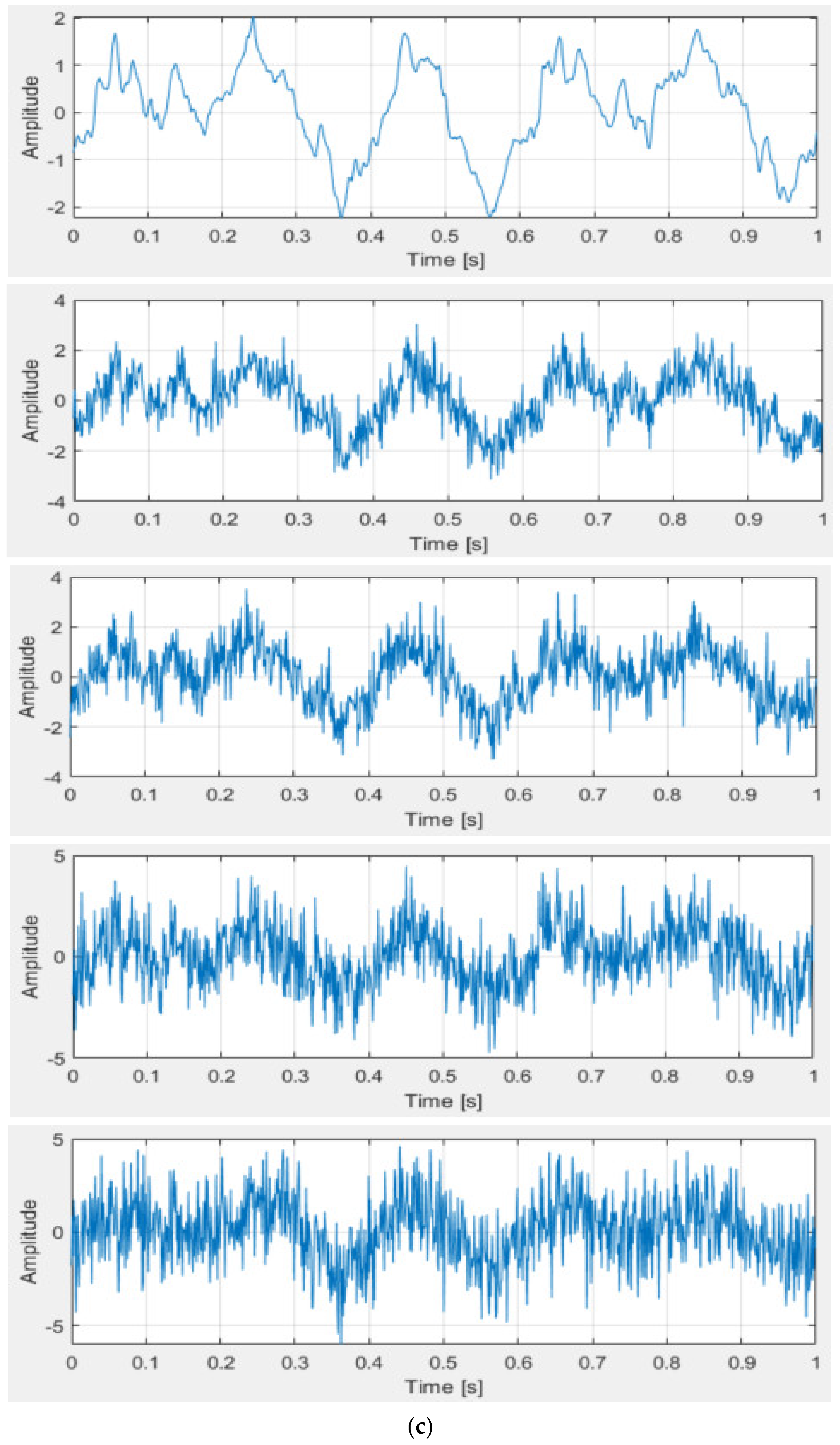
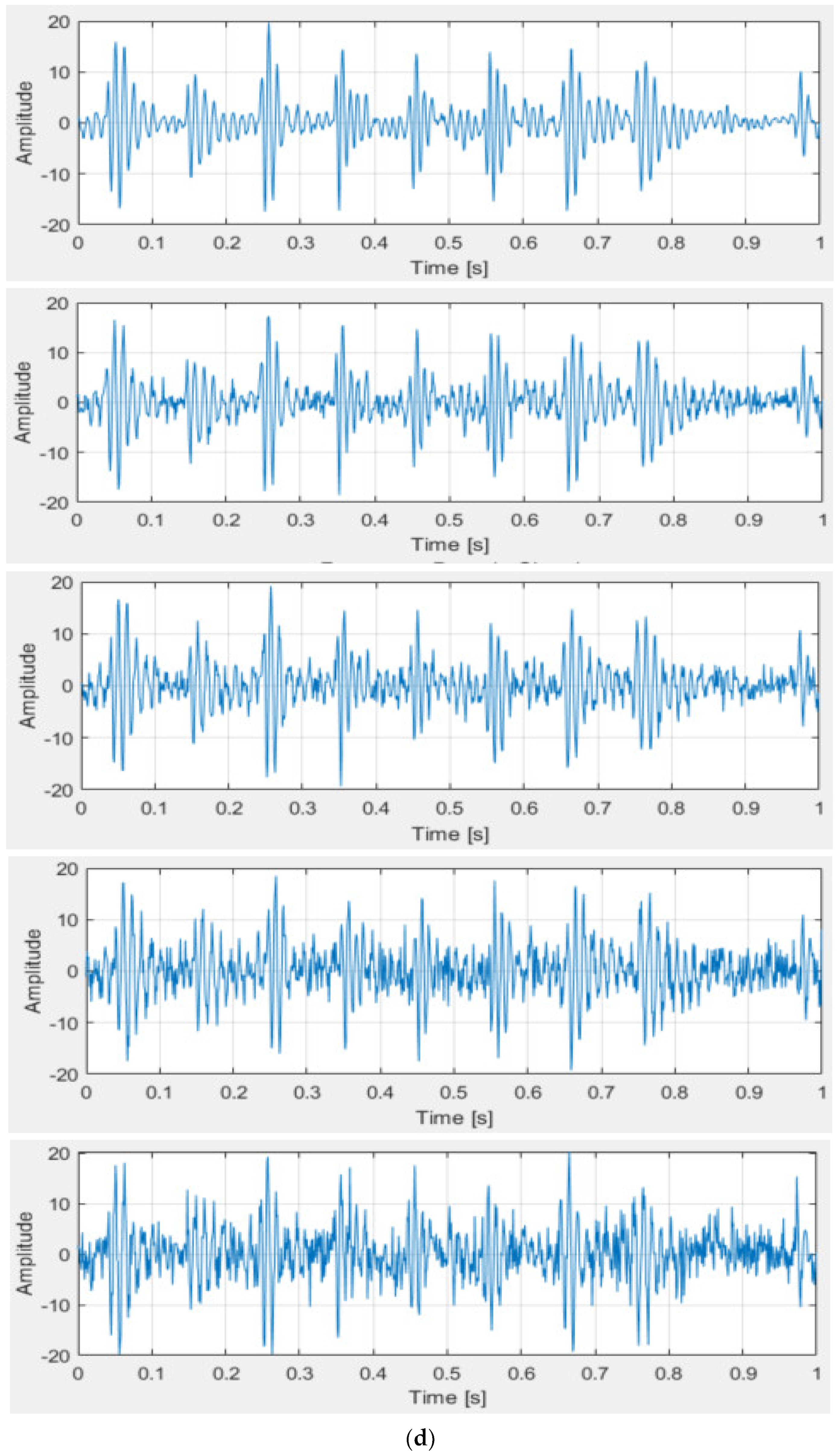
- Experimental data presentation and processing
- (2)
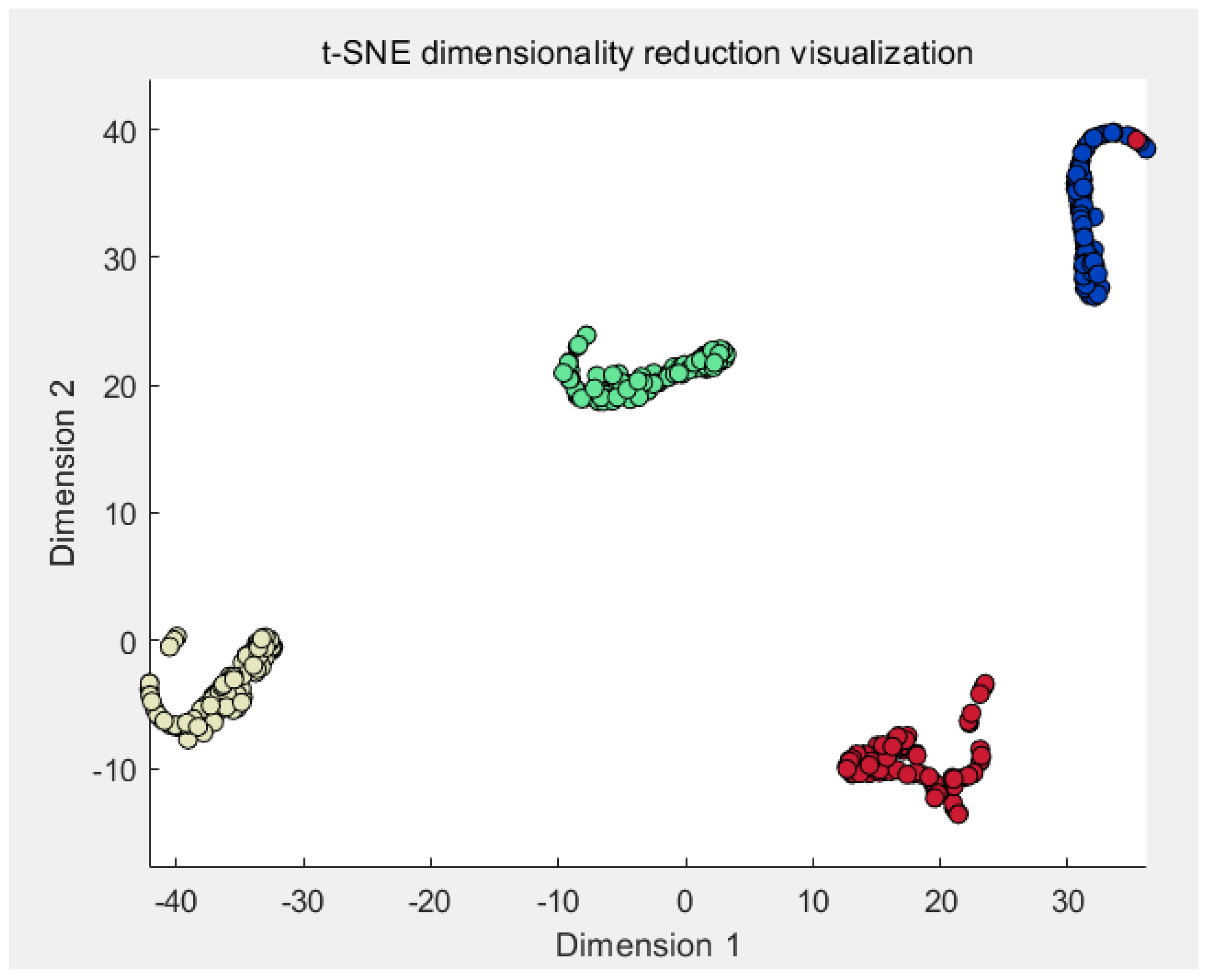
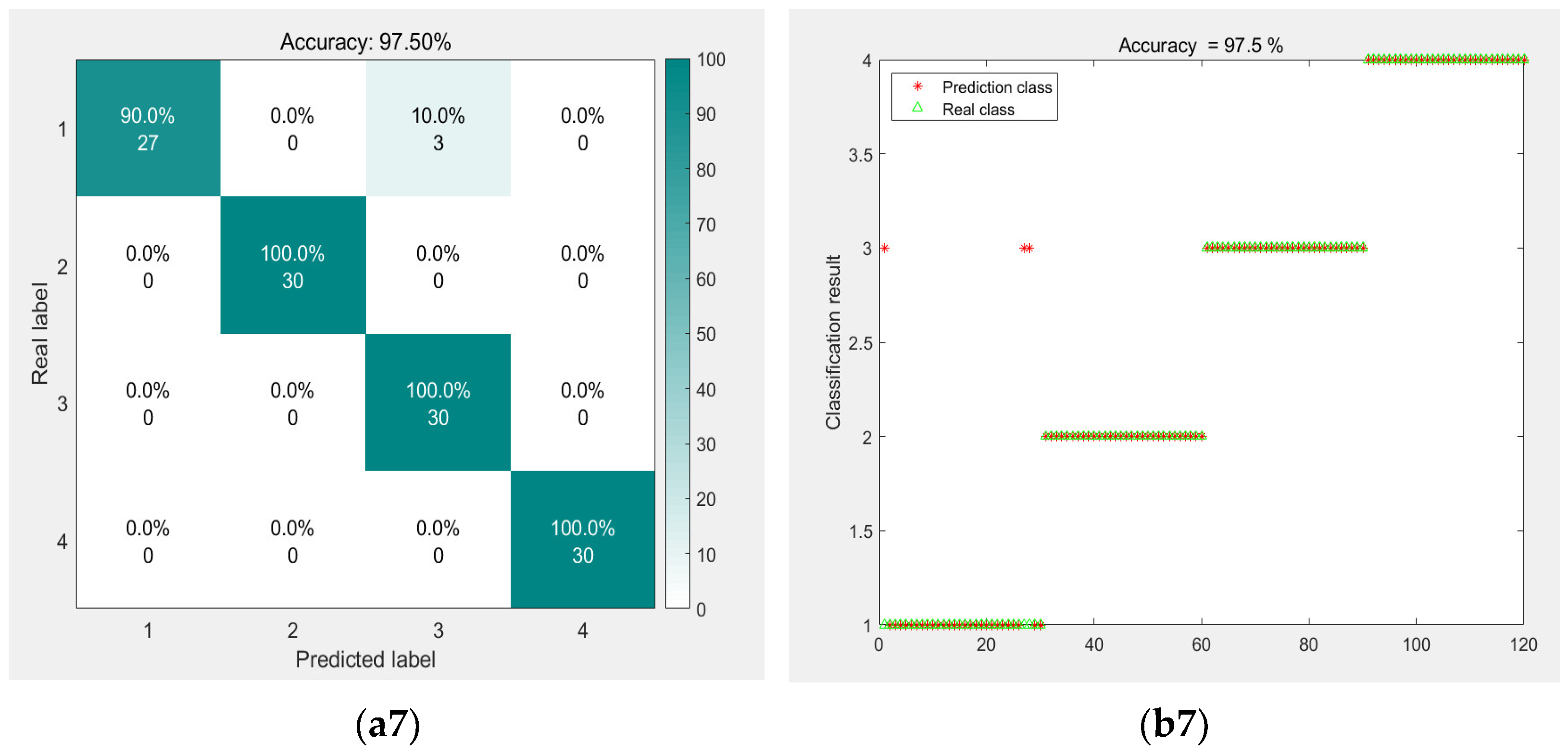
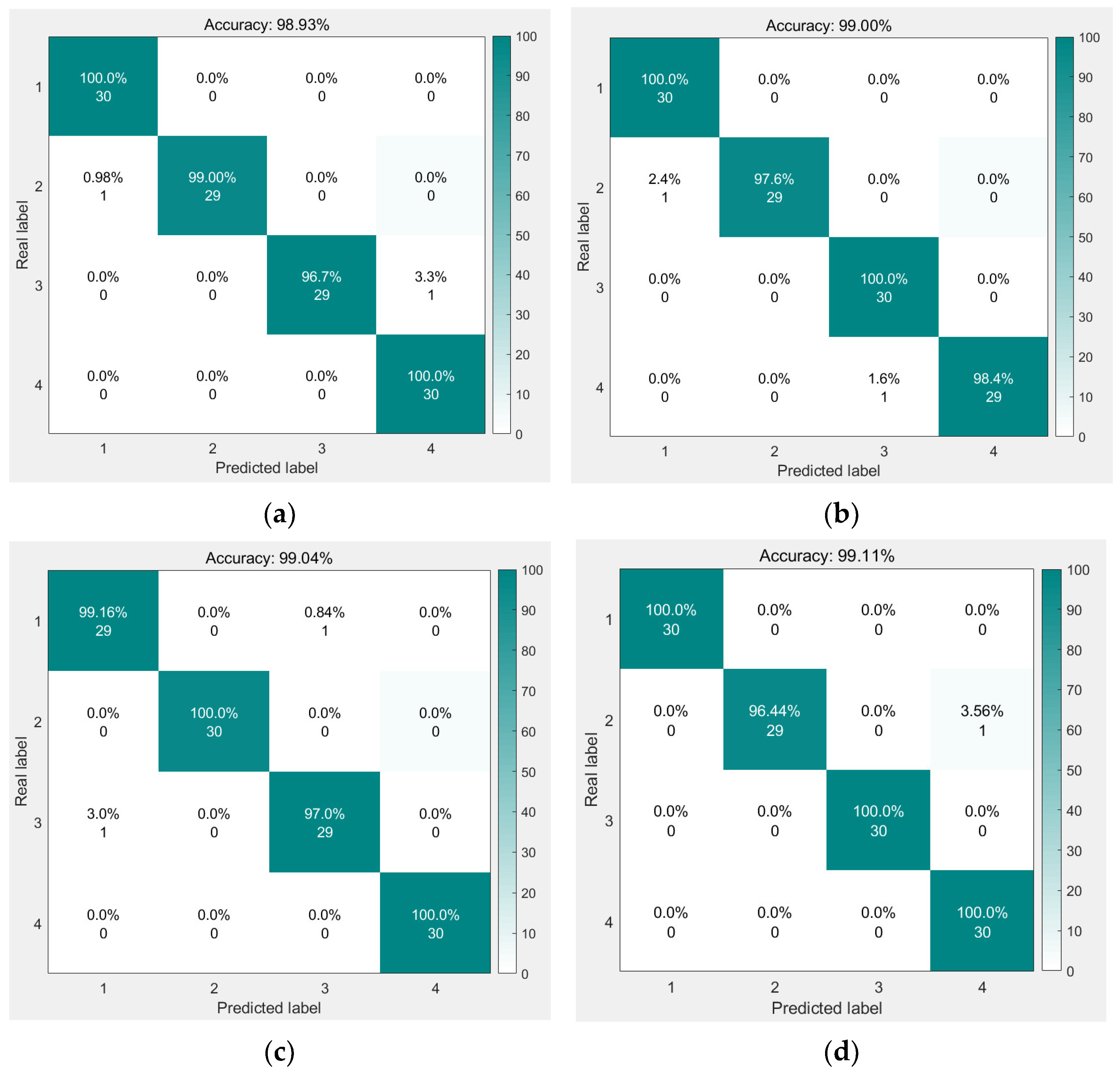
- Analysis of experimental results
- (3)
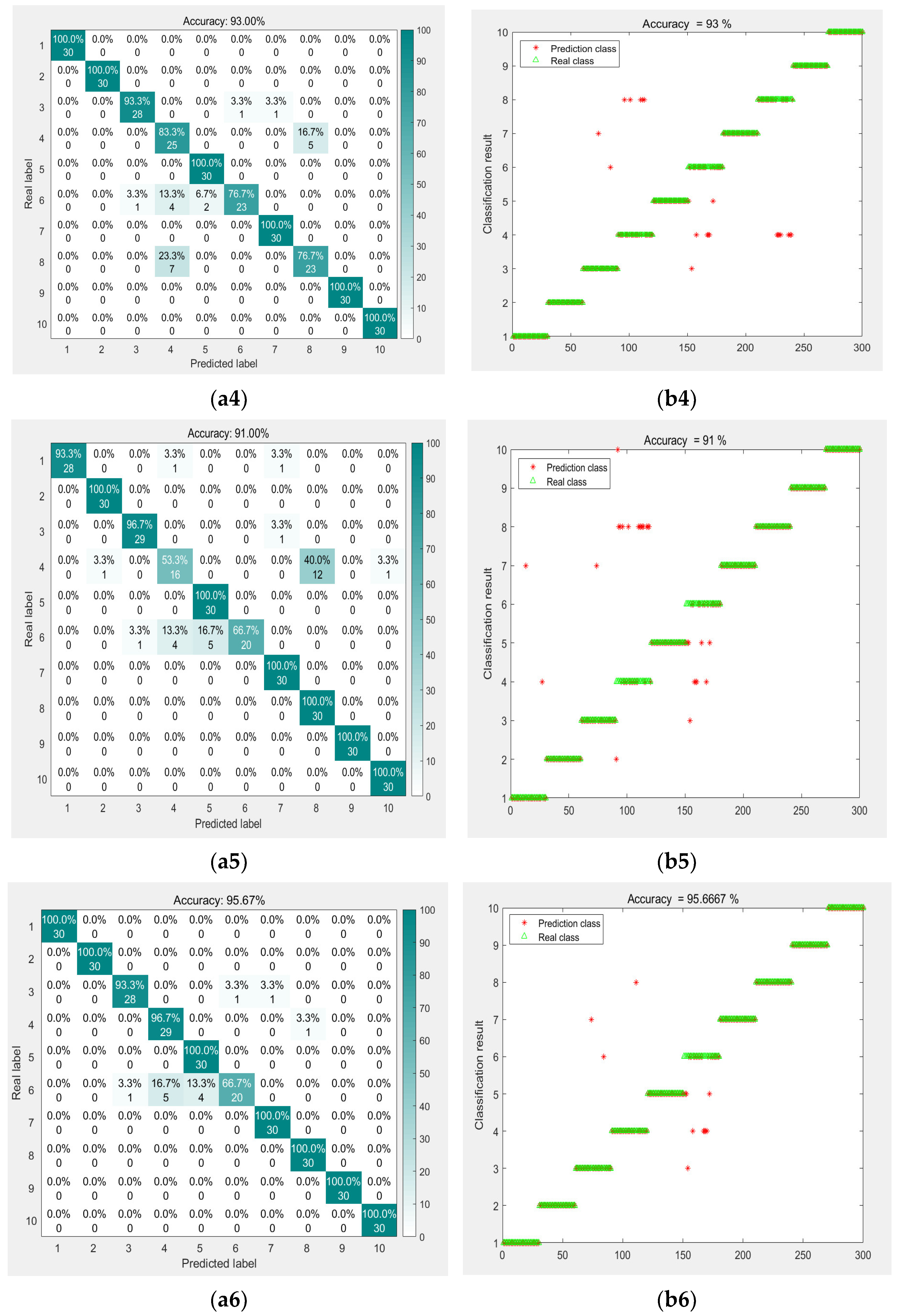
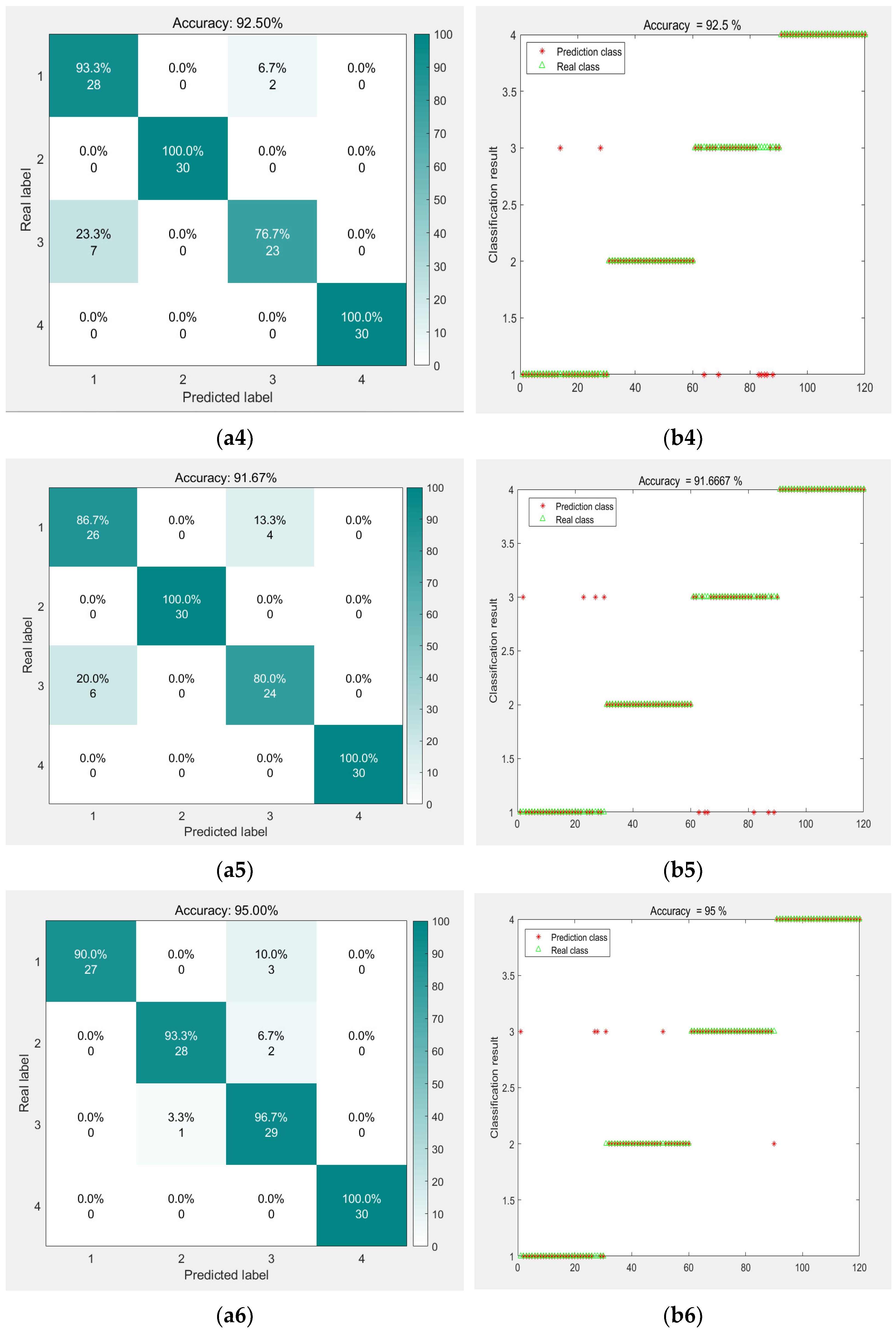
- Model comparison
- (4)
- Noise test
4. Discussion
- (1)
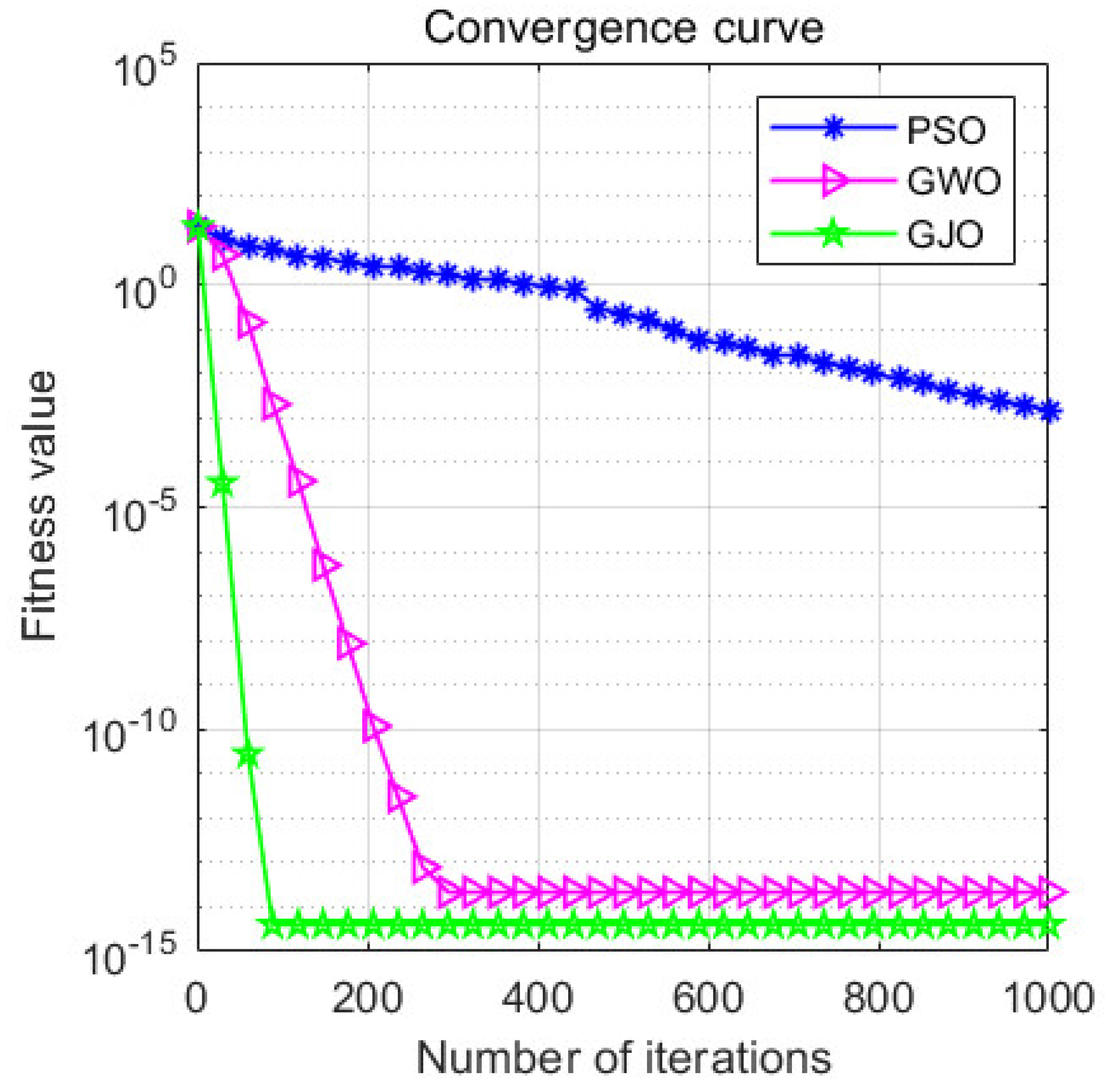
- In this paper, GJO is used to optimize VMD in order to select the key parameters, PSO and GWO algorithms are compared, and the results demonstrate that the GJO algorithm converges rapidly and maintains high accuracy.
- (2)
- The VMD-decomposed signals are filtered and reconstructed using the kurtosis and cross-correlation coefficient, and the nine time-domain features of the reconstructed signals are calculated while simultaneously constructing the feature vectors, which serve as inputs for the neural network so that the neural network can be provided with more meaningful and easy-to-interpret inputs, which then help the model to learn better, thus improving the accuracy and robustness of the model.
- (3)
- The SVM is utilized to replace the SoftMax classifier in the traditional CNN network to improve the classification ability of the CNN network, which is more conducive to the problems mentioned in this paper.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fang, Q.; Wu, D. ANS-net: Anti-noise Siamese network for bearing fault diagnosis with a few data. Nonlinear Dyn. 2021, 104, 2497–2514. [Google Scholar] [CrossRef]
- Cui, B.; Weng, Y.; Zhang, N. A feature extraction and machine learning framework for bearing fault diagnosis. Renew. Energy 2022, 191, 987–997. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, B.; Lin, Y. Machine learning based bearing fault diagnosis using the case western reserve university data: A review. IEEE Access 2021, 9, 155598–155608. [Google Scholar] [CrossRef]
- Han, T.; Zhang, L.; Yin, Z.; Tan, A.C. Rolling bearing fault diagnosis with combined convolutional neural networks and support vector machine. Measurement 2021, 177, 109022. [Google Scholar] [CrossRef]
- Rai, A.; Upadhyay, S.H. A review on signal processing techniques utilized in the fault diagnosis of rolling element bearings. Tribol. Int. 2016, 96, 289–306. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Z.; Wang, S.; Li, W.; Sarkodie-Gyan, T.; Feng, S. A hybrid deep-learning model for fault diagnosis of rolling bearings. Measurement 2021, 169, 108502. [Google Scholar] [CrossRef]
- Khorram, A.; Khalooei, M.; Rezghi, M. End-to-end CNN+ LSTM deep learning approach for bearing fault diagnosis. Appl. Intell. 2021, 51, 736–751. [Google Scholar] [CrossRef]
- Quendo, C.; Rius, E.; Person, C.; Michel, N. Integration of optimized low-pass filters in a bandpass filter for out-of-band improvement. IEEE Trans. Microw. Theory Tech. 2001, 49, 2376–2383. [Google Scholar] [CrossRef]
- Zhang, Y.; Yong, L.; Mao, G. Complementary ensemble adaptive local iterative filtering and its application to rolling bearing fault diagnosis. IEEE Access 2021, 9, 47275–47293. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, S.; Wei, Y.; Zhang, H. A novel feature adaptive extraction method based on deep learning for bearing fault diagnosis. Measurement 2021, 185, 110030. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Yeh, J.R.; Shieh, J.S.; Huang, N.E. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P.A. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; IEEE: Piscataway, NJ, USA; pp. 4144–4147. [Google Scholar]
- Duan, R.; Liao, Y.; Wang, S. Adaptive morphological analysis method and its application for bearing fault diagnosis. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Li, Y.; Cheng, G.; Liu, C. Research on bearing fault diagnosis based on spectrum characteristics under strong noise interference. Meas. 2021, 169, 108509. [Google Scholar] [CrossRef]
- Ye, M.; Yan, X.; Jia, M. Rolling bearing fault diagnosis based on VMD-MPE and PSO-SVM. Entropy 2021, 23, 762. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, W.; Zhao, X.; Wu, X.; Liu, N. Application of WOA-VMD algorithm in bearing fault diagnosis. Noise Vib. Control 2021, 41, 86. [Google Scholar]
- Wang, M.; Wang, W.; Zeng, J.; Zhang, Y. An integrated method based on sparrow search algorithm improved variational mode decomposition and support vector machine for fault diagnosis of rolling bearing. J. Vib. Eng. Technol. 2022, 10, 2893–2904. [Google Scholar] [CrossRef]
- Li, H.; Liu, T.; Wu, X.; Chen, Q. An optimized VMD method and its applications in bearing fault diagnosis. Measurement 2020, 166, 108185. [Google Scholar] [CrossRef]
- Antoni, J. The spectral kurtosis: A useful tool for characterising non-stationary signals. Mech. Syst. Signal Process. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Nayana, B.R.; Geethanjali, P. Analysis of statistical time-domain features effectiveness in identification of bearing faults from vibration signal. IEEE Sens. J. 2017, 17, 5618–5625. [Google Scholar] [CrossRef]
- Sawalhi, N.; Randall, R.B. The application of spectral kurtosis to bearing diagnostics. In Proceedings of the ACOUSTICS 2004, Gold Coast, Australia, 3–5 November 2004; pp. 3–5. [Google Scholar]
- Liu, X.; Sun, W.; Li, H.; Hussain, Z.; Liu, A. The method of rolling bearing fault diagnosis based on multi-domain supervised learning of convolution neural network. Energies 2022, 15, 4614. [Google Scholar] [CrossRef]
- You, K.; Qiu, G.; Gu, Y. Rolling bearing fault diagnosis using hybrid neural network with principal component analysis. Sensors 2022, 22, 8906. [Google Scholar] [CrossRef]
- Chopra, N.; Ansari, M. Golden jackal optimization: A novel nature-inspired optimizer for engineering applications. Expert Syst. Appl. 2022, 198, 116924. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Peng, D.; Cheng, Z. Attention-guided joint learning CNN with noise robustness for bearing fault diagnosis and vibration signal denoising. ISA Trans. 2022, 128, 470–484. [Google Scholar] [CrossRef]
- Jiang, Z.; Li, Y.; Gao, J.; Wu, C. A fault detection of aero-engine rolling bearings based on CNN-BiLSTM network integrated cross-attention. Meas. Sci. Technol. 2024, 35, 126116. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, S.; Dai, J.; Tang, J. A Novel Bearing Fault Diagnosis Methodology Based on SVD and One-Dimensional Convolutional Neural Network. Shock. Vib. 2020, 2020, 1850286. [Google Scholar] [CrossRef]







| Fault Diameter | Typology | (k, α) |
|---|---|---|
| 0 | Normal | (10, 1847) |
| 0.1778 mm | Inner ring failure | (3, 2500) |
| 0.1778 mm | Rolling body failure | (10, 754) |
| 0.1778 mm | Outer ring failure | (4, 100) |
| 0.3556 mm | Inner ring failure | (4, 2304) |
| 0.3556 mm | Rolling body failure | (10, 1213) |
| 0.3556 mm | Outer ring failure | (10, 2352) |
| 0.5334 mm | Inner ring failure | (5, 1621) |
| 0.5334 mm | Rolling body failure | (3, 2099) |
| 0.5334 mm | Outer ring failure | (7, 196) |
| Component | Steepness | Correlation Number |
|---|---|---|
| IMF1 | 4.2514 | 0.7536 |
| IMF2 | 3.5846 | 0.4531 |
| IMF3 | 2.4561 | 0.2847 |
| IMF4 | 2.7615 | 0.2354 |
| IMF5 | 2.6513 | 0.2411 |
| Network Layer | Parameter Setting |
|---|---|
| Convolutional layer 1 | 16@3X1, Step 1 |
| Pooling layer 1 | 3X1, Step 2 |
| Convolutional layer 2 | 32@2X1, Step 1 |
| Pooling layer 2 | 2X1, Step 2 |
| Convolutional layer 3 | 64@2X1, Step 1 |
| Pooling layer 3 | 2X1, Step 2 |
| Flatten | - |
| SVM | - |
| Model | Precision/% | Recall/% | F1-Score | Average Accuracy/% |
|---|---|---|---|---|
| CNN | 89 | 87 | 0.87 | 87.33 |
| LSTM | 96 | 96 | 0.96 | 96.00 |
| BILSTM | 97 | 97 | 0.97 | 97.00 |
| CNN-SVM | 93 | 93 | 0.93 | 93.00 |
| VMD—CNN | 91 | 91 | 0.91 | 91.00 |
| VMD—CNN—SVM | 95 | 95 | 0.94 | 95.67 |
| GJO—VMD—CNN—SVM | 96 | 96 | 0.95 | 96.67 |
| GJO-VMD combining time domain features and CNN-SVM | 99 | 99 | 0.99 | 99.05 |
| Model | Precision/% | Recall/% | F1-Score | Average Accuracy/% |
|---|---|---|---|---|
| CNN | 91 | 91 | 0.91 | 90.83 |
| LSTM | 96 | 96 | 0.95 | 95.83 |
| BILSTM | 98 | 98 | 0.98 | 98.33 |
| CNN-SVM | 93 | 93 | 0.92 | 92.50 |
| VMD—CNN | 92 | 92 | 0.92 | 91.67 |
| VMD—CNN—SVM | 95 | 95 | 0.95 | 95.00 |
| GJO—VMD—CNN—SVM | 98 | 98 | 0.97 | 97.50 |
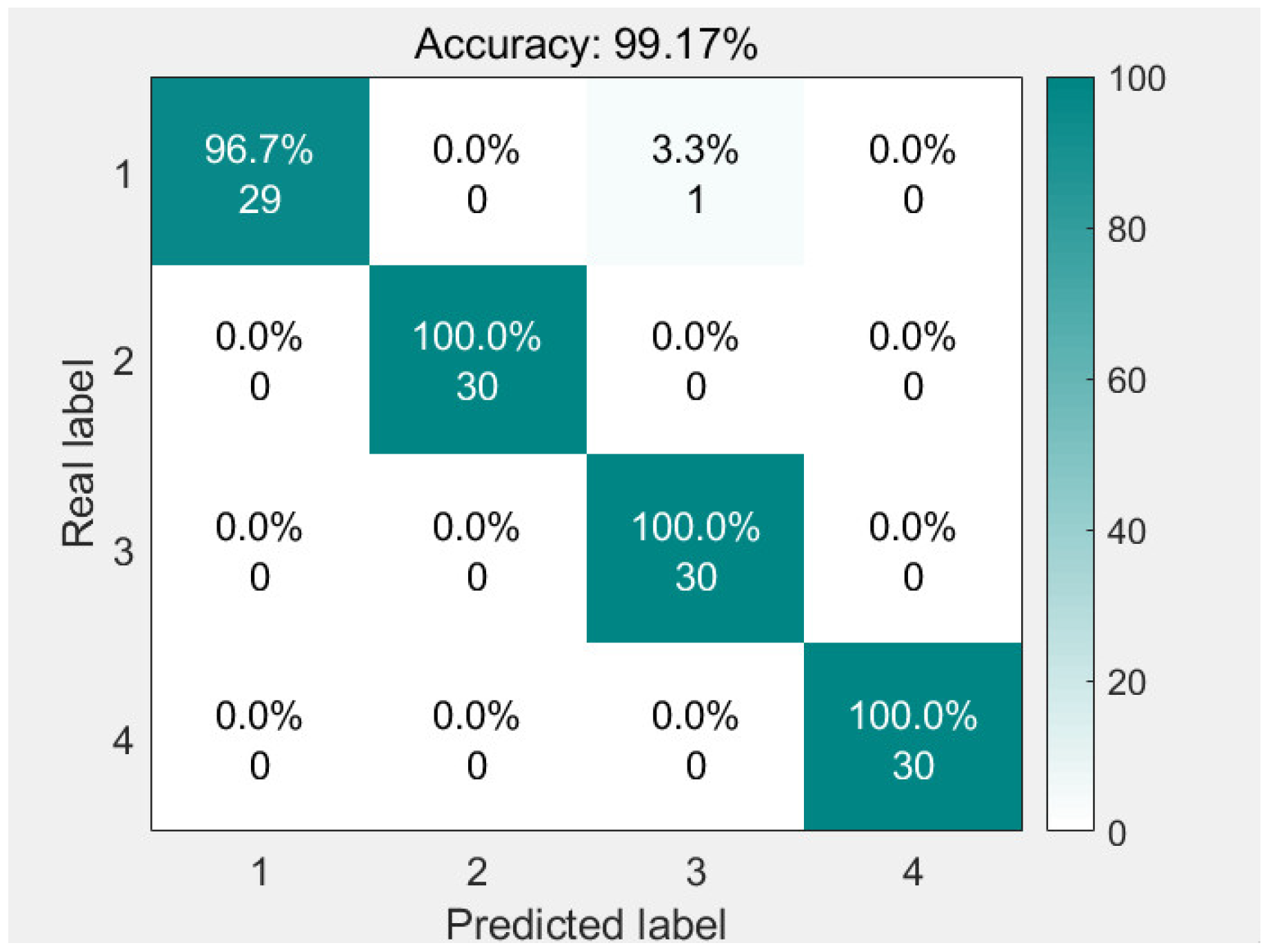
| GJO-VMD combining time domain features and CNN-SVM | 99 | 99 | 0.99 | 99.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, Y.; Zhang, X.; Zhao, W.; Liu, T. Rolling Bearing Fault Diagnosis Based on Optimized VMD Combining Signal Features and Improved CNN. World Electr. Veh. J. 2024, 15, 544. https://doi.org/10.3390/wevj15120544
Zou Y, Zhang X, Zhao W, Liu T. Rolling Bearing Fault Diagnosis Based on Optimized VMD Combining Signal Features and Improved CNN. World Electric Vehicle Journal. 2024; 15(12):544. https://doi.org/10.3390/wevj15120544
Chicago/Turabian StyleZou, Yingyong, Xingkui Zhang, Wenzhuo Zhao, and Tao Liu. 2024. "Rolling Bearing Fault Diagnosis Based on Optimized VMD Combining Signal Features and Improved CNN" World Electric Vehicle Journal 15, no. 12: 544. https://doi.org/10.3390/wevj15120544
APA StyleZou, Y., Zhang, X., Zhao, W., & Liu, T. (2024). Rolling Bearing Fault Diagnosis Based on Optimized VMD Combining Signal Features and Improved CNN. World Electric Vehicle Journal, 15(12), 544. https://doi.org/10.3390/wevj15120544






