Path-Following Control of Unmanned Vehicles Based on Optimal Preview Time Model Predictive Control
Abstract
1. Introduction
- (1)
- An unmanned vehicle path-following control strategy based on optimal preview time MPC(OP-MPC) for unmanned vehicles is proposed, which includes the longitudinal speed limit, the optimal preview time surface, and the MPC controller.
- (2)
- The particle swarm optimization (PSO) algorithm was used to obtain the optimal preview time under different vehicle speeds, and road curvatures. The linear interpolation was used to obtain the optimal preview time surface.
- (3)
- The longitudinal speed limit controls speed to prevent vehicle rollover and sideslip.
2. Longitudinal Speed Limit
2.1. Sideslip Constraint
2.2. Rollover Constraint
3. Path-Following Control Based on Model Predictive Control (MPC)
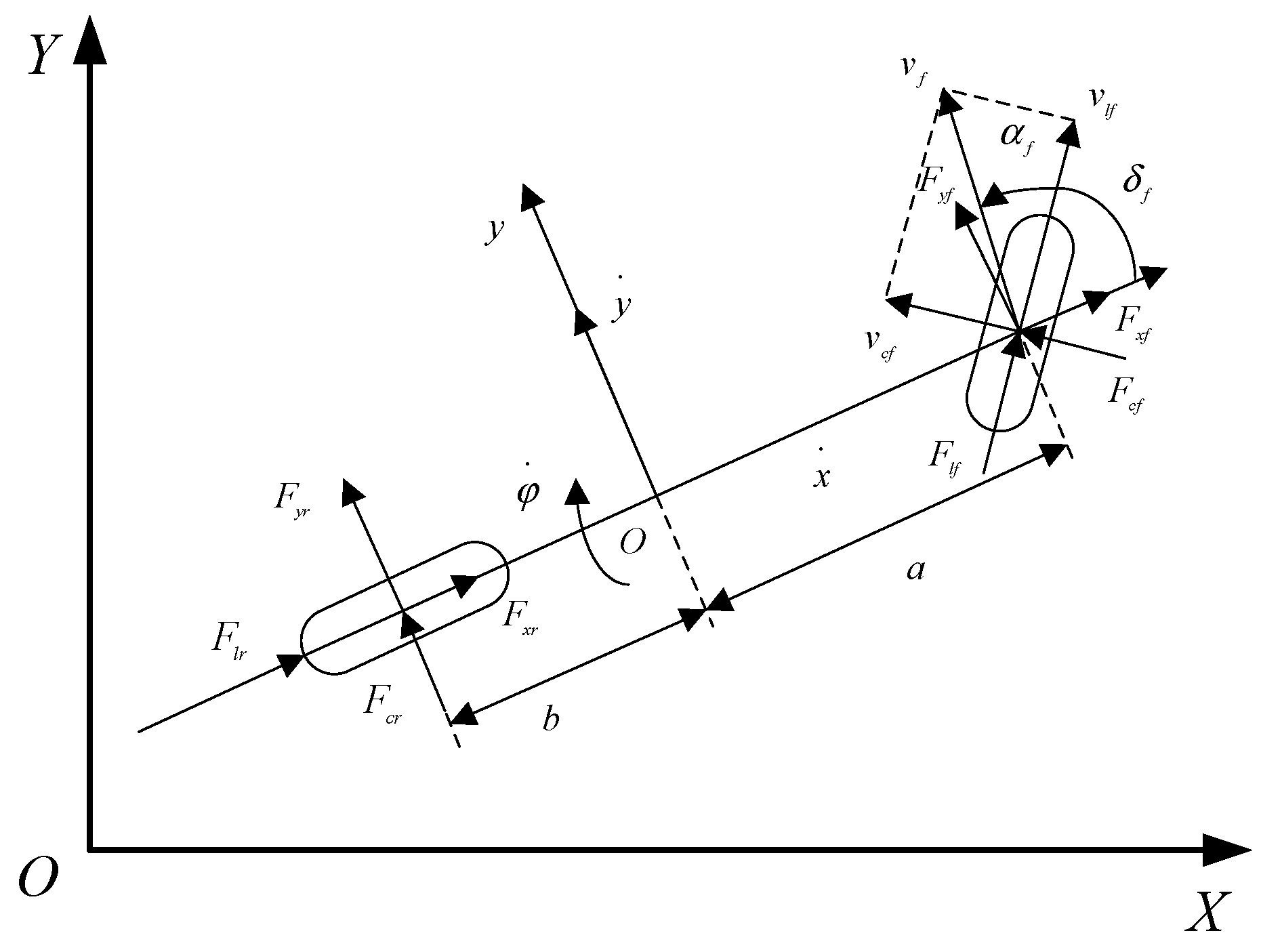
3.1. Vehicle Model
3.2. Model Predictive Control
- ,
4. Design of Adaptive Preview Time Regulator
4.1. Vehicle Preview Model
4.2. Preview Time Analysis
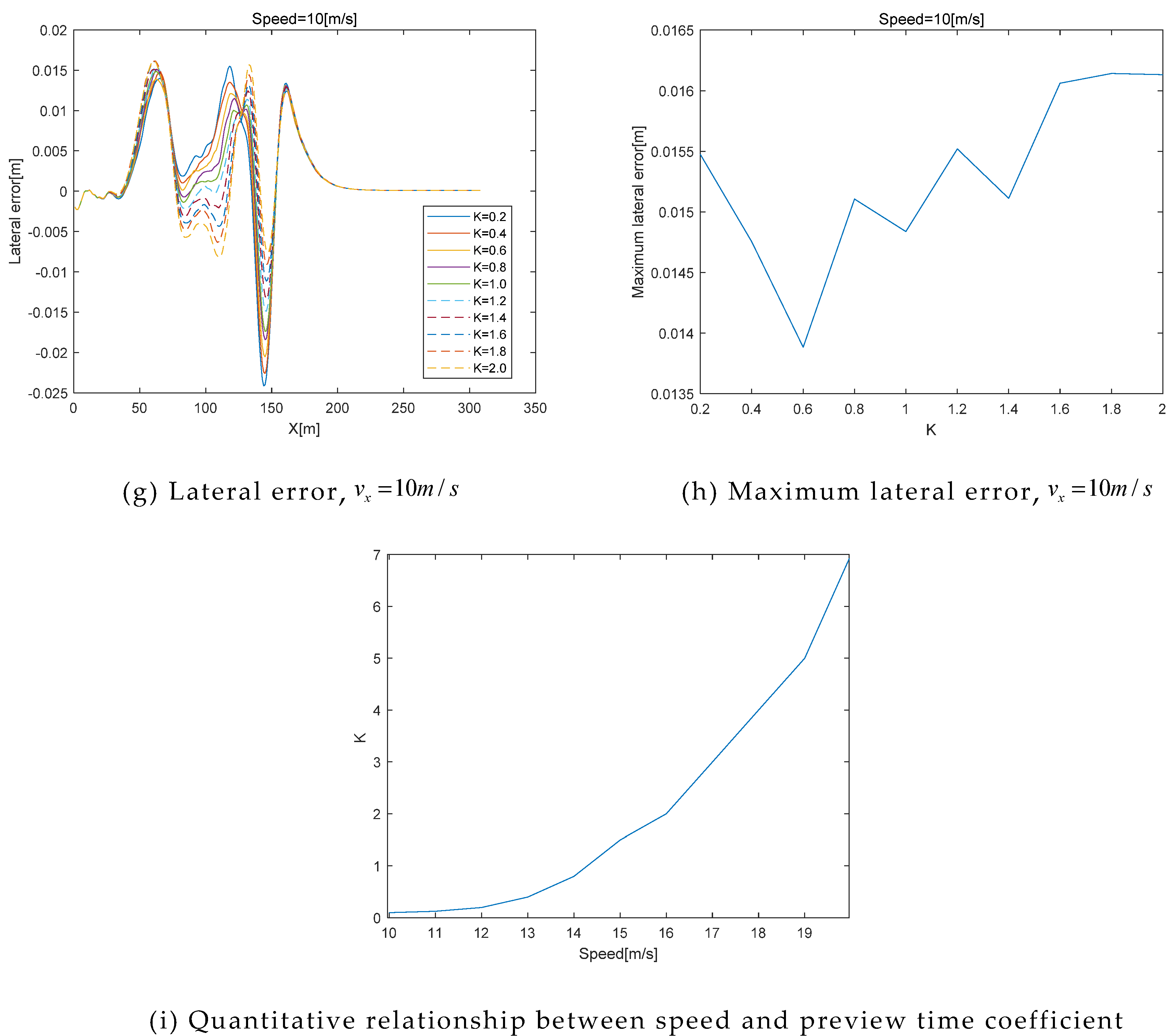
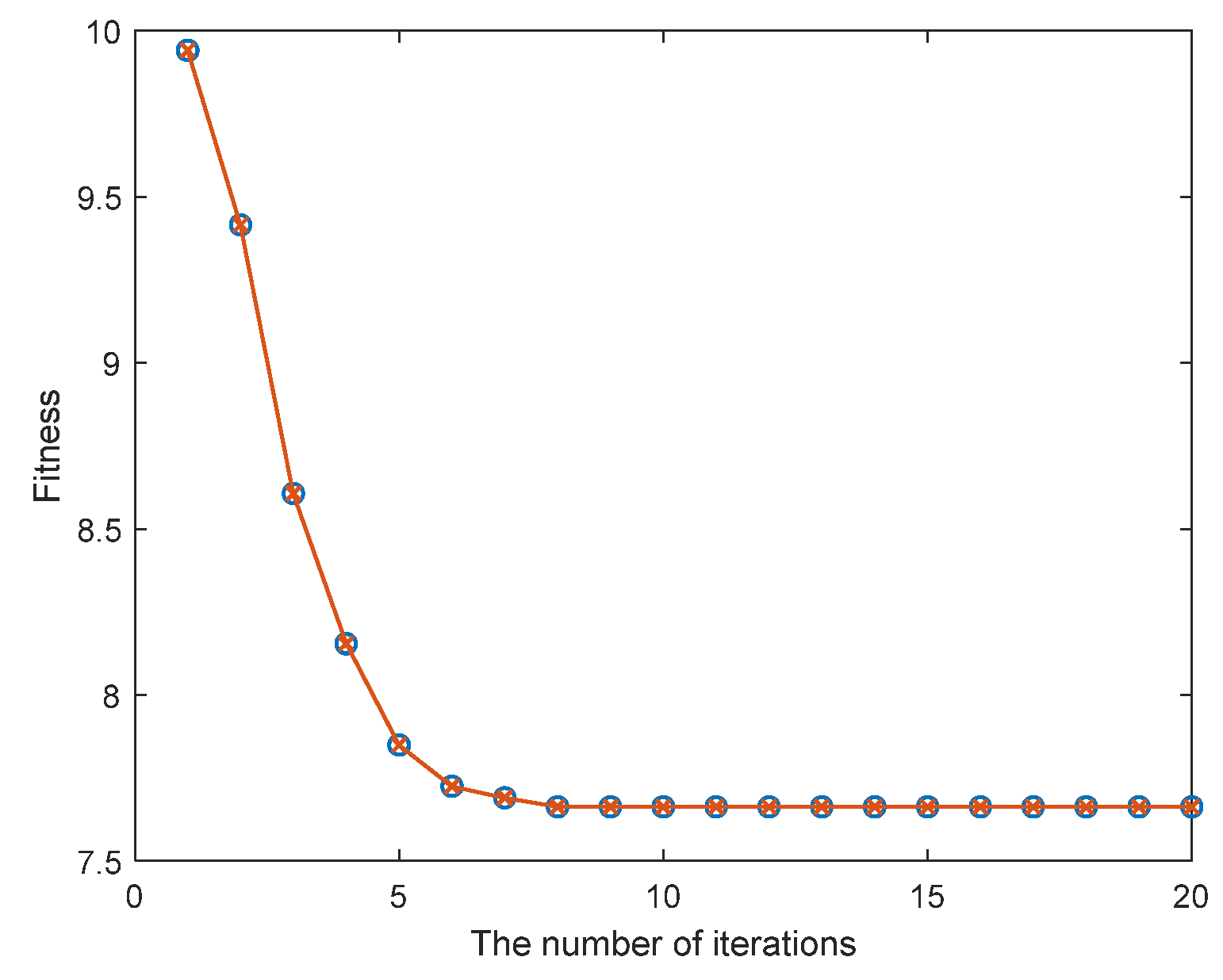
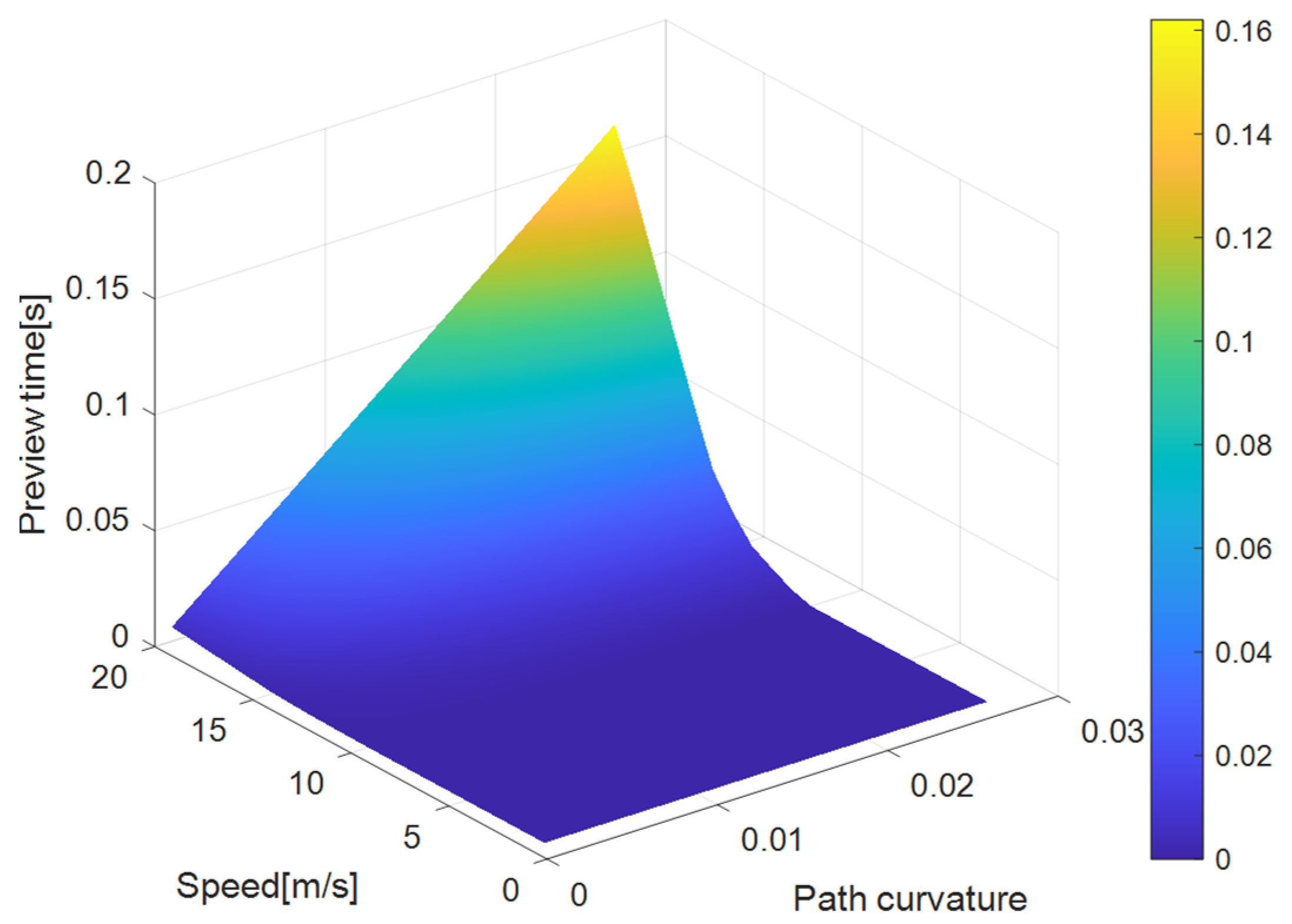
4.3. Optimal Preview Time
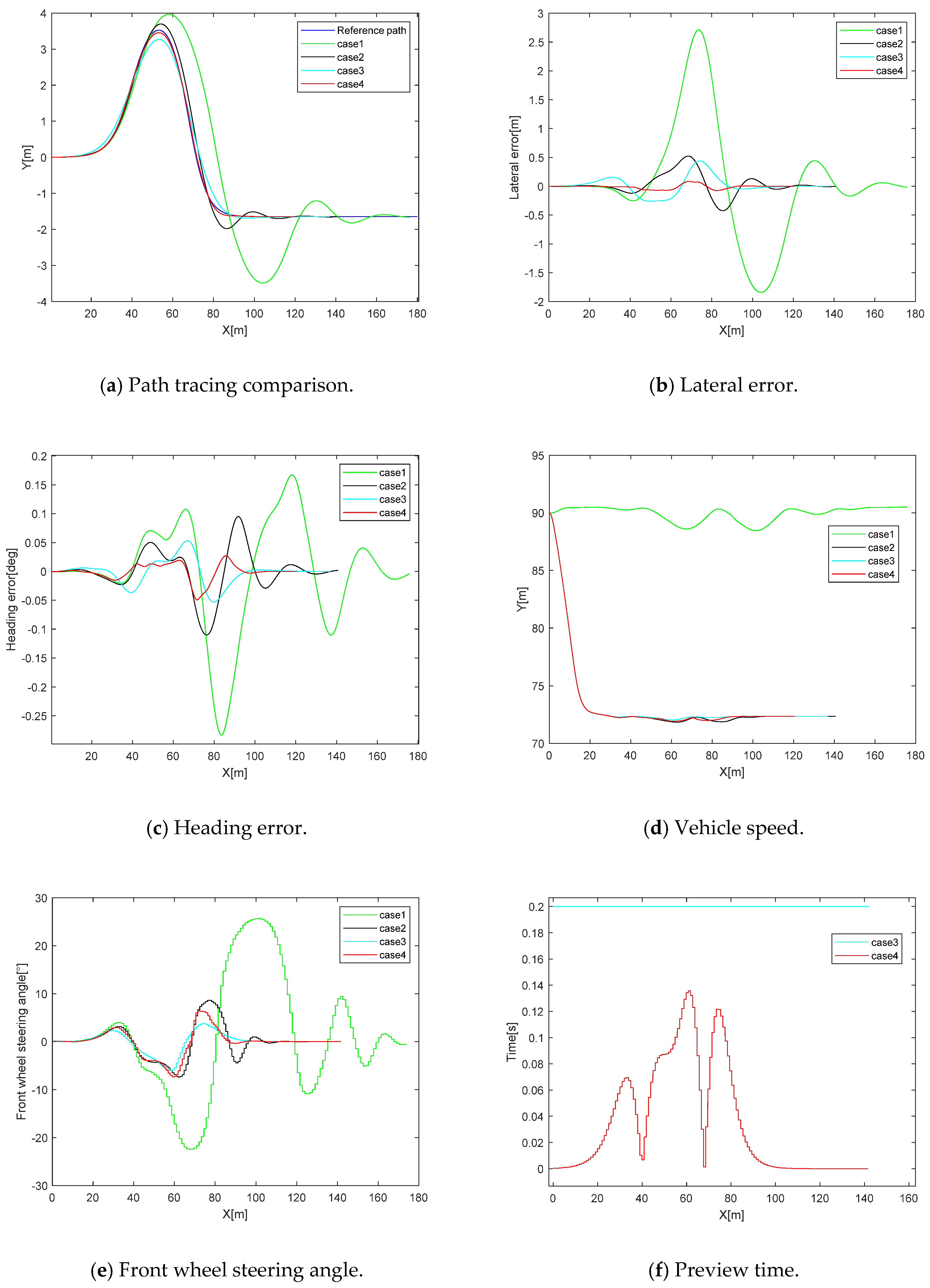
5. Simulation and Real Vehicle Testing
5.1. Simulation Analysis
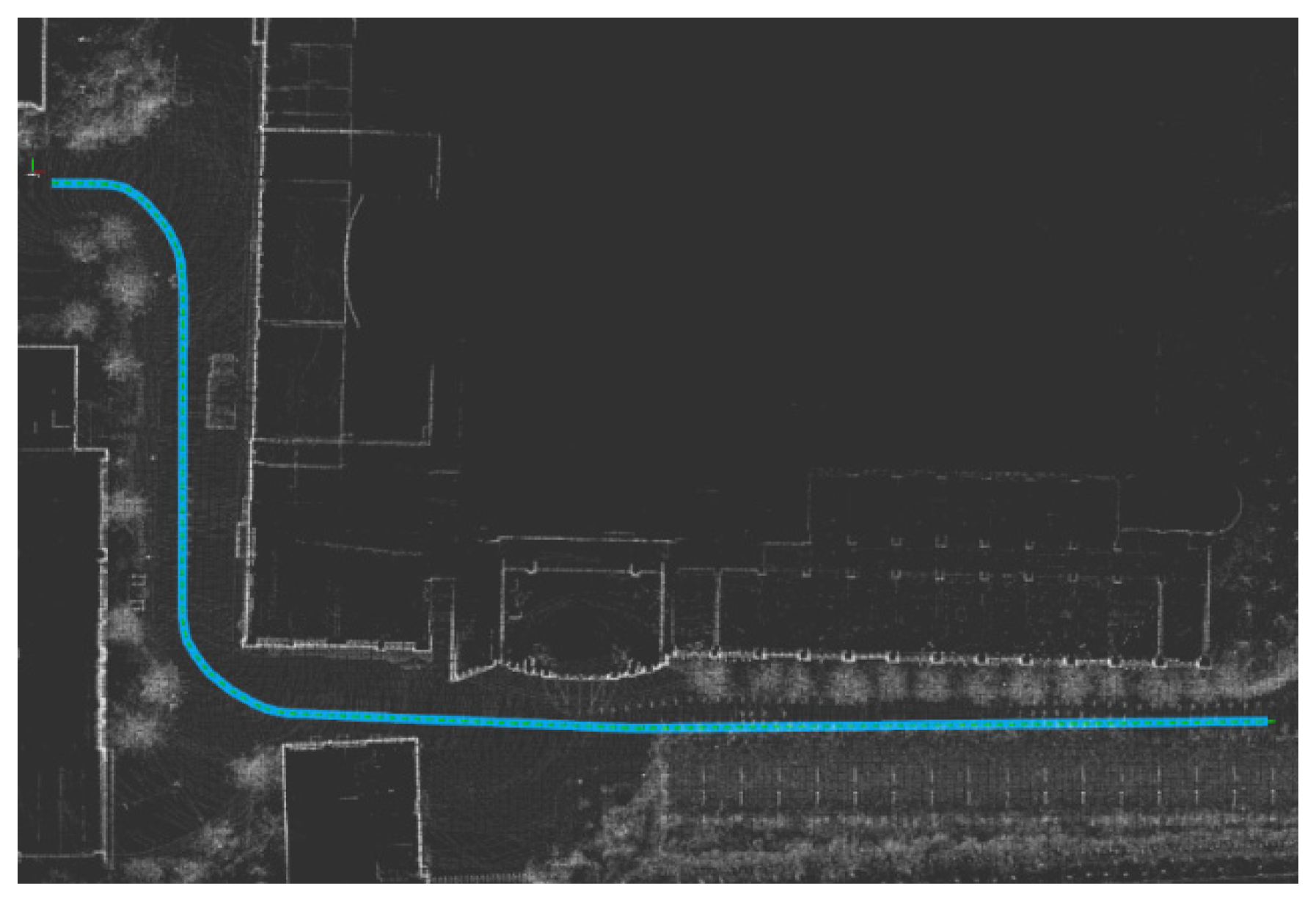
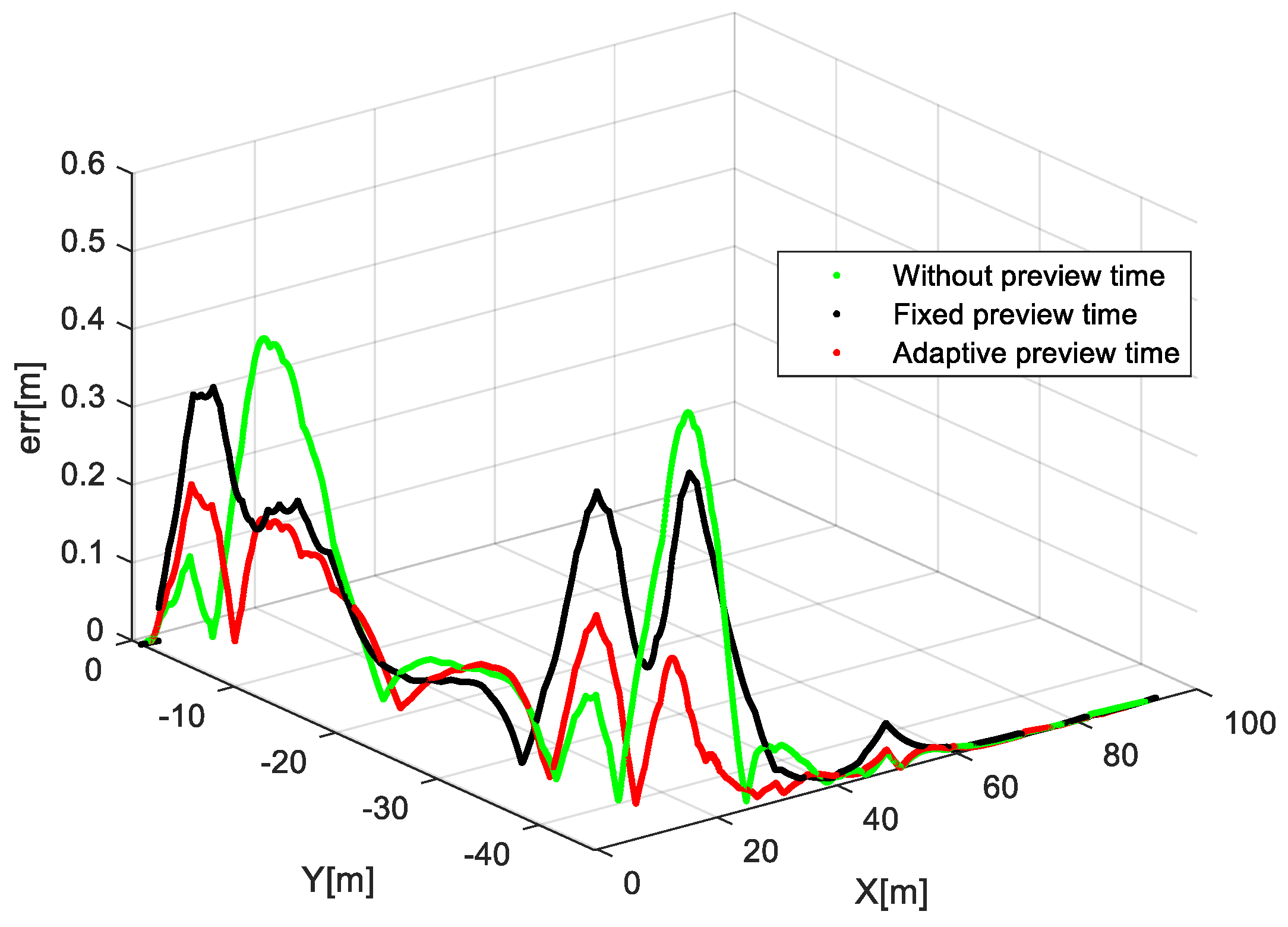
5.2. Real Car Verification
5.3. Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- König, M.; Neumayr, L. Users’ resistance towards radical innovations: The case of the self-driving car. Transp. Res. Part F Traffic Psychol. Behav. 2017, 44, 42–52. [Google Scholar] [CrossRef]
- Paden, B.; Čáp, M.; Yong, S.Z.; Yershov, D.; Frazzoli, E. A survey of motion planning and control techniques for self-driving urban vehicles. IEEE Trans. Intell. Veh. 2016, 1, 33–55. [Google Scholar] [CrossRef]
- Dudziak, A.; Stoma, M.; Kuranc, A.; Caban, J. Assessment of Social Acceptance for Autonomous Vehicles in Southeastern Poland. Energies 2021, 14, 5778. [Google Scholar] [CrossRef]
- Li, X.; Sun, Z.; Cao, D.; Liu, D.; He, H. Development of a new integrated local trajectory planning and tracking control framework for autonomous ground vehicles. Mech. Syst. Signal Process. 2017, 87, 118–137. [Google Scholar] [CrossRef]
- Kayacan, E.; Ramon, H.; Saeys, W. Robust trajectory tracking error model-based predictive control for unmanned ground vehicles. IEEE/ASME Trans. Mechatron. 2015, 21, 806–814. [Google Scholar] [CrossRef]
- Tian, Y.; Huang, K.; Cao, X.; Liu, Y.; Ji, X. A hierarchical adaptive control framework of path tracking and roll stability for intelligent heavy vehicle with MPC. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 2933–2946. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, X.; Zhou, Q.; Tian, Y. A model predictive controller with switched tracking error for autonomous vehicle path tracking. IEEE Access 2019, 7, 53103–53114. [Google Scholar] [CrossRef]
- Du, X.; Htet, K.K.K.; Tan, K.K. Development of a genetic-algorithm-based nonlinear model predictive control scheme on velocity and steering of autonomous vehicles. IEEE Trans. Ind. Electron. 2016, 63, 6970–6977. [Google Scholar] [CrossRef]
- Falcone, P.; Borrelli, F.; Asgari, J.; Tseng, H.E.; Hrovat, D. Predictive active steering control for autonomous vehicle systems. IEEE Trans. Control Syst. Technol. 2007, 15, 566–580. [Google Scholar] [CrossRef]
- Bai, G.; Liu, L.; Meng, Y.; Luo, W.; Gu, Q.; Ma, B. Path tracking of mining vehicles based on nonlinear model predictive control. Appl. Sci. 2019, 9, 1372. [Google Scholar] [CrossRef]
- Xu, S.; Peng, H. Design, analysis, and experiments of preview path tracking control for autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2019, 21, 48–58. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, X.; Xi, L.; Tian, Y. Design of a path-tracking steering controller for autonomous vehicles. Energies 2018, 11, 1451. [Google Scholar] [CrossRef]
- Guo, H.; Liu, J.; Cao, D.; Chen, H.; Yu, R.; Lv, C. Dual-envelop-oriented moving horizon path tracking control for fully automated vehicles. Mechatronics 2018, 50, 422–433. [Google Scholar] [CrossRef]
- Ji, X.; He, X.; Lv, C.; Liu, Y.; Wu, J. Adaptive-neural-network-based robust lateral motion control for autonomous vehicle at driving limits. Control Eng. Pract. 2018, 76, 41–53. [Google Scholar] [CrossRef]
- Yang, L.; Yue, M.; Ma, T. Path following predictive control for autonomous vehicles subject to uncertain tire-ground adhesion and varied road curvature. Int. J. Control Autom. Syst. 2019, 17, 193–202. [Google Scholar] [CrossRef]
- Bai, G.; Meng, Y.; Liu, L.; Luo, W.; Gu, Q.; Li, K. A new path tracking method based on multilayer model predictive control. Appl. Sci. 2019, 9, 2649. [Google Scholar] [CrossRef]
- Yu, R.; Guo, H.; Sun, Z.; Chen, H. MPC-based regional path tracking controller design for autonomous ground vehicles. In Proceedings of the 2015 IEEE International Conference on Systems, Man, and Cybernetics, Hong Kong, China, 9–12 October 2015; pp. 2510–2515. [Google Scholar]
- Cao, H.; Song, X.; Zhao, S.; Bao, S.; Huang, Z. An optimal model-based trajectory following architecture synthesising the lateral adaptive preview strategy and longitudinal velocity planning for highly automated vehicle. Veh. Syst. Dyn. 2017, 55, 1143–1188. [Google Scholar] [CrossRef]
- Yang, W.; Li, C.; Zhou, Y. A Path Planning Method for Autonomous Vehicles Based on Risk Assessments. World Electr. Veh. J. 2022, 13, 234. [Google Scholar] [CrossRef]





| Symbol | Parameter | Value |
|---|---|---|
| Wheelbase | 2.910 [m] | |
| Mass | 1412 [kg] | |
| Front wheel cornering stiffness | 148,970 | |
| Rear wheel cornering stiffness | 82,204 | |
| Distance from front wheel to center of mass | 1.015 [m] | |
| Distance from rear wheel to center of mass | 1.895 [m] | |
| Moment of inertia | 1536.7 | |
| Vehicle track | 1.89 [m] |
| Parameter | Value |
|---|---|
| Prediction time domain () | 20 |
| Control time domain () | 20 |
| The sampling period () | 0.05 (s) |
| Front wheel slip angle control amount () | –35°~35° |
| Front wheel slip angle control increment () | −0.47~0.47 |
| Q | |
| R | 1000 |
| Experiment Number | Experimental Situation | Initial Velocity | Maximum Lateral Deviation (m) | Maximum Heading Deviation (°) |
|---|---|---|---|---|
| Case 1 | Without the longitudinal speed controller | 25 m/s | 2.709 | 16.044 |
| Case 2 | The longitudinal speed controller | 25 m/s | 0.522 | 6.303 |
| Case 3 | Fixed preview time | 25 m/s | 0.437 | 3.036 |
| Case 4 | Adaptive preview time | 25 m/s | 0.145 | 2.809 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Ye, X.; Zhou, Y.; Li, C. Path-Following Control of Unmanned Vehicles Based on Optimal Preview Time Model Predictive Control. World Electr. Veh. J. 2024, 15, 221. https://doi.org/10.3390/wevj15060221
Wang X, Ye X, Zhou Y, Li C. Path-Following Control of Unmanned Vehicles Based on Optimal Preview Time Model Predictive Control. World Electric Vehicle Journal. 2024; 15(6):221. https://doi.org/10.3390/wevj15060221
Chicago/Turabian StyleWang, Xinyu, Xiao Ye, Yipeng Zhou, and Cong Li. 2024. "Path-Following Control of Unmanned Vehicles Based on Optimal Preview Time Model Predictive Control" World Electric Vehicle Journal 15, no. 6: 221. https://doi.org/10.3390/wevj15060221
APA StyleWang, X., Ye, X., Zhou, Y., & Li, C. (2024). Path-Following Control of Unmanned Vehicles Based on Optimal Preview Time Model Predictive Control. World Electric Vehicle Journal, 15(6), 221. https://doi.org/10.3390/wevj15060221





