The Fault-Tolerant Control Strategy for the Steering System Failure of Four-Wheel Independent By-Wire Steering Electric Vehicles
Abstract
1. Introduction
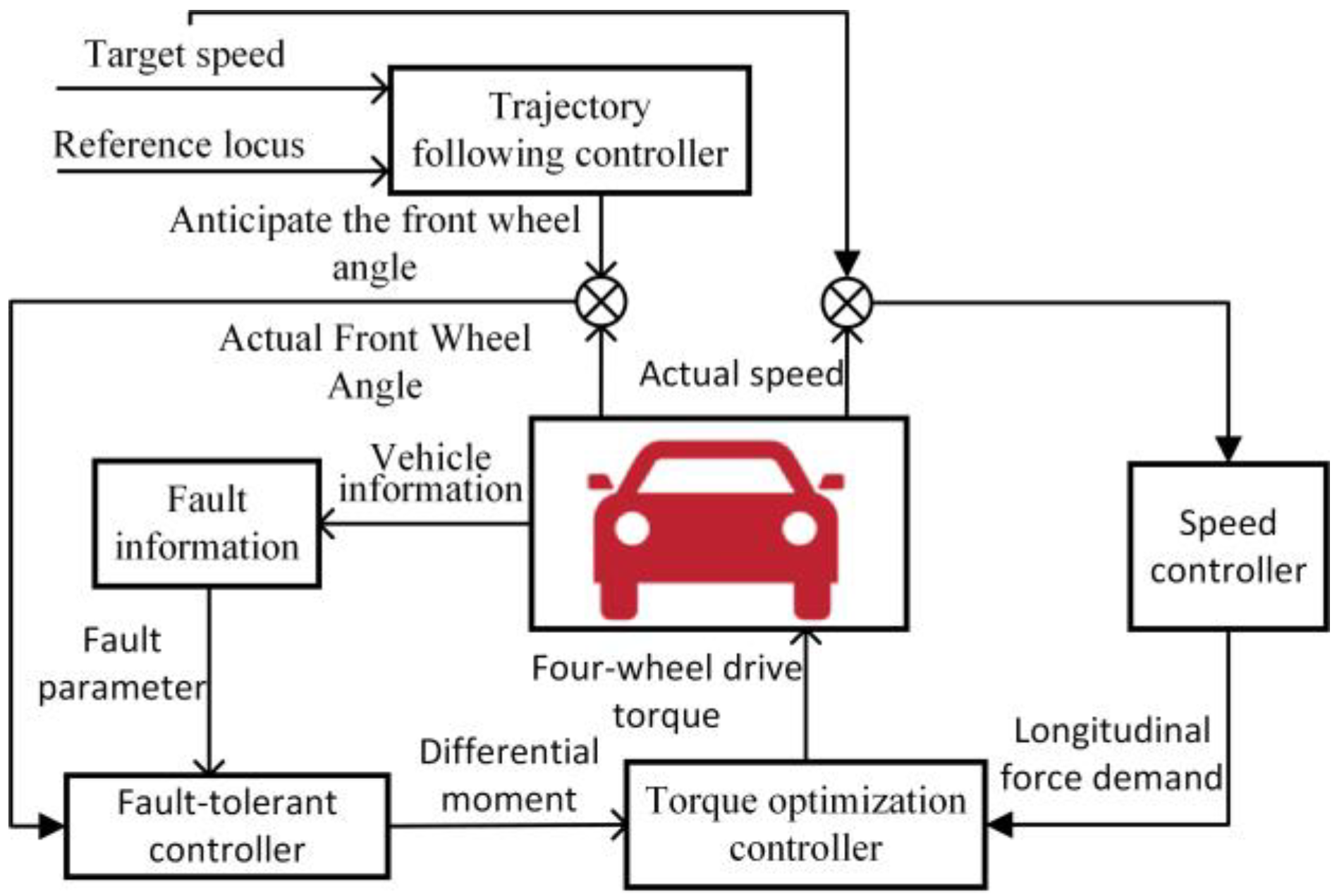
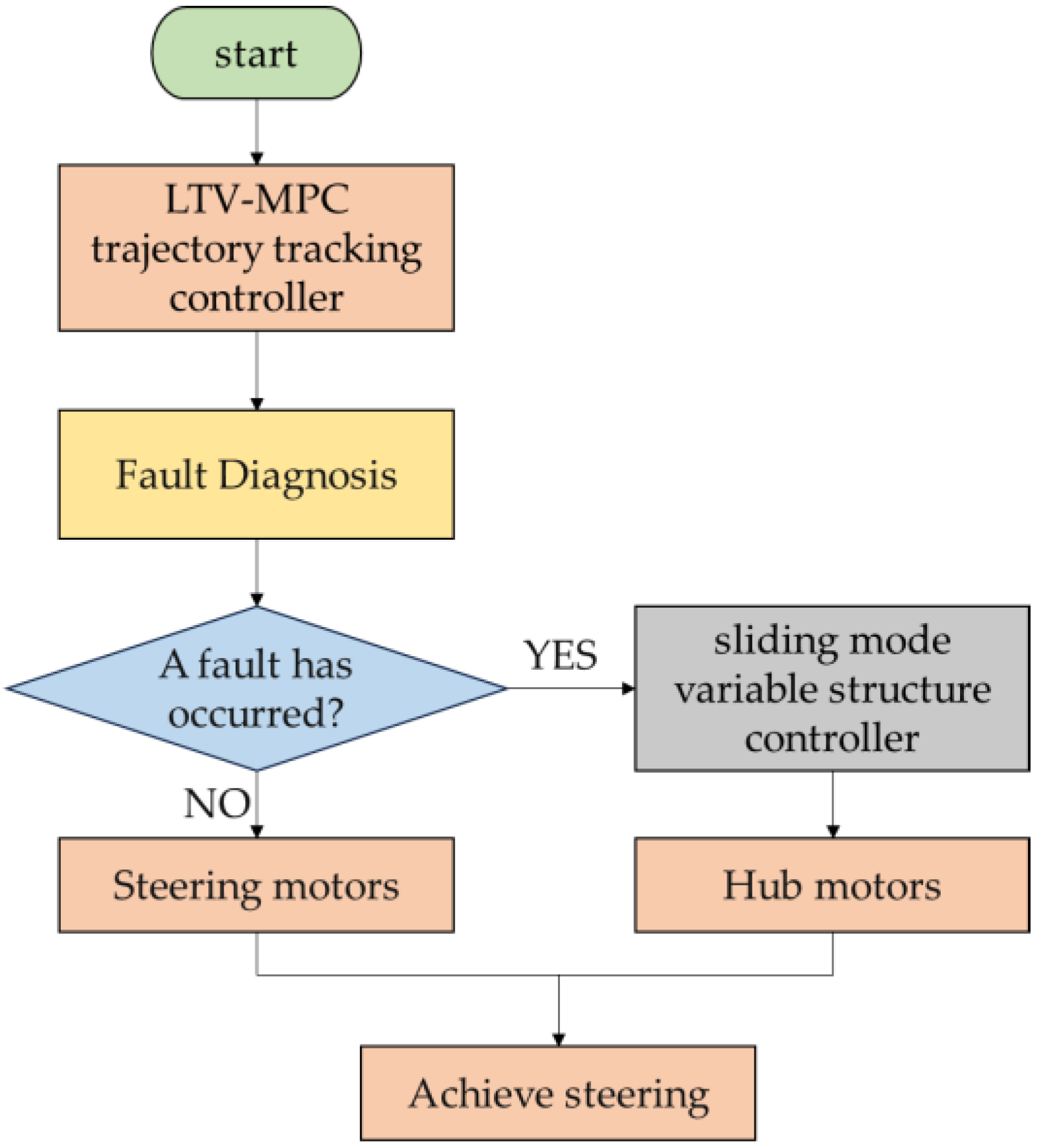
2. Control Architecture
3. Design of the Upper-Level Trajectory Tracking Controller
3.1. Linear Time-Varying Model Predictive Control
3.1.1. The Model of Vehicle Dynamics
3.1.2. Model Predictive Trajectory Tracking Control
3.1.3. Optimal Motion Control
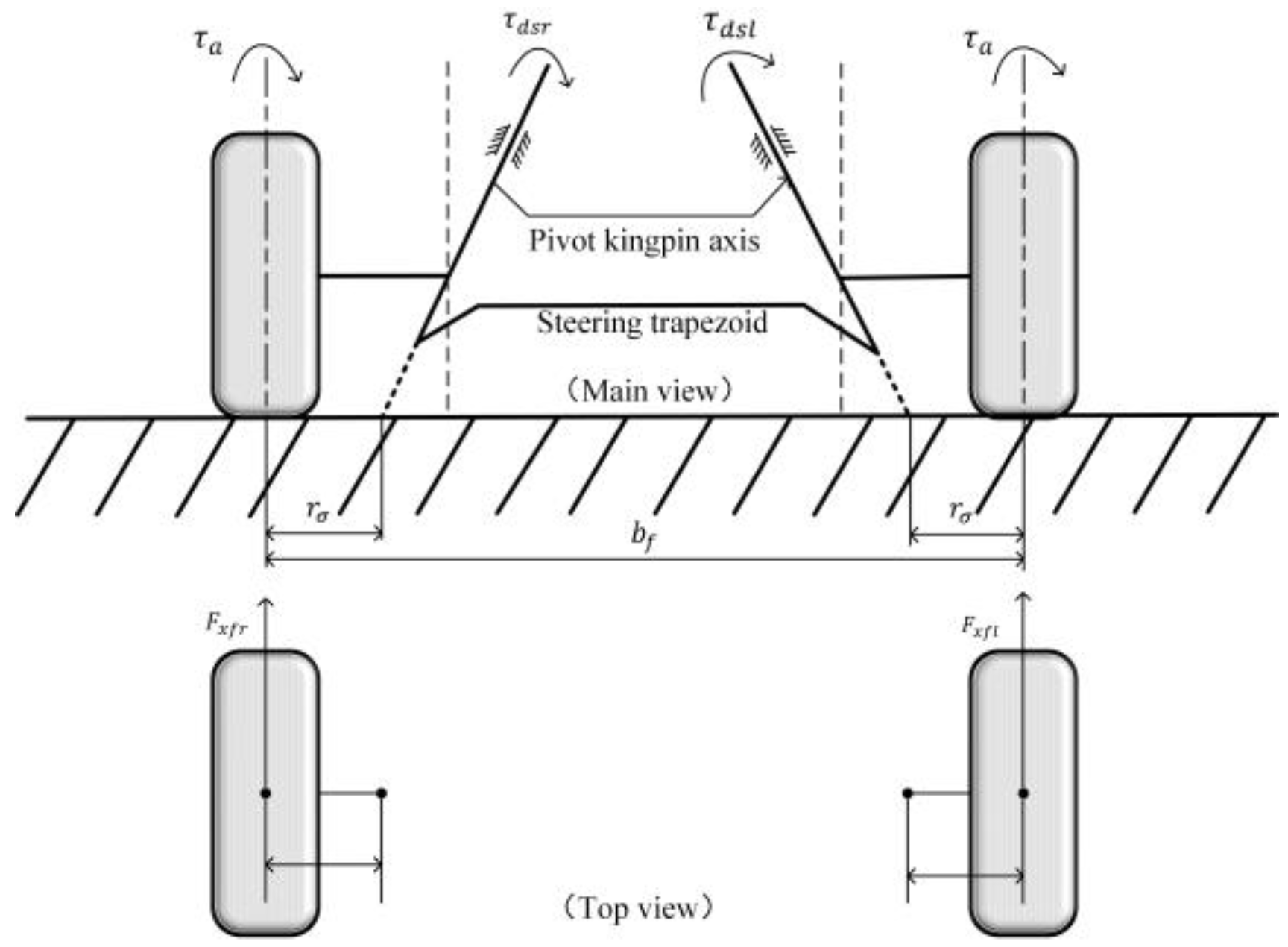
3.2. The Design of Corner Controller
4. The Design of the Lower-Level Torque Optimization Distribution Controller
5. Simulation Analysis of Typical Operating Conditions
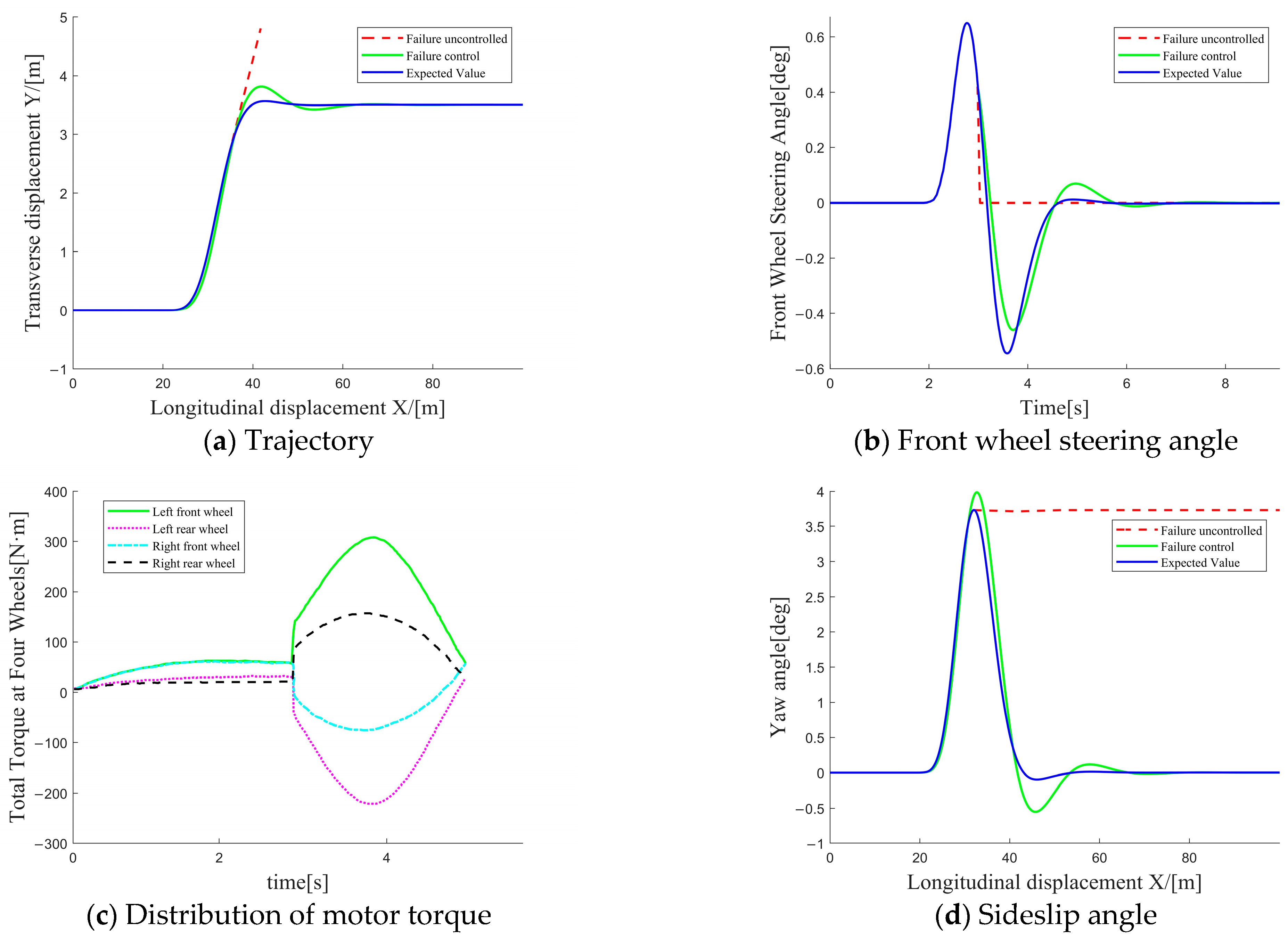
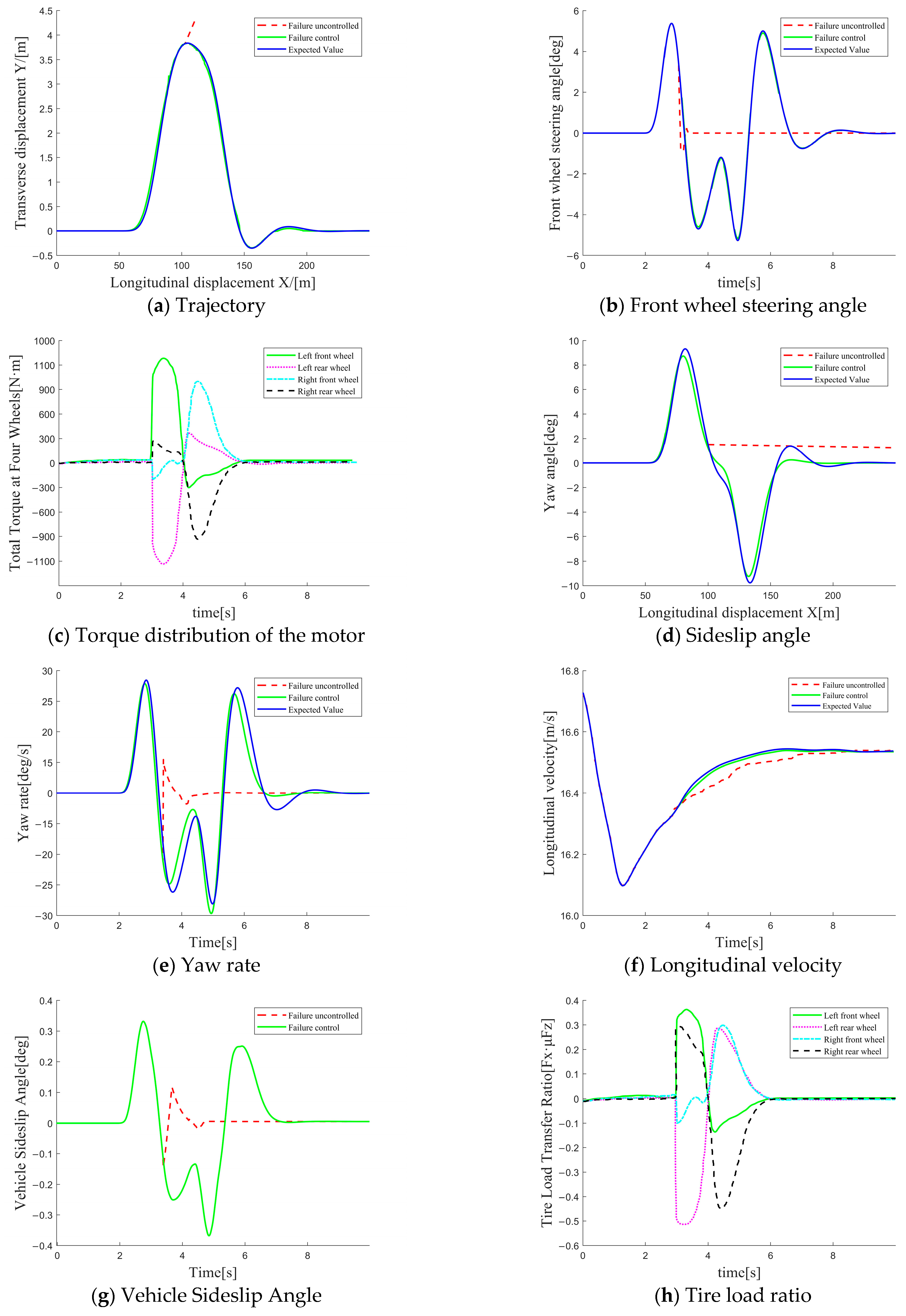
5.1. Single Shift-Line Operating Condition
5.2. Double Shift-Line Operating Condition
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, K.; Chen, T.; Luo, Y.; Wang, J. Intelligent Environment-Friendly Vehicles: Concept and Case Studies. IEEE Trans. Intell. Transp. Syst. 2012, 13, 318–328. [Google Scholar] [CrossRef]
- Qu, X.; Pi, D.; Zhang, L.; Lv, C. Advancements on unmanned vehicles in the transportation system. Green Energy Intell. Transp. 2023, 2, 100091. [Google Scholar] [CrossRef]
- Mortazavizadeh, S.A.; Ghaderi, A.; Ebrahimi, M.; Hajian, M. Recent Developments in the Vehicle Steer-by-Wire System. IEEE Trans. Transp. Electrif. 2020, 6, 1226–1235. [Google Scholar] [CrossRef]
- Zong, C.; Li, G.; Zhang, H.; He, L.; Zhang, Z. Study progress and outlook of chassis control technology for X-by-wire automobile. China J. Highw. Transp. 2013, 26, 160–176. [Google Scholar]
- Zhang, X.; Cocquempot, V. Fault tolerant control scheme based on active fault diagnosis for the path tracking control of a 4WD electric vehicle. In Proceedings of the 2014 IEEE International Symposium on Intelligent Control (ISIC), Juan Les Pins, France, 8–10 October 2017; pp. 2189–2195. [Google Scholar]
- Hasan, M.; Anwar, S. Sliding Mode Observer and Long Range Prediction Based Fault Tolerant Control of a Steer-by-Wire Equipped Vehicle. SAE Tech. Pap. 2008, 41, 8534–8539. [Google Scholar]
- Shi, G.B.; Guo, C.; Wang, S.; Liu, T.Y. Angle Tracking and Fault-Tolerant Control of Steer-by-Wire System with Dual Three-Phase Motor for Autonomous Vehicle. IEEE Trans. Intell. Transp. Syst. 2024, 25, 5842–5853. [Google Scholar] [CrossRef]
- Yang, K.; Kang, D.; Lee, D. Fault tolerant control using self-diagnostic smart actuator. In Proceedings of the 2009 ICCAS-SICE, Fukuoka, Japan, 18–21 August 2009; pp. 5674–5678. [Google Scholar]
- Zhang, B.; Lu, S. Fault-tolerant control for four-wheel independent actuated electric vehicle using feedback linearization and cooperative game theory. Control. Eng. Pract. 2020, 101, 104510. [Google Scholar] [CrossRef]
- Li, H.; Zhang, N.; Wu, G.; Li, Z.; Ding, H.; Jiang, C. Active Fault-Tolerant Control of a Four-Wheel Independent Steering System Based on the Multi-Agent Approach. Electronics 2024, 13, 748. [Google Scholar] [CrossRef]
- Meléndez-Useros, M.; Viadero-Monasterio, F.; Jiménez-Salas, M.; López-Boada, M.J. Static Output-Feedback Path-Tracking Controller Tolerant to Steering Actuator Faults for Distributed Driven Electric Vehicles. World Electr. 2025, 16, 40. [Google Scholar] [CrossRef]
- Im, J.S.; Ozaki, F.; Yeu, T.K.; Kawaji, S. Model-based fault detection and isolation in steer-by-wire vehicle using sliding mode observer. J. Mech. Sci. Technol. 2009, 23, 1991–1999. [Google Scholar] [CrossRef]
- Huang, C.; Naghdy, F.; Du, H. Delta Operator Based Fault Detection Filter Design for Uncertain Steer-by-Wire Systems with Time Delay. In Proceedings of the 2018 Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 7730–7735. [Google Scholar]
- Chen, T.; Cai, Y.; Chen, L.; Xu, X.; Sun, X. Trajectory tracking control of steer-by-wire autonomous ground vehicle considering the complete failure of vehicle steering motor. Simul. Model. Pract. Theory 2021, 109, 102235. [Google Scholar] [CrossRef]
- Seiffer, A.; Schütz, L.; Frey, M.; Gauterin, F. Constrained Control Allocation Improving Fault Tolerance of a Four Wheel Independently Driven Articulated Vehicle. IEEE Open J. Intell. Transp. Syst. 2023, 4, 187–203. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, R.; Hu, Y. Active fault-tolerant control based on MFAC or 4WID EV with steering by wire system. J. Mech. Eng. 2019, 55, 131–139. [Google Scholar]
- Asperti, M.; Vignati, M.; Sabbioni, E. Design of Electric Power Steering Control for Compensating the Torque Steer Effect due to Torque Vectoring Control. SAE Int. J. Veh. Dyn. Stab. NVH 2025, 9, 17. [Google Scholar] [CrossRef]
- Jo, S.-J.; Baek, S.-W.; Hwang, K.-Y. Optimization Design of Novel Consequent Pole Motor for Electric Power Steering System. Machines 2024, 12, 893. [Google Scholar] [CrossRef]
- Zhu, S.; Lu, J.; Zhu, L.; Chen, H.; Gao, J.; Xie, W. Coordinated Control of Differential Drive-Assist Steering and Direct Yaw Moment Control for Distributed-Drive Electric Vehicles. Electronics 2024, 13, 3711. [Google Scholar] [CrossRef]
- Hu, C.; Wang, R.; Yan, F. Differential steering based yaw stabilization using ISMC for independently actuated electric vehicles. IEEE Trans. Intell. Transp. Syst. 2018, 19, 627–638. [Google Scholar] [CrossRef]
- Xin, P.; Wang, Z.; Sun, H.; Zhang, B. Model Predictive Control of Unmanned Mine Vehicle Trajectory Tracking. In Proceedings of the 2021 Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; pp. 4757–4762. [Google Scholar]
- Hans, P. Tyre and Vehicle Dynamics; Butterworth-Heinemann: Oxford, UK, 2002. [Google Scholar]
- Lu, S. Study on Vehicle Chassis Key Subsystems and Its Integrated Control Strategy; Chongqing University: Chongqing, China, 2009. [Google Scholar]
- Wang, Q.; Wang, J.; Jin, L. Differential assisted steering applied on electric vehicle with electric motored wheels. J. Jinlin Univ. 2009, 39, 1–6. [Google Scholar]
- Jiao, G. Study on Longitudinal and Lateral Force Coordinated Control of Four wheel Independent Driving/Steering Electric Vehicle; Chongqing University: Chongqing, China, 2018. [Google Scholar]


| a0 | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 |
|---|---|---|---|---|---|---|---|---|
| 1.406 | −8.759 | 1011.783 | 8.062 | 34,788.69 | 0.022 | −0.006 | 0.096 | 0.272 |
| b0 | b1 | b2 | b3 | b4 | b5 | b6 | b7 | b8 |
| 1.412 | −10 | 1025.022 | 3906 | 2 | 0.039 | 8.168 × 10−6 | 3.495 × 10−4 | −0.282 |
| Parameter | Values |
|---|---|
| Vehicle curb weight/kg | 1880 |
| The length from the center of mass to the front axle/m | 1.015 |
| The distance between the center of mass and the rear axle/m | 1.895 |
| Axis length/m | 1.675 |
| ) | 152,500 |
| ) | 135,400 |
| Radius of the tire/m | 0.33 |
| Road surface adhesion coefficien (μ) | 0.8 |
| Boundary values of torque output of in-wheel motor/(N·m) | 800 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Q.; Liu, C.; Zhao, J.; Liu, H. The Fault-Tolerant Control Strategy for the Steering System Failure of Four-Wheel Independent By-Wire Steering Electric Vehicles. World Electr. Veh. J. 2025, 16, 183. https://doi.org/10.3390/wevj16030183
Han Q, Liu C, Zhao J, Liu H. The Fault-Tolerant Control Strategy for the Steering System Failure of Four-Wheel Independent By-Wire Steering Electric Vehicles. World Electric Vehicle Journal. 2025; 16(3):183. https://doi.org/10.3390/wevj16030183
Chicago/Turabian StyleHan, Qianlong, Chengye Liu, Jingbo Zhao, and Haimei Liu. 2025. "The Fault-Tolerant Control Strategy for the Steering System Failure of Four-Wheel Independent By-Wire Steering Electric Vehicles" World Electric Vehicle Journal 16, no. 3: 183. https://doi.org/10.3390/wevj16030183
APA StyleHan, Q., Liu, C., Zhao, J., & Liu, H. (2025). The Fault-Tolerant Control Strategy for the Steering System Failure of Four-Wheel Independent By-Wire Steering Electric Vehicles. World Electric Vehicle Journal, 16(3), 183. https://doi.org/10.3390/wevj16030183





