Multi-Agent Deep Reinforcement Learning Cooperative Control Model for Autonomous Vehicle Merging into Platoon in Highway
Abstract
1. Introduction
1.1. Platoon Longitudinal Control
1.2. Single-Autonomous-Vehicle Merging Control
1.3. Single-Autonomous-Vehicle Trajectory Planning
2. Problem Formulation
2.1. AVs Merging into Platoon Environment
2.2. State and Action
2.3. Reward
2.3.1. AV Reward
2.3.2. Platoon Reward
2.3.3. Energy Reward
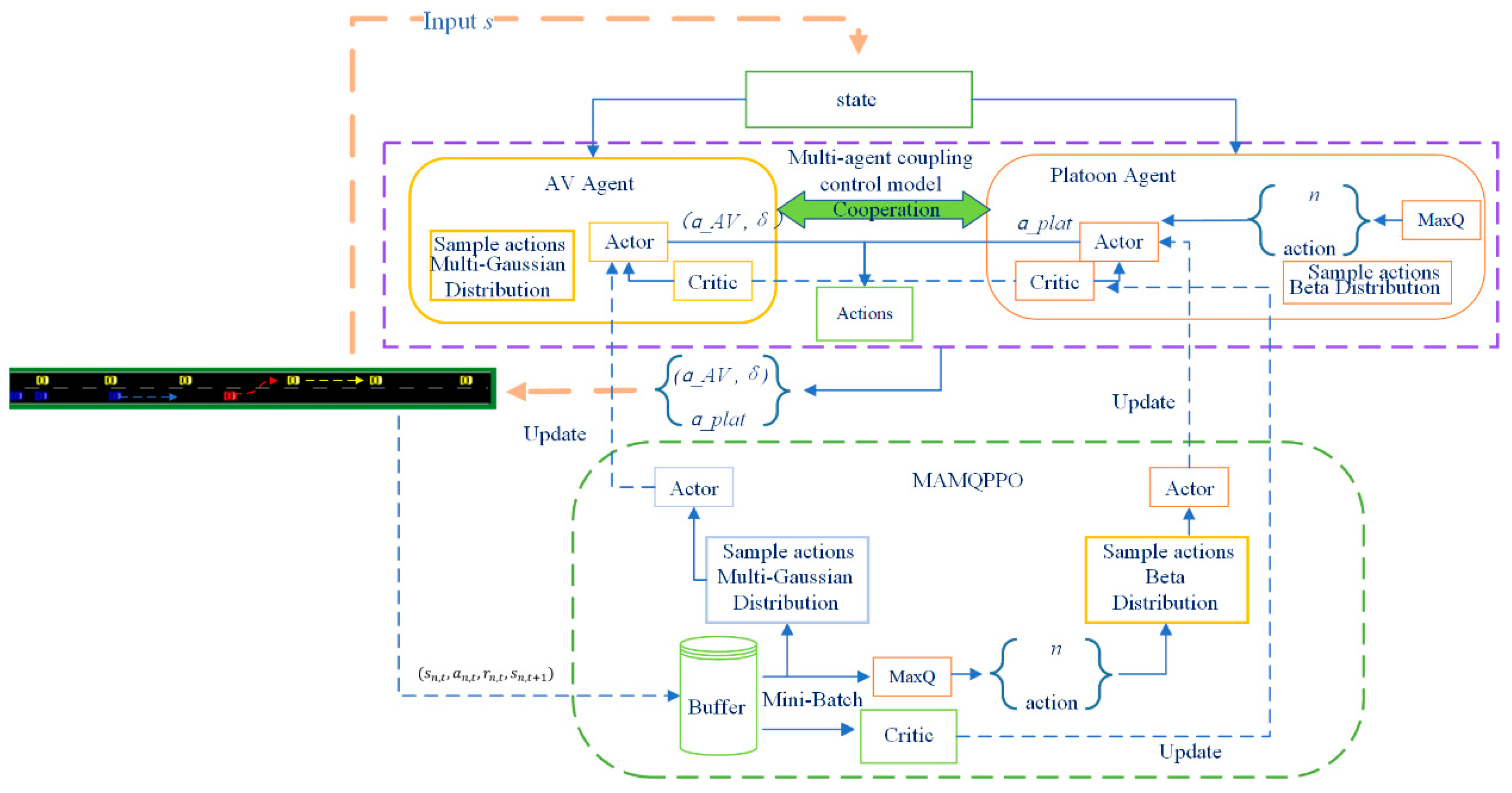
3. Multi-Agent-Based Deep Reinforcement Learning Coupled Model and Train Details
3.1. Model Structure
3.1.1. Modeling Framework
3.1.2. Interaction and Decision-Making Processes
3.2. Vehicle Dynamics Modeling
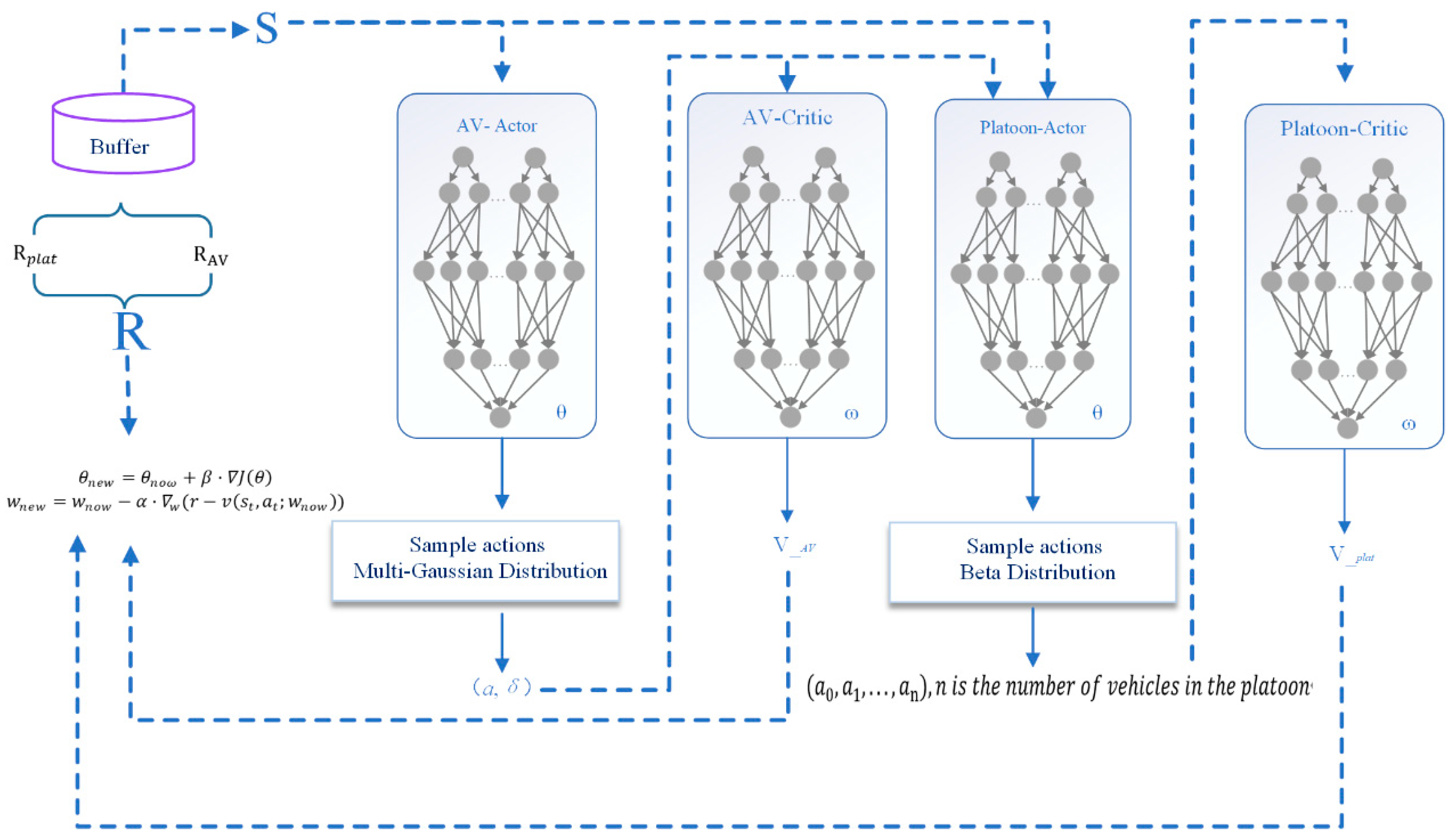
3.3. MAMQPPO Training Algorithm
3.3.1. Structure of the MAMQPPO Algorithm
3.3.2. MAMQPPO Pseudocode
| Algorithm 1. MAMQPPO |
| Initialize the AV Actor and Platoon Actor networks, and critic networks, with weights and , w. Initialize the batch size B, iteration steps α and β, and done = 0. Sample data of the specified length from the Buffer to obtain {}. Retrieve state information st from the database. for episode = 0, 1, 2, … until convergence done = 1 while not done = 1 Initialize the parameters of AV Actor, Platoon Actor, and critic networks. AV Actor: i = 2 (two-dimensional action space) Sample AAV (a, δ) from the multivariate Gaussian distribution Save the action strategy Platoon Actor: n is the output dimension of the platoon Select platoon gap J = , Choose Discrete action action = maxaQ(), and action = {−1, 1}, compute plat Sampling plat from normal distribution Beta, if action = 1 the range is [0, 3] m/s2 else the range is [−3, 0] m/s2 Aplat = {J, plat} Send t = {AAV, Aplat} Compute the advantage function and return, = {} end for for perform Compute Update the network parameters using a gradient method. Update the platoon reward Update the AV reward Calculate the accumulated reward Calculate the policy gradient Update the Actor parameters Calculate the target value Update the Critic parameters end for |
4. Experimental Analysis
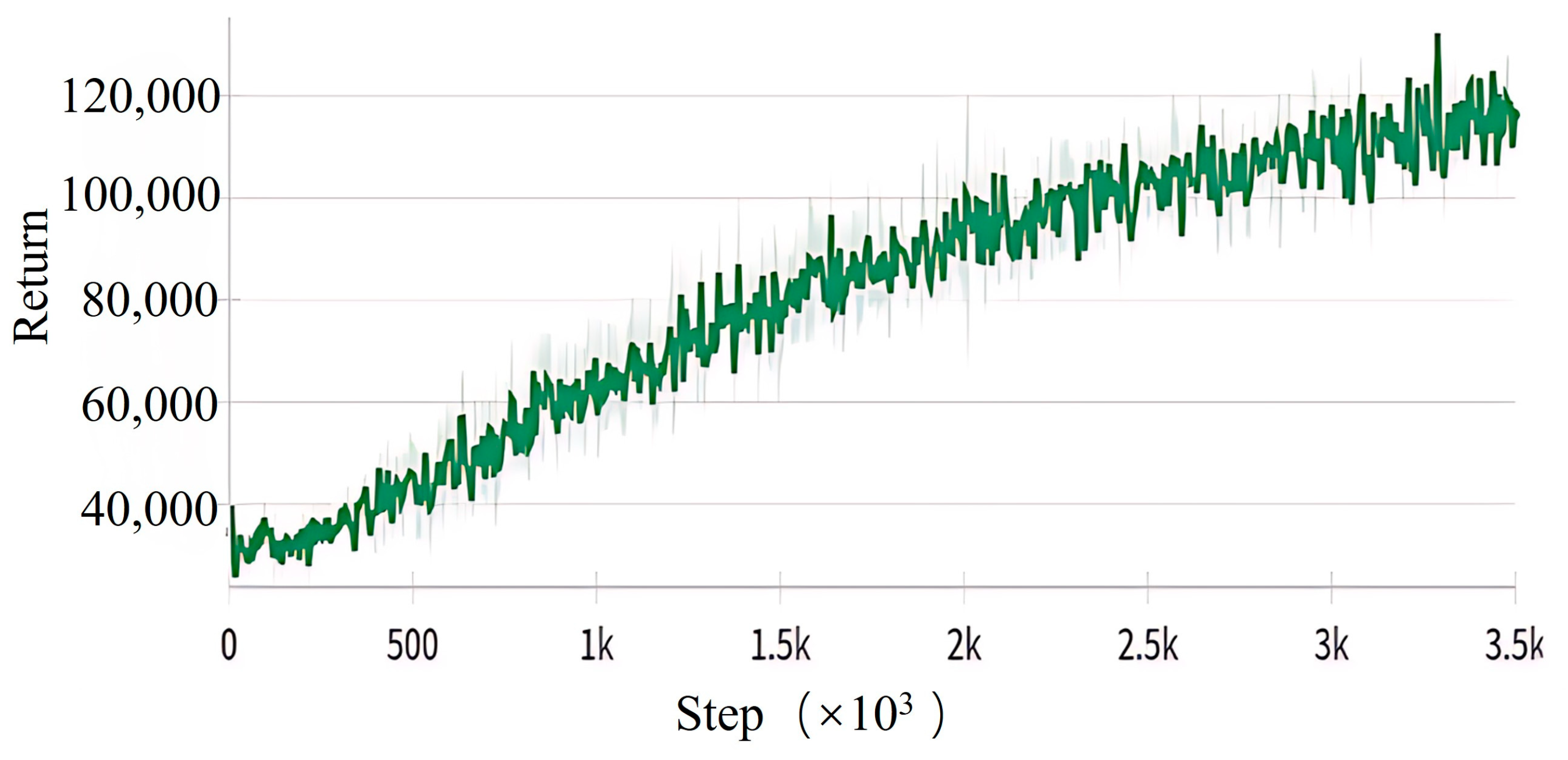
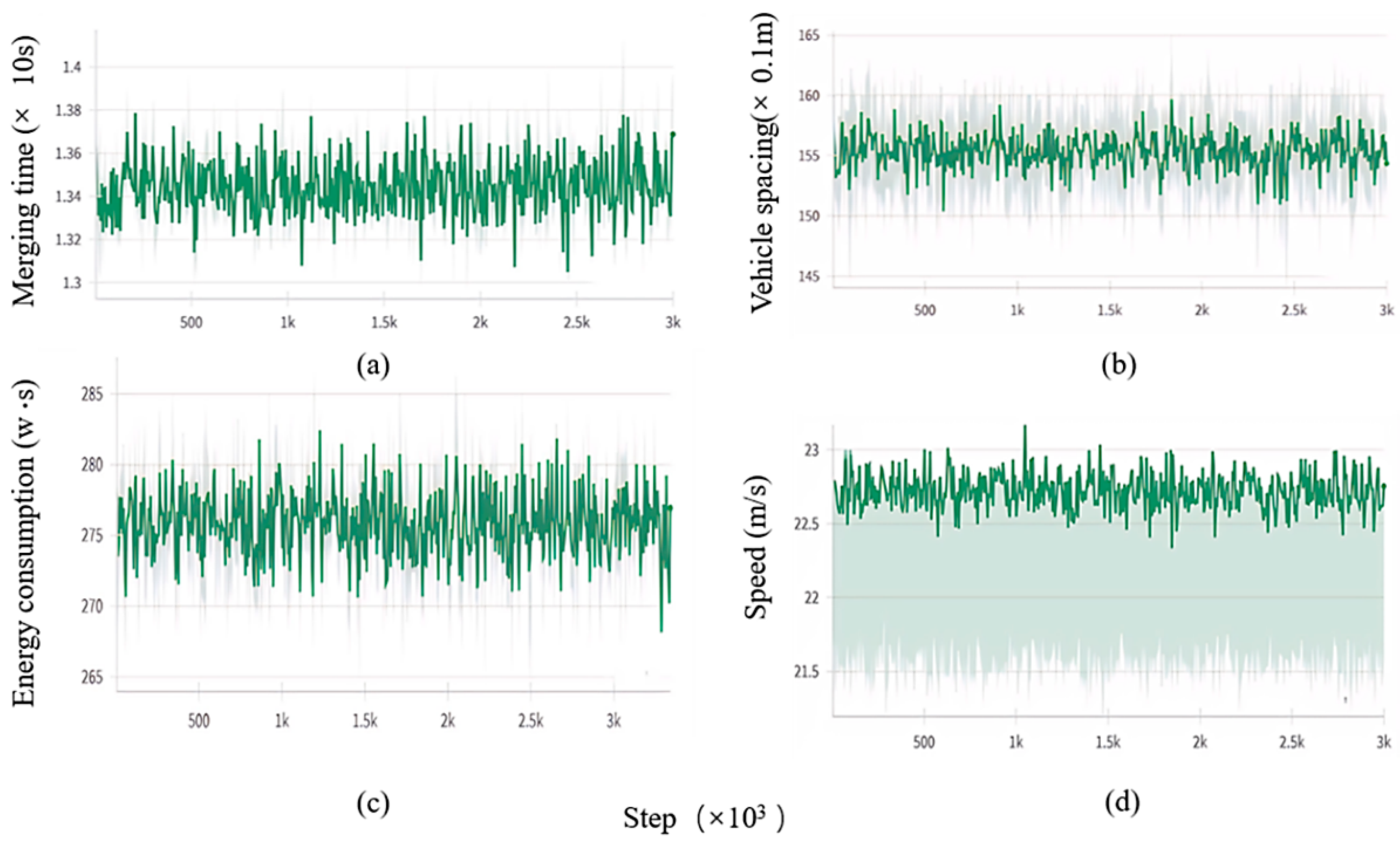
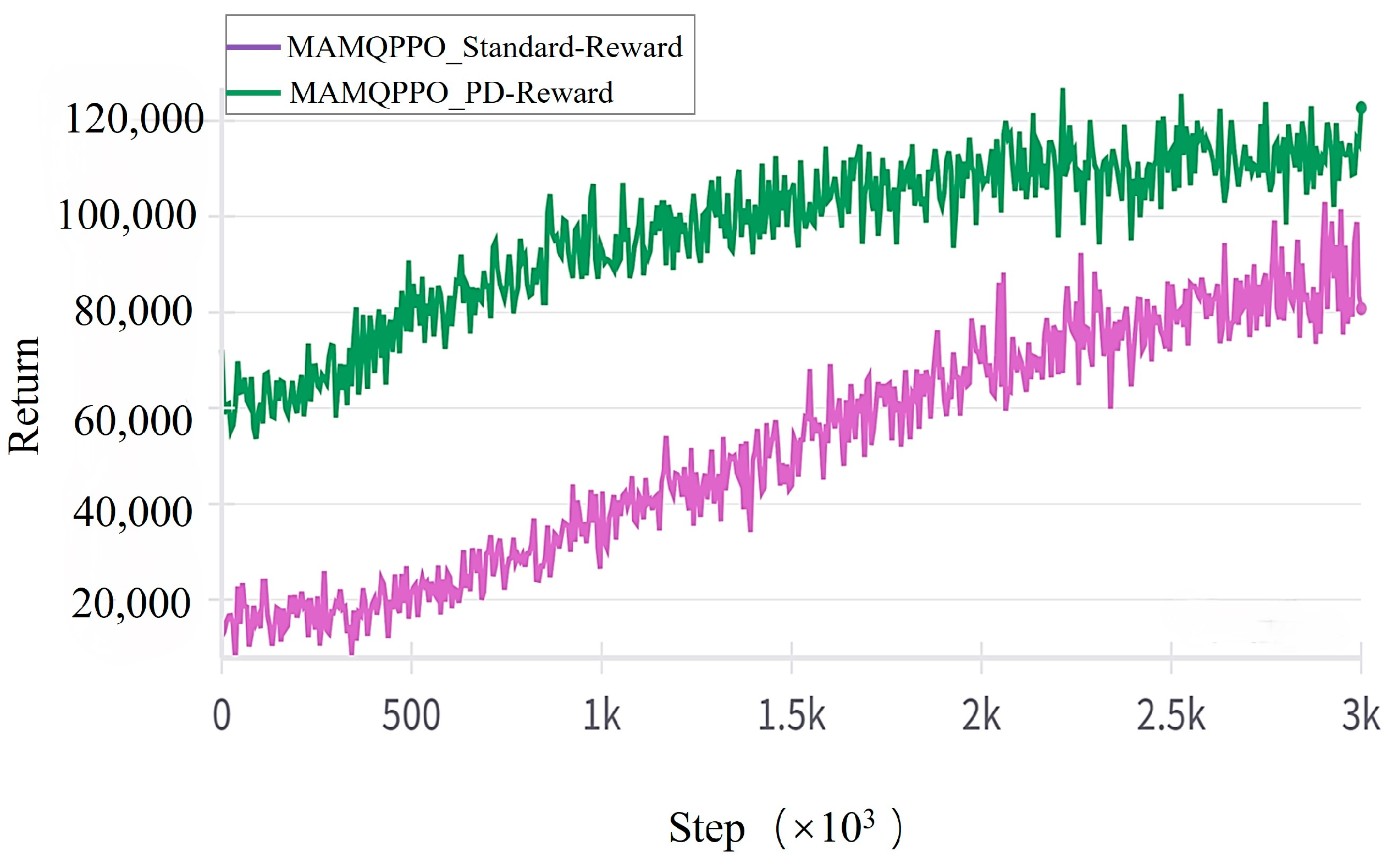
4.1. Simulation Experiment
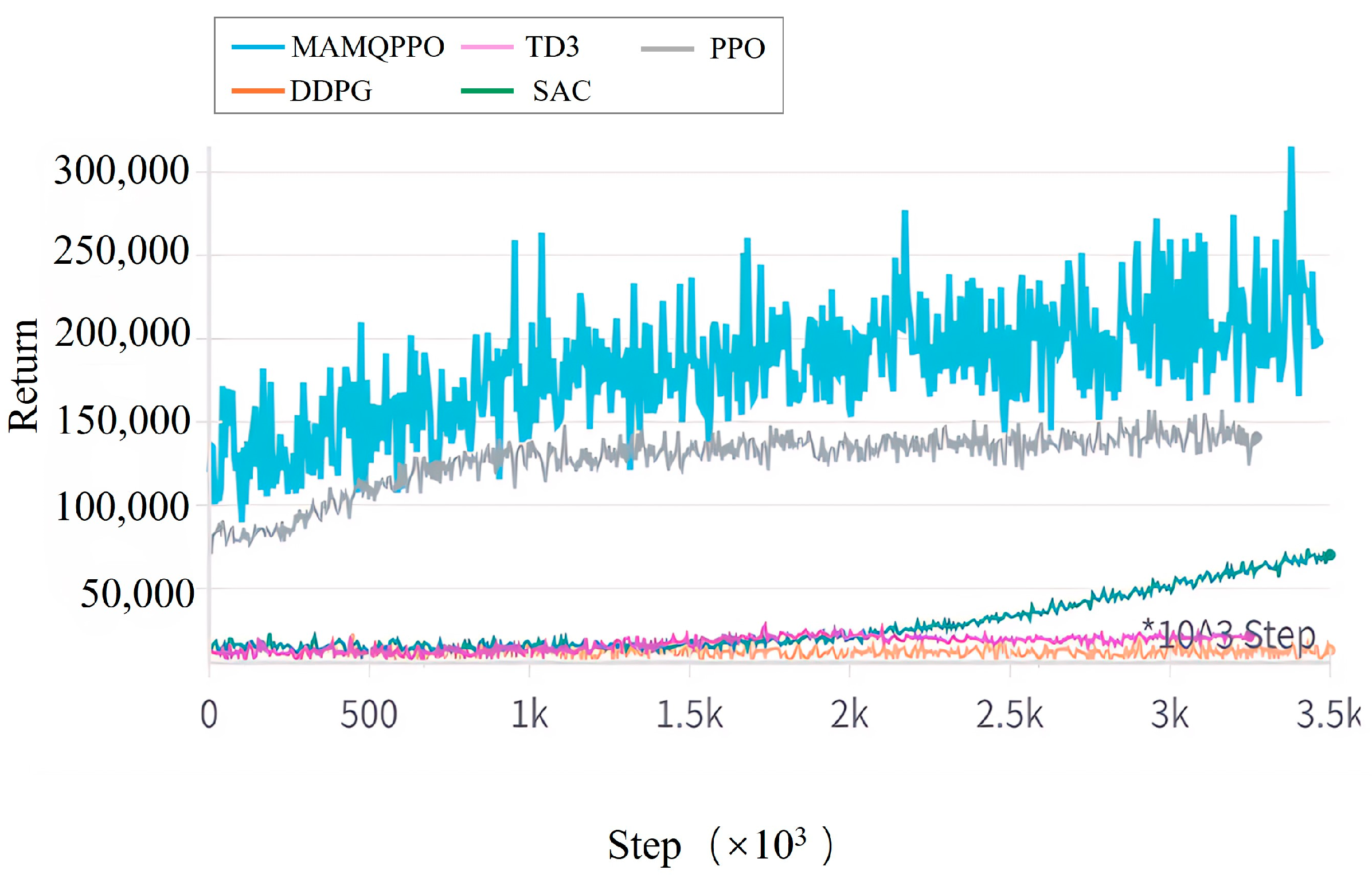
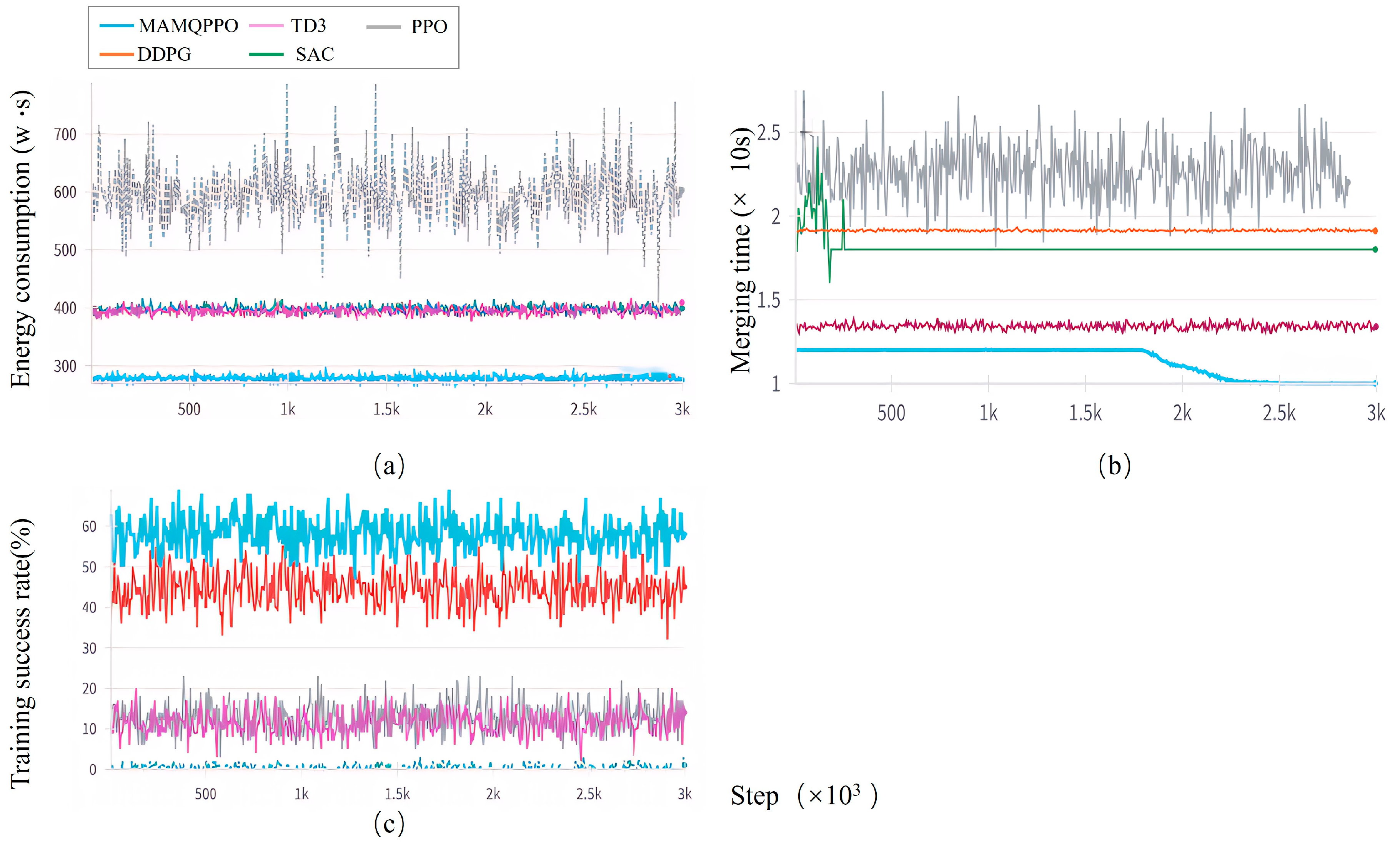
4.2. Comparison Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameter Name | Interpretation | Value | Unit |
| Atmospheric drag | -- | N | |
| Vehicle longitude power | -- | N | |
| Frictional resistance | -- | N | |
| Gradient resistance | -- | N | |
| Front wheel lateral force | -- | N | |
| Rear wheel lateral force | -- | N | |
| Vehicle lateral force | -- | N | |
| Lateral angular velocity | -- | ||
| Front wheel angle | -- | ||
| Lateral acceleration | -- | ||
| Wheelbase | 7.8 | ||
| Front wheel lateral deflection stiffness | 15,000 | ||
| Rear wheel lateral deflection stiffness | 14,000 | ||
| Vehicle rear axle | 2.75 | ||
| Vehicle front axle | 3.55 | ||
| Vehicle lateral speed | -- | ||
| Air density | 1.28 | ||
| Wind resistance | 0.564 | -- | |
| Windward side | 5.8 | ||
| Vehicle longitude speed | -- | ||
| Wind speed | 5.0 | ||
| Vehicle quality | 20,000 | ||
| Vehicle longitude acceleration | -- | ||
| Slope angle | -- | ||
| Gravitational acceleration | 9.8 | ||
| Return | -- | -- | |
| Discount rate | 0.05 | -- | |
| Learning rate | -- | ||
| Learning rate | -- | ||
| Value of Critic networks | -- | -- | |
| Weight of Critic networks | -- | -- | |
| Reward | -- | -- | |
| Target value | -- | -- | |
| The immediate reward for t | -- | -- | |
| Updated value network parameters | -- | -- | |
| Current value network parameters | -- | -- | |
| The gradient of w in value network | -- | -- | |
| W | Width of AV | 2.8 | m |
Appendix B
| ID | (m/s) | (m/s) | (m/s2) | (m/s2) | (m) | (m) | (rad) |
| AV | 23 | 0 | 0 | 0 | 70 | 1.75 | 0 |
| EV | Random (17, 25) | 0 | Random (−3, 3) | 0 | Random (0, 1000) | 1.75 or 5.25 | 0 |
| PV0 | 22 | 0 | 0 | 0 | 0 | 5.25 | 0 |
| PV1 | 22 | 0 | 0 | 0 | 20 | 5.25 | 0 |
| PV2 | 22 | 0 | 0 | 0 | 40 | 5.25 | 0 |
| PV3 | 22 | 0 | 0 | 0 | 60 | 5.25 | 0 |
| PV4 | 22 | 0 | 0 | 0 | 80 | 5.25 | 0 |
| PV5 | 22 | 0 | 0 | 0 | 100 | 5.25 | 0 |
| PV6 | 22 | 0 | 0 | 0 | 120 | 5.25 | 0 |
| PV7 | 22 | 0 | 0 | 0 | 140 | 5.25 | 0 |
References
- Ding, J.; Li, L.; Peng, H.; Zhang, Y. A rule-based cooperative merging strategy for connected and automated vehicles. IEEE Trans. Intell. Transp. Syst. 2019, 21, 3436–3446. [Google Scholar] [CrossRef]
- Shaju, A.; Southward, S.; Ahmadian, M. PID-Based Longitudinal Control of Platooning Trucks. Machines 2023, 11, 1069. [Google Scholar] [CrossRef]
- Ying, Y.; Mei, T.; Song, Y.; Liu, Y. A Sliding Mode Control approach to longitudinal control of vehicles in a platoon. In Proceedings of the 2014 IEEE International Conference on Mechatronics and Automation, Tianjin, China, 3–6 August 2014; pp. 1509–1514. [Google Scholar]
- Gaagai, R.; Horn, J. Distributed Predecessor-Follower Constrained Platooning Control of Linear Heterogeneous Vehicles. In Proceedings of the 2024 UKACC 14th International Conference on Control (CONTROL), Winchester, UK, 10–12 April 2024; pp. 274–280. [Google Scholar]
- Tapli, T.; Akar, M. Cooperative Adaptive Cruise Control Algorithms for Vehicular Platoons Based on Distributed Model Predictive Control. In Proceedings of the 2020 IEEE 16th International Workshop on Advanced Motion Control (AMC), Kristiansand, Norway, 14–16 September 2020; pp. 305–310. [Google Scholar]
- Huang, Z.; Chu, D.; Wu, C.; He, Y. Path planning and cooperative control for automated vehicle platoon using hybrid automata. IEEE Trans. Intell. Transp. Syst. 2018, 20, 959–974. [Google Scholar] [CrossRef]
- Sala, M.; Soriguera, F. Macroscopic modeling of connected autonomous vehicle platoons under mixed traffic conditions. Transp. Res. Procedia 2020, 47, 163–170. [Google Scholar] [CrossRef]
- Xu, Y.; Shi, Y.; Tong, X.; Chen, S.; Ge, Y. A Multi-Agent Reinforcement Learning Based Control Method for CAVs in a Mixed Platoon. IEEE Trans. Veh. Technol. 2024, 73, 16160–16172. [Google Scholar] [CrossRef]
- Lin, H.; Lyu, C.; He, Y.; Liu, Y.; Gao, K.; Qu, X. Enhancing State Representation in Multi-Agent Reinforcement Learning for Platoon-Following Models. IEEE Trans. Veh. Technol. 2024, 73, 12110–12114. [Google Scholar] [CrossRef]
- Dasgupta, S.; Raghuraman, V.; Choudhury, A.; Teja, T.N.; Dauwels, J. Merging and splitting maneuver of platoons by means of a novel PID controller. In Proceedings of the 2017 IEEE Symposium Series on Computational Intelligence (SSCI), Honolulu, HI, USA, 27 November–1 December 2017; pp. 1–8. [Google Scholar]
- Liu, H.; Zhuang, W.; Yin, G.; Tang, Z.; Xu, L. Strategy for heterogeneous vehicular platoons merging in automated highway system. In Proceedings of the Chinese Control And Decision Conference, Shenyang, China, 9–11 June 2018. [Google Scholar]
- Min, H.; Yang, Y.; Fang, Y.; Sun, P.; Zhao, X. Constrained Optimization and Distributed Model Predictive Control-Based Merging Strategies for Adjacent Connected Autonomous Vehicle Platoons. IEEE Access 2019, 7, 163085–163096. [Google Scholar] [CrossRef]
- An, G.; Talebpour, A. Vehicle Platooning for Merge Coordination in a Connected Driving Environment: A Hybrid ACC-DMPC Approach. IEEE Trans. Intell. Transp. Syst. 2023, 24, 5239–5248. [Google Scholar] [CrossRef]
- Chen, D.; Hajidavalloo, M.R.; Li, Z.; Chen, K.; Wang, Y.; Jiang, L.; Wang, Y. Deep Multi-Agent Reinforcement Learning for Highway On-Ramp Merging in Mixed Traffic. IEEE Trans. Intell. Transp. Syst. 2023, 24, 11623–11638. [Google Scholar] [CrossRef]
- Zhou, W.; Chen, D.; Yan, J.; Li, Z.; Yin, H.; Ge, W. Multi-agent reinforcement learning for cooperative lane changing of connected and autonomous vehicles in mixed traffic. Auton. Intell. Syst. 2022, 2, 5. [Google Scholar] [CrossRef]
- Wang, C.; Wang, L.; Qin, J.; Wu, Z.; Duan, L.; Li, Z.; Cao, M.; Ou, X.; Su, X.; Li, W.; et al. Path planning of automated guided vehicles based on improved A-Star algorithm. In Proceedings of the 2015 IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015; pp. 2071–2076. [Google Scholar]
- Li, Y.; Li, L.; Ni, D. Dynamic trajectory planning for automated lane changing using the quintic polynomial curve. J. Adv. Transp. 2023, 2023, 6926304. [Google Scholar] [CrossRef]
- Bergman, K.; Ljungqvist, O.; Axehill, D. Improved Path Planning by Tightly Combining Lattice-Based Path Planning and Optimal Control. IEEE Trans. Intell. Veh. 2021, 6, 57–66. [Google Scholar] [CrossRef]
- Hu, H.; Wang, Y.; Tong, W.; Zhao, J.; Gu, Y. Path Planning for Autonomous Vehicles in Unknown Dynamic Environment Based on Deep Reinforcement Learning. Appl. Sci. 2023, 13, 10056. [Google Scholar] [CrossRef]
- Yang, K.; Liu, L. An Improved Deep Reinforcement Learning Algorithm for Path Planning in Unmanned Driving. IEEE Access 2024, 12, 67935–67944. [Google Scholar] [CrossRef]
- Kapoor, A.; Freed, B.; Choset, H.; Schneider, J. Assigning Credit with Partial Reward Decoupling in Multi-Agent Proximal Policy Optimization. arXiv 2024, arXiv:2408.04295. [Google Scholar]
- Zhou, J.; Tkachenko, P.; del Re, L. Gap Acceptance Based Safety Assessment Of Autonomous Overtaking Function. In Proceedings of the 2019 IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; pp. 2113–2118. [Google Scholar]
- Li, M.; Cao, Z.; Li, Z. A Reinforcement Learning-Based Vehicle Platoon Control Strategy for Reducing Energy Consumption in Traffic Oscillations. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5309–5322. [Google Scholar] [CrossRef] [PubMed]
- Mindermann, S.; Shah, R.; Gleave, A.; Hadfield-Menell, D. Active inverse reward design. arXiv 2018, arXiv:1809.03060. [Google Scholar]
- Gillespie, T.D. Tire-Road Interaction. In Fundamentals of Vehicle Dynamics; Society of Automotive Engineers: Warrendale, PA, USA, 1992; pp. 53–110. [Google Scholar]
- Jiang, T.; Shi, Y.; Xu, P.; Li, Z.; Wang, L.; Zhang, W. Simulation of wind resistance and calculation of fuel saving rate of heavy truck formation driving. Intern. Combust. Engine Powerpl. 2022, 39, 81–85. [Google Scholar]
- Di, H.-Y.; Zhang, Y.-H.; Wang, B.; Zhong, G.; Zhou, W. A review of research on lateral control models and methods for autonomous driving. J. Chongqing Univ. Technol. Nat. Sci. 2021, 35, 71–81. [Google Scholar]
- Kerner, B.S.; Rehborn, H. Experimental properties of phase transitions in traffic flow. Phys. Rev. Lett. 1997, 79, 4030. [Google Scholar] [CrossRef]
- Li, J.; Chen, C.; Yang, B.; He, J.; Guan, X. Energy-Efficient Cooperative Adaptive Cruise Control for Electric Vehicle Platooning. IEEE Trans. Intell. Transp. Syst. 2024, 25, 4862–4875. [Google Scholar] [CrossRef]
- Goli, M.; Eskandarian, A. Evaluation of lateral trajectories with different controllers for multi-vehicle merging in platoon. In Proceedings of the 2014 International Conference on Connected Vehicles and Expo (ICCVE), Vienna, Austria, 3–7 November 2014; pp. 673–678. [Google Scholar]
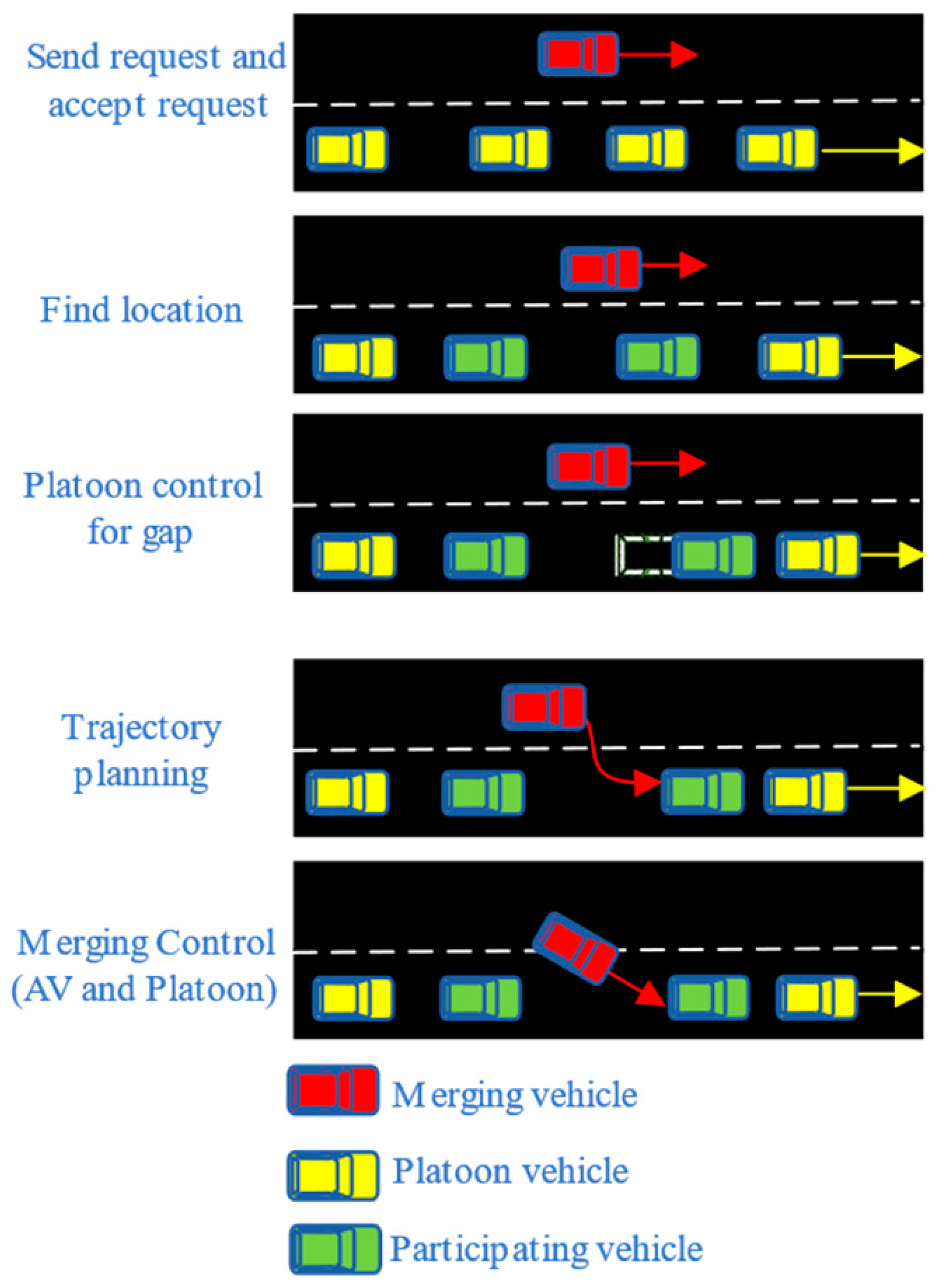


| Control | |||||
|---|---|---|---|---|---|
| Method | Applicable Environment | Advantages | Disadvantages | Study on Platoon | Study on AV |
| classical control | For static or simple scenarios where the vehicle dynamics model is known and relatively accurate. | The algorithm structure is simple, and the controller is mature and well-developed. | Less adaptable to nonlinear, dynamically changing traffic environments. | [2,3] | [10] |
| optimal control | Suitable for scenarios requiring precise control and balancing of multi-objectives (such as platoon coordination and merging control). | Optimize safety, comfort, and efficiency simultaneously by using mathematical modeling and cost function design to achieve optimal performance. | More rigid model assumptions, strong reliance on a priori information, high computational complexity, limited real-time adaptability. | [4,5] | [11,12,13] |
| learning-based | Suitable for dynamic, variable, nonlinear environments (e.g., complex interactions, heterogeneous traffic). | Model liberalization, adaptive to complex scenes, strong multi-objective coordination, good real-time feedback. | Convergence and stability challenges remain. | [6,7,8,9] | [14,15] |
| Trajectory planning | |||||
| classical | Suitable for structured maps | The method is mature and highly stable. | Difficult to handle dynamic obstacles and complex interactions. | - | [16,17] |
| optimal | Dynamic obstacle avoidance and real-time adjustment. | Smoother trajectory for comfort | High computational complexity and real-time dependence on simplified models. | - | [18] |
| learning-based | Dynamic and complex traffic scenarios. | Adaptation to high-dimensional state spaces and complex interactions. | Less interpretable, longer training time. | - | [19,20] |
| Reward Weight | |
|---|---|
| Name | Value |
| 1.2 | |
| 1.5 | |
| 0.9 | |
| 1.5 | |
| 1.1 | |
| 0.1569 | |
| 0.0245 | |
| 0.07224 | |
| 0.09681 | |
| 0.001075 | |
| Algorithm | Return | Success Rate (%) | Consumption (W·s) |
|---|---|---|---|
| TD3 | 13.5 | 391.5 | |
| DDPG | 45.3 | 393.2 | |
| SAC | 2.37 | 392.8 | |
| 17.4 | 694.4 | ||
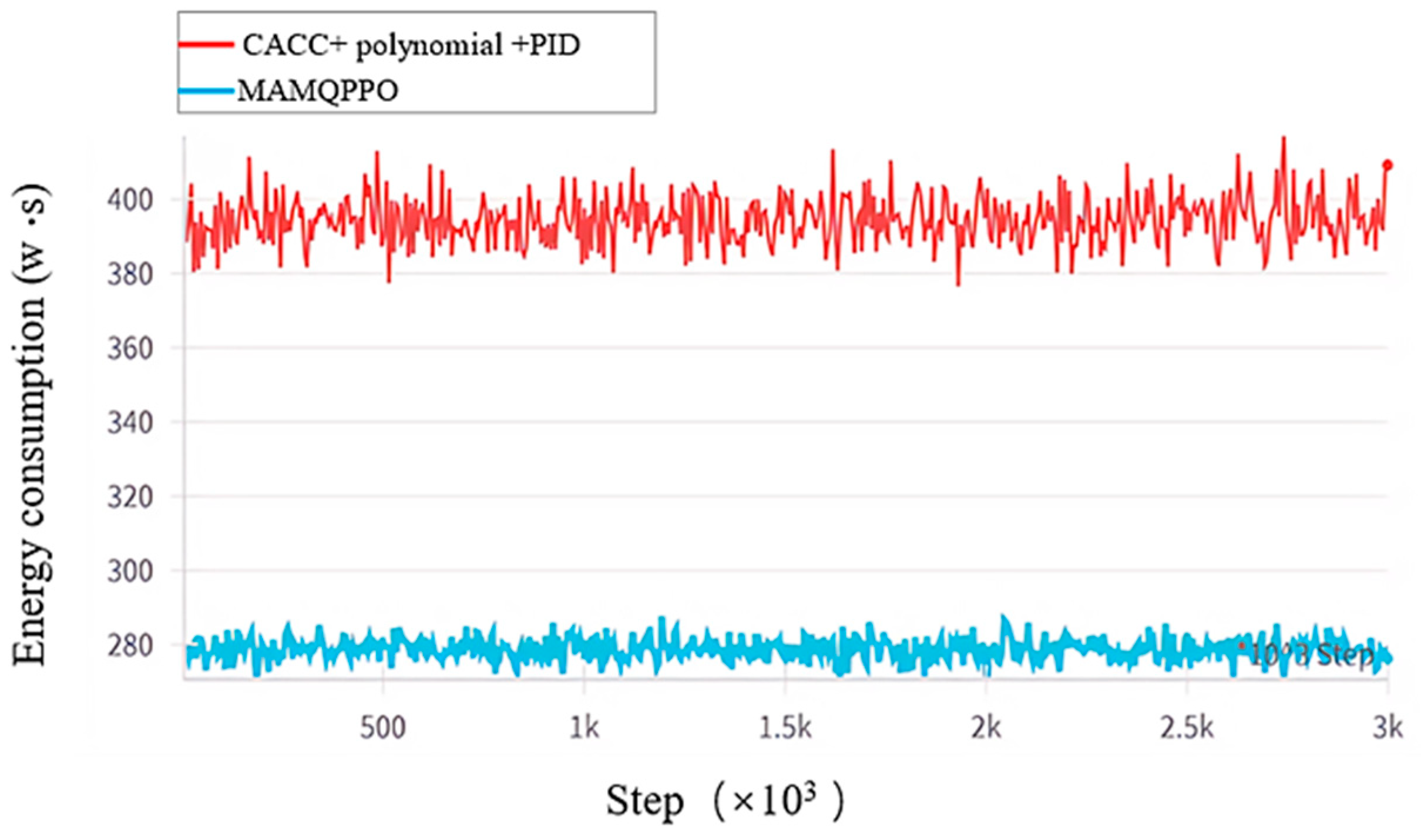
| MAMQPPO | 62.4 | 276.1 |
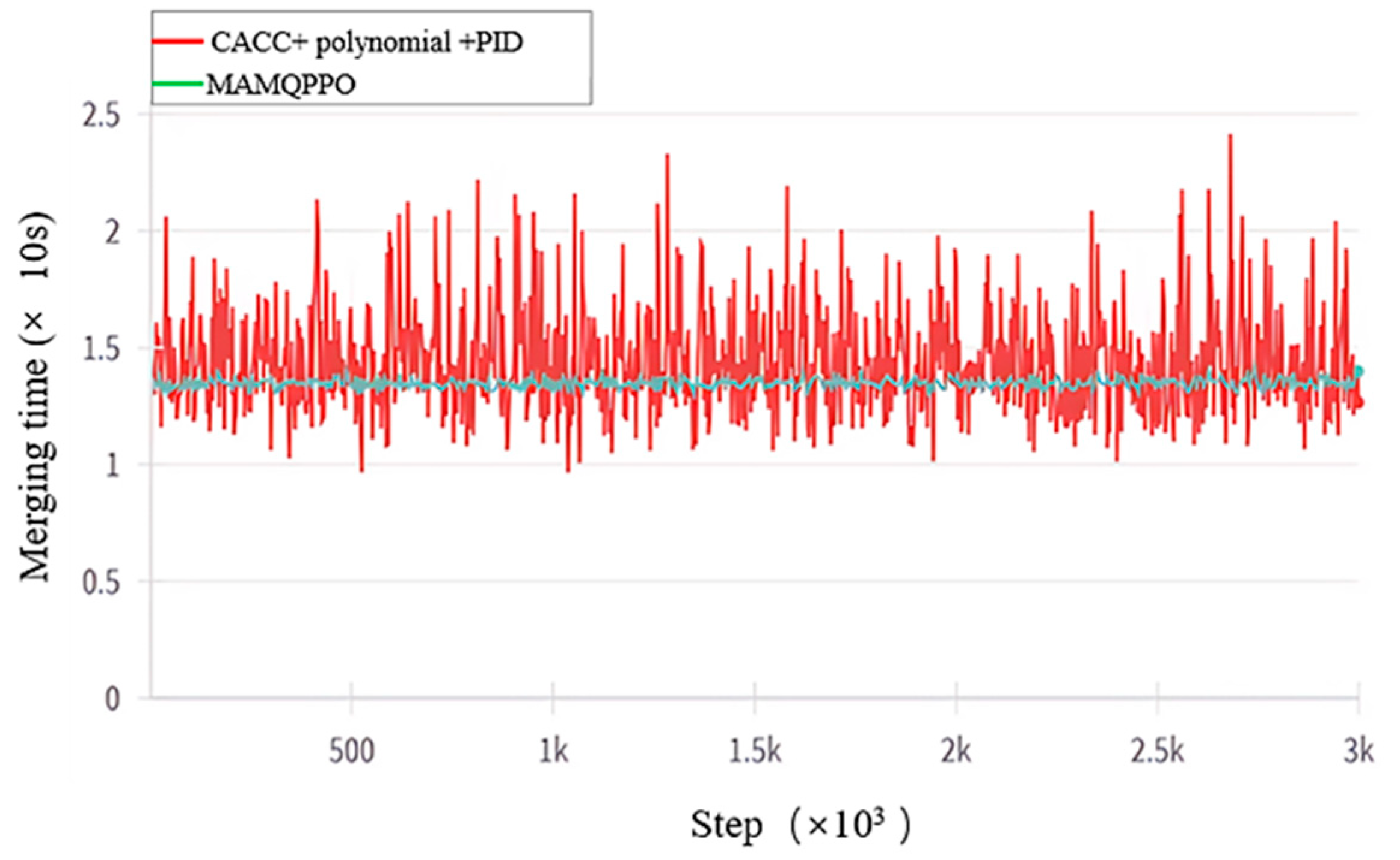
| Algorithm | Merging Time (s) | Consumption (W) |
|---|---|---|
| Polynomial + PID + CACC | 19.9 | 425.6 |
| MAMQPPO | 12.4 | 288.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Zhu, B.; Zhang, M.; Ling, X.; Ruan, X.; Deng, Y.; Guo, N. Multi-Agent Deep Reinforcement Learning Cooperative Control Model for Autonomous Vehicle Merging into Platoon in Highway. World Electr. Veh. J. 2025, 16, 225. https://doi.org/10.3390/wevj16040225
Chen J, Zhu B, Zhang M, Ling X, Ruan X, Deng Y, Guo N. Multi-Agent Deep Reinforcement Learning Cooperative Control Model for Autonomous Vehicle Merging into Platoon in Highway. World Electric Vehicle Journal. 2025; 16(4):225. https://doi.org/10.3390/wevj16040225
Chicago/Turabian StyleChen, Jiajia, Bingqing Zhu, Mengyu Zhang, Xiang Ling, Xiaobo Ruan, Yifan Deng, and Ning Guo. 2025. "Multi-Agent Deep Reinforcement Learning Cooperative Control Model for Autonomous Vehicle Merging into Platoon in Highway" World Electric Vehicle Journal 16, no. 4: 225. https://doi.org/10.3390/wevj16040225
APA StyleChen, J., Zhu, B., Zhang, M., Ling, X., Ruan, X., Deng, Y., & Guo, N. (2025). Multi-Agent Deep Reinforcement Learning Cooperative Control Model for Autonomous Vehicle Merging into Platoon in Highway. World Electric Vehicle Journal, 16(4), 225. https://doi.org/10.3390/wevj16040225







