Congestion Relief and Economic Optimization of Integrated Power Stations with Charging and Swapping Functions
Abstract
1. Introduction
- Proposed an innovative intention-reshaping model based on the ABC attitude change theory. This model could coordinate the CAS demands of EVs, balance the utilization rate of CAS equipment during peak hours, and thus alleviate congestion in ICSS.
- Proposed an out-station scheduling model based on vehicle and road conditions. This model could effectively manage out-station EVs, enhance the equipment utilization rate during off-peak hours, and consequently enhance the ICSS’s overall revenue.
- Proposed an innovative method for adjusting the SOC threshold of inventory batteries. This method could ensure a consistent supply of inventory batteries. In addition, a novel battery charging strategy based on charging duration zoning has been introduced to optimize the charging economy.
- To maximize ICSS revenue, a two-stage economic dispatch model based on on-station and off-station scheduling has been developed. This model considers economic and operational indicators and utilizes an INGO for optimization, resulting in an optimal economic dispatch for the ICSS.
2. EV
2.1. EV Queuing Model Based on Wealth Points and Battery Degradation Trust
2.1.1. Wealth Points Management Mechanism
2.1.2. Battery Degradation Trust Management Mechanism
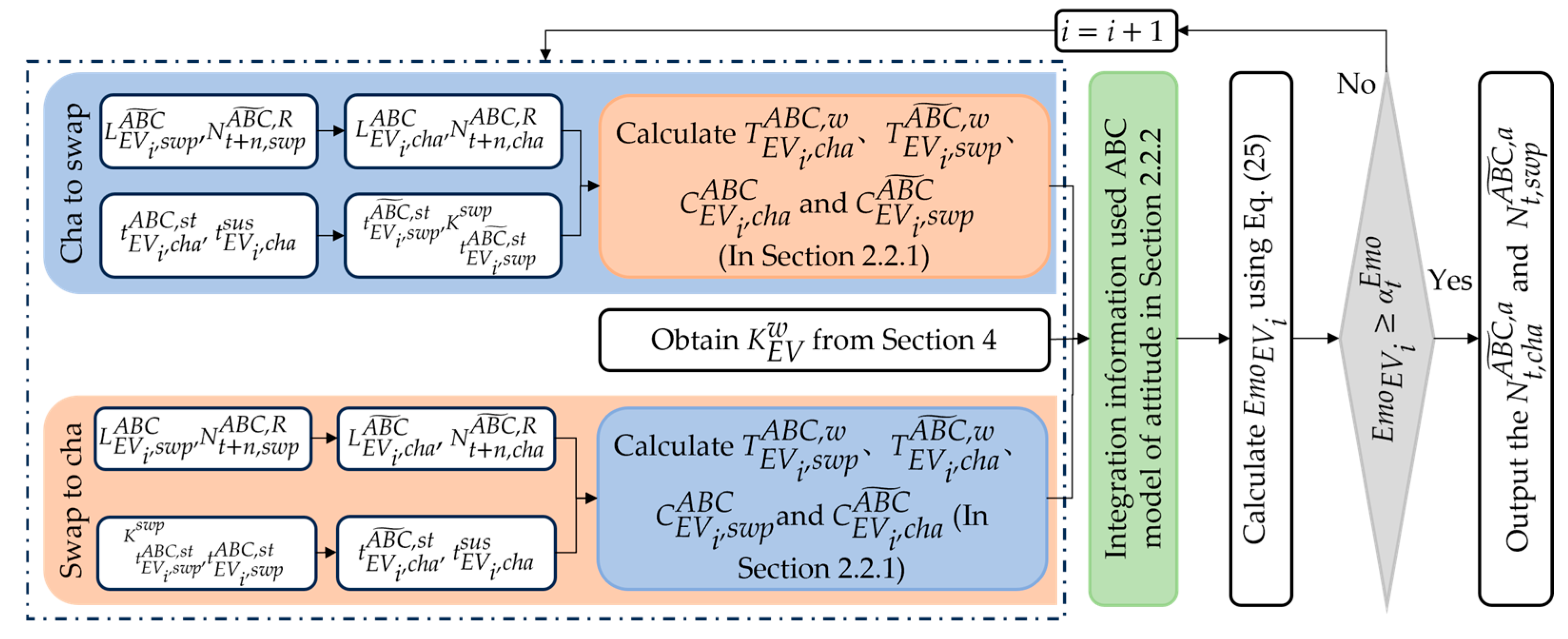
2.2. Intention-Reshaping Model
2.2.1. Waiting Time and Cost Change Model for EVs
- Scenario 1: charging to swapping
- Scenario 2: swapping to charging
2.2.2. ABC Model of Attitudes
- C
- A
- B
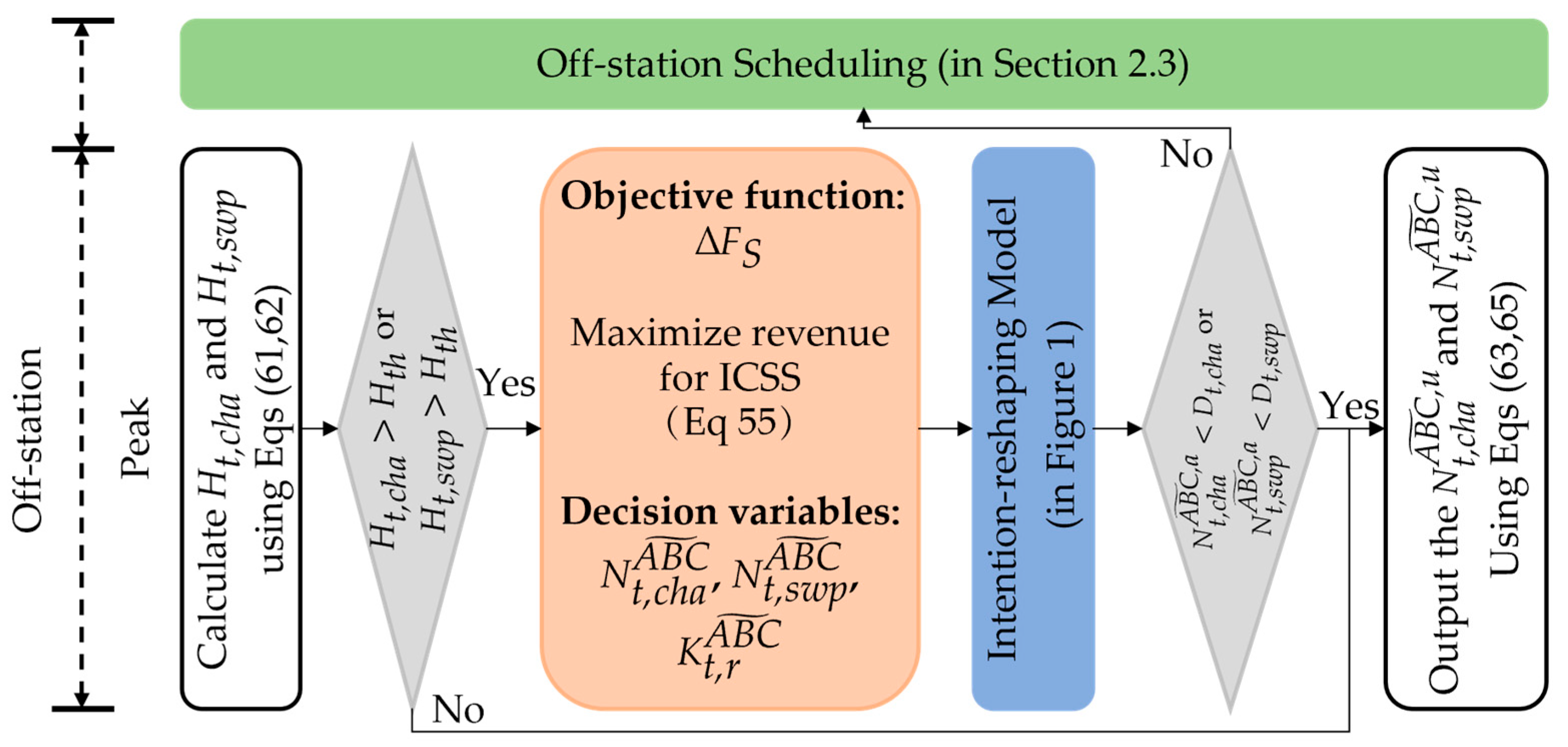
2.3. Off-Station Scheduling Model Based on Vehicle and Road Conditions
3. Battery Compartment Management
3.1. Battery Threshold Adjustment Strategy
3.2. Charging Strategy for Battery Compartment
4. Economic Dispatch Model
4.1. Objective Function
4.2. Constraint
5. Two-Stage Scheduling Strategy Based on In-Station and Off-Station Scheduling
- Step1:
- Set the number of swarms and iterations ;
- Step2:
- Set upper and lower limits for variables , , , , and ;
- Step3:
- Generate the of the northern eagle and the position of the prey;
- Step4:
- Calculate initial fitness of each by Section 4.1;
- Step5:
- Update the of each eagle after the first stage according to Equation (69);
- Step6:
- Update the of each eagle after the second stage according to Equation (71);
- Step7:
- Calculate the updated and save the best solution found so far;
- Step8:
- Repeat steps 3 and 7 until the desired number of iterations is reached;
- Step9:
- Output the optimal solution obtained by the INGO algorithm.
6. Case Study
6.1. Simulation System
6.2. Results Analysis
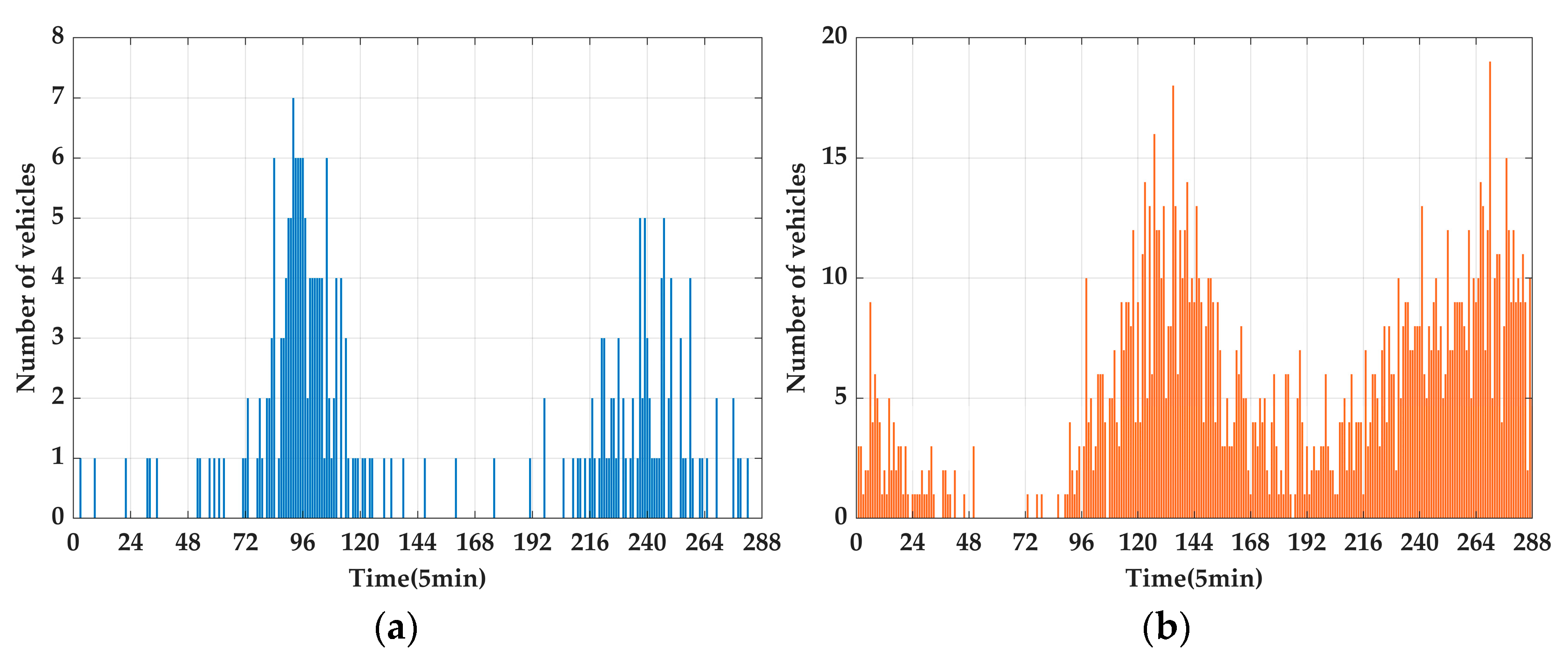
6.2.1. The ICSS’s Number of EVs Prediction Results
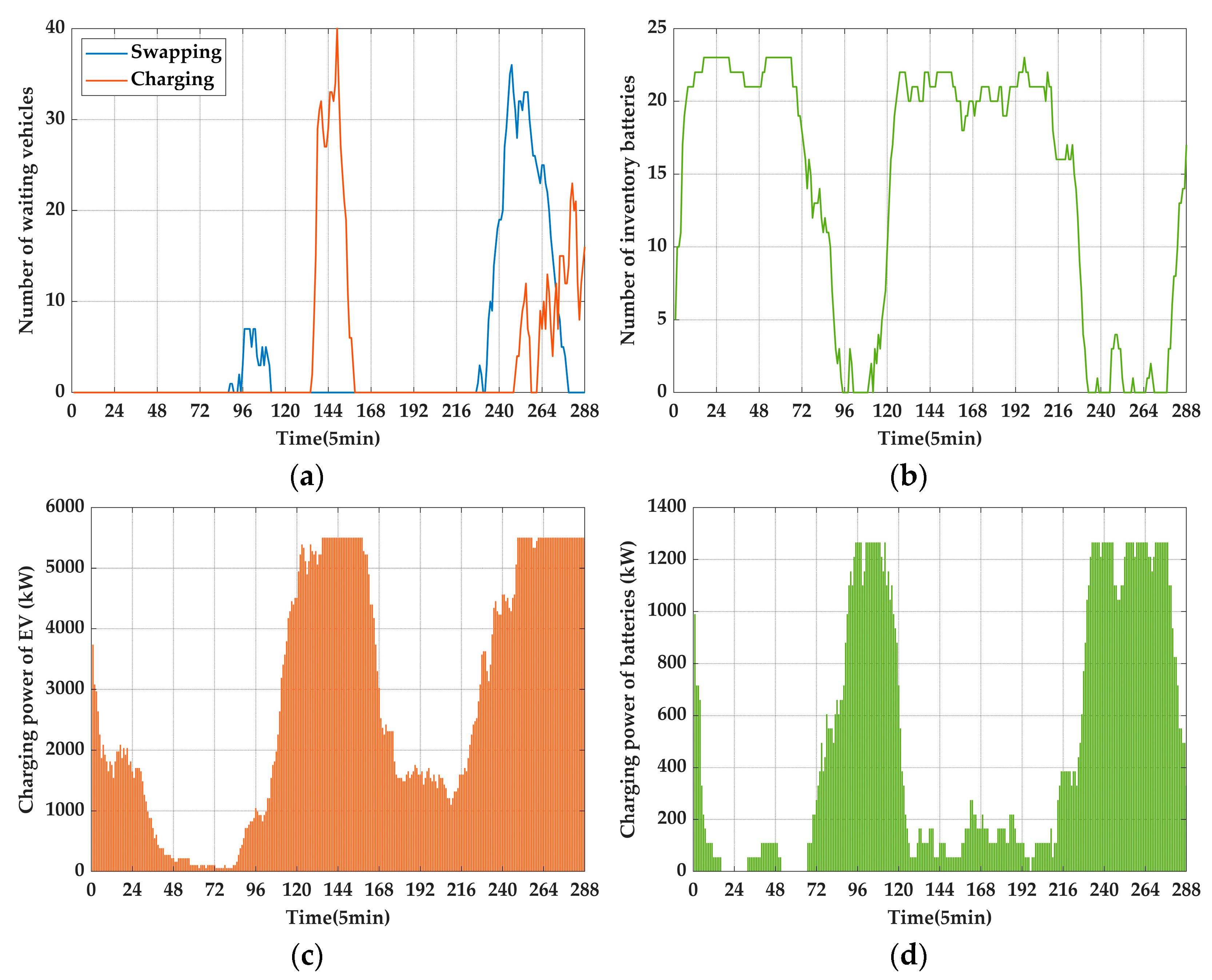
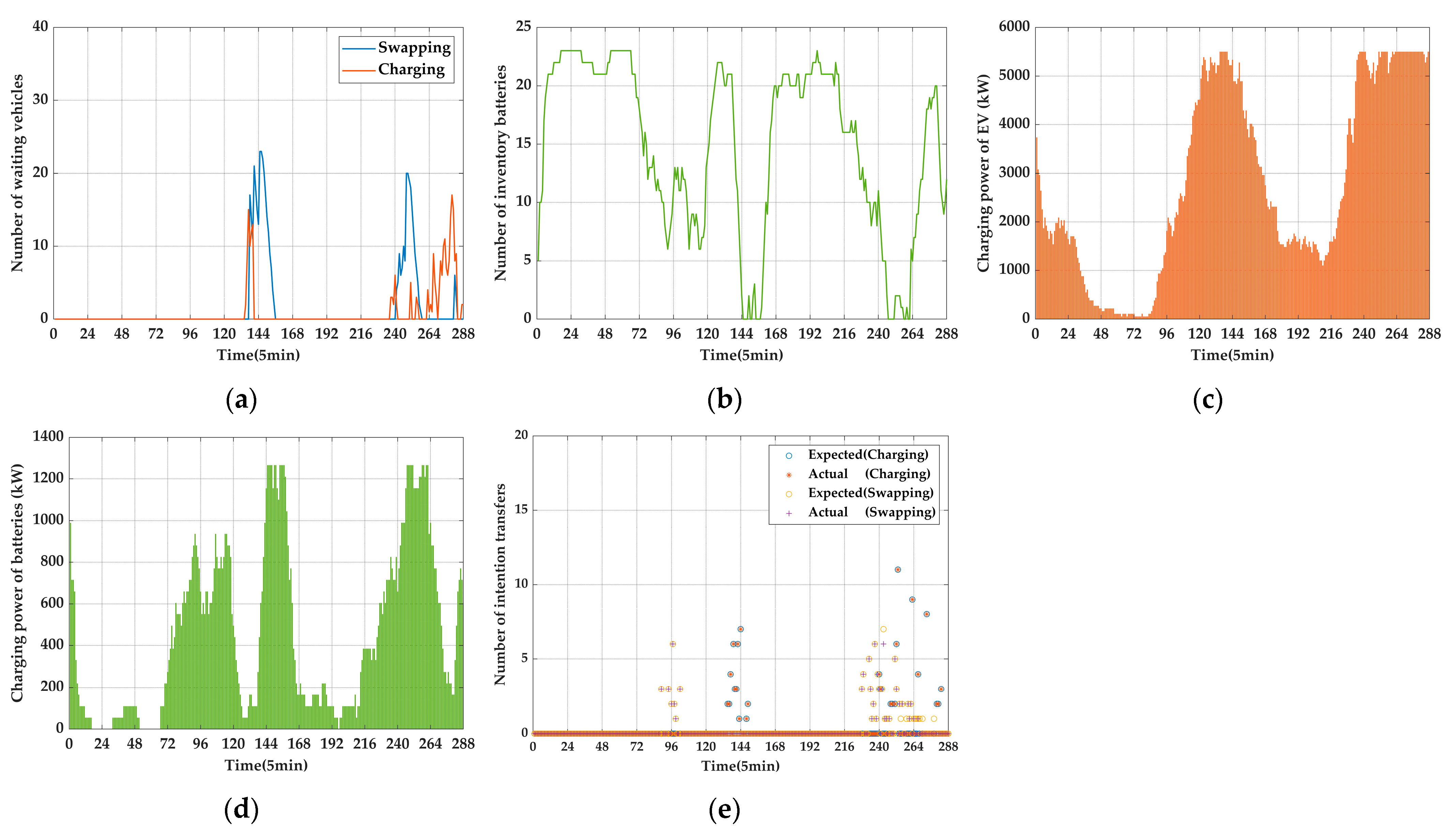
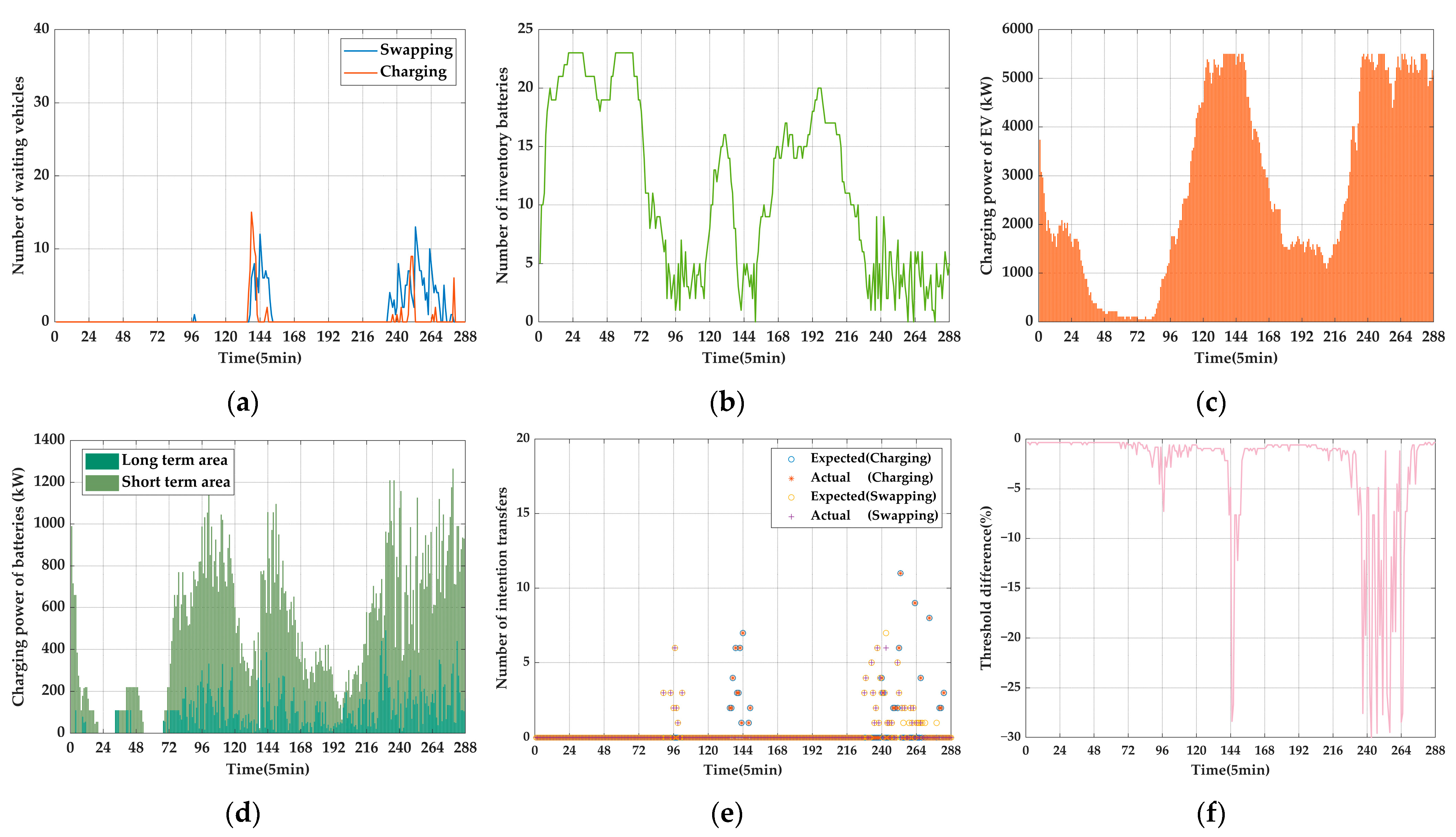
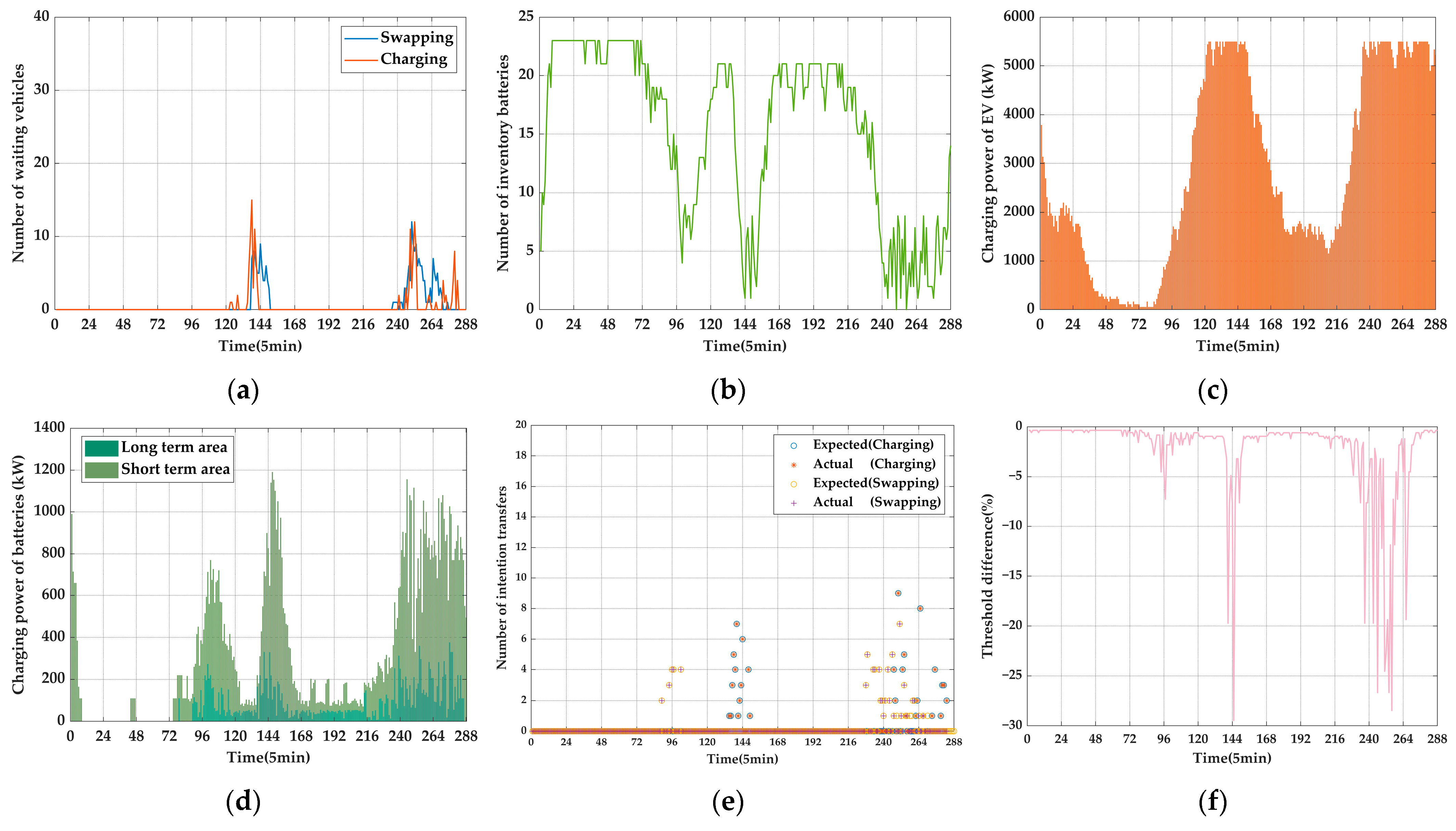
6.2.2. Results and Analysis
- Case 1
- Case 2
- Case 3
- Case 4
- Net profit of annual average
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhan, W.; Wang, Z.; Zhang, L.; Liu, P.; Cui, D.; Dorrell, D.G. A Review of Siting, Sizing, Optimal Scheduling, and Cost-Benefit Analysis for Battery Swapping Stations. Energy 2022, 258, 124723. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Li, Y.; Zheng, Y.; Liu, J. A Green-Fitting Dispatching Model of Station Cluster for Battery Swapping under Charging-Discharging Mode. Energy 2023, 276, 127600. [Google Scholar] [CrossRef]
- Wei, S. A Sequential Game Analysis on Carbon Tax Policy Choices in Open Economies: From the Perspective of Carbon Emission Responsibilities. J. Clean. Prod. 2021, 283, 124588. [Google Scholar] [CrossRef]
- Gonyan Research Institute. Report on the Comprehensive Survey and Market Evaluation of China’s New Energy Swap Station Industry from 2025 to 2031. 2025. Available online: https://www.gonyn.com/about/ (accessed on 2 March 2024).
- National Development and Reform Commission. Several Measures to Promote Automobile Consumption. 2023. Available online: https://www.gov.cn/zhengce/zhengceku/202307/content_6893476.htm (accessed on 28 March 2024).
- Ministry of Industry and Information Technology. Notice on Organizing the Pilot Work of Comprehensive Electrification of Public Vehicles in the Pilot Zone. 2023. Available online: https://www.gov.cn/zhengce/zhengceku/2023-02/03/content_5739955.htm (accessed on 20 April 2024).
- Energy Internet Research Institute. Blue Book on the Development of Electric Vehicle Swapping Industry (2022–2023). 2022. Available online: https://www.cnenergynews.cn/peixun/2024/06/03/detail_20240603163043.html (accessed on 26 July 2024).
- Dou, Y.; Zhang, T.; Meng, X. A Theoretical Model of Sequential Combinatorial Games of Subsidies and Penalties: From Waste to Renewable Energy. Front. Energy Res. 2021, 9, 719214. [Google Scholar] [CrossRef]
- Hemmati, R. Dynamic Expansion Planning in Active Distribution Grid Integrated with Seasonally Transferred Battery Swapping Station and Solar Energy. Energy 2023, 277, 127719. [Google Scholar] [CrossRef]
- Al-Zaidi, W.K.M.; Inan, A. Optimal Planning of Battery Swapping Stations Incorporating Dynamic Network Reconfiguration Considering Technical Aspects of the Power Grid. Appl. Sci. 2024, 14, 3795. [Google Scholar] [CrossRef]
- Tang, M.; Zhang, C.; Zhang, Y.; Yan, Y.; Wang, W.; An, B. A Dual-Layer MPC of Coordinated Control of Battery Load Demand and Grid-Side Supply Matching at Electric Vehicle Swapping Stations. Energies 2024, 17, 879. [Google Scholar] [CrossRef]
- Wang, Z.; Hou, S. Optimal Participation of Battery Swapping Stations in Frequency Regulation Market Considering Uncertainty. Energy 2024, 302, 131815. [Google Scholar] [CrossRef]
- Zhang, K.; Xu, Y.; Sun, H. Bilevel Optimal Coordination of Active Distribution Network and Charging Stations Considering EV Drivers’ Willingness. Appl. Energy 2024, 360, 122790. [Google Scholar] [CrossRef]
- Menghwar, M.; Yan, J.; Chi, Y.; Asim Amin, M.; Liu, Y. A Market-Based Real-Time Algorithm for Congestion Alleviation Incorporating EV Demand Response in Active Distribution Networks. Appl. Energy 2024, 356, 122426. [Google Scholar] [CrossRef]
- He, Z.; Hou, H.; Hou, T.; Fang, R.; Tang, J.; Xie, C. Multi-Objective Optimization for Improving EV Users’ Adhesion with Hybrid Demand Response Strategy. Energy Rep. 2023, 9, 316–322. [Google Scholar] [CrossRef]
- Deb, S.; Goswami, A.K.; Chetri, R.L.; Roy, R. Charging Coordination of Plug-in Electric Vehicles Considering Machine Learning Based State-of-Charge Prediction for Congestion Management in Distribution System. Electr. Power Compon. Syst. 2023, 51, 131–150. [Google Scholar] [CrossRef]
- Yan, P.; Yu, K.; Chao, X.; Chen, Z. An Online Reinforcement Learning Approach to Charging and Order-Dispatching Optimization for an e-Hailing Electric Vehicle Fleet. Eur. J. Oper. Res. 2023, 310, 1218–1233. [Google Scholar] [CrossRef]
- Wang, F.Y.; Chen, Z.; Hu, Z. Comprehensive Optimization of Electrical Heavy-Duty Truck Battery Swap Stations with a SOC-Dependent Charge Scheduling Method. Energy 2024, 308, 132773. [Google Scholar] [CrossRef]
- Chen, X.; Yang, Y.; Wang, J.; Song, J.; He, G. Battery Valuation and Management for Battery Swapping Station. Energy 2023, 279, 128120. [Google Scholar] [CrossRef]
- Zhou, K.; Cheng, L.; Wen, L.; Lu, X.; Ding, T. A Coordinated Charging Scheduling Method for Electric Vehicles Considering Different Charging Demands. Energy 2020, 213, 118882. [Google Scholar] [CrossRef]
- Tan, M.; Dai, Z.; Su, Y.; Chen, C.; Wang, L.; Chen, J. Bi-Level Optimization of Charging Scheduling of a Battery Swap Station Based on Deep Reinforcement Learning. Eng. Appl. Artif. Intell. 2023, 118, 105557. [Google Scholar] [CrossRef]
- Zhang, M.; Yu, S.S.; Yu, H.; Li, P.; Li, W.; Muyeen, S.M. Dispatchable Capacity Optimization Strategy for Battery Swapping and Charging Station Aggregators to Participate in Grid Operations. Energy Rep. 2023, 10, 734–743. [Google Scholar] [CrossRef]
- Liu, W.; Xin, S.; Zhang, Z.; Fan, C.; Hao, G.; Xu, Q. Collaborative Planning of Electric Vehicle Integrated ICSS Stations and Distribution Network for Carbon Emission Reduction. Energy Rep. 2024, 12, 5846–5862. [Google Scholar] [CrossRef]
- Saha, M.; Thakur, S.S.; Bhattacharya, A. Hybrid Differential Evolution-Prairie Dog Optimization Algorithm Approach for Optimal Scheduling of Battery Swapping Charging Station Considering Uncertainty. J. Energy Storage 2025, 112, 115494. [Google Scholar] [CrossRef]
- Yi, H.; Zhang, H.; Li, J.; Zhao, Y. Hybrid Intelligent Optimization Strategy of Battery Swapping Station for Electric Vehicles Based on Reinforcement Learning. Comput. Urban Sci. 2025, 5, 6. [Google Scholar] [CrossRef]
- Zhang, Y.; Han, T.; He, W.; Xia, J.; Cui, L.; Ma, Z.; Liu, S. Battery Swapping Scheduling for Electric Vehicles: A Non-Cooperative Game Approach. Front. Energy Res. 2024, 12, 1488234. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Li, Y.; Xue, J. A Bi-Objective Battery Dispatching Model of Taxi Battery Swapping Station Network Considering Green Power Consumption. Renew. Energy 2025, 239, 122162. [Google Scholar] [CrossRef]
- Duan, L.; Taylor, G.; Lai, C.S. Solar–Hydrogen-Storage Integrated Electric Vehicle Charging Stations with Demand-Side Management and Social Welfare Maximization. WEVJ 2024, 15, 337. [Google Scholar] [CrossRef]
- Cha, J.; Han, C.; Song, S.; Kang, S.; Lee, D.; Chang, M.; Jang, G. Hierarchical Co-Optimization of EV Scheduling Considering Customer and System in Distribution Networks. Sustain. Energy Grids Netw. 2024, 38, 101361. [Google Scholar] [CrossRef]
- Nayak, D.S.; Misra, S. An Operational Scheduling Framework for Electric Vehicle Battery Swapping Station under Demand Uncertainty. Energy 2024, 290, 130219. [Google Scholar] [CrossRef]
- Puhua Policy. Market Research Report on the Battery Swap Service Industry. 2023. Available online: https://baijiahao.baidu.com/s?id=1818778726660670306&wfr=spider&for=pc (accessed on 20 June 2024).
- Baidu Maps. 2023 China Urban Transportation Report. 2023. Available online: https://jiaotong.baidu.com/cms/reports/traffic/2023/index.html (accessed on 20 April 2024).
- Iresearch. China New Energy Vehicle Battery Swap Market Research Report. 2022. Available online: https://www.xdyanbao.com/doc/zh7he93eil?userid=57555079&bd_vid=11066103399936229079 (accessed on 2 January 2024).
- Liu, B.; Xu, Y.; Yang, Y.; Lu, S. How Public Cognition Influences Public Acceptance of CCUS in China: Based on the ABC (Affect, Behavior, and Cognition) Model of Attitudes. Energy Policy 2021, 156, 112390. [Google Scholar] [CrossRef]
- Xu, Y.; Mohd Hasan, N.A.; Mohd Jalis, F.M. Purchase Intentions for Cultural Heritage Products in E-Commerce Live Streaming: An ABC Attitude Theory Analysis. Heliyon 2024, 10, e26470. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, K.; Yu, Y. Industrial Transformation for Synergistic Carbon and Pollutant Reduction in China: Using Environmentally Extended Multi-Regional Input-Output Model and Multi-Objective Optimization. Energy 2025, 318, 134830. [Google Scholar] [CrossRef]
- Derzsi, Z.; Volcic, R. Not Only Perception but Also Grasping Actions Could Obey Weber’s Law. Cognition 2023, 237, 105465. [Google Scholar] [CrossRef]
- García-Cuesta, E.; Gómez-Vergel, D.; Gracia-Expósito, L.; López-López, J.M.; Vela-Pérez, M. Prediction of Opinion Keywords and Their Sentiment Strength Score Using Latent Space Learning Methods. Appl. Sci. 2020, 10, 4196. [Google Scholar] [CrossRef]
- Li, D.; Du, J.; Sun, M.; Han, D. How Conformity Psychology and Benefits Affect Individuals’ Green Behaviours from the Perspective of a Complex Network. J. Clean. Prod. 2020, 248, 119215. [Google Scholar] [CrossRef]
- Ding, Z. Optimizing Economic Management Paths on Consumer Conformity Psychology from a Psychological Perspective. CNS Spectr. 2023, 28, S129. [Google Scholar] [CrossRef]
- Ma, M.; Xu, E.; Zheng, W.; Qin, J.; Huang, Q. The Optimized Real-Time Energy Management Strategy for Fuel-Cell Hybrid Trucks through Dynamic Programming. Int. J. Hydrogen Energy 2024, 59, 10–21. [Google Scholar] [CrossRef]
- Liang, Y.; Hu, X.; Hu, G.; Dou, W. An Enhanced Northern Goshawk Optimization Algorithm and Its Application in Practical Optimization Problems. Mathematics 2022, 10, 4383. [Google Scholar] [CrossRef]
- Ministry of Public Security. Opinions on Accelerating the Comprehensive Green Transformation of Economic and Social Development. 2024. Available online: https://news.qq.com/rain/a/20240815A09OIS00 (accessed on 2 January 2024).
- National Energy Administration. Action Plan for Accelerating the Construction of a New Power System (2024–2027). Available online: https://www.ndrc.gov.cn/xxgk/jd/jd/202408/t20240809_1392336.html (accessed on 26 January 2024).
- The State Council. Development Plan for New Energy Vehicle Industry (2021–2035). Available online: https://www.gov.cn/xinwen/2020-11/02/content_5556762.htm (accessed on 20 April 2024).
- China Charging Alliance. Operation of National Electric Vehicle Charging and Swapping Infrastructure in September 2024. Available online: https://chd.in-en.com/html/chd-2447788.shtml (accessed on 25 June 2024).
- NIO. NIO Official Website. Available online: https://app.nio.com/ (accessed on 17 June 2024).
- China Energy Research Association. Blue Book on the Development of Electric Vehicle Swapping Industry (2022–2023). Available online: https://www.163.com/dy/article/J2VJJ3N80519QIKK.html (accessed on 17 June 2024).
- China Electric Vehicle Promotion Alliance. 2022 White Paper on Charging Behavior of Chinese Electric Vehicle Users. Available online: https://www.nea.gov.cn/2023-03/20/c_1310703965.htm? (accessed on 13 October 2024).
- Beijing Transport Institute. The Beijing Transport Development Annual Report of 2023. Available online: https://www.bjtrc.org.cn/List/index/cid/7.html (accessed on 1 August 2023).
- U.S. Department of Transportation. Summary of Travel Trends: 2022 National Household Travel Survey. Available online: https://nhts.ornl.gov/assets/2022/pub/2022_NHTS_Summary_Travel_Trends.pdf (accessed on 1 January 2024).
- Cavus, M.; Dissanayake, D.; Bell, M. Next Generation of Electric Vehicles: AI-Driven Approaches for Predictive Maintenance and Battery Management. Energies 2025, 18, 1041. [Google Scholar] [CrossRef]
- Cavus, M.; Ayan, H.; Bell, M.; Oyebamiji, O.K.; Dissanayake, D. Deep Charge-Fusion Model: Advanced Hybrid Modelling for Predicting Electric Vehicle Charging Patterns with Socio-Demographic Considerations. Int. J. Transp. Sci. Technol. 2025, in press. [Google Scholar] [CrossRef]
| Conversion Reward Funds | Costs | Waiting Time | |
|---|---|---|---|
| Cha to swap | Output | Increase (Input) | Increase (Input) |
| Output | Increase (Input) | Reduce (Output) | |
| Swap to cha | Output | Reduce (Output) | Increase (Input) |
| Output | Reduce (Output) | Reduce (Output) |
| Type | Parameters | Character | Value | Unit |
|---|---|---|---|---|
| Charging pile | Rated power | 64.5 | kW | |
| Rated efficiency | 90 | % | ||
| Service life | - | 10 | year | |
| Swapping facility | Service life | - | 15 | year |
| Battery | Upper limit of SOC | 90 | % | |
| Lower limit of SOC | 20 | % | ||
| Rated power | 64.5 | kW | ||
| Rated efficiency | 90 | % | ||
| Service life | - | 8 | year | |
| Capacity | 75 | kWh |
| Type | Parameters | Character | Value | Unit |
|---|---|---|---|---|
| Economy | Waiting time cost | 0.23 | CNY | |
| Depreciation cost of batteries | 0.46 | CNY | ||
| Investment of charging pile | 26,000 | CNY/piece | ||
| Investment of swapping facility | 300,000 | CNY/piece | ||
| Investment of battery | 80,000 | CNY/piece | ||
| O&M of ICSS | 500,000 | CNY/year | ||
| Battery rent | 728 | CNY/piece/month | ||
| Other | Empirical multiple | 1.5 | - | |
| Standard threshold | 90 | % | ||
| Average swapping capacity | 40 | kWh |
| Intention Reshaping | Battery Management | Off-Station Scheduling | |
|---|---|---|---|
| Case 1 | |||
| Case 2 | √ | ||
| Case 3 | √ | √ | |
| Case 4 | √ | √ | √ |
| Amount | |||||
|---|---|---|---|---|---|
| Annual | 85,099.57 | 37,595.81 | 148,410.61 | 0 | 25,715.23 |
| Amount | |||||
|---|---|---|---|---|---|
| Annual | 84,560.39 | 35,767.88 | 147,588.35 | 947 | 26,313.08 |
| Amount | |||||
|---|---|---|---|---|---|
| Annual | 81,995.21 | 34,952.59 | 147,087.5 | 789 | 29,350.71 |
| Amount | |||||
|---|---|---|---|---|---|
| Annual | 80,643.21 | 34,165.95 | 151,775.61 | 643 | 36,323.48 |
| Case | Gross Revenue | Net Profit |
|---|---|---|
| 1 | 938.61 | 600.78 |
| 2 | 960.43 | 622.60 |
| 3 | 1071.30 | 733.47 |
| 4 | 1325.81 | 987.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Zhang, X.; Yan, Q.; Zhang, X.; Li, Y. Congestion Relief and Economic Optimization of Integrated Power Stations with Charging and Swapping Functions. World Electr. Veh. J. 2025, 16, 230. https://doi.org/10.3390/wevj16040230
Wang Z, Zhang X, Yan Q, Zhang X, Li Y. Congestion Relief and Economic Optimization of Integrated Power Stations with Charging and Swapping Functions. World Electric Vehicle Journal. 2025; 16(4):230. https://doi.org/10.3390/wevj16040230
Chicago/Turabian StyleWang, Zhaoyi, Xiaohong Zhang, Qingyuan Yan, Xiaokang Zhang, and Yanxue Li. 2025. "Congestion Relief and Economic Optimization of Integrated Power Stations with Charging and Swapping Functions" World Electric Vehicle Journal 16, no. 4: 230. https://doi.org/10.3390/wevj16040230
APA StyleWang, Z., Zhang, X., Yan, Q., Zhang, X., & Li, Y. (2025). Congestion Relief and Economic Optimization of Integrated Power Stations with Charging and Swapping Functions. World Electric Vehicle Journal, 16(4), 230. https://doi.org/10.3390/wevj16040230






