A Dynamic Bayesian Model for Identifying High-Mortality Risk in Hospitalized COVID-19 Patients
Abstract
:1. Introduction
2. Materials and Methods
2.1. Case Selection and Data Extraction
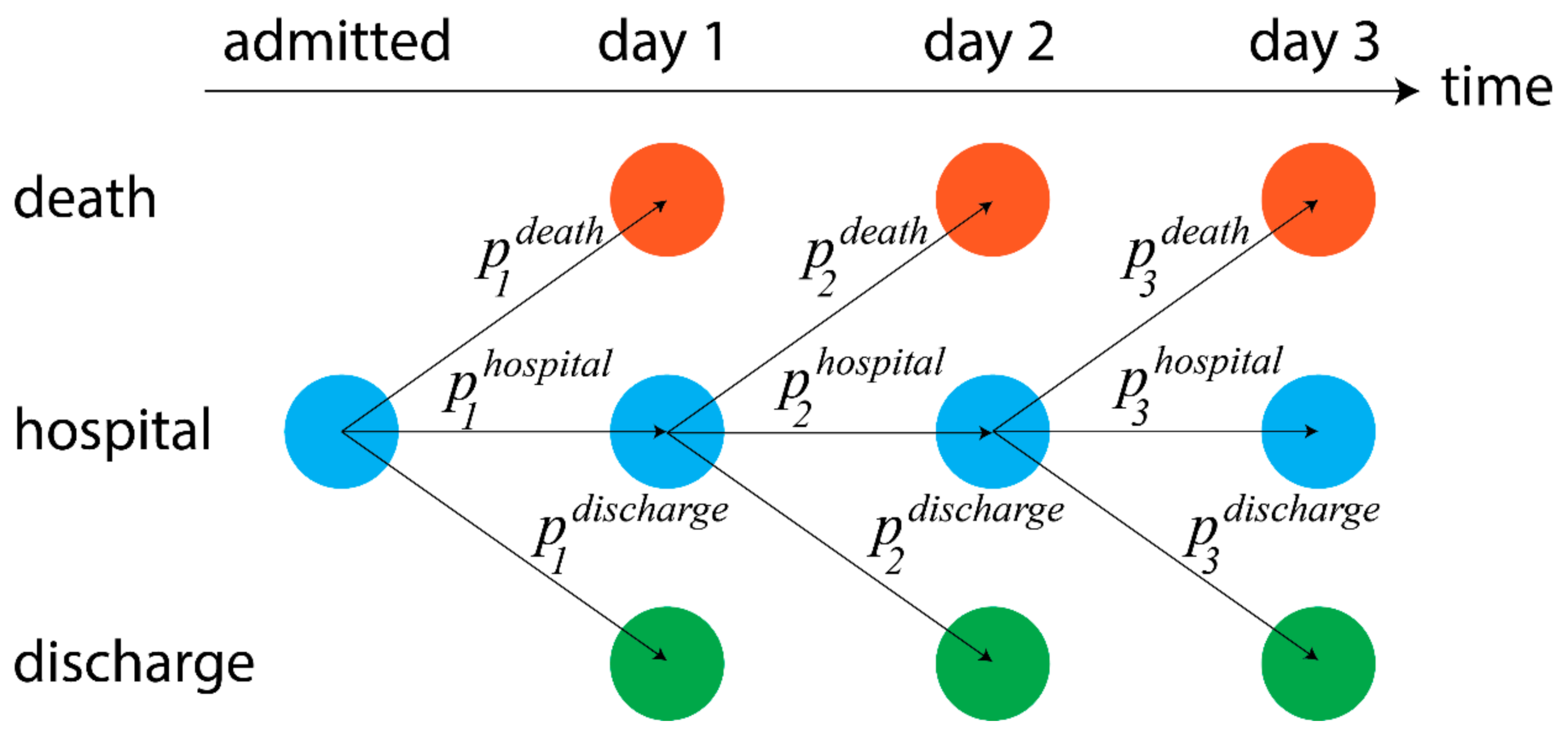
2.2. Models of Dynamic Risk
3. Results
3.1. Patient Characteristics
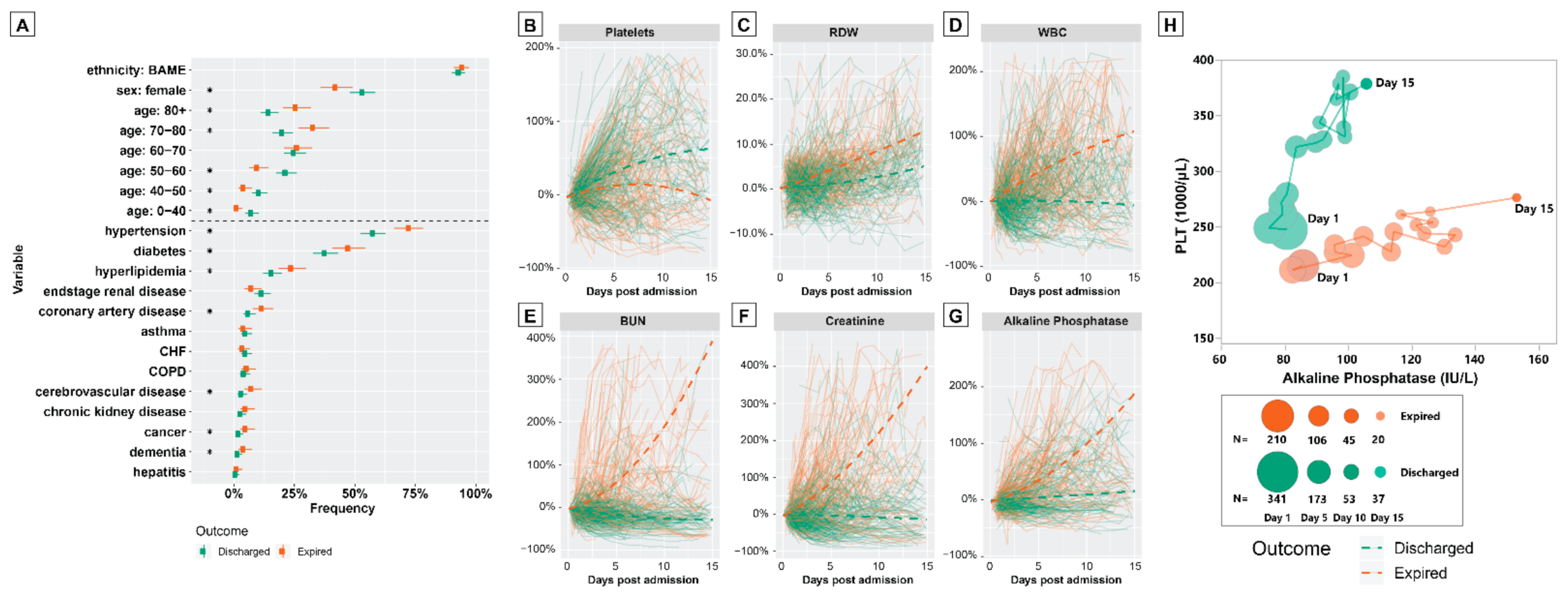
3.2. Characteristics of Discharged and Expired Patients
3.3. Analysis of Dynamic Patient Risk
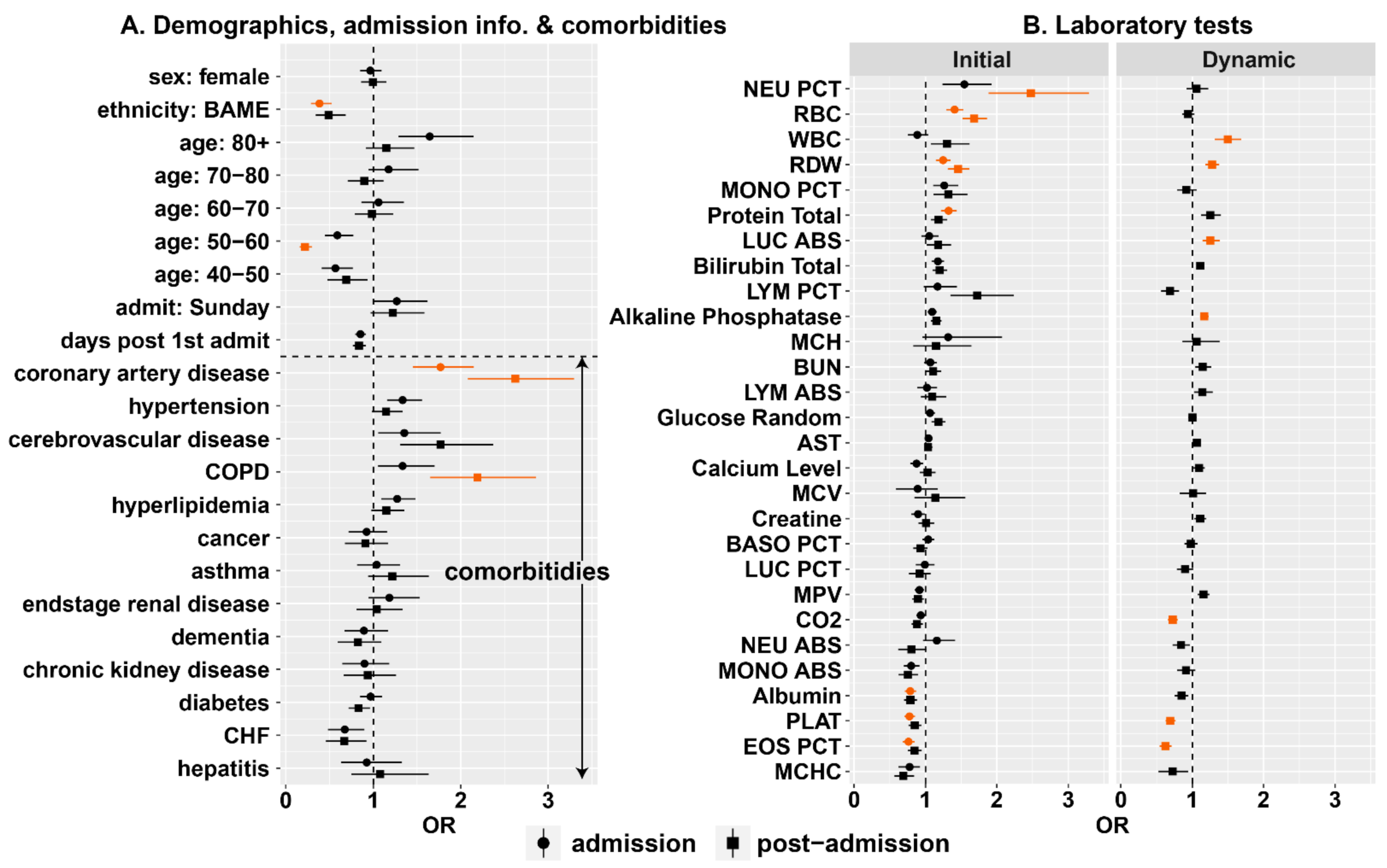
3.3.1. Univariate Analysis
3.3.2. Multivariate Analysis
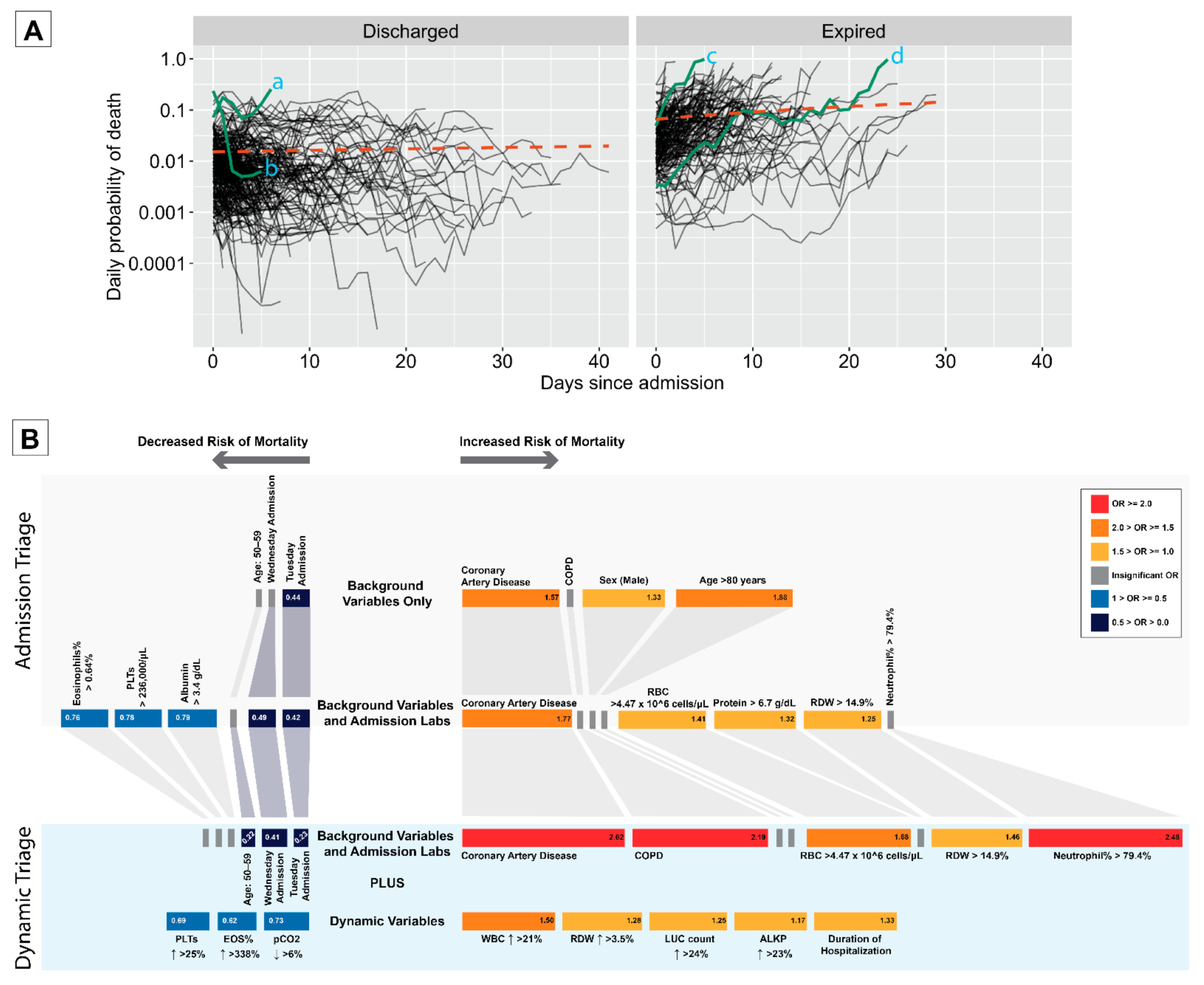
3.4. Dynamic Measure of Risk
3.5. Dynamic Triage
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Dong, E.; Du, H.; Gardner, L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect. Dis. 2020, 20, 533–534. [Google Scholar] [CrossRef]
- O’Driscoll, M.; Dos Santos, G.R.; Wang, L.; Cummings, D.A.; Azman, A.S.; Paireau, J.; Fontanet, A.; Cauchemez, S.; Salje, H. Age-specific mortality and immunity patterns of SARS-CoV-2. Nature 2020, 590, 140–145. [Google Scholar] [CrossRef] [PubMed]
- Armocida, B.; Formenti, B.; Ussai, S.; Palestra, F.; Missoni, E. The Italian health system and the COVID-19 challenge. Lancet Public Health 2020, 5, e253. [Google Scholar] [CrossRef]
- McCabe, R.; Schmit, N.; Christen, P.; D’Aeth, J.C.; Løchen, A.; Rizmie, D.; Nayagam, S.; Miraldo, M.; Aylin, P.; Bottle, A.; et al. Adapting hospital capacity to meet changing demands during the COVID-19 pandemic. BMC Med. 2020, 18, 329. [Google Scholar] [CrossRef] [PubMed]
- Grasselli, G.; Pesenti, A.; Cecconi, M. Critical Care Utilization for the COVID-19 Outbreak in Lombardy, Italy: Early Experience and Forecast During an Emergency Response. JAMA 2020, 323, 1545–1546. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Solomon, M.Z.; Wynia, M.K.; Gostin, L.O. Covid-19 crisis triage—Optimizing health outcomes and disability rights. N. Engl. J. Med. 2020, 383, e27. [Google Scholar] [CrossRef]
- Vyas, D.A.; Eisenstein, L.G.; Jones, D.S. Hidden in Plain Sight—Reconsidering the Use of Race Correction in Clinical Algorithms. Obstet. Gynecol. Surv. 2021, 76, 5–7. [Google Scholar] [CrossRef]
- Steinberg, E.; Balakrishna, A.; Habboushe, J.; Shawl, A.; Lee, J. Calculated decisions: COVID-19 calculators during extreme resource-limited situations. Emerg. Med. Pract. 2020, 22, CD1–CD5. [Google Scholar]
- Laing, A.G.; Lorenc, A.; Del Barrio, I.D.M.; Das, A.; Fish, M.; Monin, L.; Muñoz-Ruiz, M.; McKenzie, D.R.; Hayday, T.S.; Francos-Quijorna, I. A dynamic COVID-19 immune signature includes associations with poor prognosis. Nat. Med 2020, 26, 1623–1635. [Google Scholar] [CrossRef]
- Steyerberg, E.W.; Moons, K.G.; van der Windt, D.A.; Hayden, J.A.; Perel, P.; Schroter, S.; Riley, R.D.; Hemingway, H.; Altman, D.G.; Group, P. Prognosis Research Strategy (PROGRESS) 3: Prognostic model research. PLoS Med. 2013, 10, e1001381. [Google Scholar] [CrossRef] [Green Version]
- Gupta, R.K.; Marks, M.; Samuels, T.H.; Luintel, A.; Rampling, T.; Chowdhury, H.; Quartagno, M.; Nair, A.; Lipman, M.; Abubakar, I. Systematic evaluation and external validation of 22 prognostic models among hospitalised adults with COVID-19: An observational cohort study. Eur. Respir. J. 2020, 56, 2003498. [Google Scholar] [CrossRef] [PubMed]
- Wynants, L.; Van Calster, B.; Collins, G.S.; Riley, R.D.; Heinze, G.; Schuit, E.; Bonten, M.M.; Dahly, D.L.; Damen, J.A.; Debray, T.P. Prediction models for diagnosis and prognosis of covid-19: Systematic review and critical appraisal. BMJ 2020, 369, m1328. [Google Scholar]
- Zhou, F.; Yu, T.; Du, R.; Fan, G.; Liu, Y.; Liu, Z.; Xiang, J.; Wang, Y.; Song, B.; Gu, X. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: A retrospective cohort study. Lancet 2020, 395, 1054–1062. [Google Scholar] [CrossRef]
- Cummings, M.J.; Baldwin, M.R.; Abrams, D.; Jacobson, S.D.; Meyer, B.J.; Balough, E.M.; Aaron, J.G.; Claassen, J.; Rabbani, L.E.; Hastie, J.; et al. Epidemiology, clinical course, and outcomes of critically ill adults with COVID-19 in New York City: A prospective cohort study. Lancet 2020, 395, 1763–1770. [Google Scholar] [CrossRef]
- Ssentongo, P.; Ssentongo, A.E.; Heilbrunn, E.S.; Ba, D.M.; Chinchilli, V.M. Association of cardiovascular disease and 10 other pre-existing comorbidities with COVID-19 mortality: A systematic review and meta-analysis. PLoS ONE 2020, 15, e0238215. [Google Scholar] [CrossRef]
- Paranjpe, I.; Russak, A.J.; De Freitas, J.K.; Lala, A.; Miotto, R.; Vaid, A.; Johnson, K.W.; Danieletto, M.; Golden, E.; Meyer, D.; et al. Retrospective cohort study of clinical characteristics of 2199 hospitalised patients with COVID-19 in New York City. BMJ Open 2020, 10, e040736. [Google Scholar] [CrossRef] [PubMed]
- Du, R.-H.; Liang, L.-R.; Yang, C.-Q.; Wang, W.; Cao, T.-Z.; Li, M.; Guo, G.-Y.; Du, J.; Zheng, C.-L.; Zhu, Q.; et al. Predictors of Mortality for Patients with COVID-19 Pneumonia Caused by SARS-CoV-2: A Prospective Cohort Study. Eur. Respir. J. 2020, 55, 2000524. [Google Scholar] [CrossRef] [Green Version]
- Haigney, M.C.; Zareba, W.; Gentlesk, P.J.; Goldstein, R.E.; Illovsky, M.; McNitt, S.; Andrews, M.L.; Moss, A.J. QT interval variability and spontaneous ventricular tachycardia or fibrillation in the Multicenter Automatic Defibrillator Implantation Trial (MADIT) II patients. J. Am. Coll. Cardiol. 2004, 44, 1481–1487. [Google Scholar] [CrossRef] [Green Version]
- Fan, E.; Beitler, J.R.; Brochard, L.; Calfee, C.S.; Ferguson, N.D.; Slutsky, A.S.; Brodie, D. COVID-19-associated acute respiratory distress syndrome: Is a different approach to management warranted? Lancet Respir. Med. 2020, 8, 816–821. [Google Scholar] [CrossRef]
- Bilaloglu, S.; Aphinyanaphongs, Y.; Jones, S.; Iturrate, E.; Hochman, J.; Berger, J.S. Thrombosis in Hospitalized Patients With COVID-19 in a New York City Health System. JAMA 2020, 324, 799–801. [Google Scholar] [CrossRef]
- Perez-Guzman, P.N.; Daunt, A.; Mukherjee, S.; Crook, P.; Forlano, R.; Kont, M.D.; Løchen, A.; Vollmer, M.; Middleton, P.; Judge, R. Clinical characteristics and predictors of outcomes of hospitalized patients with coronavirus disease 2019 in a multiethnic London national health service trust: A retrospective cohort study. Clin Infect Dis 2020, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Hu, B.; Hu, C.; Zhu, F.; Liu, X.; Zhang, J.; Wang, B.; Xiang, H.; Cheng, Z.; Xiong, Y.; et al. Clinical Characteristics of 138 Hospitalized Patients With 2019 Novel Coronavirus–Infected Pneumonia in Wuhan, China. JAMA 2020, 323, 1061–1069. [Google Scholar] [CrossRef]
- Wolff, R.F.; Moons, K.G.M.; Riley, R.D.; Whiting, P.F.; Westwood, M.; Collins, G.S.; Reitsma, J.B.; Kleijnen, J.; Mallett, S. PROBAST: A Tool to Assess the Risk of Bias and Applicability of Prediction Model Studies. Ann. Intern. Med. 2019, 170, 51–58. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ye, W.; Chen, G.; Li, X.; Lan, X.; Ji, C.; Hou, M.; Zhang, D.; Zeng, G.; Wang, Y.; Xu, C. Dynamic changes of D-dimer and neutrophil-lymphocyte count ratio as prognostic biomarkers in COVID-19. Respir. Res. 2020, 21, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.; Sang, L.; Jiang, M.; Yang, Z.; Jia, N.; Fu, W.; Xie, J.; Guan, W.; Liang, W.; Ni, Z. Longitudinal hematologic and immunologic variations associated with the progression of COVID-19 patients in China. J. Allergy Clin. Immunol. 2020, 146, 89–100. [Google Scholar] [CrossRef]
- Liu, Y.; Tan, W.; Chen, H.; Zhu, Y.; Wan, L.; Jiang, K.; Guo, Y.; Tang, K.; Xie, C.; Yi, H. Dynamic changes in lymphocyte subsets and parallel cytokine levels in patients with severe and critical COVID-19. BMC Infect. Dis. 2021, 21, 1–10. [Google Scholar] [CrossRef]
- Abers, M.S.; Delmonte, O.M.; Ricotta, E.E.; Fintzi, J.; Fink, D.L.; de Jesus, A.A.A.; Zarember, K.A.; Alehashemi, S.; Oikonomou, V.; Desai, J.V.; et al. An immune-based biomarker signature is associated with mortality in COVID-19 patients. JCI Insight. 2021, 6, e144455. [Google Scholar] [CrossRef]
- Berzuini, C.; Hannan, C.; King, A.; Vail, A.; O’Leary, C.; Brough, D.; Galea, J.; Ogungbenro, K.; Wright, M.; Pathmanaban, O.; et al. Value of dynamic clinical and biomarker data for mortality risk prediction in Covid-19: A multicentre retrospective cohort study. BMJ Open 2020, 10, e041983. [Google Scholar] [CrossRef]
- Wolbers, M.; Koller, M.T.; Witteman, J.C.; Steyerberg, E.W. Prognostic models with competing risks: Methods and application to coronary risk prediction. Epidemiology 2009, 20, 555–561. [Google Scholar] [CrossRef]
- Abner, E.L.; Charnigo, R.J.; Kryscio, R.J. Markov chains and semi-Markov models in time-to-event analysis. J. Biom. Biostat. 2013, e001, 19522. [Google Scholar]
- Cox, D.R. Regression models and life-tables. J. R. Stat. Soc. Ser. B 1972, 34, 187–202. [Google Scholar] [CrossRef]
- Ayebare, R.R.; Flick, R.; Okware, S.; Bodo, B.; Lamorde, M. Adoption of COVID-19 triage strategies for low-income settings. Lancet Respir. Med. 2020, 8, e22. [Google Scholar] [CrossRef]
- Williamson, E.J.; Walker, A.J.; Bhaskaran, K.; Bacon, S.; Bates, C.; Morton, C.E.; Curtis, H.J.; Mehrkar, A.; Evans, D.; Inglesby, P. Factors associated with COVID-19-related death using OpenSAFELY. Nature 2020, 584, 430–436. [Google Scholar] [CrossRef]
- Price-Haywood, E.G.; Burton, J.; Fort, D.; Seoane, L. Hospitalization and mortality among black patients and white patients with Covid-19. N. Engl. J. Med. 2020, 382, 2534–2543. [Google Scholar] [CrossRef] [PubMed]
- Baqui, P.; Bica, I.; Marra, V.; Ercole, A.; van der Schaar, M. Ethnic and regional variations in hospital mortality from COVID-19 in Brazil: A cross-sectional observational study. Lancet Glob. Health 2020, 8, e1018–e1026. [Google Scholar] [CrossRef]
- Couchoud, C.G.; Beuscart, J.-B.R.; Aldigier, J.-C.; Brunet, P.J.; Moranne, O.P. Development of a risk stratification algorithm to improve patient-centered care and decision making for incident elderly patients with end-stage renal disease. Kidney Int. 2015, 88, 1178–1186. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Devereaux, A.V.; Dichter, J.R.; Christian, M.D.; Dubler, N.N.; Sandrock, C.E.; Hick, J.L.; Powell, T.; Geiling, J.A.; Amundson, D.E.; Baudendistel, T.E. Definitive care for the critically ill during a disaster: A framework for allocation of scarce resources in mass critical care: From a Task Force for Mass Critical Care summit meeting, January 26–27, 2007, Chicago, IL. Chest 2008, 133, 51S–66S. [Google Scholar] [CrossRef]
- Antommaria, A.H.M.; Gibb, T.S.; McGuire, A.L.; Wolpe, P.R.; Wynia, M.K.; Applewhite, M.K.; Caplan, A.; Diekema, D.S.; Hester, D.M.; Lehmann, L.S. Ventilator triage policies during the COVID-19 pandemic at US hospitals associated with members of the association of bioethics program directors. Ann. Intern. Med. 2020, 173, 188–194. [Google Scholar] [CrossRef]
- Gupta, A.; Madhavan, M.V.; Sehgal, K.; Nair, N.; Mahajan, S.; Sehrawat, T.S.; Bikdeli, B.; Ahluwalia, N.; Ausiello, J.C.; Wan, E.Y.; et al. Extrapulmonary manifestations of COVID-19. Nat. Med. 2020, 26, 1017–1032. [Google Scholar] [CrossRef]
- Russell, J.A. Management of Sepsis. N. Engl. J. Med. 2006, 355, 1699–1713. [Google Scholar] [CrossRef] [Green Version]
- Bates, D.; Maechler, M.; Bolker, B.; Walker, S. Fitting linear mixed-effects models using lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Piironen, J.; Vehtari, A. Sparsity information and regularization in the horseshoe and other shrinkage priors. Electron. J. Statist. 2017, 11, 5018–5051. [Google Scholar] [CrossRef]
- Betancourt, M. A conceptual introduction to Hamiltonian Monte Carlo. arXiv 2017, arXiv:170102434. [Google Scholar]
- Goodrich, B.; Gabry, J.; Ali, I.; Brilleman, S. rstanarm: Bayesian Applied Regression Modeling via Stan. R Package v. 2.19. 2. 2020. Available online: https://mc-stan.org/rstanarm/ (accessed on 11 March 2021).
- Vehtari, A.; Gelman, A.; Simpson, D.; Carpenter, B.; Bürkner, P.-C. Rank-normalization, folding, and localization: An improved Ȓ for assessing convergence of MCMC. Bayesian Anal. 2021, 1, 1–28. [Google Scholar]
- Lambert, B. A Student’s Guide to Bayesian Statistics; Sage Publications: Thousand Oaks, CA, USA, 2018. [Google Scholar]
| Category | Variable | Count | Frequency |
|---|---|---|---|
| Outcome | Outcome: Discharged | 342 | 61.8% |
| Outcome: Expired | 211 | 38.2% | |
| Demographic | Sex: Female | 271 | 50.3% |
| Sex: Male | 268 | 49.7% | |
| Age: 0–40 | 26 | 4.8% | |
| Age: 40–50 | 43 | 7.9% | |
| Age: 50–60 | 93 | 17.2% | |
| Age: 60–70 | 140 | 25.8% | |
| Age: 70–80 | 137 | 25.3% | |
| Age: 80–100 | 103 | 19.0% | |
| Ethnicity: Black | 472 | 86.8% | |
| Ethnicity: Caucasian | 25 | 4.6% | |
| Ethnicity: Hispanic | 17 | 3.1% | |
| Ethnicity: Other or Unrecorded | 39 | 7.1% | |
| Comorbidities | Asthma | 24 | 4.4% |
| Cancer | 16 | 2.9% | |
| Cerebrovascular Disease | 25 | 4.6% | |
| Congestive Heart Failure | 23 | 4.2% | |
| Chronic Kidney Disease | 19 | 3.5% | |
| Chronic Obstructive Pulmonary Disease | 25 | 4.6% | |
| Coronary Artery Disease | 44 | 8.0% | |
| Dementia | 13 | 2.4% | |
| Diabetes | 229 | 41.9% | |
| End-Stage Renal Disease | 54 | 9.9% | |
| Hepatitis | 4 | 0.7% | |
| Hyperlipidemia | 103 | 18.8% | |
| Hypertension | 350 | 64.0% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Momeni-Boroujeni, A.; Mendoza, R.; Stopard, I.J.; Lambert, B.; Zuretti, A. A Dynamic Bayesian Model for Identifying High-Mortality Risk in Hospitalized COVID-19 Patients. Infect. Dis. Rep. 2021, 13, 239-250. https://doi.org/10.3390/idr13010027
Momeni-Boroujeni A, Mendoza R, Stopard IJ, Lambert B, Zuretti A. A Dynamic Bayesian Model for Identifying High-Mortality Risk in Hospitalized COVID-19 Patients. Infectious Disease Reports. 2021; 13(1):239-250. https://doi.org/10.3390/idr13010027
Chicago/Turabian StyleMomeni-Boroujeni, Amir, Rachelle Mendoza, Isaac J. Stopard, Ben Lambert, and Alejandro Zuretti. 2021. "A Dynamic Bayesian Model for Identifying High-Mortality Risk in Hospitalized COVID-19 Patients" Infectious Disease Reports 13, no. 1: 239-250. https://doi.org/10.3390/idr13010027
APA StyleMomeni-Boroujeni, A., Mendoza, R., Stopard, I. J., Lambert, B., & Zuretti, A. (2021). A Dynamic Bayesian Model for Identifying High-Mortality Risk in Hospitalized COVID-19 Patients. Infectious Disease Reports, 13(1), 239-250. https://doi.org/10.3390/idr13010027





