Simulating the Impact of Carbon Taxes on Greenhouse Gas Emission and Nutrition in the UK
Abstract
:1. Introduction
2. Literature Review
3. Data Used in the Analysis
3.1. Food Expenditure and Nutritional Data
3.2. Carbon Emissions Data
4. Methodology
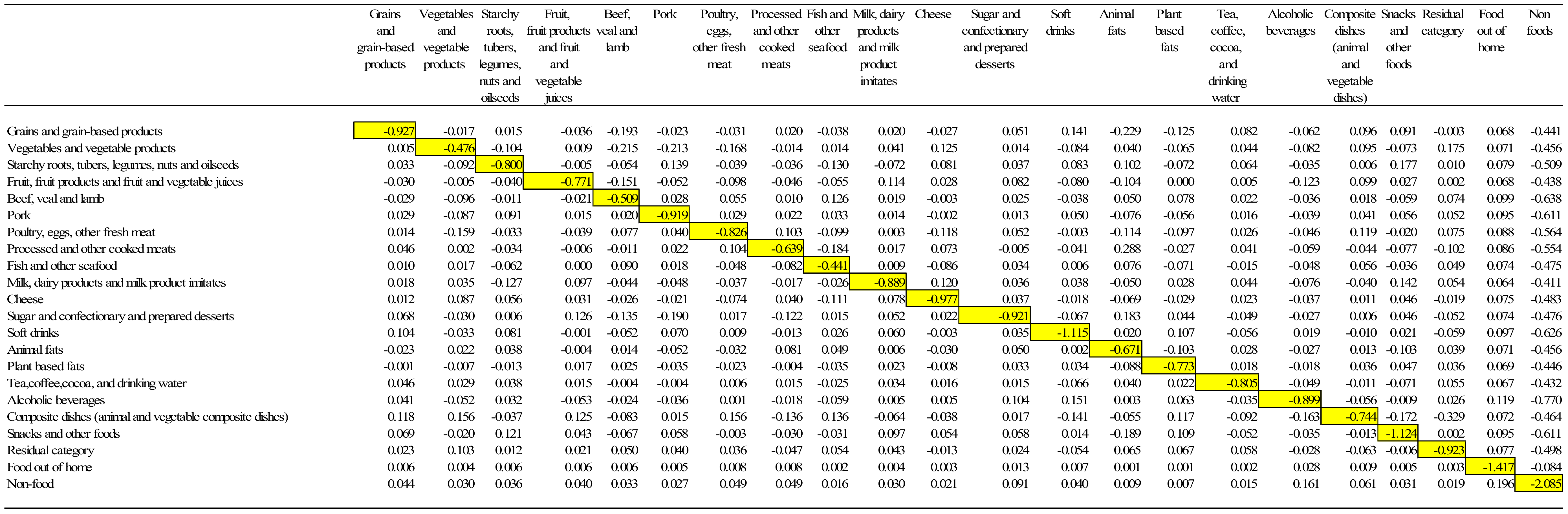
4.1. Estimation of the Demand Elasticities
- Homogeneity restriction implies constraints: . Thus, in each share equation, the price coefficients sum to zero.
- Symmetry restriction implies Hence, with J share equations (i.e., goods), there are J(J − 1)/2 such restrictions (i.e., the number of non-diagonal elements of a J × J matrix divided by 2).
- Adding-up restrictions imply that the sum of the J coefficients associated with the constant of each share equation (denoted ) is equal to unity; and the sum of the J coefficients associated with any other variable (i.e., price, socio-demographic, or expenditure) is equal to zero:
4.2. Ad Valorem and Carbon Consumption Taxes
4.3. Simulations of the Tax on Household Carbon Footprint and Nutrient Intake
5. Results and Discussion
5.1. Impact of Taxes on GHG Emissions
5.2. Impact of Taxes on Nutrition
5.3. Trade-Off between Nutrition and Environment under Different Taxes
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Group | Categories | Products inside the Categories |
|---|---|---|
| 1 | Grains and grain-based products | White bread, standard, sliced and unsliced; White bread, soft grain, sliced and unsliced; Brown bread, sliced and unsliced; Wholemeal and granary bread, sliced and unsliced; Rolls—white, brown or wholemeal; Malt bread and fruit loaves; Other breads; Flour; Crispbread; Oatmeal and oat products; Sweetened breakfast cereals; Other breakfast; Dried rice cereals; Cooked rice; Canned pasta; Dried and fresh pasta; Other cereal foods, frozen and not frozen. |
| 2 | Vegetables and vegetable products | Fresh cabbages; Fresh Brussels sprouts; Fresh cauliflower; Lettuce and leafy salads; Prepared lettuce salads; Other fresh green vegetables; Fresh carrots; Fresh turnips and swede; Other fresh root vegetables; Fresh onions, leeks and shallots; Fresh cucumbers; Fresh mushrooms; Fresh tomatoes; Fresh stem vegetables; Fresh marrow, courgettes, aubergine, pumpkin and other vegetables; Fresh herbs; Tomatoes, canned or bottled; Other canned beans and pulses; Other canned vegetables; Tomato puree and vegetable purees; Other frozen vegetables. |
| 3 | Starchy roots, tubers, legumes, nuts and oilseeds | Fresh new potatoes; Fresh baking potatoes; Other fresh potatoes; Chips—frozen or not frozen; Instant potato; Canned potatoes; Fresh peas; Fresh beans; Peas, canned; Baked beans in sauce; Peas, frozen; Beans, frozen; Nuts and edible seeds |
| 4 | Fruit, fruit products and fruit and vegetable juices | Fresh oranges; Other fresh citrus fruits; Fresh apples; Fresh pears; Fresh grapes; Other fresh soft fruit; Fresh bananas; Fresh melons; Other fresh fruit; Tinned peaches, pears and pineapples; All other tinned or bottled fruit; Dried fruit; Frozen strawberries, apple slices, peach halves, oranges and other frozen fruits; Pure fruit juices; Beef joints—boned and on the bone; Beef steak—less expensive; Beef steak—more expensive; Minced beef; All other beef and veal; Lamb joints; Lamb chops; All other lamb; All other liver; All offal other than liver. |
| 5 | Beef, veal and lamb | Beef joints—boned and on the bone; Beef steak—less expensive; Beef steak—more expensive; Minced beef; All other beef and veal; Lamb joints; Lamb chops; All other lamb; All other liver; All offal other than liver |
| 6 | Pork | Pork joints; Pork chops; Pork fillets and steaks; All other pork; Bacon and ham joints, uncooked; Bacon and ham rashers, uncooked |
| 7 | Poultry, eggs, other fresh meat | Chicken and turkey, cooked; Chicken, uncooked—whole chicken or chicken pieces; Turkey, uncooked—whole turkey or turkey pieces; Poultry other than chicken or turkey, uncooked; Other fresh, chilled and frozen meat; Eggs |
| 8 | Processed and other cooked meats | Bacon and ham, cooked; Corned beef, canned or sliced; Other cooked meat; Other canned meat and canned meat products; Sausages, uncooked—pork; Meat pies, pasties and puddings, frozen or not frozen; Burgers, frozen or not frozen; Pate; Meat pastes and spreads |
| 9 | Fish and other seafood | White fish, fresh or chilled; Herrings and other blue fish, fresh or chilled; Salmon, fresh or chilled; Shellfish, fresh or chilled; Salmon, tinned; Other tinned or bottled fish |
| 10 | Milk, dairy products and milk product imitates | UHT milk; Sterilised; Pasteurised/homogenised; Fully skimmed milk; Semi-skimmed milk; Condensed or evaporated milk; Yoghurt; Fromage frais; Cottage cheese; Soft natural cheese; Dried milk products; Milk drinks and other milks; Non-dairy milk substitutes; Canned or fresh carton custard |
| 11 | Cheese | Hard cheese—cheddar type; Hard cheese—other UK or foreign equivalent; Hard cheese—edam or other foreign; Processed cheese |
| 12 | Sugar and confectionary and prepared desserts | Sugar; Syrup, treacle; Honey; Cakes and pastries, not frozen; Buns, scones and teacakes; Chocolate biscuits; Sweet biscuits (not chocolate) and cereal bars; All canned milk puddings; Puddings; Cake, pudding and dessert mixes; Jelly squares or crystals; Ice cream tub or block; Ice cream cornets, choc-ices, lollies with ice cream; Ice lollies, sorbet, frozen mousse, frozen yoghurt; Jams and fruit curds; Marmalade; Artificial sweeteners; Chewing gum; Takeaway confectionery. |
| 13 | Soft drinks | Soft drinks, concentrated, not low calorie; Soft drinks, not concentrated, not low calorie; Soft drinks, not concentrated, low calorie |
| 14 | Animal fats | Cream; Butter; Lard, cooking fat; Suet and dripping |
| 15 | Plant based fats | Soft margarine; Other margarine; Olive oil; Other vegetable and salad oils; Peanut butter; Low fat spreads |
| 16 | Tea, coffee, cocoa and drinking water | Tea; Coffee beans and ground coffee; Instant coffee; Coffee essences; Cocoa and chocolate drinks; Malt drinks and chocolate versions of malted drinks; Fruit teas, instant tea, herbal tea, rosehip tea; Mineral or spring waters |
| 17 | Alcoholic beverages | Beers; Lagers and continental beers; Ciders and Perry; Champagne, sparkling wines and wine with mixer; Table wine; Fortified wines; Spirits; Liqueurs and cocktails |
| 18 | Composite dishes | Complete meat-based ready meals, frozen or not frozen; Ready meals and other fish products—frozen or not frozen; Ready meals and other vegetable products, frozen or not frozen; Quiches and flans, frozen and not frozen; Pizzas, frozen and not frozen; Meat pies, ready to eat; Sausage rolls, ready to eat; Other convenience meat products, frozen or not frozen; Soups—canned or cartons; Soups—dehydrated or powdered |
| 19 | Snacks and other foods | Crisps and potato snacks; Takeaway crisps, savoury snacks, popcorn, poppadums, prawn crackers; Cream crackers and other unsweetened biscuits; Other takeaway food brought home |
| 20 | Residual category | Invalid foods, slimming foods and sports foods; Salad dressings; Pickles; Sauces; Takeaway sauces and mayonnaise; Stock cubes and meat and yeast extracts; Salt; Vinegar; Spices and dried herbs; Bisto, gravy granules, stuffing mix, baking powder, yeast. |
| Categories | Elasticity |
|---|---|
| Grains and grain-based products | 0.2982 |
| Vegetables and vegetable products | 0.3088 |
| Starchy roots, tubers, legumes, nuts and oilseeds | 0.3447 |
| Fruit, fruit products and fruit and vegetable juices | 0.2962 |
| Beef, veal and lamb | 0.4320 |
| Pork | 0.4138 |
| Poultry, eggs, other fresh meat | 0.3820 |
| Processed and other cooked meats | 0.3749 |
| Fish and other seafood | 0.3214 |
| Milk, dairy products and milk product imitates | 0.2781 |
| Cheese | 0.3271 |
| Sugar and confectionary and prepared desserts | 0.3219 |
| Soft drinks | 0.4233 |
| Animal fats | 0.3083 |
| Plant based fats | 0.3018 |
| Tea, coffee, cocoa and drinking water | 0.2921 |
| Alcoholic beverages | 0.5208 |
| Composite dishes | 0.3141 |
| Snacks and other foods | 0.4137 |
| Residual category | 0.3370 |
| Food out of home | 1.1520 |
| Non-food | 2.4040 |


References
- World Meteorological Organization. Provisional WMO Statement on the Status of the Global Climate. 2016. Available online: http://public.wmo.int/en/media/press-release/provisional-wmo-statement-status-of-global-climate-2016 (accessed on 15 December 2016).
- Intergovernmental Panel on Climate Change IPCC. Fifth Assessment Synthesis Report: Summary for Policymakers. 2014. Available online: https://www.ipcc.ch/pdf/assessment-report/ar5/syr/AR5_SYR_FINAL_SPM.pdf (accessed on 15 December 2016).
- Audsley, E.; Brander, M.; Chatterton, J.C.; Murphy-Bokern, D.; Webster, C.; Williams, A.G. How Low Can We Go? An Assessment of Greenhouse Gas Emissions from the UK Food System and the Scope to Reduce Them by 2050; WWF-UK: Gland, Switzerland, 2009. [Google Scholar]
- Bingzhen, D.; Zhen, L.; de Groot, R.; Long, X.; Xiaochang, C.; Ruizi, W.; Chuanzhun, S.; Chao, W. Changing food consumption patterns and impact on water resources in the fragile grassland of Northern China. Sustainability 2015, 7, 5628–5647. [Google Scholar]
- World Health Organization. Diet, Nutrition and the Prevention of Chronic Diseases. 2003. Available online: http://apps.who.int/iris/bitstream/10665/42665/1/WHO_TRS_916.pdf (accessed on 15 December 2016).
- Briggs, A.D.M.; Kehlbacher, A.; Tiffin, R.; Garnett, T.; Rayner, M.; Scarborough, P. Assessing the impact on chronic disease of incorporating the societal cost of greenhouse gases into the price of food: An econometric and comparative risk assessment modelling study. BMJ Open 2013, 3, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Panzone, L.A.; Perino, G.S.; Swanson, T. Leung, D. Testing for the Best Instrument to Generate Sustainable Food Consumption. Int. J. Food Syst. Dyn. 2012, 2, 237–252. [Google Scholar]
- Mazzocchi, M.; Cagnone, S.; Bech-Larsen, T.; Niedźwiedzka, B.; Saba, A.; Shankar, B.; Verbeke, W.; Traill, W.B. What is the public appetite for healthy eating policies? Evidence from a cross-European survey. Health Econ. Policy Law 2015, 10, 267–292. [Google Scholar] [CrossRef] [PubMed]
- Mytton, O.T.; Clarke, D.; Rayner, M. Taxing unhealthy food and drinks to improve health. Br. Med. J. 2012, 15, 344–351. [Google Scholar] [CrossRef] [PubMed]
- Baumol, W.J. On taxation and the control of externalities. Am. Econ. Rev. 1972, 36, 307–322. [Google Scholar]
- Edjabou, L.; Smed, S. The effect of using consumption taxes on foods to promote climate friendly diets—The case of Denmark. Food Policy 2013, 39, 84–96. [Google Scholar] [CrossRef]
- García-Muros, X.; Markandya, A.; Romero-Jordán, D.; González-Eguino, M. The distributional effects of carbon-based food taxes. J. Clean. Prod. 2017, 140, 996–1006. [Google Scholar] [CrossRef]
- Defra. Family Food 2015. 2017. Available online: https://www.gov.uk/government/uploads/system/uploads/attachment_data/file/597667/Family_Food_2015-09mar17.pdf (accessed on 15 June 2017).
- EFSA Survey Details. MicroStrategy. 2017. Available online: https://dwh.efsa.europa.eu/bi/asp/Main.aspx?src=Main.aspx.2048001&evt=2048001&hiddensections=header%2Cpath%2CdockTop&documentID=D8333A2B48842E699881C7ABD939A1FB¤tViewMedia=8&visMode=0&Server=-Ua9CyBjZZt7uhDs5YGU9JVQclRg%3D&Port=-2GGlYxbTqwGp__US&Project=-ap8dUKIlSMMMc25PJi4N8wEJ7mb6UlCetqsSSLyLZxXLpEB-mAsG6wpKOqm-DnfT6uSh2NPk_gXXMo_Z&encryptedByRedir=true& (accessed on 15 June 2017).
- Public Health England. National Diet and Nutrition Survey. 2016. Available online: https://www.gov.uk/government/collections/national-diet-and-nutrition-survey (accessed on 15 June 2017).
- Hartikainen, H.; Pulkkinen, H. 2016 Summary of the chosen methodologies and practices to produce GHGE-estimates for an average European diet. In Natural Resources and Bioeconomy Studies 58/2016; Natural Resources Institute Finland: Helsinki, Finland, 2017. [Google Scholar]
- Lewbel, A.; Pendakur, K. Tricks with Hicks: The EASI demand system. Am. Econ. Rev. 2009, 99, 827–863. [Google Scholar] [CrossRef]
- Deaton, A.; Muellbauer, J. An Almost Ideal Demand System. Am. Econ. Rev. 1980, 70, 312–326. [Google Scholar]
- Pendakur, K. EASI Made Easier. In Quantifying Consumer Preferences (Contributions to Economic Analysis, Volume 288); Slottje, D.J., Ed.; Emerald Group Publishing Limited: Bingley, UK, 2009; Chapter 7; pp. 179–206. [Google Scholar]
- Carpentier, A.; Guyomard, H. Unconditional elasticities in two-stage demand systems: An approximate solution. Am. J. Agric. Econ. 2001, 83, 222–229. [Google Scholar] [CrossRef]
- The Scottish Index of Multiple Deprivation. Available online: http://www.gov.scot/Topics/Statistics/SIMD (accessed on 15 June 2017).
- Caillavet, F.; Fadhuile, A.; Nichelle, V. Taxing animal-based foods for sustainability: Environmental, nutritional and social perspectives in France. Eur. Rev. Agric. Econ. 2016, 43, 537–560. [Google Scholar] [CrossRef]
- Vieux, F.; Soler, L.; Touazi, D.; Darmon, N. High nutritional quality is not associated with low greenhouse gas emissions in self-selected diets of French adults. Am. J. Clin. Nutr. 2013, 97, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Huang, K.S. Nutrient elasticities in a complete food demand system. Am. J. Agric. Econ. 1996, 78, 21–29. [Google Scholar] [CrossRef]
- Lustig, R.H.; Schmidt, L.A.; Brindis, C.D. Public health: The toxic truth about sugar. Nature 2012, 482, 27–29. [Google Scholar] [CrossRef] [PubMed]



| Scenarios | Tax 1 | Tax 2 |
|---|---|---|
| Ad Valorem | per KgCO2 eq | |
| (%) | (per kg Product) 1/ | |
| 1. Beef and veal, other meats, not preserved | ||
| 1.1 Beef and veal, other meats, not preserved | 20 | Price(i) × 40 |
| 2. All meat and eggs (by KgCO2 eq per kg product) | ||
| 2.1 Beef and veal, other meats, not preserved | 20 | Price(i) × 40 |
| 2.2 Pork | 20 | Price(i) ×7.1 |
| 2.3 Processed and other cooked meats | 20 | Price(i) × 7.1 |
| 2.4 Poultry, eggs, other fresh meat | 20 | Price(i) × 4.3 |
| 3. All animal-based products (by KgCO2 eq per kg product) | ||
| 3.1 Beef and veal, other meats, not preserved | 20 | Price(i) × 40 |
| 3.2 Animal fats | 20 | Price(i) × 8.3 |
| 3.3 Cheese | 20 | Price(i) × 8.3 |
| 3.4 Pork | 20 | Price(i) × 7.1 |
| 3.5 Processed and other cooked meats | 20 | Price(i) × 7.1 |
| 3.6 Fish, seafood and their products | 20 | Price(i) × 5 |
| 3.7 Poultry, eggs, other fresh meat | 20 | Price(i) × 4.3 |
| 3.8 Milk, milk products | 20 | Price(i) × 2.3 |
| 4. All products (tax rate proportional to emissions per Kg of product, with varying rates) 2/ | ||
| 4.1 Beef and veal, other meats, not preserved | 30 | Price(i) × 40 |
| 4.2 Animal fats | 20 | Price(i) × 8.3 |
| 4.3 Cheese | 20 | Price(i) × 8.3 |
| 4.4 Pork | 20 | Price(i) × 7.1 |
| 4.5 Processed and other cooked meats | 20 | Price(i) × 7.1 |
| 4.6 Fish, seafood and their products | 20 | Price(i) × 5 |
| 4.7 Poultry, eggs, other fresh meat | 10 | Price(i) × 4.3 |
| 4.8 Plant based fats | 10 | Price(i) × 3.38 |
| 4.9 Milk, milk products | 10 | Price(i) × 2.3 |
| 4.10 Vegetables, fresh and processed | 10 | Price(i) × 2 |
| 4.11 Sweet products and substitutes | 10 | Price(i) × 1.6 |
| 4.12 Alcoholic beverages | 10 | Price(i) × 1.43 |
| 4.13 Cereals, cereal products and substitutes | 5 | Price(i) × 0.98 |
| 4.14 Potatoes, tubers, nuts, legumes and their products | 5 | Price(i) × 0.86 |
| 4.15 Fruit, fresh and processed | 5 | Price(i) × 0.71 |
| 4.16 Tea, coffee, cocoa, drinking water | 5 | Price(i) * 0.26 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Revoredo-Giha, C.; Chalmers, N.; Akaichi, F. Simulating the Impact of Carbon Taxes on Greenhouse Gas Emission and Nutrition in the UK. Sustainability 2018, 10, 134. https://doi.org/10.3390/su10010134
Revoredo-Giha C, Chalmers N, Akaichi F. Simulating the Impact of Carbon Taxes on Greenhouse Gas Emission and Nutrition in the UK. Sustainability. 2018; 10(1):134. https://doi.org/10.3390/su10010134
Chicago/Turabian StyleRevoredo-Giha, Cesar, Neil Chalmers, and Faical Akaichi. 2018. "Simulating the Impact of Carbon Taxes on Greenhouse Gas Emission and Nutrition in the UK" Sustainability 10, no. 1: 134. https://doi.org/10.3390/su10010134
APA StyleRevoredo-Giha, C., Chalmers, N., & Akaichi, F. (2018). Simulating the Impact of Carbon Taxes on Greenhouse Gas Emission and Nutrition in the UK. Sustainability, 10(1), 134. https://doi.org/10.3390/su10010134





