Study on Added-Value Sharing Ratio of Large EPC Hydropower Project Based on Target Cost Contract: A Perspective from China
Abstract
:1. Introduction
1.1. Project Delivery Methods and EPC
1.2. Literature Review
1.3. Uniqueness and Contributions
- (1)
- While DBB is a common project-delivery method adopted in China’s hydropower projects, EPC has not been widely used. Based on the current situation, the authors call for innovation on the contract payment method, and to use TCC to better incentivize the contractors’ motivation.
- (2)
- This paper identifies the added-value sharing ratio as the core element in the implementation of TCC and looks at the added-value sharing ratio closely, and builds a mathematical model based on the principle agent theory. The mathematical model can better investigate how the added-value sharing ratio is influenced by various factors, and how the added-value sharing ratio influences the owner, the contractor, and their relationship.
- (3)
- Since the added-value problem has many influencing factors, as a first step, this paper simplifies the model by assuming that the added value and the level of effort of the EPC contractor are discrete logical functions.
- (4)
- On the basis of the simplified model, the authors construct a principle-agent model considering various factors in continuous conditions. By calculating the partial derivatives of the mathematical equations with each variable, the authors can better observe the relationship between each factor and added-value sharing ratio.
- (5)
- Besides from getting insights from the mathematical model, the authors also give some suggestions on current practice in applying TCC in EPC hydropower projects in China.
2. Added-Value Sharing Problem of EPC Hydropower Projects
3. Sharing Ratio in Discrete Simplified Condition
3.1. Basic Assumptions
- (1)
- Suppose the project’s added value, , presents two states. When the actual cost is lower than or equal to the target cost , that is, , the project’s added value is positive. Otherwise, when the actual cost is higher than the target cost , i.e., , the project’s added value is negative.
- (2)
- Assume that the level of effort of the EPC general contractor in the contract performance process is , and it also has two states, positive effort and zero effort. When the EPC general contractor makes efforts to optimize the project for cost savings, it means that their effort is a positive effort, denoted as = 1. When the EPC general contractor does not make any effort in design optimization for cost saving, it indicates its effort level is zero, expressed as = 0. It is assumed that the total cost of the EPC general contractor due to positive effort is , and the total cost due to zero effort is .
- (3)
- Because the factors affecting the project’s added value are very complicated, positive added value may not necessarily be achieved when the EPC general contractor makes positive effort, and it is not necessarily impossible to achieve positive added value with zero effort, but the possibility of gaining positive added value is obviously much greater than zero effort. Based on past engineering experiences, it is possible to estimate the probability distribution of the EPC general contractor’s effort affecting the project’s added value. Here, suppose , , and .
- (4)
- Both the owner and the EPC general contractor are risk neutral, thus their utilities and their expected returns are equivalents.
- (5)
- Assume that the sharing ratio, denoted as , has only one value—that is, it is not set by segmentation.
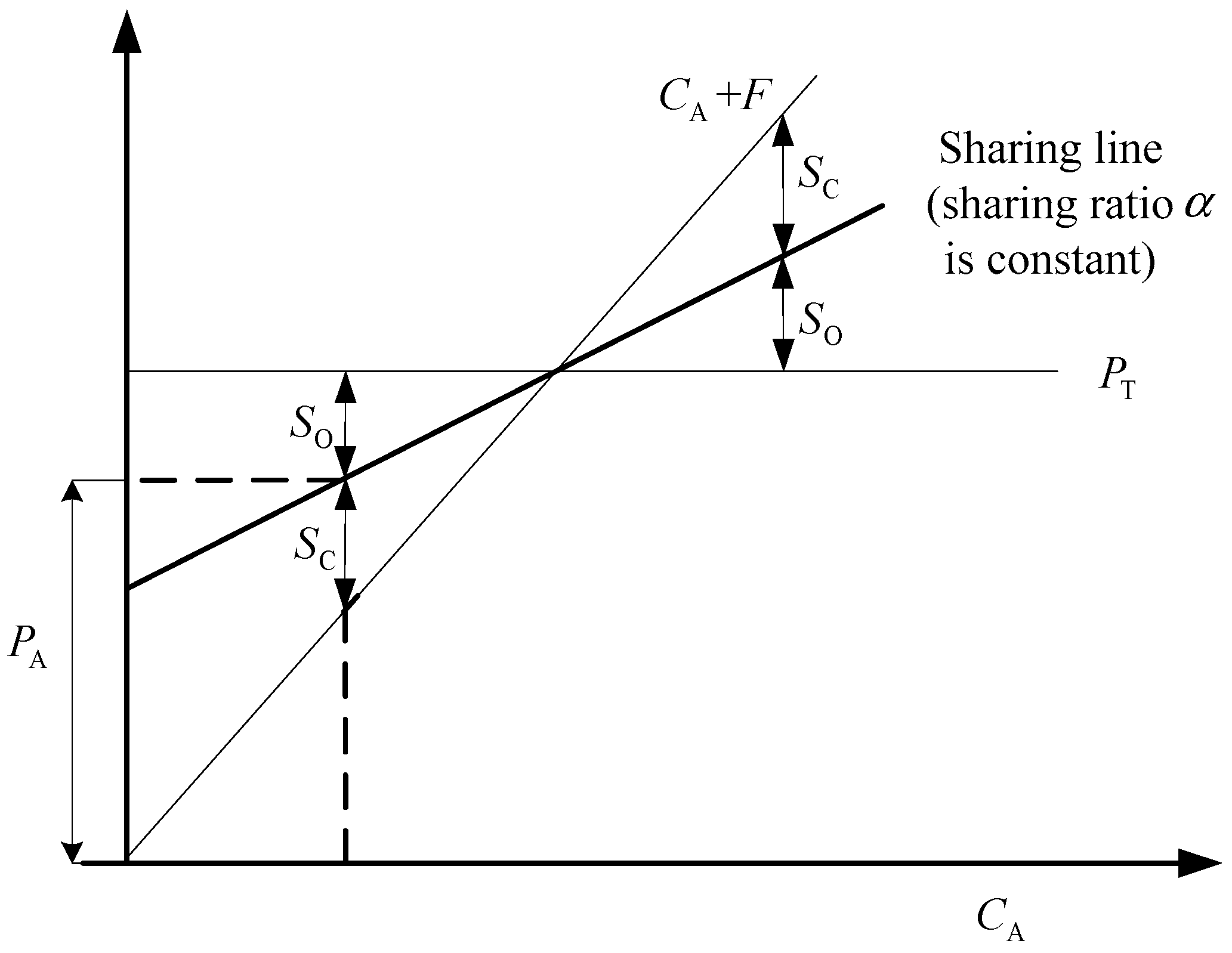
3.2. Added-Value Sharing Model
4. Sharing Ratio of Added Value in Continuous Condition
4.1. Principal-Agent Model in Continuous Condition
- , , in other words, cost savings are an increasing function of the level of effort of the EPC general contractor, but the marginal effects are decreasing;
- , meaning cost savings reach the maximum when the EPC general contractor makes the highest level of effort. That is to say, the potential added value comes true completely. Let be the potential EPC added value. Then, .
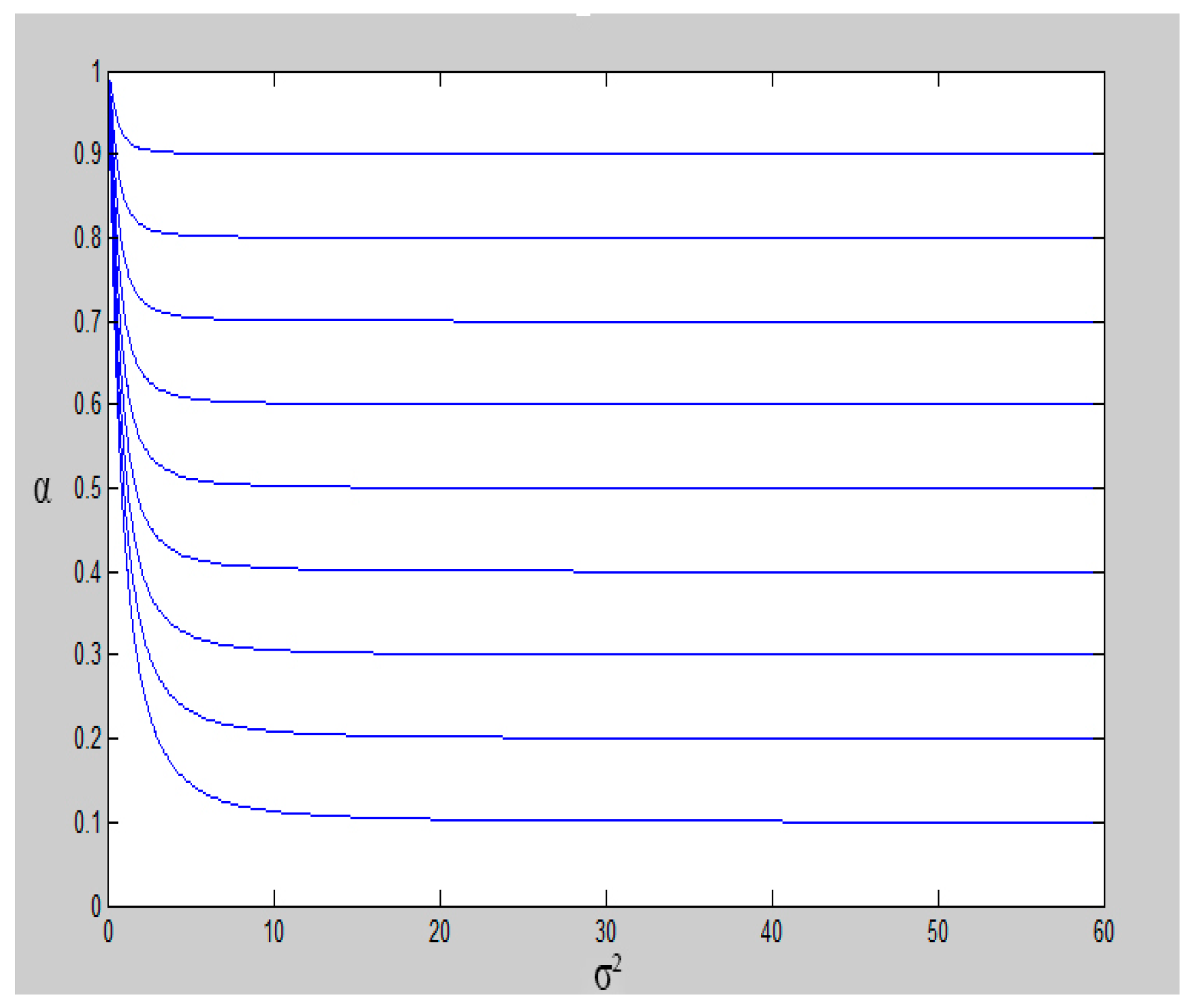
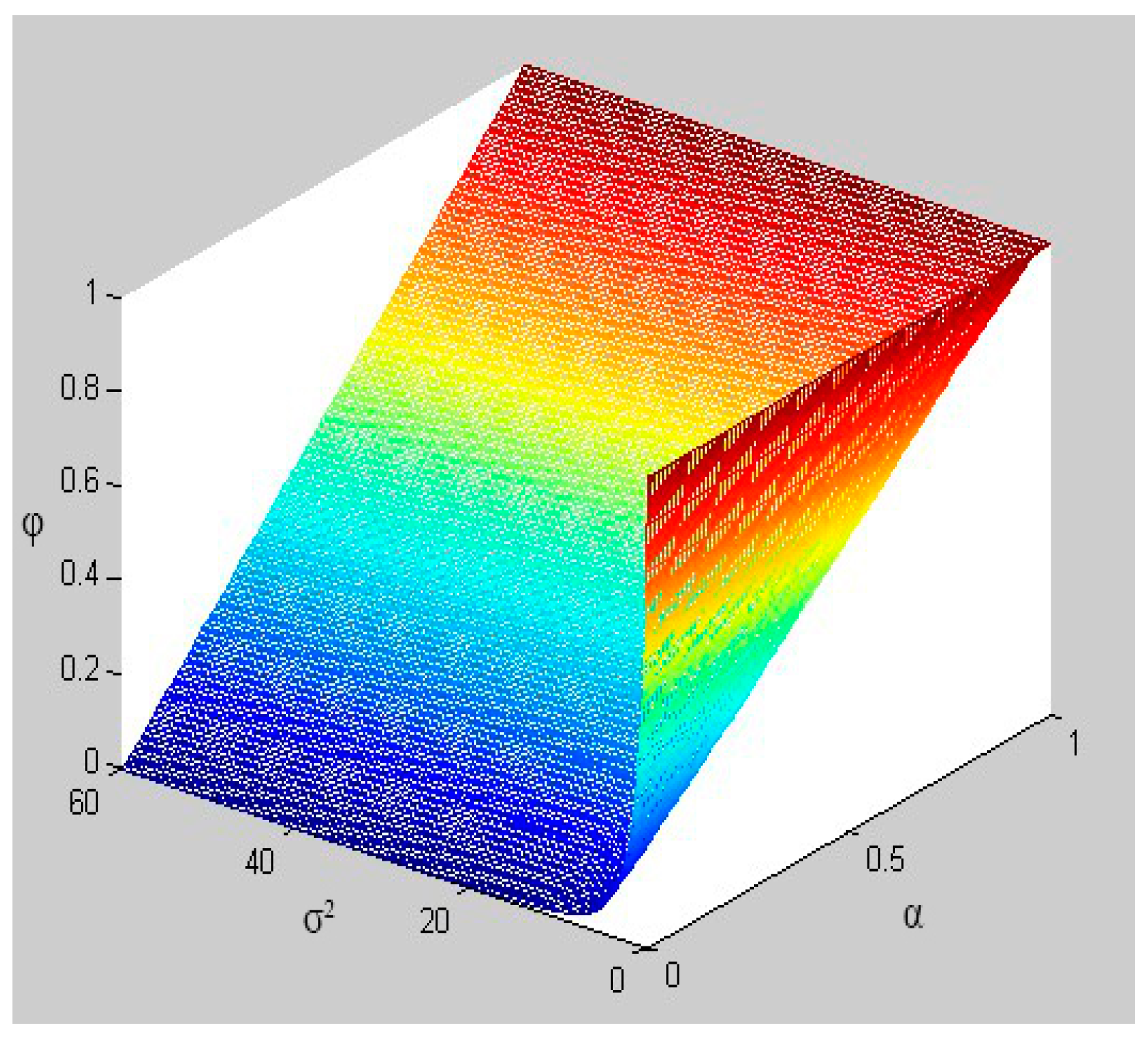
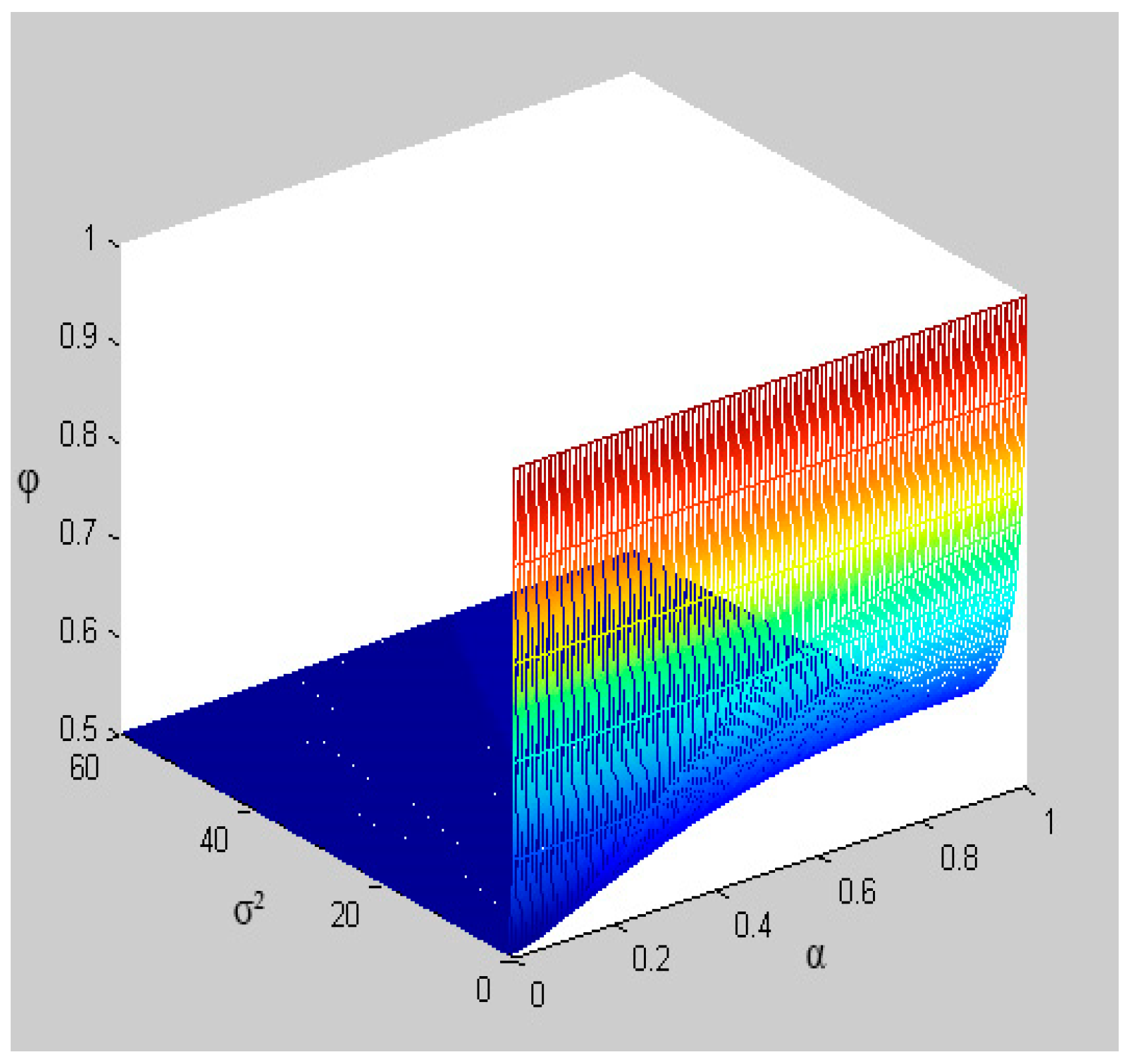
4.2. Analysis of Value-Added Sharing Ratio
- (1)
- The overrun risk degree of project cost, expressed by project cost variance . Obviously, the greater is, the greater the sharing ratio should be.
- (2)
- The owner’s risk aversion, denoted as . The bigger is, the bigger the value-added sharing ratio should be. That is to say, the worse the owner’s risk tolerance is, the smaller the share of risk the owner is willing to bear (negative added value). Thus, the owner tends to allow the EPC general contractor to get larger added-value sharing.
- (1)
- The greater the relative risk-aversion of the owner towards the EPC general contractor is, the greater the added-value sharing ratio will be. Compared with the EPC general contractor, if the owner’s relative risk-aversion is bigger, it means that the risk tolerance of the owner is worse in contrast to EPC general contractor. Thus, the owner is willing to bear less share of risk (negative added-value). Therefore, he would like to allow the EPC general contractor to get a larger added-value share.
- (2)
- The greater the relative effort cost coefficient of the EPC general contractor is, the greater the added-value sharing ratio should be. If the EPC general contractor’s relative effort cost coefficient is larger relative to the effort effect coefficient, it means that the EPC general contractor will take a higher cost to get the same effort effect. Therefore, if the owner cannot provide an added-value sharing ratio which is big enough, then the EPC general contractor tends to make less effort.
- (3)
- The greater the risk of cost overruns is, the smaller the added-value sharing ratio should be. As for an EPC hydropower project with a high risk of cost overruns, if the sharing ratio is big, it means that the EPC general contractor will take high risk, which may be beyond its risk-bearing capacity. Under this situation, the contractor may take measures to transfer the risk to the owner, thus causing damage to the owner’s interests. Therefore, it is not reasonable to set a big value for the sharing ratio when the risk of cost overruns is high.
5. Discussion on Actual Situation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.M.; López-Jiménez, P.A. Energy Recovery in Existing Water Networks: Towards Greater Sustainability. Water 2017, 9, 97. [Google Scholar] [CrossRef]
- Bernd, S. Current status and future prospects of hydropower in Saxony (Germany) compared to trends in Germany, the European Union and the World. Renew. Sustain. Energy Rev. 2014, 30, 518–525. [Google Scholar]
- National Bureau of Statistics of China. 2017. Available online: http://data.stats.gov.cn/ (accessed on 22 August 2018).
- China’s Hydropower Industry Chain is Speeding up to “Go Global”. 2015. Available online: http://finance.people.com.cn/n/2015/0520/c1004-27027018.html (accessed on 22 August 2018).
- Skitmore, R.M.; Marden, D.E. Which procurement system? Towards a universal procurement selection technique. Construct. Manag. Econ. 1998, 6, 71–89. [Google Scholar]
- Love, P.E.D.; Skitmore, R.M.; Earl, G. Selecting a suitable procurement method for a building project. Construct. Manag. Econ. 1998, 16, 221–233. [Google Scholar] [CrossRef]
- Wang, Z.F.; Yang, G.S.; Hong, W.M. Construction Project Transaction Theories and Modes; China Waterpower Press: Beijing, China, 2010. [Google Scholar]
- Ding, J.Y.; Wang, Z.F.; Anumba, C.; Wang, D.G. A review of research on delivery methods and project performance of construction projects. China Civ. Eng. J. 2014, 47, 131–144. [Google Scholar]
- Ding, J.Y.; Wang, N.; Hu, L.C. Framework for designing project delivery and contract strategy in Chinese construction industry based on value-added analysis. Adv. Civ. Eng. 2018, 2018, 5810357. [Google Scholar] [CrossRef]
- Ding, J.Y.; Wang, Z.F.; Ling, Y.M.X.; Ren, X.Q. Innovation and key scientific issues of China’s general contracting transaction model in water conservancy project. J. Econ. Water Resour. 2016, 34, 33–37, 80. [Google Scholar]
- An, X.W.; Wang, Z.F.; Ding, J.Y.; Li, H.M. Negotiation model of union general contracting project optimization profit distribution. Syst. Eng. Theory Pract. 2018, 38, 1183–1192. [Google Scholar]
- Wang, T.F.; Tang, W.Z.; Du, L.; Duffield, C.F.; Wei, Y. Relationships among risk management, partnering, and contractor capability in international EPC project delivery. J. Manag. Eng. 2016, 32, 04016017. [Google Scholar] [CrossRef]
- Galloway, P. Design-build/EPC contractor’s heightened risk changes in a changing world. J. Leg. Aff. Disput. Resolut. Eng. Construct. 2009, 1, 7–15. [Google Scholar] [CrossRef]
- Hohai University. Research Report of the Management Guidelines for Guangdong EPC Water Conservancy and Hydropower Projects; Hohai University: Nanjing, China, 2011. [Google Scholar]
- Bian, L.M. Problems and Countermeasures in the Application of EPC General Contracting Mode in Water Conservancy Project Construction; Guangdong Water Resources and Hydropower: Dongguan, China, 2013; pp. 73–75. [Google Scholar]
- Zhang, K.; Wang, Z.F.; Ding, J.Y. Discussion on the valuation method of standardized general contract conditions. J. Civ. Eng. Manag. 2014, 31, 98–102. [Google Scholar]
- Cai, S.K. Theory and practice of EPC general contracting project management in hydropower engineering. J. Tianjin Univ. 2008, 1091–1095. [Google Scholar] [CrossRef]
- Shorney-Darby, H.L. Design-Build for Water and Waste-Water Projects; American Water Works Association: Denver, CO, USA, 2012. [Google Scholar]
- Feng, J.C.; Qian, Y.; Zhao, J. Empirical study of developmental dynamic on hydraulic engineering general-contract mode. J. Hydroelectr. Eng. 2014, 33, 227–233. [Google Scholar]
- Wang, Z.F.; Ding, J.Y.; Wang, D.G.; Zhu, Y.C. Decision-making analysis framework for application of lump-sum contracting to hydropower projects from value-added perspective. J. Hydroelectr. Eng. 2014, 33, 317–323, 330. [Google Scholar]
- Jian, Y.H.; Zhang, Y. A study of the general contract delivery method of the water conservancy project with intuitionistic fuzzy IFWA operator. China Rural Water Hydropower 2012, 2, 142–145, 148. [Google Scholar]
- Zhao, M.L.; Chen, J.; Yi, X. Risk management on theory of TOC and SPA in hydropower engineering EPC program. J. Civ. Eng. Manag. 2017, 34, 103–107. [Google Scholar]
- Parrod, N.; Thierry, C.; Fargier, H. Cooperative subcontracting relationship within a project supply chain: A simulation approach. Simul. Model. Pract. Theory 2007, 15, 137–152. [Google Scholar] [CrossRef]
- Guan, B.H.; Hu, P. Interest distribution mechanism of the general contractor in repetitive cooperation consortium project. J. Syst. Manag. 2009, 18, 172–176. [Google Scholar]
- Zhang, Y.; Lv, P.; Song, Y.Q. Research on profit distribution model of supply chain in general contracting construction projects. Chin. J. Manag. Sci. 2011, 19, 98–104. [Google Scholar]
- Hu, W.F.; Zhu, Y.; He, X.H. Multi-level benefit distribution and incentive mechanism for engineering project contractors. J. Tongji Univ. (Nat. Sci.) 2014, 42, 1437–1443. [Google Scholar]
- Rusk, J. Target Cost Contracts. Available online: http://www.agilekiwi.com/estimationandpricing/target-cost-contracts/ (accessed on 30 July 2018).
- Chan, D.W.M.; Chan, A.P.C.; Lam, P.T.I. Risk ranking and analysis in target cost contracts: Empirical evidence from the construction industry. Int. J. Proj. Manag. 2011, 29, 751–763. [Google Scholar] [CrossRef] [Green Version]
- Yan, M.H. Research on Engineering Project Cost Management System Based on Target Cost Contract; Tianjin University: Tianjin, China, 2011. [Google Scholar]
- Gandhi, D.K. A strategy for risk reduction in incentive contracting. Decis. Sci. 1979, 10, 371–385. [Google Scholar] [CrossRef]
- Chen, X.X. Economic Analysis of Project Management; China Economic Publishing House: Beijing, China, 2006. [Google Scholar]
- Cao, J.; Yang, C.J.; Li, P.; Zhou, G.G. Research on linear separation contract design of supply chain under asymmetric information. Chin. J. Manag. Sci. 2009, 12, 19–30. [Google Scholar]
- Wen, S.B.; Yang, W.; Li, C.Z. Research on the design of incentive mechanism under information asymmetry. J. Chongqing Univ. Soc. Ed. 1999, 5, 127–129. [Google Scholar]
- Bidding Documents for the Comprehensive Improvement Project of Water Environment in Mazhou River Basin (Baoan Area) in Shenzhen City of China. 2016. Available online: http://www.bidcenter.com.cn/news-23676674-1.html (accessed on 20 May 2016).


| Authors | Topics and Methods |
|---|---|
| Cai [17] | Theories and practices of EPC hydropower project management, including supervision system under EPC model, the management contents and tasks of general contractors and owners, and risk analysis, etc. Theoretic analysis and case studies. |
| Shorney-Darby et al. [18] | DB method applied to water/wastewater projects. Collection of 30 articles which can provides a basic template of how DB projects can be planned, procured and executed. |
| Feng et al. [19] | Driving factors for the development of general contracting modes including EPC in the water conservancy project. Value chain theory and SEM (Structural Equation Modeling). |
| Wang et al. [20] | Value-added approach for the adoption of general contracting modes including EPC in hydropower projects. Value-added analysis matrix. |
| Jian et al. [21] | Selection of general contracting delivery methods for hydropower projects. Intuition fuzzy selection method. |
| Zhao et al. [22] | Risk Identification of EPC hydropower projects. TOC (Theory of Constraints) and SPA (Set Pair Analysis). |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, J.; Chen, C.; An, X.; Wang, N.; Zhai, W.; Jin, C. Study on Added-Value Sharing Ratio of Large EPC Hydropower Project Based on Target Cost Contract: A Perspective from China. Sustainability 2018, 10, 3362. https://doi.org/10.3390/su10103362
Ding J, Chen C, An X, Wang N, Zhai W, Jin C. Study on Added-Value Sharing Ratio of Large EPC Hydropower Project Based on Target Cost Contract: A Perspective from China. Sustainability. 2018; 10(10):3362. https://doi.org/10.3390/su10103362
Chicago/Turabian StyleDing, Jiyong, Chen Chen, Xiaowei An, Na Wang, Wujuan Zhai, and Chenhao Jin. 2018. "Study on Added-Value Sharing Ratio of Large EPC Hydropower Project Based on Target Cost Contract: A Perspective from China" Sustainability 10, no. 10: 3362. https://doi.org/10.3390/su10103362
APA StyleDing, J., Chen, C., An, X., Wang, N., Zhai, W., & Jin, C. (2018). Study on Added-Value Sharing Ratio of Large EPC Hydropower Project Based on Target Cost Contract: A Perspective from China. Sustainability, 10(10), 3362. https://doi.org/10.3390/su10103362






