Big Geospatial Data Analytics for Global Mangrove Biomass and Carbon Estimation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.2. Methods
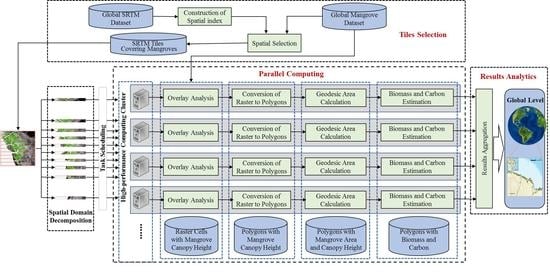
2.2.1. Selection of SRTM Tiles
2.2.2. Extraction of Mangrove Canopy Height
2.2.3. Calculation of Mangrove Area
2.2.4. The Estimation of Biomass and Carbon in Mangrove Forest
2.2.5. Parallel Computing for Accelerated Geospatial Analysis of Mangrove Data
3. Results
3.1. Parallel Computing Performance
3.2. Estimation Results of Global Mangrove Area, Biomass and Carbon
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Country | Fatoyinbo and Simard (2013) | This Study | ||||
|---|---|---|---|---|---|---|
| Area | Total AGB | Mean Biomass | Area | Total AGB | Mean Biomass | |
| (km2) | (Mg) | (Mg ha−1) | (km2) | (Mg) | (Mg ha−1) | |
| Angola | 154 | 1,441,200 | 93 | 295.57 | 3,626,791.37 | 122.70 |
| Benin | 18 | 137,719 | 76 | 30.76 | 214,831.39 | 69.84 |
| Cameroon | 1483 | 25,334,900 | 171 | 2122.16 | 38,866,367.62 | 183.15 |
| Congo | 15 | 267,603 | 178 | - | - | - |
| Côte d’Ivoire | 32 | 406,516 | 124 | 39.67 | 553,696.47 | 139.59 |
| Djibouti | 17 | 1,653,170 | 90 | 5.41 | 61,204.65 | 113.19 |
| DRC | 183 | 51,570 | 140 | 212.83 | 2,250,885.94 | 105.76 |
| Egypt | 1 | 8344 | 117 | 0.33 | 1923.45 | 58.14 |
| Equatorial Guinea | 181 | 2,922,420 | 161 | 220.06 | 3,960,141.62 | 179.96 |
| Eritrea | 49 | 640,038 | 129 | 46.90 | 443,969.75 | 94.67 |
| Gabon | 1457 | 23,840,000 | 162 | 1526.49 | 26,882,131.01 | 176.10 |
| Gambia | 519.11 | 5,509,300 | 106 | 666.14 | 5,694,597.99 | 85.49 |
| Ghana | 76 | 742,925 | 97 | 71.91 | 547,573.70 | 76.15 |
| Guinea | 1889 | 18,153,800 | 108 | 2286.30 | 22,873,857.63 | 100.05 |
| Guinea Bissau | 2806 | 31,712,300 | 113 | 2715.50 | 30,303,032.21 | 111.59 |
| Kenya | 192 | 2,294,820 | 119 | 381.96 | 3,580,841.84 | 93.75 |
| Liberia | 189 | 2,141,860 | 113 | 94.47 | 961,997.24 | 101.83 |
| Madagascar | 2059 | 24,856,900 | 121 | 2314.22 | 29,867,914.35 | 129.06 |
| Mauritania | 0.4 | 4156 | 95 | 0.51 | 4141.48 | 81.99 |
| Mozambique | 3054 | 30,974,100 | 101 | 2901.51 | 30,887,485.61 | 106.45 |
| Nigeria | 8573 | 94,788,000 | 111 | 6136.63 | 75,061,148.06 | 122.32 |
| Senegal | 1200 | 11,462,100 | 95 | 1197.74 | 9,149,049.33 | 76.39 |
| Sierra Leone | 955 | 10,655,600 | 112 | 1365.66 | 14,065,427.62 | 102.99 |
| Somalia | 30 | 436,907 | 143 | 17.36 | 136,751.57 | 78.79 |
| Sudan | 4 | 135,626 | 113 | 2.49 | 16,510.70 | 66.32 |
| South Africa | 12 | 40,018 | 100 | 16.96 | 225,023.10 | 132.71 |
| Togo | 2 | 15,861 | 78 | 4.74 | 36,790.55 | 77.68 |
| Tanzania | 809 | 11,037,800 | 136 | 966.45 | 13,493,199.77 | 139.62 |
| Africa | 25,960 | 301,665,553 | 116 | 25,640.71 | 313,767,286.04 | 122.37 |
References
- Alongi, D.M. Mangrove forests: Resilience, protection from tsunamis, and responses to global climate change. Estuar. Coast. Shelf Sci. 2008, 76, 1–13. [Google Scholar] [CrossRef]
- Donato, D.C.; Kauffman, J.B.; Murdiyarso, D.; Kurnianto, S.; Stidham, M.; Kanninen, M. Mangroves among the most carbon-rich forests in the tropics. Nat. Geosci. 2011, 4, 293–297. [Google Scholar] [CrossRef]
- Alongi, D.M. Carbon cycling and storage in mangrove forests. Annu. Rev. Mar. Sci. 2014, 6, 195–219. [Google Scholar] [CrossRef] [PubMed]
- Pendleton, L.; Donato, D.C.; Murray, B.C.; Crooks, S.; Jenkins, W.A.; Sifleet, S.; Craft, C.; Fourqurean, J.W.; Kauffman, J.B.; Marbà, N. Estimating global “blue carbon” emissions from conversion and degradation of vegetated coastal ecosystems. PLoS ONE 2012, 7, e43542. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fatoyinbo, T.E.; Simard, A.M. Height and biomass of mangroves in Africa from ICESat/GLAS and SRTM. Int. J. Remote Sens. 2013, 34, 668–681. [Google Scholar] [CrossRef]
- Saenger, P.; Hegerl, E.; Davie, J.D. Global Status of Mangrove Ecosystems; International Union for Conservation of Nature and Natural Resources: Gland, Switzerland, 1983. [Google Scholar]
- Saenger, P.; Snedaker, S.C. Pantropical trends in mangrove above-ground biomass and annual litterfall. Oecologia 1993, 96, 293–299. [Google Scholar] [CrossRef] [PubMed]
- Stringer, C.E.; Trettin, C.C.; Zarnoch, S.J.; Tang, W. Carbon stocks of mangroves within the Zambezi River Delta, Mozambique. For. Ecol. Manag. 2015, 354, 139–148. [Google Scholar] [CrossRef]
- Kauffman, J.B.; Donato, D. Protocols for the Measurement, Monitoring and Reporting of Structure, Biomass and Carbon Stocks in Mangrove Forests; Center for International Forestry Research (CIFOR): Bogor, Indonesia, 2012. [Google Scholar]
- Twilley, R.; Chen, R.; Hargis, T. Carbon sinks in mangroves and their implications to carbon budget of tropical coastal ecosystems. Water Air Soil Pollut. 1992, 64, 265–288. [Google Scholar] [CrossRef]
- Sanders, C.J.; Maher, D.T.; Tait, D.R.; Williams, D.; Holloway, C.; Sippo, J.Z.; Santos, I.R. Are global mangrove carbon stocks driven by rainfall? J. Geophys. Res. Biogeosci. 2016, 121, 2600–2609. [Google Scholar] [CrossRef]
- Giri, C.; Ochieng, E.; Tieszen, L.L.; Zhu, Z.; Singh, A.; Loveland, T.; Masek, J.; Duke, N. Status and distribution of mangrove forests of the world using earth observation satellite data. Glob. Ecol. Biogeogr. 2011, 20, 154–159. [Google Scholar] [CrossRef]
- Tang, W.; Feng, W.; Jia, M.; Shi, J.; Zuo, H.; Trettin, C.C. The assessment of mangrove biomass and carbon in West Africa: A spatially explicit analytical framework. Wetl. Ecol. Manag. 2016, 24, 153–171. [Google Scholar] [CrossRef]
- Hutchison, J.; Manica, A.; Swetnam, R.; Balmford, A.; Spalding, M. Predicting global patterns in mangrove forest biomass. Conserv. Lett. 2014, 7, 233–240. [Google Scholar] [CrossRef]
- Spalding, M. World Atlas of Mangroves; Earthscan: London, UK, 2010. [Google Scholar]
- Fatoyinbo, T.E.; Simard, M.; Washington-Allen, R.A.; Shugart, H.H. Landscape-scale extent, height, biomass, and carbon estimation of Mozambique’s mangrove forests with Landsat ETM+ and Shuttle Radar Topography Mission elevation data. J. Geophys. Res. Biogeosci. 2008, 113. [Google Scholar] [CrossRef]
- Manyika, J.; Institute, M.G.; Chui, M.; Brown, B.; Bughin, J.; Dobbs, R.; Roxburgh, C.; Byers, A.H. Big Data: The Next Frontier for Innovation, Competition, and Productivity; McKinsey Global Institute: Washington, DC, USA, 2011. [Google Scholar]
- Tang, W.; Feng, W. Parallel map projection of vector-based big spatial data: Coupling cloud computing with graphics processing units. Comput. Environ. Urban Syst. 2017, 61, 187–197. [Google Scholar] [CrossRef]
- Yang, C.; Huang, Q.; Li, Z.; Liu, K.; Hu, F. Big Data and cloud computing: Innovation opportunities and challenges. Int. J. Digit. Earth 2017, 10, 13–53. [Google Scholar] [CrossRef]
- Lu, D. The potential and challenge of remote sensing-based biomass estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- Samet, H. Foundations of Multidimensional and Metric Data Structures; MOrgan Kaufmann: San Francisco, CA, USA, 2006. [Google Scholar]
- Eldawy, A.; Mokbel, M.F. A demonstration of spatialhadoop: An efficient mapreduce framework for spatial data. Proc. VLDB Endow. 2013, 6, 1230–1233. [Google Scholar] [CrossRef]
- Li, Z.; Hu, F.; Schnase, J.L.; Duffy, D.Q.; Lee, T.; Bowen, M.K.; Yang, C. A spatiotemporal indexing approach for efficient processing of big array-based climate data with MapReduce. Int. J. Geogr. Inf. Sci. 2017, 31, 17–35. [Google Scholar] [CrossRef]
- Tang, W. Parallel construction of large circular cartograms using graphics processing units. Int. J. Geogr. Inf. Sci. 2013, 27, 2182–2206. [Google Scholar] [CrossRef]
- Hamilton, S.E.; Collins, S. Livelihood responses to mangrove deforestation in the northern provinces of Ecuador. Bosque 2013, 34. [Google Scholar] [CrossRef]
- Torge, W.; Müller, J. Geodesy; Walter de Gruyter: Berlin, Germany, 2012. [Google Scholar]
- Komiyama, A.; Ong, J.E.; Poungparn, S. Allometry, biomass, and productivity of mangrove forests: A review. Aquat. Bot. 2008, 89, 128–137. [Google Scholar] [CrossRef]
- Atkins, D. Revolutionizing Science and Engineering through Cyberinfrastructure: Report of the National Science Foundation Blue-Ribbon Advisory Panel on Cyberinfrastructure; The University of Arizona Libraries: Tucson, AZ, USA, 2003. [Google Scholar]
- National Science Foundation (NSF). Cyberinfrastructure Vision for 21st Century Discovery; Report of NSF Council; Cyberinfrastructure Council, NSF: North Arlington, VA, USA, 2007.
- Wilkinson, B.; Allen, M. Parallel Programming: Techniques and Applications Using Networked Workstations and Parallel Computers, 2nd ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- Tang, W.; Jia, M. Global sensitivity analysis of a large agent-based model of spatial opinion exchange: A heterogeneous multi-GPU acceleration approach. Ann. Assoc. Am. Geogr. 2014, 104, 485–509. [Google Scholar] [CrossRef]
- Ding, Y.; Densham, P.J. Spatial strategies for parallel spatial modelling. Int. J. Geogr. Inf. Syst. 1996, 10, 669–698. [Google Scholar] [CrossRef]
- Trettin, C.C.; Stringer, C.E.; Zarnoch, S.J. Composition, biomass and structure of mangroves within the Zambezi River Delta. Wetl. Ecol. Manag. 2016, 24, 173–186. [Google Scholar] [CrossRef]
- Trettin, C.C.; Stringer, C.E.; Zarnoch, S.J.; Tang, W.; Dai, Z. Mangrove Carbon Stocks in Zambezi River Delta, Mozambique; Forest Service Research Data Archive: Fort Collins, CO, USA, 2017.
- Lefsky, M.A.; Harding, D.J.; Keller, M.; Cohen, W.B.; Carabajal, C.C.; Del Bom Espirito, F.; Hunter, M.O.; de Oliveira, R. Estimates of forest canopy height and aboveground biomass using ICESat. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Zhang, G.; Ganguly, S.; Nemani, R.R.; White, M.A.; Milesi, C.; Hashimoto, H.; Wang, W.; Saatchi, S.; Yu, Y.; Myneni, R.B. Estimation of forest aboveground biomass in California using canopy height and leaf area index estimated from satellite data. Remote Sens. Environ. 2014, 151, 44–56. [Google Scholar] [CrossRef]
- Hey, T.; Tansley, S.; Tolle, K. (Eds.) The Fourth Paradigm: Data Intensive Scientific Discovery; Microsoft Research: Redmond, WA, USA, 2009. [Google Scholar]









| Dataset | Year | Links | Type | Data Size | Spatial Resolution |
|---|---|---|---|---|---|
| Shuttle Radar Topography Mission (SRTM) 1 Arc-Second Global DEM | 2000 | https://lta.cr.usgs.gov/SRTM1Arc | Raster (GeoTIFF) | 315 GB | 30 m |
| Global Mangrove Coverage | 2000 | http://data.unep-wcmc.org/datasets/4 | Vector (Shapefile) | 0.9 GB | - |
| Global Administrative Area data for country boundary | 2015 | http://www.gadm.org/ | Vector (Shapefile) | 1.96 GB | - |
| Year | Area (km2) | Aboveground Biomass (Pg) | Belowground Biomass (Pg) | Carbon (Pg C) | |
|---|---|---|---|---|---|
| This Study | 2000 | 130,420 | 1.908 | 0.725 | 1.32 |
| Twilley et al. (1992) | 1986 | 240,000 | 2.34 | 1.69 | - |
| Giri et al. (2011) | 2000 | 137,760 | - | - | - |
| Alongi (2014) | 2000 | 138,000 | - | - | 1.82 |
| Hutchison et al. (2014) | 1999–2003 | 153,141 | 2.83 | 1.11 | - |
| Sanders et al. (2016) | 2000 | 137,760 | - | - | 1.568 |
| Country | This Study | Hutchison et al. (2014) | ||||
|---|---|---|---|---|---|---|
| Aboveground Biomass | Belowground Biomass | Total Carbon | Area | Aboveground Biomass | Area | |
| (Pg) | (Pg) | (Pg C) | (km2) | (Pg) | (km2) | |
| Indonesia | 0.511 | 0.194 | 0.35 | 26,422 | 0.729 | 29,865 |
| Brazil | 0.167 | 0.063 | 0.115 | 10,145 | 0.227 | 13,480 |
| Australia | 0.106 | 0.04 | 0.073 | 9283 | 0.085 | 6322 |
| Mexico | 0.072 | 0.027 | 0.05 | 6528 | 0.135 | 9644 |
| Nigeria | 0.075 | 0.029 | 0.052 | 6137 | 0.152 | 7789 |
| Malaysia | 0.089 | 0.034 | 0.061 | 5455 | 0.179 | 7097 |
| Papua New Guinea | 0.098 | 0.037 | 0.068 | 4515 | 0.099 | 4186 |
| Myanmar | 0.058 | 0.022 | 0.04 | 4469 | 0.089 | 5143 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, W.; Zheng, M.; Zhao, X.; Shi, J.; Yang, J.; Trettin, C.C. Big Geospatial Data Analytics for Global Mangrove Biomass and Carbon Estimation. Sustainability 2018, 10, 472. https://doi.org/10.3390/su10020472
Tang W, Zheng M, Zhao X, Shi J, Yang J, Trettin CC. Big Geospatial Data Analytics for Global Mangrove Biomass and Carbon Estimation. Sustainability. 2018; 10(2):472. https://doi.org/10.3390/su10020472
Chicago/Turabian StyleTang, Wenwu, Minrui Zheng, Xiang Zhao, Jiyang Shi, Jianxin Yang, and Carl C. Trettin. 2018. "Big Geospatial Data Analytics for Global Mangrove Biomass and Carbon Estimation" Sustainability 10, no. 2: 472. https://doi.org/10.3390/su10020472
APA StyleTang, W., Zheng, M., Zhao, X., Shi, J., Yang, J., & Trettin, C. C. (2018). Big Geospatial Data Analytics for Global Mangrove Biomass and Carbon Estimation. Sustainability, 10(2), 472. https://doi.org/10.3390/su10020472