Actual and Balanced Stand Structure: Examples from Beech-Fir-Spruce Old-Growth Forests in the Area of the Dinarides in Bosnia and Herzegovina

Abstract

Old-growth forests are spontaneously developed forest ecosystems without direct human influence in which only natural processes take place. In this study we analyzed the structural sustainability of beech-fir-spruce old-growth forests on dolomite and limestone in the Bosnian Dinaric Mountains. The field work was carried out on permanent experimental plots of 1.0 hectare in size. Thereby, the diameters (d_1.30) and the height (h) of all trees within the plots were measured. Based on the available literature, we hypothesized that the structure of old-growth forests provides sustainability through tree-size demographic equilibrium. Thus, the data collected were used to test possible differences between the actual and the theoretically balanced structure in the studied old-growth forests. Statistically significant difference in the actual structure between the two old-growth forests on limestone and dolomite was determined. However, both of them exhibited sustainable diameter distributions. These results point to the importance of preserving old-growth forests for future research as they exemplify the tree-size demographic sustainability and can thus serve as an appropriate reference to managed forests. Concretely, certain structural attributes from old-growth forests could be embedded into the management objectives for increased resilience of managed forests.

1. Introduction

Sustainability in forestry was first mentioned in 1713 by Hans Carl von Carlowitz [1] and was first defined by Georg-Ludwig Hartig at the end of the 18th century [2]: “All wise foresters use the woods as much as possible, but in such a way that later generations will be able to derive at least as much benefit from them as the present generation claims for itself”. The concept of sustainable, natural and diverse forests has evolved from the idea of sustainability. It is in terms of research into the development process and structure best represented by old-growth forests. The application of natural principles in the managed beech-fir-spruce forests should provide sustainability at the landscape scale. These forests, if they are in equilibrium (close to normal) by composition and structure, express the naturalness, stability and dynamics of the processes similar to those in old-growth forests. Therefore, the application of close-to-nature silviculture as a concept has long been known in forestry [3] and enables the sustainable development of forest ecosystems on the basis of natural processes [4].

The notion of the balanced forest structure in European forestry appeared at the beginning of practical application of selection management system and it refers to sustainable tree-size structure of selection forests. The constant availability of different-sized wood products from selection forests requires adequate distribution of wood volume or the number of trees through the whole range of diameter classes [5,6]. In defining the normal state, some authors have also used the amount of volume increment [7,8], the value of the increment [9,10] or the yield [11]. Mitscherlich [12] considered the normal state of a selection forest to be the state in which the most valuable increment is achieved based on the quantity of assortments and the prices on the timber market. In most cases, especially if the balanced state is determined based on the number of trees and volume, the basis is the diameter structure which ensures permanent forest productivity. The balanced state has most often been determined by mathematical models. One of the best-known mathematical models is known as Liocourt’s distribution of the number of trees per diameter classes [13]. This distribution is often understood as Liocourt’s law because the exponential growth of the number of trees from the upper to the lowest diameter classes is determined by the constant of geometric progression [14]. Actually, the ideal theoretical distribution of the number of trees per diameter classes is very difficult to achieve in reality, but there is a possibility of gradually reaching the desired state of forests by using proper silvicultural treatments. Selection forest management has been traditionally applied in the Dinaric region [15], and the knowledge of the declining number of trees per diameter classes is important for large-scale management of these forests in terms of establishing a normal state.

The balanced state does not refer only to the regulation of the stand structure for commercial purposes, but also to the sustainable provision of a range of non-timber forest services for the sustainable development of forest ecosystems. Although the stage in which old-growth forests assume an inverse-J diameter distribution is often called the steady stage [16,17], recent studies [14,18] have revealed that the steadiness might not be the most appropriate term as stand structures can be rather dynamic without losing the tree-size demographic equilibrium [19,20]. Investigating the possible balanced stand structures of old-growth forests is thus important to understand as such knowledge may be practically transferred or, at least, adapted to management of uneven-aged forests on the landscape scale. To ensure sustainability of increased forest productivity, both in managed or unmanaged forests, the degree of alignment of the actual distribution of the number of trees needs to fit the theoretical model.

Fortunately, Dinaric mixed old-growth forests have been isolated without experiencing direct human influence. Therefore current structure and tree species composition have been shaped only by natural processes. Recent research has shown that these forests exhibit high structural heterogenity [21] which is one of the major prerequisites for sustaining biodiversity on the landscape scale [22] and the regulation of the carbon cycle [23]. Moreover, the provision of multiple forest benefits is better guaranteed if the management follows natural structures and regeneration patterns. Thus, the increasing forest resilience to disturbance events which have recently intensified due to climate change [24] is today one of the major challenges faced by scientists and forest managers [15]. In the last few decades, the importance of sustainability of forests has been widely recognized [25]. Practically, due to large demands for wood products worldwide, it is increasingly difficult to ensure the sustainability and multipurpose functionality of forests (ecological, economic and social functions). The sustainability of managed selection forests composed of beech, fir and spruce is usually assessed based on structural features such as actual tree diameter distribution and its alignment with the theoretical model of the balanced state. This approach is not merely related to the regulation of stand structure but also to the understanding of a dynamically balanced state and new experimental methods for determining the normal state [26,27].

Therefore, the major aim of this study was to determine and compare the actual stand structure with the theoretical balanced state in the old-growth forests Janj and Lom. Thereby, we hypothesized that no significant differences occur between the actual and the theoretical diameter distributions.

2. Materials and Methods

2.1. Study Site

The research was carried out in the old-growth forests Janj (1359 m above sea level) and Lom (1323 m above sea level) in central and western Bosnia (Figure 1). These old-growth forests are classified according to IUCN (International Union for the Conservation of Nature and Natural Resources) classification system of the international union for the conservation of nature, that is, the World conservation union for protected areas in the category of strict nature reserves (Ia). The old-growth forest Janj covers a total area of 295 ha and the old-growth forest Lom 297 ha. The dominant plant communities in these old-growth forests are mixed stands of European beech, silver fir and Norway spruce (Piceo-Abieti–Fagetum dinaricum) which also occupy significant areas of the interior Dinarides [28,29]. There are few plant species which are found only in one old-growth forest. The dominant beadrock in the old-growth forest Janj is dolomite, while it is limestone in Lom. The dominant soil types are calcomelanosol, calcocambisol and luvisol. According to the ecological and vegetation classification of Bosnia and Herzegovina [30], the research stands belong to Eurosiberian-North American region as a secondary community within the regional community of mixed forests of beech, fir and spruce. The average annual temperature in the area of the old-growth forest Janj is 6.5 °C and the annual amount of precipitation is 1200 mm. In the old-growth forest Lom, the average annual temperature is around 5.0 °C and the annual amount of precipitation is 1600 mm.

2.2. Analysis

The field data collection was carried out on permanent experimental surfaces of 1.0 ha. Each of the research stands had one polygon shape experimental surface established for the purpose of data collection. All trees on the experimental surfaces had two diameters cross-measured at a height of 1.3 m above the ground, whereby the degree of accuracy was 1.0 mm and the inventory threshold 5.0 cm. The height of all trees with a diameter larger than the inventory threshold was measured. Measurements were made using a Vertex IV instrument with a degree of accuracy of 0.1 m. The cores were taken at a height of 1.3 m by using Presler’s drill in order to determine the diameter increment. The width of the last 10 growth rings was measured, as well as the number of tree rings with a width of 2.5 cm. The sample included 5 randomly selected trees of each diameter class. In order to determine the diameter structure of the stands, 5.0 cm diameter classes were formed for each stand with the distribution of the number of trees per diameter classes. The measured heights and diameters of trees were used to construct the height curves for beech, fir and spruce using Prodan’s function of growth [31]. This function was applied for site class determination by comparing the constructed height curves with the average site class height curves for the analyzed tree species [32]. In order to define site classes, the collected data were fitted by Prodan’s function:

$$h=\frac{d_{1.30}^2}{a+b{d}_{1.3}+c{\mathrm{d}}_{1.3}^2}+1.30$$

(1)

where h is the height of trees (m) and d_1.3 represents the diameter of trees (cm) at 1.30 m above the ground.

Mayer’s differential method was used for determining the current diameter increment [31], whereas the total volume was determined using the tables of structural elements for high forests in B&H [32]. In order to compare the distributions of the real number of trees with the normal number of trees, Mayer’s function (modified Liocourt’s function) of normal distribution of the number of trees per diameter classes was used [33,34].

$$Y_i=k{e}^{-a{d}_i}$$

(2)

where Y_i is the number of trees, d_i is the diameter (cm), k, a—coefficients of function, e is the base of natural logarithm (2.71...).

To determine the elements of the normal state, Susmel’s equations for fir and spruce and Collete’s equations for beech, were used [35,36].

For fir and spruce:

$$D_{\max }=2.33H_{dom}$$

(3)

$$V_{norm}=\frac{H_{dom}{}^2}{3}$$

(4)

$$G_{norm}=0.97H_{dom}$$

(5)

$$q=\frac{4.3}{\sqrt[3]{H_{dom}}}$$

(6)

For beech:

$$D_{\max }=2.64H_{dom}$$

(7)

$$V_{norm}=\frac{H_{dom}{}^2}{4.23}$$

(8)

$$G_{norm}=0.73H_{dom}$$

(9)

$$q=\frac{4.54}{\sqrt[3]{H_{dom}}}$$

(10)

where D_max is the tree’s physiological maturity (cm), H_dom is the average height (m) of the trees whose diameter is higher d_1.30 > 50 cm, V_norm is the balanced (normal) volume (m³/ha), G_norm is the balanced (normal) basal area (m²/ha) and q coefficient of geometric progression.

Kolmogorov-Smirnov’s test was used for determining the significance of differences between the actual and the normal diameter distributions [37,38].

$$D=\max |F_n(x)-F_t(x)|$$

(11)

where F_n is the cumulative of real frequencies and F_t is the cumulative of theoretical frequencies.

3. Results

3.1. The Quality of Stands

According to the majority of authors, the age and average stand height are not significant in the site class determination of selection and uneven-aged stands [7,31,39]. However, each diameter class corresponds to the average height, which is of great importance for site class determination in selection and uneven-aged stands [31]. Trees of thinner diameter classes are not favorable indicators of site conditions because in selection and uneven-aged forests these trees belong to the lower stratum of the stand, they are shaded and their growth stagnates. Consequently, no significant height differences occur between such trees. The principle of site class determination based on heights is difficult to apply in the study area because old-growth forests are usually composed of three layers: thin trees, medium-sized trees and large upperstory trees with site classes III, II and I, respectively [39,40,41]. In the old-growth forest Janj, the fir height curve generally shows a uniform flow and it is more flattened for the heights that correspond to diameters above 60 cm (Figure 2). The rise of the spruce height curve is strong, regular and uniform up to the diameter of 40 cm; between 40 and 50 cm, the height increase is smaller and the height curve is more laid. The upward reallocation of height curves is higher in lower than in higher diameter classes which is especially noticeable for spruce, whereas the fir height curves move upward more uniformly. The diameter class in which a clearly pronounced decrease and the difference in the height increment of fir and spruce occur cannot be observed. The only exception is the spruce in the old-growth forest Janj at site class II which shows a more horizontal flow of the height curve for the diameter of 47.5 cm.

The curve is more horizontal when the tree reaches more light, which is in the middle diameter classes. The height increment is then smaller and the diameter increment is more intensive. This was also noticed in even-aged stands of low stocking [41]. The fir trees in the old-growth forest Lom belong to a better site class compared to the fir trees in Janj, while the spruce belongs to the same site class in both old-growth forests. The shape of fir height curves in the two old-growth forests is very similar. However, the fir in Lom attains greater heights at the same diameters. The spruce trees with a diameter up to 17.5 cm in the old-growth forest Janj attain lower heights than the trees in Lom, but medium and large-diameter trees of this species have on average about 3.0 m greater heights in Janj compared to Lom. The obtained statistical correlations among tree diameters and their heights showed high determination coefficients (

Table 1. Basic statistical indicators of height curves according to Prodan’s function.

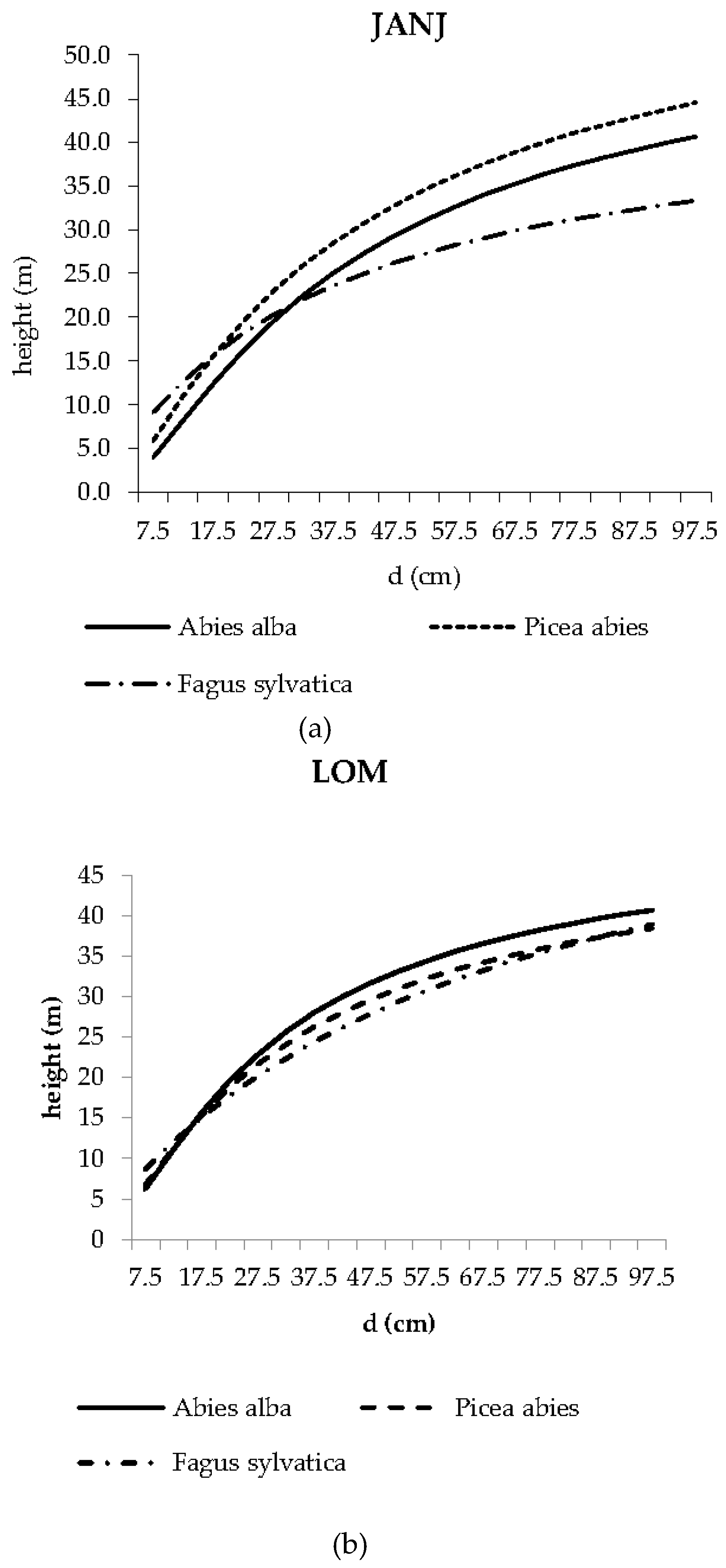
Stand	Species	a	b	c	R2	Se (m)	Site Class
Janj	Fir	5.5046	0.6630	0.0202	98.5	1.14	II
	Spruce	9.5387	0.2340	0.0228	89.6	2.86	II
	Beech	−0.9180	0.7823	0.0220	75.6	3.01	III
Lom	Fir	6.8039	0.4840	0.0197	71.4	4.37	I
	Spruce	4.5473	0.6313	0.0200	83.7	3.88	II
	Beech	−1.2380	1.0639	0.0158	79.0	4.07	II

R²—coefficient of determination; Se—standard error.

).

Within the same site classes of the old-growth forests, spruce trees reach on average greater heights compared to fir trees. This difference in heights increases from lower to higher diameter classes and in the middle diameter classes the difference reaches a maximum of about 4.0 m, after which the difference decreases. The differences are negligible between large-sized upperstory trees of these species in the old-growth forest Janj. The lowered curve flow is more pronounced for the spruce compared to fir in both old-growth forests. Height differentiation can be noticed even in small-diameter trees, which is caused by differences in the stand structure.

3.2. Actual and Balanced Tree Diameter Distributions

The theoretical (normal) distribution of the number of trees per diameter classes was determined for the main tree species, based on the corresponding values of Susmel’s and Colette’s correlations (

Table 2. Susmel’s and Colette’s correlations for fir, spruce and beech in old-growth forests.

Stand		Hdom.	Dmax.	Gnorm.	Vnorm.	q
Janj	Fir	38.1	100.3	36.9 35.9	483.9 458.8	1.28
	Spruce	37.1	97.7			1.29
	Beech	36.0	83.4	26.6	305.6	1.37
Lom	Fir	42.2	110.9	40.9 35.0	593.6 434.4	1.24
	Spruce	36.1	95.0			1.30
	Beech	35.0	81.6	25.5	288.9	1.39

H_dom—the average height of trees which diameter is higher from 50 cm.

).

Diameter structure of the stands in the old-growth forests Janj and Lom is distinguished by the presence of old trees with very large diameters and specific phenotypes (Figure 3). The number of trees in Janj amounts to 588 trees per hectare and 548 trees per hectare in Lom. In Janj, fir trees are most abundant (41.4%), whereas beech with 209 trees per ha and spruce with 135 trees per ha have lower shares in the tree species composition. In Lom, beech trees are most abundant with 261 trees per ha or 47.6%, while fir and spruce follow with 35.4% and 17.0% of the total number of trees, respectively (

Table 3. Experimental and theoretical number of trees in the old-growth forests.

d	Experimental Number of Trees Per Hectare								Theoretical Number of Trees Per Hectare
	JANJ				LOM				JANJ				LOM
cm	A.a.	P.a.	F.s.	Total	A.a.	P.a.	F.s.	Total	A.a.	P.a.	F.s.	Total	A.a.	P.a.	F.s.	Total
7.5	93	23	69	185	88	18	105	211	49	40	29	118	38	42	30	110
12.5	14	7	36	57	5	11	22	38	38	31	21	91	31	32	22	85
17.5	21	7	21	50	5	5	16	27	30	24	15	70	25	25	16	65
22.5	14	14	24	53	18	7	25	51	23	19	11	53	20	19	11	50
27.5	14	5	14	33	7	4	11	22	18	14	8	41	16	15	8	39
32.5	5	9	4	18	9	3	18	30	14	11	6	31	13	11	6	30
37.5	13	11	9	32	7	5	15	27	11	9	4	24	11	9	4	23
42.5	5	13	7	25	7	1	18	26	9	7	3	19	9	7	3	18
47.5	13	7	9	29	5	4	15	24	7	5	2	14	7	5	2	14
52.5	8	6	4	17	7	1	6	14	5	4	2	11	6	4	2	11
57.5	6	6	3	15	2	2	4	9	4	3	1	9	5	3	1	9
62.5	7	5	5	17	8	6	2	16	3	2	1	7	4	2	1	7
67.5	6	5	3	14	4	3	1	8	3	2	1	5	3	2	1	5
72.5	8	6	1	14	4	5	2	12	2	1		3	2	1		4
77.5	6	3	1	10	4	3		8	2	1		3	2	1		3
82.5	2	3		5	4	5		8	1	1		2	2	1		2
87.5	2	2		4	1	3		4	1	1		2	1	1		2
92.5	2	1		3	2	2		4	1	1		1	1			1
97.5	1	1		2	1	2		3	1			1	1			1
102.5	1	1		2	1	1		2					1			1
107.5	1	1		2	1			1					1			1
112.5					1			1
117.5					1			1
122.5					1			1
Total	243	136	209	588	194	93	261	548	223	177	105	505	195	180	106	481

A.a.—Abies alba; P.a.—Picea abies; F.s.—Fagus sylvatica.

). The maximum number of trees in both old-growth forests occurs in the lowest diameter class (7.5 cm) where fir is most represented. The site classes determined for each tree species and the distribution of the number of trees per diameter classes were used to determine the total volume of both stands. In the old-growth forest Janj, the total volume was 1007 m³/ha and the current volume increment amounted to 11 m³/ha, while in the old-growth forest Lom, the volume amounted to 893 m³/ha and the current volume increment to 13 m³/ha. Large volume in the old-growth forest Lom (763.1 m³/ha) had already been determined in earlier research [42]. For both stands, the actual number of fir and beech trees in the lowest diameter class was higher than the theoretically modeled values (Table 3).

By comparing the differences between the cumulative experimental values and the cumulative theoretical distributions of tree frequencies, we tested the starting hypothesis about the absence of statistically significant differences between the actual and theoretical distributions (Figure 4).

The maximum absolute values of these differences (deviations) are higher than table values with probability 0.05. They occur at diameter classes 32.5 cm (Janj) and 37.5 cm (Lom). Therefore, we can conclude that there is statistically significant difference between the theoretical and the actual tree-size distributions in both old-growth forests (

Table 4. Parameters of Mayer’s modified function and results of Kolmogorov-Smirnov’s test.

Old-Growth Forests	k	a	max|Fn − Ft|	${\mathit{D}}_{\left(\mathbf{n};0.05\right)}=\frac{1.36}{\sqrt{\mathbf{n}}}$
Janj	84.67	0.03	0.126	0.056
Lom	57.62	0.02	0.079	0.058

).

4. Discussion

The differences in the heights of the stand trees did not cause significant differences in site classes. However, regarding the main tree species, site conditions were more favorable in the old-growth forest Lom. Earlier research conducted on 8 experimental surfaces in the old-growth forests Janj and Lom found that spruce trees belonged to site class II [41]. In the same study area, Tregubov found that there were no significant differences considering heights of beech, fir and spruce up to the diameter of 30 cm. In old-growth forests on Grmeč the differences were not noticeable up to the diameter of 20 cm [40]. However, this research shows that there are significant differences in the heights between these species considering thin trees (Figure 2). Similar results had been determined in previous research of the old-growth forests Janj and Lom as well as the old-growth forest Perućica [41]. The lower height of the fir compared to the spruce was due to the longer period of fir growth stagnation. In the old-growth forest of Bern-Emmental, fir growth stagnation can be 40–60 years long, while it is 10 years for spruce [43]. Suppressed trees mostly use diffuse light. The spruce in the old-growth forest Janj reached higher average heights than the fir in all diameter classes. The differences in height increased from the lowest diameter classes and in the middle diameter class of 42.5 cm they reached the maximum, which amounted to 4.0 m, whereas the differences in height between larger-diameter trees decreased. The reduction in the differences was caused by a more horizontal flow of the spruce height curve, especially after the diameter class of 42.5 cm. The spruce had greater height increments up to the diameter of 37.5 cm, whereas the fir height increments were higher. This indicates that in the period when fir trees are suppressed in shade, they do not have intensive height increments, and when they reach favourable light conditions, they respond by increasing the height. Spruce trees had greater height increments up to the diameter of 37.5 cm. The fir in Lom reached greater heights than the spruce. In thinner diameter classes, there was no significant difference in heights. The flow of height curves of both tree species point to the possibility of intensifying the height increment at an old age when trees have large diameters. Significant differences in the flow of height curves occurred in middle diameter classes and after that the differences diminished, whereas the curves of the largest trees became virtually parallel. The fir height increment was on average greater than that of the spruce, up to the diameter of 77.5 cm, and after that there were no differences in the height increment. Up to the diameter of 17.5 cm, the beech reached greater heights than the fir and spruce of the same diameters in both old-growth forests. That was also noted in the old-growth forests Klekovača and Grmeč [40]. In the case of beech trees with diameters between 20 and 30 cm, the height curve is more flattened. Beech trees with diameters >37.5 cm in Janj and >22.5 cm in Lom had smaller heights than the trees of fir and spruce with the same diameters. The occurrence of intense height increment in thinner diameter classes and a sharp decrease in middle diameter classes was also determined by Leibundgut [44].

By analyzing the diameter structure, several generations of trees were observed in both old-growth forests. The characteristic increase in the number of beech trees compared to the fir and spruce, especially in old-growth forests of the Dinarides after the disruption of stand canopy is caused by adverse effects of abiotic and biotic factors [44,45,46,47]. Intensive regeneration of the beech and its dominance in thinner diameter classes in old-growth forests usually occurs after a fire or wind disasters [48,49], which leads to the development of structural forms that are characteristic for stands with fast and short regeneration [6]. The significantly higher actual number of beech trees than the normal number of trees in the lowest diameter class is the consequence of the pronounced process of beech ingrowth above the inventory threshold. It is very difficult to suppress beech in the lower and middle stand layer in canopy gaps [50]. The process of natural regeneration of beech is more intensive in the old-growth forest Lom, but due to the dolomite bedrock and the less rocky terrain in the old-growth forest Janj the growing stock and the total number of trees are higher per unit area.

Bedrock has significant influence on the benefits of natural regeneration. The area of the old-growth forest Janj is mostly on dolomite. Together with the favourable light conditions in the stand understory, it makes a larger active surface for natural regeneration than the limestone bedrock in the old-growth forest Lom. The actual number of fir and beech trees is much closer to the normal state than in the case of spruce. In the case of fir and spruce trees in thinner diameter classes, there is an absence of significant numbers of trees in comparison with the theoretical sustainability values. That absence of trees in diameter classes from 12.5 to 42.5 cm is more pronounced in the old-growth forest Janj. In higher diameter classes of both old-growth forests, the real number of trees was higher than the number of trees which was theoretically determined as normal. The number of fir and spruce trees in commercial forests is on average higher than in old-growth forests [51,52,53]. The mixed forests of fir, spruce and beech (Piceo-Fago-Abietum) with selection structure on medium deep brown soil on limestone in Serbia [54] reported 628 trees per ha and the fir share of 66%, spruce 22% and beech 12%. For the ecological association of beech and fir Abieti-Fagetum Illyricum on brown soil over limestone in Croatia, in order to establish a normal state, the share of fir is recommended to be above 30% [55]. The actual number of trees in both old-growth forests was higher than the theoretical number of trees. This difference was more expressed in the old-growth forest Janj, which is caused by the more intensive regeneration of beech trees in the stand understory. Compared to other old-growth forests with similar structure, the old-growth forests Janj and Lom are distinguished by a larger number of trees per unit area (larger stocking). By comparing them with the old-growth forests of fir and spruce in the Carpathian region [56], it can be concluded that in addition to the larger number of trees, Janj and Lom have larger volumes. The difference is influenced by the presence of edifying tree species which are bio-ecologically different in terms of the use of habitat, as opposed to the old-growth forests in the Carpathian region with the dominant presence of two species—fir and spruce. The results of Kolmogorov–Smirnov’s test suggested that the cumulative values of Mayer’s function can successfully describe the diameter structure of the studied stands. Based on the obtained results, it can be concluded that the old-growth stands deviate from the structure which is typical of selection stands.

The high variability of the left parts of diameter distribution curves points to the need to increase the inventory threshold in the analysis of diameter structure of old-growth forests. Namely, at the inventory threshold of 5.0 cm, the results of the tests indicate that the stands significantly deviate from the structure which is characteristic for selection forests. However, if the inventory threshold was 10 cm, the results of the distribution of the number of trees per diameter classes might be closer to the theoretical model or the structure which is characteristic for selection forests. In this context, a different sampling approach with a larger number of small plots across the old-growth forests Janj and Lom revealed a number of structural similarities with adjacent managed selection forests [21]. Based on the results of Kolmogorov–Smirnov’s approval test obtained for one sample by accumulating the actual number of trees per diameter classes and comparing them with the expected cumulative theoretical distribution, it can be also found that selection managed forests do not have the distribution of the number of trees characteristic for selection forests. The normal distribution of trees shows that the two old-growth forests have similar lines of distribution of the normal number of trees. The difference exists only in the lowest diameter classes where the number of trees in the old-growth forest Janj should be higher than in the forest of Lom. The research showed that the normal number of fir trees in the smallest diameter classes (up to 32.5 cm) should be higher in Janj than in the old-growth forest Lom (Table 2). The number of trees of the other two species (spruce and beech) should be, according to the normal distribution of the number of trees, almost equally represented in all diameter classes.

Old-growth forests, however, are distinguished by a specific structure that deviates from typical selection stands. The selection structure can be maintained as such in commercial forests with silvicultural treatments during management over a longer period of time. The particular physiognomy of old-growth forests is provided by old dying or dead trees which make specific micro-habitats which are important for the preservation and improvement of biodiversity. The corresponding volume of preserved stands of the old-growth forest type is a prerequisite for many functions of the forest ecosystem [57]. These functions can be significantly reduced if uncontrolled harvesting is carried out, especially with the cutting of highest quality parts of commercial forests. Therefore, it is important to improve the research about old-growth forests as they serve as natural laboratories and often as references to sustainable management of uneven-aged and mixed stands.

5. Conclusions

The beech-fir-spruce old-growth forests in the Dinarides area are the rare remnants of former untouched ancient forests in Europe. They are distinguished by specific landscapes formed by ancient trees of a special phenotype. A deeper insight into the balanced state, temporal and spatial development dynamics of these forests is important for their sustainability and the application of the principle of close-to-nature silviculture. Selection management system has proved to be sustainable in practice as well as by scientific analysis, particularly when considering conditions for the so-called demographic equilibrium [58]. This system is especially suitable for the forests with the dominance of coniferous shade-tolerant species. Leibundgut stated in earlier research [59]: “Our quest is to derive from pristine forest such stand forms which are efficient and stable enough but at the same time also satisfy mankind’s interests in terms of sustainable qualitative product.” Therefore, for the sustainable development of forest ecosystems, forest management should be directed towards establishing a balanced state and the distribution of trees of different tree species by diameter classes in a way that best meets the set of management objectives (biodiversity preservation, increased productivity, quality improvement and successful natural regeneration).

The old-growth forests Janj and Lom are distinguished by a specific structure that differs from the structure of typical selection forests. The real distribution of the number of trees per diameter classes is significantly different from the theoretical model of distribution which is characteristic for the stands with selection structure at the physiological maturity of trees. The diameter structure of trees in old-growth forests is characterized by the high share of veteran trees of large dimensions and a specific phenotype which gives these stands a special physiognomy. The real number of trees in the old-growth forest Janj is smaller than the normal, while it is higher in the old-growth forest Lom, which results from the intensive regeneration of beech ingrowth. The theoretical distributions of the number of spruce and beech trees in the old-growth forests are similar, while the distribution of the number of fir trees, especially in the diameter classes up to 37.5 cm, is significantly different. The old-growth forest Lom has more favourable site conditions, especially for fir, and the site classes of the main tree species are higher on average. Beech is a bio-ecologically more aggressive species compared to fir and spruce, especially in canopy gaps. It also has a more intensive development in youth and dominates in the category of thinner trees, especially in Lom forest. Old-growth forests undergo developmental stages [60] which interact with each other on a relatively small area. Their formation is conditioned by changes in the horizontal and vertical structure of the stands, degree of regeneration, health state [61,62], as well as the creation of canopy gaps as a result of the extinction and fall of veteran trees [48,49]. The state of the stands investigated points to the need to preserve them and improve the research of the temporal dynamics regarding the changes in diameter structure and canopy openings which are influenced by the developmental stages of old-growth forests.

The old-growth forests of the Dinarides in Bosnia-Herzegovina are extremely important for naturalistic, cultural and scientific purposes, not only at the regional scale but also at the continental scale (species, forest types). Furthermore, forestry sectors in many states are adapting policy and management instruments towards the multi-functional use of forests [63,64]. In the future, the interest in the research of old-growth forests will increase as the processes taking place in them can serve as recommendations for the future sustainable development of forest ecosystems.