Optimal Locating of Electric Vehicle Charging Stations by Application of Genetic Algorithm
Abstract
:1. Introduction
2. Charging Modes for EVs Charging Stations
- Mode 1: Charging refers to the connection of an EV to the AC supply network through a single phase AC line not exceeding 250 V AC or a three phase AC line not exceeding 480 V AC at 50–60 Hz, using national plug and socket system not exceeding 16 A with protective earth conductors, depending on the country and standardization. This low power vehicle charging mode is the slowest mode and can refill a battery overnight reaching full capacity before morning. This type of overnight recharge ensures a low electric load for the grid and the car is recharged economically using a low cost night rate power. This recharging mode is mainly used at home and office, since no additional infrastructures are required.
- Mode 2: Charging refers to the connection of an EV to the AC supply network with the same voltage limits as for Mode 1, using standard wall sockets and plugs not exceeding 32 A with protective earth conductors. The difference with Mode 1 consists in the fact that the vehicle inlet and connector present a control pin. The supply network side of the cable does not require a control pin as the control function is provided by an integrated control box with the further function of in cable protection device. This recharging mode is primarily used for dedicated private facilities.
- Mode 3: Charging refers to the connection of the EV to the AC supply network using an Electric Vehicle Supply Equipment (EVSE), not exceeding 63 A, where the control pilot function is extended from Mode 2 to control equipment permanently connected to the AC supply. In this case, connectors with a group of control and signal pins are required for both sides of the cable. This recharging mode is typical of public charging stations and is generally supplied from three-phase AC mains at 50/60 Hz. It is also called “semi-fast” charging solution since it is possible to charge a battery in few hours when the driver is at work or during every day activity.
- Mode 4: It has been implemented by the CHAdeMO consortium and is characterized by the use of off-board chargers where the control pilot function is extended also to the equipment permanently connected to the AC supply. The supply AC power is converted in the charging station to DC and the plug ensures that only a matching electric vehicle can be connected. Typical charging times of Mode 4 are in a range from 20 to 30 min. In this case, the charging time is limited by the allowable current of 125 A and voltage of 500 V of the CHAdeMO standard connector.
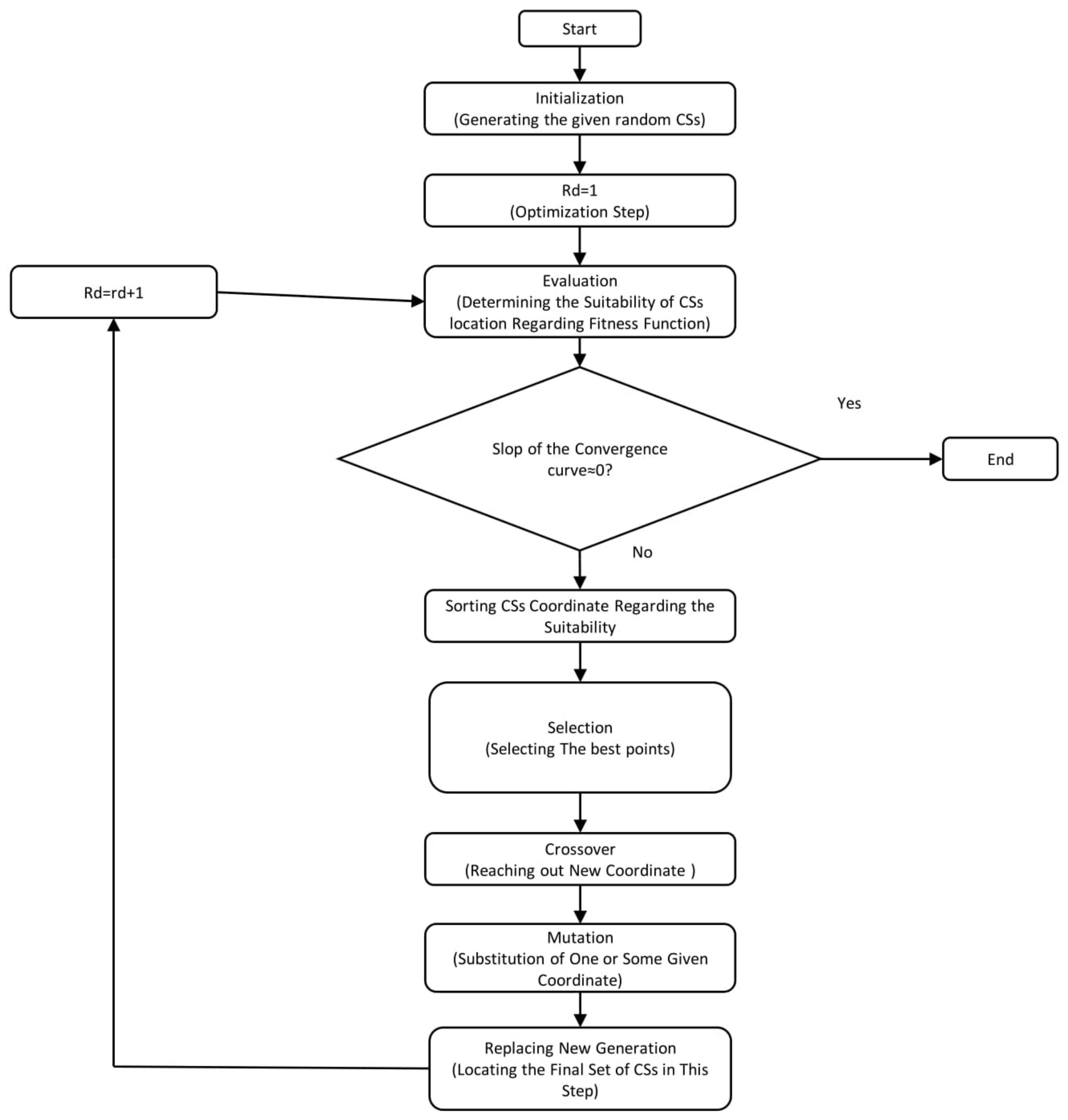
3. Description of Genetic Algorithm
4. Optimization Performance by Genetic Algorithm
Objective Function Optimizer
- Mode 2: It is a slow charging mode applied by a household type socket-outlet with an inner cable protection component in AC.
- Mode 3: It is a medium to fast speed charging mode utilizing a specific EV socket-outlet with control and protection function installed in AC.
- Mode 4: It is an ultra-fast charging mode with an external charger in DC.
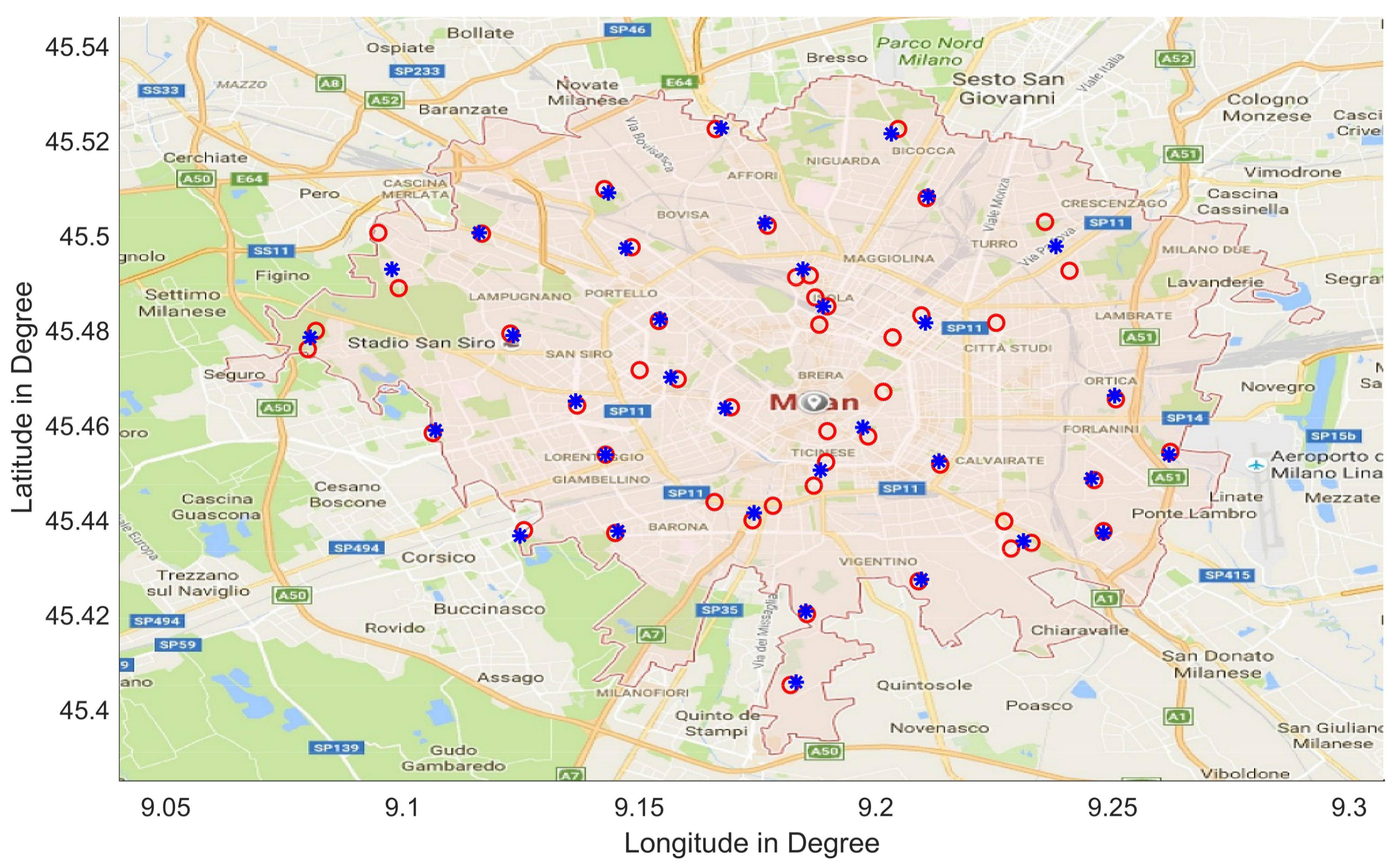
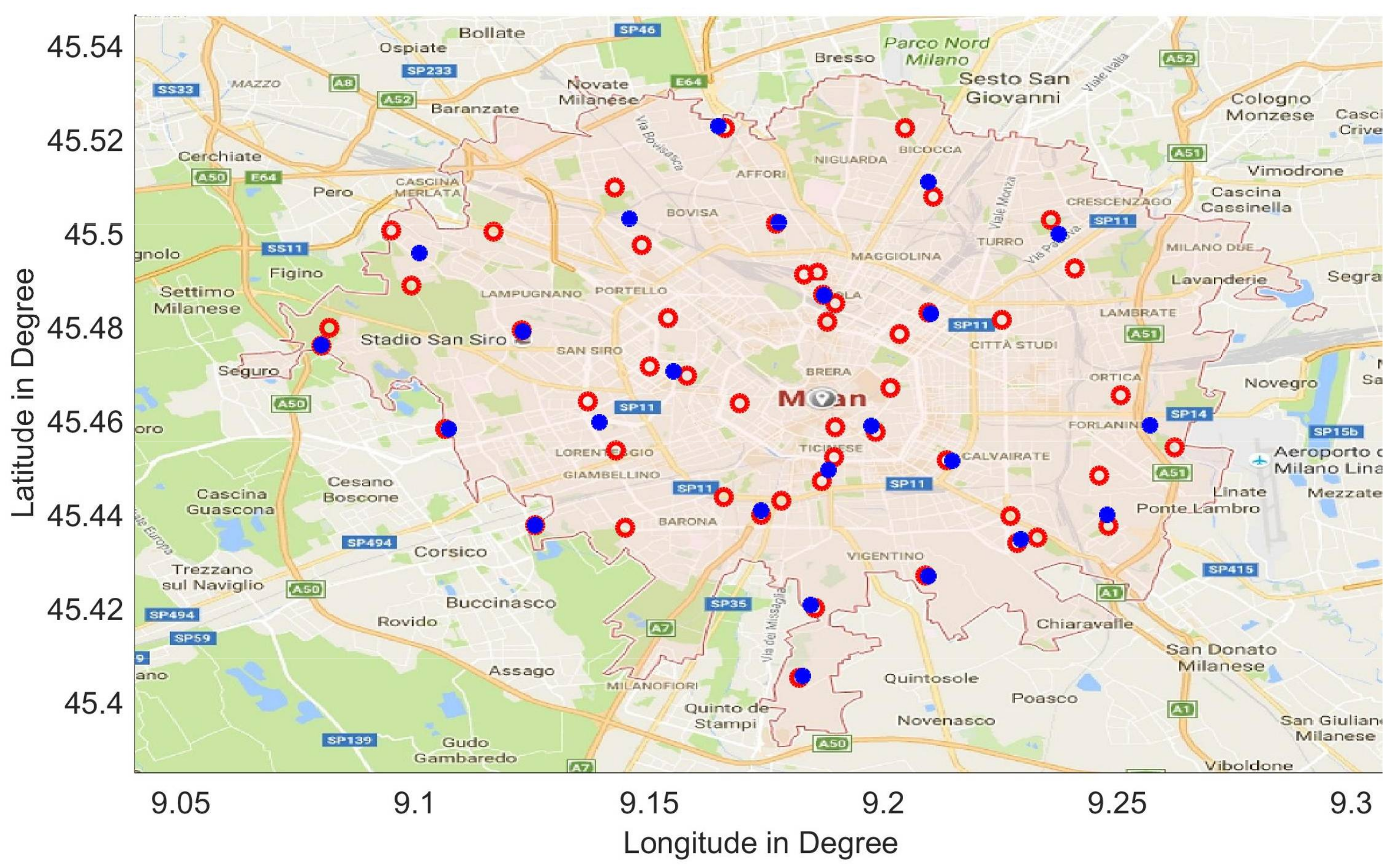
5. Case Study
6. Distance and Costs Obtained in Different Modes
7. Conclusions
Author Contributions
Conflicts of Interest
Nomenclature
| CS | Charging Stations |
| EV | Electric Vehicle |
| GA | Genetic Algorithm |
| ICE | Internal Combustion Engine |
| C1 | the cost for clients caused within traveling the path |
| C2 | the cost of the power consumed within the path |
| C3 | the cost of controlling the populace |
| C | total costs |
| the average constant cost per kilometre for the clients | |
| the constant cost of electricity generating per kWh | |
| R | the constant cost of contamination controlling for production of kWh |
| P | the power utilization of an EV for every kilometre |
| the charging stations coordinate | |
| , | the settlements coordinate |
| φ | latitude |
| λ | longitude |
| R | earth’s radius |
| D | the summation of distances between settlements and the closest charging station |
| N(t) | estimated number of electric vehicles |
| calculated number of charging stations | |
| W | the acquired electric vehicles’ power consumption per day |
| µs | the balancing factor |
| Ps | the charging station’s power |
| the required average time for recharging | |
| the electric vehicle’s average power consumption | |
| the average number of charge cycles in a day | |
| an electric vehicle’s power consumption | |
| the average distance that client travels per day |
References
- Jayakumar, A.; Chalmers, A.; Lie, T.T. Review of prospects for adoption of fuel cell electric vehicles in New Zealand. IET Electr. Syst. Transp. 2017, 7, 259–266. [Google Scholar] [CrossRef]
- Un-Noor, F.; Padmanaban, S.; Mihet-Popa, L.; Nurunnabi Mollah, M.; Hossain, E. A comprehensive study of key electric vehicle (EV) components, technologies, challenges, impacts, and future direction of development. Energies 2017, 10, 1217. [Google Scholar] [CrossRef]
- Wang, G.; Xu, Z.; Wen, F.; Wong, K.P. Traffic-constrained multiobjective planning of electric-vehicle charging stations. IEEE Trans. Power Deliv. 2013, 28, 2363–2372. [Google Scholar] [CrossRef]
- Hajimiragha, A.; Caizares, C.A.; Fowler, M.W.; Elkamel, A. Optimal transition to plug-in hybrid electric vehicles in Ontario, Canada, considering the electricity-grid limitations. IEEE Trans. Ind. Electron. 2010, 57, 690–701. [Google Scholar] [CrossRef]
- Lam, A.Y.; Leung, Y.-W.; Chu, X. Electric vehicle charging station placement: Formulation, complexity, and solutions. IEEE Trans. Smart Grid 2014, 5, 2846–2856. [Google Scholar] [CrossRef]
- Liu, Z.; Wen, F.; Ledwich, G. Optimal planning of electric-vehicle charging stations in distribution systems. IEEE Trans. Power Deliv. 2013, 28, 102–110. [Google Scholar] [CrossRef]
- Sadeghi-Barzani, P.; Rajabi-Ghahnavieh, A.; Kazemi-Karegar, H. Optimal fast charging station placing and sizing. Appl. Energy 2014, 125, 289–299. [Google Scholar] [CrossRef]
- Hanabusa, H.; Horiguchi, R. A study of the analytical method for the location planning of charging stations for electric vehicles. In Proceedings of the International Conference on Knowledge-Based and Intelligent Information and Engineering Systems, Kaiserslautern, Germany, 12–14 September 2011. [Google Scholar]
- Jia, L.; Hu, Z.; Song, Y.; Luo, Z. Optimal siting and sizing of electric vehicle charging stations. In Proceedings of the 2012 IEEE International Electric Vehicle Conference (IEVC), Greenville, SC, USA, 4–8 March 2012. [Google Scholar]
- Mehar, S.; Senouci, S.M. An optimization location scheme for electric charging stations. In Proceedings of the 2013 International Conference on Smart Communications in Network Technologies (SaCoNeT), Paris, France, 17–19 June 2013. [Google Scholar]
- Pazouki, S.; Mohsenzadeh, A.; Haghifam, M.-R.; Ardalan, S. Simultaneous allocation of charging stations and capacitors in distribution networks improving voltage and power loss. Can. J. Electr. Comput. Eng. 2015, 38, 100–105. [Google Scholar] [CrossRef]
- Iversen, E.B.; Morales, J.M.; Madsen, H. Optimal charging of an electric vehicle using a Markov decision process. Appl. Energy 2014, 123, 1–12. [Google Scholar] [CrossRef]
- Dong, J.; Liu, C.; Lin, Z. Charging infrastructure planning for promoting battery electric vehicles: An activity-based approach using multiday travel data. Transp. Res. Part C 2014, 38, 44–55. [Google Scholar] [CrossRef]
- Jaramillo, J.H.; Bhadury, J.; Batta, R. On the use of genetic algorithms to solve location problems. Comput. Oper. Res. 2002, 29, 761–779. [Google Scholar] [CrossRef]
- Barrero, R.; van Mierlo, J.; Tackoen, X. Energy saving in public transport. IEEE Veh. Technol. Mag. 2008, 3, 26–36. [Google Scholar] [CrossRef]
- Guo, F.; Liu, Q.; Liu, D.; Guo, Z. On Production and Green Transportation Coordination in a Sustainable Global Supply Chain. Sustainability 2017, 9, 2071. [Google Scholar] [CrossRef]
- International Electrotechnical Commission (IEC). 61851-1: Electric Vehicle Conductive Charging System-Part 1: General Requirements; IEC: Geneva, Switzerland, 2010. [Google Scholar]
- Veneri, O.; Ferraro, L.; Capasso, C.; Iannuzzi, D. Charging infrastructures for EV: Overview of technologies and issues. In Proceedings of the Electrical Systems for Aircraft, Railway and Ship Propulsion (ESARS), Bologna, Italy, 16–18 October 2012. [Google Scholar]
- Hõimoja, H.; Rufer, A. Infrastructure Issues Regarding the Ultrafast Charging of Electric Vehicles. In Proceedings of the International Advanced Mobility Forum. 2012. Available online: https://infoscience.epfl.ch/record/175699/files/Hoimoja%20Hardi%20_Infrastructure%20Issues_EPFL_IAMF2012.pdf (accessed on 19 March 2018).
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1989; Volume xiii, pp. 2104–2116. [Google Scholar]
- Shao, Z.; Ma, Z.; Liu, S.; Lv, T. Optimization of a Traffic Control Scheme for a Post-Disaster Urban Road Network. Sustainability 2018, 10, 68. [Google Scholar] [CrossRef]
- Mayet, C.; Horrein, L.; Bouscayrol, A.; Delarue, P.; Verhille, J.-N.; Chattot, E.; Lemaire-Semail, B. Comparison of Different Models and Simulation Approaches for the Energetic Study of a Subway. IEEE Trans. Veh. Technol. 2014, 63, 556–565. [Google Scholar] [CrossRef]
- Oremland, M.; Laubenbacher, R. Optimization of Agent-Based Models: Scaling Methods and Heuristic Algorithms. J. Artif. Soc. Soc. Simul. 2014, 17, 1–6. [Google Scholar] [CrossRef]
- Hu, Y.; Song, X.; Cao, W.; Ji, B.; New, S.R. Drive With Integrated Charging Capacity for Plug-In Hybrid Electric Vehicles (PHEVs). IEEE Trans. Ind. Electron. 2014, 61, 5722–5731. [Google Scholar] [CrossRef]
- Bocharnikov, Y.V.; Tobias, A.M.; Roberts, C.S.; Hillmansen, S.; Goodman, C.J. Optimal driving strategy for traction energy saving on DC sub-urban railways. IET Electr. Power Appl. 2007, 1, 675–682. [Google Scholar] [CrossRef]
- Song, L.; Wang, J.; Yang, D. Optimal placement of electric vehicle charging stations based on Voronoi diagram. In Proceedings of the 2015 IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015. [Google Scholar]
- Riva Sanseverino, E.; Domenico Genco, V.; Scaccianoce, G.; Vaccaro, V.; Riva Sanseverino, R.; Zizzo, G.; Di Silvestre, M.L.; Arnone, D.; Paternò, G. Urban Energy Hubs and Microgrids: Smart Energy Planning for Cities. In From Smart Grids to Smart Cities: New Challenges in Optimizing Energy Grids; Wiley: Hoboken, NJ, USA, 2017; pp. 129–175. [Google Scholar]
- Di Silvestre, M.L.; Riva Sanseverino, E.; Zizzo, G.; Graditi, G. An optimization approach for efficient management of EV parking lots with batteries recharging facilities. J. Ambient Intell. Hum. Comput. 2013, 4, 641–649. [Google Scholar] [CrossRef]
- Lilien, G.L.; Rangaswamy, A.; Bruyn, A. The Bass model: Marketing engineering technical note. In Principles of Marketing Engineering; DecisionPro, Inc.: State College, PA, USA, 2007. [Google Scholar]
- Marmaras, C.; Xydas, E.; Cipcigan, L.M. D4. 4 Report Scenario Modeling eBRIDGE: Empowering e-Fleets for Business and Private Purposes in Cities. September 2015. Available online: http://ebridge-project.eu/images/ebridge/docs/ebridge-d4-4-scenarios-modelling.pdf (accessed on 19 March 2018).
- Scripts, M.T. Calculate Distance, Bearing and More between Latitude/Longitude Points. 2013. Available online: http://www. movable-type.co.uk/scripts/latlong.html (accessed on 19 March 2018).










| Charging Mode | Max Current per Phase | Charging Time | Vehicle Battery Charger |
|---|---|---|---|
| Mode 1 | 16 A | 4–8 h | On Board |
| Mode 2 | 32 A | 2–4 h | On Board |
| Mode 3 | 63 A | 1–2 h | On Board |
| Mode 4 | 400 A DC | 5–30 min | Off Board |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akbari, M.; Brenna, M.; Longo, M. Optimal Locating of Electric Vehicle Charging Stations by Application of Genetic Algorithm. Sustainability 2018, 10, 1076. https://doi.org/10.3390/su10041076
Akbari M, Brenna M, Longo M. Optimal Locating of Electric Vehicle Charging Stations by Application of Genetic Algorithm. Sustainability. 2018; 10(4):1076. https://doi.org/10.3390/su10041076
Chicago/Turabian StyleAkbari, Milad, Morris Brenna, and Michela Longo. 2018. "Optimal Locating of Electric Vehicle Charging Stations by Application of Genetic Algorithm" Sustainability 10, no. 4: 1076. https://doi.org/10.3390/su10041076
APA StyleAkbari, M., Brenna, M., & Longo, M. (2018). Optimal Locating of Electric Vehicle Charging Stations by Application of Genetic Algorithm. Sustainability, 10(4), 1076. https://doi.org/10.3390/su10041076






