A Study on the Development and Application of Spatial-TDR Sensor for the Management of Groundwater at Riverside
Abstract
:1. Introduction
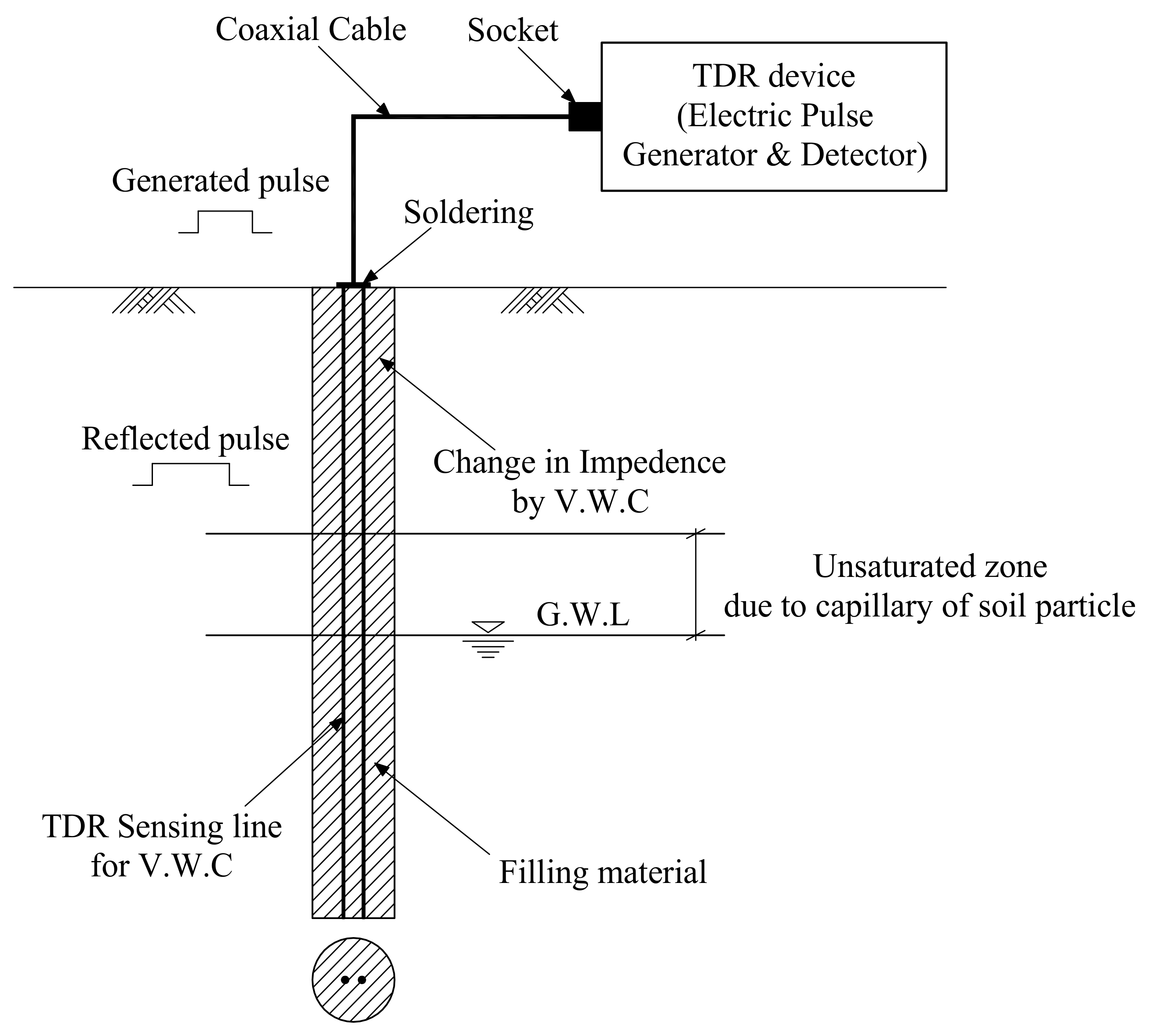
2. Spatial-TDR Sensor for Measurement of Groundwater Table and Unsaturated Zone
2.1. Point-TDR Sensor for Measurement of Water Content and Density of Soil
2.2. Spatial-TDR Sensor for Measurement of Groundwater Table and Unsaturated Area
3. Laboratory Experiment
3.1. Laboratory Experiments to Calculate the Calibration Equations for Voltage of Electric Pulse and Degree of Saturation of Soil
3.2. Laboratory Model Simulation for Verifying the Applicability of Spatial-TDR Sensor
4. Field Experiment
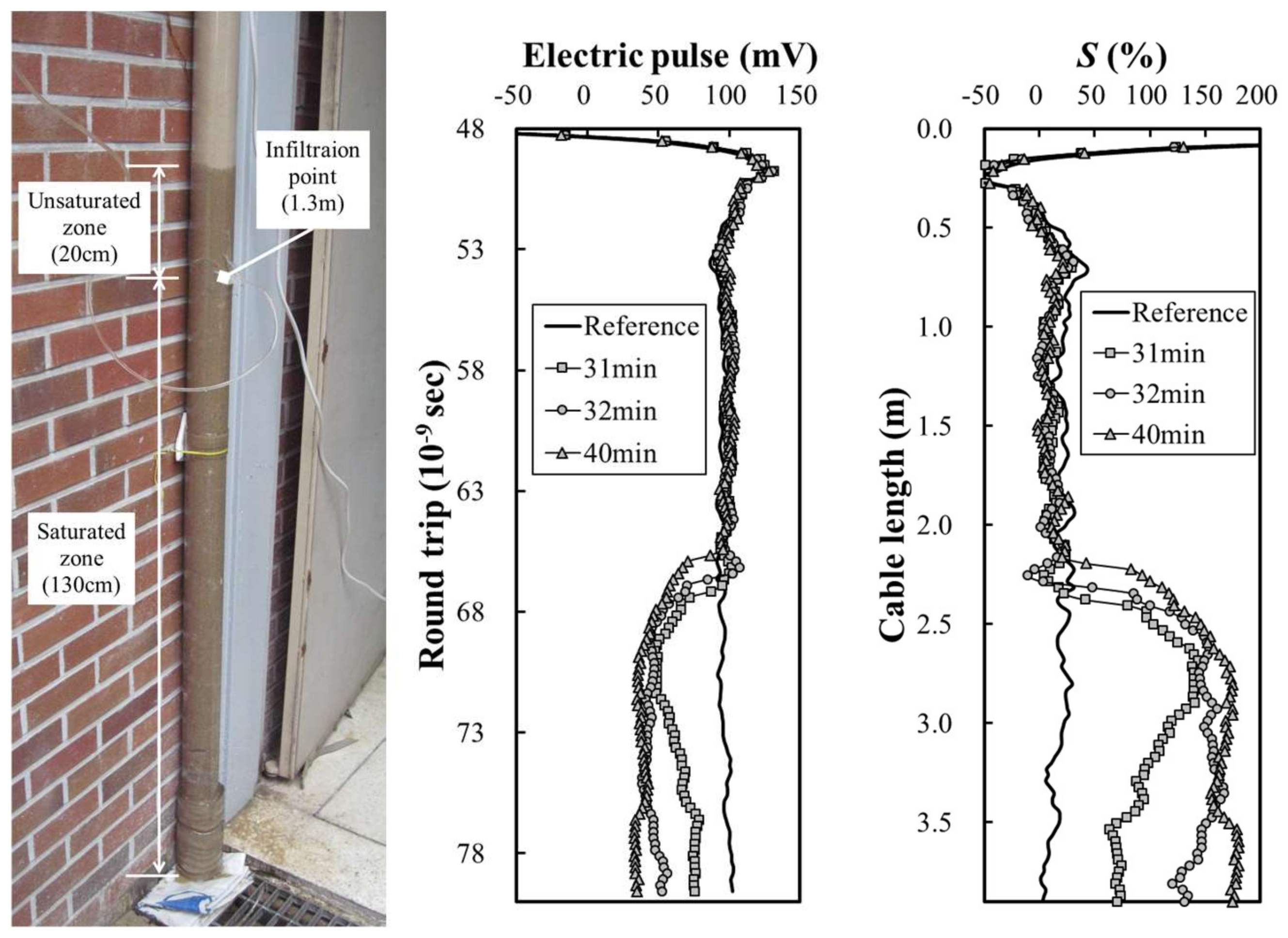
4.1. Site Preparation
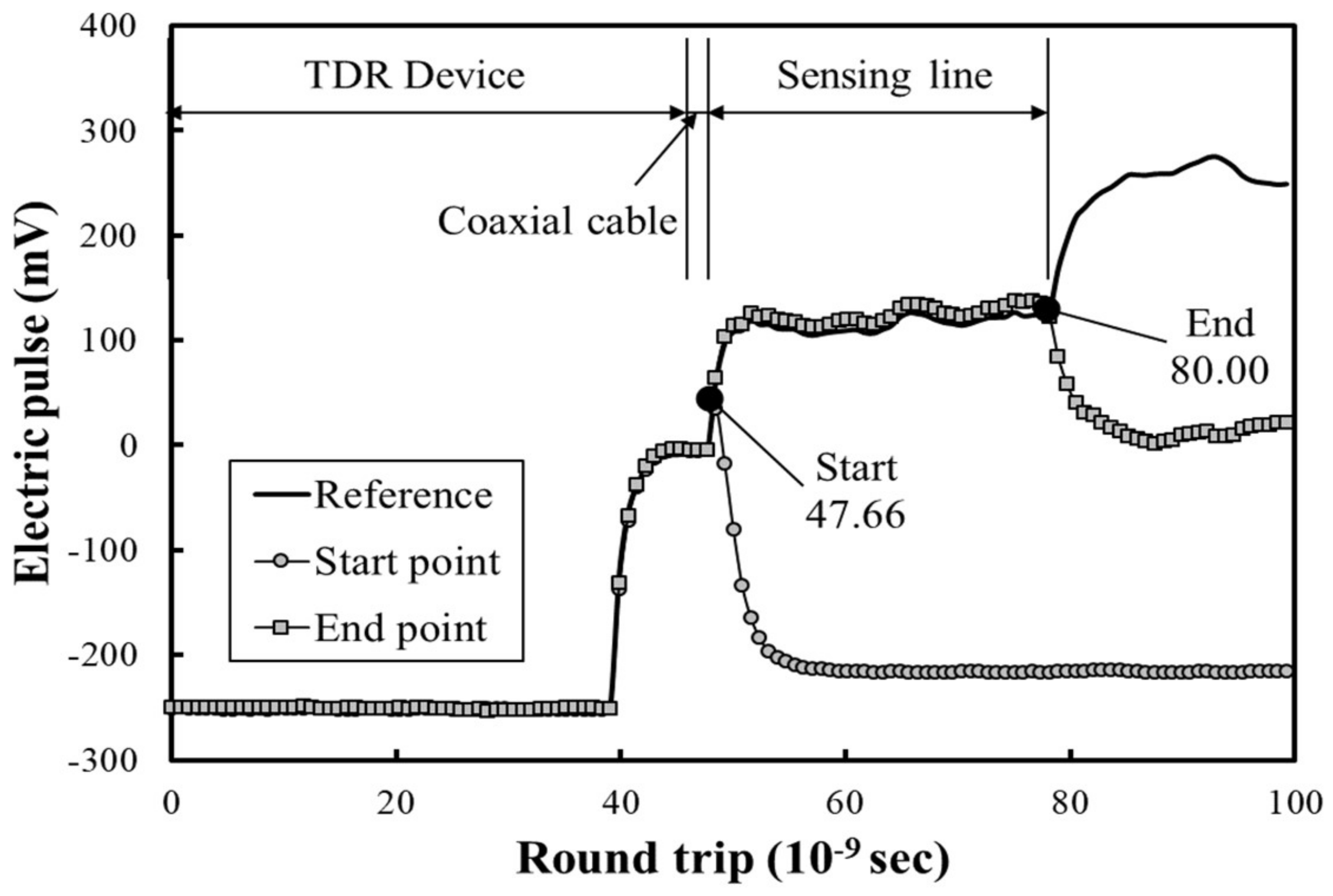
4.2. Two-Dimensional Electric Waveform of the Spatial-TDR Sensor Measured in the Field Experiment
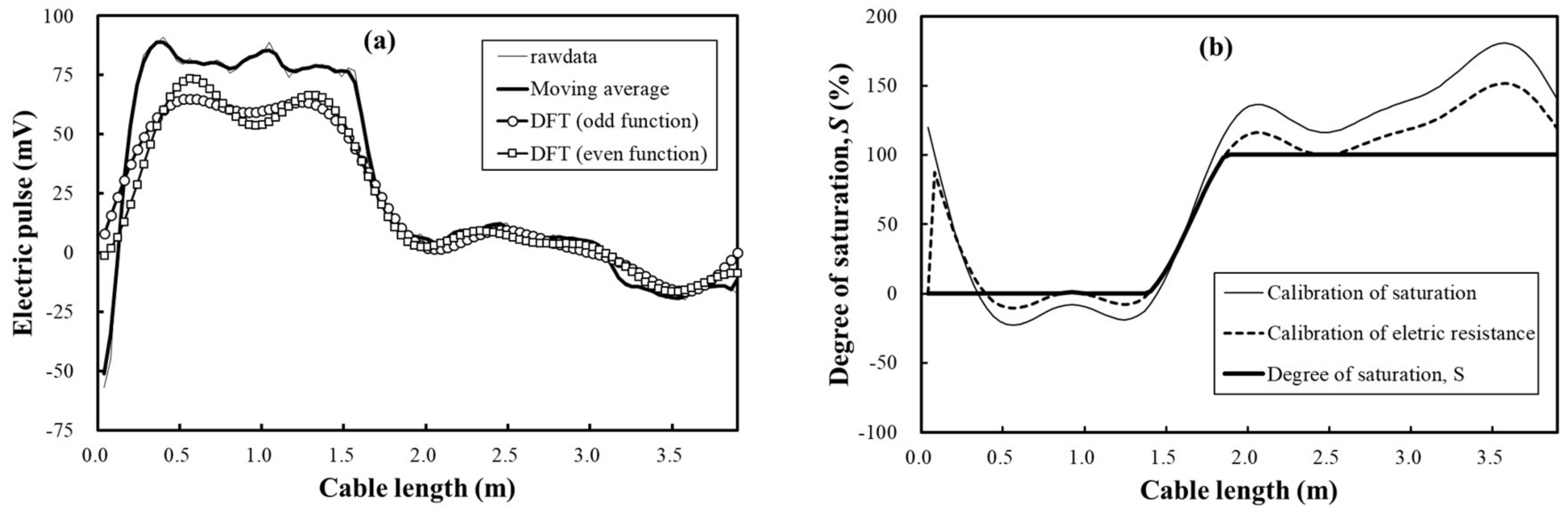
4.3. Filtering and Calibration Algorithm for Two-Dimensional Electric Waveforms
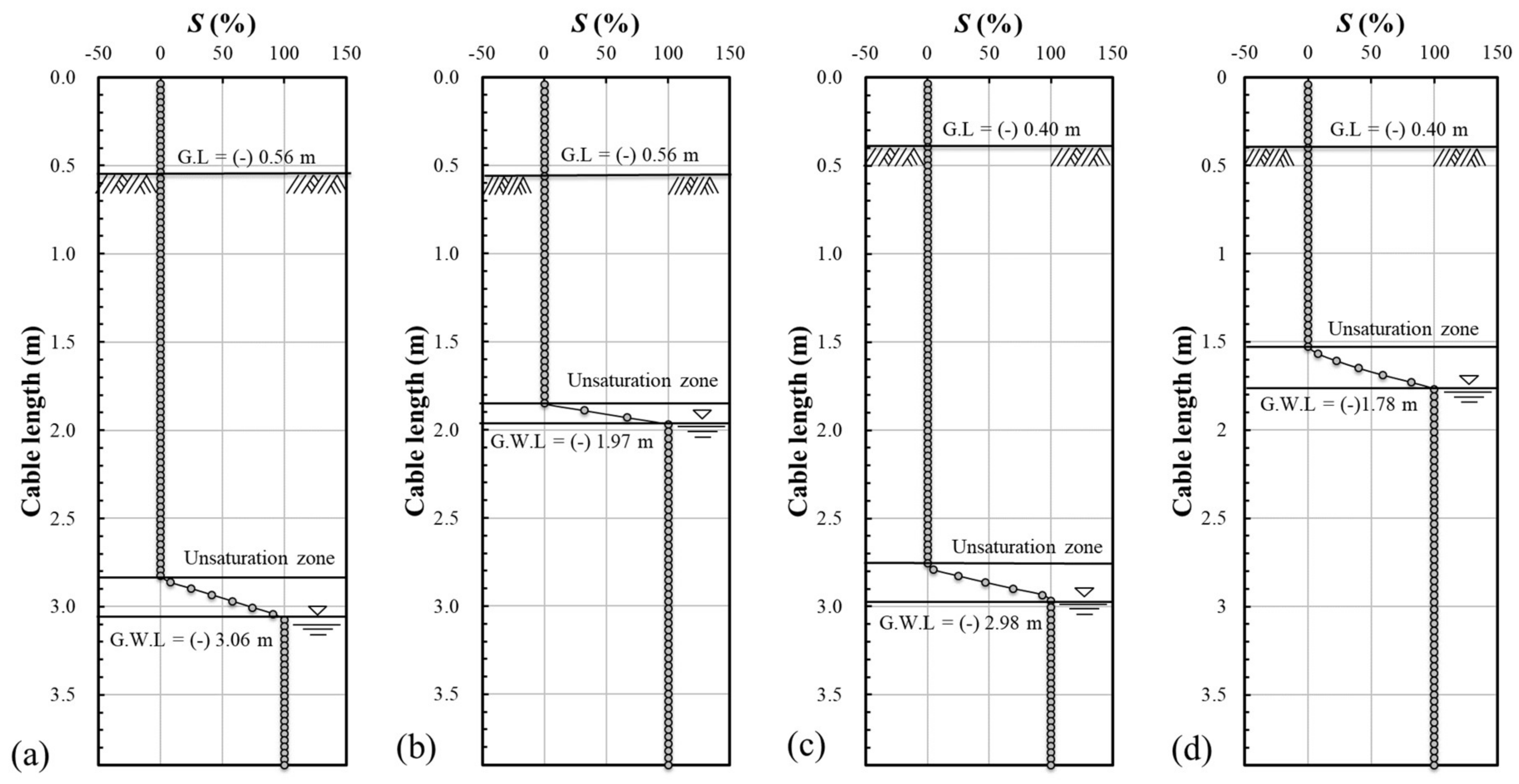
4.4. Estimation Results of Groundwater and Unsaturated Areas
5. Conclusions
Conflicts of Interest
References
- Indrawan, I.G.B.; Rahardjo, H.; Leong, E.-C.; Tan, P.-Y.; Fong, Y.-K.; Sim, E.-K. Field instrumentation for monitoring of water, heat, and gas transfers through unsaturated soils. Eng. Geol. 2012, 151, 24–36. [Google Scholar] [CrossRef]
- Park, M.C. Behavior analysis by model slope experiment of artificial rainfall. Nat. Hazards Earth Syst. Sci. 2016, 16, 789–800. [Google Scholar] [CrossRef]
- Tohari, A.; Nishigaki, M.; Komatsu, M. Laboratory rainfall-induced slope failure with moisture content measurement. J. Geotech. Geoenviron. Eng. 2007, 133, 575–587. [Google Scholar] [CrossRef]
- Tami, D.; Rahardjo, H.; Leong, E.-C. Effects of hysteresis on steady-state infiltration in unsaturated slopes. J. Geotech. Geoenviron. Eng. 2004, 130, 956–967. [Google Scholar] [CrossRef]
- Davis, J.; Chudobiak, W. In situ meter for measuring relative permittivity of soils. Geol. Surv. Can. Pap. 1975, 75, 75–79. [Google Scholar]
- Topp, G.C.; Davis, J.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef]
- Zegelin, S.; White, I.; Russell, G. A critique of the time domain reflectometry technique for determining field soil-water content. In Advances in Measurement of Soil Physical Properties: Bringing Theory into Practice; Soil Science Society of America: Madison, WI, USA, 1992; pp. 187–208. [Google Scholar]
- ASTM. Standard Test Method for Water Content and Density of Soil in Place by Time Domain Reflectometry (TDR); ASTM International: West Conshohocken, PA, USA, 2002; Volume 4. [Google Scholar]
- Drnevich, V.P. Some New Uses of Time Domain Reflectometry in Geotechnical Engineering. In Proceedings of the Soil Dynamics Symposium in Honor of Professor Richard D. Woods, Austin, TX, USA, 24–26 January 2005; pp. 1–16. [Google Scholar]
- Chen, R.; Drnevich, V.P.; Yu, X.; Nowack, R.L.; Chen, Y. Time domain reflectometry surface reflections for dielectric constant in highly conductive soils. J. Geotech. Geoenviron. Eng. 2007, 133, 1597–1608. [Google Scholar] [CrossRef]
- Chen, R.; Xu, W.; Chen, Y. Measuring dielectric constant in highly conductive soils based on surface reflection coefficients. J. Geotech. Geoenviron. Eng. 2009, 135, 1883–1891. [Google Scholar] [CrossRef]
- Dowding, C.; Pierce, C. Use of time domain reflectometry to detect bridge scour and monitor pier movement. In Proceedings of the Symposium on Time Domain Reflectometry in Environmental, Infrastructure, and Mining Applications, Evanston, IL, USA, 7–9 September 1994; pp. 7–9. [Google Scholar]
- Worsching, H.; Becker, R.; Schlaeger, S.; Bieberstein, A.; Kudella, P. Spatial-TDR moisture measurement in a large scale levee model made of loamy soil material. In Proceedings of the 3rd International Symposium on Time Domain Reflectometry for Innovative Soils Applications, Purdue University, West Lafayette, IN, USA, 17–20 September 2006. [Google Scholar]
- Scheuermann, A.; Huebner, C.; Schlaeger, S.; Wagner, N.; Becker, R.; Bieberstein, A. Spatial time domain reflectometry and its application for the measurement of water content distributions along flat ribbon cables in a full-scale levee model. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Wagner, N.; Trinks, E.; Kupfer, K. Determination of the spatial TDR-sensor characteristics in strong dispersive subsoil using 3D-FEM frequency domain simulations in combination with microwave dielectric spectroscopy. Meas. Sci. Technol. 2007, 18, 1137. [Google Scholar] [CrossRef]
- Graeff, T.; Zehe, E.; Schlaeger, S.; Morgner, M.; Bauer, A.; Becker, R.; Creutzfeldt, B.; Bronstert, A. A quality assessment of spatial TDR soil moisture measurements in homogenous and heterogeneous media with laboratory experiments. Hydrol. Earth Syst. Sci. 2010, 14, 1007–1020. [Google Scholar] [CrossRef] [Green Version]
- Fan, J.; Scheuermann, A.; Guyot, A.; Baumgartl, T.; Lockington, D.A. Quantifying spatiotemporal dynamics of root-zone soil water in a mixed forest on subtropical coastal sand dune using surface ERT and spatial TDR. J. Hydrol. 2015, 523, 475–488. [Google Scholar] [CrossRef]
- Giese, K.; Tiemann, R. Determination of the complex permittivity from thin-sample time domain reflectometry improved analysis of the step response waveform. Adv. Mol. Relax. Processes 1975, 7, 45–59. [Google Scholar] [CrossRef]
- Yu, X.; Drnevich, V.P. Soil water content and dry density by time domain reflectometry. J. Geotech. Geoenviron. Eng. 2004, 130, 922–934. [Google Scholar] [CrossRef]
- Das, B.M. Advanced soil Mechanics; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Yang, H.; Rahardjo, H.; Xiao, D. Laboratory Study of Steady-State Vertical Infiltration in Layered Soils. In Geo-Frontiers 2011: Advances in Geotechnical Engineering; American Society of Civil Engineers: Reston, VA, USA, 2011; pp. 1382–1391. [Google Scholar]
- Kim, Y. Soil Slope Design and Stability Evaluation Methodology Considering Hydraulic Conductivity and Rainfall Characteristics; Korea Advanced Institute of Science and Technology: Daejeon, Korea, 2009. [Google Scholar]










© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, M. A Study on the Development and Application of Spatial-TDR Sensor for the Management of Groundwater at Riverside. Sustainability 2018, 10, 1213. https://doi.org/10.3390/su10041213
Park M. A Study on the Development and Application of Spatial-TDR Sensor for the Management of Groundwater at Riverside. Sustainability. 2018; 10(4):1213. https://doi.org/10.3390/su10041213
Chicago/Turabian StylePark, Mincheol. 2018. "A Study on the Development and Application of Spatial-TDR Sensor for the Management of Groundwater at Riverside" Sustainability 10, no. 4: 1213. https://doi.org/10.3390/su10041213
APA StylePark, M. (2018). A Study on the Development and Application of Spatial-TDR Sensor for the Management of Groundwater at Riverside. Sustainability, 10(4), 1213. https://doi.org/10.3390/su10041213



