1. Introduction
Nowadays, generating different types of waste and the outbreak of its social, economic and environmental inconsistencies has caused many problems of collecting, transporting, processing and disposing of such waste for urban service management. Since, the main cost of the waste management is related to the transportation [
1], evaluation and optimization of this system would play an important role in reducing the imposed cost and solving the problems of urban service management.
Determining the optimal routes would lead to reduce transportation costs and improve service quality as one of the vital operational decisions in urban services organization [
2,
3,
4]. Transportation imposes some irreparable impacts on the environment. Consumption of resources, land use, toxic effects on the ecosystem and human beings, noise pollution, emission of greenhouse gases and contaminants are examples of the hazardous impacts. Besides the mentioned negative impacts, emission of the greenhouse gases is directly related to people’s health and indirectly associated with the destruction of the ozone layer. The necessity of paying attention to this topic comes from the fact that, the greenhouse gases emitted by the transportation sector are the causes for a major portion of pollution in different countries around the world [
5]. In other words, climate change has attracted a lot of attention around the world in recent years, particularly the global warming, which significantly resulted by greenhouse gas (GHG). Carbon dioxide (CO
2) is a major part of GHG. According to the Baidu Index [
6], CO
2 concentration has increased rapidly in recent years and this is going on. Therefore, minimizing fossil fuel consumption and CO
2 emissions due to vehicles’ transportation by optimizing transportation operations is a very helpful way for controlling the global warming [
7].
As such, increased concerns about the reduction of such hazardous impacts indicates the necessity of implementing a well-planned program for transportation sector, for which green routing models based on consumed fuel and air pollution can be helpful.
There are two main categories presented in routing problems related to urban waste collection [
8]. First, a set of given nodes are distributed throughout the urban graph network and the objective is to find the best routes that traverse all the nodes. The best-known problem in this category is Vehicle Routing Problem (VRP). Second, there are some predefined edges/arcs in the urban graph network and the objective is to find the best routes that traverse all the edges/arcs with positive demand. In fact, the edges/arcs denote the streets or alleys of the urban area in which the waste are distributed along them. The most applicable problem in the second category is Capacitated Arc Routing Problem (CARP).
In this research, the problem is modeled as a CARP on an undirected graph and solved accordingly. The reported results in this area mentioned that several real world activities can be modeled as CARP, headmost among them are waste collection, street sweeping, snow removal and mail collection or delivery. Whereas the CARP is a robust problem model, which was first introduced by Golden and Wong [
9], have been studied by many researchers. Dror [
10] presented the most applications of CARP variants and of related solution methods. For a further survey, the reader can also see the research done by Assad and Golden [
11].
Even though CARP is a well-known concept in operational research but only limited research and extensions have been studied in this respect. This important routing problem was first introduced by Golden and Wong [
9]. CARP refers to the set of problems wherein a fleet of vehicles originally located in one or more depots delivering services on road networks; the main examples of these services include municipal waste collection, snow removal, pouring salt on snows and road surveying. The roads are represented by edges or arcs across these networks. Each edge contains two arcs with different directions. The services should be delivered in such a way to minimize the associated cost. By starting from the associated central depot, the vehicle delivers the planned service and then returns back to the depot. Each vehicle has a certain capacity and all routes are both originated from and terminated to the origin (central depot).
Most of the research works performed in this respect have attempted to achieve economic objectives by focusing on minimization of traveled distance, required time, or the number of vehicles required but failing to take environmental objectives and pollution reduction into consideration is so remarkable. So, the crucial aspects of the research are listed as below:
- -
Environmental involvement
- -
Economic transportation system
- -
Real world assumptions
- -
Mathematical model limitations
- -
Efficient solution methods
We survey the literature for three different parts of solution methods and possible extensions of the problem, green aspects of the problem with different existed solution methods and some novel studies in the vehicular technologies and related solution methodologies applicable to the routing problems. In the first part, some important research is investigated in terms of different solution methods and different applications of the CARP. Ghiani et al. [
12] solved CARP with intermediate facilities (CARP-IF) by considering capacity and distance constraints using a new Ant Colony Optimization (ACO) that an auxiliary graph is used in it. Experimental results indicated that their proposed algorithm was able to make substantial improvements over the known heuristics. Li et al. [
13] solved a waste collection problem in Porto Alegre, Brazil that has a population of over 1.3 million people and consists of 150 districts. They made a truck scheduling operational plan with the objective of minimizing operating costs and fixed costs of trucks. Furthermore, they proposed a heuristic approach to balance number of travels between facilities. Computational results indicated that they could reduce the average number of required vehicles and the average traveled distance of 27.21% and 25.24% respectively.
Laporte et al. [
14] presented a CARP problem considering stochastic demands which will cause failure in paths because of exceeding from vehicle capacity. They solved the problem by a neighborhood search heuristic algorithm. Khosravi et al. [
15] presented a periodic CARP (PCARP) with mobile disposal sites specific to the urban waste collection. They tested two versions of the Simulated Annealing (SA) algorithm to solve the problem. Their proposed algorithm showed an appropriate performance in comparison with CPLEX.
Babaee Tirkolaee et al. [
16] investigated a novel mathematical model for the robust CARP. The objective function of their proposed model aimed to minimize the traversed distance considering the demand uncertainty of the edges. To solve the problem, they developed a hybrid metaheuristic algorithm based on a SA algorithm and a heuristic algorithm.
Recently, Tirkolaee et al. [
1] developed a Mixed-Integer Linear Programming (MILP) model for the multi-trip CARP in order to minimize total cost in the scope of the urban waste collection. In the proposed model, depots and disposal facilities were located in different places specific to the urban waste collection. They proposed a hybrid algorithm using the Taguchi parameter design method based on an Improved Max-Min Ant System (IMMAS) to solve well-known test problems and large-sized instances. They could demonstrate the high efficiency of their proposed algorithm. Hannan et al. [
17] proposed a Particle Swarm Optimization (PSO) algorithm in order to solve a Capacitated VRP (CVRP) with the aim of finding the best waste collection way and optimal routes. They could prove the efficiency of their algorithm in different datasets.
Rey et al. [
18] developed a hybrid solution method based on ACO heuristics, Route First-Cluster Second methods and Local search improvements to obtain high quality solutions for VRP in comparison with other metaheuristic solvers.
Tirkolaee et al. [
19] proposed a novel mathematical model for the robust PCARP considering working time of the vehicles. They developed a hybrid SA algorithm in order to solve the problem approximately. The obtained results showed that their proposed algorithm could generate appropriate robust solutions.
In the second part of the literature, Green VRP (G-VRP) and its different applications are investigated which deal with the optimization of energy consumption of transportation. The G-VRP was mainly studied since 2006 [
19]. Lin et al. [
20] presented a review research in the field of G-VRP and its past and future trends. Miden et al. [
21] investigated time window-constrained VRP wherein speed was dependent on travel time. They further proposed a heuristic for solving the problem and ended up with 7% saving in CO
2 emission in a case study in England.
Erdoğan and Miller-Hooks [
22] formulated a G-VRP and developed some solution methods to consider fuel-powered vehicles to cope with the limited refueling infrastructure in the problem. They could generate acceptable solutions using the modified Clarke and Wright Savings heuristic and the Density-Based Clustering (DBC) algorithm.
Kopfer et al. [
23] did some research on the analysis of different costs incurred through pollution and environmental impacts. They presented a mathematical model and evaluated it by CPLEX solver. Tavares et al. [
24] studied the effects of road slope and vehicle load on consumed fuel in waste collection problem; however, they considered three levels of load only: half load (during waste collection), full load (traveling to the disposal site) and no load (when returning to the depot). In their research, the relationship between fuel consumption rate and load was not considered. In the meantime, it is obvious that, when a vehicle serves a node, its losses some its load, which translates into lower fuel consumption along the rest of the route. Therefore, it is necessary to consider load-dependent fuel consumption for calculating total cost more accurately.
Mirmohammadi et al. [
5] presented a multi-trip time-dependent periodic G-VRP considering time windows for serving the customers with this assumption that urban traffic would disrupt timely services. The objective function of the proposed problem was to minimize the total amount of carbon dioxide emissions produced by the vehicle, earliness and lateness penalties costs and costs of used vehicles. They used CPLEX solver to solve the problem exactly.
Stochastic G-VRP has been investigated in some research in which some parameters are considered to be stochastic such as vehicle speed, breakdown rate of vehicles [
25,
26]. Recently, Poonthalir and Nadarajan [
27] presented a bi-objective G-VRP, considering various speeds and fuel efficiency. They minimized the travelling cost and fuel consumption using goal programming and Particle Swarm Optimization (PSO). As a recent applied high efficiency solution method in the field of study, Kulkarni et al. [
28] proposed a novel two-stage heuristic based on the inventory formulation for the recreational Vehicle Scheduling Problem (VSP).
As the last part of the literature, Wang et al. [
29,
30,
31] proposed some mobile sink based routing methods to the routing process, which can largely improve network performance such as energy consumption and network lifetime. On the other hand, there are some novel technologies that would be applicable to the problem such as conversion of CO
2 into clean fuels, autonomous vehicle control and so on [
32,
33,
34,
35,
36,
37].
Uebel et al. [
35] conducted the study of a novel approach that combines discrete state-space Dynamic Programming and Pontryagin’s Maximum Principle for online optimal control of hybrid electric vehicles (HEV). They considered engine state and gear, kinetic energy and travel time are considered states in this paper besides electric energy storage. They could demonstrate the high quality of the generated solutions in comparison with a benchmark method. Woźniak and Polap [
36] developed a hybrid neuro-heuristic methodology for intelligent simulation and the control of dynamic systems over time interval specific to the model of electric drive engine vehicle.
Alcala et al. [
37] presented the control of an autonomous vehicle using a Lyapunov-based technique with a LQR-LMI tuning. They could apply a non-linear control strategy based on Lyapunov theory for solving the autonomous guidance control problem.
After reviewing the literature in different aspects, it is perceived that all of the research contains different solution methods so that each has its own advantages. Therefore, in this research, the most applied metaheuristic algorithms that is, SA and GA are combined together in order to keep the advantageous of each one. On the other hand, the applied local search procedures are defined innovatively in line with the problem solution space.
Accordingly, this research is aimed at presenting a novel model for the multi-trip CARP of urban waste collection which not only brings about economic benefits (minimizing the fixed cost of used vehicles) but also reduces adverse impacts of the CO2 emission in air pollution considering advantages for the environment and people’s health. Also, a Hybrid Genetic Algorithm (HGA) is developed to solve the problem efficiently.
Therefore, the main novelties of the present paper are briefly as follows: (1) presentation of the multi-trip Green Capacitated Arc Routing Problem (G-CARP) which has not been yet introduced in the literature to the best of our knowledge; (2) since this paper is related to municipal solid waste management, loading, unloading sites and vehicle depots are commonly located in different places so that two separate locations are considered for the depot and unloading site in the model to make it closer to real world; and (3) developing a customized efficient solution method.
The remaining of the paper is organized as follows:
Section 2 describes the distance-oriented green capacitated arc routing problem studied in this paper.
Section 3 presents the proposed algorithm.
Section 4 discusses the computational results. Finally, the concluding remarks and outlook of the research are presented in
Section 5.
2. Distance-Oriented Green Capacitated Arc Routing Problem
The assessment of fuel consumption and CO
2 emission for vehicles requires performing complicated computations which only shows an estimation and approximation due to the difficulty of determining some of the fundamental variables values such as road slope, driving mode, weather conditions, accidents and so on [
38].
The investigations performed on CO
2 emission are based on either fuel consumption or traveled distance. Based on an initiative approach of greenhouse gases protocol [
39],
Table 1 lists the required criteria for determining feasibility of each of these methods [
39]. In one hand, in the fuel-oriented method, the fuel consumption is multiplied by CO
2 emission factor for the fuel type. On the other hand, in the distance-oriented method, CO
2 emission can be calculated using the distance-oriented emission factors. A fuel-oriented emission factor is developed based on fuel heat values, the fraction of fuel carbon which reacts with oxygen and carbon content coefficient. The distance-oriented method can be used when the data related to the traveled distance by the vehicle is available. Making a decision regarding which of these two methods is used, depends on the data accessibility.
It is clear that trying to obtain a theoretical formulation of this problem, the distance-oriented method (wherein CO2 emission is calculated based on traveled distance and distance-based emission factors) is easier to apply. This requires taking two main steps: (1) collecting data on traveled distance by a given vehicle and fuel type (e.g., km or ton-km); and (2) converting the distance estimations to CO2 emissions by multiplying the obtained results from step 1 by the distance-based emission factors.
In addition, the CO
2 emission calculations are based on the assumption that all of this computation depends mainly on two factors: type of the vehicle and type and quantity of the consumed fuel. Furthermore, this means that the emission is a function of two factors: transportation types (the vehicle and its load) and traveled distance [
40]. Therefore, CO
2 emission estimations differ depending on the vehicle mass and transported load, which is an important parameter [
41].
As it is presented in
Table 2, emission estimation factor goes through the two main steps mentioned earlier. The first step includes estimating a fuel conversion factor using chemical reaction of fuel combustion (C
13H
28 + 20 O
2 → 13 CO
2 + 14 H
2O) [
42]. Given the molecular mass of diesel (C
13H
28) and CO
2 (184 and 24, respectively) and knowing that there are 13 CO
2 molecules for each diesel molecule, one can simply find that for each kg of diesel, 13 × 44/184 = 3.11 kg of CO
2 is produced. Then, using diesel density (0.84 kg/L), one can calculate the produced CO
2 per liter of consumed diesel (3.11 × 0.84 = 2.61 kg). It is observed that this estimated theoretical conversion factor is well close to that experimentally obtained by Defra (2.63 kg) [
43], providing conversion factors for greenhouse gases, so as to use existing data resources and convert them to equivalent CO
2 emission data. Subsequently, having the fuel conversion factor (2.61 kg of CO
2/L of diesel), the second step is to estimate emission factor (
ε). In this step, a function incorporating the data on average consumption depending on load is defined.
Table 2 shows estimated value of this factor for several different capacity scenarios for a truck of 10 tons in capacity [
39].
Accordingly, the presented information is generalized to our problem by considering the impact of CO2 emission and conversion factors.
2.1. Mathematical Model of G-CARP in the Scope of Municipal Services
As the main difference between VRP and CARP, CARP consists of determining optimal routes that traverse all the edges with positive demands (required edges), however, VRP consists of finding optimal routes that traverse all the nodes defined in a graph network [
1].
Consider a graph of G = (V, E) including the set of V for all the nodes constituting the edges and the set of E for all the edges defined in the network. The proposed G-CARP involves determining the optimal number of vehicles and optimal routes for each vehicle to minimize an overall objective function involving the cost of using the vehicles and the cost of total CO2 emission throughout the network which has a direct relation with total traveled distance. The vehicles are originally located in depot; then start traveling (their first trip) to serve the required arcs and once their capacity limitation is reached, proceed to the unloading site to empty their loads. If possible, they continue traveling (their second trip) from the unloading site to the operational area. Having more than one trip for each vehicle directly depends on the capacity constraint and the maximum available time of vehicles. When the remaining time for a vehicle becomes zero, it shall return to the unloading site where it is unloaded before returning back to the depot.
Node 1 denotes the depot and node n denotes the unloading site in the network graph.
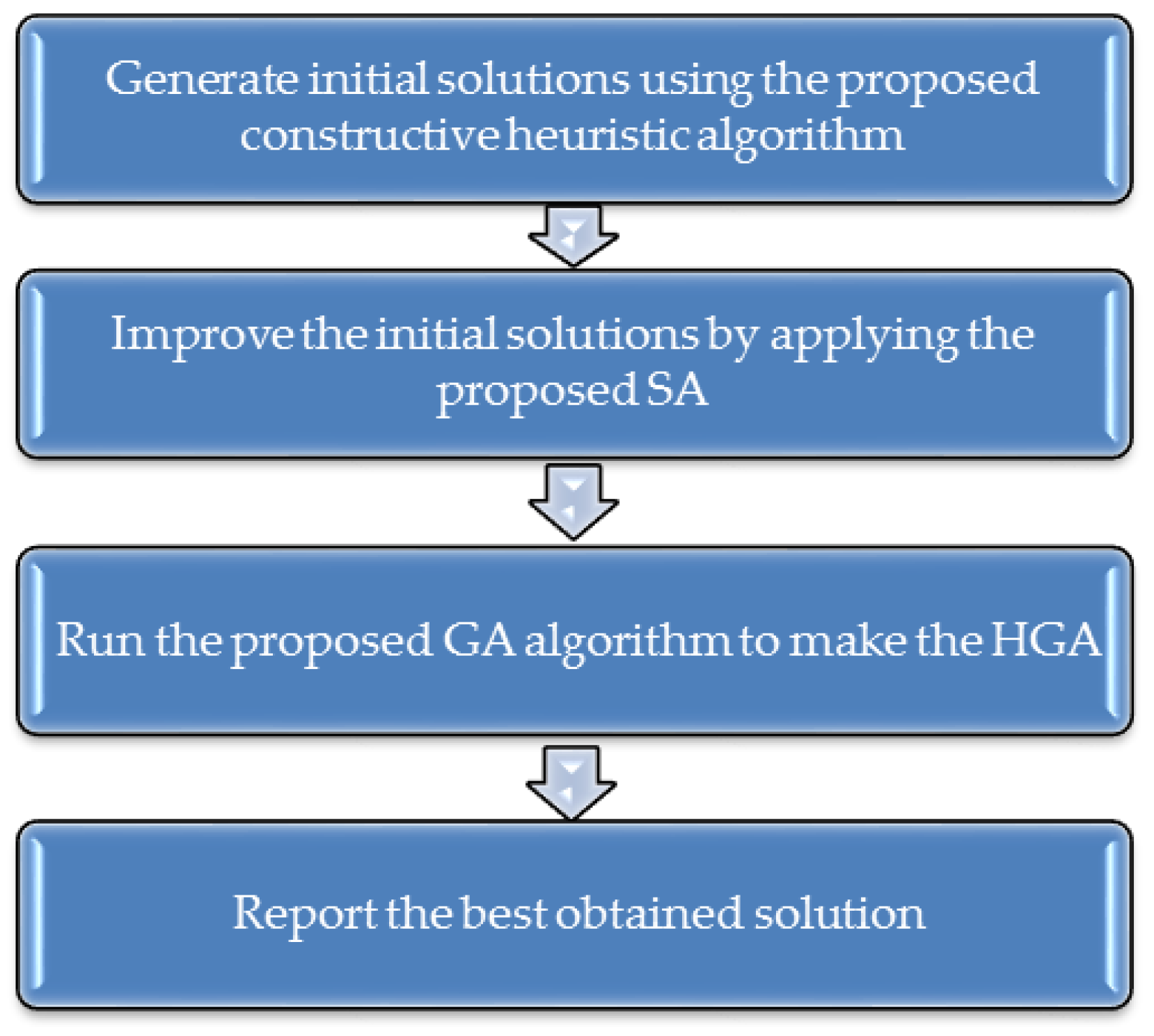
The main steps of the research and modeling the problem are described in
Figure 1 before the model being presented.
Sets
| V | The set of the network nodes |
| K | The set of the available vehicles |
| Pk | The set containing pth trip by the kth vehicle |
| E | The set of all edge defined across the network |
| ER | The set of all required edge defined in the network |
| S | An optional set of all edges defined in the network |
| V[S] | The set of nodes defined in the set S |
Parameters
| tij | The time it takes to traverse the edge (i, j), where (i, j) ∈ E |
| dij | Demand of the edge (i, j), where (i, j) ∈ E |
| cij | Distance (length) of the edge (i, j), where (i, j) ∈ E |
| eij | CO2 emission along the edge (i, j), where (i, j) ∈ E |
| Ψ | Cost conversion factor per CO2 emission unit |
| cvk | Cost of activating kth vehicle |
| Tmax | Maximum time available for each vehicle |
| Wk | Capacity of kth vehicle |
| G | A very large number |
Decision variables
Mathematical model
The objective function consists of two parts. The first part includes minimization of total CO2 emission cost while the second part attempts to minimize the cost of using (renting) the kth vehicle. Constraints (5) denote the flow balance for each vehicle, that is, it controls input to output from each intermediate node constituting two arcs. Constraint (6) ensures that each required edge is served by one of its two constituting arcs. Constraint (7) indicates the capacity constraint of the kth vehicle. Constraint (8) expresses that the required edge is served by the vehicle traveling through it (or there are chances that a vehicle travels through an edge without having the edge served). Constraint (9) stipulates that the kth vehicle will be used when the associated cost is paid. Constraint (10) represents the maximum time limitation considered for each vehicle. Constraints (11) and (12) ensure that the first trip of the vehicle starts from the depot and ends at unloading site. Constraints (13) and (14) make sure that from the second trip to the next (if any), the trips start and end at the unloading site. Constraint (15) ensures that no sub-tour will be constructed.
Total CO
2 emission is based on the environmental matrix (
e) which is calculated by considering the matrix containing distances between each pair of nodes constituting edge (
i,
j) and respective emission factor (
ε).
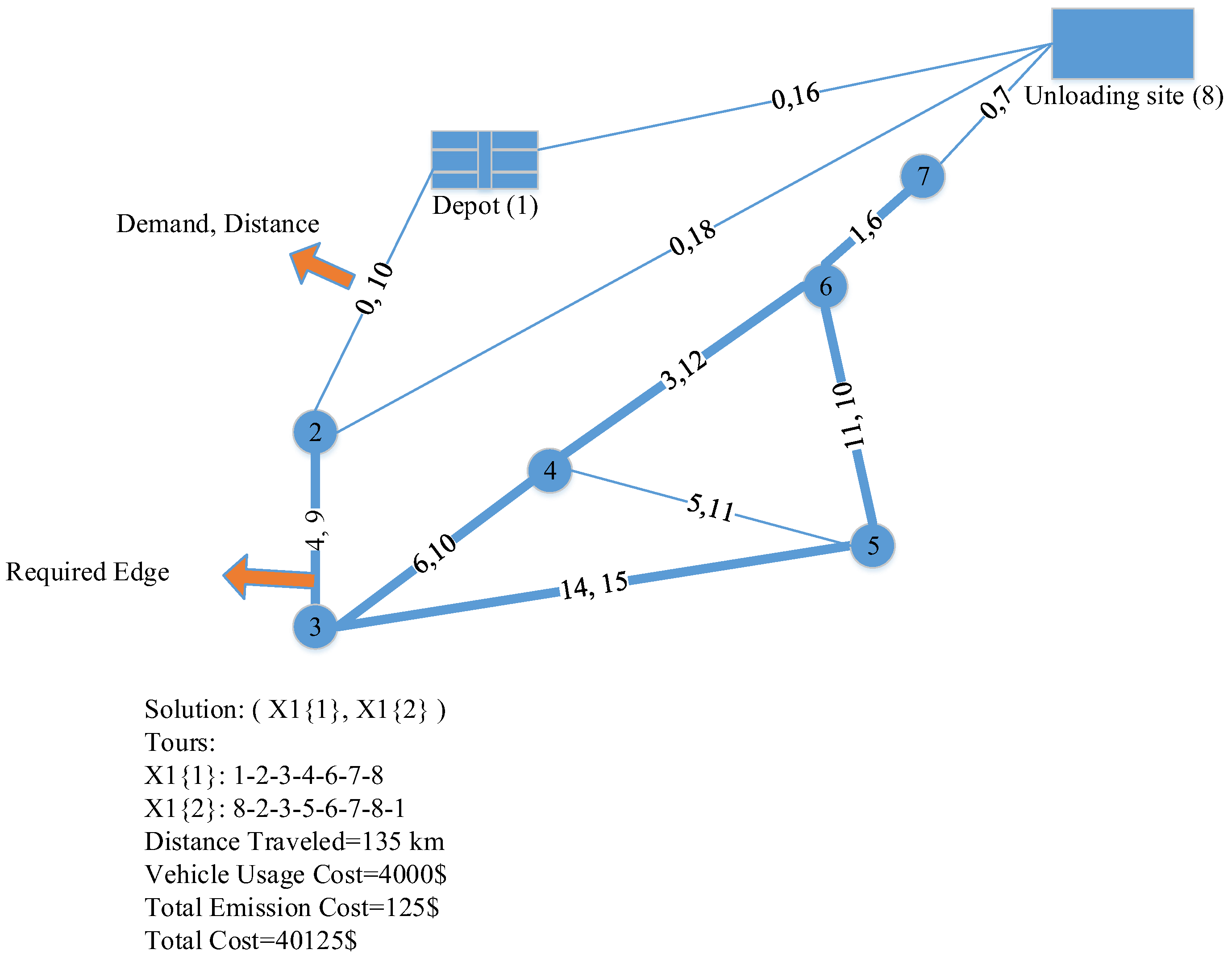
In order to gain a better understanding, an example with four required edges and two available vehicles is demonstrated in
Figure 2. Nodes 1 and 8 represent the depot and unloading site, respectively. In this figure, the numbers indicated on each edge refer to the demand and length of the edge. It is assumed that the lengths of the edges are equal to their traversing time. The required edges are marked by solid lines (e.g., the edge (2, 3)). Vehicle 1 has the capacity of 40 units and the usage cost of 4000
$. Vehicle 2 has the capacity of 50 units and the usage cost of 5000
$. Maximum available time for each vehicle is equal to 200 units. In this example, vehicle 1 is used and constructs two trips in order to serve all the required edges.
By solving the final proposed model considering appropriate input parameter value and considering time periods, the obtained results will be reliable and applicable in an urban area and would definitely lead to huge cost savings as a real time application.
2.2. Limitations of the Adopted Model
The applicable limitations of the proposed adopted model are listed as below:
- (1)
It is just applicable for a specific time period and it cannot include a planning horizon. As it is obvious the demand of different periods may be different and it would change the obtained results.
- (2)
The exact fuel consumption rate is not accessible due to the hardness of computing the exact effects of the road slope, temperature conditions, load volume and so forth.
4. Numerical Results
In this section, in order to validate the proposed mathematical model and to evaluate the performance of the proposed algorithm, 15 random instances of various sizes are generated. After solving instances with the exact method and analyzing the obtained results, it has been revealed that the proposed model has passed its validity test.
For all of the instances, two types of vehicle (types 1 and 2) with capacities and activation costs of 5 and 7 tons and 400
$ and 500
$, respectively, were considered. Supporting information and network structure are demonstrated in
Table 4. The input parameters values are generated randomly with a uniform distribution.
In
Table 4, column 1 denotes the instance number, column 2 defines the total number of edges, column 3 gives the number of required edges and columns 4 and 5 show numbers of available vehicles of types 1 and 2, respectively, for each instance. The emission factors of the vehicles are described in
Table 5. Also,
Ψ is equal to 10 in all instances.
The 15 instances are then solved using CPLEX solver of GAMS Software, the proposed SA and HGA separately for the applied run time constraint of 3600 s. The aim of investigating SA and HGA separately is to make the impact of applying GA on SA more obvious. In fact, HGA is the result of applying GA on SA.
The obtained results are shown in
Table 5. The solution methods are executed on a Laptop equipped with Core i7 CPU @ 2.60 GHz processor and 12.00 GB of RAM.
As it is obvious in
Table 6, CPLEX is not capable of finding a solution for some problems by applying the 3600 s run time limitation. Results have shown that the proposed HGA has appropriate efficiency in comparison with SA and CPLEX. However, SA could solve the problems at a lower run time against HGA, however, this difference is negligible due to the significant better Gap percentage (
Figure 5). The average gaps obtained by SA and HGA are 2.66% and 1.64%, respectively. On the other hand, the capability of the proposed solution methods is evaluated through solving P15–P18. As it is obvious, CPLEX could report the best found solution up to the first 15 problems. For P16–P17, there is a significant increase in run time of SA and HGA and for P18, none of the algorithms are able to find any solution within 3600 run time limitation. It shows that some additional modification may be needed to be applied to improve the efficiency of for solving very large sized problems. The number of used vehicles in each instance problems is presented in
Table 7 for different solution methods. As it is obvious, there are no significant differences between the number of used vehicle types 1 and 2.
As another advantage of the proposed algorithm, it can solve the large sized problems with a reasonable low run time in comparison with the algorithms proposed in the literature like Improved Max-Min Ant System (IMMAS) [
1].
Sensitivity Analysis
In order to investigate the effects of changing some parameters on the value of the objective function, a sensitivity analysis is performed on these parameters of the first fifteen problems by HGA. In fact, the behavior of the objective is studied in front of the uncertain environment if the considered value of a parameter changed. On the other hand, managers are willing to know how much benefits would be gained if they assign more resources. In fact, they want to know about the relation defined between objective function and the value of the assigned resources. In this research, the effects of the maximum available time of each vehicle on the objective are analyzed. Four different executive values (i.e., 360, 480, 550 and 600 min) are considered for the parameter while the other parameters are constant.
Results of the sensitivity analysis on
Tmax are given in
Table 8. The most important conclusion drawn from the analysis is that the higher the
Tmax is, the lower objective function and the lower number of the used vehicles are.
As it is clear in
Figure 6, the objective value will increase significantly by changing
Tmax to 360 min. In other words, the worst case is obtained by
Tmax of 360. The difference between the objective values obtained by
Tmax of 550 and 600 is proportionally the lowest.
Table 9 shows the cost savings obtained by different
Tmax value.
In order to optimize associated costs, managers should consider the impact of these maximum vehicle usage times and set an appropriate upper limit to gain maximum cost saving. As it is presented in
Table 9, the average cost saving for
Tmax of 360 is not a positive value that is, it causes the loss for all instances. The average cost savings for
Tmax of 550 and 600 are equal to 374.00 and 507.80, respectively. Finally, the performed sensitivity analysis can be used as a managerial tool to be applicable in decision making processes.