1. Introduction
The Korean steel industry as a whole has been recently trying to secure new overseas markets. The companies choosing to look overseas for work are taking on significant risks in this venture due to the uncertainty of international investments, much larger than that of domestic investments. Many of them have suffered major losses from poor investments caused by entering international markets hastily. To mitigate these risks, companies prefer to organize a consortium consisting of local companies rather than make a direct, sole overseas investment. When several companies as investment sponsors (or developers) establish a Special Purpose Company (SPC), the required capital for resultant project(s) must be financed through Project Financing (PF). However, PF has higher interest rates than Corporate Financing (CF) because PF is a type of credit loan without recourse to the sponsors, whereas CF is financed by a company’s own assets with collateral securities, typically used on domestic projects. For sponsors to be successful internationally, a method is needed to lower project interest rates, ensuring sustainable profits. Moreover, as major collateral securities for the investment sponsors for PF, offtake-agreements (as purchasing agreements so-called long-term forward contracts with the recourse buyers) have not been arranged historically for the steel production industry. Instead, the trade of the production steel resources has been done at steel spot markets as a commodity like LME (London Metal Exchange). Therefore, PF has not been fully utilized in the steel industry and has big risks when used in investments abroad. For these reasons, the authors will consider the feasibility of sponsors using MF, which is a type of PF that could provide a comparatively lower interest rate.
This study investigates the feasibility of using option-based MF to supplement the high interest rates of PF. To set this discussion, the paper begins with an overview of previous literature on project capital procurement methods followed by a description of the basic concepts and characteristics of PF and MF. The possibility of improving the profitability through combination of PF and MF is analyzed by conducting an MCS of the profitability. These findings are validated through a case study [
1,
2].
2. Literature Review
A literature review for previous studies was carried out to understand how PF is implemented to improve profitability of the sponsors. Milton Haris and Artur Raviv [
3] proposed the capital structure theories based on agency costs, asymmetric information, product/input market interactions, and cooperate control consideration. They tried to prove the capital structures based on the mathematical models and showed the relationship between leverage and exogenous factors like profitability and characteristics of the product market. However, as they applied the traditional CF for financing modeling, the increase in the project’s profitability was not found.
Alternatively, Sandalkhan Bakatjan [
4] proposed an interest scheme in the Build/Operate/Transfer (BOT) for infrastructure projects that were rapidly growing. They presented a simplified model to determine the optimum equity level for the decision makers and sponsors at the beginning of the evaluation stage of BOT hydro-electric power plants. Similar to the study of this paper, they tried to make a ‘combination’ between a financial model and a linear programming model to incorporate the objective of maximizing the benefit from the equity. Through research, they found different equity levels for optimal capital structure in BOT projects which supports the project sponsors to ensure the required equity level. Although they proposed a meaningful idea to merge a financing model and a programming model, they could not evaluate and prove the increase in profitability.
Finally, James A. Milers and John R. Ezzell [
5] found that for financial management to make properly informed decisions concerning maximizing capital budgeting, a correct determination is required for a project’s levered cash flows. However, although many good solutions based on existing CF or PF have been suggested in the paper, a new concept such as the combination of PF and MF has not been suggested. Therefore, they could not propose lower interest rates as long as the rate was fixed according to the model of CF or PF, and also could not expect high profitability in comparison to present financing methods.
Contrary to the previous studies by others, in this paper, the result of the MF study shows that it is the optimal capital structure when considering different factors, which directly affects sustainable profitability based on the low interest rate when compared to PF depending on the type of capital used by the company. In addition, either method can be used to evaluate the firm value because the result is the same when evaluating the firm value through capital costs, which are the Weighted Average Cost of Capital (WACC) and Adjusted Present Value (APV). A review of studies related to PF now follows [
5].
Even though many studies have been done for PF and CF respectively, no proper alternative types of financing have been suggested. Therefore, this paper could change the fundamental idea for historical financing methodologies.
3. Definition for Financing Terminologies
As the publication of this paper is not a financial one, the readership of this paper may be of varying financial competency. To ensure the reader has a basic understanding of the terminology used, below is a basic definition of the fundamental financing terms used in this paper.
3.1. Classification of Financing
Financing is needed to start a business and ramp it up to profitability. There are several sources to consider when looking for start-up financing. First one needs to consider how much and at what time money is needed. The financial needs of a business will vary according to the type and size of the business. For example, processing businesses are usually capital intensive, requiring large amounts of capital. Retail businesses usually require less capital [
6].
Debt and equity are the two major sources of financing. Government grants to finance certain aspects of a business may be an option. Also, incentives may be available in certain communities to encourage activities in particular industries. These are described below.
3.1.1. Equity Financing
Equity financing is the exchanging of a portion of the business ownership for a financial investment. Said ownership stake resulting from an equity investment allows the investor to share in the company’s profits. Equity involves a permanent investment in a company and is not repaid by the company at a later date. The investment is also properly defined in a formally created business entity. An equity stake in a company can be in the form of membership units, as in the case of a limited liability company, or in the form of common or preferred stock as in a corporation. Companies may establish different classes of stock to control voting rights among shareholders. Similarly, companies may use different types of preferred stock. For example, common stockholders can vote while preferred stockholders generally cannot. Common stockholders are last in line for the company’s assets in case of default or bankruptcy. Preferred stockholders receive a predetermined dividend before common stockholders. Equity financing incudes personal savings, friends and relatives, venture capital, angel investors, governmental grants, equity offerings, public offerings and warrants [
7].
3.1.2. Debt Financing
Debt financing involves borrowing funds from creditors with the stipulation of repaying the borrowed funds plus interest at a specified future time. For the creditors (those lending the funds to the business), the reward for providing the debt financing is the interest on the amount lent to the borrower. Debt financing may be secured or unsecured. Secured debt has collateral (a valuable asset which the lender can attach to satisfy the loan in case of default by the borrower). Conversely, unsecured debt does not have collateral and places the lender in a less secure position relative to repayment in case of default. Debt financing (loans) may be short term or long term in their repayment schedules. Generally, short-term debt is used to finance current activities, such as operations, while long-term debt is used to finance assets such as buildings and equipment. Debt financing includes friends and relatives, banks and other commercial lenders, commercial finance companies, governmental programs and bonds [
7].
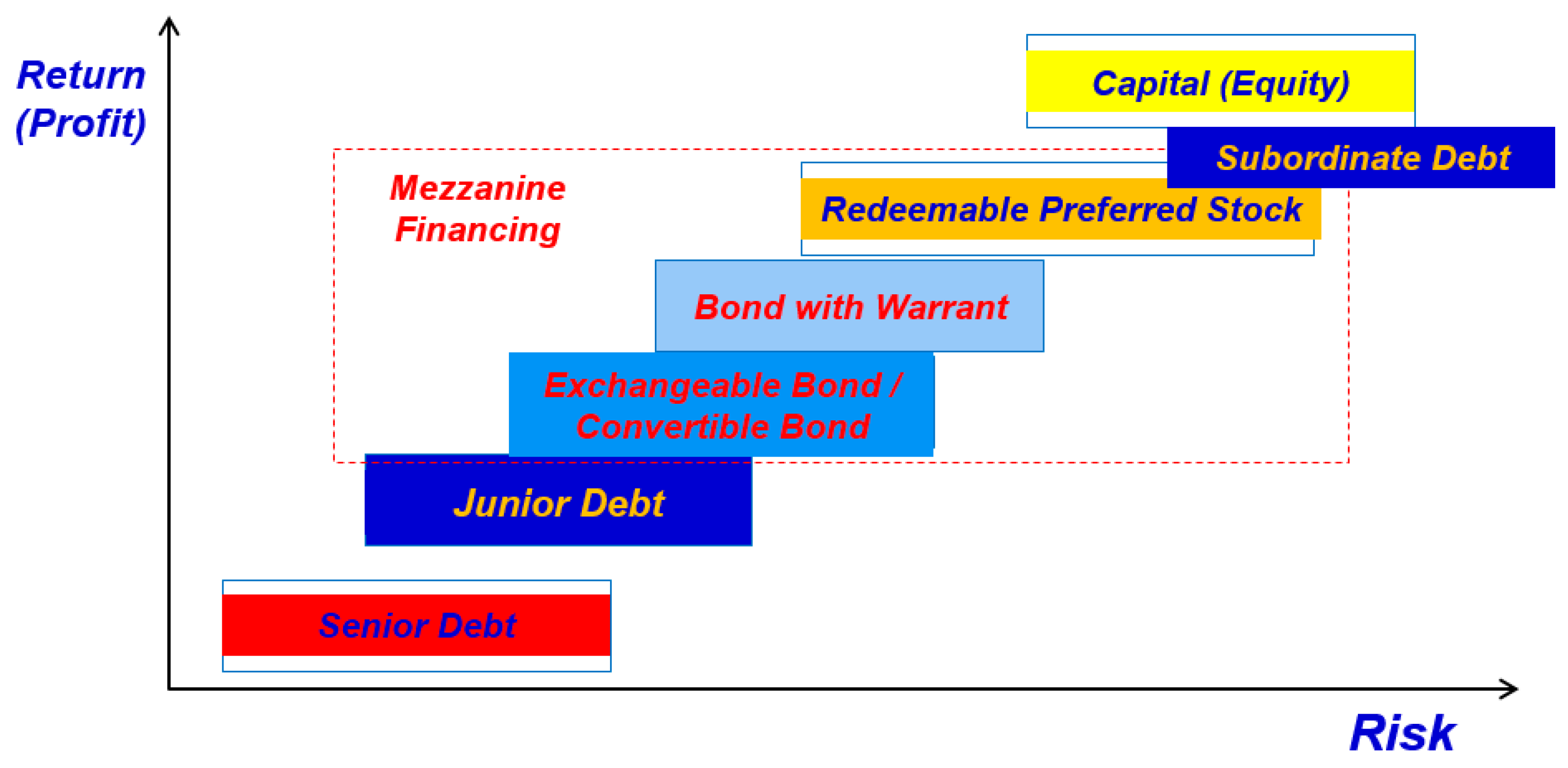
There are two types of loans for debt financing, senior and junior loans. Senior loan is debt that takes priority over other unsecured loans and has greater seniority in the issuer’s capital structure than subordinated debt, as shown in
Figure 1. In the event the issuer goes bankrupt, senior debt theoretically must be repaid before other creditors receive any payment. Senior debt is often secured by collateral on which the lender has put in place a first lien. Usually, this covers all the assets of a corporation and is often used for revolving credit lines. On the other hand, in the event of insolvency, junior debt is prioritized lower than other classes of debt. The most common kind of junior debt is an unsecured loan, which has no collateral. Another kind of junior debt is a secured loan in which another loan has priority on the collateral; a second mortgage is an example of a secured junior debt. This class of debt carries higher risk but also pays higher interest than other classes [
7].
Figure 1 shows the classification of debt financing:
3.1.3. Option
One of the benefits of MF is that the lender can provide the appropriate option (call or put option), thereby allowing the sponsor to borrow at a lower interest rate than PF or CF. An option is a financing derivative that allows you to exercise your rights, which is trading underlying assets at a specified price. In contrast to futures and forward trading, the option is based on whether the option owner exercises the right to choose. That is, the option is not the obligation, but the right to trade. There are two types of options by the property of trading, one is a call option that allows you to buy an underlying asset at a set price according to the nature of the rights option, and another is a put option that can be sold at a fixed price. Also, the option can be classified as per the time of exercise. One is the American option, which allows you to exercise your rights at any time prior to the maturity of options, and another is the European option, which allows you to exercise your rights only at the time of maturity [
7].
3.1.4. Lease
A lease is a method of obtaining the use of assets for the business without using debt or equity financing. It is a legal agreement between two parties that specifies the terms and conditions for the rental use of a tangible resource such as a building and equipment. Lease payments are often due annually. The agreement is usually between the company and a leasing or financing organization and not directly between the company and the organization providing the assets. When the lease ends, the asset is either returned to the owner, the lease renewed, or the asset is purchased [
7].
3.2. Financing Methods
3.2.1. Corporate Financing and Project Financing
In organizations where CF is practiced, the objective is to maximize the wealth of the shareholders. CF mainly deals with the sources of funds and how the optimum capital structure is achieved. For example, a hypothetical company, ABC Ltd., acquires 50% of their funds from creditors with an assurance to give back 15% within 5 years. The remaining amount is sourced from their equity shareholders. In this example, ABC Ltd. will pay a dividend cost of 10% on the profit. The 15% payback and 10% profit sharing are their cost of capital which they want to reduce by any means. This is done by optimizing the debt-equity ratio (50:50 in the current example) to reduce the cost of capital. At the same time, if they can reduce their total cost of capital (debt and equity included), they are able to keep better profits or think of re-investing the profit into the business. CF allows for flexibility to discover an optimum solution.
In cases where finance is required for a large industrial or renewable energy project, PF is used. In PF, the full required financing is not invested upfront. With PF, the financial institution finances the project based on projected cash flow versus the balance sheet upfront. The institution will invest in the project if the cash flow is beneficial to the financial institution. For example, X project contacts a bank or a financial institution to request 10% of the required financing, outlying the projected future cash flow. The bank or financial institution has complete discretion on whether or not to invest in X project. If the choice is to invest, there is usually a number of equity investors who invest as sponsors. The loans given are typically non-recourse (secured) loans, given against project property. The loans are paid completely from the project cash flow. If the parties default to pay back the loan, then the project properties are seized. To conduct the process properly, an SPC entity is created for the entire project.
Both CF and PF are commonly used on steel mill projects. As a means of comparison and description,
Table 1 shows the basic elements of each. PF is a financing method that collates project assets and has the main repayment source through future cash-flows. SPC manages the project, and the recourse is limited when there is a problem to repay borrowings.
Figure 2 depicts a standard organization of PF.
3.2.2. Benefits of Project Financing
PF has been expanded into various industries, and related research has been conducted. Salman [
9] summarized the reasons to use PF and explained it in relation to the optimal capital structure. Afterwards, John Teresa [
10] conducted a PF optimization study to conduct a comparison with CF, and Benjamin [
11] focused on its economic advantages. These studies indicate that PF has many advantages in that it lowers the project risk, uncertainty, and agency costs while also resolving overdrafts. Enzo Scannella [
12] found advantages of PF as a new financial model, especially in the energy industry [
13].
3.2.3. Disadvantages of PF
In spite of these advantages, PF is quite complex and costly to assemble. The cost of capital arranged through this route is high in comparison to capital arranged through conventional routes. The complexity of PF deals is due to the need to structure a set of contracts that must be negotiated by all of the parties to the project. This also leads to higher transaction costs on account of the legal expenses involved in designing the project structure, dealing with project-related tax and legal issues, and the preparation of necessary project ownership, loan documentation, and other contracts [
13]. MF can potentially mitigate PF’s disadvantages due to its ability to lower the interest, which is described in greater detail below.
3.2.4. Mezzanine Financing
MF refers to derivatives in the middle stage between stocks and bonds. MF can be flexibly funded because it can combine equities and debt components to respond appropriately to a given situation. It provides incentives to investors to finance unsecured funds because securing senior debt is not appropriate when business risk is high, or the credit rate of the lender is low. Investors receive lower interest rates than regular bonds but have a higher return on investment than general bonds because they have stable interest income as well as performance-based options. If a company is liquidated due to bankruptcy, it is subordinated to senior debt, which is borrowed money that a company must repay first if it goes out of business. This debt is more senior to equity, so the expected profit and risk are intermediate between equity and debt [
14,
15,
16,
17].
MF is an offshoot of traditional financial instruments that combine the characteristics of stocks and bonds to pursue both profitability and stability. In addition to fixed interest rates, investors can exercise additional rights as these provide a high risk and high return and in the worst case, the investor can obtain a fixed interest income. MF can be classified into two categories: option portion and priority portion. These are shown in
Table 2. The convertible bond (CB) and bond with warrant (BW) are optional products with additional options by agreement. An option is a product that has the right to buy or sell an underlying asset at a specific time or within a set period of time. In the position of an issuer who raises funds, they have the advantage of lowering the capital cost through options and relatively financing. In addition, debts are debited at the time of the initial issuance, but the property changes to Equity is applied at the time the option is exercised, thus improving the financial state of the enterprise. On the other hand, investors who lend money have an opportunity to earn stable, high profits at the same time, so there is merit as an investment product.
Table 2 shows the types and characteristics of MF [
18,
19].
As stated, due to the consortium of companies developed for overseas steel projects, PF is the required financing model. However, this model has high interest rates, and a method is needed to mitigate these interest rates and improve a project’s profitability. The author proposes utilizing an option-based MF for this purpose, and its use is defended in the sections below. As such, the features of PF and MF are discussed in the following section.
4. Research Methods
For initiating a project, the project owner needs to raise funds though PF or CF. However, as mentioned above, PF needs a high interest rate in return for low risks in the case of project failure, while CF entails a significantly high level of liability to the owner in the case of failure. In order to find a better way in which the owner can obtain lower interest rates while keeping a low level of failure impact, MF is reconsidered. This study investigates the feasibility of using option-based MF to supplement and mitigate the high interest rates of PF. This process includes the following research methodologies: (1) literature review; (2) Monte-Carlo simulation modeling; (3) a case study.
4.1. Literature Review
A literature review was conducted on the basics in project capital procurement methods and the three financing methods within this paper: CF, PF, and MF. Much of these findings are discussed in the introduction section as background for the problem. The literature used for this research includes previous discussions on methods to test project profitability and how to convert cash-flow findings into option pricing.
4.2. Monte-Carlo Simulation Modelling
From literature findings, the authors have developed a three-step process to calculate the optimal ratio of MF, shown below in
Figure 3 and is as follows: (1) calculate project cash-flow and volatility through two @Risk Monte-Carlo analyses; (2) determine the adjusted interest rate of MF with consideration of the option value, calculated by inserting results from step 1 into the BSM formula; and (3) apply the adjusted interest rate from step 2 to the Net Present Value (NPV) calculations to determine the effects of MF on the project with a final output of the optimal MF ratio.
4.3. Implementation of Case Study
The project chosen for the case study is an Iranian Public Knowledge Project (PKP) integrated steel mill project with an annual production capacity of 1.5 million tons that utilizes FINEX and CEM (Continuous Endless Milling). FINEX is an iron making technology developed by Siemens VAI and POSCO. Molten iron is produced directly using iron ore fines and non-coking coal rather than traditional blast furnace methods through sintering and reduction with coke. Elimination of preliminary processing is claimed to make the plant for FINEX less expensive to build than a blast furnace facility of the same scale. Additionally, a 10–15% reduction in production costs is expected/claimed through cheaper raw materials, reduction of facility cost, pollutant exhaustion, maintenance staff and production time. The process is claimed to produce less pollutants such as SOx, NOx, and carbon dioxide than traditional methods. This process is essentially a combination of FINMET’s Fluidized Bed and COREX’s Melter Gasifier, hence its name “FINEX”. Both methods are unique to the domestic company P and is to be constructed in the Chabahar economic zone on the coast of Oman, southern Iran. The total investment (CAPEX) is about 1.8 billion USD.
The main conditions are as shown in
Table 3, and the production capacity, the investment cost, construction period, and production products are obtained from the official announcement data when the Memorandum of Understanding (MOU) was concluded. Tax, market risk, beta are assumed with the reference paper. The risk-free rate uses the last 4-year average of 10-year US Treasury yields, and the consequences of a change in the country risk premium are simulated through a sensitivity analysis after applying the same numerical value as that of Brazil, Indonesia, and India, since the country risk of premium of Iran is not defined [
20,
21,
22].
Concerning the financing structure for this project, the total investment cost of 2 billion USD is raised with 50% equity and 50% debt. The joint venture between Iran PKP and domestic company P will invest 1 billion USD in equity, and the SPC will raise the remaining 1 billion USD from the lender. Debt at this time is procured as a general senior debt, and the interest rate is later defined according to the weighting.
5. Literature Review Findings
The conventional engineering economic analysis with discounted cash-flow (DCF), which typically yields IRR (internal rate of Return) and payback period has been traditionally used as an industry practice to assess the profitability of overseas investment projects, at least for major Korean steel companies. However, in this study, the authors suggested to use a more advanced methodology such as Mezzanine Financing with Call or Put option values in order to reinforce the profitability of the investors by lowering the interest rate of financing.
Along with a better understanding of the problem, the literature review shed light on how to calculate and compare different options. Kim, Yong-gu calculated the volatility from the project profitability using the outputs to calculate the option value based on the measured volatility [
23]. Because this study has the same goals, it also uses this methodology. The basic structure is to calculate the option value of the MF based on the volatility of the Project profitability, reflect this in the interest rate, and borrow at this low interest rate [
24]. Lee, Cheuk Wing studied the feasibility of applying a hybrid bond, which is a type of MF for Renewable Energy, but analyzed it in terms of only reducing risk, not in deriving the economic value [
18]. This paper applies the option value to the MF reviewed by Lee, Cheuk Wing [
18] based on the volatility of the project profitability used by Kim, Yong-gu [
24] and Jung, Young Ki [
25] to calculate the interest rate of PF. These results are used to find the optimal ratio of the MF while re-calculating the capital procurement cost and project profitability.
Next, the authors needed a way to convert the NPV volatility into an adjusted interest rate. The total value of the option mezzanine products, which is the subject of this study on MF, can be divided into the value as a general bond and as the value of an option. In other words, when compared to junior loans, which is a priority order mezzanine product under the same conditions, the interest value can lower only the remaining interest profit after subtracting the option value from the total value that needs to be obtained.
This paper attempts to evaluate the value of CB among option MF and assumes that the CB is a European call option product that can be converted only at maturity, with the option value measured using BSM. An option can be regarded as a means to avoid the volatility of the underlying assets, and studies have been conducted to evaluate the value of the options as trading becomes more active in the market.
Black and Scholes were awarded the Nobel Prize by presenting a systematic option pricing model for the first time, and their model is widely used although it is based on unrealistic assumptions. BSM is a European option that allows investors to borrow under risk-free rate and the full capital market, and the execution is allowable only on the maturity day and assumes no basic dividend. The pricing model of the European call option presented under this assumption can be expressed as Equations (1) and (2) [
20,
24,
26].
where,
- -
C: Call premium
- -
S: Current stock price
- -
N: Cumulative standard normal distribution
- -
K: Option striking price
- -
R: Risk-free interest rate
- -
T: Time until option exercise
- -
e: Exponential term
- -
ln: Natural log
6. Simulation Modeling for Optimizing MF
As shown in sub-sections below, the project NPV Simulation process is divided into three stages. The first step is developing a cash-flow model through two MCS to obtain the volatility of the NPV. The option value of the MF and adjusted interest rate are then calculated using the Black-Scholes equations and the results from the first step. Since the option value varies depending on the portion of the MF borrowing, this work should be repeated for each borrowing weight section. In the final step, the project NPV is simulated according to the ratio of the senior debt and MF, and the optimal Mezzanine interest ratio is obtained. The profitability of the project is expressed as NPV, discounting the future cash flow (inflow and outflow) as the present value. The project NPV Simulation Modeling is described in detail below [
22].
6.1. STEP 1a: Calculate Cash-Flow Modeling (1st Monte Carlo Simulation)
The first MCS is run with the @Risk Program to create a cash-flow diagram and calculate the project NPV. This step begins by developing a project cash-flow model in Excel. Considering that the cash inflow and outflow are the same as analyzing with the existing DCF (Discounted Cash-Flow) method, a valuation method used to estimate the attractiveness of an investment opportunity (the free cash flow needed during the construction period and operation period) is derived. DCF analyses use future free cash flow projections and discounts them with a required annual rate to arrive at present value estimates. A distribution model of the input data based on the past historical data is obtained for the simulation. In addition, if there is a correlation between the input variables, it is necessary to set the correlation to reduce unrealistic cases and improve the reliability of the results. A correlation function (formula) can be defined in the @Risk program, and it has a function to reflect the execution of the simulation (simulation). Therefore, the correlation of related variables should be defined to improve the reliability of the result. Once the probability distribution of the input variables and the correlation are defined, the simulation is ready to be run. To obtain reliable results, the number of repetitions should be high, generally 10,000 times. When the simulation is run, the program will output the results in a short time and will display these as a probability distribution graph for project NPV as shown in
Figure 4a [
27]. The advantage of the MCS using @Risk software is to easily perform a sensitivity analysis, which represents the relative impact and consequently, the sensitivity of input parameters to the project NPV on a so-called “Tornado-chart”, as illustrated in
Figure 4b.
6.2. STEP 1b: Project NPV Volatility (2nd Monte Carlo Simulation)
Since the NPV is calculated as the basis of the volatility analysis, the volatility for basic assets that can be used to evaluate the option value is obtained through an analysis. MCS is run once more to obtain the volatility of the NPV. The MCS is the process to standardize the normal distribution of the mean and the standard deviation of the NPV obtained previously using an Excel Macro. First, 10,000 random numbers (mean variance) with a mean of 0 and a standard deviation of 1 are generated through a Gaussian distribution in Excel. By multiplying the random variables by the standard deviation of the NPV and adding the mean, the NPV can be a standardized normal distribution. The NPV volatility is obtained by obtaining the log method of 10,000 generated results, and the standard deviation of the log method. This is called the Wiener Process as defined by Black-Scholes and must be satisfied to utilize the BSM [
20,
24].
6.3. STEP 2: Adjustment of MF Interest Rate Reflecting the Option Value
As mentioned earlier, CB periodically receives interest, and at the time of conversion at a certain point, the status as a general bond ends and holds stock. Therefore, the total value of the CBs can be divided into bond value and convertible value. In other words, the value as a general bond held until the conversion right is exercised is the expected profit due to the interest rate, and the total value can be obtained by adding the value of the conversion right obtained using the BSM. When compared to the junior loan, which is a priority order mezzanine product under the same condition, the interest value can be reduced because it needs to obtain only the remaining interest profit, which is the subtracted option value from the total value. The first step is to calculate the option value of the CB by substituting the NPV and the NPV volatility of the project into the BSM, and the second step is to deduct it from the value of the junior loan to obtain the adjusted interest rate. Since the option value varies depending on the size of issuance of the CB, the previous two steps must be repeated for each size, as shown in
Figure 5 [
28].
The option value (C) is calculated according to the value (S), the conversion price (K), the maturity (T), and the volatility (σ) of the underlying asset after defining BSM formula in Excel. Since the underlying asset is the NPV of the project, the calculated NPV value can be substituted. However, since the effect on the NPV varies depending on the loan, the NPV value calculated by multiplying the total NPV by the portion of the loan is used as the value of the underlying asset. Since the CB receives the principal of the loan at maturity or exercises the conversion right, the exercise price is the loan itself. Since the maturity (T) of the CB is the same as the maturity of the bonds at issue, it is necessary to include the maturity of the bond, which is set to 10 years as the general loan period. Finally, the volatility is calculated by substituting values derived from the two MCS of the previous section.
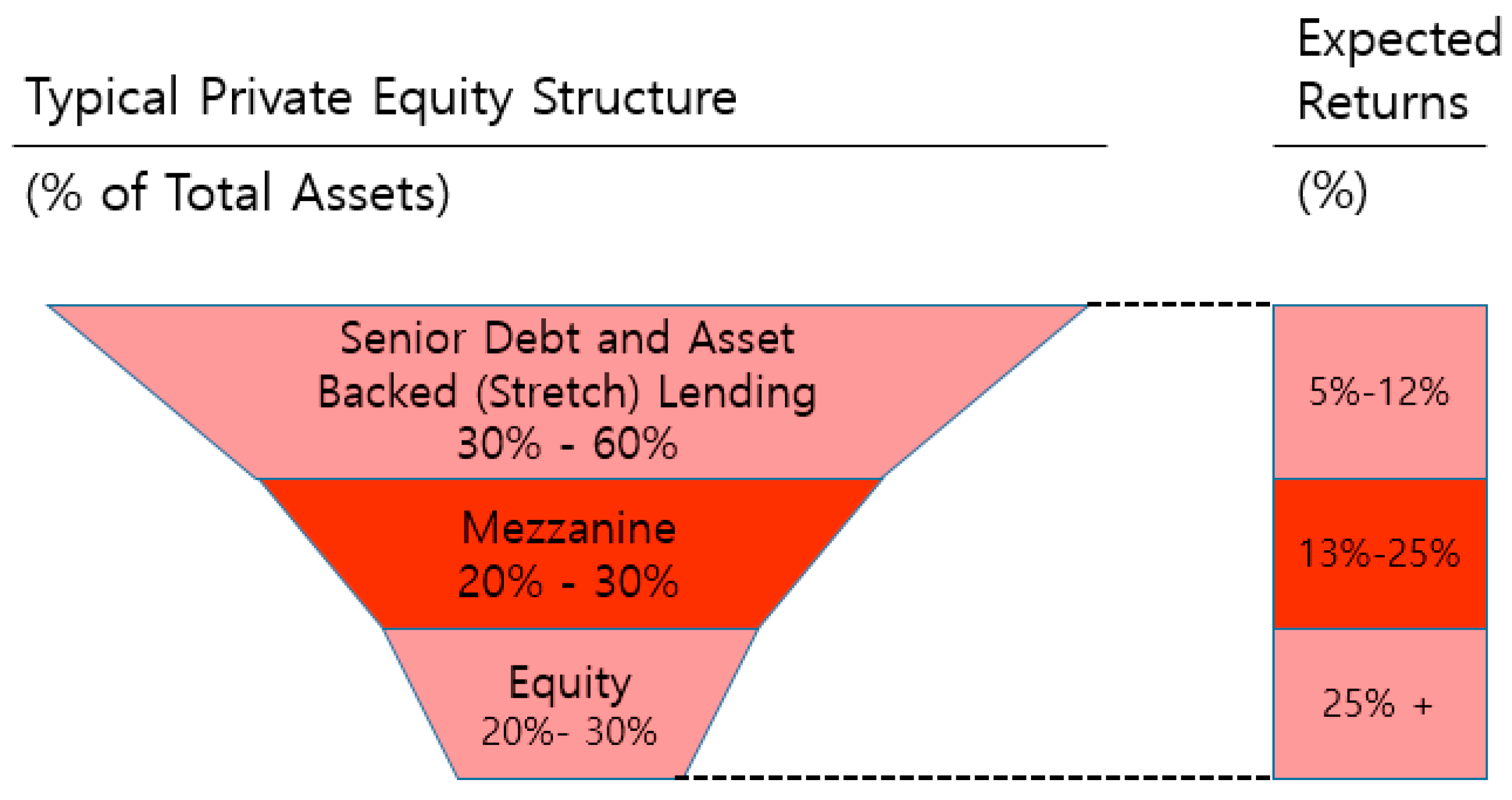
For companies issuing CB, the investment profitability can be expected to increase as much as the interest rate paid annually is decreased. The interest rate for each CB should be assessed per issue, as the convertible value varies according to the −issuing CB volume with its lender’s different expectations and its portion amongst the total loan as well. In addition, since CB is a substitute for senior debt while keeping the same debt rate, not a substitute for existing equity, the interest rate of the senior debt should also be changed. To conduct a comparison, the reference interest rate is required. The authors used data from Bond Capital, which has analyzed and studied MF since the early 2000s.
The expected return rate of the senior debt and MF is defined to consist of 50% Equity and 50% Debt based on the above data in the following manner, as shown in
Figure 6.
- (1)
Interest rate based on senior debt: 12% (maximum loan portion: 50%)
- (2)
Interest rate variation due to a 10% decrease in borrowing weight: −0.5%
- (3)
Interest rate based on MF: 13% (minimum borrowing portion: 10%)
- (4)
Interest rate variation due to a 10% increase in borrowing weight: +1.0%.
6.4. STEP 3: Deriving Mezzanine Optimum Utilization Ratio
Based on the adjusted interest rate of the MF calculated in the previous section and the interest rate of the senior debt, the change in the NPV is simulated according to the ratio of borrowing for both capitals. The optimal capital structure for which the value of WACC is minimum and NPV is maximum is also calculated. The simulation is conducted by changing the ratio of the MF to the base case for which equity is 50% and the debts are 50%, with senior debts only. A total of four cases are compared where the Equity is fixed at 50% and senior debt is replaced by MF in increments of 10%, from 10 to 40%. The case of no senior debt is excluded in this study because the MF itself has a senior position and the basic interest rate is lowered, so there is no meaning in a comparison. Based on the simulation model set up here, the next chapter simulates the NPV according to the utilization ratio of the MF applied to the overseas steel project, which company P in Korea is promoting together with PKP of Iran, taking into account the optimal ratio of MF.
7. MF Case Study Project with Monte-Carlo Simulation
As stated in
Section 4.3, the project chosen for the project case study was an Iranian PKP integrated steel mill project. The above steps are executed for the project case study obtained data below.
7.1. STEP 1a: Project NPV Calculation (1st Monte Carlo Simulation)
For the same probabilistic analysis as the DCF, a deterministic analytical method, the cash-flow model needs to be implemented in Excel. The net cash flow needs to be found during the construction period and the operation period considering the cash inflow and cash outflow. Unlike the DCF method, it is necessary to set the distribution of the input variables into the simulation. Using the distribution fitting function in the @Risk program with the data from the last four years (2013–2016), as shown in
Table 4, a distribution model is obtained for each variable.
The distribution model is obtained using monthly data over four years, and the figure is produced with a total of 48 data values for each factor. Once the distribution model of the input variables is obtained from historical data, a Cash-flow model using it as a boundary condition needs to be implemented. The revenue is comprised of revenue from product sales, intermediate goods, and by-product sales. Expenses are comprised of selling and administrative expenses and maintenance expenses based on cost of materials, labor, expenses, and others. The ratio of each item is adjusted to the present situation by referring to the paper that examined the existing PKP. The income statement is made based on the annual income and expenses, thereby the tax and after-tax profit can be sequentially obtained. Based on this, the cash outflow, inflow, and free cash flow are obtained during the construction period and the operation period. The sum of discounted free cash flow is calculated reflecting the present value, that is the Project’s NPV using the DCF method. Now that one representative project NPV has been obtained using the DCF method, the @Risk Program is now used to reflect the correlation of the input variables to implement the MCS. The product price and raw materials consisting of iron ore and coking coal showed a positive correlation of 0.9 using the correlation function of Excel. @Risk’s Define Correlations function can be used to define the correlation between the above variables, and a value of 0.9 is entered. To obtain reliable results, a simulation is performed by selecting 10,000 cycles, which is the maximum number of simulation cycles that can be selected in the program [
15].
The average NPV of the PKP project financial model was 583 million USD and the standard deviation was 270 million USD. The second MCS is run based on these values to determine the volatility of the NPV.
7.2. STEP 1b: Project NPV Volatility (2nd Monte Carlo Simulation)
The mean and standard deviations of the project NPV that are the basis of the volatility analysis are obtained, and the volatility that satisfies the Black-Scholes’ Wiener process [
7] can be obtained. The results of the MCS using the Excel macro shows that the volatility of the NPV is 87.06%. An option product is traded as a risk hedge against such volatility. Generally, the greater the volatility, the greater the option value. Based on the volatility of the NPV and NPV calculated above, the value of option-based MF is calculated, and based on this value, the process of adjusting the appropriate interest rate reflecting MF is shown.
7.3. STEP 2: Adjustment of MF Interest Rate Reflecting the Option Value
A standard interest rate should exist to calculate the appropriate interest rate by reflecting the option value to the interest rate of the option MF. Based on the data of the bond capital as defined above, the following amendment to the SPC is applied in accordance with the cost of equity procurement in the project. The interest rate for senior debt, which was recalculated based on the equity fund procurement cost of the PKP project, is 2.8–6.7%, and the interest rate of the MF is 7–14%. Based on the data, the standard interest rate to be applied to the actual simulation should be defined by the borrowing weight. Iran has the highest risk rate of 6.7% when the debt ratio of senior debt is 50% because of the country risk premium (3.4%), which is higher than that of developed countries. The interest rate of the MF rate is defined as 7.2% when the ratio of borrowing is at least 10%, and it is defined according to the ratio of borrowing by the following criteria.
- (1)
Interest rate based on senior debt: 6.7% (maximum loan portion, 50%)
- (2)
Interest rate variation due to a 10% decrease in borrowing weight: −0.5%
- (3)
Interest rate based on MF: 7.2% (minimum borrowing portion, 10%)
- (4)
Interest rate variation with a 10% increase in borrowing portion: +1%
- (5)
Interest rate variation according to the increase and decrease in the borrowing ratio of the MF is a factor that can influence the result in the future as the basis to derive the optimal utilization ratio, and the simulation is performed by changing it in the sensitivity analysis and will compare the results.
Since all data required to calculate the option value of the MF is calculated, the option value is calculated according to the following process, and the interest rate is adjusted by reflecting this value.
Figure 7 shows the process of the mezzanine option value and the interest rate adjustment.
Amongst the MF options, only the value of CB is evaluated, and the option value is calculated using the BSM as setting a European call option with a 10-year maturity product that is converted only upon maturity. Based on the calculated option value, the interest rate should be adjusted according to the interest rate based on the MF defined in the previous section. The base case is where the ratio of equity and debt is 50%, the WACC for capital procurement is 9.29%, and the target rate (hurdle rate) is 12.69, which is the sum of the WACC and country risk premium 3.4%.
In the case of an international investment, the hurdle rate is the discount rate, and the NPV calculated based on the base case of the Iranian PKP Project is 580 million USD. A total of 4 cases are compared while the Equity remains fixed at 50% and senior debt is replaced by 10% MF increments from 10 to 40%. The option value for Case 1 can be calculated, where the loan amount of the MF is 10% and the loan period is 10 years out of the total investment cost of 2 billion USD. Among the total investment of 2 billion USD, 10% of the borrowing portion is worth 208.7 million USD, and the interest rate when borrowing from a subordinated loan (junior loan) is 7.23%, and the present value of the revenue expected by the mezzanine lender is 30.22 million USD. The total NPV of the project is 580 million USD, and the portion of the MF is 10%. Therefore, the NPV of the CB is 58 million USD. The volatility of the NPV is 87.06%, on applying this to the BSM, the conversion value of the CB is obtained as 42.3 million USD. Therefore, the lender needs to earn only 259.9 million USD, which is the profit from 302.2 million USD obtained from the subordinated loan (junior loan) minus the value of 42.3 million USD which is the value of conversion right, and the interest rate at that time is 4.95%. Based on the calculated interest rate, the WACC is lowered from 9.29 to 9.03% of the original base case, and the discount rate decreases from 12.69 to 12.43%.
When the figure is converted to the present value with the condition of no cash-flow change in the Iran PKP project’s financing model, if NPV is recalculated reflecting 12.43% as the modified discount rate, the value is 620 million USD, which is 40 million higher compared to 580 million initially. The simulation is executed for cases 2, 3, 4, in the same manner as in case 1, and the obtained figures are as shown in
Table 5.
7.4. STEP 3: Deriving Mezzanine Optimum Utilization Ratio
According to the results of the case study, the maximum project NPV was obtained by minimum WACC of the capital cost and the minimum discount rate when the CB (senior debt) was 20% of the total investment. As can be seen, the WACC was reduced as the senior debt is replaced by MF up to a 20% MF. However, when the MF reached 30% and 40%, the WACC increased. The reason for this result is that MF is more dependent on the interest rate than senior debt, and the interest rate rises as the amount of the loan increases. If the borrowing amount is large, borrowing with senior debt can be more advantageous even if an option value is considered.
In summary, the WACC decreased from the base case (consisting only of senior debt) at 10% and 20% MF but then increased at 30% and 40% MF as shown in
Figure 8a (the red-circle indicates the optimal low-interest point). As illustrated on
Figure 8b there is an inverse relationship between WACC and NPV; i.e., when the WACC decreases, the NPV increases (the red-circle indicates the highest NPV point).
8. Sensitivity Analysis for the Case Study Project
Although not discussed in the NPV simulation discussion, a sensitivity analysis was conducted on the project to understand the three factors that have the greatest impact on the results of the simulation. These were determined to be the NPV’s volatility, interest rate increase and decrease with MF, and country risk premium. These variables are discussed in greater detail below.
8.1. NPV Volatility
First, the results of the simulation change are analyzed according to the NPV volatility. The NPV volatility is one of the values that represents both the project cash inflow and cash outflow, and it is a key factor that determines the option value of the MF through the BSM. The greater the volatility of the project NPV, the more likely it is that the project becomes larger or smaller than the average value, which means the option value of the MF is higher. The NPV volatility is simulated by dividing it into five categories by changing the volatility calculated from the Iranian PKP Project (87.06%) to 30%, 60%, 120% and 150%, as shown in
Figure 9.
As the volatility of the NPV increases, the option value of the MF increases, resulting in a decrease in the capital cost and an increase in the NPV. In addition, as the value of the MF increases, the optimal utilization ratio also increases, moving to the right side of the graph. On the other hand, as the NPV variability becomes smaller, the value of the option becomes smaller, so the value of the utilization becomes lower, and the optimum utilization ratio becomes smaller.
8.2. Increase/Decrease in the Interest Rate by the MF Borrowing Size
The second sensitivity analysis simulates how the Project NPV changes according to the increase/decrease in the interest rate by the amount of MF borrowed. The increase in interest rate with the MF was divided into five categories, and a simulation was performed with 0%, 0.5%, 1.5% and 2% based on the 1% used in the project.
The smaller the increase in the interest rate per CB, the greater the increase in ratio utilization of the maximum NPV, therefore the graph moves to the right. In an unrealistic case, the NPV is maximized in Case 4 due to the option value if the interest rate is the same. In the case of an interest rate increase of 0.5%, the NPV for Cases 2 and 3 is almost the same, and the NPV improves significantly compared to that of 1%. In contrast, if the increase in interest rate is large, the cost of capital procurement increases, so the value of the MF utilization becomes smaller, and the optimal utilization point moves to the left in the graph as shown in
Figure 10.
8.3. Country Risk Premium
Finally, the changes in the results are simulated according to the country risk. A simulation was conducted with two cases where the low country risk premium is 1% and 2%, and the high-country risk premium is 4% and 5% based on Iran’s country risk premium (3.4%).
As a result of simulating the change in NPV according to the country risk premium, the change in NPV is shown to change in the base case, unlike in the previous two cases. Since the country risk premium is different from the cases when the project is executed in Iran and USA, respectively, the discount rate is also different. Therefore, the project NPV changes. The results of the simulation show that a smaller country risk premium results in a better overall NPV and higher MF value. This is because as the NPV increases, the option value increases for the same loan amount. As the country risk premium increases, the NPV is lowered overall, and the value of the MF is also lowered.
The sensitivity analysis result for above three factors (i.e., (1) NPV volatility; (2) MF interest rate; and (3) county risk premium) shows that the overall effect of NPV improvement and the adjustment of optimal ratio accordingly, as the factors change. However, overall the use of MF improves the NPV, and the optimal ratio is found to exist as shown in
Figure 11.
9. Conclusions
As the domestic steel industry is saturated within the domestic market, Korean steel companies have been actively trying to advance overseas to secure new markets and improve profitability. To minimize risk, the Korean companies often strategically contract with local companies. This results in the necessity of project financing (PF) whose interest rate is higher than the traditional corporate financing (CF) used domestically increasing capital procurement, decreasing profit. As such, this paper sought to lower the interest rate, maximizing profit. Based on literature findings, the mezzanine financing (MF) method can procure funds with lower interest rate, and was investigated within this paper for its efficiency.
To investigate said efficiency, this paper used multiple Monte Carlo Simulations to achieve NPV and project volatility values, the Black-Scholes model to convert these values into adjusted interest rates, and inputting the findings into four cases (base case with 50% PF and cases 1–4 decreasing PF and increasing MF at intervals of 10%). In performing these steps on a case study Iran PKP project, it was found that the project NPV is maximum (WACC of capital cost and discount rates minimum) when the MF (using the option of a convertible bond) was 20% of total investment cost. However, when MF was increased to 30% and 40%, the NPV decreased (WACC of capital cost and discount rates increased).
These results can be expected to vary depending on the conditions under which the Iranian PKP project is based and the results obtained under a specific environment. To investigate the impacts said environment can have, a sensitivity analysis was performed with the following having the most significant impact on NPV: volatility, increase/decrease in the interest rate by the MF borrowing size, and country risk premium. The results of the sensitivity analysis for these three factors show that the NPV improvement effect and optimal utilization ratio changed depending on the variation of the factors for utilizing MF. However, it is clear that usage of MF is beneficial for improving MF and the existance of an optimal point. Therefore, it can be concluded that the proper use of MF can improve project profitability by considering various conditions rather than financing only senior debt to carry out the project, which could affect a number of sponsors and stakeholders to initiate more projects easily in the future. Though this paper was used for a Korean steel company’s international investment cases, the overall results can be applicable with some relevant local adjustments for other types of international investment mega-projects in which a special purpose company (comprised of multiple investors and corporations) needs to be created.
In the course of this study, the results were calculated with a widely used program based on proven theory and data, but there are some limitations. First, the data from the last four years is similar to that used in a deterministic method to calculate the volatility of the NPV. However, considering that the project period is 15 years, this is a short period for a probabilistic analysis. Therefore, the accuracy and reliability of the probabilistic analysis can increase based on sufficiently long data. In the NPV simulation, the ratio of borrowing by MF is divided by 10%, and the total of four cases are analyzed. Therefore, the optimum utilization ratio is also calculated in units of 10%. However, since the optimal point needs to be found through a more accurate and continuous analysis in order to apply it to real projects, the ratio of the MF should be divided into smaller increments, for example, 5, 3, or 1%. In addition, applying MF was only examined from an economic perspective, without including the additional time needed to increase the number of contractors and the complex characteristics of the MF. The sensitivity analysis methodology introduced in this case study can be applied to cover a wider range of various “what-if scenarios”.
The actual project is based on a very limited amount of time, and sometimes it is necessary to maintain the timeline, even if the cost is higher, so the funding plan should be thoroughly reviewed in advance. If funds are raised without planning, money will likely be borrowed at a higher interest rate. Finally, the convertible bond was analyzed as being issued at the beginning of the business with a fixed 10-year maturity. However, the application to an actual project is higher if the time of issuance and maturity are considered to vary.