The Optimization of Emergency Evacuation from Nuclear Accidents in China
Abstract
:1. Introduction
2. Evacuation Path Network Model with Multiple Security Points
- (1)
- The paths are the same if the vehicle’s starting point and destination are the same;
- (2)
- The evacuation vehicles are buses;
- (3)
- There is an emergency vehicle garage at the farthest distance from the plant entrance inside the nuclear power plant. Once a serious nuclear accident has occurred and evacuation is needed, the vehicles start from the garage and travel through every temporary shelter to take people in the nuclear plant site to a safe area past the entrance.
- (4)
- The radiation dose of the personnel on the driving path of the emergency vehicle is within a safe value.
- (1)
- Construct an evacuation network diagram and add weight for each edge.
- (2)
- Find singularities (a singularity is the node for which the number of edges associated with it is odd).
- (3)
- In the singularities above, find a node with the longest distance (largest weight) from the origin (V0).
- (4)
- Add a virtual origin Vt to the network diagram; connect the virtual origin Vt with a singularity found in the third step and the origin (V0) separately, the weight of the connecting edges being zero.
- (5)
- In addition to the singularity found in the third step, the number of singular points in the graph must be odd. Any singular point is paired with the origin (V0), and the rest of the singularity is paired. A repeating edge is added between each pair of singularities (or between the singularity and the origin), then the number of edges associated with each node is even. At this time from the virtual origin Vt, going through the all edges (no repeat) can also return to Vt.
- (6)
- A loop that contains a repeating edge is randomly selected, and the total weights of the loop are calculated. If the sum of the weight of the repeated edges in the loop is less than half of the loop’s total weight, then the network model diagram is the optimal network, otherwise the repeating edge is adjusted until the repeated edges in the loop are less than half of the loop’s total weight.
3. Example Simulation
- (1)
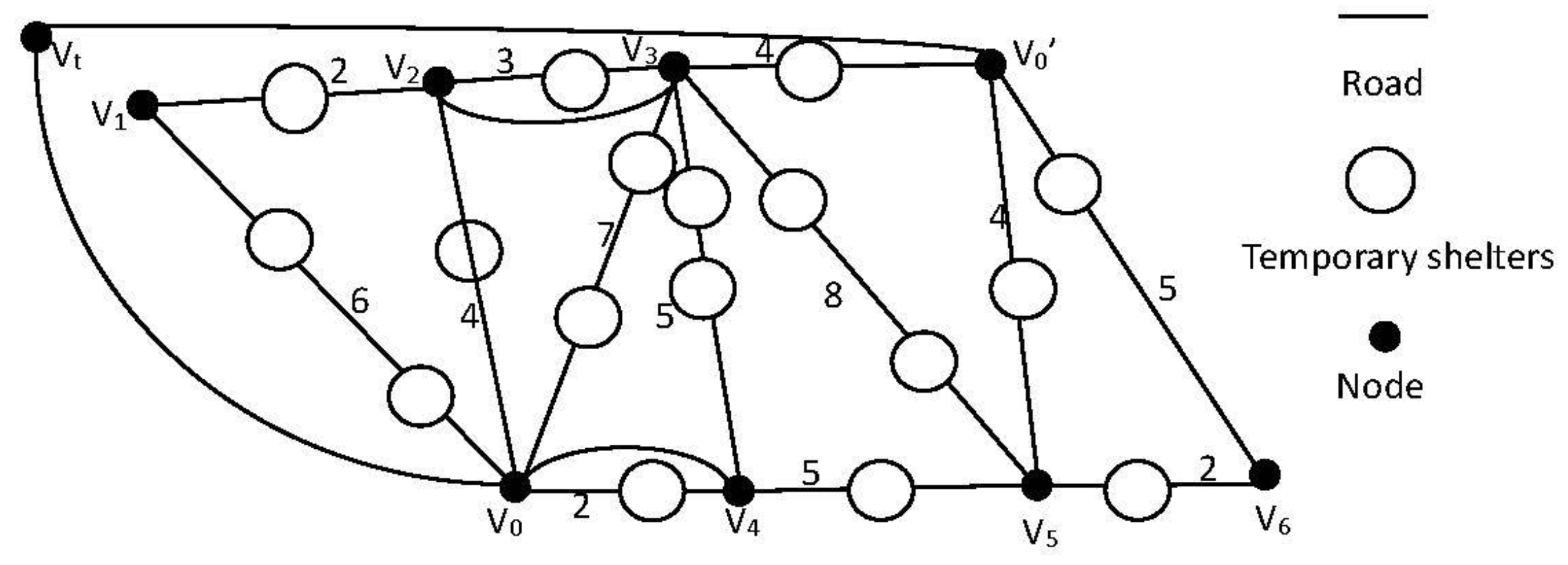
- Finding all the singularities in Figure 4: V2, V3, V4, V0′. Among all the singularities, a point with the longest path with V0 is found, and V0′ is the point to find (V0V4 = 2, V0V2 = 4, V0V3 = 7, V0V0′ = 11). A virtual origin Vt is added; Vt is connected to V0 and V0′ separately.
- (2)
- Duplicate edges are added, so that each node in the graph has an even number of degrees. From node Vt, all the edges of the graph are traced through at least once, returning to Vt. There are two duplicate edges added in the network diagram, which is shown in Figure 5.
- (3)
- In the loop of V0V2V3V4, the total loop weight = V0V2 + V2V3 + V3V4 + V4V0. The weight of the duplicate edges (5 + 4) is greater than half of the total loop weight (7). So, the duplicate edges in V0V2V3V4 loop should be changed, and we can adjust the duplicate edges as shown in Figure 6:
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Argyris, N.; French, S. Nuclear emergency decision support: A behavioural OR perspective. Eur. J. Oper. Res. 2017, 264, 180–193. [Google Scholar] [CrossRef]
- Suzuki, T.; Tajima, E.; Nozawa, M. Nuclear emergency plan and preparedness in Japan. In Proceedings of the 9th Pacific Basin Nuclear Conference, Sydney, Australia, 1–6 May 1994; Available online: https://inis.iaea.org/search/search.aspx?orig_q=RN:26057007 (accessed on 30 July 2018).
- U.S. Nuclear Regulatory Commission (NRC). Criteria for Preparation and Evaluation of Radiological Emergency Response Plans and Preparedness in Support of Nuclear Power Plants. Available online: https://www.nrc.gov/reading-rm/doc-collections/nuregs/staff/sr0654/ (accessed on 30 July 2018).
- U.S. Nuclear Regulatory Commission (NRC). General Site Suitability Criteria for Nuclear Power Stations. Available online: https://www.nrc.gov/docs/ML1218/ML12188A053.pdf (accessed on 27 July 2018).
- Kohonen, T. Essentials of the self-organizing map. Neural Netw. 2013, 37, 52–65. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Hou, J.; Gao, J.; Wang, R.; Lin, Q.; Yang, L. Estimation of Emergency Evacuation Time in Fuqing Nuclear Power Plant. Radiat. Prot. 2017, 37, 108–115. [Google Scholar]
- Lane, R.; Dagher, E.; Burtt, J.; Thompson, P.A. Radiation exposure and cancer incidence (1990 to 2008) around nuclear power plants in Ontario, Canada. J. Environ. Protect. 2013, 4. [Google Scholar] [CrossRef]
- Xu, J.; Wu, W. Theory and Method of Multi-Attribute Decision Making; Tsinghua University Press: Beijing, China, 2006. [Google Scholar]
- Zou, S.; Chi, X.; Liu, W.; Li, D. Optimization of Field Emergency Evacuate and Rescue Route in Nuclear Accident. Ind. Saf. Environ. Prot. 2018, 44, 30–33. [Google Scholar]
- Xie, T.; Zhou, X.; Wang, T.; Wang, T.; Liu, W.; Chen, J.; Guan, H.; Li, P. Integrated S-BOX Model for Nuclear Emergency Response. China Safe Prod. Sci. Technol. 2015, 11, 22–27. [Google Scholar]
- Urbanik, T.; Desrosier, A.; Lindell, M.K.; Schuller, C.R. Analysis of Techniques for Estimating Evacuation Times for Emergency Planning Zones; NUREGrCR-1745; U.S. Nuclear Regulatory Commission: Washington, DC, USA, 1980. [Google Scholar]
- Adler, J.D.; Mirchandani, P.B.; Xue, G.; Xia, M. The Electric Vehicle Shortest-Walk Problem with Battery Exchanges. Netw. Spat. Econ. 2016, 16, 155–173. [Google Scholar] [CrossRef]
- Hu, A.; Zhang, X. The Optimization Model and Algorithm of Tobacco Distribution Routing in Urban Area Based on the Chinese Postman Problem. Logist. Eng. Manag. 2016, 38, 145–149. [Google Scholar]
- Yuan, W.-W. Logistics Engineering and Management. J. Daqing Normal Univ. 2017, 37, 62–64. [Google Scholar]
- Urbanik, T., II. Evacuation Time Estimates for Nuclear Power Plants. J. Hazard. Mater. 2000, 75, 165–180. [Google Scholar] [CrossRef]





© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, Y.; Zou, S.; Niu, C. The Optimization of Emergency Evacuation from Nuclear Accidents in China. Sustainability 2018, 10, 2737. https://doi.org/10.3390/su10082737
Zou Y, Zou S, Niu C. The Optimization of Emergency Evacuation from Nuclear Accidents in China. Sustainability. 2018; 10(8):2737. https://doi.org/10.3390/su10082737
Chicago/Turabian StyleZou, Yang, Shuliang Zou, and Changming Niu. 2018. "The Optimization of Emergency Evacuation from Nuclear Accidents in China" Sustainability 10, no. 8: 2737. https://doi.org/10.3390/su10082737
APA StyleZou, Y., Zou, S., & Niu, C. (2018). The Optimization of Emergency Evacuation from Nuclear Accidents in China. Sustainability, 10(8), 2737. https://doi.org/10.3390/su10082737



