Modeling the Taxi Drivers’ Customer-Searching Behaviors outside Downtown Areas

Abstract

A popular phenomenon in the street-hailing taxi system is the imbalanced mobility services between city central and outside downtown areas, which leads to unmet demand outside downtown areas and competitions in city central areas. Understanding taxi drivers’ customer-searching behaviors is crucial to addressing the phenomenon and redistributing the taxi supply. However, the current literature ignores or simply models the taxi drivers’ behaviors, in particular, lacks the in-depth discussions on individuals’ heterogeneity. This study introduces the latent class model to identify the internal and external factors influencing the taxi drivers’ destination choice after the last drop-offs. Beyond the influencing factors, the modeling structure captures the heterogeneity in vacant taxicab drivers through introducing latent classes. The proposed model outperforms other discrete choice models, for instance, multinomial logit, nested logit, and mixed logit, based on the two study cases developed from the New York City yellow taxicab system. The empirical results first statistically indicate the existence of latent classes, which further empirically prove the heterogeneity in the choices by vacant taxicab drivers while searching customers. Moreover, we obtain a set of internal and external factors influencing the customer searching behaviors. For example, the taxicab drivers are sensitive to the demand at the search destination areas and the distance from the last drop-off location to the search destination areas and behave identically in particular under the conditions of high demand and short search distance. On the other hand, the external variables have different impacts on customer searching behaviors across the different groups of drivers in the both study cases, including peak hours, weekday, holiday, earned fare from last occupied trip, raining hours, and flight arrivals at airports. In final, the proposed modeling structure and findings are useful as a sub-model of taxi system modeling while developing strategies, as well as as a regional planning tool for taxi supply estimations.

1. Introduction

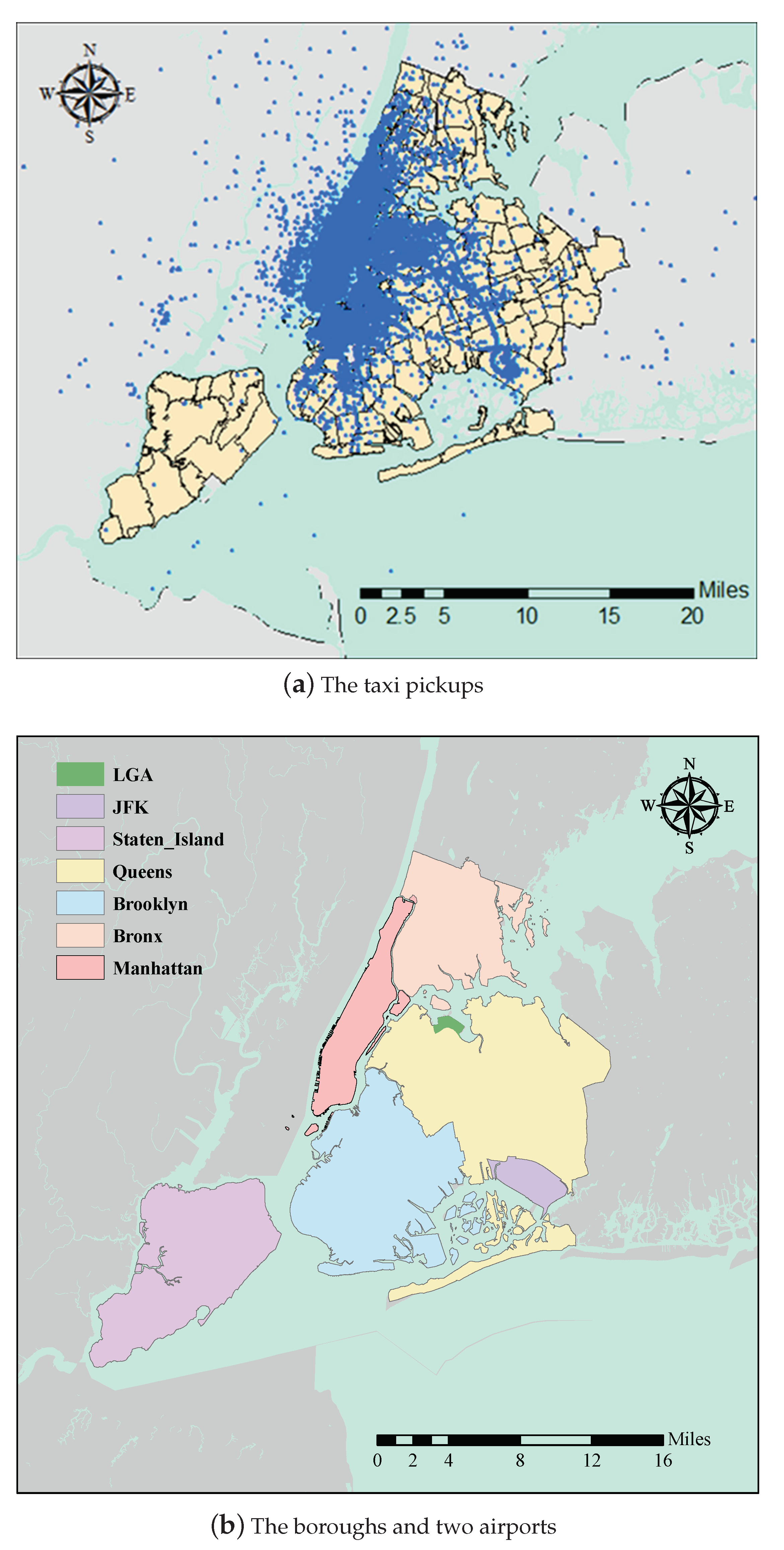
The street-hailing taxicabs are representative urban mobility services, providing convenient door-to-door rides and playing an important role in urban transportation system. For instance, the New York City (NYC) owned a taxi fleet of more than 13,000 yellow taxicabs and more than 7000 green taxicabs in 2015, which is the largest taxi market in North America and generates more than 600,000 daily customers [1]. The taxi share is about 10% in the NYC urban public transit system. However, one major characteristic of taxi activities is the spatial imbalance. Again in the NYC, almost 92% of customers are located in Manhattan, which is known as the central area of the city, as shown in Figure 1. Similar imbalanced rider distributions are observed in other big cities, such as Beijing and Shanghai [2,3]. Although the spatial differentiation is determined by the high demand and supply in the city central areas, this will result in several negative effects not only within the taxicab systems but also beyond that. First, the imbalanced taxi supply will lead to taxi shortage outside downtown areas, increased difficulties in finding available taxicabs, and longer waiting time by customers, but more competitions in the central areas. Second, more taxicabs circulating within the city central areas will load much traffic onto the limited road network and likely result in severe congestion. Finally, the emerging app-based taxi services, for instance Uber and Lyft, are competing for customers within the city central areas through providing more convenient, cheaper, and differentiated mobility services [4]. On the other hand, there is still much unmet taxi demand outside the city central areas. The NYC taxi and limousine commission began to operate a new street-hailing taxi service, called the green taxi, in 2013 to mainly serve upper Manhattan and boroughs other than Manhattan. The new taxi system completed more than 60,000 daily rides in 2015 [5]. These rides are not fully served by the yellow taxicabs. Moreover, one statistic over Uber pickups in NYC indicates that about 22% of the 4.4 million pickups were from outside Manhattan. The share of pickups from outside Manhattan is two times larger than the 14% share by yellow and green taxicabs [6]. In particular, on adverse weather days, it is much easier to observe taxi shortage outside Manhattan and at airports, since most taxicabs crush into the city central areas [7].

To build a sustainable street-hailing taxicab system under the challenges of app-based taxi services, the better way is issuance of the strategies that guide taxicab drivers to search for customers outside the city central areas. Considering the specialty of street-hailing taxicabs (i.e., the bi-blinded searching), the customer searching behaviors of taxicab drivers are mainly dominated by their experiences. We should have an in-depth understanding of their customer searching behaviors, such as why taxicab drivers do not prefer to stay outside downtown areas and what factors contribute to their decisions. Besides several preliminary statistics over taxi demand and supply variations at airports [8,9], the most common discussions on the vacant taxi drivers’ movement are in the form of multinomial logit, as a sub model of taxi system modeling [10,11]. Several studies validated the multinomial logit form with a small sample of taxicab drivers, along with external factors [12,13,14]. However, the aforementioned literature has not addressed all concerns regarding the problem. First, the multinomial logit form without any random effects cannot account for the individual heterogeneity while searching customers. Sometimes, the heterogeneity is significant between experienced and naive taxicab drivers. Second, the small sample of taxi drivers rather than the population sample of taxi drivers likely introduces the selection bias and thus results in biased empirical findings. Third, the imbalanced taxi services between city central and outside downtown areas, together with a small sample of taxi drivers, likely include a very small portion of real observations on taxi drivers’ behaviors outside downtown areas that is of great importance. Finally, the explanatory variables are mainly about the demand, distance, cost, and time-of-day. There are almost no discussions on the impacts of day-of-week, weather, and major taxi hotspots (i.e., airports). All these gaps in the literature motivate our analyses on the taxi drivers’ customer-searching behaviors, in particular, outside downtown areas.

In this study, we mainly address two problems unsolved in the current literature, including: (1) whether the vacant taxicabs behave identically while searching for customers after the last drop-offs outside downtown areas; and (2) what internal and external factors contribute to the customer-searching behaviors. The latent class model is introduced to account for taxicab customer searching behaviors (i.e., the choices of search destinations). Since the modeling structure can not only capture the internal and external factors but also investigates the heterogeneity in drivers’ preferences by clustering similar customer behaviors into multiple classes. Moreover, the rich yellow taxicab GPS trip records in NYC provide all taxicab drivers’ customer-searching behaviors, temporal characteristics, trip-level characteristics, and demand information. Along with weather and flight scheduling datasets, we validate the latent class model with two separate cases of airports and outside downtown areas of NYC.

The remaining sections are organized as follows: Section 2 presents the current studies on taxi system modeling and customer searching behavioral modeling; Section 3 shows the generalized latent class based modeling structures for taxicab customer searching behaviors; Section 4 develops the study cases; Section 5 analyzes the empirical findings from the two study cases; and Section 6 concludes our findings and future studies.

2. Literature Review

Taxi system modeling is one important topic in the field of urban transportation studies, involving demand and vehicle movement modeling. Recent years have seen many taxi related discussions [8,10,11,15,16,17,18,19,20,21,22,23,24,25]. One of the most representative studies is from Yang et al. [11], who developed the logit-based modeling structure for customer searching behaviors. However, the underlying assumptions of the logit-based modeling structure is that taxicab drivers should maximize their profits or minimize their searching times while finding their next customers. This is not empirically validated or calibrated well. Moreover, taxicab drivers’ knowledge on the large-scale taxi market is generally limited and imperfect, although they can update from experience [26].

Extending the logit-based modeling structure, multiple studies empirically examine the customer searching behaviors by vacant taxicabs. Sirisoma et al. [27] implemented a stated preference survey of 400 taxi drivers and developed a multinomial logit model to specify taxi drivers’ customer searching behaviors. They also identified the taxi trip-level characteristics that may have impacts on customer searching behaviors, including waiting time, trip time, travel distance, and fare. These findings were consistent with those in another similar study [14]. Szeto et al. [28] introduced a time-dependent logit model to model vacant taxi movements and indicated significant impacts of demand, earned fare, and time of day, utilizing GPS data from about 460 taxicabs. Wong et al. [12,29] extended the simple logit-based structure to the sequential processes (i.e., a series of decisions along the vacant taxi routes) and showed that the customer searching behaviors were significantly influenced by the probability of successfully picking up a customer along their movement routes. Vacant taxi movements at several places of interest were also explored, except for the citywide taxi system modeling. Wong et al. [13] proposed a sequential logit approach to model bi-level decisions of vacant taxi drivers at the taxi stands, including whether drivers will travel to the taxi stands and then whether they will wait there for customers after arrivals. The study was based on a stated preference survey and identified the significant impacts of distance, drivers’ preferences, and congestion on those choices. Ji et al. [9] collected data from airport terminals and introduced nonparametric statistical methods to identify the variances in characteristics of trips from/to airports, compared to other regular trips.

To sum up, the literature on customer searching behaviors by vacant taxicabs is limited in three aspects.

• Data collection and sample size. Most studies were based on the stated preference survey to capture complex dynamics in vacant taxi movements. However, the data source is less likely to have a better spatial and temporal coverage, due to the limited resources. The widespread existence of location-aware techniques has provided a new perspective for taxi studies along with the pervasive dataset, such as taxi GPS data recording detailed trip-level characteristics. The applications vary from the taxi movements tracking, the link traffic state estimation, to the taxi system efficiency measurement [30,31,32,33,34]. Szeto et al. [28] and Wong et al. [14,29] also introduced a pervasive dataset to validate customer searching modeling, but only sampled one-week GPS data from a small portion of 400 taxicabs (out of 10,000 taxicabs) in the city. A limited number of observations may exclude interesting heterogeneity in vacant taxi movements.
• The scope of modeling. The citywide analyses are more likely to ignore interesting findings on vacant taxi customer searching behaviors outside the city central areas since the taxi system is spatially imbalanced. Although several studies have examined the vacant taxi movements at the taxi stands [13], as well as at airports [8,15], we still need a special study on all suburban areas other than several points of interest.
• Methodologies. Most studies introduced simple logit-based taxi customer searching modeling, as well as further improvements with sequential processes [12,13]. However, the methods can not capture the heterogeneity in drivers’ decisions if there are no improvements with latent class or mixed logit structure.
• Explanatory variables. The aforementioned literature mainly explores the impacts of internal factors, for instance, demand, travel distance, revenues, and waiting time, as well as the impacts of time-of-day. However, there is a lack of investigations on the other external factors such as weather, day-of-week, seasons, and built environment. In particular, the airport operations have significant impacts on taxicab drivers’ customer-searching behaviors outside downtown areas.

3. Methodologies

The Latent Class model (LC) is one of the logit based modeling structures that is suitable for discrete choice behaviors. However, the existence of classes makes it different from other logit-based modeling structures, since the LC modeling structure first clusters similar customer searching behaviors into one group and then estimates internal and external impacts under each group. Specifically, the model can be presented in the following steps:

Step 1:Choose the number of latent classes. In general, we can initially choose 2.

Step 2: Estimate the parameters in Equations (1)–(3) with the maximum likelihood method. Equation (1) applies a multinomial logit model to customer searching behaviors i under each latent class c. Equation (2) obtains the possibility of one taxicab driver following each latent class. Equation (3) combines the previous two equations for the unconditional probability of taxicab driver n choosing alternative customer searching behavior i.

Step 3: Compute the Bayesian Information Criterion (BIC) shown in Equation (4), with estimation results from step 2.

Step 4: Repeat step 1 to step 3 with a different number of latent classes. The determination on the number of latent classes depends on the BIC values, since the smaller BIC is more likely to yield better results [35,36]:

$$\begin{array}{cc}\hfill P_n\left(i|c\right)& =\frac{e^{\left({\beta }_{ic}{X}_{in}\right)}}{{\sum }_I{e}^{\left({\beta }_{Ic}{X}_{In}\right)}},\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill P_n\left(c\right)& =\frac{e^{\left({\alpha }_c{Z}_n\right)}}{{\sum }_C{e}^{\left({\alpha }_C{Z}_n\right)}},\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill P_n\left(i\right)& =\sum _{\forall c\in C}{P}_n\left(c\right)\times P_n\left(i|c\right),\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill BIC& =-\frac{2\left(LL-Kln\left(K\right)\right)}{Q},\hfill \end{array}$$

(4)

where X is the vector of measurable variables, $\alpha$ and $\beta$ are the vectors of estimable coefficients, Z is the vector of variables to determine probabilities of class c for the customer searching behavior observation n, c is latent class, C is the set of latent classes, $LL$ is the log-likelihood value at convergence, K is the number of parameters, and Q is the number of observations.

Step 5: Compute the elasticity of influencing factors with optimal settings on the number of latent classes. Equations (5) and (6) show the mathematical forms of elasticity for the continuous and indicator variables, respectively. The elasticity of the continuous variables can be interpreted as the percent changes in vacant taxicab drivers’ choice probabilities by 1% change in a specific explanatory variable. The elasticity of indicator variables can be interpreted as the percent changes in vacant taxi drivers’ choice probabilities by changing a specific indicator variable from 0 to 1, which is also called pseudo-elasticity:

$$\begin{array}{cc}\hfill E_{x_{ki}}^{P\left(i\right)}& =\left(1-P\left(i\right)\right){\beta }_{ki}{x}_{ki},\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill E_{x_{ki}}^{P\left(i\right)}& =\left(\frac{e^{\left(\Delta \left({\beta }_i{X}_i\right)\right)}{\sum }_{\forall I}{e}^{\left({\beta }_{kI}{X}_{kI}\right)}}{e^{\left(\Delta \left({\beta }_i{X}_i\right)\right)}{\sum }_{\forall I_n}{e}^{\left({\beta }_{k{I}_n}{X}_{k{I}_n}\right)}+{\sum }_{\forall I\ne I_n}{e}^{\left({\beta }_{kI}{X}_{kI}\right)}}-1\right)\times 100,\hfill \end{array}$$

(6)

where X is the vector of measurable variables x, $\beta$ is the vector of estimable coefficients, $I_n$ is the set of alternate choices with $I_n$ in the function determining the choices, and I is the set of all possible choices.

4. Data

In NYC, there are five boroughs, including Manhattan, Staten Island, Brooklyn, Queen, and Bronx. Manhattan is the city central area which generates more than 90% of taxi trips. We define the outside city central area as only containing the remaining four boroughs other than the city airports since the taxi operation at airports are different from other regular areas, although the airports generally are distant from the city central area. Thus, we develop two separate study cases, one of which is the vacant taxicab customer searching at airports and another of which is that outside the city central area. The NYC taxi and limousine commission releases the detail trip records in all above areas for more than 13,000 yellow taxicabs. Each trip record contains rich information on trip characteristics and charged fares, for instance, taxi medallion id, taxi shift id, time and location of pickup or drop-off, trip travel time in seconds, trip distance, initial fare, distance-based fare, time-based fare, surcharge, toll, tax, and total fares. Other than the whole year and several consecutive days or weeks, we randomly sample about 16 days as the study case to capture temporal variations. Specifically, we randomly select one month from each of four seasons and randomly select four days in each of the selected months. To avoid no observations on weekends or holidays, the four random days in each of selected months should consist of two random days from weekdays and two random days from weekends and holidays. Moreover, we only keep taxi trip records during four typical time slots in each selected day, including 8:00 a.m. to 9:00 a.m. as morning peak, 10:00 a.m. to 11:00 a.m. as off peak, 6:00 p.m. to 7:00 p.m. as evening peak, and 11:00 a.m. to 12:00 a.m. as night. Finally, we filter out about 1.3 million occupied taxi trips in 2013 for further steps.

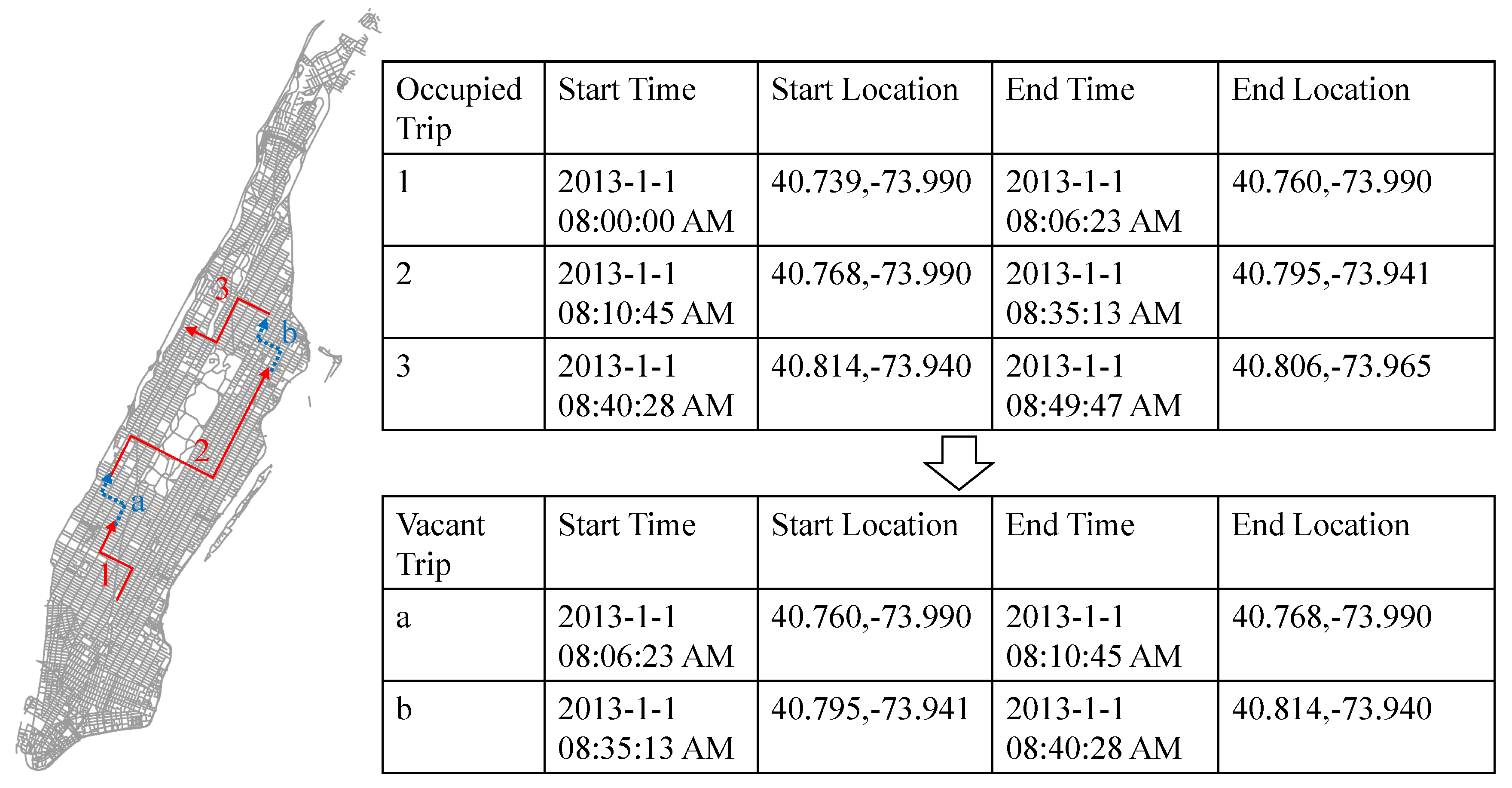
Since the taxi trips in the dataset are only with the taxicabs with passengers, we should further extract vacant taxi movement and obtain taxicab drivers’ choices of customer searching destinations. Here, we assume that the taxi and limousine commission recorded almost all taxi trips in 2013. We can simply order the whole dataset based on the medallion id and pickup time to obtain the taxicab movement sequences. For a taxicab in Figure 2, we can observe three consecutive occupied taxi trips (red line). The vacant taxi trips exist between any two consecutive occupied trips (blue dashed line). The origin of one vacant taxi trip is the drop off/end location of the last occupied taxi trip, at which the vacant taxi driver makes decisions on customer searching destinations. Similarly, the destination of one vacant taxi trip is the pickup/start location of the following occupied taxi trip. Note that the vacant taxi behaviors are identified based on location of their final destinations, other than sequential decisions or driving directions, due to data availability. In study case 1 at airports, we observe 11,857 vacant taxi trips and define four customer searching destination choices, including waiting at airports, driving to another airport, cruising outside Manhattan, and driving to Manhattan. In study case 2 outside Manhattan but without airports, we observe 52,318 vacant taxi trips and define three customer searching destination choices, including driving to Manhattan, driving to airports, and cruising outside Manhattan.

In addition, we also measure a set of internal and external variables, such as taxi trip level characteristics, aggregated demand, temporal characteristics, weather, and facilities. The taxi trip level characteristics mainly contain trip distance/travel time/earned fare of prior occupied trip and distances from drop-off location to center point of Manhattan, John F. Kennedy International Airport (JFK), and LaGuardia Airport (LGA). The taxi demand for Manhattan, outside Manhattan, JFK, and LGA are aggregated from pickups every 15 min. Note that the aggregated demand is a little lower than the exact taxi demand, since we cannot capture the unmet taxi demand. Temporal characteristics are presented by several indicator variables, for instance, weekday, winter, holiday, peak hour, and night. The 2013 NYC historical weather dataset provides hourly weather information, including temperature, humidity, wind speed and direction, precipitation, visibility, events, and conditions (e.g., overcast, cloudy, rain, and haze), obtained from [37]. An indicator variable is developed to indicate whether it is rainy in each hour. The 2013 JFK and LGA (i.e., two main airports in NYC) on-time performance dataset records all domestic flight arrivals at JFK and LGA, including date and time of flight, origin and destination airport, Computer Reservation System (CRS) arrival time, flight time in minutes, and flight distance, obtained from the United States Department of Transportation. We count the hourly number of total arrival flights and long-haul flights (i.e., time airborne during a flight is more than 6 h) for the both JFK and LGA respectively. Furthermore, 30-min and 1-h lag are introduced for the number of flight arrivals, considering the duration of disembark, baggage claim, and walking to taxi stands. The summary statistics of all internal and external variables are shown in

Table 1. Summary statistics of dependent and explanatory variables.

Variables	Case 1			Case 2
	Mean (Standard Deviation) or Percentage	Min	Max	Mean (Standard Deviation) or Percentage	Min	Max
Vacant taxi drivers’ decision: drop-off at airport, 1-waiting at
airports/2-going to other airport/3-cruising outside Manhattan/4-returning
back to Manhattan; drop-off outside Manhattan: 1-returning back to Manhattan/2-going
to airports/3-cruising outside Manhattan)	21.31/4.48/63.73/10.48	1	4	44.77/8.63/46.60	1	3
Temporal characteristics
Weekday indicator; 0 for weekend/1 for weekday	48.10/51.90	0	1	53.25/46.75	0	1
Holiday indicator; 0 for other days/1 for holiday	87.22/12.78	0	1	88.80/11.20	0	1
Winter indicator; 0 for other seasons/1 for winter	76.46/23.54	0	1	77.80/22.20	0	1
Spring indicator; 0 for other seasons/1 for spring	74.54/25.46	0	1	73.13/26.87	0	1
Summer indicator; 0 for other seasons/1 for summer	74.43/25.57	0	1	75.10/24.90	0	1
Fall indicator; 0 for other seasons/1 for fall	74.57/25.43	0	1	73.97/26.03	0	1
Morning peak indicator; 0 if otherwise/1 if drop-off between 8:00 a.m. and 9:00 a.m.	56.81/43.19	0	1	84.43/15.57	0	1
Evening peak indicator; 0 if otherwise/ 1 if drop-off between 6:00 p.m. and 7:00 p.m.	81.72/18.28	0	1	72.24/27.76	0	1
Off peak indicator; 0 if otherwise/ 1 if drop-off between 10:00 a.m. and 11:00 a.m.	63.41/36.59	0	1	83.03/16.97	0	1
Night indicator; 0 if otherwise/1 if drop-off between 11:00 p.m. and 12:00 a.m.	98.06/1.94	0	1	60.30/39.70	0	1
Trip-level characteristics
Prior occupied trip travel time in seconds	1317.45 (593.71)	0	7858	906.56 (541.36)	0	8400
Prior occupied trip travel distance in miles	10.69 (5.09)	0	36	4.61 (3.81)	0	85.30
Distance from drop-off to Manhattan in miles	10.05 (3.74)	0.77	16.73	5.72 (2.39)	2.18	25.56
Distance from drop-off to JFK airport in miles	7.65 (4.65)	0.002	16.86	12.66 (2.31)	1.22	32.36
Distance from drop-off to LGA airport in miles	3.42 (4.69)	0.01	11.89	7.09 (2.84)	0.22	31.33
Earned fare from prior occupied trip	41.50 (15.85)	2.99	170.55	19.218 (11.71)	2.5	390.5
Demand characteristics
Taxi demand in Manhattan per 15-min	4286.91 (1690.63)	1130	8339	5211.34 (1791.51)	1130	8339
Taxi demand Outside Manhattan per 15-min	170.58 (60.01)	83	717	282.38 (153.18)	83	717
Taxi demand at JFK airport per 15-min	64.33 (37.86)	15	188	89.74 (39.55)	15	188
Taxi demand at LGA airport per 15-min	103.12 (65.55)	4	306	120.08 (68.10)	2	306
Weather characteristics
Rain indicator; 0 for others/1 for rain	87.27/12.73	0	1	93.68/6.32	0	1
Airport operation
Number of hourly arrival flights at JFK	7.04 (7.41)	0	24	10.92 (6.70)	0	24
Number of hourly arrival long-haul flights at JFK	3.62 (3.92)	0	12	6.69 (3.67)	0	12
Number of hourly arrival flights at JFK-30-min lagged	1.38 (2.86)	0	10	4.19 (3.17)	0	10
Number of hourly arrival long-haul flights at JFK-30-min lagged	0.91 (1.87)	0	6	2.76 (2.09)	0	6
Number of hourly arrival flights at JFK-1-h lagged	3.04 (6.10)	0	21	9.81 (7.02)	0	21
Number of hourly arrival long-haul flights at JFK-1-h lagged	1.78 (3.65)	0	14	5.95 (4.42)	0	14
Number of hourly arrival flights at LGA	10.92 (10.05)	0	25	12.97 (7.48)	0	25
Number of hourly arrival long-haul flights at LGA	4.03 (3.79)	0	10	5.42 (2.89)	0	10
Number of hourly arrival flights at LGA-30-minute lagged	1.72 (3.56)	0	13	3.94 (3.51)	0	13
Number of hourly arrival long-haul flights at LGA-30-minute lagged	0.53 (1.21)	0	5	1.48 (1.44)	0	5
Number of hourly arrival flights at LGA-1-h lagged	3.43 (6.94)	0	21	8.97 (6.99)	0	21
Number of hourly arrival long-haul flights at LGA-1-h lagged	0.90 (1.87)	0	7	3.14 (2.52)	0	7

. Finally, we implement the multicollinearity test by computing variance inflation factor (VIF) for each variable to remove any possible correlations among variables. The thumb of rule is that all VIF values should be less than 10.

Table 2. VIF values of explanatory variables in study case 1.

Explanatory Variables	VIF
Temporal characteristics
Weekday indicator; 1 for weekday, 0 for weekend	1.837
Holiday indicator; 0 for other days/1 for holiday	2.076
Winter indicator; 0 for other seasons/1 for winter	2.418
Spring indicator; 1 for spring, 0 for other seasons	2.743
Summer indicator; 1 for summer, 0 for other seasons	1.962
Evening peak indicator; 1 if drop-off between 6:00 p.m. and 7:00 p.m., 0 if otherwise	1.661
Off peak indicator; 1 if drop-off between 10:00 a.m. and 11:00 a.m., 0 if otherwise	2.274
Trip-level characteristics
Distance from drop-off to Manhattan in miles	4.435
Distance from drop-off to JFK airport in miles	7.220
Distance from drop-off to LGA airport in miles	9.788
Earned fare from prior occupied trip	1.469
Demand characteristics
Taxi demand in Manhattan per 15-min	4.352
Taxi demand Outside Manhattan per 15-min	2.876
Taxi demand at JFK airport per 15-min	4.920
Taxi demand at LGA airport per 15-min	4.221
Weather characteristics
Rain indicator; 1 for rain, 0 for others	2.493
Airport operation
Number of hourly arrival flights at JFK-30-min lagged	2.557
Number of hourly arrival flights at JFK-1-h lagged	4.755
Number of hourly arrival flights at LGA	2.899
Number of hourly arrival flights at LGA-1-h lagged	6.802

and

Table 3. VIF values of explanatory variables in study case 2.

Explanatory Variables	VIF
Temporal characteristics
Weekday indicator; 1 for weekday, 0 for weekend	1.925
Holiday indicator; 0 for other days/1 for holiday	2.291
Winter indicator; 0 for other seasons/1 for winter	1.939
Spring indicator; 1 for spring, 0 for other seasons	1.971
Summer indicator; 1 for summer, 0 for other seasons	2.082
Morning peak indicator; 0 if otherwise/1 if drop-off between 8:00 a.m. and 9:00 a.m.	2.304
Off peak indicator; 1 if drop-off between 10:00 a.m. and 11:00 a.m., 0 if otherwise	1.592
Trip-level characteristics
Distance from drop-off to Manhattan in miles	2.128
Distance from drop-off to JFK airport in miles	2.038
Distance from drop-off to LGA airport in miles	1.717
Earned fare from prior occupied trip	1.167
Demand characteristics
Taxi demand in Manhattan per 15-min	3.605
Taxi demand Outside Manhattan per 15-min	7.051
Taxi demand at JFK airport per 15-min	4.299
Taxi demand at LGA airport per 15-min	3.481
Weather characteristics
Rain indicator; 1 for rain, 0 for others	1.623
Airport operation
Number of hourly arrival long-haul flights at JFK-30-min lagged	1.565
Number of hourly arrival long-haul flights at JFK-1-h lagged	9.259
Number of hourly arrival long-haul flights at LGA	8.349
Number of hourly arrival long-haul flights at LGA-30-min lagged	4.503
Number of hourly arrival long-haul flights at LGA-1-h lagged	1.090

present remaining explanatory variables with VIFs less than 10 after deleting relatively higher VIFs.

5. Numerical Analysis

As stated in the section of methodologies, we compare the LC model performance under three different number of latent classes which are 2, 3, and 4. Moreover, we also estimate several common discrete choice models, for instance, multinomial logit, nested logit, and mixed logit. Regarding the nested logit model, we develop all possible nested structures. In particular, for study case 1, we tested four different nested structures, including structure 1: wait at airports and driving to airports are nested; structure 2: wait at airports and driving to airports are nested, and cruising outside Manhattan and driving back to Manhattan are nested; structure 3: wait at airports, driving to airports, and cruising outside Manhattan are nested; and structure 4: wait at airports, driving to airports, and driving back to Manhattan are nested. Similarly, we tested three different nested structures, including structure 1: driving back to Manhattan and driving to nearby airports are nested; structure 2: driving back to Manhattan and cruising outside Manhattan are nested; and structure 3: driving to airports and cruising outside Manhattan are nested. The last three cells in the row of nested logit is the model performance of nested structure 1. All model estimations are performed in the econometric software of Nlogit 4 at the confidence level of 95%.

Table 4. The model performance and comparisons in both study cases.

Models	Study Case 1			Study Case 2
	Number of Parameters	BIC	Log-Likelihood	Number of Parameters	BIC	Log-Likelihood
LC (2 classes)	53	1.842	−10,665.68	61	1.623	−42,120.02
LC (3 classes)	80	1.855	−10,614.83	92	1.620	−41,867.40
LC (4 classes)	107	1.867	−10,562.70	123	1.624	−41,819.18
Multinomial logit	26	1.846	−10,819.19	30	1.639	−42,724.43
Nested logit *	25	1.847	−10,820.27	29	1.633	−42,681.97
Mixed logit	26	1.846	−10,804.02	30	1.639	−42,724.43

* The presented values in this row is from the nested structure with better model performance.

presents the number of parameters, BIC, and log-likelihood after removals of insignificant variables. Note that the definition of significant variables in the LC model is a little different from others. The variable is significant when it is significant in at least one latent class (i.e., corresponding t-static should be greater than 1.96 or less than −1.96), not necessarily when it is significant in all latent classes. From the comparison results, it is obvious that the LC model has greater log-likelihood than all other modeling structure in the both study cases. However, the LC model with more classes cannot improve log-likelihood greatly by introducing more parameter estimations, given the fact of larger BICs. Therefore, we choose LC model with two classes in study case 1. In contrast, the LC model with three classes is with better estimations in study case 2.

5.1. Study Case 1 at Airports

Among all 11,857 observations on vacant taxicab customer searching at airports, 2527 (about 21.3%) taxicabs choose to wait at airports after the last drop-off, 531 (about 4.5%) taxicabs would like to leave for another airport, 7556 (about 63.7%) drivers prefer to cruise outside Manhattan, and 1243 (about 10.5%) taxicabs drive back to Manhattan. The parameter estimations and elasticities of the significant variables are summarized in

Table 5. Parameter estimation results of study case 1.

Explanatory Variables	Latent Class 1								Latent Class 2
	Waiting at Airports		Going to Other Airports		Cruising outside Manhattan		Returning Back to Manhattan		Waiting at Airports		Going to Other Airports		Cruising outside Manhattan		Returning Back to Manhattan
	Parameter	t-Statistic	Parameter	t-Statistic	Parameter	t-Statistic	Parameter	t-Statistic	Parameter	t-Statistic	Parameter	t-Statistic	Parameter	t-Statistic	Parameter	t-Statistic
Constant
Waiting at airports	3.057	2.323	-	-	-	-	-	-	4.837	5.868	-	-	-	-	-	-
Cruising outside Manhattan	-	-	-	-	1.798	7.837	-	-	-	-	-	-	2.122	15.018	-	-
Returning back to Manhattan	-	-	-	-	-	-	8.499	3.408	-	-	-	-	-	-	6.491	4.409
Temporal characteristics
Weekday indicator; 1 for weekday, 0 for weekend	−0.092	−0.634	-	-	-	-	-	-	0.227	3.063	-	-	-	-	-	-
Spring indicator; 1 for spring,0 for other seasons	0.479	2.731	-	-	-	-	-	-	0.300	3.936	-	-	-	-	-	-
Evening peak indicator; 1 if drop-off between 6:00 p.m. and 7:00 p.m., 0 if otherwise	-	-	-	-	3.038	4.927	-	-	-	-	-	-	−0.488	−3.206	-	-
Off peak indicator; 1 if drop-off between 10:00 a.m. and 11:00 a.m., 0 if otherwise	-	-	-	-	-	-	0.967	3.680	-	-	-	-	-	-	0.399	4.191
Trip-level characteristics
Distance from drop-off to Manhattan in miles	-	-	-	-	-	-	−0.506	−3.431	-	-	-	-	-	-	−0.401	−4.446
Distance from drop-off to JFK airport in miles	-	-	−0.040	−0.199	0.401	3.414	-	-	-	-	0.262	3.582	0.093	1.279	-	-
Distance from drop-off to LGA airport in miles	−0.305	−2.628	-	-	-	-	-	-	−0.307	−4.303	-	-	-	-	-	-
Earned fare from prior occupied trip	−0.075	−10.013	-	-	-	-	-	-	0.007	2.314	-	-	-	-	-	-
Demand characteristics
Taxi demand in Manhattan per 15-min in terms of pickups	-	-	-	-	-	-	−0.001	−5.746	-	-	-	-	-	-	0.0001	4.407
Taxi demand Outside Manhattan per 15-min in terms of pickups	-	-	-	-	-	-	0.013	4.125	-	-	-	-	-	-	0.003	3.716
Taxi demand at JFK airport per 15-min in terms of pickups	0.028	8.564	-	-	-	-	−0.008	−1.238	0.002	0.934	-	-	-	-	0.008	4.038
Taxi demand at LGA airport per 15-min in terms of pickups	0.018	11.524	−0.006	−2.223	-	-	-	-	0.003	4.089	0.007	8.108	-	-	-	-
Weather characteristics
Rain indicator; 1 for rain, 0 for others	-	-	-	-	-	-	0.968	3.713	-	-	-	-	-	-	−7.185	−5.157
Airport operation
Number of hourly arrival flights at JFK-1-h lagged	0.375	7.561	-	-	-	-	-	-	−0.068	−2.579	-	-	-	-	-	-
Number of hourly arrival flights at LGA hourly-1-h lagged	−0.229	−3.851	-	-	-	-	-	-	0.064	2.623	-	-	-	-	-	-
Class Probability (t-statistic in parentheses)	0.718 (105.563)								0.282 (31.644)
Number of observations					11,851
Log Likelihood at zero					−11,759.189
Log Likelihood at convergence					−10,665.680
R2					0.351
Bayesian Information Criterion (BIC)					1.842

and

Table 6. Elasticity estimation results of study case 1.

Explanatory Variables	Waiting at Airports	Going to Other Airports	Cruising outside Manhattan	Returning Back to Manhattan
Temporal characteristics
Weekday indicator; 1 for weekday, 0 for weekend	0.028	-	-	−0.061
Spring indicator; 1 for spring, 0 for other seasons	0.047	-	-	-
Evening peak indicator; 1 if drop-off between 6 p.m. and 7 p.m., 0 if otherwise	-	-	0.066	-
Off peak indicator; 1 if drop-off between 10:00 a.m. and 11:00 a.m., 0 if otherwise	-	-	-	0.182
Trip-level characteristics
Distance from drop-off to Manhattan in miles	-	-	-	−3.241
Distance from drop-off to JFK airport in miles	-	1.572	0.370	-
Distance from drop-off to LGA airport in miles	−0.423	-	-	-
Earned fare from prior occupied trip	−0.342	-	-	-
Demand characteristics
Taxi demand in Manhattan per 15-min	-	-	-	−0.578
Taxi demand Outside Manhattan per 15-min	-	-	-	0.875
Taxi demand at JFK airport per 15-min	0.458	-	-	0.126
Taxi demand at LGA airport per 15-min	0.564	0.488	-	-
Weather characteristics
Rain indicator; 1 for rain, 0 for others	-	-	-	0.037
Airport operation
Number of hourly arrival flights at JFK-1-h lagged	0.344	-	-	-
Number of hourly arrival flights at LGA-1-h lagged	−0.225	-	-	-

, respectively. Note that several insignificant variables are not presented. The latent class 1 is with higher probability, about 71.8%. Comparing the constant parameters, we can find that vacant taxicabs in latent class 1 have a higher constant parameter for back to Manhattan than those for other choices. In contrast, the latent class 2 is with lower probability, about 28.2%. The constant parameters are relatively smaller than those in latent class 1. Thus, we can define the both latent classes as follows: the latent class 1 is the set of vacant taxicabs that are more likely to drive back to Manhattan; and the latent class 2 is the set of vacant taxicabs that may stay outside Manhattan and at airports where they drop off passengers.

5.1.1. Latent Class 1

Previous studies have empirically examined the impacts of time-of-day on vacant taxi movements [14,28]. However, our results indicate that not only time of day but also day-of-week and seasons have impacts on vacant taxicab customer searching behaviors. During evening peak hours, vacant taxicabs are more likely to stay outside Manhattan after the last drop off at airports. During off peak hours, vacant taxicabs are more likely to drive back to Manhattan. The impacts of time-of-day make sense considering the temporal variations in demand that there are high demand in most areas during evening peak hours and also high demand in Manhattan even during off peak hours. Vacant taxicabs are also more likely to wait at airports after passenger drop-off in the spring and on the weekdays, considering the flight travel peaks. The location of the last drop off has significant impacts on the customer searching behaviors. If the taxicabs drop off at a remote airport (e.g., JFK), the taxicabs are less likely to drive back to Manhattan and wait at the airport. If the taxicabs drop off at LGA, the taxicabs, however, are more likely to cruise outside Manhattan. In addition, the taxicabs are less likely to wait at airports after earning much money from the last trip. High demand at JFK and LGA will definitely attract more vacant taxicabs to wait. However, the long customer searching distance from the airports to Manhattan may prevent the taxicabs to drive back, although there is high demand in Manhattan. We also observe that taxi drivers prefer to drive back to Manhattan from airports during rainy hours. This is consistent with discussions in [8]. The number of flight arrivals have significantly positive impacts on vacant taxicabs waiting at JFK. However, this will be in effect about one hour later, considering duration of disembarking time, baggage claims, and walking to taxi stands. Interestingly, the number of flight arrivals have significantly negative impacts on taxicabs waiting at LGA. This is likely because the location of LGA is close to Manhattan and vacant taxicabs have more better customer searching choices other than waiting at LGA.

5.1.2. Latent Class 2

Compared to the customer searching behaviors in the latent class 1, the vacant taxicabs in the latent class 2 are more likely to wait at airports after the last drop-off on the weekdays and in the spring. Meanwhile, they are less likely to search customers outside Manhattan areas during evening hours. We also find that the vacant taxicabs are more likely to drive to the JFK airport after the last drop-off at LGA, as well as to wait at airports after earning much money from the last trip. However, the vacant taxicabs are also more likely to drive back to Manhattan during off peak hours, less likely to drive a long distance to Manhattan, and less likely to wait at JFK, as the latent class 1. The small difference by the latent class 2 is that the vacant taxicabs may drive back to Manhattan where there is high demand, although a long distance between drop-off location and Manhattan. Regarding the impacts of weather and flight arrivals, they are totally different for vacant taxicabs in the latent class 2. The vacant taxicabs may not drive back to Manhattan in rainy hours as most drivers do in the latent class 1. More flight arrivals may not encourage the vacant taxicabs to wait at JFK but may keep them waiting at LGA. This indicates the significant heterogeneity in drivers’ customer searching destination choices.

5.1.3. Elasticity of Internal and External Factors

The elasticity shows the net impacts of variables on the probability of customer searching destination choices by combining the both latent classes. The temporal characteristics will not lead to too many differences in the probability of customer searching destination choices, no more than 0.06. For instance, the probability of waiting at airports may increase by 0.028 and 0.047 on the weekdays and in the spring, respectively; the probability of cruising outside Manhattan may increase by 0.066 during evening peak hours; and the probability of driving back to Manhattan may decrease by 0.061 on the weekdays. The trip-level characteristics, such as distance and drop-off location, have higher changes in the probabilities of movement choices. One additional mile traveled from the drop-off location to Manhattan and LGA will decrease the probability of driving back to Manhattan by 3.241 and decrease the probability of waiting at airport by 0.423, respectively. However, one additional mile traveled from the drop-off location to JFK will increase the probability of going to another airport and cruising outside Manhattan by 1.572 and 0.370, respectively. The taxi demand and flight arrivals also show higher changes in the probability of customer searching destination choices. The probability of waiting at airports and going to another airport may change by more than 0.20, if one additional demand and flight arrival at airports. The probability of driving back to Manhattan from the airports will change more than 0.10 due to the additional demand in the different areas but increase by a lower level of 0.037 in the rainy days.

5.2. Study Case 2 outside Manhattan Other Than Airports

Among all 52,318 observations on the vacant taxi customer searching outside Manhattan, 23,422 (about 44.8%) taxicabs choose to drive back to Manhattan, 4517 (about 8.63%) prefer to drive to nearby airports, and 24,378 (about 46.6%) taxicabs would like to stay outside Manhattan. The parameter estimations and elasticities of the significant variables are summarized in Table 7 and

Table 8. Elasticity estimation results of study case 2.

Explanatory Variables	Returning Back to Manhattan	Going to Airports	Cruising outside Manhattan
Temporal characteristics
Weekday indicator; 1 for weekday, 0 for weekend	−0.026	0.039	-
Holiday indicator, 1 for holiday, 0 for other days	0.013	−0.009	-
Winter indicator; 1 for winter, 0 for other seasons	-	-	0.010
Morning peak indicator; 1 if drop-off between 8:00 a.m. and 9:00 a.m., 0 if otherwise	0.381	-	-
Off peak indicator; 1 if drop-off between 10:00 a.m. and 11:00 a.m., 0 if otherwise	-	−1.372	−0.396
Trip-level characteristics
Distance from drop-off to Manhattan in miles	−0.018	-	-
Distance from drop-off to JFK airport in miles	-	−1.731	-
Distance from drop-off to LGA airport in miles	-	−0.970	-
Earned fare from prior occupied trip	-	0.061	0.009
Demand characteristics
Taxi demand in Manhattan per 15-min	0.397	-	-
Taxi demand Outside Manhattan per 15-min	-	-	0.452
Taxi demand at JFK airport per 15-min	-	0.174	-
Taxi demand at LGA airport per 15-min	-	0.463	-
Weather characteristics
Rain indicator; 1 for rain, 0 for others	-	0.0008	-
Airport operation
Number of hourly arrival long-haul flights at JFK-1-h lagged	-	−0.793	-
Number of hourly arrival long-haul flights at LGA-1-h lagged	-	0.048	-

, respectively. The latent class 1 is with a lower probability, about 15.8%. We can find that vacant taxicabs in the latent class 1 have a higher constant parameter for cruising outside Manhattan than those for other choices. The latent class 2 is with a medium probability, about 26.0%. We can find that the vacant taxicabs in the latent class 2 have only one negatively significant constant parameter of cruising outside Manhattan. The latent class 3 is with a higher probability, about 58.2%. We can find that the vacant taxicabs in the latent class 3 have only one negatively significant constant parameter of driving back to Manhattan. Thus, we can define the latent classes as follows: the latent class 1 is the set of the vacant taxicabs who are more likely to cruise outside Manhattan; the latent class 2 is the set of the vacant taxicabs who prefer not to cruise outside Manhattan; and the latent class 3 is the set of the vacant taxicabs who are less likely to drive back to Manhattan.

5.2.1. Latent Class 1

The vacant taxicabs are less likely to drive to nearby airports or cruise outside Manhattan after the last drop-off during off peak hours. This is similar as the customer searching destination choices at airports. Meanwhile, the vacant taxicabs are more likely to drive back to Manhattan during morning peak hours. This is likely due to the spatiotemporal pattern of taxi demand that the city central area is relatively with high demand during peak hours and the outside city central areas are relatively with low demand during off peak hours. In winter, the vacant taxicabs are also less likely to cruise outside Manhattan after the last drop-off. This may be resulted from the increased demand in cold weather in Manhattan. In contrast, the vacant taxicabs are more likely to search customers around the location of the last drop-off on holidays, since more taxi rides generate across the whole city on holidays. Same as discussions in study case 1, the distance between the last drop-off location and empty trip destinations also contributes to the customer searching destination choices. Long searching distance will prevent the taxicabs to get there. More earned fares from the last trip may allow the vacant taxicabs to stay around drop-off locations to search new customers, although it may take more times to find ones due to relatively low demand in this area. High demand at airports may attract the vacant taxicabs to get there for new passengers. Moreover, the number of long-haul flight arrivals at the JFK airport also has significantly positive impacts on the decision of going to the airport. Generally, the long-haul flights take many more passengers than others and may generate more demand on taxis. However, this is in effect about one hour later, which is the same as discussions in the study case 1.

5.2.2. Latent Class 2

Compared to the latent class 1, the temporal characteristics have relatively smaller magnitude and different impacts on customer searching destination choices. The vacant taxicabs are less likely to drive back to Manhattan on the weekdays and to drive to nearby airports on the holidays. However, the distance and demand also show almost the same impact as presented in the latent class 1. The small difference is that the group of vacant taxicabs is more likely to stay outside Manhattan when there is high demand. The rainy weather will reduce the vacant taxicabs driving to nearby airports after the last drop-off, consistent with the study case 1 and the literature [8]. Interestingly, it seems that the greater number of long-haul flight arrivals at both the JFK and LGA airports may not attract more vacant taxicabs. This is different from the observations in latent class 1 that more long-haul flights can yield more vacant taxicabs waiting at airports after the last drop-off.

5.2.3. Latent Class 3

The off peak hours and morning peak hours present significantly negative and positive impacts on customer searching destination choices, respectively. This is similar to observations in the latent class 1. However, other temporal characteristics show different impacts. The vacant taxicabs are more likely to visit nearby airports on the weekends and to drive back to Manhattan on the holidays. In winter, they are also more likely to cruise outside Manhattan, instead of going elsewhere. The long distance from the drop-off location to the airports will prevent the vacant taxicabs to get there. Although there is a relatively long distance from outside Manhattan to Manhattan, the vacant taxicabs in this group are more likely to drive back to Manhattan because of high demand. More earned fares from the last trip can allow more vacant taxicabs to drive to nearby airports, which may be at risk of a long waiting time. The demand always has significantly positive impacts on customer searching destination choices except for the JFK airport. The long waiting time, about one hour, may prevent the vacant taxicabs to get there even if there is high demand. The significantly positive impact of the rainy day on going to nearby airports indicates a result different from that in [8] and other latent classes. Not all vacant taxicabs may drive back to Manhattan during the rainy hours. The long-haul flight arrivals at different airports show different impacts on going to airports. At the LGA, more long-haul flight arrivals will attract more vacant taxicabs from outside Manhattan to the airport. In contrast, more long-haul flight arrivals at JFK may not attract vacant taxicabs to drive outside of Manhattan.

5.2.4. Elasticity of Internal and External Factors

We can observe the strong impacts of the empty trip distance and demand on customer searching destination choices. The net impacts of one additional mile traveled from the drop-off location to the airports may reduce the probability of going to airport by more than 0.970. The one additional taxi demand may increase the probability of getting the corresponding area by more than 0.174. However, the negative net impact of the distance traveled from the drop-off location to Manhattan is smaller, about 0.018. This shows that the vacant taxicabs prefer Manhattan other than both remote airports after drop off outside Manhattan. The time of day also presents strong impacts on customer searching destination choices. The probability of staying outside Manhattan and going to nearby airports may decrease by 0.396 and 1.372 during off peak hours, respectively. We may observe a 0.381 increase in the probability of driving back to Manhattan during morning peak hours. All other temporal characteristics (e.g., weekday, holiday, and winter), as well as trip-level characteristic (e.g., earned fare from last occupied trip), yield weak impacts with the magnitudes less than 0.06. The impacts of the rainy weather may change the probability of going to airports by a very small level of 0.0008. Interestingly, the long-haul flight arrivals at different airports show different impacts on the probability of going to the airport. One additional long-haul flight arrival may decrease the probability by 0.793 at the JFK but increase the probability by 0.048 at the LGA.

5.3. Discussion: Policy Implications

Among all significant variables, we can see the strong impacts of taxi demand and customer searching distance on the destination choices. Both high demand and short travel distance from the last drop-off location to the searching destination areas contribute to more vacant taxicabs driving there for new passengers. The identical signs of most estimated demand and distance parameters also indicate that the taxicab drivers are sensitive to the demand and distance and are tending to behave identically only considering the demand and distance. Moreover, the taxicab drivers tend to drive back to Manhattan during off peak hours. However, the impact is stronger after drop off outside Manhattan than at airports. All remaining variables present different impacts across latent classes, which confirm the significant heterogeneity in customer searching destination choices. For instance, portions of the vacant taxicabs may stay around the last drop-off locations, instead of driving back to downtown areas, during peak hours, on the holidays, and on the weekdays. More earned fare may also allow portions of vacant taxicabs to stay outside downtown areas. Importantly, not all vacant taxicabs drive back to the city central areas during the rainy days. The airports may be alternative preferred locations for customer searching. The vacant taxicabs may also exhibit different behavioral decisions during drop off at different airports. More flight arrivals at the remote airport may not attract portions of vacant taxicabs to get or wait there, likely because of potential long waiting times at the airport.

In the taxi system modeling, the vacant taxi drivers’ customer-searching behaviors are crucial components in addition to demand generation and vehicle-passenger matching. The previous studies [21,24,25] formulated the behaviors with a routing probability matrix derived from a multinomial logit model. Our empirical findings, however, confirm the existence of individual heterogeneity in taxicab drivers. The latent class model outperforms the multinomial logit one while addressing the heterogeneity. Moreover, in addition to the popular variables of demand and distance, we also show that the weather and major transportation hubs (i.e., airports) have impacts on taxicab drivers’ customer-searching behaviors. The proposed modeling structure together with identified explanatory variables can contribute to the better estimations on the routing probability matrix used in the taxi system modeling.

Another implication of the study sheds light on the predictions of taxicab supply. Given the total number of drop-offs, the proposed methods can simulate the taxicab drivers’ destination choice behaviors and derive the routing probability matrix, as well as number of taxicabs serving the destination regions. The taxicab supply predictions are important in regional transportation and facility planning. Take the taxi waiting area design as the example for facility planning. At airports, the taxicabs operate in a different way from street-hailing. The taxicab drivers should wait and queue at a designated area and then drive to terminals for pickups. The capacity is an important concern while planning the waiting area. Reported by Conway et al. [8], the number of taxicabs waiting for passengers at the JFK exceeds the capacity of the taxicab waiting area at 2:45 p.m. and again at 4:40 p.m. on one Sunday. The general model for capacity estimation is based on queue theory with the inputs of taxicab arrival rates and service rates. Our proposed model can contribute to estimating the taxicab arrival flow in terms of how many taxicabs arrive at airports for passenger pickups.

6. Conclusions

The objective of this study is to empirically discover how the taxicab drivers find customers after drop-off outside city central areas, as well as identify what internal and external factors affect their preferences. We introduce the latent class model to specify the customer searching destination choices, considering the potential heterogeneity in the taxicab drivers. Two separate study cases are developed utilizing the 2013 taxi trip records in NYC, including the study case 1 at the two airports JFK and LGA and the study case 2 outside Manhattan Island except for two airports. Moreover, we adopt an adaptive number of latent classes by comparing model performance.

In the both study cases, the proposed latent class model outperforms the other common discrete choice models, for instance, multinomial logit, mixed logit, and nested logit. Clearly, the significance of latent classes indicates the individual heterogeneity in taxicab drivers while searching for customers. Moreover, we also identify a set of internal and external variables influencing taxicab drivers’ behaviors, including temporal characteristics, trip-level characteristics, demand, weather, and airport flight scheduling. The same as other findings, the variables of demand, distance and time of day have significant impacts. Beyond that, we also empirically measure the impacts of weather and airport operations on taxicab drivers’ customer-searching behaviors outside downtown areas. Finally, the study also discusses the potential policy implications on enhancing the taxi system modeling and regional taxi system planning.

In addition, we also suggest the following future study to improve our findings. First, the drivers’ heterogeneity is simply specified by the latent classes but without drivers’ socio-economic background. Second, our dataset only contains the origin and destination of each trip and removes detail features of routes for privacy. Thus, we can only define vacant taxi movements based on destinations, without considerations on sequential movement choices along one route.